A Comparison between Two Reduction Strategies for Shrouded Bladed Disks

Abstract

Shrouded bladed disks exhibit a nonlinear dynamic behavior due to the contact interfaces at shrouds between neighboring blades. As a result, reduced order models (ROMs) are mandatory to compute the response levels during the design phase for high cycle fatigue (HCF) life assessment. In this paper, two reduction strategies for shrouded bladed disk reduction are presented. Both approaches rely on: (i) the cyclic symmetry of the linear bladed disk with open shrouds to perform only single sector calculations, (ii) the Craig–Bampton (CB) method to reduce the number of physical degrees of freedom (dofs). The two approaches are applied to a set of test cases in order to evaluate and compare their accuracy and the associated computational effort. Although both approaches allow for generating accurate ROMs, it is found that the numerical efficiency of the two methods depends on the ratio of the number of nodes at the inter-sector interfaces over the number of inner nodes of the elementary sector model.

1. Introduction

Bladed disks (Figure 1) in gas turbine engines are interested by severe vibration problems, mainly caused by the non-stationary gas flow pressure [1], which can result in high cycle fatigue damage and failure. If resonances cannot be avoided, as in many practical cases due to the high modal density of bladed disks in certain frequency ranges, a forced response analysis is necessary to accurately assess the vibration levels [2].

Due to the presence of multiple contact surfaces in bladed disks (e.g., shrouds [3,4], underplatform dampers [5,6,7], blade roots [8,9], ring dampers [10,11], inter-stage coupling [12]), nonlinear analyses must be performed in order to take into account the friction damping due to slip phenomena at the contact interfaces [13,14] and predict accurately the response level.

Under periodic excitation, which actually occurs in steady-state regimes, the state-of-the-art approach relies on the solution of the nonlinear governing equations in the frequency domain by means of the Harmonic Balance Method (HBM) [15], which allows huge time savings with respect to the Time Domain Analysis (TDA).

Although bladed disks are supposed to be made of a set of identical sectors [16], the actual assemblies are never symmetric and small differences, called mistuning in the literature [17], always exist. Furthermore, even in case of a perfectly symmetric system, localization phenomena of the response might occur in the presence of either geometric nonlinearities [18] or scatter of the contact interface parameters [19].

Thus, on one side, for an exhaustive analysis of the dynamic response of bladed disks, it is necessary to study the full bladed disk, while, on the other side, the highly refined meshes typical of industrial bladed disks make the use of full Finite Element (FE) models unfeasible.

The solution of this dilemma comes from the properties of cyclically symmetric structures, recently reviewed in [20]. Given the set of stiffness and mass matrices of the fundamental sector, obtained by applying all the allowable cyclic symmetry boundary conditions, it is possible to obtain the stiffness and mass matrices of the full system through simple algebraic operations. In the end, it is possible to obtain the model of the full bladed disk without actually modelling it, using as a fundamental brick the stiffness and mass matrices of the fundamental sector.

Before continuing, it is worth mentioning that, although HBM allows for reducing the computational effort, the nonlinear forced response of a full bladed disk is still a formidable task. For this reason, reduced order models are commonly used. In case of localized nonlinearities, such as the contact interfaces, a typical reduction strategy is based on the Craig–Bampton (CB) method [21], originally developed for substructuring purposes.

According to the CB method, a set of master degrees of freedom (dofs) is retained in the analysis, while all the other dofs are replaced by a set of normal modes with specific boundary conditions and, in the case of systems with contact interfaces, the set of master dofs must include those that lie on the contact surfaces, whose amplitude determines the contact forces that produce the nonlinear friction damping.

In detail, in this paper, two different CB reduction strategies are described and compared. In both cases, the result of the process is a set of CB-reduced stiffness and mass matrices of the fundamental sector with cyclic symmetry boundary conditions. What is different in the two approaches is the order in which cyclic symmetry and CB reduction are applied to the fundamental sector of the bladed disk and it will be shown that the chosen sequence of operations can significantly affect the computation time necessary to obtain the ROMs.

The capability of CB-ROMs for nonlinear forced response is recognized by the scientific community [2] and it is taken for granted in this paper, which only focuses on the development of CB-ROMs, which are intended as inputs in numerical codes based on nonlinear techniques, such as HBM, not implemented here, since nonlinear forced response analyses are beyond the scope of this paper.

2. Background

The two reduction strategies described in this paper rely on the cyclic symmetry properties of bladed disks and on the CB method. Thus, in this section, both are briefly recalled for the sake of completeness.

2.1. Cyclic Symmetry

Bladed disks belong to the particular category of the so-called cyclically symmetry structures [20], which are defined as a special class of periodic structures, determined by a finite number N of identical substructures (one blade and the corresponding disk sector), each one constituted by J degrees of freedom and forming on the whole a closed ring.

The cyclically symmetric structures are characterized by the fact that the deflection of one substructure is strictly linked to the deflection of the previous one, having the same amplitude and a constant phase difference φ from it. In other words, the same instantaneous deflected shape reappears after successive intervals of time t, rotated round an additional substructure each time, thus generating what are generally called ‘rotating mode shapes’.

Figure 2 describes the simplified geometry of the fundamental section of a N-sectors bladed disk, introducing the distinction between the interface complex coordinates q_H and q_L and all the remaining inner dofs q_I. More in detail, q_H defines the nodes belonging to the High sector interface, whereas q_L identifies the coordinates at the Low interface.

The dofs vector of the fundamental sector is

$$\mathit{q}=\left\{\begin{array}{c}{\mathit{q}}_{\mathit{H}}\\ {\mathit{q}}_{\mathit{I}}\\ {\mathit{q}}_{\mathit{L}}\end{array}\right\}$$

(1)

and the cyclic symmetry conditions can be applied to it by means of a set of complex constraint equations,

$${\mathit{q}}_{\mathit{H}}={\mathit{q}}_{\mathit{L}}{e}^{j\phi },$$

(2)

which link the interface coordinates q_H and q_L, where the phase angle φ is defined as:

$$\phi =h\frac{2\pi }{N}.$$

(3)

The ‘harmonic index’ h in Equation (3) can assume any integer value between 0 and N − 1, corresponding to an integer number of waves in the circumferential direction. It is worth mentioning that mode shapes characterized by h = 0 and h = N/2 correspond to standing waves, while mode shapes with 0 < h < N/2 rotate clockwise and those with h > N/2 rotate counter-clockwise.

Once the full set of stiffness and mass matrices of the fundamental sector are obtained, the matrices of the full bladed disk can be finally assembled thanks to the circularity property of the matrices of cyclically symmetric structures. In fact, if K_BD is the block-diagonal matrix, whose h^th block is the stiffness matrix corresponding to the h^th harmonic index, the stiffness matrix of the whole bladed disk can be obtained [20] as

$$\mathit{K}=[{({\mathit{E}}_{\mathit{N}}^{\mathit{H}}\otimes {\mathit{I}}_{\mathit{P}})}^{-\mathbf{1}}·{\mathit{K}}_{\mathit{B}\mathit{D}}·{\left({\mathit{E}}_{\mathit{N}}\otimes {\mathit{I}}_{\mathit{P}}\right)}^{-\mathbf{1}}]·\mathit{N},$$

(4)

where:

−

E_N is an N × N Fourier matrix (N is the number of blocks, coincident with the number of nodal diameters h in this case), and ${\mathit{E}}_{\mathit{N}}^{\mathit{H}}$ is its conjugate transpose.

−

I_P is the identity matrix of dimension P, P being the dimension of each block of matrix K_BD.

−

⊗ is the Kronecker product.

2.2. Craig–Bampton Method

According to the CB method [21], the model dofs are divided into master dofs ${\mathit{q}}_{\mathit{M}}$ and slave dofs ${\mathit{q}}_{\mathit{S}}$ and the system response is approximated as a linear combination of constraint modes and of fixed-interface normal modes, where the constraint modes $\mathit{\Psi }$ represent the static deformed shapes due to a unitary displacement of one master dof, while the other master dofs are set to zero, and the fixed-interface modes $\mathit{\varphi }$ are the normal modes of the system with fixed (i.e., zero displacements) master dofs.

The resulting reduction matrix ${\mathit{R}}_{\mathit{C}\mathit{B}}$ is defined as

$${\mathit{R}}_{\mathit{C}\mathit{B}}=\left[\begin{array}{cc}\mathit{I}& \mathbf{0}\\ \mathit{\Psi }& \mathit{\varphi }\end{array}\right]$$

(5)

and, when ${\mathit{R}}_{\mathit{C}\mathit{B}}$ is applied to the system, the governing equations

$$\left[\begin{array}{cc}{\mathit{M}}_{\mathbf{MM}}& {\mathit{M}}_{\mathbf{MS}}\\ {\mathit{M}}_{\mathbf{SM}}& {\mathit{M}}_{\mathbf{SS}}\end{array}\right]\left\{\begin{array}{c}{\ddot{\mathit{q}}}_{\mathit{M}}\\ {\ddot{\mathit{q}}}_{\mathit{S}}\end{array}\right\}+\left[\begin{array}{cc}{\mathit{K}}_{\mathbf{MM}}& {\mathit{K}}_{\mathbf{MS}}\\ {\mathit{K}}_{\mathbf{SM}}& {\mathit{K}}_{\mathbf{SS}}\end{array}\right]\left\{\begin{array}{c}{\mathit{q}}_{\mathit{M}}\\ {\mathit{q}}_{\mathit{S}}\end{array}\right\}=\left\{\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right\}$$

(6)

become

$${\mathit{M}}_{\mathit{C}\mathit{B}}\left\{\begin{array}{c}{\ddot{\mathit{q}}}_{\mathit{M}}\\ {\ddot{\mathit{\eta }}}_{\mathit{S}}\end{array}\right\}+{\mathit{K}}_{\mathit{C}\mathit{B}}\left\{\begin{array}{c}{\mathit{q}}_{\mathit{M}}\\ {\mathit{\eta }}_{\mathit{S}}\end{array}\right\}=\left\{\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right\}$$

(7)

with

$${\mathit{M}}_{\mathit{C}\mathit{B}}={\mathit{R}}_{\mathit{C}\mathit{B}}{}^{\mathit{T}}\mathit{M}{\mathit{R}}_{\mathit{C}\mathit{B}},$$

(8)

$${\mathit{K}}_{\mathit{C}\mathit{B}}={\mathit{R}}_{\mathit{C}\mathit{B}}{}^{\mathit{T}}\mathit{K}{\mathit{R}}_{\mathit{C}\mathit{B}},$$

(9)

${\mathit{\eta }}_{\mathit{s}}$ being the vector of fixed-interface modal amplitudes.

When the CB method is applied to systems with contact interfaces to generate reduced order models suitable for the nonlinear forced response, the set of master dofs must include the set of contact dofs of the model.

3. Reduction Methods for Bladed Disks

The application of the cyclic symmetry properties and of the CB-method to bladed disks for the generation of reduced order models suitable for nonlinear forced response analyses requires some preliminary definitions.

Referring to Figure 3, where the fundamental sector of a shrouded bladed disk is depicted, the inner dofs ${\mathit{q}}_{\mathit{I}}$ of the fundamental sector include two sets of dofs. The first one, called ${\mathit{q}}_{\mathit{C}}$, includes the contact dofs and the second one, called ${\mathit{q}}_{\mathit{N}\mathit{C}}$, includes all the other non-contact dofs; it is noteworthy that, due to the local nature of contacts, the size of ${\mathit{q}}_{\mathit{C}}$ is always much smaller than the size of ${\mathit{q}}_{\mathit{N}\mathit{C}}$.

3.1. Direct Method

The first reduction strategy, called here direct (D) method, is based on the approach applied for the first time in [22] to the reduction of a mistuned bladed disk for linear analyses, extended here to the case of a bladed disk with contact interfaces.

The vector of the sector dofs $\mathit{q}$ of the fundamental sector is written as

$$\mathit{q}=\left\{\begin{array}{c}{\mathit{q}}_{\mathit{I}}\\ {\mathit{q}}_{\mathit{H}}\\ {\mathit{q}}_{\mathit{L}}\end{array}\right\}=\left\{\begin{array}{c}{\mathit{q}}_{\mathit{C}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{N}\mathit{C}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{H}}\\ {\mathit{q}}_{\mathit{L}}\end{array}\end{array}\end{array}\right\}.$$

(10)

Then, after the cyclic symmetry properties (2) are applied,

$$\left\{\begin{array}{c}{\mathit{q}}_{\mathit{C}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{N}\mathit{C}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{H}}\\ {\mathit{q}}_{\mathit{L}}\end{array}\end{array}\end{array}\right\}=\left[\begin{array}{cc}\begin{array}{cc}\mathit{I}& \mathbf{0}\\ \mathbf{0}& \mathit{I}\end{array}& \begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\\ \begin{array}{cc}\mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}& \begin{array}{c}\mathit{I}{e}^{j\phi }\\ \mathit{I}\end{array}\end{array}\right]\left\{\begin{array}{c}{\mathit{q}}_{\mathit{C}}\\ {\mathit{q}}_{\mathit{N}\mathit{C}}\\ {\mathit{q}}_{\mathit{L}}\end{array}\right\}.$$

(11)

The CB method is used, retaining ${\mathit{q}}_{\mathit{C}}$ as master dofs. As a result, the following transformation holds for the single sector:

$$\left\{\begin{array}{c}{\mathit{q}}_{\mathit{C}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{N}\mathit{C}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{H}}\\ {\mathit{q}}_{\mathit{L}}\end{array}\end{array}\end{array}\right\}=\left[\begin{array}{cc}\begin{array}{cc}\mathit{I}& \mathbf{0}\\ \mathbf{0}& \mathit{I}\end{array}& \begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\\ \begin{array}{cc}\mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}& \begin{array}{c}\mathit{I}{e}^{j\phi }\\ \mathit{I}\end{array}\end{array}\right]\left[\begin{array}{cc}\begin{array}{c}\mathit{I}\\ {\mathit{\Psi }}_{\mathit{N}\mathit{C}}\end{array}& \begin{array}{c}\mathbf{0}\\ {\mathit{\varphi }}_{\mathit{N}\mathit{C}}\end{array}\\ {\mathit{\Psi }}_{\mathit{L}}& {\mathit{\varphi }}_{\mathit{L}}\end{array}\right]\left\{\begin{array}{c}{\mathit{q}}_{\mathit{C}}\\ {\eta }_{\mathit{S}}\end{array}\right\}={\mathit{R}}_{\mathit{D}}\left\{\begin{array}{c}{\mathit{q}}_{\mathit{C}}\\ {\mathit{\eta }}_{\mathit{S}}\end{array}\right\},$$

(12)

where subscripts NC and L indicate the partition of constraint and fixed-interface modes of the single sector with cyclic symmetry boundary conditions, corresponding to ${\mathit{q}}_{\mathit{N}\mathit{C}}$ and ${\mathit{q}}_{\mathit{L}}$, respectively.

The direct method requires the reduction matrix ${\mathit{R}}_{\mathit{D}}$ to be applied N times to the matrices of the fundamental sector, one per each value of harmonic index h.

3.2. Two-Step Method

In this section, an alternative approach, hence called the two-step (2S) method is described to obtain the CB-reduced matrices of the fundamental sector with cyclic symmetry properties.

First, the vector of the dofs is written as

$$\mathit{q}=\left\{\begin{array}{c}{\mathit{q}}_{\mathit{C}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{L}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{H}}\\ {\mathit{q}}_{\mathit{N}\mathit{C}}\end{array}\end{array}\end{array}\right\}.$$

(13)

Then, the CB method is applied one first time, retaining as master dofs ${\mathit{q}}_{\mathit{C}}$, ${\mathit{q}}_{\mathit{H}}$ and ${\mathit{q}}_{\mathit{L}}$

$$\mathit{q}=\left\{\begin{array}{c}{\mathit{q}}_{\mathit{C}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{L}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{H}}\\ {\mathit{q}}_{\mathit{N}\mathit{C}}\end{array}\end{array}\end{array}\right\}=\left[\begin{array}{cccc}{\mathit{I}}_{\mathit{C}}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\mathit{I}}_{\mathit{L}}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& 0& {\mathit{I}}_{\mathit{H}}& \mathbf{0}\\ {\mathit{\Psi }}_{\mathit{C}\mathbf{1}}& {\mathit{\Psi }}_{\mathit{L}\mathbf{1}}& {\mathit{\Psi }}_{\mathit{H}\mathbf{1}}& {\mathit{\varphi }}_{\mathbf{1}}\end{array}\right]\left\{\begin{array}{c}{\mathit{q}}_{\mathit{C}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{L}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{H}}\\ {\mathit{\eta }}_{\mathit{S}\mathbf{1}}\end{array}\end{array}\end{array}\right\}={\mathit{R}}_{\mathbf{1}}\left\{\begin{array}{c}{\mathit{q}}_{\mathit{C}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{L}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{H}}\\ {\mathit{\eta }}_{\mathit{S}\mathbf{1}}\end{array}\end{array}\end{array}\right\}.$$

(14)

In this way, the fixed-interface modes ${\mathit{\varphi }}_{\mathbf{1}}$ are the modes of the fundamental sector with zero displacements at all the interfaces (contact and cyclic symmetry).

Finally, for each harmonic index h, after the cyclic symmetry properties (2) are applied

$$\left\{\begin{array}{c}{\mathit{q}}_{\mathit{C}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{L}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{H}}\\ {\mathit{\eta }}_{\mathit{S}\mathbf{1}}\end{array}\end{array}\end{array}\right\}=\left[\begin{array}{ccc}\mathit{I}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathit{I}& \mathbf{0}\\ \mathbf{0}& \mathit{I}{e}^{j\phi }& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathit{I}\end{array}\right]\left\{\begin{array}{c}{\mathit{q}}_{\mathit{C}}\\ {\mathit{q}}_{\mathit{L}}\\ {\mathit{\eta }}_{\mathit{S}\mathbf{1}}\end{array}\right\}.$$

(15)

A second CB reduction is performed, by retaining ${\mathit{q}}_{\mathit{C}}$ as master dofs. As a result, the following transformation holds:

$$\left\{\begin{array}{c}{\mathit{q}}_{\mathit{C}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{L}}\\ \begin{array}{c}{\mathit{q}}_{\mathit{H}}\\ {\mathit{\eta }}_{\mathit{S}\mathbf{1}}\end{array}\end{array}\end{array}\right\}=\left[\begin{array}{ccc}\mathit{I}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathit{I}& \mathbf{0}\\ \mathbf{0}& \mathit{I}{e}^{j\phi }& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathit{I}\end{array}\right]\left[\begin{array}{cc}\begin{array}{c}I\\ {\mathit{\psi }}_{\mathit{L}\mathbf{2}}\end{array}& \begin{array}{c}\mathbf{0}\\ {\mathit{\phi }}_{\mathit{L}\mathbf{2}}\end{array}\\ {\mathit{\psi }}_{\mathit{S}\mathbf{2}}& {\mathit{\phi }}_{\mathit{S}\mathbf{2}}\end{array}\right]\left\{\begin{array}{c}{\mathit{q}}_{\mathit{C}}\\ {\mathit{\eta }}_{\mathit{S}\mathbf{2}}\end{array}\right\}={\mathit{R}}_{\mathbf{2}}\left\{\begin{array}{c}{\mathit{q}}_{\mathit{C}}\\ {\mathit{\eta }}_{\mathit{S}\mathbf{2}}\end{array}\right\},$$

(16)

where the symbols $\mathit{\psi }$ and $\mathit{\phi }$ refer to the constraint modes and the fixed interface modes of the system after the first reduction ${\mathit{R}}_{\mathbf{1}}$.

The two-step method is not a standard approach, although it is implemented in some FE software such as Samcef (SAMTECH, Belgium) and Code-Aster (Open Source, France).

3.3. Remarks about the Two Approaches

Before testing the two approaches on a set of test cases, it is worthwhile to write some remarks about the two methods, trying to highlight some features, which will help interpret the results of the comparison.

In particular, the most important features, which characterize the two reduction approaches, are:

• The direct method requires one reduction (${\mathit{R}}_{\mathit{D}}$ matrix) for each harmonic index h, while the two-step method requires a first reduction (${\mathit{R}}_{\mathbf{1}}$ matrix), which is performed only once, followed by a second reduction (${\mathit{R}}_{\mathbf{2}}$ matrix) for each harmonic index.
• The direct method requires a lower number of constraint modes $\mathit{\Psi }$ to be computed with respect to the two-step method, where the number of static analyses necessary to generate the constraint modes ${\mathit{\Psi }}_{\mathbf{1}}$ is proportional to the number of contact dofs and to the number of inter-sector interface dofs.
• In the direct method, the linear modal analyses (one per each harmonic index h, necessary to compute the fixed-interface modes $\mathit{\varphi }$, are computed on the full model of the fundamental sector. In the two-step method, only one modal analysis of the full model of the fundamental sector is performed to obtain ${\mathit{\varphi }}_{\mathit{1}}$, and the modal analyses performed in the second reduction operate on an already reduced model.
• Fixed-interface modes $\mathit{\varphi }$ computed with the direct method respect the cyclic symmetry properties of the bladed disk, while fixed-interface modes ${\mathit{\varphi }}_{\mathbf{1}}$ assume fixed inter-sector interfaces.

Feature #1 makes the direct method easier to implement, since it only requires one step. In addition, Feature #2 seems to imply a higher numerical efficiency of the Direct method, since it requires a lower number of static analyses to generate the reduction matrix.

Feature #3, on the contrary, makes the two-step method preferable because the modal analyses with cyclic symmetry boundary conditions (one per each harmonic index) are performed on an already reduced model.

Finally, Feature #4 indicates that the modal vectors $\mathit{\varphi }$ look more suitable to represent the dynamics of the full bladed disk than modal vetctors ${\mathit{\varphi }}_{\mathbf{1}}$ obtained with fixed inter-sector interfaces.

4. Numerical Results

4.1. First Test Cases for Accuracy and Efficiency Analysis

The two reduction methods described in the previous section are applied to two numerical test cases to compare their capability to obtain a CB-ROM suitable for nonlinear forced response, considering both accuracy and numerical efficiency.

The analyses are performed on the FE models of the fundamental sector of two bladed disks, shown in

Table 1. Details of the numerical test case.

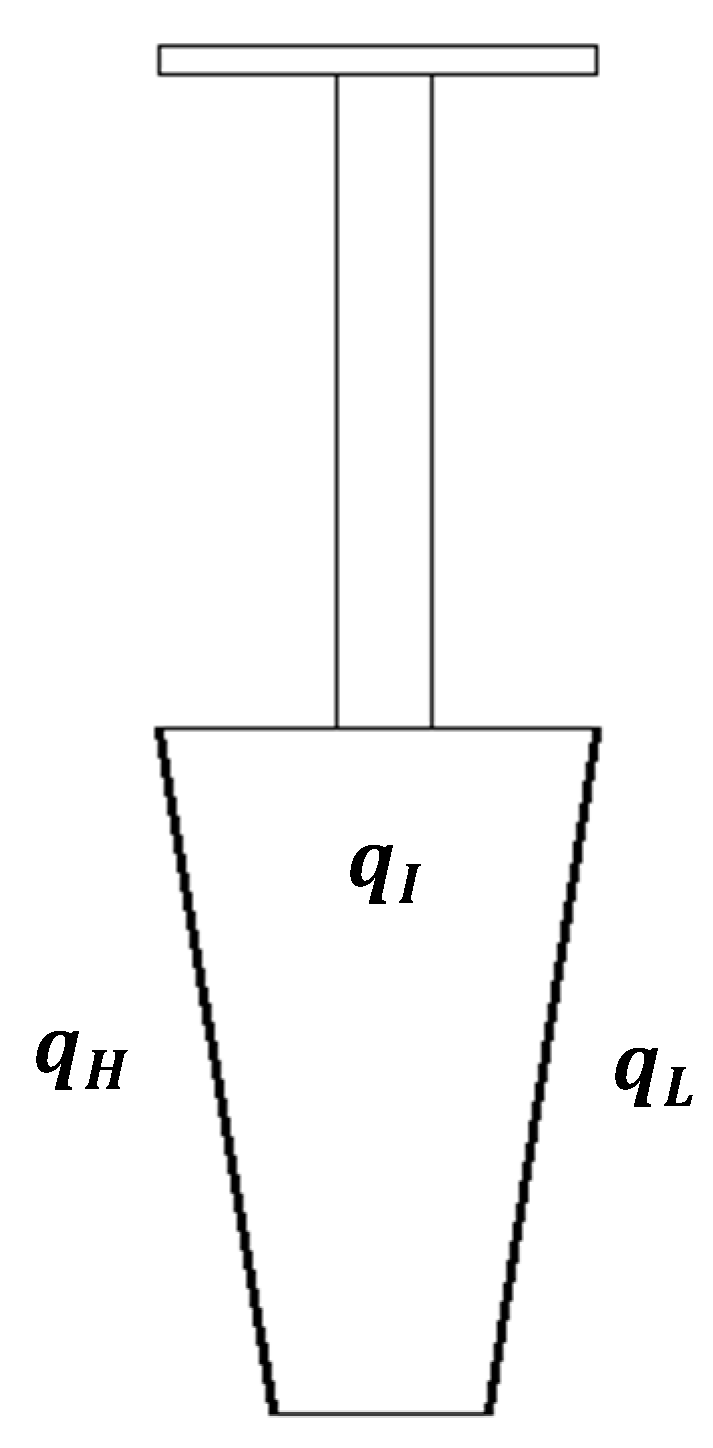
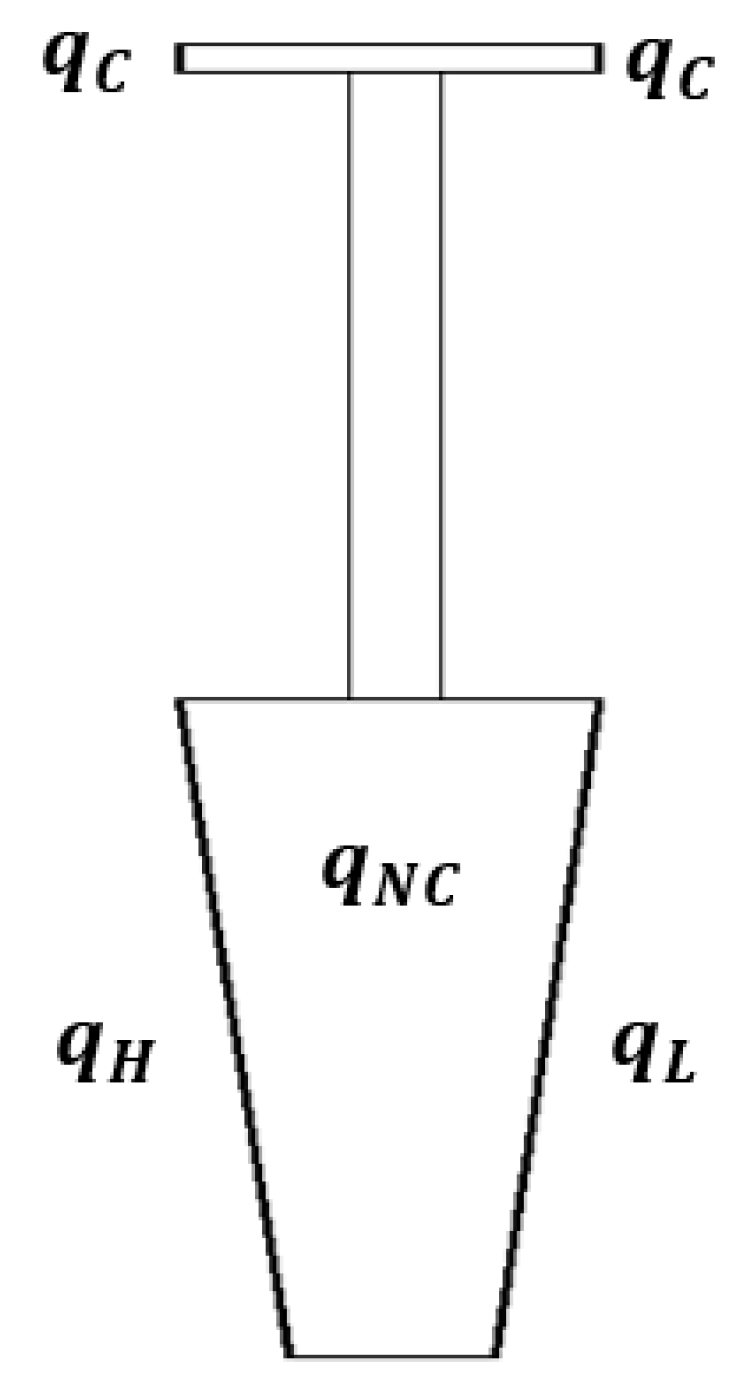
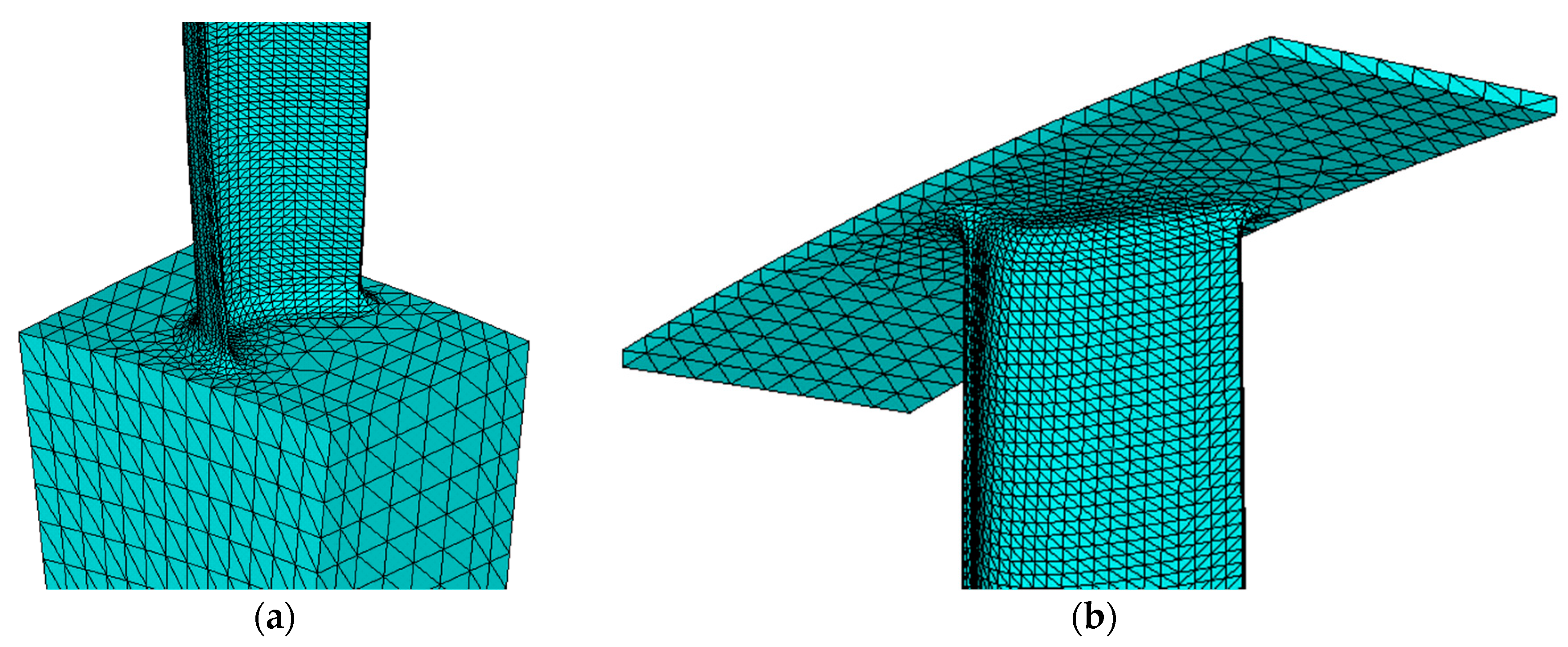
Test Case	A		B
Blades	27		81
Sector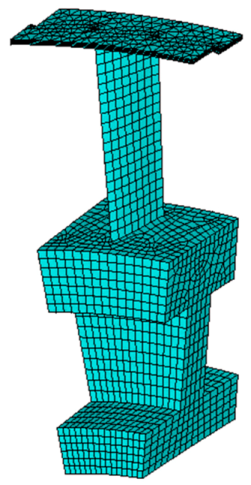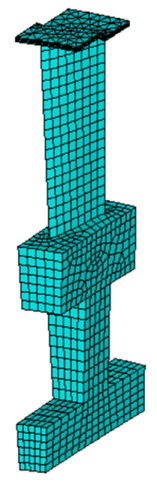
Element Type	Linear	Quadratic	Linear	Quadratic
Elements	16,561	16,561	5627	5627
Nodes	6052	30,920	2454	11,672

. The contact interfaces are located at the covers located at the blade tip, called shrouds.

For each sector, two different element types are used, linear and quadratic, to check the effect of the dofs number on the efficiency of the reduction methods. It is worth mentioning that quadratic elements are usually preferred to linear elements when the FE model is used not only for modal analysis but also for the stress analysis, since they allow computing non-uniform stresses inside each element.

To assess the efficiency and the accuracy of the two reduction techniques, multiple ROMs (

Table 2. List of ROMs generated and used for comparison.

Direct Method	Two-Step Method
	1st Set of ROMs	2nd Set of ROMs	3rd Set of ROMs
Z	(Z1; Z2)	(Z1; Z2)	(Z1; Z2)
20	60; 20	120; 20	180; 20
40	60; 40	120; 40	180; 40
60	60; 60	120; 60	180; 60

) of the fundamental sectors are generated.

First, the direct method is applied by selecting an increasing number Z of slave modes (Z = 20, 40 and 60) in order to check the convergence of the natural frequencies of the first 10 modes of the fundamental sector.

Then, the two-step method is applied. Three sets of ROMs are generated with an increasing number Z₁ of fixed-interface modes during the 1st step (Z₁ = 60, 120 and 180). For each set, three subsets are generated with an increasing number Z₂ of slave modes (Z₂ = 20, 40 and 60) in the 2nd step.

Comparisons are only performed between ROMs generated by the direct method with Z slave modes and ROMs generated by the two-step method with Z₂ slave modes in the 2nd step. In this way, ROMs with the same size are compared. Of course, for the two-step method, the overall calculation time, necessary to perform both steps, is given for a fair comparison.

The natural frequencies of the ROMs are compared to the natural frequencies computed with the full wheel model, which, in the case of industrial applications, is of course not available.

An example of the results collected for each harmonic index h is shown in

Table 3. Test Case A (linear elements, h = 1)—relative error between natural frequencies.

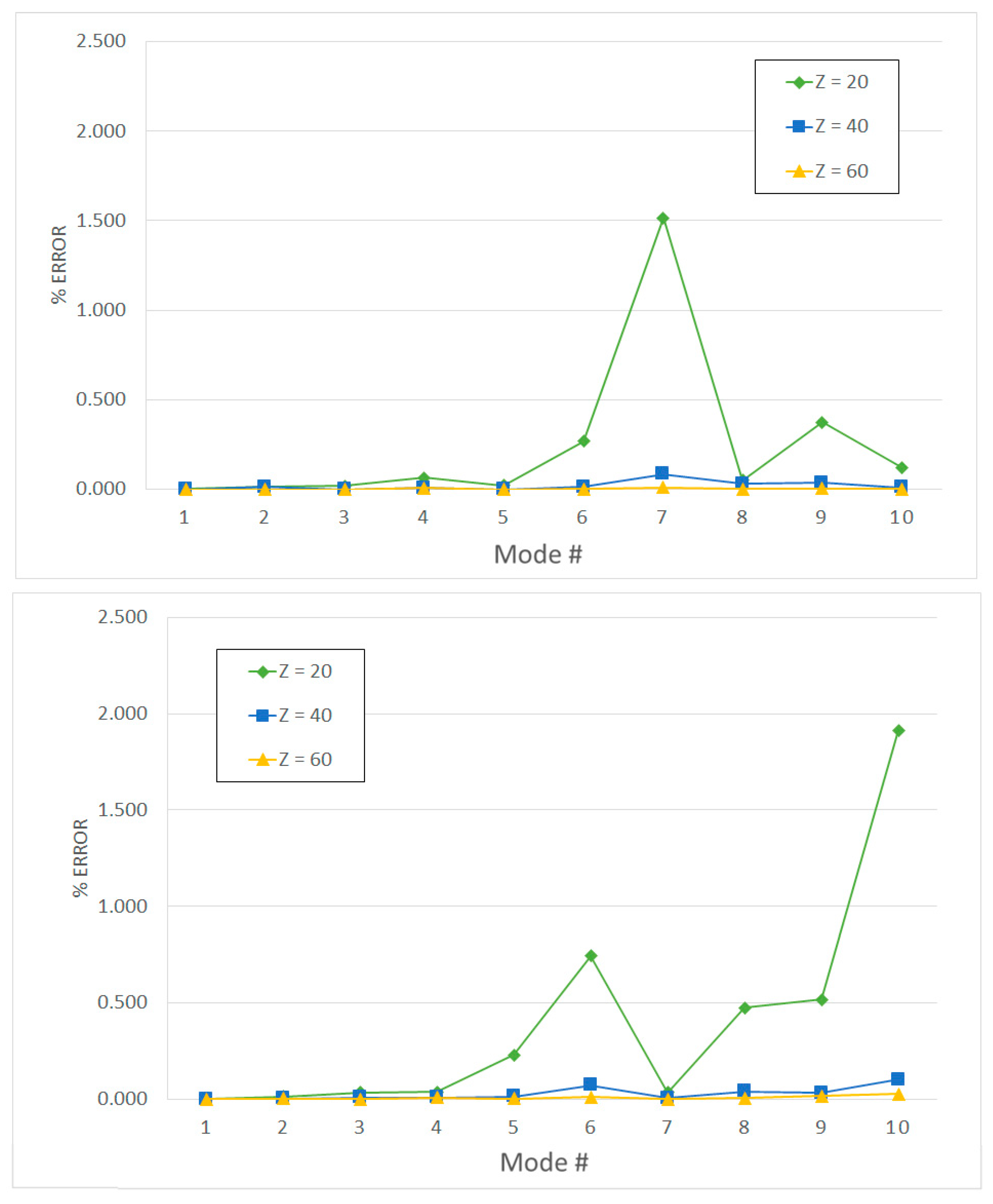
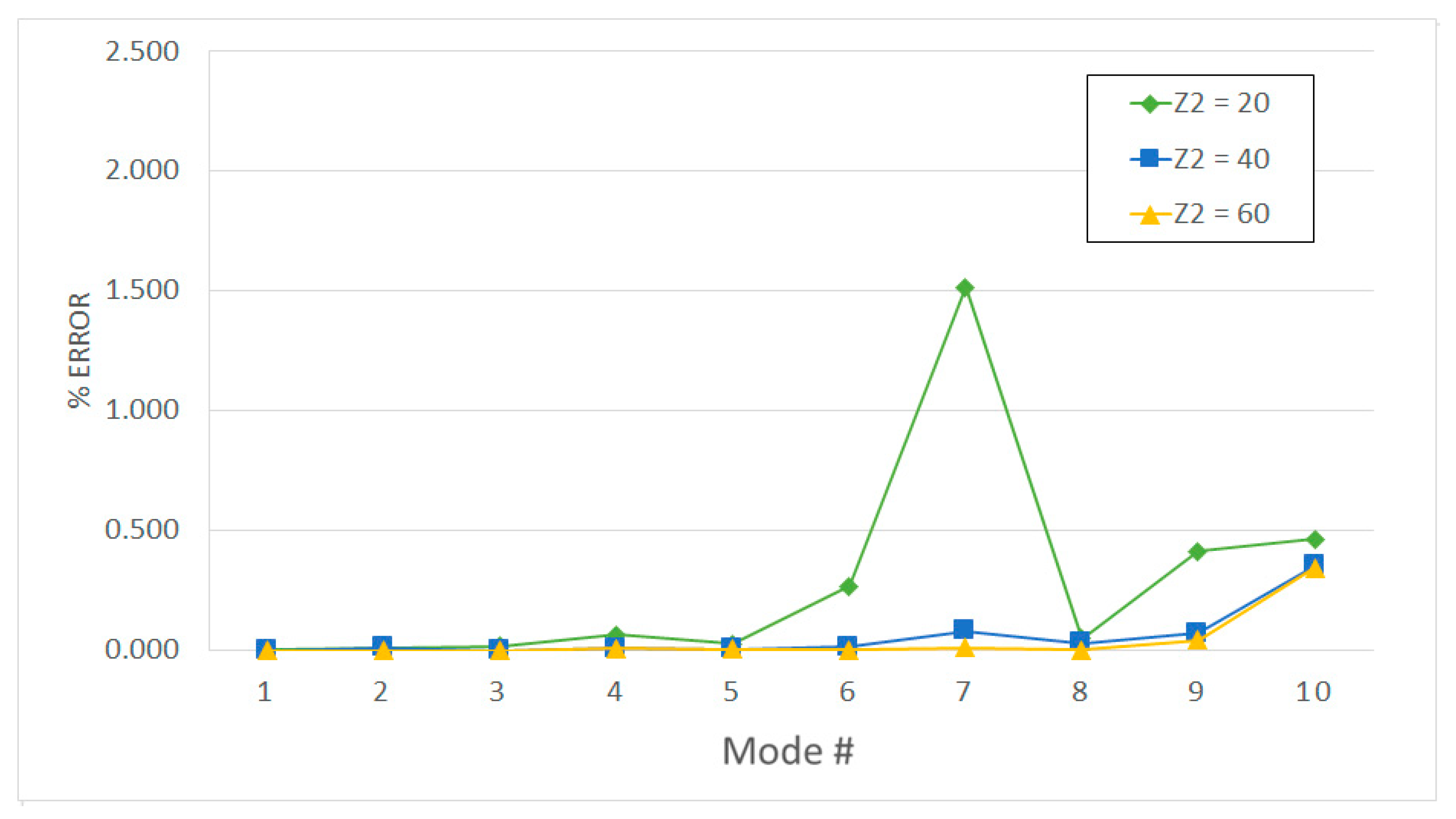
Full	Direct Method			Two-Step Method
(Hz)				Z1 = 60			Z1 = 120			Z1 = 180
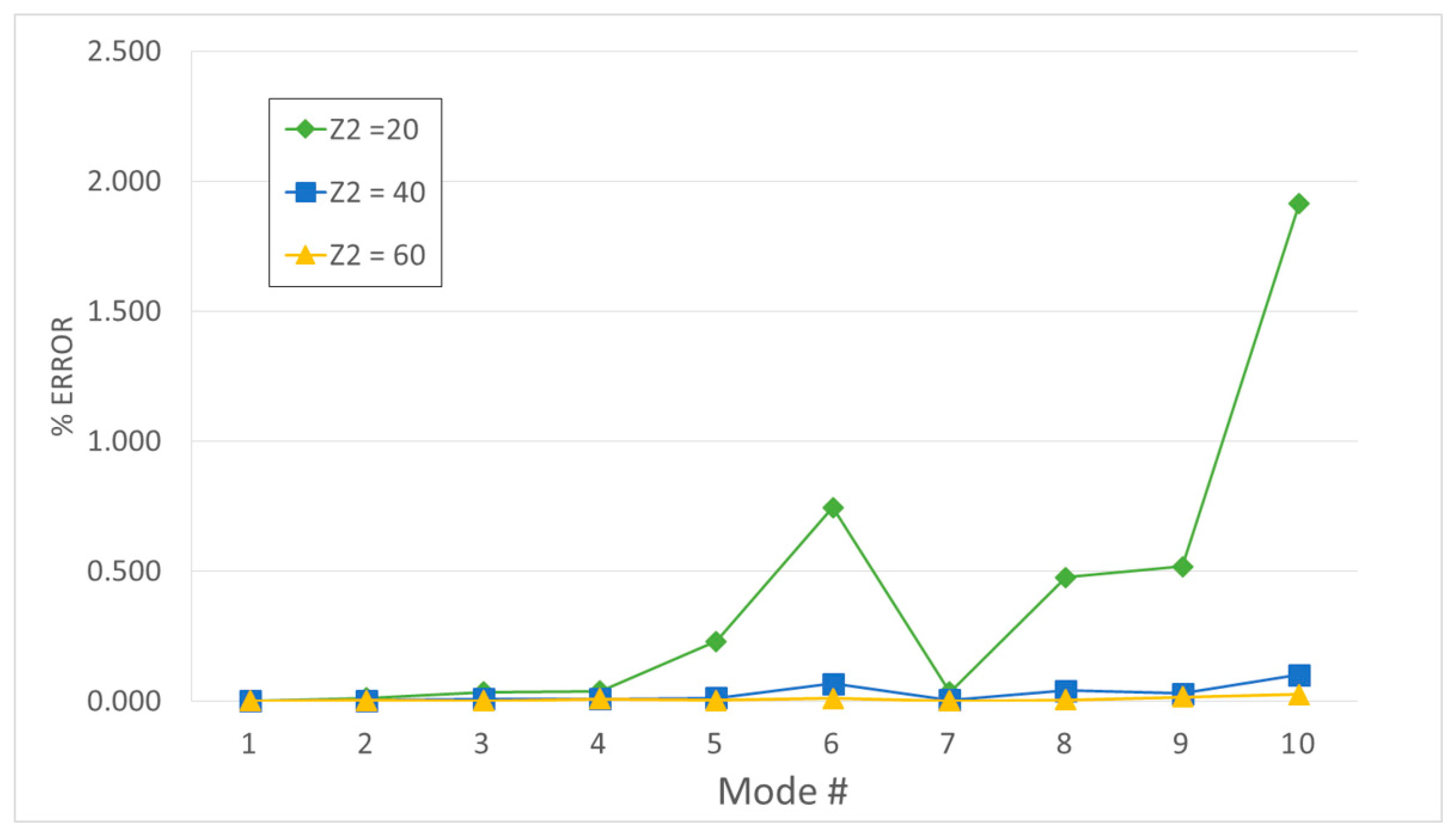
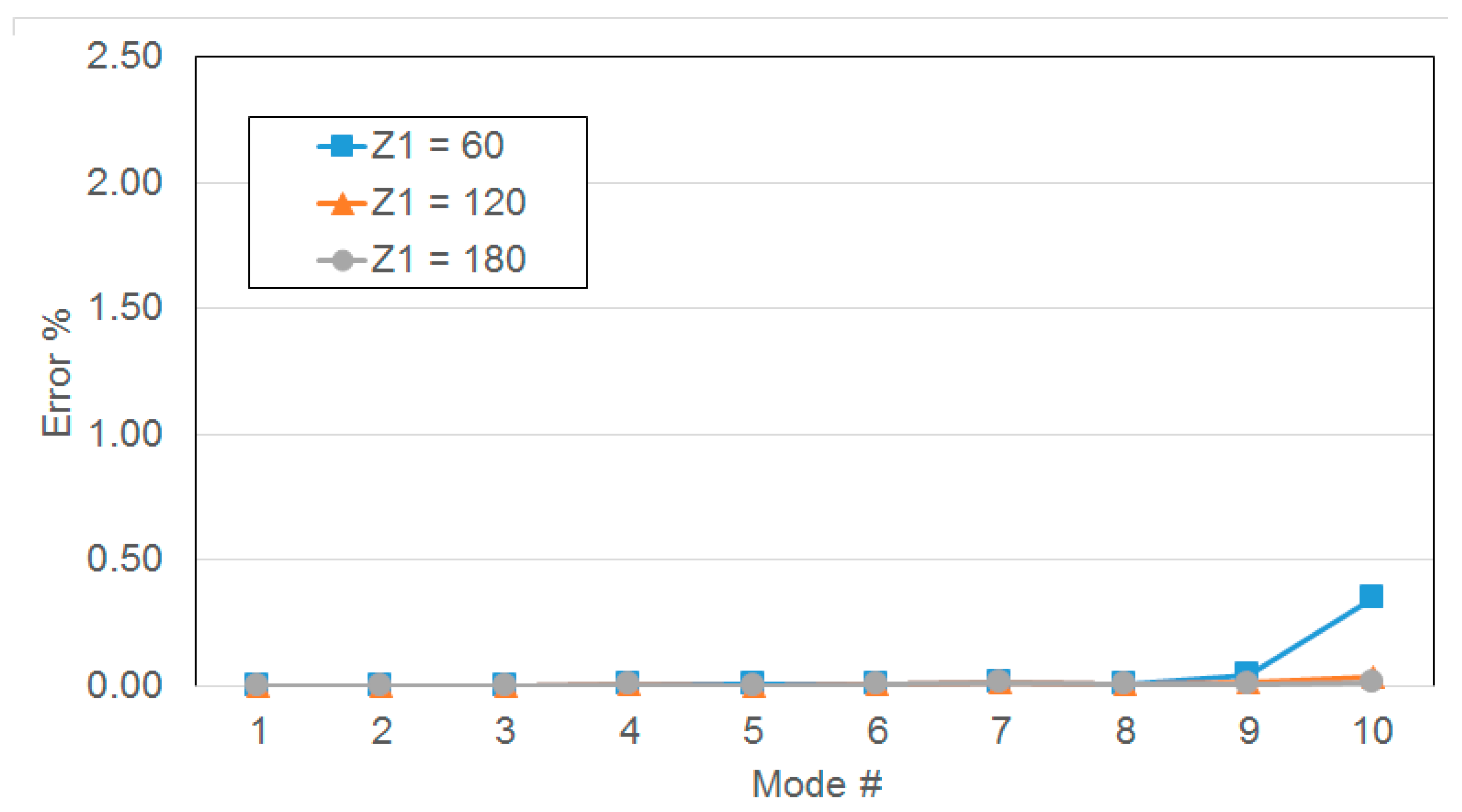
	Z = 20	Z = 40	Z = 60	Z2 = 20	Z2 = 40	Z2 = 60	Z2 = 20	Z2 = 40	Z2 = 60	Z2 = 20	Z2 = 40	Z2 = 60
200.18	0.00%	0.00%	0.00%	0.00%	0.00%	0.00%	0.00%	0.00%	0.00%	0.00%	0.00%	0.00%
488.70	0.01%	0.01%	0.00%	0.01%	0.01%	0.00%	0.01%	0.01%	0.00%	0.01%	0.01%	0.00%
1044.80	0.02%	0.00%	0.00%	0.02%	0.00%	0.00%	0.02%	0.00%	0.00%	0.02%	0.00%	0.00%
1211.40	0.07%	0.01%	0.01%	0.07%	0.01%	0.01%	0.07%	0.01%	0.01%	0.07%	0.01%	0.01%
1943.90	0.02%	0.00%	0.00%	0.03%	0.01%	0.01%	0.03%	0.01%	0.00%	0.03%	0.00%	0.00%
3439.40	0.27%	0.01%	0.00%	0.27%	0.01%	0.00%	0.27%	0.01%	0.00%	0.27%	0.01%	0.00%
3895.00	1.51%	0.08%	0.01%	1.51%	0.08%	0.01%	1.51%	0.08%	0.01%	1.51%	0.08%	0.01%
6389.70	0.05%	0.03%	0.00%	0.05%	0.03%	0.00%	0.05%	0.03%	0.00%	0.05%	0.03%	0.00%
6915.70	0.37%	0.03%	0.01%	0.41%	0.07%	0.04%	0.38%	0.04%	0.01%	0.37%	0.04%	0.01%
7775.40	0.12%	0.01%	0.00%	0.46%	0.35%	0.34%	0.16%	0.04%	0.03%	0.13%	0.02%	0.01%

, where the relative error, computed with respect to the full FE model, in computing the natural frequencies of the test case A is listed for different ROMs. In the table, errors equal to 0.00% must be interpreted as <0.01%.

Figure 4 shows the relationship between the number Z of slave modes and the accuracy of the ROMs generated with the direct method for two different harmonic indexes representative of a compliant (h = 1) and a stiff (h = 13) disk, representative of what was observed for all of the other harmonic indexes. When Z = 20, some of the natural frequencies have more than 1% error, which is reduced to 0.1% with Z = 40 and becomes negligible when Z = 60.

It is worth noting that, for each mode, the convergence rate depends on the harmonic index h. As shown in Figure 4, when Z = 20, mode #7 and mode #10 are the less accurate modes when h equals 1 and 13, respectively. This apparent inconsistency in the ROM results is due to the effect of the harmonic index on the mode shapes. When h = 1, the disk is more compliant than when h = 13, but the stiffening effect due to the harmonic index affects in different ways different blade modes. As a result, the same blade mode can change its position in the mode sequence (e.g., the 2nd blade bending mode can be mode #3 when h = 1 and it can be mode #2 when h = 13).

Afterwards, the two-step method was implemented with the objective of generating a ROM of the same size (or smaller) with the same accuracy as the one of the ROMs generated with the direct method.

The first set of ROMs was generated by selecting 60 slave modes in the 1st reduction step (Z₁ = 60). Results are summarized in Figure 5 and Figure 6.

In some cases (e.g., Figure 6), 60 modes in the 1st reduction are enough to obtain an accuracy comparable to the direct methods in all of the first 10 natural frequencies. In this case, the results obtained with the direct method (Figure 4-Low) are almost identical to each other. The reason is that, for high harmonic indices, as h = 13, the disk behavior resembles a rigid body and fixed (direct method) and cyclic (two-step method) boundary conditions are almost equivalent to each other.

Unfortunately, in other cases (e.g., Figure 5), the ROM accuracy does not improve as the number of slave modes Z₂ is increased from 40 to 60. We interpret this result as a lack of accuracy of the ROM generated in the 1st step because of the fixed-interface boundary conditions applied to the sector interface nodes ${\mathit{q}}_{\mathit{H}}$ and ${\mathit{q}}_{\mathit{L}}$.

Thus, in order to increase the accuracy of the ROM generated with the two-step approach, the 2nd and the 3rd sets of ROMs are generated with Z₁ = 120 and Z₁ = 180, respectively. In Figure 7, the effect of the number of modes of the 1st reduction (Z₁) is shown for the first 10 natural frequencies associated with h = 1.

All of the curves refer to ROMs with the same size (Z₂ = 60) as the final one generated with the direct method (Figure 4). It is observed that increasing the number of modes retained in the 1st step significantly affects the accuracy of the final ROM, specifically for modes #9 and #10. This behavior agrees with the interpretation given about the results in Figure 5 because of the (fixed) boundary conditions applied to the disk interfaces, and the reduction basis used in the 1st step must include a number of modes (Z₁) significantly higher (up to three times) than the number of modes retained in the 2nd step (Z₂), to accurately represent the dynamics of the bladed disk.

While accuracy is by far the most relevant performance index for reduction techniques, it is not the only one. Since the amount of time necessary to generate ROMs is not negligible, numerical efficiency is another parameter, which can drive the reduction technique selection.

In order to check the numerical efficiency of the two reduction approaches described in this paper versus the size of the full model, they are applied to Test Cases A and B in both their configurations (linear and quadratic elements).

In particular, the direct method is applied by retaining 60 fixed-interface modes, while the two-step method is applied by retaining Z₁ = 180 modes at the 1st step and Z₁ = 60 modes in the 2nd step. In this way, the ROMs will have the same final size and, according to the previous analysis, comparable accuracy.

The total computation times, corresponding to the time necessary to generate ROMs for all the harmonic indices needed to build the full wheel ROM by means of Equation (4), are shown in

Table 4. Total calculation times for the proposed reduction techniques (Test Cases A and B).

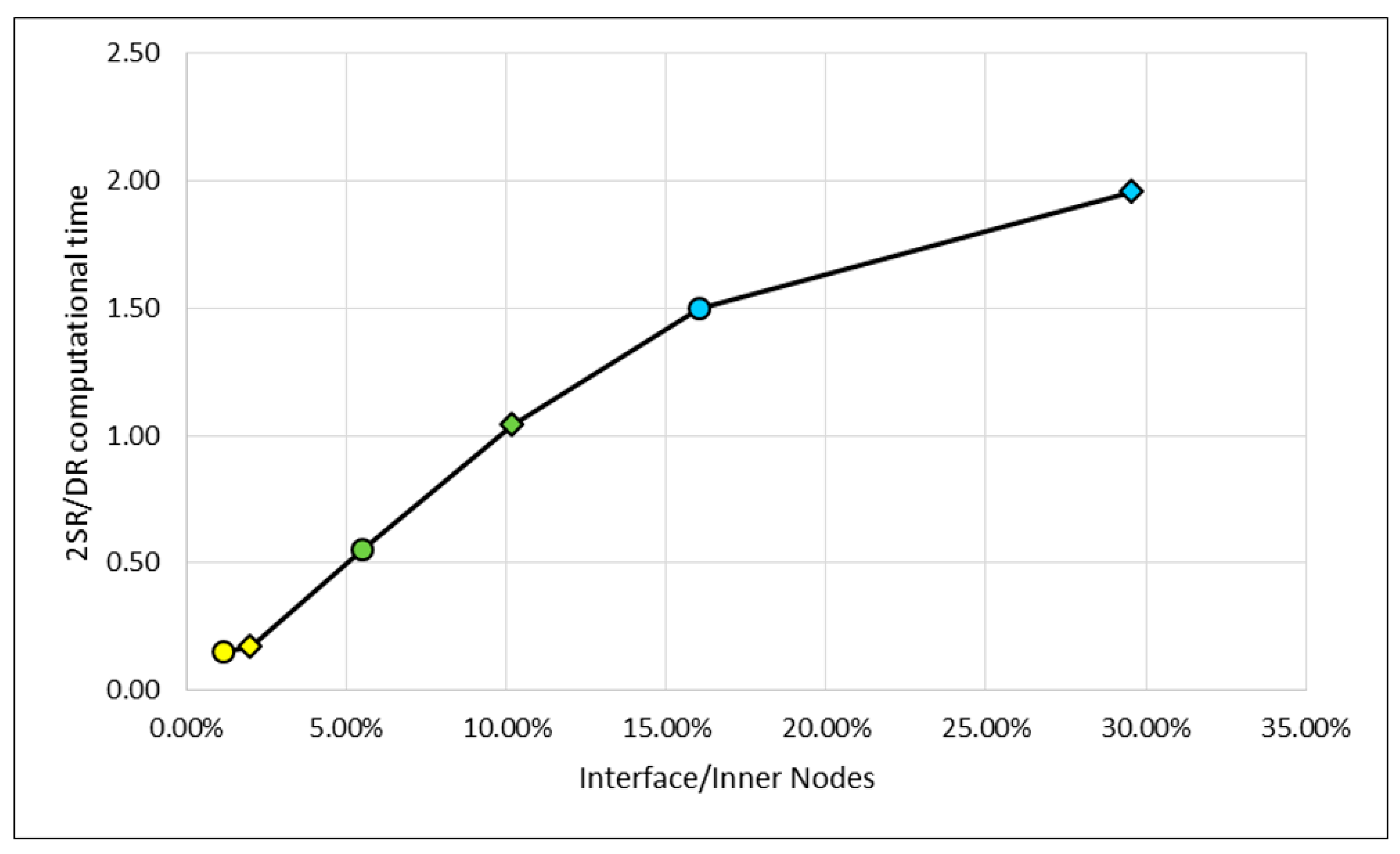
Test Case	Node #	Direct (s)	Two-Step (s)	Two-Step/Direct
B-Lin	2454	328	641	1.95
B-Quad	6052	779	1169	1.50
A-Lin	11,672	322	336	1.04
A-Quad	30,920	1120	620	0.55

, whose last column represents the ratio between the two-step and the direct method’s calculation time. A ratio higher than one means that the direct method is more efficient and vice versa. The four test cases are ordered according to the number of nodes in the fundamental sector.

The results in Table 4 suggest that the two-step method becomes more and more convenient from the computational point of view as the number of nodes (and of dofs) of the fundamental sector becomes higher. The obtained results give a preliminary indication, but they are not conclusive and, therefore, a third test case is analyzed in the next section for the sake of completeness.

4.2. Additional Test Case for Efficiency Analysis.

In order to double-check the results of Table 4, a 32-sector bladed disk is generated as Test Case C, in two configurations with linear (13,885 nodes) and quadratic (89,224 nodes) elements.

While for Test Cases A and B the mesh size was uniform over the entire sector (blade and disk), in Test Case C (Figure 8), a more realistic meshing strategy is adopted. The mesh is more refined in the blade, while it is coarser in the disk, consistently with what usually happens with FE models developed for bladed disk dynamics, since the critical component for high cycle fatigue failure is the blade.

The results listed in Table 4 are updated with the addition of the Test Case C results (

Table 5. Total calculation times for the proposed reduction techniques (Test Cases A, B and C).

Test Case	Node #	Direct (s)	Two-Step (s)	Two-Step/Direct
B-Lin	2454	328	641	1.95
B-Quad	6052	779	1169	1.50
A-Lin	11,672	322	336	1.04
C-Lin	13,885	646	110	0.17
A-Quad	30,920	1120	620	0.55
C-Quad	89,228	2244	332	0.15

). The new results contradict the conclusions drawn before, since the two-step method looks more efficient for Test Case C with linear elements that for Test Case A with quadratic elements, although the latter has a bigger size.

Based on the results in Table 5 and on the remarks in Section 3.3, it is observed here that a suitable parameter to rank the Test Cases in terms of numerical efficiency is the ratio ${\mathit{q}}_{\mathit{H}}/{\mathit{q}}_{\mathit{I}}$. (interface/inner nodes), since:

• the calculation of the constraint modes in the 1st step is the most time-consuming operation in the two-step process,
• the computation of the fixed-interface modes is the most time-consuming step of the direct method.

In Figure 9, the normalized computational time is plotted versus the ratio ${\mathit{q}}_{\mathit{H}}/{\mathit{q}}_{\mathit{I}}$ and a monotonic curve is in fact obtained.

According to these results, if the number of interface nodes is lower than 10% of the inner nodes of the fundamental sector, the two-step method is more efficient than the direct method.

Since, as mentioned above, the FE models of bladed disks are more refined in the blade than in the disk, as for Test Case C, the two-step method looks promising for industrial applications, when time is always one of the major constraints.

5. Conclusions

In this paper, two reduction strategies are described. They can be applied to generate ROMs of bladed disks in cyclic symmetry for nonlinear forced response analysis, such as shrouded bladed disks.

Both rely on the cyclic symmetry properties of the system and make use of the Craig–Bampton reduction method to reduce the size of the final model to be used for nonlinear analysis.

The first approach, here called the direct method, was already used in the literature to generate ROMs for linear forced response of mistuned bladed disk and it is extended here to the case of nonlinear forced response. The second approach, defined here as the two-step method, does not represent a classical approach although it is implemented in some commercial FE solver.

The numerical results performed on different test cases showed that both methods ensure a high accuracy in terms of natural frequencies of the system (an error or less than 0.1% on the first ten natural frequencies of each harmonic index.

In addition, test cases showed that ROMs of the same size, but obtained with the two methods, can guarantee the same accuracy.

An interesting result was obtained when the numerical efficiency of the two methods was compared. The test cases showed that the numerical efficiency of the two approaches is affected by the ratio defined by the number of disk interface nodes over the number of inner nodes in the fundamental sector. In particular, when this ratio is lower than 10%, the two-step method is more efficient. It is worth noting that those values (less than 10%) are typical of industrial FE models, developed for high cycle fatigue analysis of the blades and characterized by a more highly refined mesh in the blades than in the disk.

It is worth mentioning also here that the focus of this paper was to obtain efficiently CB-ROMs to be provided as inputs for nonlinear forced response analysis of shrouded bladed disks, but that the nonlinear simulations are not part of this work.