Role of Piezoelectric Elements in Finding the Mechanical Properties of Solid Industrial Materials

Abstract

Recent developments in ultrasonic material testing have increased the need to evaluate the current status of the different applications of piezoelectric elements (PEs). This research have reviewed state-of-the-art emerging new technology and the role of PEs in tests for a number of mechanical properties, such as creep, fracture toughness, hardness, and impact toughness, among others. In this field, importance is given to the following variables, namely, (a) values of the natural frequency to PEs, (b) type and dimensions of specimens, and (c) purpose of the tests. All these variables are listed in three tables to illustrate the nature of their differences in these kinds of tests. Furthermore, recent achievements in this field are emphasized in addition to the many important studies that highlight the role of PEs.

1. Introduction

The role of piezoelectric elements (PEs) in ultrasonic tests and smart system applications is becoming increasingly difficult to ignore, especially with regard to art using PE in finding the mechanical properties of solid materials. The classical definition of PE is a polarizing ceramic material that can convert mechanical energy to electric energy and vice versa. The mechanical wave or vibration is generated through passing an electric wave through the two electrodes of the PE then, into the material of PE itself. The piezoelectric effect causes a crystal to produce an electrical potential when it is subjected to mechanical vibration. In contrast, the reverse piezoelectric effect causes the crystal to produce vibration when it is placed in an electric field. A crystal exhibits the piezoelectric effect if its structure has no center of symmetry. A stress (tensile or compressive) applied to such a crystal will alter the separation between the positive and negative charge sites in each elementary cell leading to a net polarization at the crystal surface. The effect is practically linear, i.e., the polarization varies directly with the applied stress, and is direction-dependent, so that compressive and tensile stresses will generate electric fields and hence voltages of opposite polarity. It is also reciprocal, so that if the crystal is exposed to an electric field, it will experience an elastic strain causing its length to increase or decrease according to the field polarity [1]. There are many advantages of PEs which are very important in mechanical tests such as (1) the high electromechanical transformation efficiency; (2) a broad range of characteristics can be achieved with different material compositions (high degree of freedom in characteristics design); (3) high stability; and (4) their suitability for mass production and economic production. The purposes of this research are: (a) to summarize published articles that involve PE applications in testing material properties; (b) to report recent progress in this field; and (c) to establish a guideline for the frequency levels or ranges of PE use associated with the dimensions of test specimens for these types of tests.

2. Using Piezoelectricity to Calculate Solid-Material Properties

The properties that were taken into account are discussed in the following sub-sections.

2.1. Creep

Creep represents plastic deformation in material over time, when this material is subjected to constant stress. This stress is often less than the yield point of the material. Usually, creep does not necessarily mean failure, but it is usually not good. Acute creep tends to increase with increasing temperature.

To calculate the static creep rate of ice and a frozen soil specimen (394 mm long and 76 mm in diameter subject to −3 °C), two pieces of PE with frequency ranging from 0 Hz to 1000 Hz were used [2]. In this test, the input motion and output sample resonance are both observed and measured with piezoelectric transducer attached to the cap and base plates at passive and active ends of the specimen.

Vibrocreep in polymers means an acceleration of creep through the specimen to the cyclic loading regime. This test was used as one of many stages in an experimental program to test the creep in polymers and thin-film of piezoelectric polymer made from polyvinylidene fluoride (PVDF) [3,4]. The PVDF used can sense very small vibrations from 1 Hz to 20 Hz, slight changes in stress, after more than 10 years and 100 million pressure cycles at a pressure range from 10 kPa to 2 MPa, with approximately 10% accuracy, and about 1 ms response time [3]. In addition, the PVDF can be used in a wide temperature range (−40 °C to +160 °C). In another report, PVDF of 4 mm diameter with hosing diameter range of 8 mm to 20 mm was used, which can sense loads with frequency ranging from 0.001 GHz to 2 GHz [4]. These potential properties and their flexibility in use are very difficult to find in many available sensors or smart materials. Thus, most ultrasonic creep tests have utilized PVDF recently [5,6,7].

The Udimet 520 and IN738LC Ni nickel-based alloy is one of the important alloys in manufacturing gas turbine blades because this material has a high resistance to creep. A previous study reported the relationship between creep life and its effects on ultrasonic waves for these alloys using PE (2.25 MHz, 6 mm diameter that was manually joined to the specimen using a compliant gel) as a dual element transducer (pulse emitter and receiver from the same location) [8]. The overall length of these specimens was 15 cm and the width ranged from 2.25 cm to 3.0 cm.

To measure the creep in SUS 316L austenitic stainless steel, a control system consisting of PE with a natural frequency of 15 MHz as the valve opening to control the force which comes from the vacuum drum was designed [9]. This application reveals the ability of PE as a high-velocity actuator with small size, which can be used in special applications.

In the same manner, another report indicated that ultrasonic attenuation increases on two conditions, namely, an increase in the equivalent size of cubical shape γ’ precipitates and an increase in creep time [10]. This attenuation in ultrasonic waves can be used as a potential non-destructive parameter for evaluating the creep degree for the alloy IN738LC Ni, as shown in Figure 1. Thus, piezoelectric transducer (PT) with a center frequency of 15 MHz in a pulse echo technique was used to calculate the attenuation in this wave. Then, the degree of creep in this alloy was calculated. In addition, PE was used as a sensor to measure creep in paper peeling [11].

2.2. Fracture Toughness

In recent years, interest in fracture toughness in the ultrasonic field has increased considerably. Fracture toughness is defined as the ability of the material to resist the progression of a crack. Material failure occurs when $K_1=K_{1C}$ where: $K_1 = Y\sigma \sqrt{\pi c}$, K₁ = mode 1 stress intensity factor, Y = constant, depending on geometry/loading, σ = average stress (i.e., away from the crack), c = crack size, and K_1C = is a material property named fracture toughness.

One of the methods of measuring the increasing toughness of materials is by using a periodic residual stress model, which was explained in detail in [12]. A piezospectroscopic technique [13], a method that was described in detail in another report [14], was used to calculate the residual stress in an alumina matrix (ZrO₂-Zr) from the measured frequency shifts according to a relation of linear proportionality through the average piezospectroscopic coefficients given by He and Clarke [15]. Recently, most measurements of residual stresses in several alloys have been implemented by piezospectroscopic measurements based on the shift peak as a function of stress [16].

Table 1. Several piezoelectric element (PE) applications for measuring the fracture of toughness of metals.

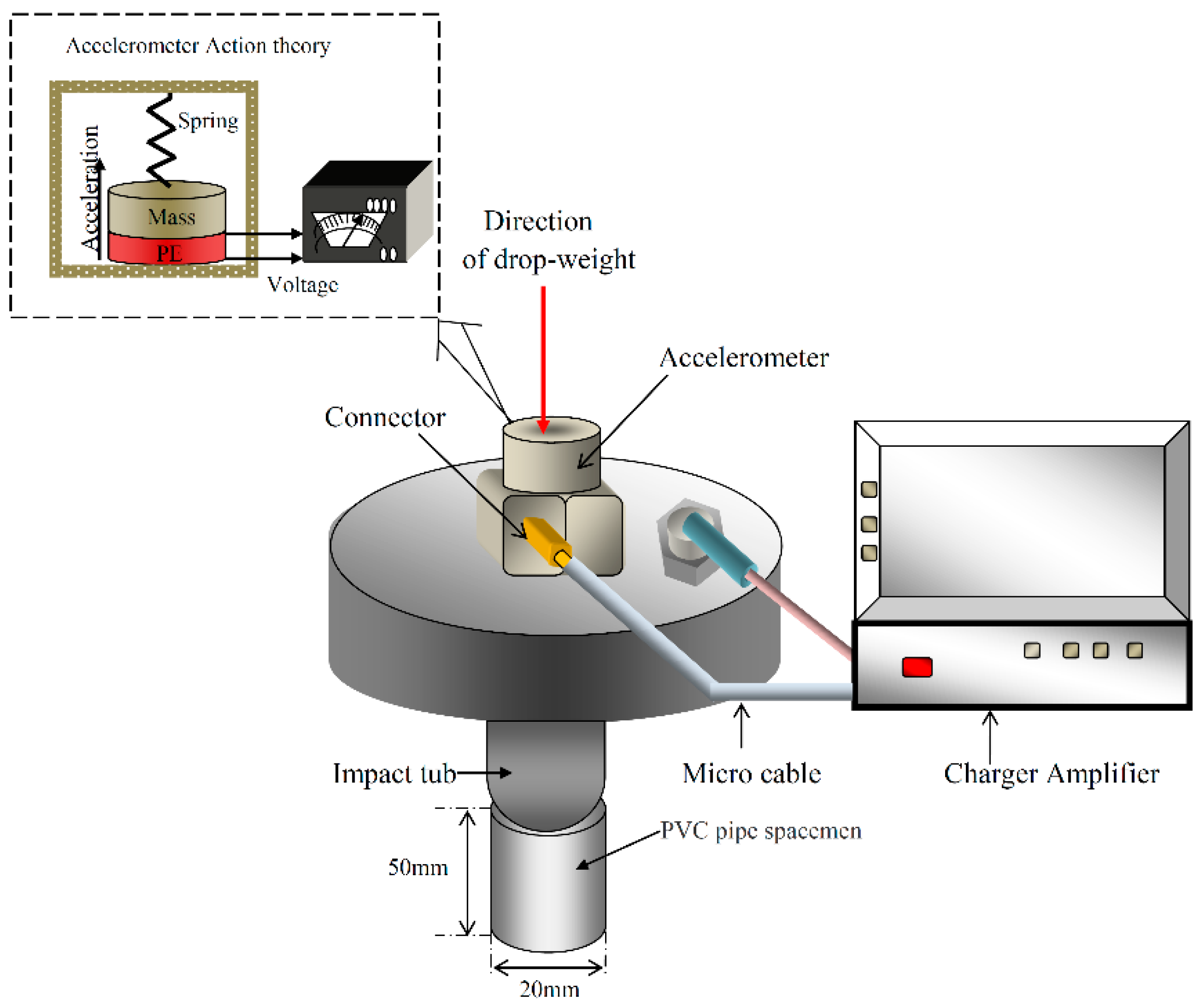
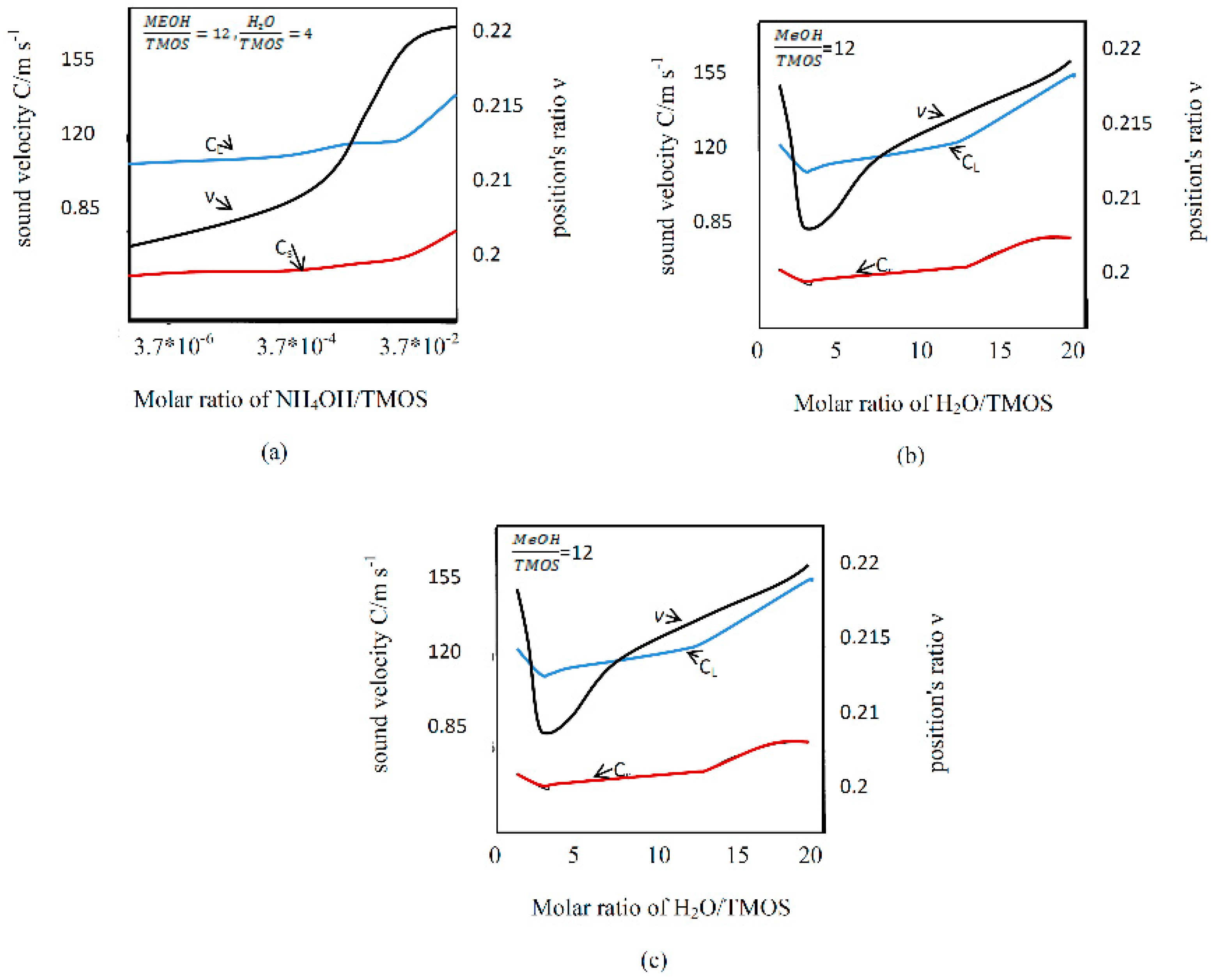
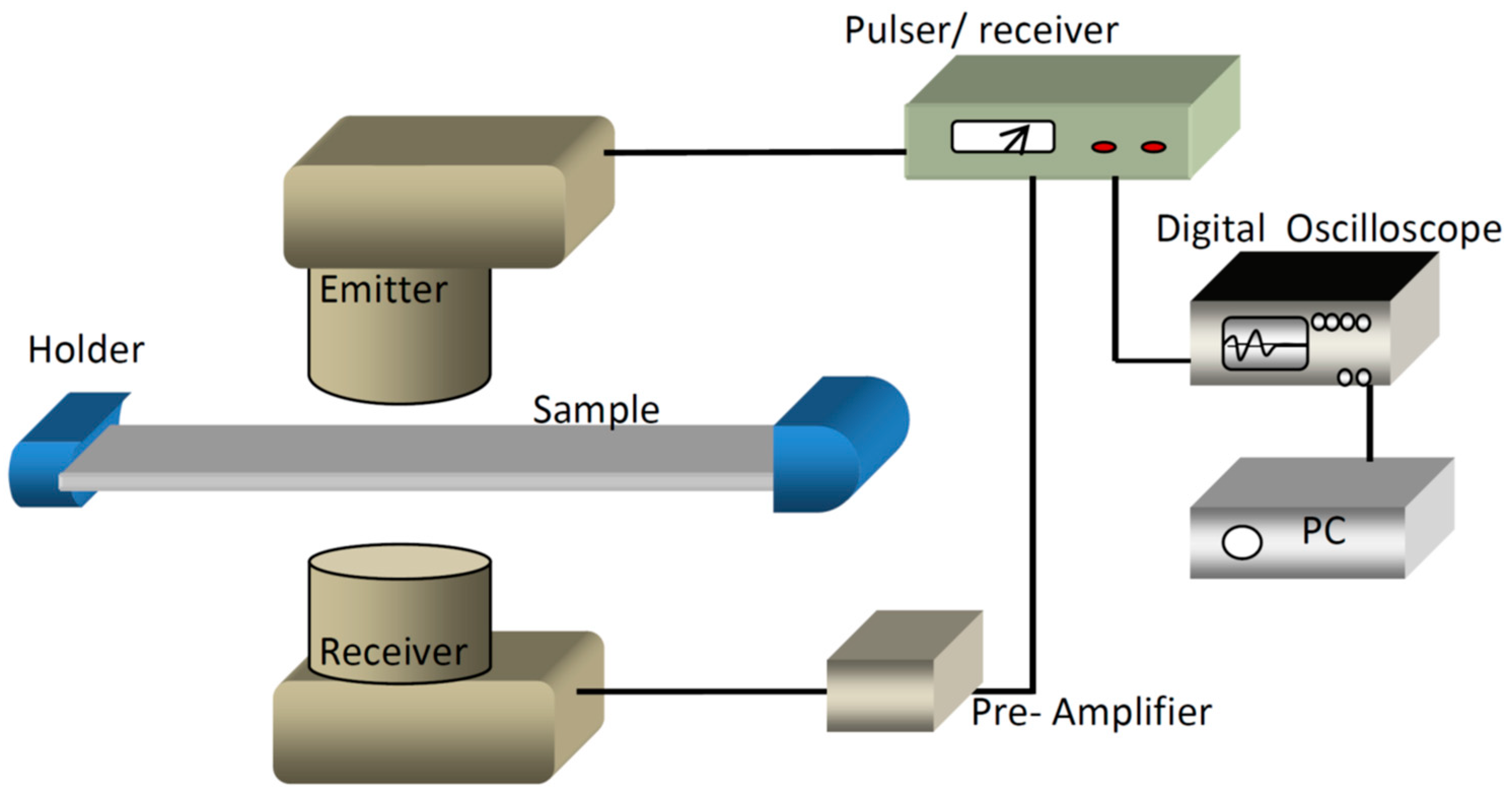
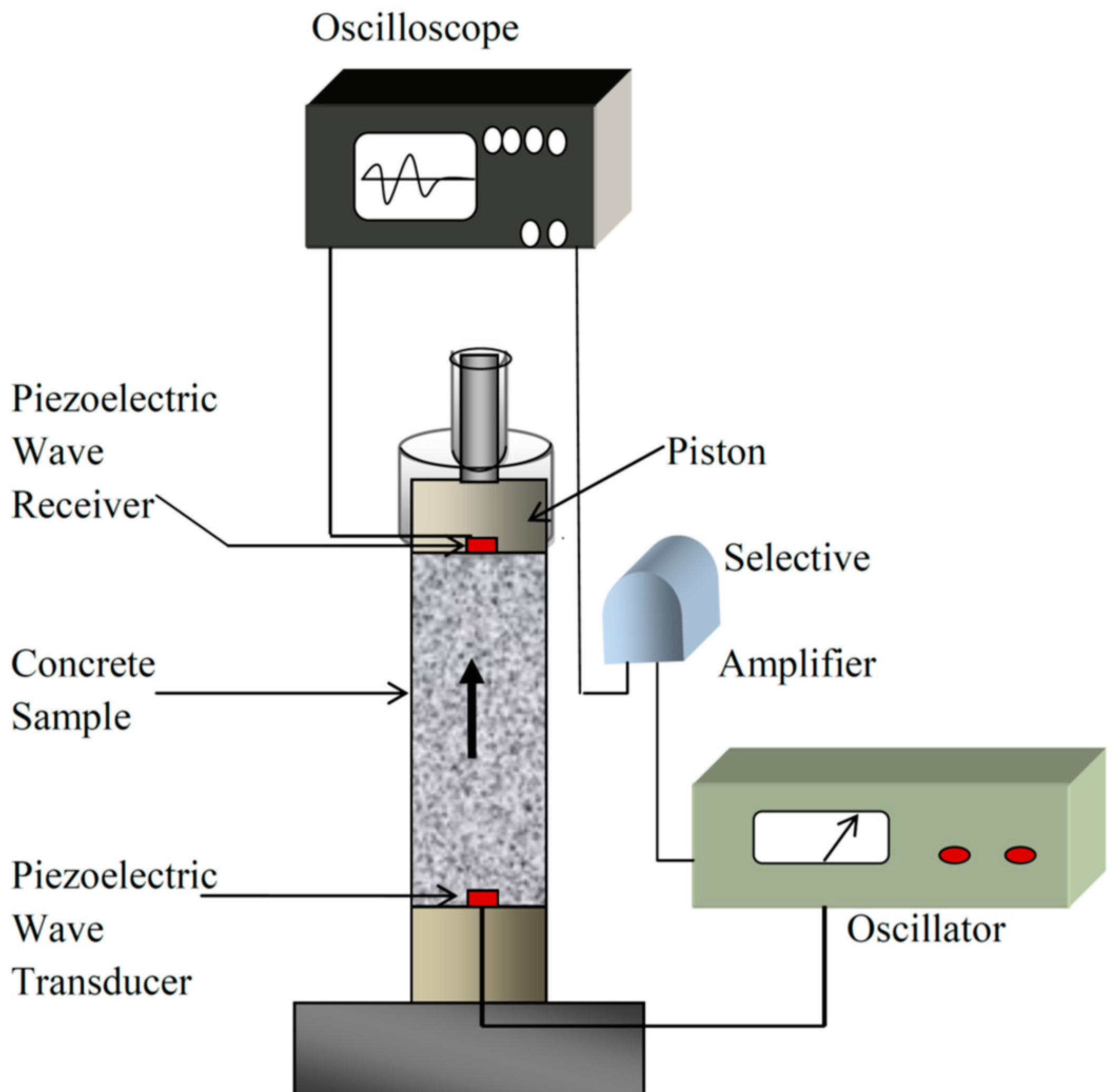
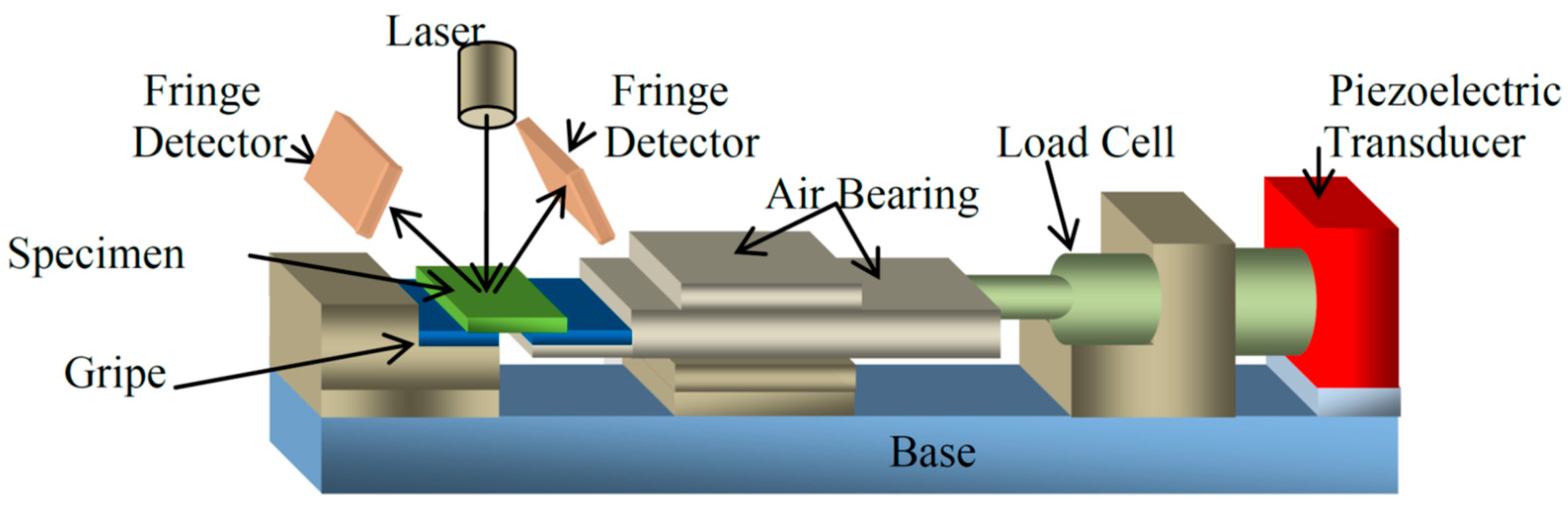
Description of PE	Role of PE	Description of the Advantage of PE
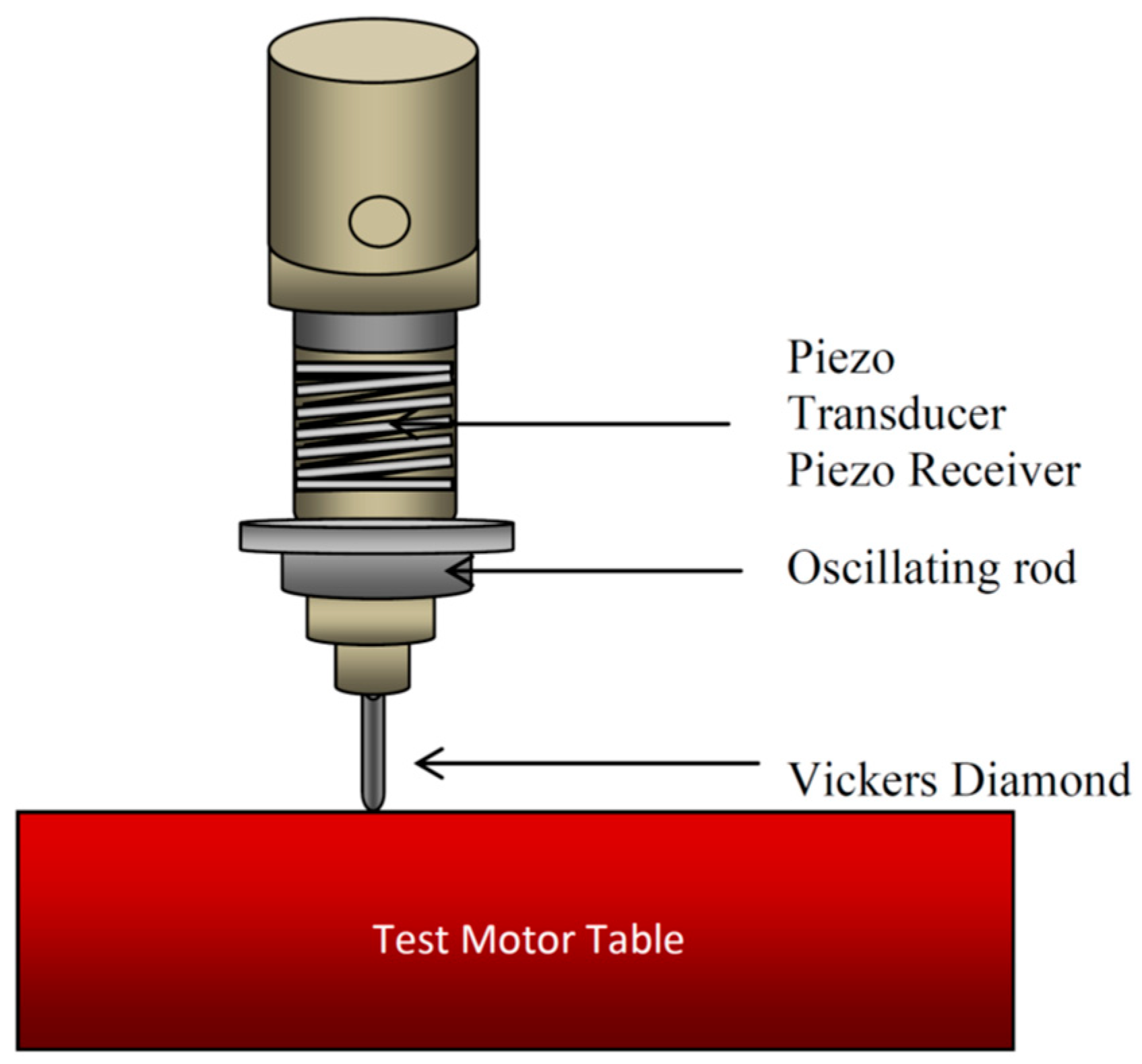
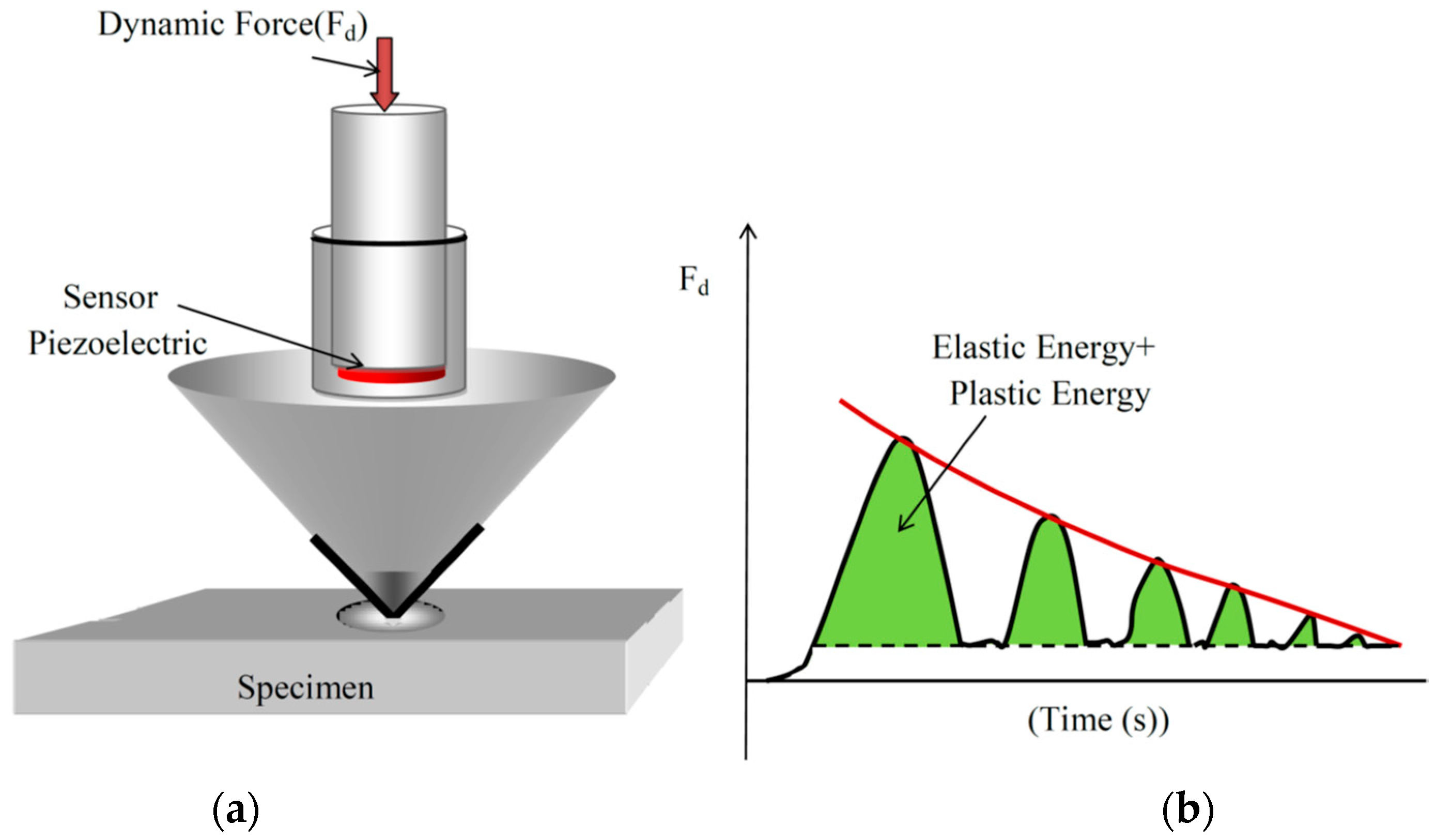
(100 kHz to 2000 kHz)	Piezo-scanner.	An indenter tip was employed to obtain a convenient nanometer-resolution imaging of test surface for measuring the slim membrane toughness of the tetrahedral amorphous carbon of diamond [17]. More details on the piezo-scanner is available in the literature [18,19].
5 MHz	Load cell in quasi-static dynamic fracture toughness tests.	PE can eliminate any inertia effects associated with the higher velocity (5000 mm/s) test rates. Results show the magnitudes of K1C within the range ($2.5\pm 0.1 \mathrm{MPa}\sqrt{m} to 1.7\pm 0.01 \mathrm{MPa}\sqrt{m}$) at an applied load rate of 1 m/s [20]. More details on using PE as a load cell has been previously reported [21,22,23].
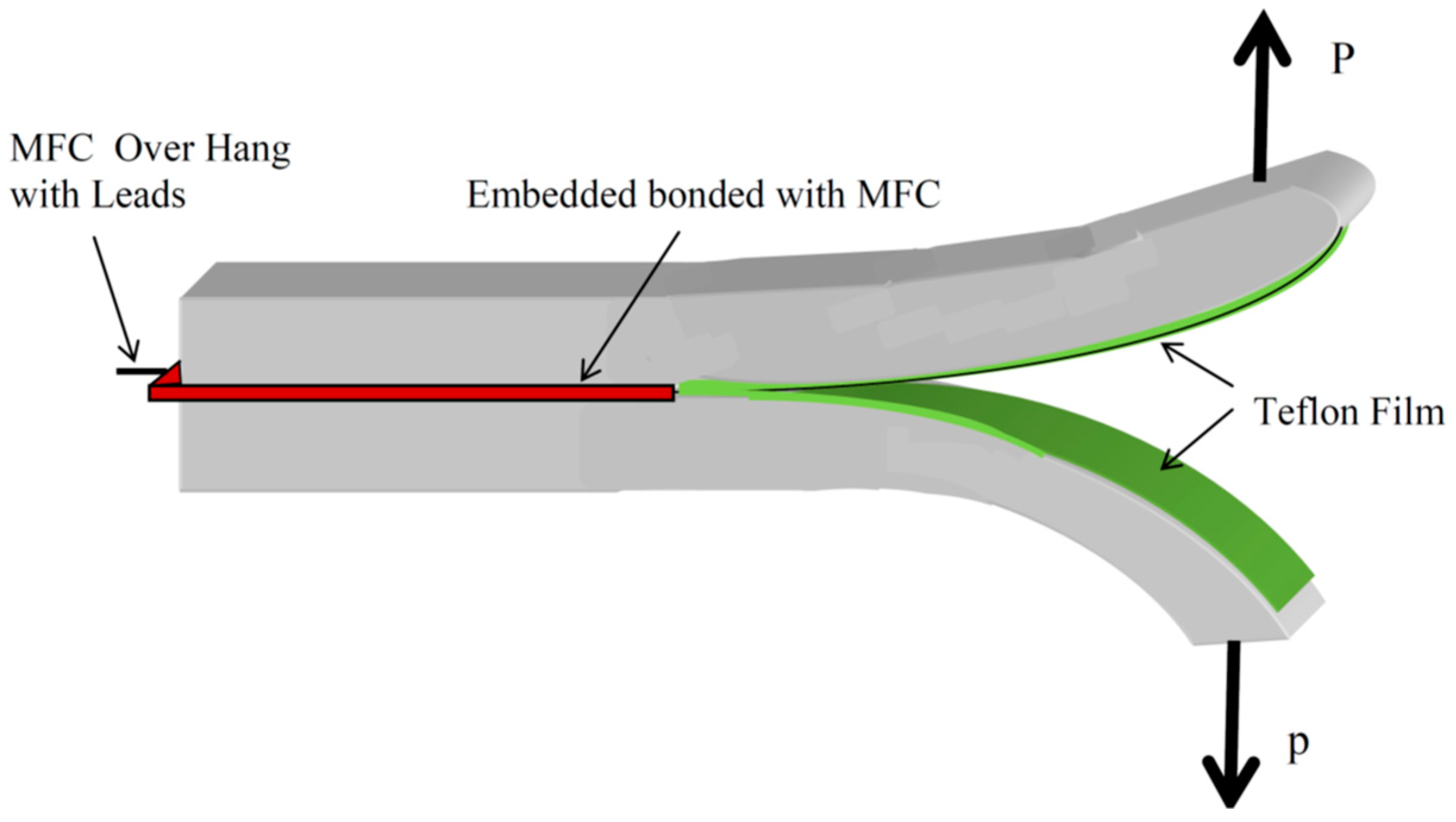
Lead zirconate titanate Pb[ZrxTi1-x]O3 (PZT) 0.79 in × 3.7 in (width× length) and thickness 0.0115 in to 0.0063 in	Embedded sensor for vibration control and health monitoring of aircraft structure.	PE was used as a sensor for load frequencies from 1 Hz to 10 Hz in epoxy and to study the effect of embedded materials on fracture toughness. Piezoelectric microfiber composite (MFC) (embedded piezoelectric sensors) was covered with a thin polymer film on its two sides. Then, the sandwich was inserted as an embedded material in glass/epoxy composite material (12-in2 unidirectional panels), as shown in Figure 2 to function as a sensor [24,25,26]. More details on embedded sensors have been reported [27,28].
	Emitter and receiver.	PE was used as a detector to determine the characteristics of several molybdenum alloys (10 mm × 10 mm × 55 mm) at various resonance frequencies [29].
	Load cell for tool cutting.	PE was used to measure cutting force in the x-direction and transverse force in the y-direction to calculate the fracture toughness of polymers with cutting widths of 3 mm to 6 mm, depths of 0.025 mm to 0.25 mm, and velocity of 10 mm/s [30].
	Monitor for the constant loading rate and equilibrium of the dynamic load on a pre-cracked specimen.	The new technology reported in references [31] proved the practicability of using the loading rate as a function of the dynamic fracture. Another article reported a similar finding [32].
Thick mode 10 MHz and 4 MHz shear mode	Sender and receiver for longitudinal and shear waves.	A thickness mode vibration PE was used for creating longitudinal waves and shear mode vibration for creating shear waves, these two types of PE were used in a crack-opening displacement method to determine the toughness of base glasses for dental restoration glass-ceramics [33].

highlights some of the roles of PEs in finding the fracture toughness property for some solid metals.

Many common methods have used attenuation in ultrasonic waves as an indicator of fracture toughness [34,35,36]. For example, in the investigation of the influence of nitrogen on the fracture toughness (K_1C) of stainless steel coatings, a 150 kHz PE was used as filter for signals (filter for interference noise during the test) for frequencies above 300 kHz and below 100 kHz [37]. In addition, the changing of the voltage values of the PE signal, within these bandwidth during the increasing of test load from 0 N to 200 N, were used as an indication of the critical magnitude of the load, which is the threshold load for crack formation (PC). Then, they used PC to calculate K_1C using Equation (1):

$$K_{1C}=0.13{\left(\frac{E_c}{H_c}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{P}_c. C_{circular}^{\raisebox{1ex}{$-3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$

(1)

where C_circular = the radial crack length in the coating, E_c= elastic modulus of the coating, and H_c= hardness of the coating.

2.3. Hardness

Hardness is defined as the resistance to plastic deformation, such as scratching, cutting, or abrasion. Several classic methods to determine the hardness of a material include the Rockwell hardness test, Brinell hardness, Vickers, Knoop hardness, and Shore. A number of researchers suggested different methods to use PE in finding the hardness of materials. PE was used as a 1 Hz actuator in a nano/micro-hardness tester to apply load on a specimen to check the hardness [38].

Similarly, PE was regarded as load actuator in the hardness measurements for JNl, JN2, SUS304, SUS 316L, Ti alloy, and copper at cryogenic temperatures less than 4.2 K, where the piezo-actuator is expected to maintain the given load constant when the applied load fluctuates [39]. Another application in this field is PE as a piezoscanner [40].

As a sensor of load, PE with a frequency of 5 MHz, was connected with an amplifier and displayed on a memory oscilloscope. PE was used to calculate the dynamic and static hardness of different materials [41]. In the same context, five piezo-elements in series were used as a force sensor, where the maximum displacement of dynamic part in that device was 15 µm [42,43].

The authors in [44,45,46,47,48,49] used the PE in the ultrasonic contact impedance (UCI) method to measure the frequency shift. However, MIC10 and MIC20 can be also used for standardization according to ASTM A 1038 and DIN 50159 to evaluate the hardness of the material, as indicated in Figure 3 [46]. When a 70 kHz PE excite s the metal rod, the end of this rod will penetrate the specimen as provided by Vickers Diamond. This penetration will cause a frequency shift and allow the indentation area to be electronically detected by measuring the shift of an ultrasonic frequency using a piezoelectric receiver. The frequency shift is proportional to the size of the Vickers test indentation. Then, hardness can be evaluated using Equation (2):

Δf = f (Eeff, A); HV = F/A

(2)

where Δf is the frequency shift, A is the area of indentation, Eeff is the effective Young’s modulus, HV is the Vickers hardness value, and F is the test load.

To characterize and identify a traffic-hardened layer in a rail surface and to identify a minimum detectable hardness gradient requirement in this rail, three different frequency angle-wedge PEs (ultrasonic transducers) were used to develop the handled prototype (Lunch Box PC) [50,51]. This box has the ability to produce Sezawa waves that have been used in inspections for rail specimens, as shown in Figure 4a,b. These PE pieces, with frequencies ranging from 1 MHz to 5 MHz, were included after a grinding cycle to the rail specimen (to use in pulse echo technique). Then, this process was repeated for several depths at 1.9 mm to 5.65 mm of grinding to check the amplitude of the Sezawa wave after each grinding cycle. Afterward, they compared these results (maximum amplitudes of the Sezawa wave) from the different depths of the grinding cycles with a standard rail hardness profile and used the amplitude of these waves as an indication of hardness.

The design of Gutt [52] is regarded as one of the modern apparatuses in the field of using an acoustic technique for testing the properties of materials, because they used PE as a device for sensing the elastic reaction force from a specimen after force removal. This PE was located after a press part, as shown in Figure 5a, and the output voltage from this PE suits the dynamic force F_d, as shown in Figure 5b. The shadowed area represents the elastic and plastic deformation energy. This energy is relative to the kinetic energy of impact calculated from a connected superior photo barrier coupled to an electronic counter and other facilities, and it is proportional to dynamic hardness. The references [53,54,55]provide more details about how to create equivalent voltage from mechanical load by using PE.

Recently, guide waves have been used in determining the hardness of metals. Guide waves suffer from changes in attenuation and dispersion with the changing of material microstructure due to several reasons, such as rolling, heat treatment, and so on. Thus, to test the hardness of six specimens of aluminum 2024 alloy plates (152. 4 mm × 50.8 mm × 4.0 6 mm) difference in heat treatments using Lamb waves, ref. [56] employed two pairs of PTs at the two frequencies of 1 and 3.5 MHz in pitch catch technique to achieve this aim.

The role of PE in this area is not limited to determining the mechanical properties of materials but also to studying the effect of external factors on these characteristics. For example, ref. [57] recently published a new article on the relationship between the levels of hardness and the performance of coated carbide tool for AISI 4340 steel. This study was performed using a three-component of the PE KISTLER Type 9257A as dynamometer to measure the average values of the force components of the cutting.

2.4. Impact Toughness

Impact is a high load that strikes one or more bodies during a specific short time, but the strength of the impact is the ability to resist or to withstand shock loading. Popular methods used to determine the strength of impact are those of Charpy and Izod. Typically, this work focuses on using PE in an impact test. Many authors used a PE as a sensor to obtain a constant output signal in impact toughness tests. This advantage of PE (as a sensor) was used to measure the impact toughness of glass/polyester face sheet/polyvinyl chloride (PVC) foam core sandwich structure [58], which is widely used in automotive, aerospace, and marine industries because it has high superior bending stiffness, acoustic damping, and low weight.

Authors in [59,60] developed a new instrument to determine the impact energy by employing a suitable frequency PE as a strain gage to obtain real-time information such as force-versus-time behavior for the material and the magnitude of peak force, which Charpy and Izod cannot provide.

Given the wide usage of PVC pipes in mechanical and civil engineering, authors in [61] employed this material as a specimen to illustrate the impact strength of 25% and 33% VE/FLYASH using the drop-weight test. This test contains a “Bruel and Kjaer” piezoelectric delta shear type (Type: 4371) to be real-looking as shown in Figure 6. The advantages of using piezoelectric accelerometers over other types of accelerometers are a broad frequency range, good linearity in dynamic applications and performance in a wider range of environmental conditions, and the ability of data to be integrated. The output signal appearing on the oscilloscope screen is analyzed by the MATLAB program to solve the equation of velocity C(t), is as shown in Equation (3). The data obtained from an oscilloscope represented the changing velocity with time (acceleration). The value of velocity is calculated through integration the equation of acceleration a(t) as shown in Equation (3a).

$$\mathrm{C}\left(\mathrm{t}\right)={\int }_{{\mathrm{t}}_0}^{{\mathrm{t}}_1}\mathrm{a}\left(\mathrm{t}\right)\mathrm{dt}\left(3-\mathrm{a}\right)$$

(3a)

$${\mathrm{P}}_{\mathrm{Energy}}=\mathrm{mgh},{\mathrm{P}}_{\mathrm{Energy}}={\mathrm{K}}_{\mathrm{energy}}=\frac{1}{2}{\mathrm{mC}}^2$$

(3b)

where P_Energy is potential energy and K_Energy is kinetic energy.

The use of PE in this test allowed access to important data, such as the distribution of power, peak force, duration, and the energy required to activate the crack and its propagation as shown in Equation (3b). More information on using piezoelectric accelerometers has been reported previously [62,63].

To indicate the effect of aluminum particles and milled fibers in the toughness impact of epoxy matrix as a composite material, authors in [64] needed a piezoelectric accelerometer with 1.008 PC/m s⁻² sensitivity (Bruel and Kjaer 4371, Denmark) to complete his tester device [pendulum machine H.20 (Tensometer Ltd., Croydon, UK)]. An acceleration/time curve that was produced from a piezoelectric accelerometer was used. A force/time curve can be plotted to evaluate the absorbed energy that refers to the strength of impact for this composite material.

2.5. Longitudinal Velocity of Sound

Longitudinal waves in materials refer to the particles of the material that are moving in the same or maybe opposite in direction with respect to the exciting vibration wave, such as a compression wave. The popular expression of longitudinal wave velocity v(C_L) is $C_L = \lambda \times f$ where λ is the wavelength and f is the frequency or $C_L=$ w⁄k where w is the angular frequency and k is the propagation constant.

Considering that PE is often used as a generator of sonic and ultrasonic waves, many researchers have attempted to study the longitudinal velocity of sound in PE itself. Authors in [65] studied the effect of many different variables, such as thickness (t), volume percentage, density (ρ), and the modulus of elasticity (E), on the longitudinal velocity of sound (C_L) for ceramic materials with PE (1 MHz to 10 MHz). Lead zirconate titanate Pb[ZrxTi1-x]O₃ (PZT ) using the formula $C_L = {(E_t/\rho )}^{0.5}$ where E_t, as an elastic modulus, was regarded as a function of volume fraction of PZT. This function was calculated by [66,67], who found the relationship between the volume percentage of PZT and the longitudinal velocity of sound as an inverse relationship.

Then, authors in [68] studied the effect of lateral dimensions of un-poled and poled PZT-5H ceramics (15 MHz) and the longitudinal velocity of sound was generated from it. The same result was obtained (an inverse relationship between the dimensions of PE and the longitudinal velocity generated from it) in which the transducer’s diameter (un-poled and poled PZT-5H) increased to 14%, and the longitudinal velocity of sound will increase to 1.4% and 0.9% respectively. In the same context, authors in [69] used picoseconds in ultrasonic devices to calculate the longitudinal velocity in PE (111) epilayers of In_xGa_(1-x)As.

As a sensor, authors in [70] utilized a 300 kHz PE to calculate the longitudinal velocity for the following samples: polycrystalline metals (Al and Cu), single-crystalline alkali-halides (LiF and KCl), poly-crystalline Al₂O₃, fused silica (SiO₂), and an invar alloy. The samples were square-shaped plates with a common dimension of approximately 40 mm × 40 mm × 10 mm except for Cu, which was 35 mm × 35 mm × 10 mm.

To evaluate the velocity of sound in the single crystal YBazCu307 under the effect of temperature change, the authors in [71] needed a PE as a generator of short 10 ns to 20 ns pulses of ultrasonic waves (500 MHz bandwidth).

The relationship between the relative velocity ∆v/v of sound in a single crystal YBazCu307 to temperature is non-linear. Also, an inverse relationship was found. authors in [72] found a positive relationship between longitudinal and transverse velocity with temperature. The experiment was performed using two PEs, one as an emitter transducer and another as a receiver, for sending and receiving ultrasonic pulse waves (405 kHz), on silica aerogels 10-cm wide where, aerogels undoubtedly come under a class of fascinating materials having high porosity, low density, low thermal conductivity, large surface area, transparency in the visible range, and many more peculiar properties for scientific and industrial uses [68]. They succeeded obtaining a longitudinal wave by cutting piezoelectric crystal in the x-direction, and then they obtained a transverse wave by cutting piezoelectric crystals in the y-direction. In addition, they illustrated a behavior of longitudinal and transfer waves with a different molar ratio of silica aerogels, where, silica aerogels was a function of molar ratios of tetramethoxysilane (TMOS) precursor, ammonia (NH₄OH) catalyst, methanol (MeOH) solvent, and water, as shown in Figure 7.

Authors in [73,74] studied an air-coupling technique to explain the effect of velocities of transferred longitudinal waves on different samples of paper as shown in Figure 8. These paper samples involved differences in density from 80 g/m³ to 300 g/m³ and difference in magnitudes of angles for the paper (angle of inclination of the paper). Two pairs of specially designed air-coupled piezoelectric transducers were used as emitters and receivers. The center frequency was 0.9 MHz for one pair and 1.7 MHz for the other. The active elements were 1 to 3 piezocomposite disks made by the dice and filling technique (PZ-26, Ferroperm and Araldite-D), which were 2-mm thick for the 0.9 MHz transducers and 1 mm thick for the 1.7 MHz transducers.

Using the same technique (air coupled), authors in [75] PE 750 kHz to show a good match between the theoretical calculations and the experimental results of the longitudinal behavior of the waves for the following materials(1) copper sheets with 0.35 mm width and 0.45 mm thickness (2) 0.1 mm width and 0.5 mm thickness, and finally (3) CW508L copper with width 0.0762 mm and thickness of 0.381 mm).

PE with a resonance frequency of 7 MHz was employed by [76] as a transducer to investigate and measure the longitudinal sound waves in liquid and selenium. The authors in [77] succeeded to replace the disturbance force effects on a steel square plate (19 mm × 19 mm × 305 mm) by a PE with a center frequency of 2.2 MHz and attached it by using cyanoacrylate adhesive to create longitudinal sound waves. The transducer was driven by a five-cycle windowed sinusoid voltage waveform [78] where the used pulses generator in [76] was arbitrary. Waveform generatorscan produce waves of any shape such as the function in Equation (4). They noted the first arrival of the wave at 52.6 μs, and this corresponded to the group velocity of sound in the steel (5.8 km/s). Equation (4) represents two sine waves multiplied together with the deference phase angle for producing modulated waves (Ton berst wave).

$$C\left(t\right) = \left(\begin{array}{c}{c}_o\sin \left(2\pi ft\right).{\left(\sin \frac{ft}{20\pi }\right)}^{2}t <\frac{5}{f}\\ 0 t \ge \frac{5}{f}\end{array}\right).$$

(4)

The authors in [79] used longitudinal velocity, which was measured by utilizing two pieces of PE (one as an emitter and the other as a sensor) for a set of various Fe₄Sb₁₂ and Co₄Sb₁₂-based skutterudites filled by mischmetal, didymium, or alkaline earths (Ca, Sr, and Ba) in order to calculate some of the mechanical properties which are: modulus of elasticity, transfer velocity, shear modulus of elasticity, bulk modulus, and Poisson’s ratio for the above materials, where time-of-flight sound pulse measurements were performed on cylinders (height = 10 mm, diameter = 10 mm) with a frequency of 10 MHz were also measured.

Recently, many researchers have considered piezoelectric shunt damping techniques as a renewable technology in this field, where the periodic arrays of shunted piezoelectric patches are utilized to control the wave host plate. The tunable characteristics that belong to shunted piezo-patches allow the band gaps to be tuned over desired frequency ranges. The authors in [80] used this technology to explain the mechanism of resonant piezoelectric shunt scan to be tuned over desired frequency ranges. They achieved this aim by bonding squire-shunted piezo-patches with frequencies ranging from (1 kHz to 1.6 kHz), dimensions 40 mm × 40 mm × 0.2 mm) to a plat made of epoxy (Young’s modulus of 4.35 × 10⁹ N/m², Poisson’s ratio of 0.37 and density of 1.18 × 10³ kg/m³) with dimensions of 80 mm × 80 mm × 5 mm. This study describes how resonant piezoelectric shunts can be used to affect the equivalent mechanical characteristics of an elastic waveguide and suggests their application for enhancing the tunable band gaps.

2.6. Modulus of Elasticity

In mechanical applications, the modulus of elasticity (E) of material is a measure of its stiffness. E is considered as an important material property. The famous rule for this factor is $E=\sigma /ϵ$, where σ is stress and ϵis strain. The tensile test is regarded as a classic method. To measure E for non-traditional specimens, non-traditional methods are needed.

PE was used as an electric force measurement system (sensor, nominal range 0 N to 50 N). This PE was put just below the central bending point of the specimens (length = 70 mm, width = 4.021 mm to 4.2 mm, and thickness = 0.1 mm to 0.25 mm) to measure E for magnetron-sputtered thin films of different materials (C, W, W(C), Cr, TIN) with different thicknesses [81].

Two pairs of PEs were used with each pair three pieces of PE, type (air-transducers KG100-0.25, KG100-0.5, and KG100-1 with center frequencies of 250 kHz, 500 kHz, and 1 MHz)in the system shown Figure 8 [82]. This approach was used to detect E based on the relationship $c = {(E/\rho )}^{0.5}$ for 13 types of test paper made of different materials with thicknesses ranging from 60 µm to 700 µm. The term $f{\left(\sin \theta \right)}^2$ was considered as a function of velocity (c). Then, they detected the term ($f{\left(\sin \theta \right)}^2)$ from the method, as explained in the air-coupling technique discussed in Section 2.5. This method was explained in detail previously [83].

The most popular method in acoustic tests for the material properties test is the method of calculation of the time of flight of the wave (TOF). Several studies have been dependent on the TOF method, which depends on conversion formulas of elastic module for homogeneous materials as shown in Equation (5):

$$E_{TOF} = 2\rho C_s^2\left(1 + v\right)$$

(5)

where E_TOF is in MPa, ρ is in kg/m³, C_s is the acoustic shear wave velocity in m/s, ν is the Poisson’s ratio $\left(v = \frac{C_L^2 - 2C_s^2}{2\left(C_L^2 - C_s^2\right)}\right)$ and C_L is the longitudinal wave velocity. Many published studies used acoustic tests and regarded the two factors E_TOF and E is the same factor (no difference between them), and mentioned them as the modulus of elasticity (E); for example, Osamura et al. [84] estimated E_TOF for. Bismuth strontium calcium copper oxide (BSCCO) tapes and regarded E_TOF is the same with E, Vendra and Rabiei [85] evaluated the E_TOF for composite metal foams by experimental and numerical techniques without mention of this difference, in the same contract Diaz et al. [86] estimated E_TOF and regarded it E for plastics and wood plastic composites using a Taber stiffness tester.Genga et al. [87] studied the effect of Mo₂C additions on the properties of spark plasma sintering (SPS) manufactured WC–TiC–Ni cemented carbides without mention to this difference too.

To study the relationship of E with hydrostatic pressure (HP) and moisture content (µ), the same relationship (Equation (5)) was used to calculate E for a bulk of cereal grains [88]. The initial state of the cylindrical sample was a length of 150 mm and a diameter of 70 mm in (for five levels of moisture 10%, 12.5%, 15%, 17.5%, and 20%). To achieve this relationship, a magnitude of ν was taken from a Polish standard. Then, a PE was used as an emitter and receiver of acoustic shear waves (C_s) (1 KHz) as shown in Figure 9. The values of C_s were measured for each increasing of magnitude of HP. These values of ν and C_s were employed to complete the Equation (5) requirements in order to calculate the value of E. The positive relationship between E and Hp was found, but the relationship between E and µ was negative.

To generate a longitudinal wave in a tree trunk has dimensions (1.2 m × 50 mm × 50 mm), the authors in [89] made a hole in the tree trunk to insert PE in order to study the relationship between E with the longitudinal wave. This study proved a positive relationship between these two parameters.

Authors in [90] calculated the E for different types of granite according to another formula: $E\left(GPa\right)=4 \times T \times L^2 \times F_l^2 \times \rho$ where T is a factor depending on the relative specimen dimensions, L is specimen length, F_l is a resonance frequency in Hz, and ρ is the density of granite. To achieve the conditions of this equation, an Erudite MK3 test system (CNS Farnell) was used. This device worked in the range 1 kHz to 100 kHz to receive an optimization for the acoustic technique depending on the measure of the essential mode for the longitudinal wave resonance frequency. This measure was based on the use of PE as a receiver of the vibrational longitudinal wave that was changed to a voltage wave and then emitted to Erudite MK3.

As indicated in Section 2.3, authors in [52] declared that “the tangent of the curve in the plateau of the elastic rebound after impact is proportional to the size of dynamic elastic modulus of indentation”, as shown in Figure 5b. A general technique as was described previously in [52] and the traditional technique in [91] have been recently regarded as techniques in finding E and ν.

Arshed et al. [92,93] noted that there is a big difference between the standard values of E, according to ASTM from one side, and the values of E calculated from TOF tests, for a group of metals which are the refractory metals, from another side. To address this issue, Refs. [92,93] provided a new relationship between pressure transmission coefficient (PTC) and E × ρ of the test specimen (TS) as shown in Equations (6)–(8) to calculate E for refractory and non-refractory metals:

$$Z_{TS}=C_{L for TS}\times {\rho }_{ for TS}$$

(6)

$$PTC = \frac{\left(39.9Z_{TS}\right)}{\left(1.5 + Z_{TS}\right)\left(Z_{TS} + 9.97612\right)}$$

(7)

The following equations were derived:

$$E_{}= \frac{-5.66211 + 73.0387PTC- 275.856PT{C}^2 + 425.253PT{C}^3- 234.885PT{C}^4}{\rho } \times {10}^7$$

(8a)

The Equation (8a) can be used for the solid materials that have an acoustic impedance (Z_TS) equals or less than 51 × 10⁶ kg/m² s (Z_TS ≥ 51 × 10⁶ kg/m² s). The Equation (8b) is used for the materialshave values ofZ_TSwithin range of 51 × 10⁶ ≤ Z_TS ≤ 29 × 10⁶ kg/m² s:

$$E = \frac{-6.86293+ 58.1587PTC-102.833PT{C}^2+52.8154PT{C}^3}{\rho }\times {10}^6$$

(8b)

While for values of Z_TS are around Z_TS ≤ 29 × 10⁶ kg/m² the equation is

$$E_{} = \frac{2.55909-8.2542PTC+9.8896PT{C}^2-5.196PT{C}^3+1.0075PT{C}^4}{\rho } \times {10}^8$$

(8c)

According [92,93], the set of Equation (8) depends on the value of PTC only to find the value of E where, ρ is already known. PTC is based on the calculation of Z_TS as shown in Equation (7) and this Z_TS is equals to ρ × C_L as shown in Equation (6). Therefore, the calculation of E according to the method proposed by [93] depends on measuring C_L only, while the TOF method needs measuring two types of waves (C_L and C_S) to calculation E as shown in Equation (5), where $v = \frac{C_L^2 - 2C_s^2}{2\left(C_L^2 - C_s^2\right)}$. Figure 10 illustrates the difference between the proposed method by Arshed et al. and the TOF method represented by one of the OLYMPUS company products, 38DL PLUS, that uses this technique.

Recently, the authors in [94] used the same setup as [92,93], which includes two piezoelectric transducers, one as emitter and the other as receiver, to calculate E but this time by using a Hilbert Huang transformer

2.7. Poisson’s Ratio

In most studies, ν is associated to E. Poisson’s ratio is the ratio between a strain perpendicular to the load axis and a strain that occurs with the load axis. Authors in [95] utilized a PE with 0.5 MHz, and [96] also utilized it as an emitter and a sensor in the TOF method by measuring the longitudinal and transverse velocities of the wave to calculate ν and several properties of materials for cement paste, mortar, and rock.

Authors in [97,98] succeeded in measuring ν, E, and tensile strength for polysilicon by using PE as a motion generator to the load cell (4.5 N) and the linear air bearing. The advantage of using the air bearing is the absence of friction, which is shown in Figure 11. The motion of PE was controlled by a laboratory computer. This motion system was used to generate strain in a polysilicon specimen. The specimen strain was measured using an interferometric strain/displacement gage.

To determine ν and E for a thin film of fused silica and TiN/NbN, the authors in [99] developed the contact area technique using an acoustic microscope to measure surface elastic properties quantitatively. They needed a piezoelectric thin-film transducer in a pulse-echo acoustic microscope, which was used in this work, to generate an ultrasonic wave that is focused by a hemispherical sapphire lens. The focused wave passes through a coupling fluid, usually water, and interacts with the sample surface, producing bulk shear and longitudinal waves as well as a surface wave. These waves were used in the contact area technique to calculate ν and E.

The flexibility to use a thin film of PE associated with the ability of generating deference types of waves, cannot be found in other smart materials except PE. The authors in [100] preferred to utilize piezo-spectroscopy to measure the stress and strain to calculate ν in aluminum-alumina.

The authors in [101] measured the ν and E for a thin golden film using a micro tensile testing unit. This unit consisted of a piezoelectric actuator, as a load cell, a microscope, and two CCD cameras. After the results were obtained from the tensile test unit, the results were compared with those from the visual image tracing (VIT). The results were in good agreement.

To evaluate the ν and shear E for a concrete specimen, the authors in [102] used three pieces of PE (piezo-blender element), one as sender (500 kHz) and two pieces as receivers. The first receiver was in front of the actuator to detect the C_L and the other was beside it to detect the C_S as shown in Figure 12a,b. Then, the velocities of these two types of waves were calculated using B-scan images. Poisson’s ratio was calculated from the equation below:

$$v = \frac{C_L^2 - 2C_s^2}{2\left(C_L^2 - C_s^2\right)}.$$

2.8. Shear Modulus of Elasticity

For materials subjected to shear force, an important parameter that must be taken into account is the shear modulus of elasticity, which is defined as the ratio between shear stress to shear strain. Instead of using direct shear forces to excite the three samples of granular materials (Fontainebleau sand, first and second class of natural alluvial deposits of the Seine River) to measure the shear modulus of elasticity (G_w), refs. [103,104] used a PE (bender elements) to generate and receive a shear wave. Moreover, they calculated the propagation time t_w (the time that the wave took to pass through the sand specimens) by recording the input and output electric signal on an oscilloscope. The equations below were used to calculate the shear modulus where L_w is the length between the tips of the bender elements and m is the unit mass of the materials.

$$C_S = L_w/t_w\to G_w = m \times C_S^2.$$

Then, the authors in [105] used PE as an emitter (1 and 10 MHz) and receiver of a shear wave but it was placed at opposite corners in the cubic and cylindrical specimens with the length of an isotropic cube side or cylinder height L₁ (10.1 mm brass cube of mass 8.175 g). This procedure was performed for many reasons, such as to provide a weak elastic couple (torsional couple) on the piezoelectric pieces and for minimum parasitic damping. Resonant ultrasound spectroscopy was also employed, which involved scanning the resonance structure (γ) for a compact specimen and then by using Equation (9) the shear modulus was calculated:

$$G_w = \frac{\mathsf{\rho }{\left({\mathrm{L}}_1\mathsf{\pi }.\mathsf{\gamma }\right)}^2}{2}$$

(9)

The authors in [106] utilized PE(LiNbO₃) to generate a wave from 300 kHz to 1 MHz with the Curie temperature at 1200 °Cto calculate G_w for metallic glass under this condition equation.

An interesting study was conducted by [107,108] to study the difference between the static and dynamic factors. Two couples of piezoelectric transducers were used as an actuator, which required a trigger with dimensions of 10 mm × 10 mm × 20 mm and an actual frequency of 69 kHz to generate a compressive wave (longitudinal wave (C_L)) and shear waves C_S. Three couples of piezoelectric transducers were used as a cylindrical accelerometer of 60 kHz with a diameter of 3.6 mm and a thickness of 3 mm to receive these waves. Two small piezoelectric-type bender elements was fixed first at the top of the cylindrical specimen (Toyoura sand, 5 cm in diameter and 10 cm in thickness), as shown in Figure 13, and the other at the bottom. The equation $E_D=\rho \times C_S^2$ was considered as the equation of dynamic modulus of elasticity and $G_D=\rho \times C_L^2$ as the equation of dynamic shear modulus of elasticity. For shear modulus, the results were in good agreement with the results from those that used C_L and C_S waves. However, for the dynamic modulus of elasticity, the results revealed a large difference between the dynamic and static values and the difference increased with increasing specimen density. Using the similar technique, the authors in [109] utilized three plate transducers of 3.9, 7.8, and 15.9 kHz to calculate G_D from the equation $G_D=\rho \times C_s^2$ for a soil.

The authors in [2] reported using torsional resonant frequencies as a recent technique in this field to measure shear modulus for isotropic bars.

$$f_r = \frac{C_s}{2l} = \frac{\sqrt{(G_w/\rho )}}{2l}$$

where f_r is the fundamental frequency of torsional resonance. PE has been used as an actuator (electro-mechanic) driver to excite both flexural and torsional vibrations in isotropic bars [110,111,112].

2.9. Tensile Strength

The tensile strength of a material is its ability to bear tensile load before failure. As a mathematical concept, it is the ratio between the greatest tensile forces allowed (before destruction) to the cross section area of a specimen. Most of the users of PE in this type of test have used it as a sensor. Among the first who used PE as a pressure sensor in a tensile test was [113,114] for a specimen with dimensions 1.5 cm × 0.5 cm.

Authors in [115] employed eight PEs (Physical Acoustics model S9225) with frequencies ranging from 0.1 MHz to 2 MHz to calculate the tensile strength of a rock of quasi-brittle material with size (span × height) of approximately 800 mm × 300 mm and 400 mm × 150 mm for the granite and 900 mm × 300 mm for the sandstone and 200 mm × 75 mm for the granite and sandstone.

A 150 kHz acoustic emission was also used by [116] as a detector to determine the strength of glass-fibre bundles or as a sensor for energy produced from a fibre fracture during the tension process, as shown in Figure 14.

PE was used in a tensile setting, and the authors in [117] measured the tensile strength of a piezoelectric specimen made of PZT (150) kHz fibre-epoxy with dimensions of 25 mm × 50 mm composites and explained the strong effect of matrix material on the tensile strength of PE.

The authors in [118] placed two PEs as an emitter and receiver with an operating frequency range of 200 kHz to 750 kHz. The relationship between the tensile stress and acoustic wave velocity (acoustoelectric calibration test) was measured in a case of loading and unloading for seven-wire steel strands (T15.7), which had the following dimensions: core wire diameter of 5.4 mm, helical wire diameter of 5.22 mm, and strand diameter of 5.7 mm. The results of this research revealed an induced positive relationship between an increase in transit wave velocity (through this type of wire) and an increase in the stress percentage in it.

The authors in [119] used a piezoelectric sensor with a frequency range of 1 kHz to 1.5 MHz to evaluate the tensile strength of epoxy-impregnated Kevlar^® 49 composites (25 mm × 1.4 mm × 1.1 mm). PE was used as a load washer (load sensor with 33 kHz) to measure the tensile strength of sisal fibre cement composites (152.4 mm × 25.4 × 12 mm) [120].

The progress in the areas of manufacturing enabled researchers to use piezoelectric actuators of high speed and frequency. The authors in [121,122] designed a high strain rate tensile test machine for DP780, DP980, and TRIP780 steels using a PE (Kistler 9071A) as a high speed load cell (20 m/s).

3. Statistical Study and Discussion

There are several points worthy of discussion raised in this research: One is the rapid increase in utilizing PE for determining the proprieties of solid materials, as shown in Figure 15. Another is the pulse echo technique that has acquired the largest share in using this type of testing, as well as the attention of researchers in the use of PZT as a material of PT.

The frequency ranges of dual-use PEs (emitter and receiver) including specimen dimensions are listed in

Table 2. Frequencies used for determining properties of solid materials associated with the dimensions of the test samples.

Material Properties	Emitter and Receiver Frequency Range	Rough Dimension Sample Size in mm, L = Length, W = Width, D = Depth
Creep	2.25 MHz to 15 MHz	150, 22–30, -
Fracture toughness	4 MHz to 10 MHz	10, 10, -
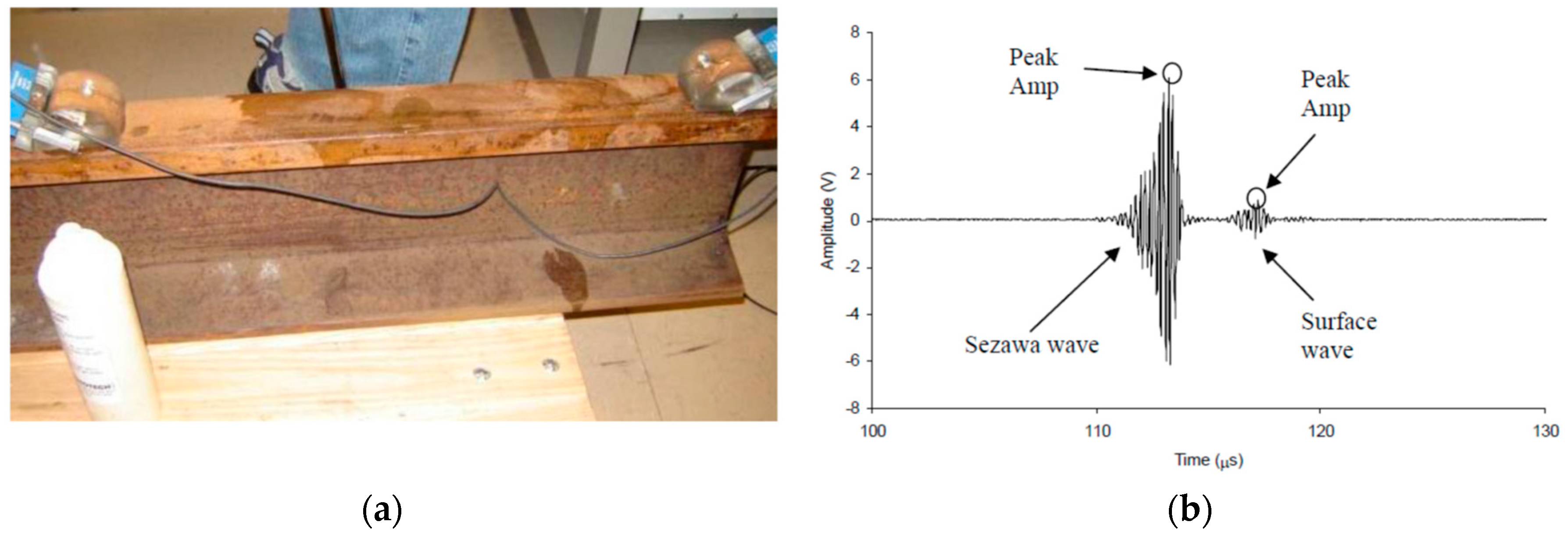
Hardness	Sezawa wave (1 MHz to 5 MHz)	-, -, 1.9–5.65
Longitudinal velocity	Guide wave (1 MHz to 3.5 MHz)	152, 10~20, 30
	405 kHz to 15 MHz	19–100, 10, 305
Modulus of elasticity	Air Coupled 750 KHz to 1.7 MHz	Paper-, -, 1–2; metal -, -, 0.1~0.5
	1 kHz to 1 MHz	60–150, 13~70, 5
Poisson’s ratio	Air coupled 250 kHz to 1 MHz	paper 60–700, -, -
	500 kHz
Shear modulus	60 kHz to 10 MHz	Diameter = 50, 100
Tensile strength	1 kHz to 2 MHz	Rock 200–800 span = 75–300; Metal 25, 1.4, 1.1

.

Another classification for PE according to the type of application and range of frequency is shown in

Table 3. Types of applications for PE according to frequency range.

Frequency (fr) Range in MHz	Type of Application	Rough Description of the Samples
Less than 0.5	Piezo-spectroscope, shaker load cell, filter for interface noise, emitter only, pickup sensor only, shock wave generator, active and passive velocity transducer, polyvinylidene fluoride (PVDF), Piezo-scanner, load cell, monitor to the constant load, dynamometer, strain gauge, accelerometers	Most dimensions for length, width and depth are less than 100 mm. Weight loads ranged between 4 N to 200 Grain size (0.3 µm to 1.5 µm)
0.5 < fr < 2	PVDF, Piezo-electroscope, and pickup sensor
2 < fr < 5	Shaker load cell, pickup sensor only, monitor for constant load and PVDF.
5 < fr < 15	High-speed actuator, PVDF.

.

Another category based on material type is shown in

Table 4. Different types of material with suitable frequency ranges for PE.

Material Type	Range of Frequency of PE	Dimension of Samples (mm)
Plexiglas, glass, metallic glass	300 kHz to 8 MHz
Polycrystaline metals Aluminium, copper, Al2O3	10 Hz to 2000 kHz (bulk wave), 1 MHz to 3.5 MHz (surface wave)	200 × 25 × 2, 152 × 50 × 4
Ice	1 Hz to 1000 Hz	394 × 76
Polymer	1 Hz to 20 Hz	8 to 20 (circle diameter)
IN738IC nickel base	2.25~15 MHz	150 × (22.5–30)
Stainless steel 316L	100 Hz to 15 MHz
Tetrahedral amorphous carbon diamond	100 kHz to 2000 kHz
Rail specimen	1 MHz to 5 MHz	1.9–5.65
Ceramic	1 MHz to 10 MHz
Silica aerogels	405 kHz
Paper of writing	0.9 MHz to 1.7 MHz	80–300 g/m3
Fe4Sb12, Co4Sb12, didymium akaline	10 MHz	10 (diameter) and 10 (height)
Seismogenic rock, concert, bulk of cereal grains	75 kHz to 1 MHz	60 × 13 × 5
Epoxy-impregnated Kevlar	1 kHz to 1.5 kHz	25 × 1.4 × 1.1

.

4. Conclusions

Many corporations and factories need PE in finding the mechanical properties of solid materials especially when the purchase orders of their needed materials have non-uniform shapes or long specimens such as long shafts or wide and thick plates where long or wide materials cannot be tested within the tensile test devices. In addition, the need it to lower the costs of these types of test which are mostly non-destructive. A number of impressions can be gained from this review. A quick in-depth analysis on all the research that has been reviewed in the art of using piezoelectric elements in finding the mechanical properties of solid materials, which amounted to 121 studies, reveals that the PE frequencies in this kind of tests did not exceed 15 MHz and most of the research used PE frequencies less than 500 kHz. In addition, most of the dimensions of the samples that were used did not exceed 100 mm. In addition, in this review three tables were classified based on the range of PE frequencies for each test, type of test such as impact tests, toughness tests, etc. and classification of tests according to material properties.

On the other hand, many technical advantages in using PEs can be concluded, as follows:

• Most of the ultrasonic creep tests have preferred of using PVDF because it can sense: (a) the low and high vibrations; (b) the slight changes in stress for more than 10 years and 100 million pressure cycles; (c) and can be used in a wide temperature range (−40 °C to +160 °C).
• PE can eliminate any inertia effects associated with the higher velocity; therefore, many applications focus on using the PEs as a load cell, instead of any type of actuators, in quasi-static dynamic fracture toughness tests.
• PE could be used as a strain gage to obtain real-time information such as force-versus-time behavior for the material and the magnitude of peak force, which Charpy and Izod cannot provide us in impact tests.
• The advantages of using piezoelectric accelerometers over other types of accelerometers in impact tests are the broad frequency range, good linearity in dynamic applications and performance in a wider range of environmental conditions, and the ability of data to be integrated.
• There is an inverse relationship between the dimensions of PE and the longitudinal velocity generated from it.
• The resonant piezoelectric shunts can be used to affect the equivalent mechanical characteristics of an elastic waveguide and suggests their application for enhancing the tunable band gaps.
• Tests of the shear modulus of elasticity, putting the PEs at the opposite corners for specimens that have cube shapes or at opposite edges for the short cylinders, show (a) weakness in elastically coupling for the piezoelectric transducers (b) reducing the perturbation of the vibration (c) minimal shift in resonant frequency, and finally (d) minimum parasitic damping. The main challenge of the use of PE in finding mechanical properties are that these tests do not include all mechanical properties such as yield stresses, ultimate tensile stress, and melting point etc. In addition, there are some of difference in results, for some of the special materials such as radiation materials, between the result coming from these tests (PE tests) from one side, and from traditional tests from the other side. Therefore, these tests need more study and research.

5. Recommendations

• Study using PE in finding other properties of materials such as yield stress, tensile strength and melting point.
• Study using PE in finding the materials properties in high temperature.