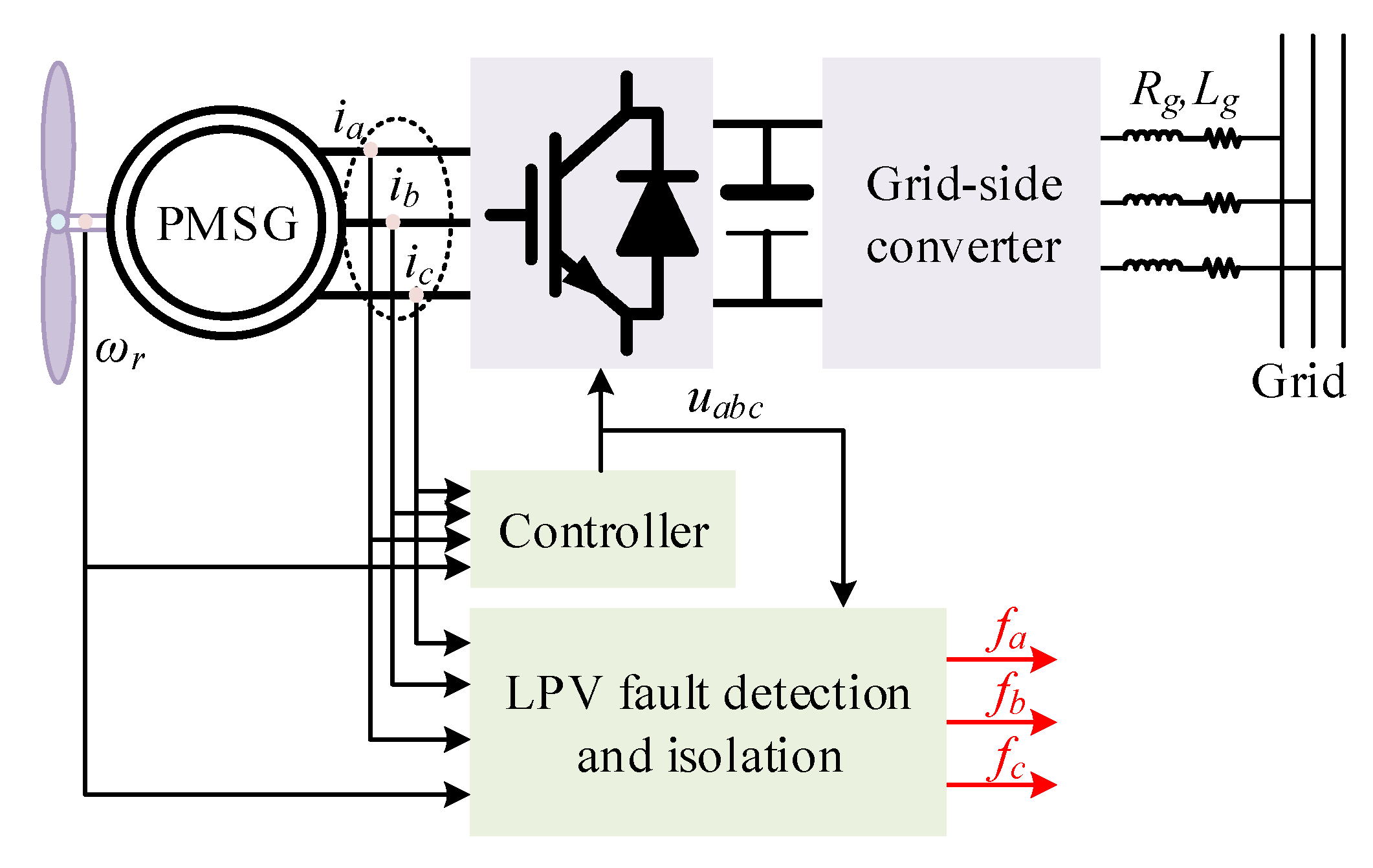
LPV Model Based Sensor Fault Diagnosis and Isolation for Permanent Magnet Synchronous Generator in Wind Energy Conversion Systems
Abstract
1. Introduction
- (1)
- A scheme is proposed for detection and isolation of multiple sensor faults. Compared with the existing methods, the proposed method is capable of isolating three-phase current sensor faults while most existing schemes are presented to isolate faults in stationary frame or synchronous reference frame.
- (2)
- The proposed isolator is based on a fault estimation scheme. Fault estimates contain all the fault information, which makes it possible to deal with both additive and multiplicative faults.
- (3)
- All of the measurements are available in the control loop. No additional hardware or measurements are required. Furthermore, the proposed method is implemented in closed-loop operation.
2. Problem Statement
2.1. LPV Model of PMSG
2.2. Polytopic Decomposition of the System Model
2.3. Extended Bounded Real Lemma
3. Current Sensor Fault Detection
3.1. Parameter-Dependent Observer Design
3.2. Current Sensor Fault Detection
- , sensor fault alarm,
- , no fault alarm.
4. Sensor Fault Isolation Scheme
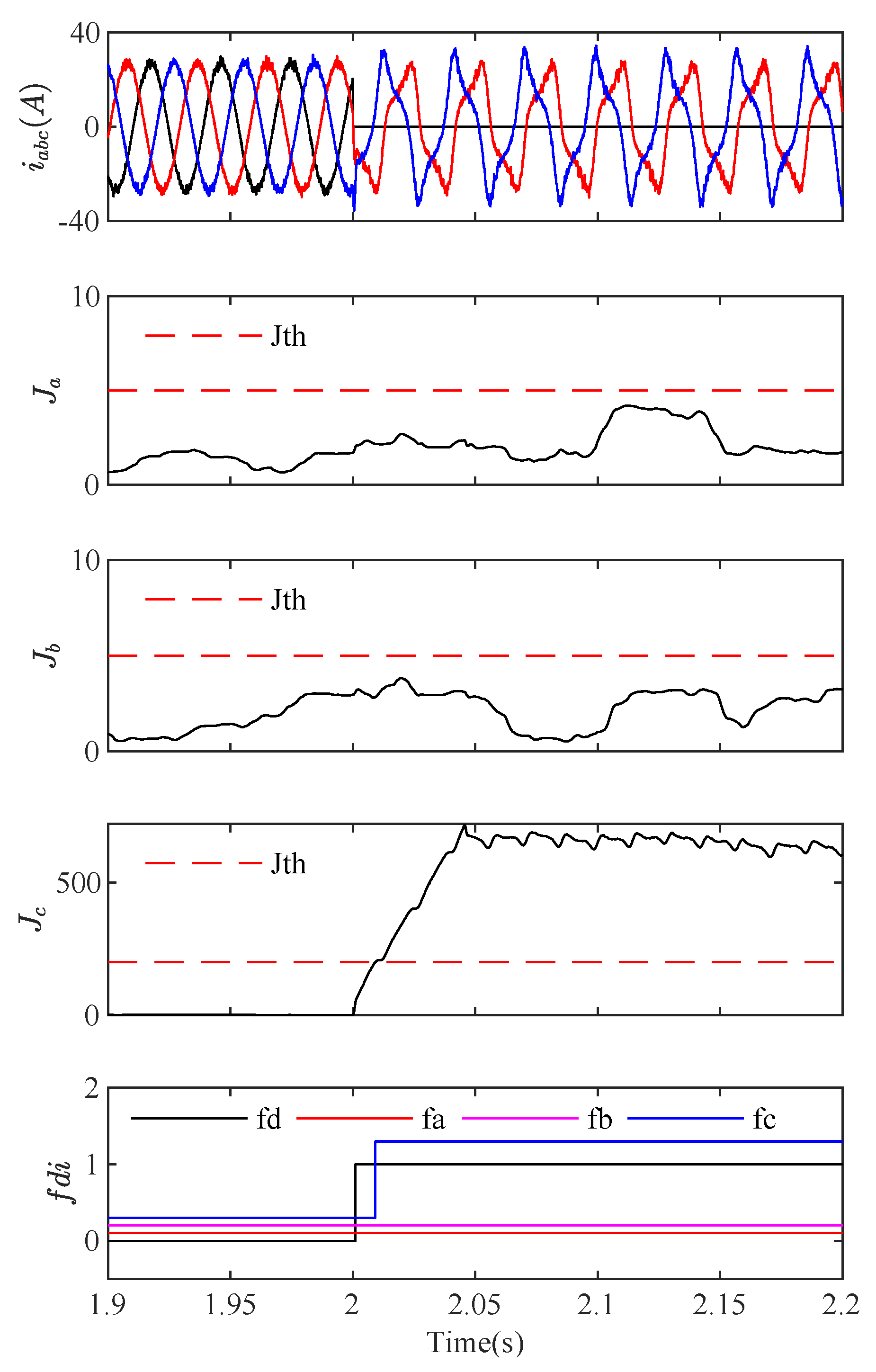
5. Simulation Results and Discussion
- Type a: gain error in phase a sensor, only 80% of the measured value fed to the controller,
- Type b: bias fault in phase b sensor, 4 A is added to the measured value,
- Type c: disconnection of phase c sensor, the measurement output becomes zero.
5.1. Performance for Single Sensor FDI with External Disturbance
5.2. Multiple Fault Detection and Isolation
- Type a and Type b fault at s and s,
- Type b and Type c fault at s and s,
- Type a and Type c fault at s and s,
- Three type faults occur simultaneously at s, s and s.
5.3. Comparison with the Existing Sensor FDIs
5.4. Discussions
- The component parameters of simulation model come from the real laboratory prototype with rated power 2.5 kW. Its controller parameters are designed on the simulation file and can guarantee the control performance. The real waveforms and power characteristics are the same as those of simulation results. The observer design is a dual problem of controller design. Thus, the parameters designed in SIMULINK environment can be applied to the real experiments.
- The threshold selection is the most challenging problem in implementing the proposed algorithm. In real application, the mechanical torque and measurement noise are different from the simulation configuration. This will be further introduced into the observer and error dynamics. These effects can be modeled as generalized unknown disturbances. The upper bound of the disturbances in real application is slightly different from simulation scenarios. However, this does not affect the performance since the upper bounds of disturbances and faults hold for real applications.
- The harmonics is another issue for current sensor fault diagnosis. The influences of harmonics on system behavior need to be further discussed with respect to system parameter and dynamics variation. However, few results have been presented for dealing with this problem, even for the controller designs in [20,21,22]. Recalling the FDI schemes in Table 2, only the method in [2] utilizes the harmonic model of PMSG to diagnose additive and multiplicative faults in current sensors. The state space model and output equation are linear combinations of each order harmonic in frequency domain, which indicates that the residuals can be modeled as the combination of finite harmonics. The proposed FDI takes the time domain behaviors of residuals into consideration. The average value of each fault estimate is calculated with a sliding window. Current sensor faults are evaluated via the threshold function defined in Equation (32). From this perspective, the harmonics will not affect the residual evaluation in time domain analysis.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Wu, C.; Guo, C.; Xie, Z.; Ni, F.; Liu, H. A Signal-Based Fault Detection and Tolerance Control Method of Current Sensor for PMSM Drive. IEEE Trans. Ind. Electron. 2018, 65, 9646–9657. [Google Scholar] [CrossRef]
- Beddek, K.; Merabet, A.; Kesraoui, M.; Tanvir, A.A.; Beguenane, R. Signal-Based Sensor Fault Detection and Isolation for PMSG in Wind Energy Conversion Systems. IEEE Trans. Instrum. Meas. 2017, 66, 2403–2412. [Google Scholar] [CrossRef]
- Song, Y.; Wang, B. Survey on Reliability of Power Electronic Systems. IEEE Trans. Power Electron. 2013, 28, 591–604. [Google Scholar] [CrossRef]
- Yang, Z.; Chai, Y. A survey of fault diagnosis for onshore grid-connected converter in wind energy conversion systems. Renew. Sustain. Energy Rev. 2016, 66, 345–359. [Google Scholar] [CrossRef]
- Yang, S.; Xiang, D.; Bryant, A.; Mawby, P.; Ran, L.; Tavner, P. Condition Monitoring for Device Reliability in Power Electronic Converters: A Review. IEEE Trans. Power Electron. 2010, 25, 2734–2752. [Google Scholar] [CrossRef]
- Rothenhagen, K.; Fuchs, F.W. Current Sensor Fault Detection, Isolation, and Reconfiguration for Doubly Fed Induction Generators. IEEE Trans. Ind. Electron. 2009, 56, 4239–4245. [Google Scholar] [CrossRef]
- Rothenhagen, K.; Fuchs, F.W. Doubly Fed Induction Generator Model-Based Sensor Fault Detection and Control Loop Reconfiguration. IEEE Trans. Ind. Electron. 2009, 56, 4229–4238. [Google Scholar] [CrossRef]
- Aguilera, F.; de la Barrera, P.; Angelo, C.D.; Trejo, D.E. Current-sensor fault detection and isolation for induction-motor drives using a geometric approach. Control Eng. Pract. 2016, 53, 35–46. [Google Scholar] [CrossRef]
- Abdelmalek, S.; Barazane, L.; Larabi, A.; Bettayeb, M. A novel scheme for current sensor faults diagnosis in the stator of a DFIG described by a T-S fuzzy model. Measurement 2016, 91, 680–691. [Google Scholar] [CrossRef]
- Boulkroune, B.; Gálvez-Carrillo, M.; Kinnaert, M. Combined Signal and Model-Based Sensor Fault Diagnosis for a Doubly Fed Induction Generator. IEEE Trans. Control Syst. Technol. 2013, 21, 1771–1783. [Google Scholar] [CrossRef]
- Akrad, A.; Hilairet, M.; Diallo, D. Design of a Fault-Tolerant Controller Based on Observers for a PMSM Drive. IEEE Trans. Ind. Electron. 2011, 58, 1416–1427. [Google Scholar] [CrossRef]
- Mwasilu, F.; Jung, J. Enhanced Fault-Tolerant Control of Interior PMSMs Based on an Adaptive EKF for EV Traction Applications. IEEE Trans. Power Electron. 2016, 31, 5746–5758. [Google Scholar] [CrossRef]
- Kommuri, S.K.; Defoort, M.; Karimi, H.R.; Veluvolu, K.C. A Robust Observer-Based Sensor Fault-Tolerant Control for PMSM in Electric Vehicles. IEEE Trans. Ind. Electron. 2016, 63, 7671–7681. [Google Scholar] [CrossRef]
- Kommuri, S.K.; Lee, S.B.; Veluvolu, K.C. Robust Sensors-Fault-Tolerance With Sliding Mode Estimation and Control for PMSM Drives. IEEE/ASME Trans. Mech. 2018, 23, 17–28. [Google Scholar] [CrossRef]
- Foo, G.H.B.; Zhang, X.; Vilathgamuwa, D.M. A Sensor Fault Detection and Isolation Method in Interior Permanent-Magnet Synchronous Motor Drives Based on an Extended Kalman Filter. IEEE Trans. Ind. Electron. 2013, 60, 3485–3495. [Google Scholar] [CrossRef]
- Wang, Y.; Meng, J.; Zhang, X.; Xu, L. Control of PMSG-Based Wind Turbines for System Inertial Response and Power Oscillation Damping. IEEE Trans. Sustain. Energy 2015, 6, 565–574. [Google Scholar] [CrossRef]
- Badihi, H.; Zhang, Y.; Hong, H. Wind Turbine Fault Diagnosis and Fault-Tolerant Torque Load Control Against Actuator Faults. IEEE Trans. Control Syst. Technol. 2015, 23, 1351–1372. [Google Scholar] [CrossRef]
- Bifaretti, S.; Iacovone, V.; Rocchi, A.; Tomei, P.; Verrelli, C. Nonlinear speed tracking control for sensorless PMSMs with unknown load torque: From theory to practice. Control Eng. Pract. 2012, 20, 714–724. [Google Scholar] [CrossRef]
- Tomei, P.; Verrelli, C.M. Observer-Based Speed Tracking Control for Sensorless Permanent Magnet Synchronous Motors With Unknown Load Torque. IEEE Trans. Autom. Control 2011, 56, 1484–1488. [Google Scholar] [CrossRef]
- Kang, C.M.; Lee, S.; Chung, C.C. Discrete-Time LPV 2 Observer With Nonlinear Bounded Varying Parameter and Its Application to the Vehicle State Observer. IEEE Trans. Ind. Electron. 2018, 65, 8768–8777. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, S.; Chung, C.C. LPV ∞ Control with Disturbance Estimation for Permanent Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2018, 65, 488–497. [Google Scholar] [CrossRef]
- Lee, Y.; Shin, D.; Kim, W.; Chung, C.C. Nonlinear 2 Control for a Nonlinear System With Bounded Varying Parameters: Application to PM Stepper Motors. IEEE/ASME Trans. Mech. 2017, 22, 1349–1359. [Google Scholar] [CrossRef]
- De Souza, C.E.; Barbosa, K.A.; Neto, A.T. Robust ∞ filtering for discrete-time linear systems with uncertain time-varying parameters. IEEE Trans. Signal Process. 2006, 54, 2110–2118. [Google Scholar] [CrossRef]
- Pandey, A.P.; de Oliveira, M.C. Discrete-time ∞ control of linear parameter-varying systems. Int. J. Control 2018. [Google Scholar] [CrossRef]
- Pandey, A.P.; de Oliveira, M.C. A new discrete-time stabilizability condition for Linear Parameter-Varying systems. Automatica 2017, 79, 214–217. [Google Scholar] [CrossRef]
- Pandey, A.P.; de Oliveira, M.C. On the Necessity of LMI-Based Design Conditions for Discrete Time LPV Filters. IEEE Trans. Autom. Control 2018, 63, 3187–3188. [Google Scholar] [CrossRef]
- Li, L.; Ding, S.X.; Qiu, J.; Yang, Y.; Zhang, Y. Weighted Fuzzy Observer-Based Fault Detection Approach for Discrete-Time Nonlinear Systems via Piecewise-Fuzzy Lyapunov Functions. IEEE Trans. Fuzzy Syst. 2016, 24, 1320–1333. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, Z.; Xu, D.; Zhou, T.; Xu, R. Speed and Current Sensor Fault Detection and Isolation Based on Adaptive Observers for IM Drives. J. Power Electron. 2014, 14, 967–979. [Google Scholar] [CrossRef]
- Zhang, X.; Foo, G.; Vilathgamuwa, M.D.; Tseng, K.J.; Bhangu, B.S.; Gajanayake, C. Sensor fault detection, isolation and system reconfiguration based on extended Kalman filter for induction motor drives. IET Electr. Power Appl. 2013, 7, 607–617. [Google Scholar] [CrossRef]
- Najafabadi, T.A.; Salmasi, F.R.; Jabehdar-Maralani, P. Detection and Isolation of Speed-, DC-Link Voltage-, and Current-Sensor Faults Based on an Adaptive Observer in Induction-Motor Drives. IEEE Trans. Ind. Electron. 2011, 58, 1662–1672. [Google Scholar] [CrossRef]
- Saha, S.; Haque, M.E.; Mahmud, M.A. Diagnosis and Mitigation of Sensor Malfunctioning in a Permanent Magnet Synchronous Generator Based Wind Energy Conversion System. IEEE Trans. Energy Convers. 2018, 33, 938–948. [Google Scholar] [CrossRef]






| Quantity | Value | Quantity | Value |
|---|---|---|---|
| Magnet steel | NdFeB permanent magnet | Insulation class | Class F |
| Protection | IP54 | Stator winding connection | Star connection |
| Rated voltage | 110 V | Rated frequency | 32.67 Hz |
| Stator resistance | 0.3667 | Rated power | 2.5 kW |
| Stator inductance | 3.29 mH | Rated speed | 335 r/min |
| Flux linkage | 0.283 Wb | DC-link voltage | 300 V |
| Generator inertia | 0.1133 Kg· m | Grid inductance | 2 mH |
| Viscous damping | 0.008 N·m·s | Grid resistance | 0.19 |
| Pole pairs | 7 | Grid voltage | 110 V |
| FD Scheme | Measurements | Fault Types | Isolability | System Model | Detection Variables |
|---|---|---|---|---|---|
| Bank of observers [28] | 1 voltage, 3 currents, 1 speed | Type c | Single | IM model in | Estimation errors of rotor flux and speed |
| EKF [29] | 1 voltage, 2 currents, 1 speed | Type c | Single | IM model in | Estimation errors of phase currents |
| Adaptive observer [30] | 1 voltage, 2 currents, 1 speed | Type c | Single | IM model in | Fault inference based on current errors |
| Bank of observers [8] | 1 voltage, 2 currents, 1 speed | Type a, Type b, Type c | 2 faults | IM model in | Geometric residuals |
| TS fuzzy observers [9] | 2 currents, 1 speed | Type b | 2 faults | DFIG model in | Estimation errors of the states |
| Integrated filters [10] | 2 currents, 1 speed, 1 position | Type a, Type b, Type c | 2 faults | DFIG model in and | Generalized likelihood ratio of residuals |
| TVKF [2] | 2 currents, 1 speed | Type a, Type b, Type c | 3 faults | PMSG model in harmonic domain | Generalized likelihood ratio of residuals |
| Sliding mode observer [31] | 3 currents, 1 speed, 1 position | Type c | 2 faults | PMSG model in | Evaluation of estimation errors |
| This method | 3 currents, 1 speed, 1 position | Type a, Type b, Type c | 3 faults | PMSG model in | Evaluation of the fault estimates |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Chai, Y.; Yin, H.; Tao, S. LPV Model Based Sensor Fault Diagnosis and Isolation for Permanent Magnet Synchronous Generator in Wind Energy Conversion Systems. Appl. Sci. 2018, 8, 1816. https://doi.org/10.3390/app8101816
Yang Z, Chai Y, Yin H, Tao S. LPV Model Based Sensor Fault Diagnosis and Isolation for Permanent Magnet Synchronous Generator in Wind Energy Conversion Systems. Applied Sciences. 2018; 8(10):1816. https://doi.org/10.3390/app8101816
Chicago/Turabian StyleYang, Zhimin, Yi Chai, Hongpeng Yin, and Songbing Tao. 2018. "LPV Model Based Sensor Fault Diagnosis and Isolation for Permanent Magnet Synchronous Generator in Wind Energy Conversion Systems" Applied Sciences 8, no. 10: 1816. https://doi.org/10.3390/app8101816
APA StyleYang, Z., Chai, Y., Yin, H., & Tao, S. (2018). LPV Model Based Sensor Fault Diagnosis and Isolation for Permanent Magnet Synchronous Generator in Wind Energy Conversion Systems. Applied Sciences, 8(10), 1816. https://doi.org/10.3390/app8101816