Vector-Based Eddy-Current Testing Method

Abstract

We present a type of eddy-current testing (ECT) method based on measuring the reaction of the Lorentz force by using a small permanent magnet (PM) as the probe. The means of measuring impedance is superseded by measuring force. By analyzing the variations in different components of the reaction of Lorentz force, the defects characteristics within the measured conductor can be revealed. The results indicate that the vector-based eddy-current testing method obtains good quantitative results and precisely evaluates the lift-off effect during measurement along two orthogonal directions. Numerical simulations are performed to provide supports for the experimental results. The method described in this paper may have great potential for use in industrial nondestructive testing applications.

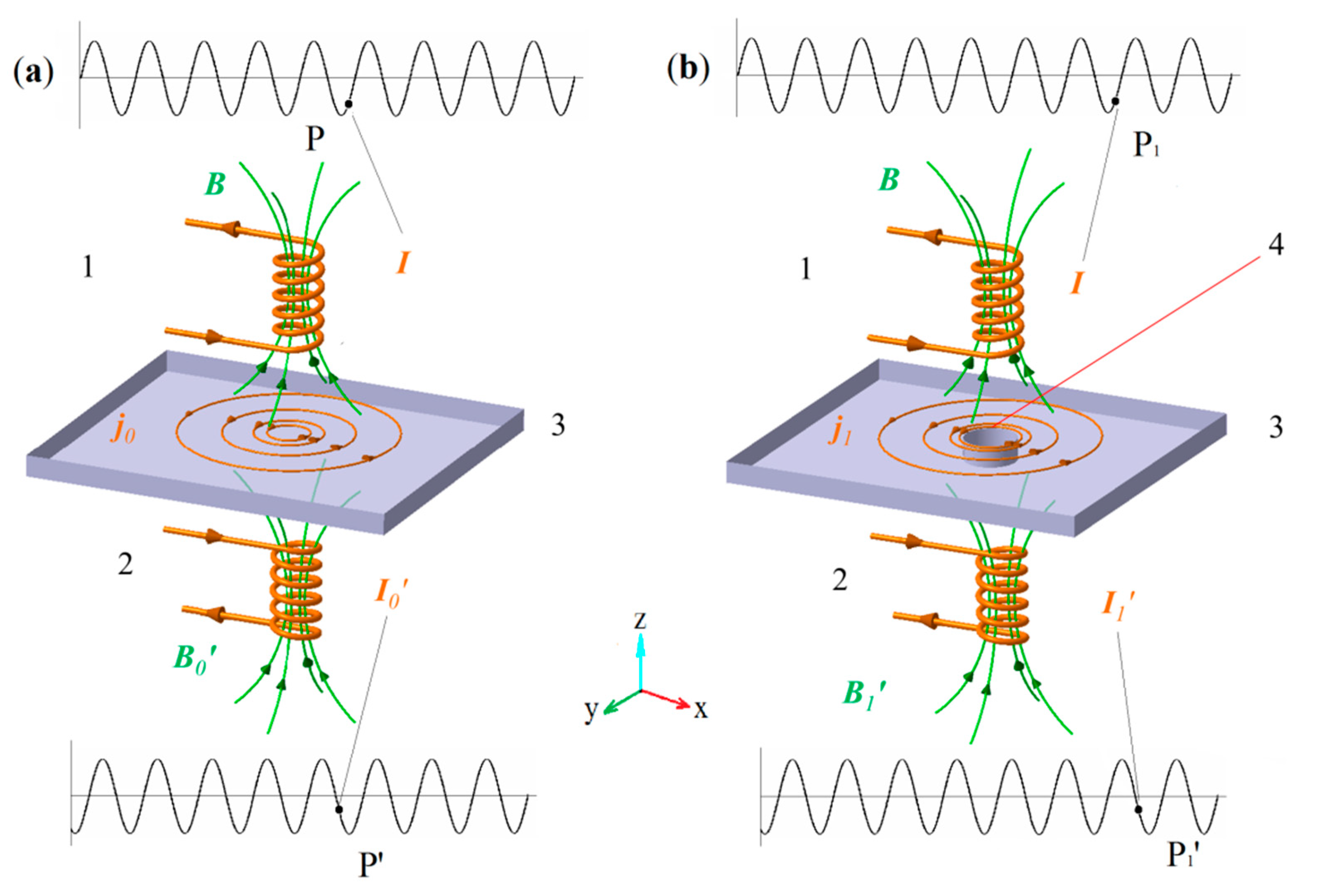
1. Introduction

Current technological developments typically require materials with improved properties. Therefore, methods of detecting and locating defects both on the surface and inside these materials without causing damage are becoming increasingly important. The widely applied industrial methods for addressing those demands are called non-destructive testing (NDT) methods, including the methods of eddy current testing (ECT), radiography testing, ultrasonic testing, magnetic particle testing, penetrant testing and so on. The ECT (Figure 1) is a specialized NDT method for testing conductor material and has been widely used in inspections of aerospace structures and engines, equipment in the nuclear industry, fossil fuel power facilities and pipelines, wires, and plates in the manufacturing process [1,2,3,4]. The ECT method can also be applied in tasks applicable to many industries such as thickness measurements, quality inspections, coating applications and surface treatments. Compared with other NDT methods, the ECT method has many advantages such as high detection sensitivity, no requirement for a coupling agent, and suitability for the on-line detection of work pieces. Moreover, this method is appropriate for magnetic and non-magnetic conductors at common or high temperatures. However, as the frequency increases, the eddy current tends to be distributed on the surface due to the skin effect, therefore comprehensive considerations are required to determine the input parameters for the ECT method.

The principle of the ECT is shown in Figure 1. An exciting coil with an alternative current is placed on one side of the material, and a pick-up coil is placed on the other side. In some cases, it is impossible to place the exciting coil and pick-up coil on two sides of sample, they can be set on the same side. The magnetic field generated by the exciting coil will induce eddy current j inside the material, which also induces an alternative magnetic field. The magnetic field generated by the exciting coil and inducing eddy current are detected by measuring the impedance of the pick-up coil. When a defect is present, the induced eddy current will change correspondingly and yield to a signal change in the pick-up coil. Note that a phase difference occurs between the exciting coil and pick-up coil as shown in Figure 1a,b. By identifying this signal, the defect in the test sample can be identified as well [5,6].

Magnetic sensors (AMR (anisotropic magnetoresistance), Hall and GMR (giant magnetoresistance)) have been introduced in the ECT system in recent years to provide improved sensitivity and allow for lower frequencies during testing. Postolache designed and implemented neural network classification schemes to establish a reduced number of features for two types of defects induced in an aluminium plate [7]. Espina-Hernández estimated the crack’s dimension in aluminium based on two extracted parameters from the GMR output voltage [8]. Ramos also proposed a velocity induced eddy current testing (VIECT) excited by a permanent magnet (PM) or a DC coil, in which relative motion occurs between the sample and the excitation [9].

Uhlig proposed the Lorentz force eddy current testing (LET) method that utilizes a PM to test the defects, which induces eddy current by the relative motion. They use a force sensor to measure the reaction of the Lorentz force acting on the PM [10,11,12]. Wang used a laser cantilever magnet (LCM) system to measure the Lorentz force [13,14,15] and Dai detected cracks by array probes consisting of PMs based on speckle pattern interferometry [16].

However, the traditional ECT method has a few disadvantages. For example, the output signal of the traditional ECT method is very sensitive to the distance between the probe and the test sample; thus, the signal can be disturbed easily in practice by factors such as varied coating thicknesses, irregular samples surface or operator movement (lift-off). Gui proposed an approach using normalization and two reference signals to reduce the lift-off problem using pulsed eddy current techniques, and this approach is primarily suitable for sub-surface corrosion detection, whereas it is unsuitable for detection of surface defect [17]. C. Mandache and J. H. V. Lefebvre proposed that the lift-off intersection (LOI) can be used to eliminate the lift-off noise [18]. Yin arranged the exciting and pick-up coils in a special range and found that the output signal phase only slightly varied in space with the liftoff value [5].

In this paper, we introduce the Lorentz force principle into the ECT system and present a vector-based ECT method [19]. After building our test system, we successfully obtained reproducible measurements of the reaction of the Lorentz force. By carefully analyzing different components, more detailed information can be extracted regarding defects and lift-off.

2. Methods

The principle of our method is shown in Figure 2 and briefly reviewed as follows: An eddy current is induced by the exciting coil and then an alternative current of sinusoid form is applied. A PM interacts with the eddy current and functions as the probe. Similar to the process in ECT and LET, defects in the test sample would induce a redistribution of the eddy current, thus leading to a change in the Lorentz force on the conductor. The Lorentz force is a vector, with all its components reflecting different features of the eddy current and its reaction force acts on the PM. A laser cantilever magnet (LCM) system, similar to the laser-cantilever-tip system used in Atomic Force Microscopy (AFM) [20], is applied to measure all components of this force via displacement measurements. Just as the traditional ECT, the PM and exciting coil can be on the same side or on both sides, the form with the PM and exciting coil on both sides are used to illustrate the principle in Figure 2. The detailed form of the net force is discussed as follows.

By applying an alternating input current $I=I_0\sin \omega t$ to the exciting coil, the exciting coil generates a magnetic field, which can be described as follows:

$${\mathit{B}}_p=\mathit{B}(x,y,z)\sin \omega t$$

(1)

As the PM interacts with this primary magnetic field, the exciting coil exerts a magnetostatic force on the PM. This magnetostatic force has the same phase as the primary magnetic field, and its dependence on time can be simply described as follows:

$$F_{\mathrm{c}}(t)=F_c(x,y,z)\sin \omega t$$

(2)

According to Maxwell’s equations and Ohm’s law, this alternating magnetic field induces an eddy current inside the conductor. σ is the electrical conductivity of the sample, and the eddy current satisfies the following:

$$\nabla \times j=-\sigma \frac{\partial B}{\partial t}$$

(3)

Thus, its dependence on time can be written as follows:

$$j(t)=j\cos \omega t$$

(4)

Note that $B_p$ and j have a π/2 phase difference.

The interaction between the PM’s static magnetic field and the eddy current produces the Lorentz force acting on the conductor, equally obvious but less widely recognized is the fact that by virtue of Newton’s law, an opposite force (reaction force) acts on the PM [11]. In our study, this force is time-dependent and has the same phase as the eddy current, thus can be described as following form:

$$F_L=F_L(x,y,z)\cos \omega t$$

(5)

Thus, the total force acting on the PM is described as follows:

$$F_{PM}(t)=F_c(x,y,z)\sin \omega t+F_L(x,y,z)\cos \omega t$$

(6)

Note that, although both $F_c$ and $F_L$ are dependent on the magnetic field generated by the exciting coil, there is no direct relation between them and they both proportional to the input current I. If the PM and the coil are on the same side, $F_c$ can be more significant because of the reduced distance between them. For the sake of readily operation, our experiment set them on the different sides with the conductor.

For any component i (x, y or z) of this force, we have the following:

$$F_{PMi}(t)=F_{ci}\sin \omega t+F_{Li}\cos \omega t=\sqrt{F_{ci}^2+F_{Li}^2}\sin (\omega t+\phi )$$

(7)

where $\phi =\arctan (F_{Li}/F_{ci})$. We can calculate the above relation through the trigonometric functions. Thus, the force acting on the PM also has a sinusoidal form, leading to an oscillation motion for the PM. When a defect is present, the Lorentz force part undergoes a small disturbance.

$${{\mathit{F}}^{\prime }}_L=F_L+\delta$$

(8)

Here $F_L^{\prime }$ is the reaction of the Lorentz force with the defect. δ is the small disturbance. Because this disturbance is minor, the net force acting on the PM in any direction can be described as follows:

$$F_{PMi}{}^{\prime }(t)=\sqrt{F_{ci}^2+{F_{Li}^{\prime }}^2}\sin (\omega t+{\phi }^{\prime })~(\sqrt{F_{ci}^2+F_{Li}^2}+\frac{F_{Li}}{\sqrt{F_{ci}^2+F_{Li}^2}}{\delta }_i)\sin (\omega t+{\phi }^{\prime })$$

(9)

where ${\phi }^{\prime }=\arctan (F_{Li}^{\prime }/F_{ci})$.

In the LCM system, the displacement of the PM is considered proportional to the force on it. Therefore, the force given by Equation (9) causes the PM to oscillate, and defects can be detected by observing change in the amplitude of the PM oscillation. Note that, similar to the tapping mode of AFM [19], the oscillation generated by the force is optimized for detecting near the resonance frequency of the cantilever (200 Hz in our experiment setup).

In our experiments, this force is measured by measuring the displacement of the cantilever, and the output is voltage signals as shown in Figure 3. The displacement of the cantilever is considered to be proportional to the force acting on it in a certain range, where our measuring range is involved. Therefore, the force is proportional to the measured voltage.

3. Experimental Setup

Our experimental setup is shown in Figure 3. The exciting coil (6) and the PM (8) are placed on two sides of the test sample (7). The sample is placed on a stage, and can move in one direction via the controller (2). $F_{PM}$ represents the force exerted on the PM (8), and it is measured by an LCM system (8, 9 and 10) [20,21,22,23] due to its high sensitivity and quick response. Two components of the force are measured by changing the alignment of the LCM system and then repeating the procedure: One component is perpendicular to the sample surface (z) (Figure 3b), and the other is parallel to the sample and is the same as the direction of the defect movement (x) (Figure 3c).

The PM is composed of NbFeB with a size of 1 mm × 1 mm × 1 mm. The cantilever is made of stainless steel (12CrNi177) with a size of 7 mm × 1.2 mm × 40 μm (length × width × thickness). The sample board is made of copper (σ = 5.9 × 10⁷ S/m) with a thickness of 1 mm. The sample board contains through-holes of various diameters (0.3~2 mm) to simulate defects. The sample board is placed on a stage that can be controlled to move in the x-direction at a speed of 2.45 mm/s (with an accuracy of positioning of 0.005 mm, and a range of 25 mm). Note that the slow relative movement between the sample and the magnetic field at this speed induces a negligible eddy current. A precision translation stage is used to adjust the position of the PM to guarantee the same measurement conditions. The distance between the PM and the surface of the testing sample is d = 0.5 mm, which is called lift-off distance.

During the experiment, a sinusoid current (200 Hz) is applied to the exciting coil, which causes oscillation of the cantilever. The reason for choosing this frequency is to adapt to the LCM system so that the cantilever beam is in a sensitive state. Moreover, a low frequency can provide a better penetration depth, which is 4.6 mm. This oscillation is detected by a Microtrak3 displacement sensor (made by the MTI company, New York, USA), which has a measuring range of ±5 mm and a resolution of 1.25 μm. The error caused by the cantilever’s deformation is in a range of 0.05~0.1%, which is negligible. The test sample moves uniformly in one direction driven by the stage, so that different areas of the sample are scanned by the exciting coil PM system. A MDO3022 Tektronix oscilloscope collects the data from the displacement sensor as the scanned area moves, and thus provides information regarding oscillation as a function of the defect position.

To better understand the mechanics of our system and interpret the experimental results, numerical simulation work based on the finite element method is performed to study the force acting on the PM. The simulation work is carried out in a commercial software package of COMSOL Multiphysics 5.3 under the following conditions: the exciting coil and PM are aligned to each other (both located at origin in x-y plane) and placed on two sides of the sample conductor as the set of the experiment; the sample contains a defect, which is moving along the x-axis; the parameters (size, position etc.) in the simulation are the same as those in experiments and the amplitude of the force acting on the PM is calculated as the defect moves.

4. Results and Discussion

4.1. Data Processing

Figure 4 presents a sample of the data collected by the oscilloscope. The period of the oscillation is 5 ms, which matches the frequency of the input to the exciting coil. Note that this frequency is slightly inconsistent with the resonance frequency of the LCM system to avoid noise from frequency disturbance.

As discussed in the method section, the change in oscillation amplitude is proportional to the change in the Lorentz force caused by defects. Thus, we obtain the difference value between the maximum and the minimum value in each period. Based on these data, we plotted the amplitude as a function of time for the later data analysis as shown at the top right figure. Note that, time can be converted to a position by multiplying preset motion speed (2.45 mm/s). By plotting the points obtained from all cycles, the inset graph is obtained.

4.2. Force Acting on the PM

In our experiment, we measured two components of the force acting on the PM. One is perpendicular to the sample surface (z), and the other is parallel to it and the same as the direction that the defect moves along (x). The y-component is not measured because the defect is always located along the x-axis in our measurement, thus significant change is not observed in the y-component of the force due to symmetry. Figure 5 shows the measured force as the defect is at different positions and in Figure 6 the distribution of the Lorentz force density in the z-direction is shown and the arrows represent the direction of the Lorentz force density in x-y plane. In both Figure 5 and Figure 6, x = 0 refers to the position where the defect aligned with the PM.

Figure 5a shows the z-component of the force acting on the PM. The z-component is the perpendicular component of the Lorentz force and yields the most significant results. Two peaks can be observed although only one defect is present. The reason for the two peaks is illustrated in Figure 6. Because of the geometry of the exciting coil, when no defect is present, the Lorentz force density distribution inside the sample yields the shape of a “ring” and a locally minimal value appears at the center of the “ring” (Figure 6a). When the defect is present, the signal will increase as the defect moves close to this “ring”, the signal reaches the maximal value as the defect is on top of this “ring” (Figure 6b,c). The signal then decreases as the defect moves to the local minimal value (Figure 6d). The leaving process of the defect is completely symmetrical with the change of the z-direction Lorentz force density during the process of entering, leading to a second peak. The experimental and numerical results are consistent with each other as shown in Figure 5a, and the positions of two peaks are nearly identical with a slight difference caused by experimental error. The reason for the asymmetric experimental result is that the lift-off distance is changed caused by the uneven surface of the testing copper plate. Thus, because of the changed lift-off distance the eddy current is not symmetric in the measurement process, and the force acting on the PM is different at the positions of the two peaks.

Compared with the perpendicular direction (z), force measured in the horizontal direction has not been fully studied. Figure 5b shows the x-component of the force acting on the PM. The measured force is 0 at x = 0 and has two opposite peaks around it. The direction of this x-component Lorentz force density can be either positive or negative as the arrows indicate in Figure 6a, therefore, the defect could cause the net x-component of the Lorentz force density to be either positive or negative (Figure 6b,c). Note that when there is no defect or the defect is located at x = 0, the Lorentz force density in the x-component has a symmetric feature and thus the net force is zero (Figure 6a,d). The experimental results agree with the simulation results as shown in Figure 5b.

By measuring the reaction of the Lorentz force, the size of the defects can also be quantitatively evaluated. Figure 7 shows the measured force acting on the PM for defects of various sizes. Here defects are simulated by through holes. As shown in Figure 7a, in the z-direction, more intensive signals can be obtained for larger defects. Note that for a large defect, the two peaks we observed in Figure 5a overlap with each other. We calculate the areas under the corresponding curves by integrating the voltage above the baseline (baseline voltage = 0.285 V in Figure 7a) and the results are shown in Figure 8. The graph shows a strong linear correlation between the integral and the volume information of defects within experimental error. This correlation is confirmed by theoretical analysis in the range where the size of the defect is comparable or smaller than the PM probe (1 mm³). Therefore, the z-component of our force can be used to quantitatively determine the size of the defect thin test sample with small defect.

In the x-direction, we observed stronger signals for larger defects, which is similar to the observations in the z-direction but with a different feature. We may utilize this feature specific to the horizontal component to evaluate the lift-off effect, which will be discussed next.

4.3. Distinguish and Precisely Evaluate Lift-off Effect

Lift-off effect is one of the major problems of the ECT method and is caused by the electromagnetic field weakening or strengthening due to variation of the lift-off distance. Signals caused by such lift-off are usually difficult to distinguish from those caused by those defects. However, as discussed, the Lorentz force in the horizontal direction has a specific feature different than that in the vertical direction, this feature has different sensitivity to defects and lift-off factors such as the varied coating thicknesses, an irregular sample surfaces or an operator movement. This feature can be utilized to reflect the extent of the lift-off.

The simulation results of the measured force in the z and x-direction are shown when a sample without and with a defect undergoes a “lift-off” as shown in Figure 9. Figure 9a, we see that in the z-direction a lift-off forms a signal which could be difficult to distinguish from signals refer to defect in practice. Nevertheless, in the x-direction no signal is detected, indicating that the x-component is resistant to lift-off. When a lift-off occurs with a defect (Figure 9b), the z-component is disturbed by the lift-off, note that in Figure 5a the experimental curve has a similar shape as the $F_z$ simulation result in Figure 9b. However, the signal of the x-component is still mostly unaffected as compare to that in Figure 5b. It is confirmed that a lift-off occurs in our experiment. The above results show that, horizontal components are much insensitive to lift-offs compared to vertical component, and some curves of the Lorentz force in the x-direction is invisible because there is much overlap among these forces, namely they vary very consistently. Consequently, we can take advantage of this feature to identify lift-offs.

5. Conclusions

In conclusion, we propose that the eddy current change induced by the defect can be depicted more clearly by measuring the reaction of the Lorentz force vector. Based on that, we developed an altered ECT method by introducing a probe PM and the LCM measuring system. In our method, two components of Lorentz force acting on the probe PM are measured, respectively. The vertical component (z) of the force gives a quantitative estimation of the defect size for a thin sample with small defects, and the horizontal component (x) of the force has a specific feature that is insensitive to the lift-off effect, which can be used to distinguish defects from “lift-off”.

In future work, the current system may be improved in the following aspects: to further decrease the sizes of exciting coil till less than 1 mm and to optimize the dimensions and the shape of the LCM system may improve the sensitivity and obtain a high resolution of the defects; To investigate the intrinsic mechanic oscillating relationship between the input frequency and the LCM system; to improve force measurement means, i.e., adapting 3-axis force sensor, in order to obtain the force acting on the PM with three components of the reaction of the Lorentz force simultaneously.