Experimental and Simulation Study of Low-Velocity Impact on Glass Fiber Composite Laminates with Reinforcing Shape Memory Alloys at Different Layer Positions
Abstract
:1. Introduction
2. Methods: Experiment and Numerical Simulation
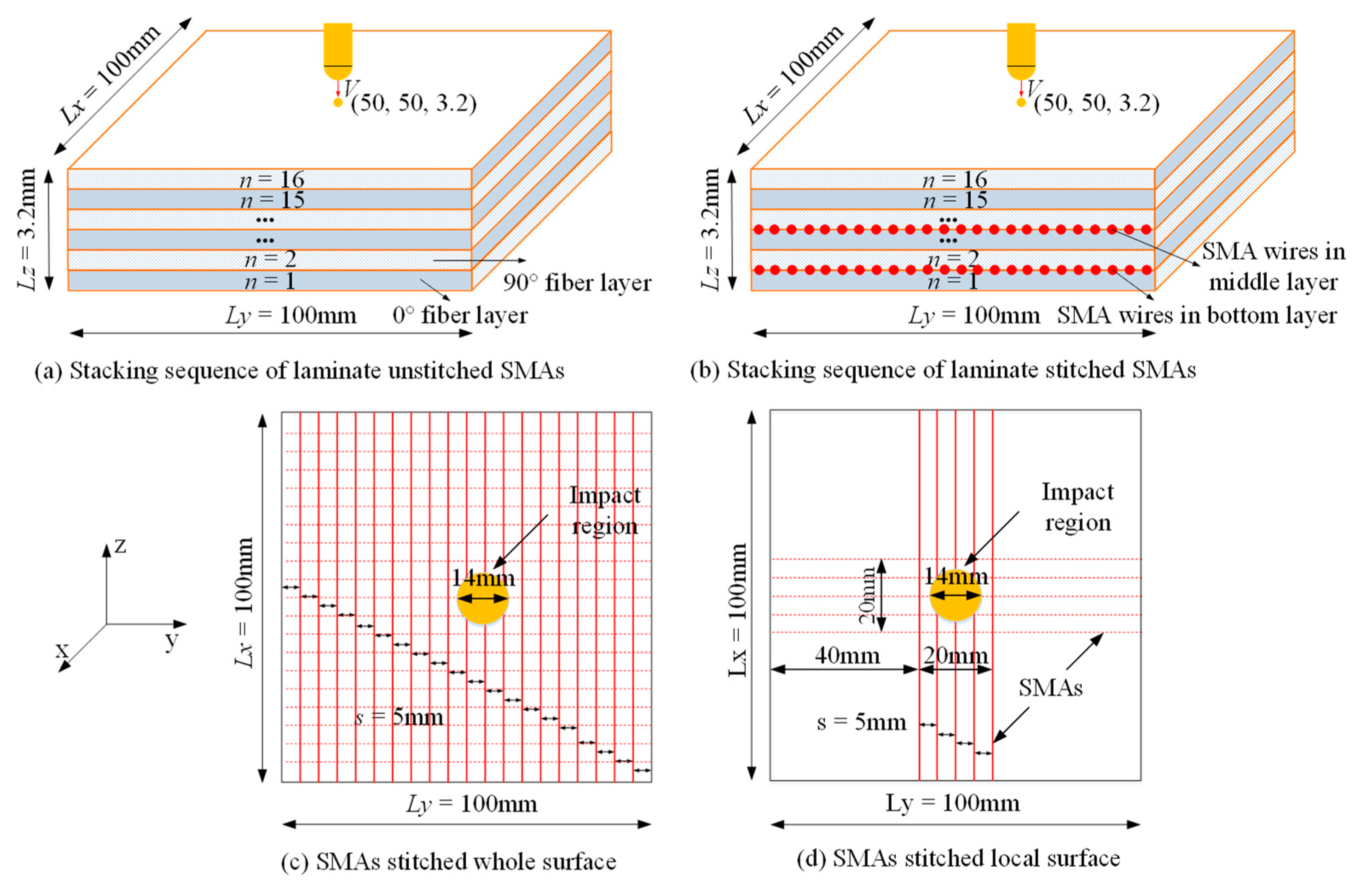
2.1. Low-Velocity Impact Experimental Tests
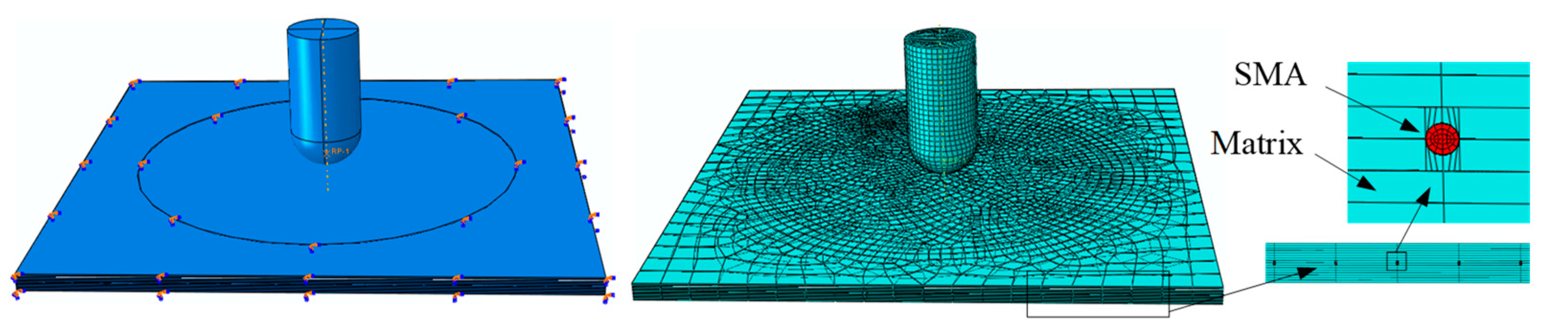
2.2. Numerical Models
2.2.1. SMA Model
2.2.2. Failure Criterion
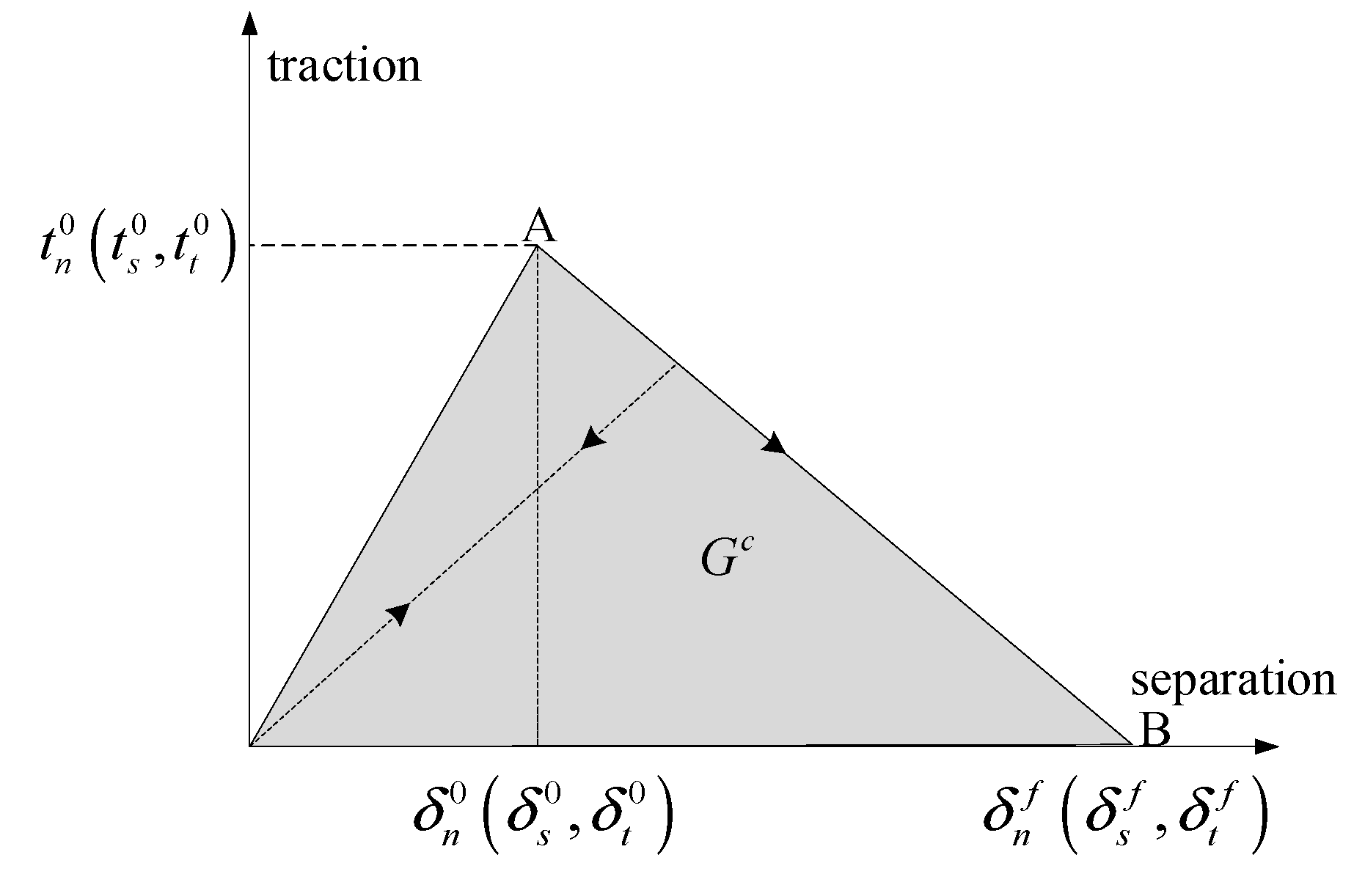
2.2.3. Interlaminar Damage Model
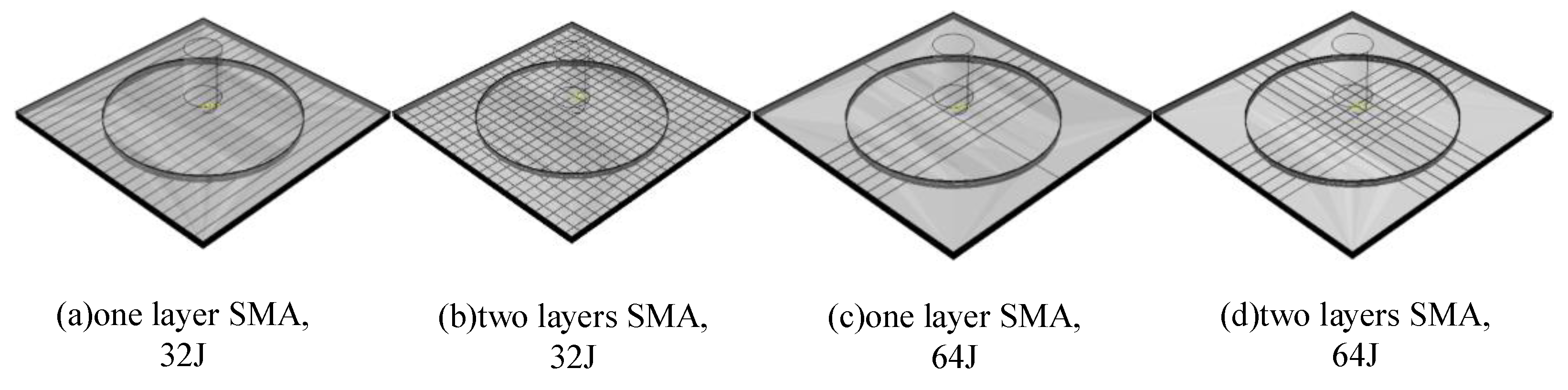
2.2.4. Modeling of Composite Laminates
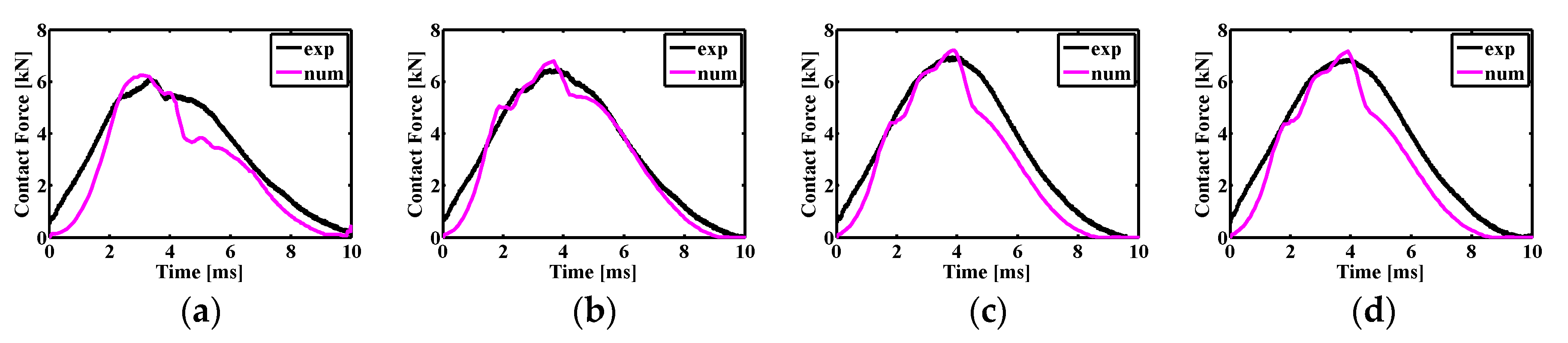
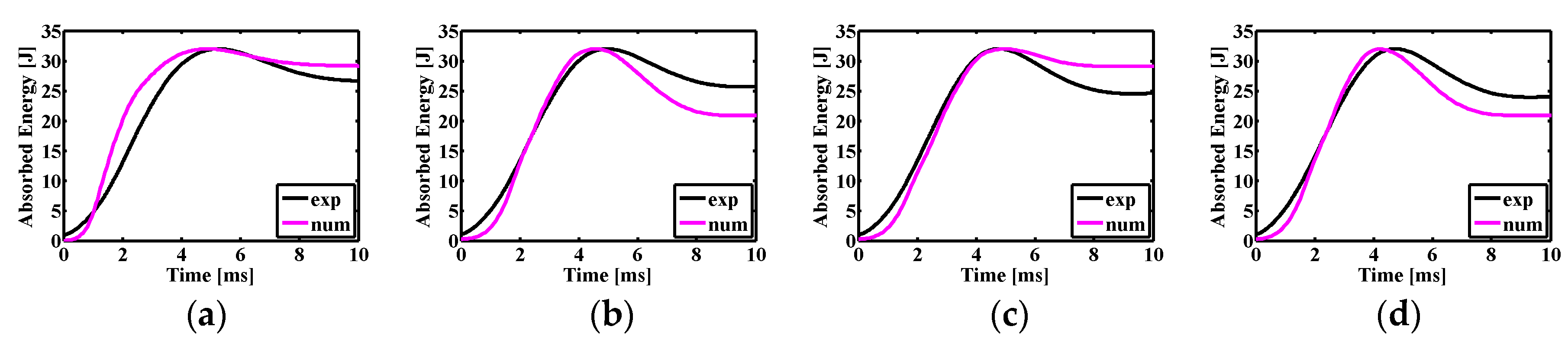
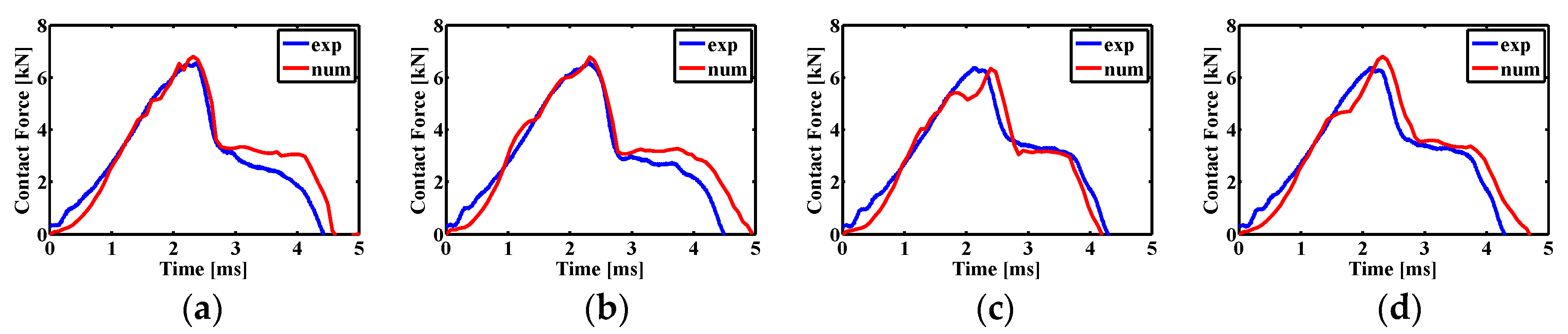
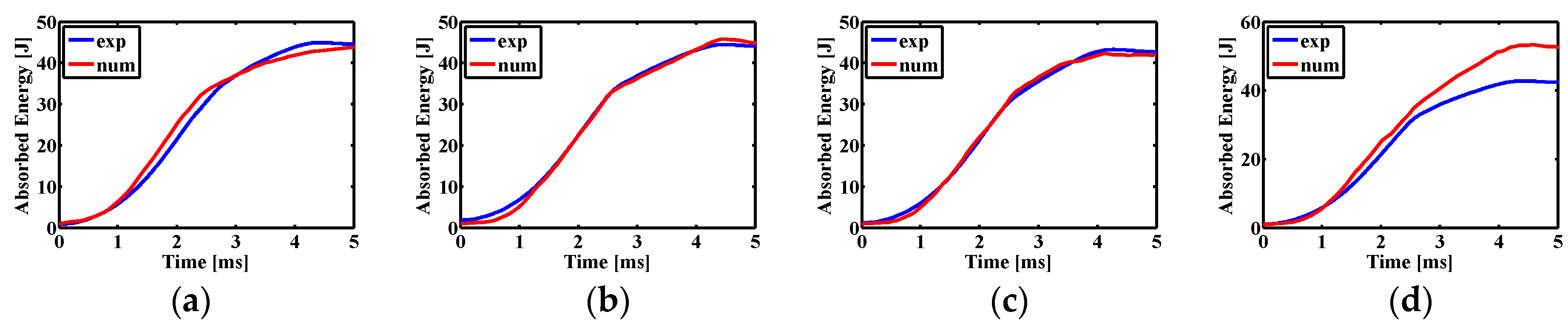
3. Results and Discussions
3.1. Impact Dynamics
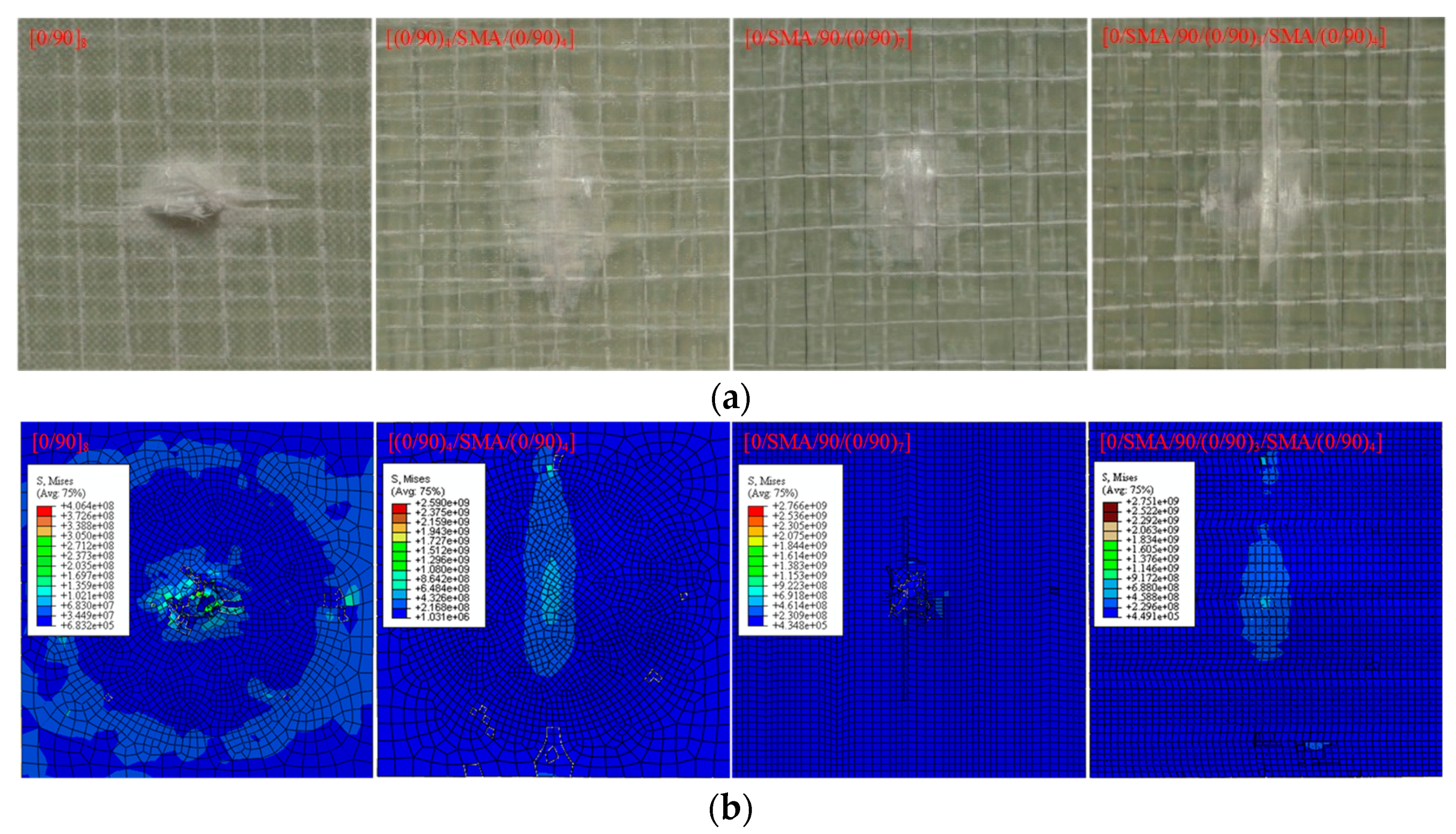
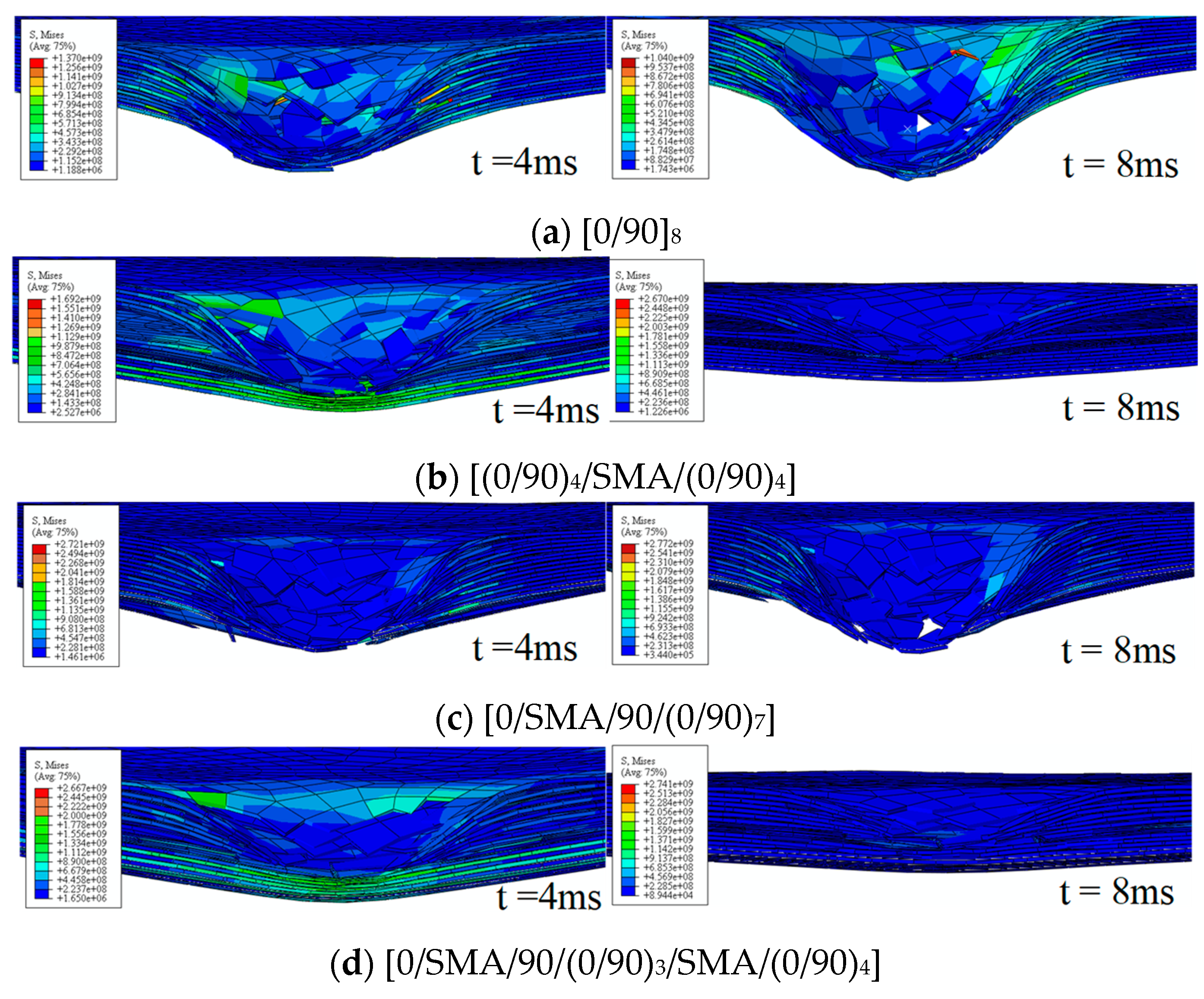
3.2. Damage Morphology
3.3. Impact Damage Mechanism
4. Conclusions
- (1)
- The reported numerical results show a reasonable agreement with the experimental results.
- (2)
- Local indentation, delamination, and matrix crack are the main damage mechanisms of composite laminates at the initial stage of the impact, and fiber breakage occurs later than matrix fracture and delamination during the impact penetration process.
- (3)
- For the case of 32-J impact energy, impact damages are mainly caused by matrix cracks and delamination in the interlayers or the SMA–composite interface of composite laminates. For the case of 64-J impact energy, impact damages are mainly caused by fiber breakage in composite laminates.
- (4)
- The impact resistance property of composite laminates can be significantly improved by embedding the SMA wires into the composites.
Author Contributions
Funding
Conflicts of Interest
References
- Haider, M.F.; Majumdar, P.K.; Angeloni, S.; Reifsnider, K.L. Nonlinear anisotropic electrical response of carbon fiber-reinforced polymer composites. J. Compos. Mater. 2018, 52, 1017–1032. [Google Scholar] [CrossRef]
- Atas, C.; Sayman, O. An overall view on impact response of woven fabric composite plates. Compos. Struct. 2008, 82, 336–345. [Google Scholar] [CrossRef]
- Sevkat, E.; Liaw, B.; Delale, F. Drop-weight impact response of hybrid composites impacted by impactor of various geometries. Mater. Des. 2013, 52, 67–77. [Google Scholar] [CrossRef]
- De Moura, M.; Marques, A.T. Prediction of low velocity impact damage in carbon epoxy laminates. Compos. A Appl. Sci. Manuf. 2002, 33, 361–368. [Google Scholar] [CrossRef]
- Buehler, W.J.; Gilfrich, J.V.; Wiley, R.C. Effect of low-temperature phase changes on the mechanical properties of alloys near composition TiNi. J. Appl. Phys. 1963, 34, 1475–1477. [Google Scholar] [CrossRef]
- Buehler, W.J.; Wiley, R.C. Nickel-Base Alloys. U.S. Patent 3174851, 1965. [Google Scholar]
- Lagoudas, D.C. Shape Memory Alloys; Springer: Boston, MA, USA, 2008; ISBN 978-0-387-47685-8. [Google Scholar]
- Aurrekoetxea, J.; Zurbitu, J.; de Mendibil, I.O.; Agirregomezkorta, A.; Sánchez-Soto, M.; Sarrionandia, M. Effect of superelastic shape memory alloy wires on the impact behavior of carbon fiber reinforced in situ polymerized poly (butylene terephthalate) composites. Mater. Lett. 2011, 65, 863–865. [Google Scholar] [CrossRef]
- Kang, K.W.; Kim, J.K. Effect of shape memory alloy on impact damage behavior and residual properties of glass/epoxy laminates under low temperature. Compos. Struct. 2009, 88, 455–460. [Google Scholar] [CrossRef]
- Pappadà, S.; Gren, P.; Tatar, K.; Gustafson, T.; Rametta, R.; Rossini, E.; Maffezzoli, A. Mechanical and vibration characteristics of laminated composite plates embedding shape memory alloy superelastic wires. J. Mater. Eng. Perform. 2009, 18, 531–537. [Google Scholar] [CrossRef]
- Pappadà, S.; Rametta, R.; Toia, L.; Coda, A.; Fumagalli, L.; Maffezzoli, A. Embedding of superelastic SMA wires into composite structures: Evaluation of impact properties. J. Mater. Eng. Perform. 2009, 18, 522–530. [Google Scholar] [CrossRef]
- Roh, J.H.; Kim, J.H. Hybrid smart composite plate under low velocity impact. Compos. Struct. 2002, 56, 175–182. [Google Scholar] [CrossRef]
- Tsoi, K.A.; Stalmans, R.; Schrooten, J.; Wevers, M.; Mai, Y.W. Impact damage behaviour of shape memory alloy composites. Mater. Sci. Eng. A 2003, 342, 207–215. [Google Scholar] [CrossRef]
- Paine, J.S.N.; Rogers, C.A. The response of SMA hybrid composite materials to low velocity impact. J. Intell. Mater. Syst. Struct. 1994, 5, 530–535. [Google Scholar] [CrossRef]
- Meo, M.; Antonucci, E.; Duclaux, P.; Giordano, M. Finite element simulation of low velocity impact on shape memory alloy composite plates. Compos. Struct. 2005, 71, 337–342. [Google Scholar] [CrossRef]
- Kim, E.H.; Lee, I.; Roh, J.H.; Choi, R.H.; Koo, K.N. Effects of shape memory alloys on low velocity impact characteristics of composite plate. Compos. Struct. 2011, 93, 2903–2909. [Google Scholar] [CrossRef]
- Shariyat, M.; Hosseini, S.H. Accurate eccentric impact analysis of the preloaded SMA composite plates, based on a novel mixed-order hyperbolic global–local theory. Compos. Struct. 2015, 124, 140–151. [Google Scholar] [CrossRef]
- Birman, V.; Chandrashekhara, K.; Sain, S. An approach to optimization of shape memory alloy hybrid composite plates subjected to low-velocity impact. Compos. Part. B Eng. 1996, 27, 439–446. [Google Scholar] [CrossRef]
- Khalili, S.M.R.; Shokuhfar, A.; Malekzadeh, K.; Ghasemi, F.A. Low-velocity impact response of active thin-walled hybrid composite structures embedded with SMA wires. Thin. Wall. Struct. 2007, 45, 799–808. [Google Scholar] [CrossRef]
- Shariyat, M.; Niknami, A. Impact analysis of strain-rate-dependent composite plates with SMA wires in thermal environments: Proposing refined coupled thermoelasticity, constitutive, and contact models. Compos. Struct. 2016, 136, 191–203. [Google Scholar] [CrossRef]
- Sun, M.; Wang, Z.Q.; Yang, B.; Sun, X.K. Experimental investigation of GF/epoxy laminates with different SMAs positions subjected to low-velocity impact. Compos. Struct. 2017, 171, 170–184. [Google Scholar] [CrossRef]
- Hashin, Z.; Rotem, A. A fatigue failure criterion for fiber reinforced materials. J. Compos. Mater. 1973, 7, 448–464. [Google Scholar] [CrossRef]
- Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. Int. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Puck, A.; Schürmann, H. Failure analysis of FRP laminates by means of physically based phenomenological models. Compos. Sci. Technol. 1998, 58, 1045–1067. [Google Scholar] [CrossRef]
- Shi, Y.; Swait, T.; Soutis, C. Modelling damage evolution in composite laminates subjected to low velocity impact. Compos. Struct. 2012, 94, 2902–2913. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- Lopes, C.S.; Camanho, P.P.; Gürdal, Z.; Maimí, P.; González, E.V. Low-velocity impact damage on dispersed stacking sequence laminates. Part II: Numerical simulations. Compos. Sci. Technol. 2009, 69, 937–947. [Google Scholar] [CrossRef]
- Camanho, P.P.; Davila, C.G. Mixed-Mode Decohesion Finite Elements for the Simulation of Delamination in Composite Materials; NASA/TM-2002-211737; NASA Langley Research Center: Hampton, VA, USA, June 2002. [Google Scholar]
- Feng, D.; Aymerich, F. Finite element modelling of damage induced by low-velocity impact on composite laminates. Compos. Struct. 2014, 108, 161–171. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics-Fundamentals and Applications; CRC Press: New York, NY, USA, 1995. [Google Scholar]
- Abrate, S. Impact Engineering of Composite Structures; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]



| Codes/Stacking Sequence | Layer Number of SMAs | Root Number of SMAs | Initial Impact Energy (J) |
|---|---|---|---|
| I: [0/90]8 | 0 | 0 | 32 |
| II: [(0/90)4/SMA/(0/90)4] | 1 | 21 | |
| III: [0/SMA/90/(0/90)7] | 1 | 21 | |
| IV: [0/SMA/90/(0/90)3/SMA/(0/90)4] | 2 | 42 | |
| V: [0/90]8 | 0 | 0 | 64 |
| VI: [(0/90)4/SMA/(0/90)4] | 1 | 5 | |
| VII: [0/SMA/90/(0/90)7] | 1 | 5 | |
| VIII: [0/SMA/90/(0/90)3/SMA/(0/90)4] | 2 | 10 |
| Yield stress (MPa) | 440.3 | 455.1 | 453.1 | 455.1 | 451.4 | 453.1 | 453.4 |
| Equivalent plastic strain | 0 | 0.032 | 0.045 | 0.060 | 0.074 | 0.082 | 0.092 |
| Yield stress (MPa) | 457.1 | 492.6 | 624.1 | 772.2 | 952.4 | 1111.9 | 1226.3 |
| Equivalent plastic strain | 0.102 | 0.111 | 0.121 | 0.130 | 0.141 | 0.151 | 0.160 |
| Mechanical Constants (Symbols) | Values |
|---|---|
| Young’s modulus () | 55.2 GPa, 18.4 GPa, 18.4 GPa |
| Poisson’s ratio () | 0.269, 0.269, 0.428 |
| Shear modulus () | 13.8 GPa, 13.8 GPa, 13.8 GPa |
| Ultimate tensile stress () | 1656 MPa, 73.8 MPa, 73.8 MPa |
| Ultimate compressive stress () | 1656 MPa, 91.8 MPa, 91.8 MPa |
| Ultimate shear stress () | 117.6 MPa, 117.6 MPa, 117.6 MPa |
| Symbols | Interlayer Interfaces | SMA–Layer Interfaces | |
|---|---|---|---|
| Cohesive damage (GPa/m) | , , | 15, 15, 15 | 1.5, 1.5, 1.5 |
| Initiation (MPa) | , , | 123, 96, 96 | 12.3, 19.6, 19.6 |
| Evolution (N/m) | , , | 0.831, 1.99, 1.99 | 0.167, 0.398, 0.398 |
| Stacking Sequence | Experiments | Simulations | ||
|---|---|---|---|---|
| Peak Force (kN) | Absorbed Energy (J) | Peak Force (kN) | Absorbed Energy (J) | |
| [0/90]8 | 6.1012 | 26.2039 | 6.2480 | 29.0969 |
| [(0/90)4/SMA/(0/90)4] | 6.4666 | 25.0616 | 6.7845 | 20.9080 |
| [0/SMA/90/(0/90)7] | 6.9370 | 24.0008 | 7.2166 | 29.0764 |
| [0/SMA/90/(0/90)3/SMA/(0/90)4] | 6.8569 | 23.2786 | 7.1506 | 20.9550 |
| Stacking Sequence | Experiments | Simulations | ||
|---|---|---|---|---|
| Peak Force (kN) | Absorbed Energy (J) | Peak Force (kN) | Absorbed Energy (J) | |
| [0/90]8 | 6.4438 | 45.3494 | 6.7991 | 45.1237 |
| [(0/90)4/SMA/(0/90)4] | 6.5688 | 43.8837 | 6.7771 | 44.9752 |
| [0/SMA/90/(0/90)7] | 6.3605 | 43.3652 | 6.3418 | 41.9943 |
| [0/SMA/90/(0/90)3/SMA/(0/90)4] | 6.5549 | 43.0796 | 6.7991 | 52.7428 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Chang, M.; Wang, Z.; Li, H.; Sun, X. Experimental and Simulation Study of Low-Velocity Impact on Glass Fiber Composite Laminates with Reinforcing Shape Memory Alloys at Different Layer Positions. Appl. Sci. 2018, 8, 2405. https://doi.org/10.3390/app8122405
Sun M, Chang M, Wang Z, Li H, Sun X. Experimental and Simulation Study of Low-Velocity Impact on Glass Fiber Composite Laminates with Reinforcing Shape Memory Alloys at Different Layer Positions. Applied Sciences. 2018; 8(12):2405. https://doi.org/10.3390/app8122405
Chicago/Turabian StyleSun, Min, Mengzhou Chang, Zhenqing Wang, Hao Li, and Xiaokun Sun. 2018. "Experimental and Simulation Study of Low-Velocity Impact on Glass Fiber Composite Laminates with Reinforcing Shape Memory Alloys at Different Layer Positions" Applied Sciences 8, no. 12: 2405. https://doi.org/10.3390/app8122405




