Finite Element Analysis of Thermal Stress and Thermal Deformation in Typical Part during SLM
Abstract
:Featured Application
Abstract
1. Introduction
2. Mobile Heat Source and Thermal–Mechanical Coupling Algorithm
2.1. Heat Source
2.2. Heat-Transfer Equation
2.3. Thermal–Mechanical Coupling
2.4. Stress–Strain Equations
2.5. Initial Conditions and Boundary Conditions
σ,ε,τ,γ | t=20 = 0
u, v, w | t=20 = 0
2.6. Material Properties of 316L
3. Simulation Process and Operation
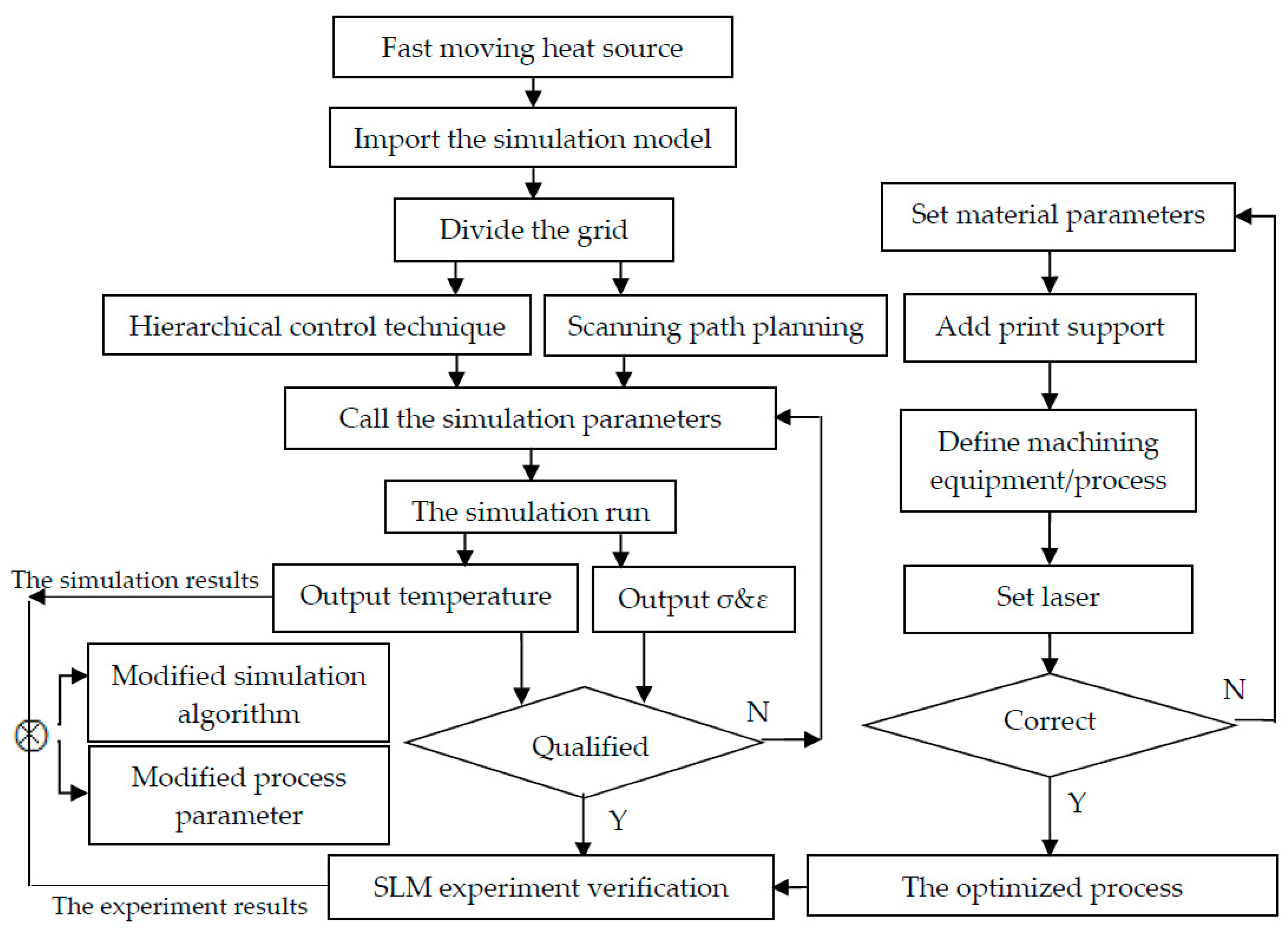
3.1. Simulation Flow
3.2. Simulation Parameters
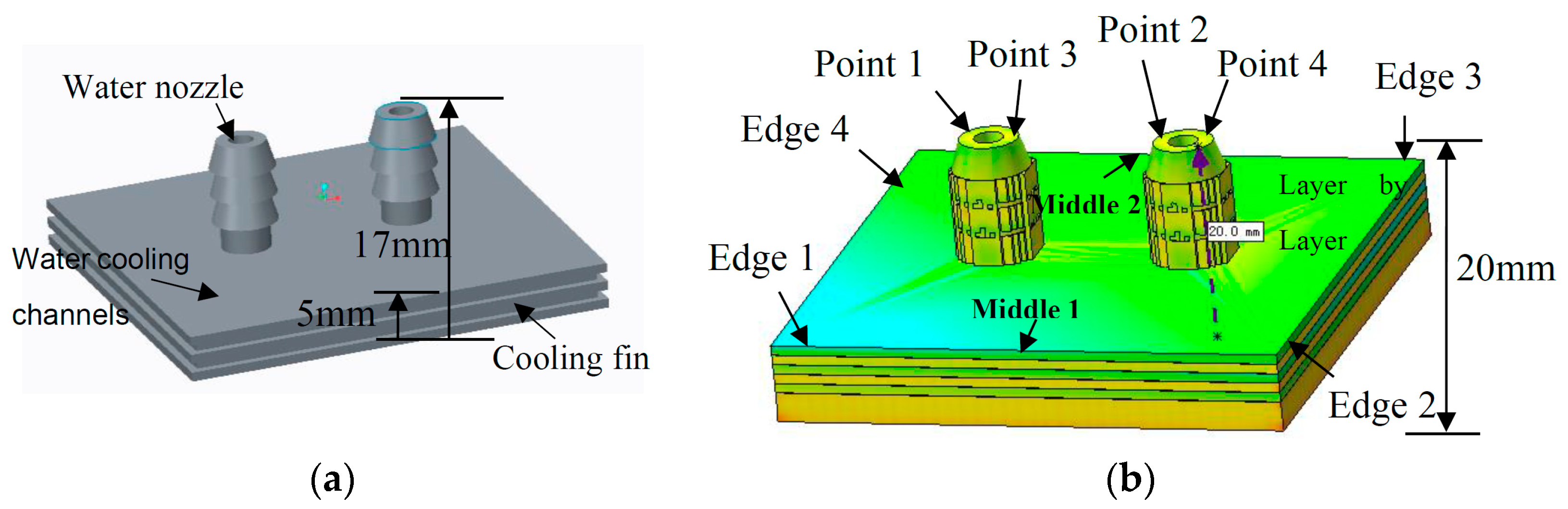
3.3. Simulation Runs
4. Emulation Results and Discussion
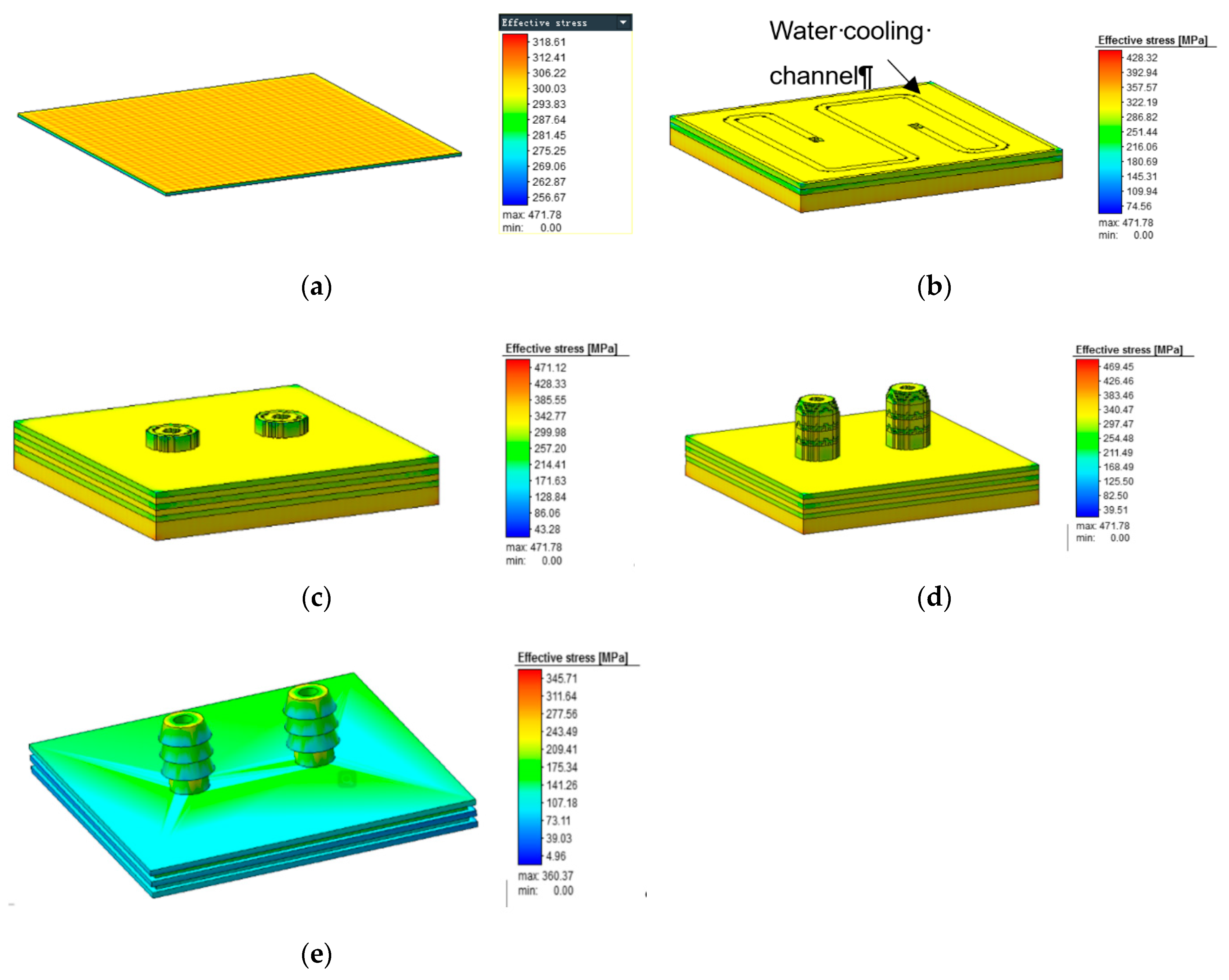
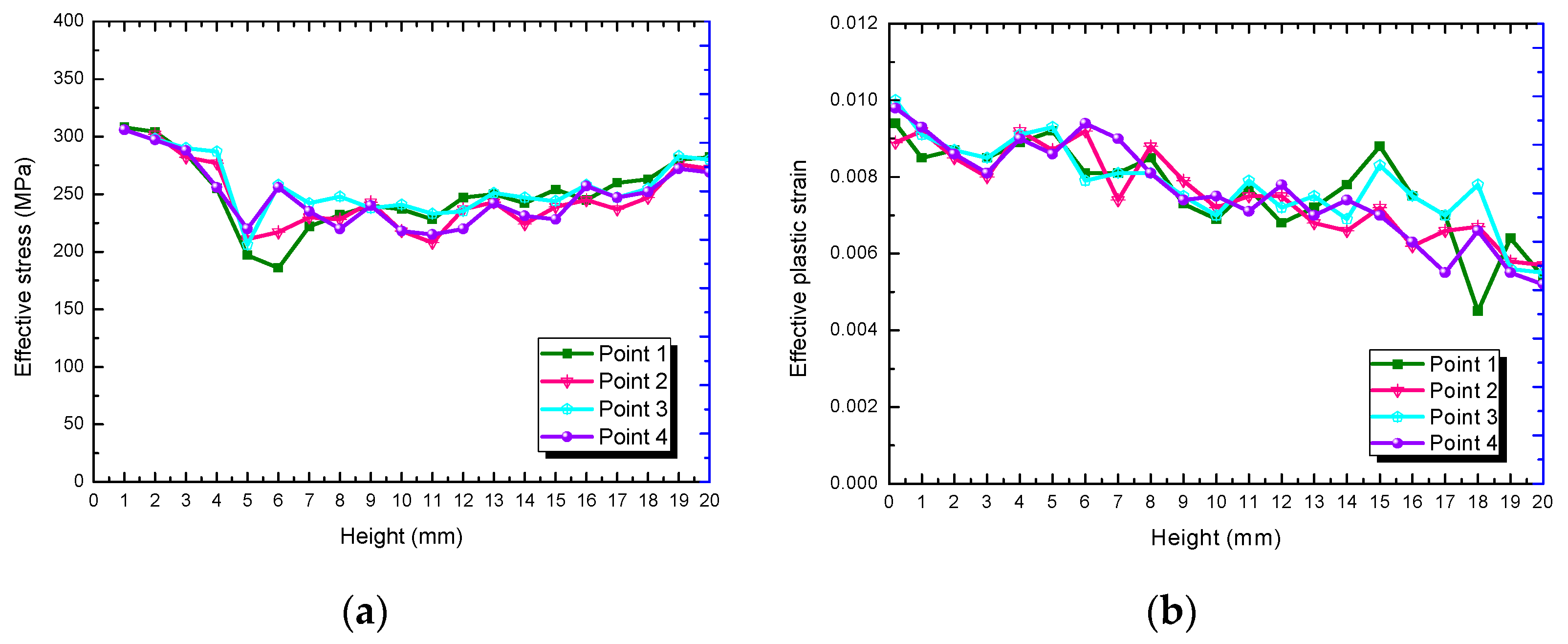
4.1. Effective Stress and Strain
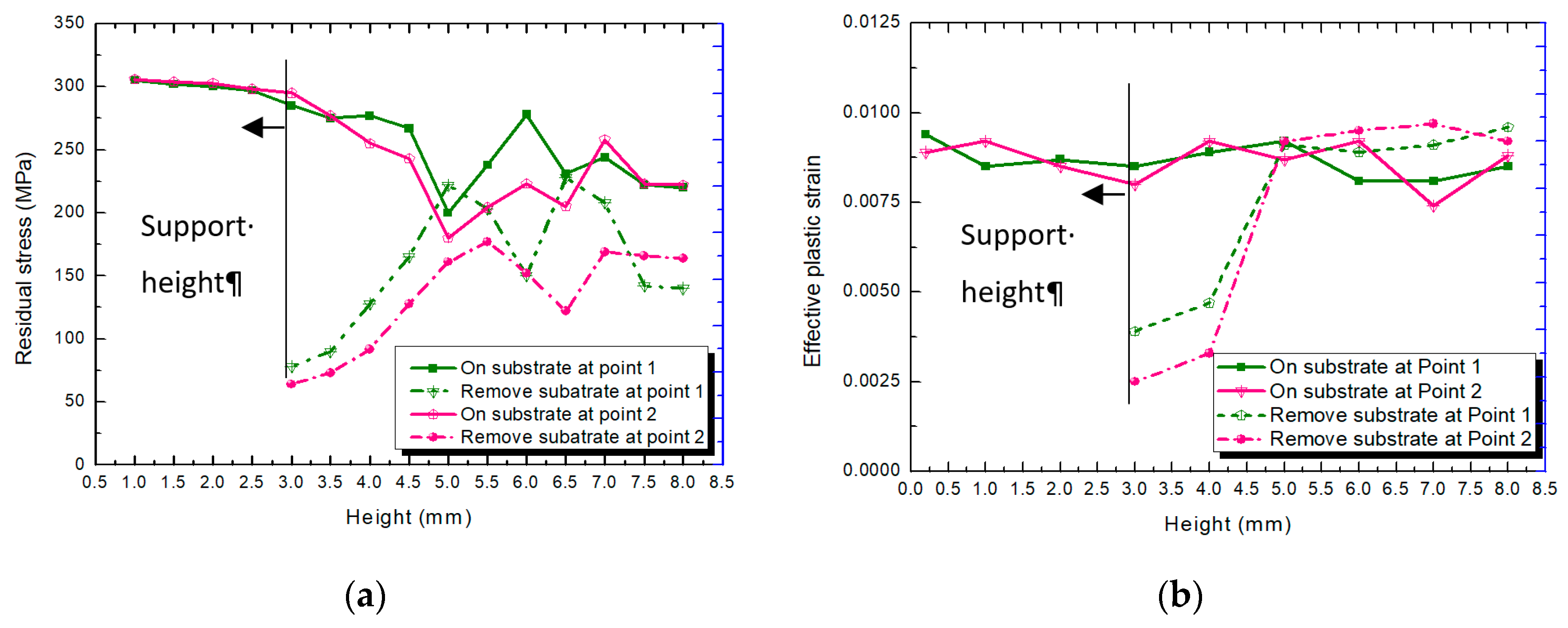
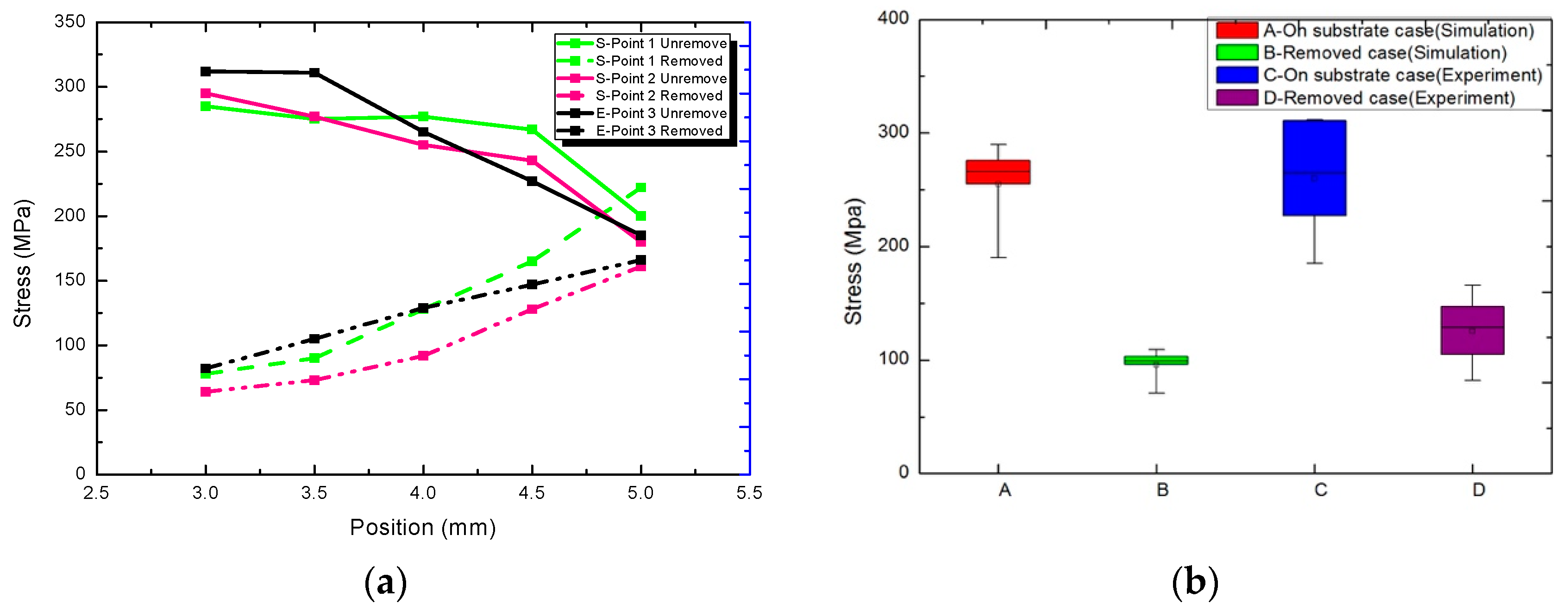
4.2. Stress Release in Removed Substrate
4.3. X/Y/Z Uniaxial Plane Stress
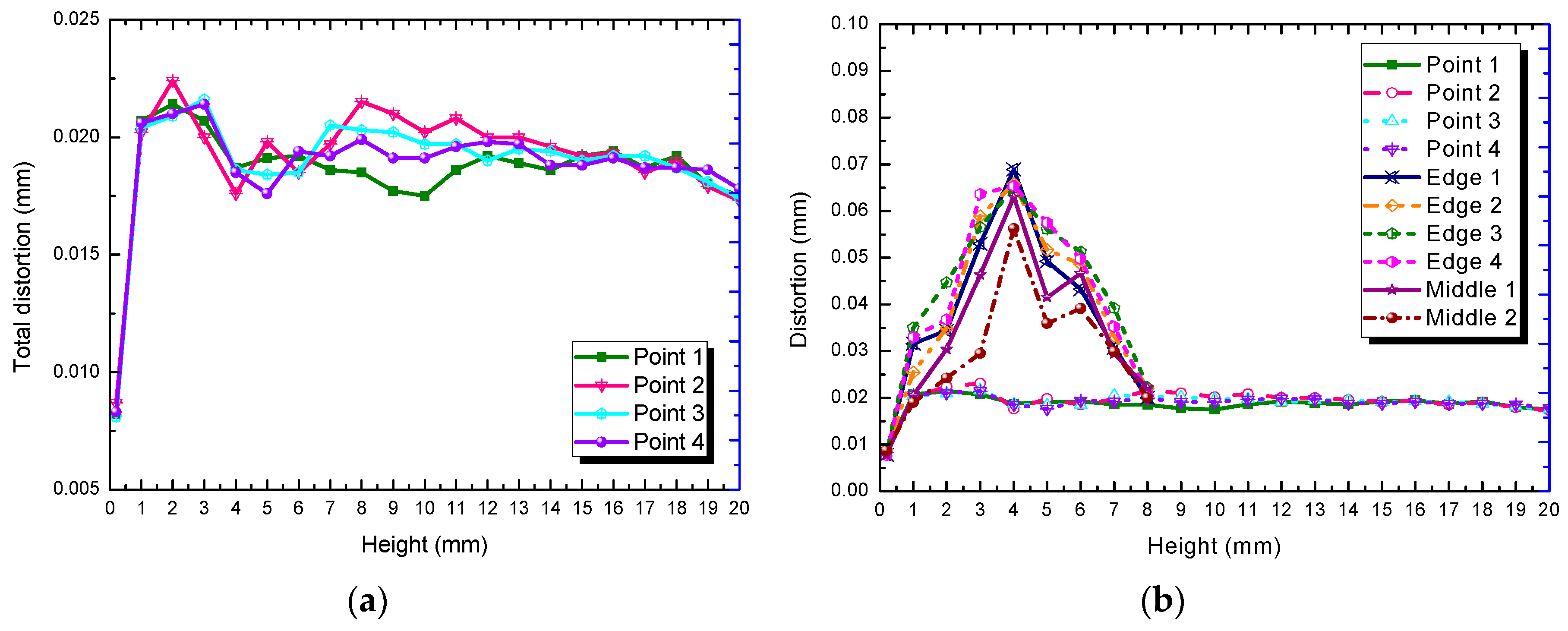
4.4. Thermal Deformation
5. Experimental Results and Analysis
5.1. Residual Stress
5.2. Residual Deformation
6. Conclusions
- According to the reasonable design simulation algorithm and process parameters, the simulation process of the SLM parts was completed. Consequently, the thermodynamic coupling algorithm was simple and effective, while the thermal stress and thermal strain data were calculated to draw the curve.
- For the simulated sample, the thermal stress increased from the substrate to the upper surface layer by layer. While the stress was reduced when the substrate was removed, the stress decreased from the substrate to the upper surface.
- For the forming plane, the uniaxial stress reached the tension and pressure equilibrium state. Through the σx/σy/σz comparison, the same three areas—Areas I, II, and III (in Figure 7d–f)—showed tensile and compressive stress, but the amplitude and breadth were highly different. Furthermore, the maximum residual stresses of the 316L stainless steel under these process parameters were σxMax = 295 MPa, σyMax = 283 MPa, and σzMax = 305 MPa.
- The changes of strain and thermal stress trends were relative, while the macroscopic geometric deformation occurred. From the simulation results, it could be deduced that the thermal deformation and thermal stress were in positive proportion. The higher deformation occurred at the corner of the same plane and the maximum deformation amount was located at the support toward the solid parts.
- After the simulation, a set of optimizing technological parameters in the experiment was printed in the case model. The characteristics of the experimentally formed parts were consistent with the simulation results. It was observed that the simulation analysis could effectively predict the quality of the forming parts, which proved instructive to the practical production.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hitzler, L.; Merkel, M.; Hall, W.; Öchsner, A. A Review of Metal Fabricated with Laser- and Powder-Bed Based Additive Manufacturing Techniques: Process, Nomenclature, Materials, Achievable Properties, and its Utilization in the Medical Sector. Adv. Eng. Mater. 2018, 20, 1700658. [Google Scholar] [CrossRef]
- Debroy, T.; Wei, H.; Zuback, J.; Mukherjee, T.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Yap, C.Y.; Chua, C.K.; Dong, Z.L.; Liu, Z.H.; Zhang, D.Q.; Loh, L.E. Review of selective laser melting: Materials and applications. Appl. Phys. Rev. 2015, 2, 041101. [Google Scholar] [CrossRef]
- Ren, X.; Shao, H.; Lin, T.; Zheng, H. 3d gel-printing—an additive manufacturing method for producing complex shape parts. Mater. Des. 2016, 101, 80–87. [Google Scholar] [CrossRef]
- Lee, H.; Lim, C.H.J.; Low, M.J.; Tham, N.; Murukeshan, V.M.; Kim, Y.J. Lasers in additive manufacturing: A review. Int. J. Precis. Eng. and Manuf. Green Technol. 2017, 4, 307–322. [Google Scholar] [CrossRef]
- Van Belle, L.; Agazzi, A. Inverse thermal analysis of melting pool in selective laser melting process. Key Eng. Mater. 2015, 651, 1519–1524. [Google Scholar] [CrossRef]
- Debroy, T.; Zhang, W.; Turner, J.; Babu, S.S. Building digital twins of 3d printing machines. Scr. Mater. 2017, 135, 119–124. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A.T.; Rubenchik, A.; King, W.E. Laser powder-bed fusion additive manufacturing: Physics of complex melt flow and formation mechanisms of pores, spatter, and denudation zones. Acta Mater. 2016, 108, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Yang, L.J.; Du, X.Z.; Yang, Y.P. Finite element analysis of thermal behavior of metal powder during selective laser melting. Int. J. Therm. Sci. 2016, 104, 146–157. [Google Scholar] [CrossRef]
- Foroozmehr, A.; Badrossamay, M.; Foroozmehr, E.; Golabi, S. Finite element simulation of selective laser melting process considering optical penetration depth of laser in powder bed. Mater. Des. 2016, 89, 255–263. [Google Scholar] [CrossRef]
- Zohdi, T.I. Dynamic thermomechanical modeling and simulation of the design of rapid free-form 3d printing processes with evolutionary machine learning. Comput. Meth. Appl. Mech. Eng. 2018, 331, 343–362. [Google Scholar] [CrossRef]
- Wu, A.S.; Brown, D.W.; Kumar, M.; Gallegos, G.F.; King, W.E. An experimental investigation into additive manufacturing-induced residual stresses in 316l stainless steel. Metall. Mater. Trans. A 2014, 45, 6260–6270. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Wang, D. A study on the residual stress during selective laser melting (slm) of metallic powder. Int. J. Adv. Manuf. Technol. 2016, 87, 647–656. [Google Scholar] [CrossRef]
- An, K.; Yuan, L.; Dial, L.; Spinelli, I.; Stoica, A.D.; Gao, Y. Neutron residual stress measurement and numerical modeling in a curved thin-walled structure by laser powder bed fusion additive manufacturing. Mater. Des. 2017, 135, 122–132. [Google Scholar] [CrossRef]
- Matsumoto, M.; Shiomi, M.; Osakada, K.; Abe, F. Finite element analysis of single layer forming on metallic powder bed in rapid prototyping by selective laser processing. Int. J. Mach. Tools Manuf. 2002, 42, 61–67. [Google Scholar] [CrossRef]
- Krol, T.A.; Seidel, C.; Zaeh, M.F. Prioritization of process parameters for an efficient optimisation of additive manufacturing by means of a finite element method. Proced. Cirp. 2013, 12, 169–174. [Google Scholar] [CrossRef]
- Hussein, A.; Hao, L.; Yan, C.; Everson, R. Finite element simulation of the temperature and stress fields in single layers built without-support in selective laser melting. Mater. Des. 2013, 52, 638–647. [Google Scholar] [CrossRef]
- Criales, L.E.; Arısoy, Y.M.; Özel, T. Sensitivity analysis of material and process parameters in finite element modeling of selective laser melting of inconel 625. Int. J. Adv. Manuf. Technol. 2016, 86, 1–14. [Google Scholar] [CrossRef]
- Vastola, G.; Zhang, G.; Pei, Q.X.; Zhang, Y.W. Controlling of residual stress in additive manufacturing of ti6al4v by finite element modeling. Addit. Manuf. 2016, 12, 231–239. [Google Scholar] [CrossRef]
- Parry, L.; Ashcroft, I.A.; Wildman, R.D. Understanding the effect of laser scan strategy on residual stress in selective laser melting through thermo-mechanical simulation. Addit. Manuf. 2016, 12, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Gu, D.; He, B. Finite element simulation and experimental investigation of residual stresses in selective laser melted ti–ni shape memory alloy. Comput. Mater. Sci. 2016, 117, 221–232. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, P.; Cheng, L.; Min, Z.; Chyu, M.; To, A.C. Finite element modeling and validation of thermomechanical behavior of ti-6al-4v in directed energy deposition additive manufacturing. Addit. Manuf. 2016, 12, 169–177. [Google Scholar] [CrossRef]
- Pei, W.; Wei, Z.; Zhen, C.; Li, J.; Zhang, S.; Du, J. Numerical simulation and parametric analysis of selective laser melting process of alsi10mg powder. Appl. Phys. A 2017, 123, 540. [Google Scholar] [CrossRef]
- Zhao, X.; Iyer, A.; Promoppatum, P.; Yao, S.C. Numerical modeling of the thermal behavior and residual stress in the direct metal laser sintering process of titanium alloy products. Addit. Manuf. 2017, 14, 126–136. [Google Scholar] [CrossRef]
- Belle, L.V. Numerical simulation of complex part manufactured by selective laser melting process. In Proceedings of the International Conference of Global Network for Innovative Technology and Awam International Conference in Civil Engineering, Penang, Malaysia, 8–9 August 2017. [Google Scholar]
- Li, Y.; Zhou, K.; Tan, P.; Shu, B.T.; Chua, C.K.; Leong, K.F. Modeling temperature and residual stress fields in selective laser melting. Int. J. Mech. Sci. 2018, 136, 24–35. [Google Scholar] [CrossRef]
- Ali, H.; Ghadbeigi, H.; Mumtaz, K. Residual stress development in selective laser-melted ti6al4v: A parametric thermal modelling approach. Int. J. Adv. Manuf. Technol. 2018, 97, 2621–2633. [Google Scholar] [CrossRef]
- Luo, C.; Qiu, J.; Yan, Y.; Yang, J.; Uher, C.; Tang, X. Finite element analysis of temperature and stress fields during the selective laser melting process of thermoelectric snte. J. Mater. Process. Technol. 2018, 261, 74–85. [Google Scholar] [CrossRef]
- Arni, R.; Gupta, S.K. Manufacturability analysis of flatness tolerances in solid freeform fabrication. J. Mech. Des. 2001, 123, 148–156. [Google Scholar] [CrossRef]
- Rattanawong, W.; Masood, S.H.; Iovenitti, P. A volumetric approach to part-build orientations in rapid prototyping. J. Mater. Process. Technol. 2001, 119, 348–353. [Google Scholar] [CrossRef]
- Masood, S.H.; Rattanawong, W. A generic part orientation system based on volumetric error in rapid prototyping. Int. J. Adv. Manuf. Technol. 2002, 19, 209–216. [Google Scholar] [CrossRef]
- Nagahanumaiah; Subburaj, K.; Ravi, B. Computer aided rapid tooling process selection and manufacturability evaluation for injection mold development. Comput. Ind. 2008, 59, 262–276. [Google Scholar] [CrossRef]
- Ollison, T.; Berisso, K. Three-dimensional printing build variables that impact cylindricity. J. Ind. Technol. 2010, 26, 1–10. [Google Scholar]
- Lynn-Charney, C.; Rosen, D.W. Usage of accuracy models in stereolithography process planning. Rapid Prototyp. J. 2000, 6, 77–87. [Google Scholar] [CrossRef]
- Paul, R.; Anand, S. Optimal part orientation in rapid manufacturing process for achieving geometric tolerances. J. Manuf. Syst. 2011, 30, 214–222. [Google Scholar] [CrossRef]
- Paul, R.; Anand, S. Material Shrinkage Modeling and Form Error Prediction in Additive Manufacturing Processes. In Proceedings of the 41st NAMRC 2013, University of Wisconsin-Madison, Madison, WI, USA, 10–14 June 2013. [Google Scholar]
- Paul, R.; Anand, S.; Gerner, F. Effect of thermal deformation on part errors in metal powder based additive manufacturing processes. J. Manuf. Sci. Eng. 2014, 136, 031009. [Google Scholar] [CrossRef]
- Hitzler, L.; Hirsch, J.; Heine, B.; Merkel, M.; Hall, W.; Öchsner, A. On the Anisotropic Mechanical Properties of Selective Laser Melted Stainless Steel. Materials 2017, 10, 1136. [Google Scholar] [CrossRef]
- Hitzler, L.; Hirsch, J.; Tomas, J.; Merkel, M.; Hall, W.; Öchsner, A. In-plane Anisotropy of Selective Laser Melted Stainless Steel: The Importance of the Rotation Angle Increment and the Limitation Window. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2018, 1464420718757068. [Google Scholar] [CrossRef]
- Thijs, L.; Kempen, K.; Kruth, J.P.; Van Humbeeck, J. Fine-structured aluminium products with controllable texture by selective laser melting of pre-alloyed alsi10mg powder. Acta Mater. 2013, 61, 1809–1819. [Google Scholar] [CrossRef]
- Sun, Z.; Tan, X.; Tor, S.B.; Yeong, W.Y. Selective laser melting of stainless steel 316L with low porosity and high build rates. Mater. Des. 2016, 104, 197–204. [Google Scholar] [CrossRef]
- Prashanth, K.G.; Eckert, J. Formation of metastable cellular microstructures in selective laser melted alloys. J. Alloys Compd. 2017, 707, 27–34. [Google Scholar] [CrossRef]
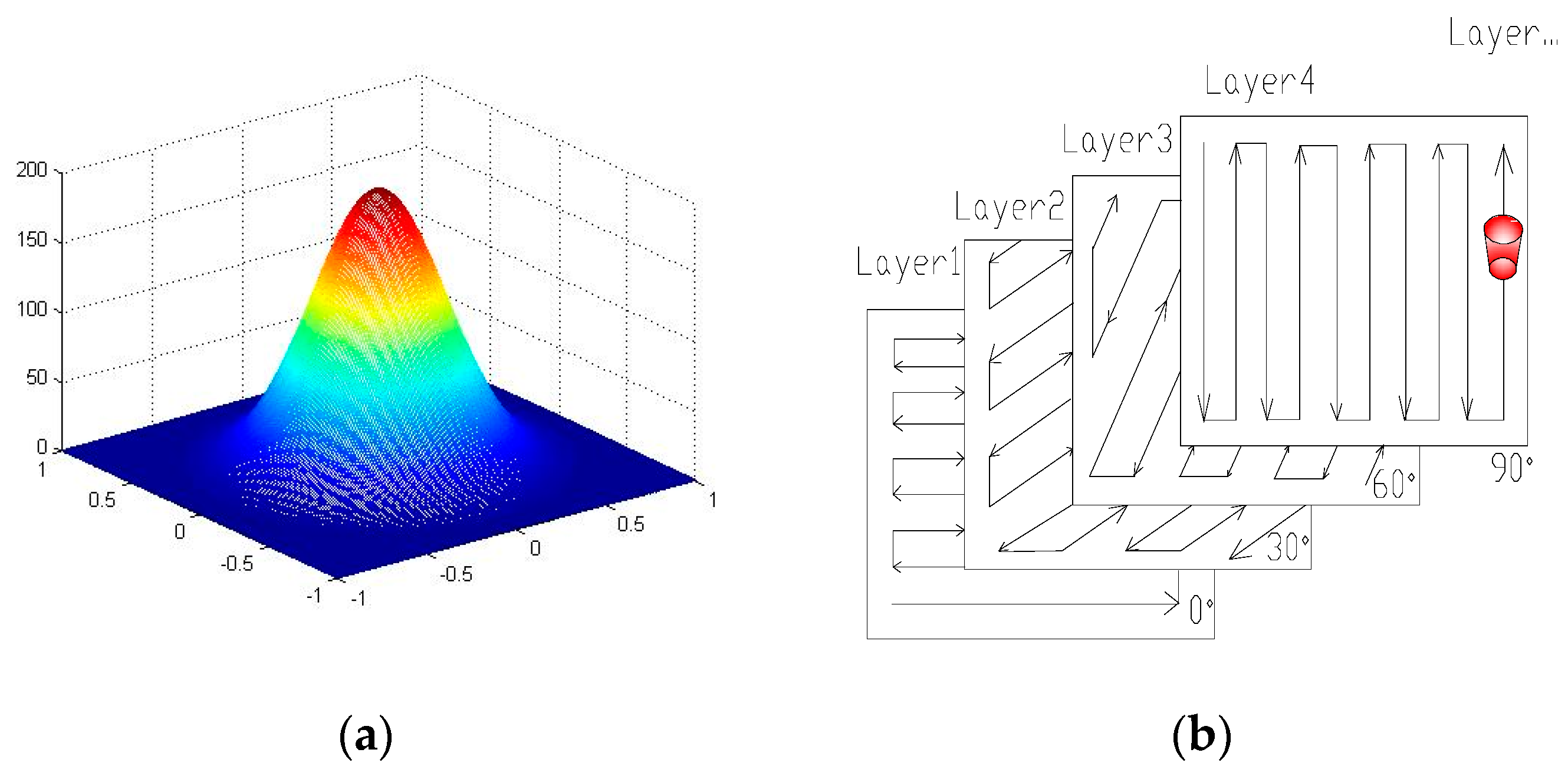



| Temperature T(K) | 273 | 1563 | 1713 | 2793 | 3153 | |
|---|---|---|---|---|---|---|
| 316L Stainless Steel Powder | Thermal conductivity, K (W/m K) | 0 | 0 | 32 | 40 | 45 |
| Specific heat capacity, C (J/kg K) | 0 | 110 | 180 | 290 | 800 | |
| Density, ρ (kg/m3) | 4750 | 4450 | 7000 | 6000 | 5750 | |
| Solid 316L Stainless Steel | Thermal conductivity, K (W/m K) | 12 | 30 | 32 | 40 | 45 |
| Specific heat capacity, C (J/kg K) | 470 | 700 | 820 | 820 | 820 | |
| Density, ρ (kg/m3) | 8000 | 7250 | 7000 | 6000 | 5750 | |
| Thermal expansion, α (1/K) Young’s modulus, E (GPa) Poisson’s ratio, μ | 12 × 10−6 206 0.3 | 14 × 10−6 20 0.4 | 14.2 × 10−6 13.5 0.41 | 14.5 × 10−6 0.2 0.43 | 15 × 10−6 0.02 0.45 | |
| Parameters | Simulation | Experiment |
|---|---|---|
| Laser power | 100 W | 100 W |
| Scan speed | 500 mm/s | 500 mm/S |
| Thickness | 0.03 mm | 0.03 mm |
| Laser absorptivity | 0.7 | 0.7 |
| Substrate Temperature | 20 °C | 20 °C |
| Materials | 316L powder | 316L powder |
| Equipment | — | Concept |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, P.; Shao, X.; Du, J. Finite Element Analysis of Thermal Stress and Thermal Deformation in Typical Part during SLM. Appl. Sci. 2019, 9, 2231. https://doi.org/10.3390/app9112231
Bian P, Shao X, Du J. Finite Element Analysis of Thermal Stress and Thermal Deformation in Typical Part during SLM. Applied Sciences. 2019; 9(11):2231. https://doi.org/10.3390/app9112231
Chicago/Turabian StyleBian, Peiying, Xiaodong Shao, and Jingli Du. 2019. "Finite Element Analysis of Thermal Stress and Thermal Deformation in Typical Part during SLM" Applied Sciences 9, no. 11: 2231. https://doi.org/10.3390/app9112231
APA StyleBian, P., Shao, X., & Du, J. (2019). Finite Element Analysis of Thermal Stress and Thermal Deformation in Typical Part during SLM. Applied Sciences, 9(11), 2231. https://doi.org/10.3390/app9112231





