A CFOA-Based Voltage-Mode Multifunction Biquadratic Filter and a Quadrature Oscillator Using the CFOA-Based Biquadratic Filter
Abstract
:1. Introduction
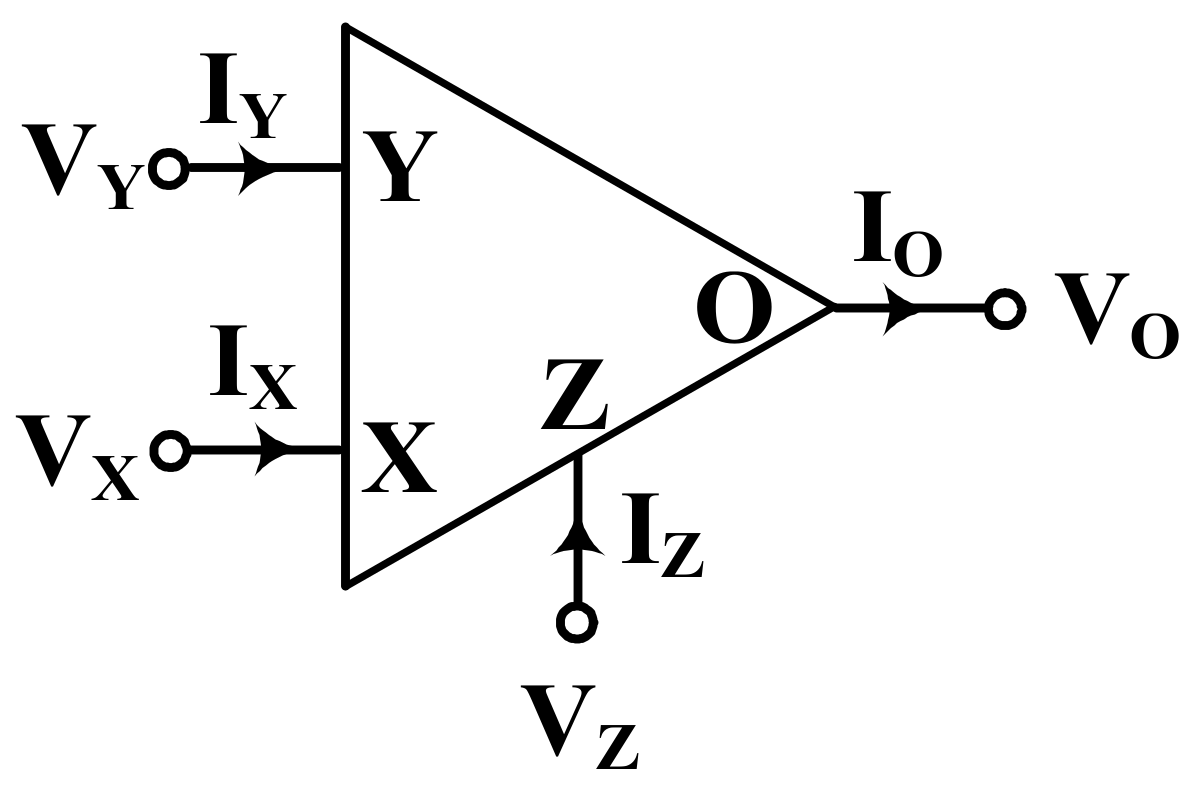
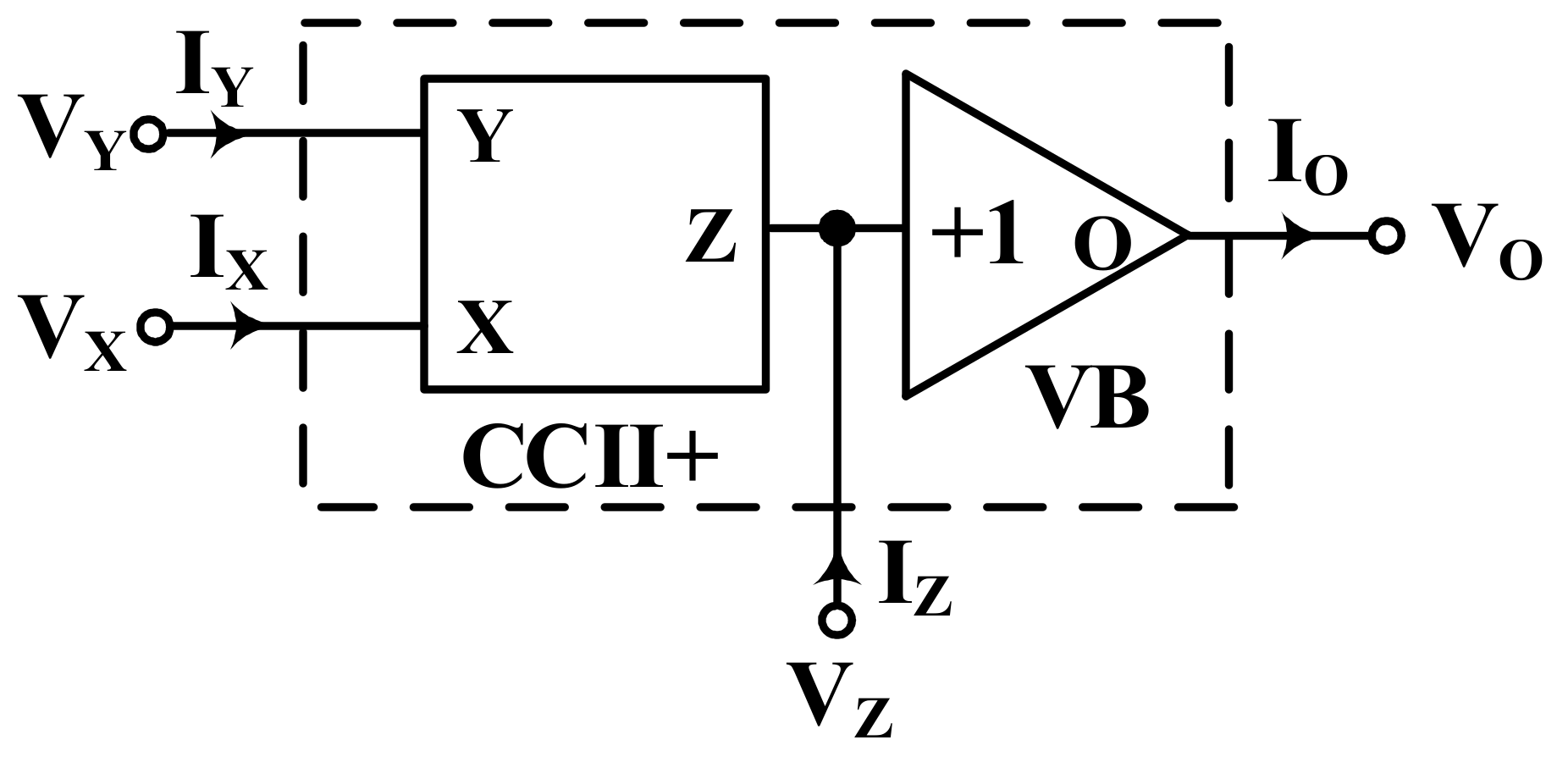
2. Proposed Circuits
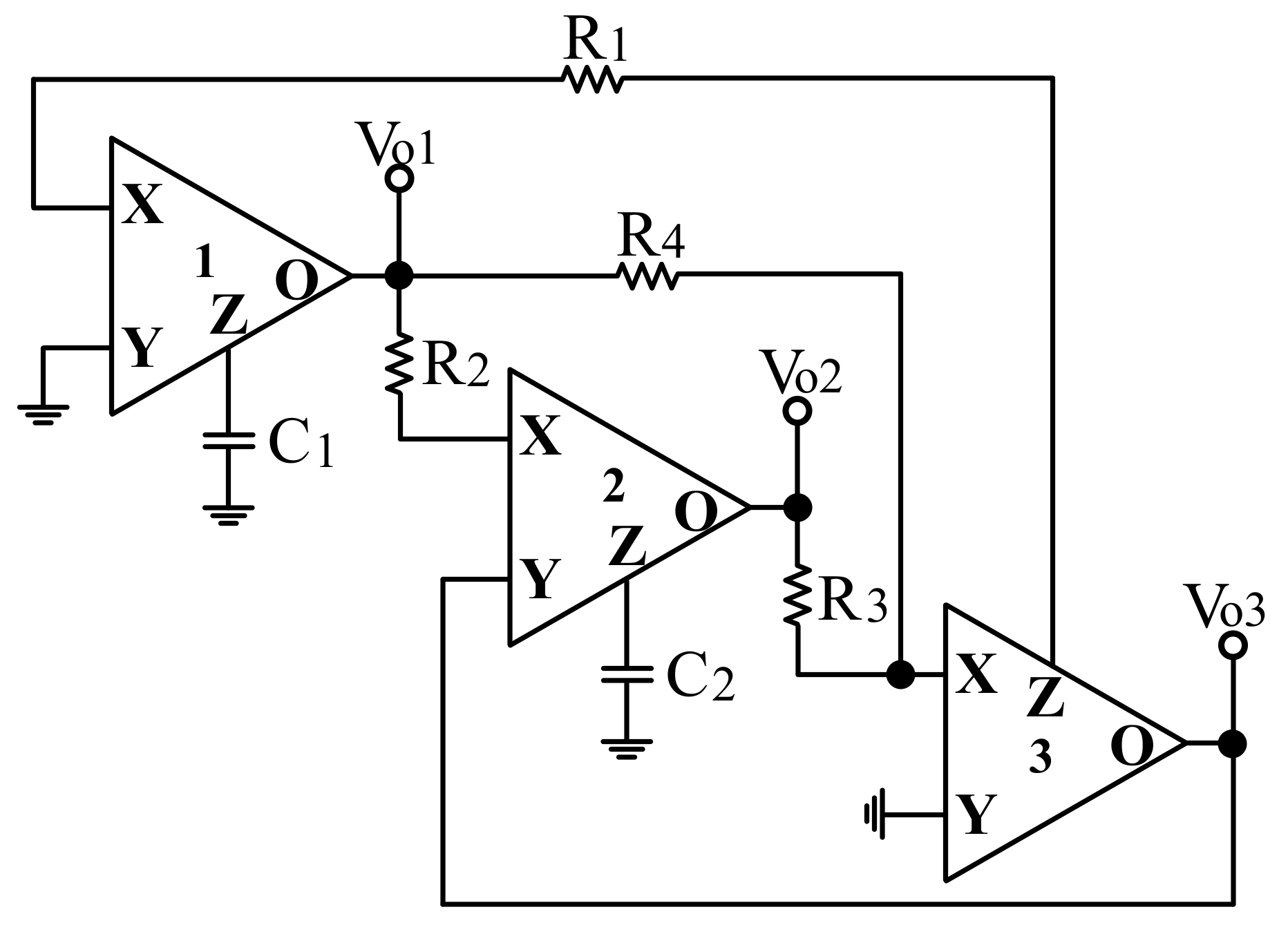
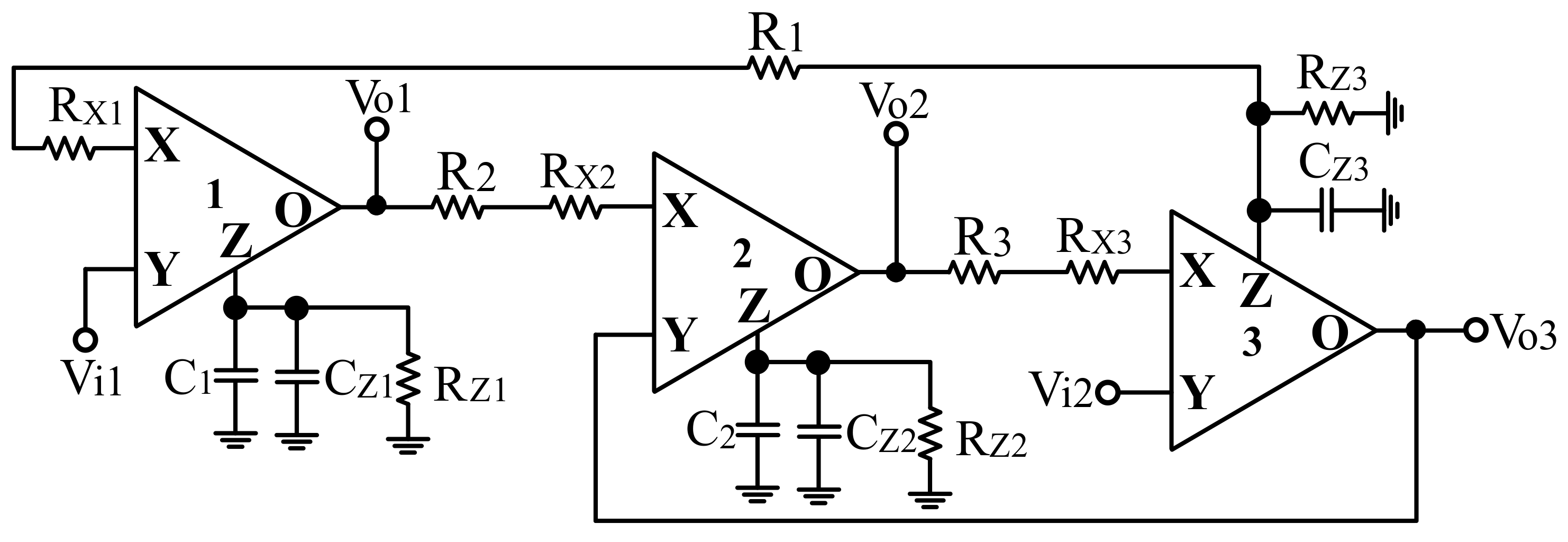
2.1. Voltage-Mode Multifunction Biquadratic Filter
2.2. Voltage-Mode Quadrature Sinusoidal Oscillator
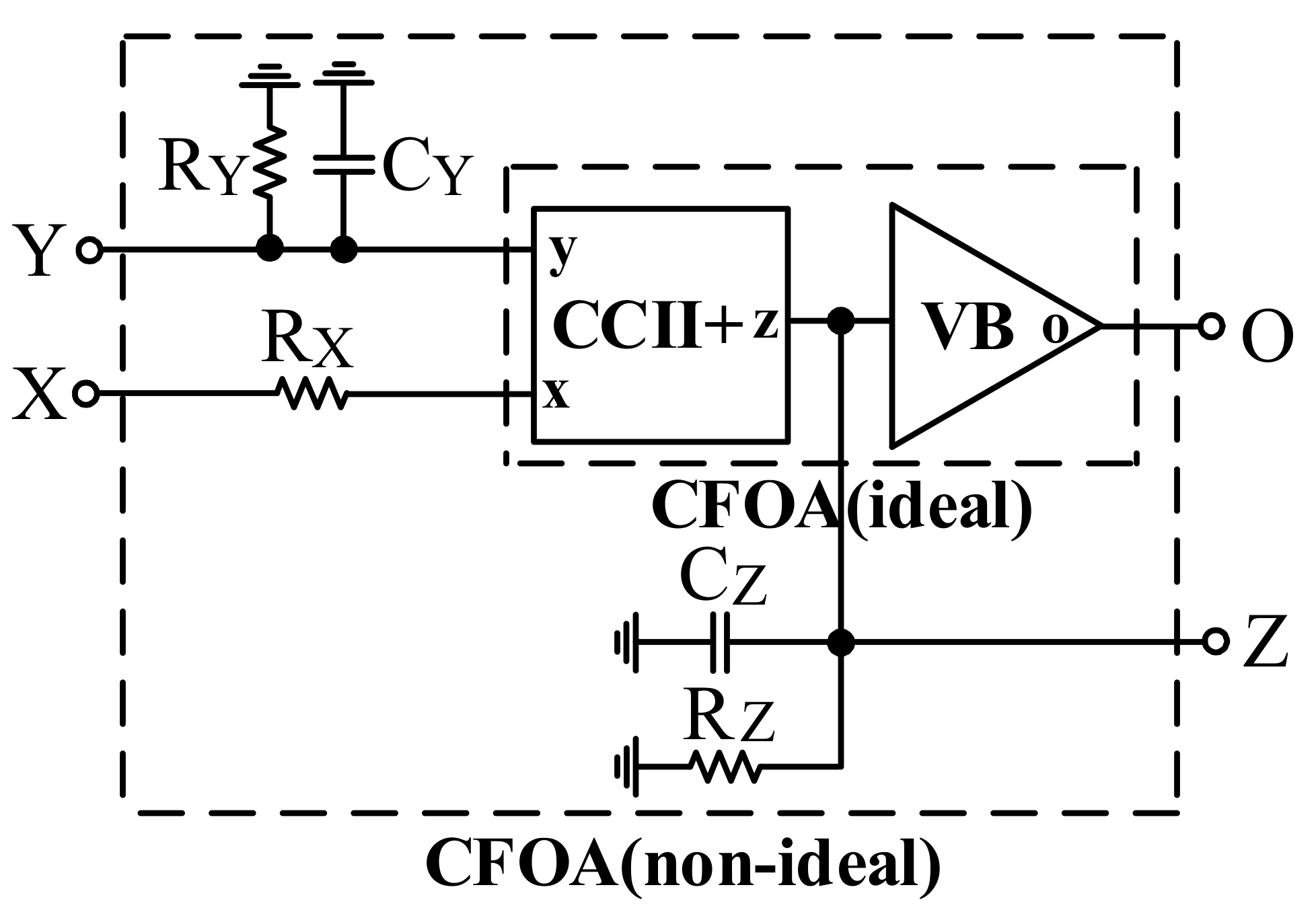
3. Non-Idealities Analysis
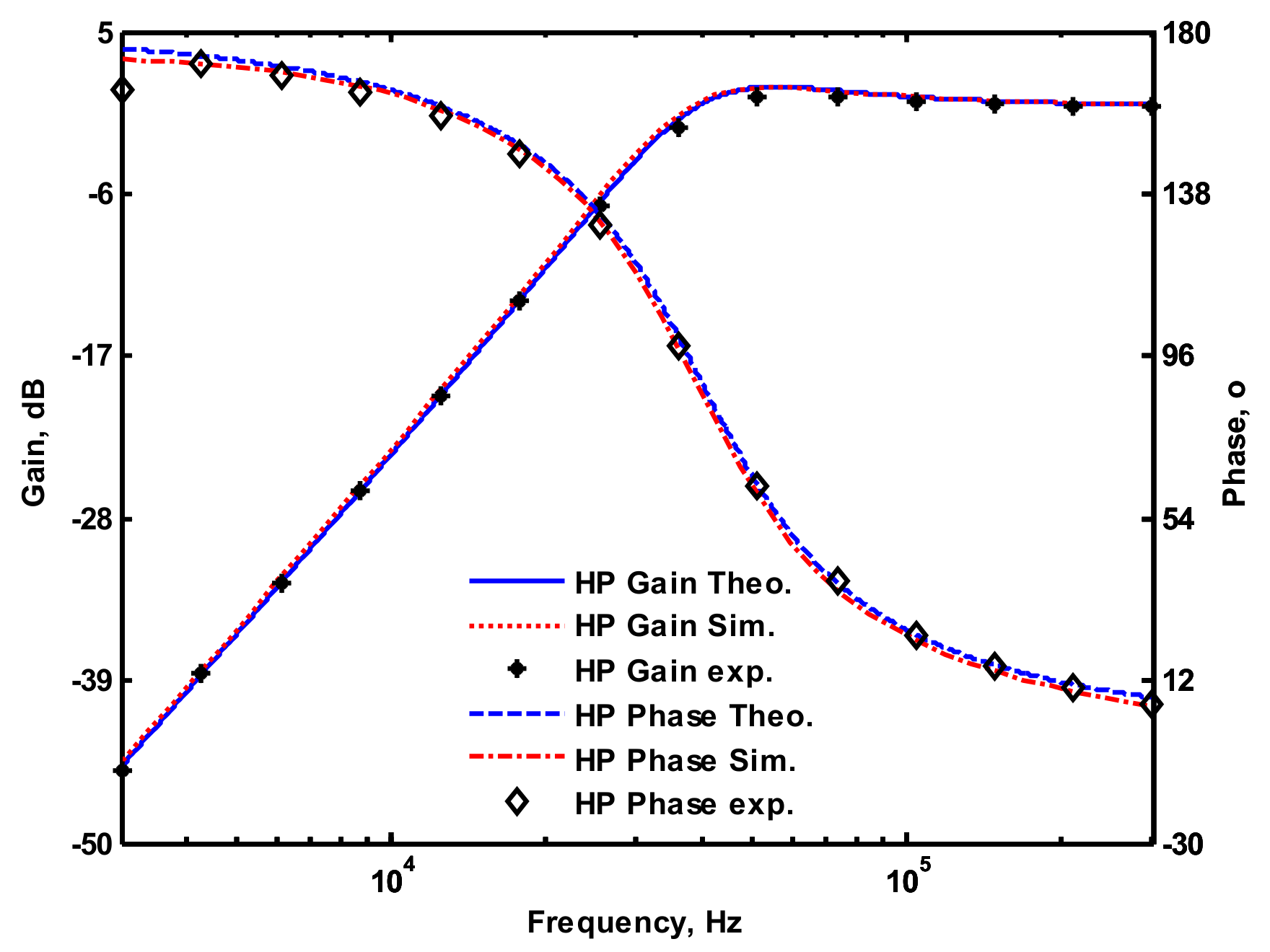
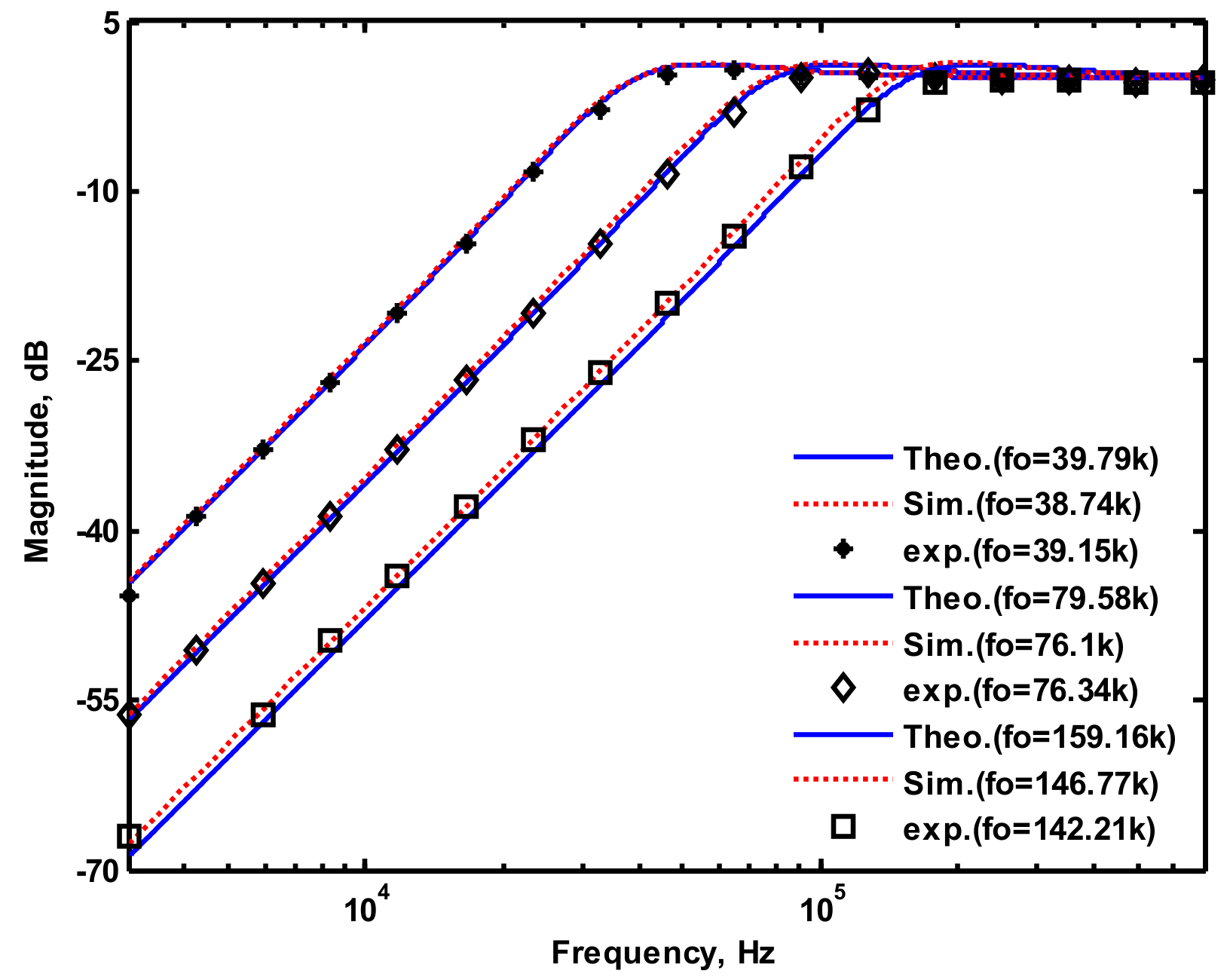
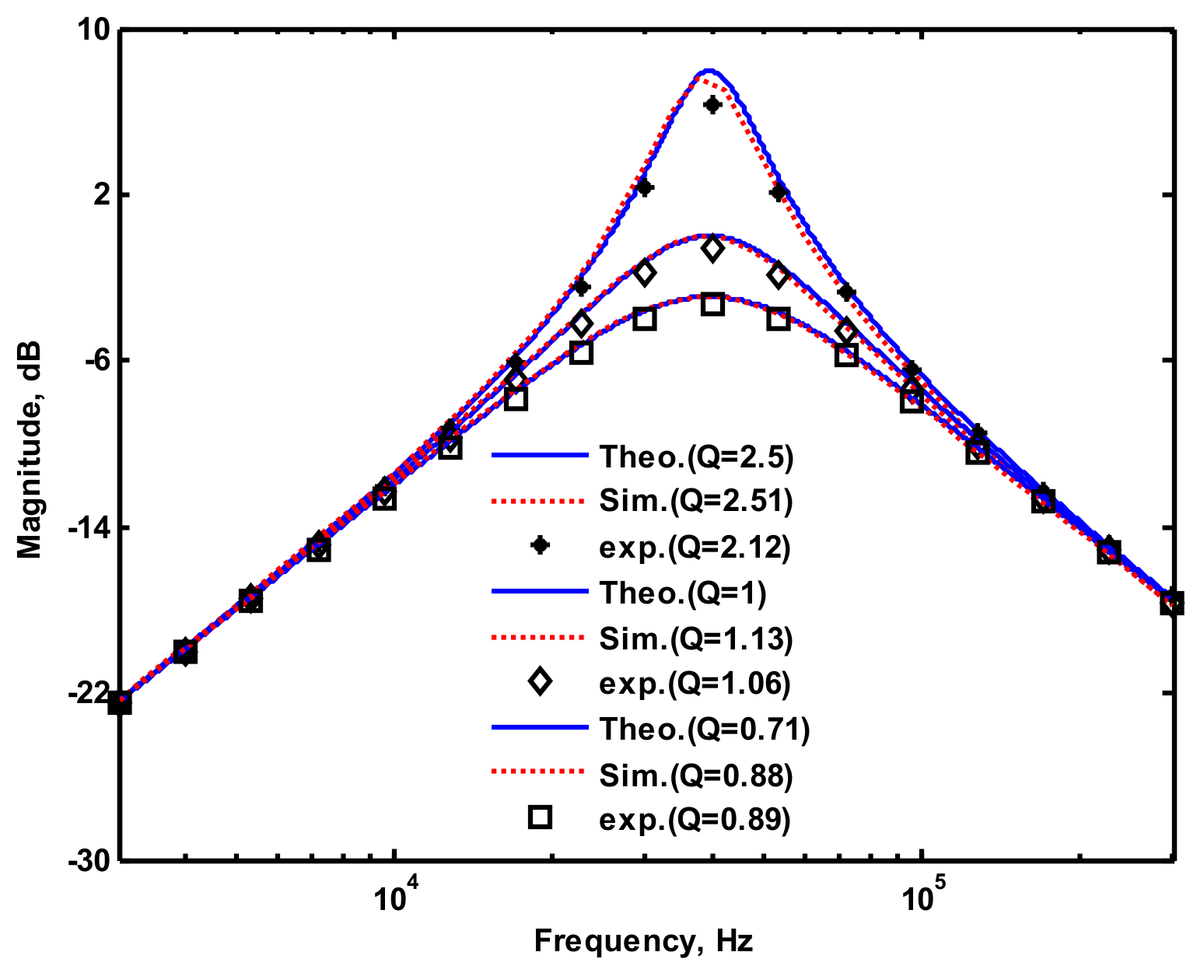
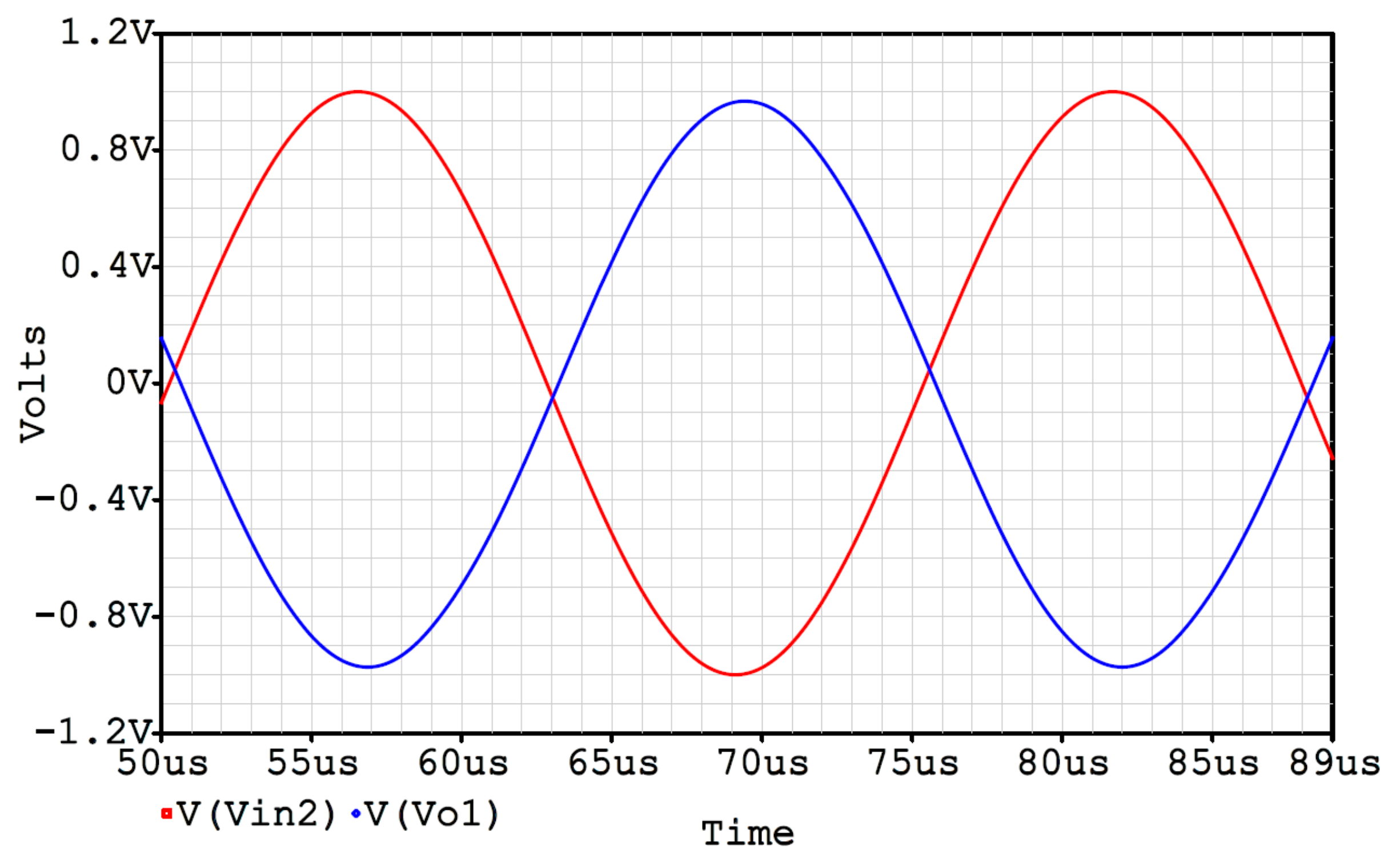
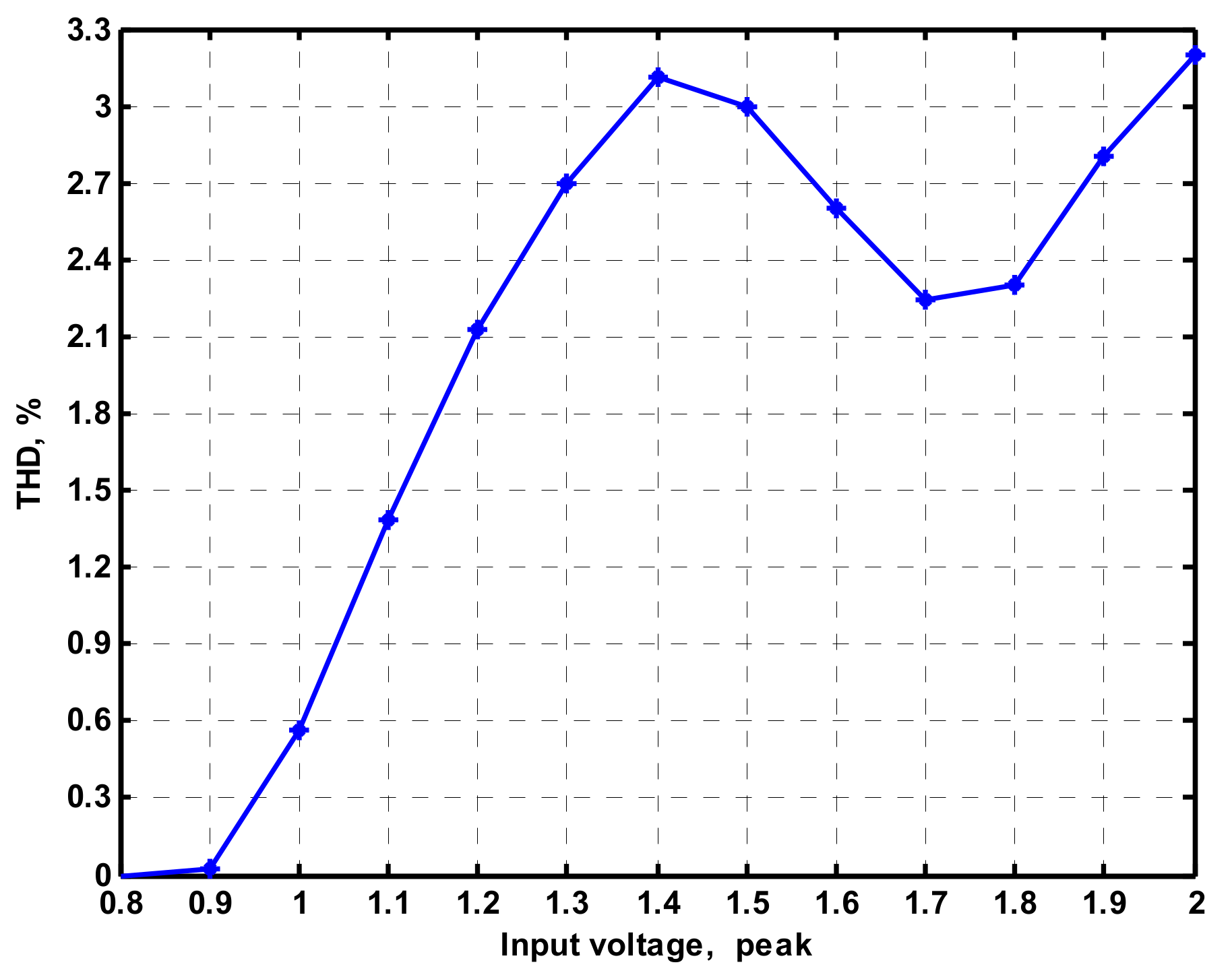
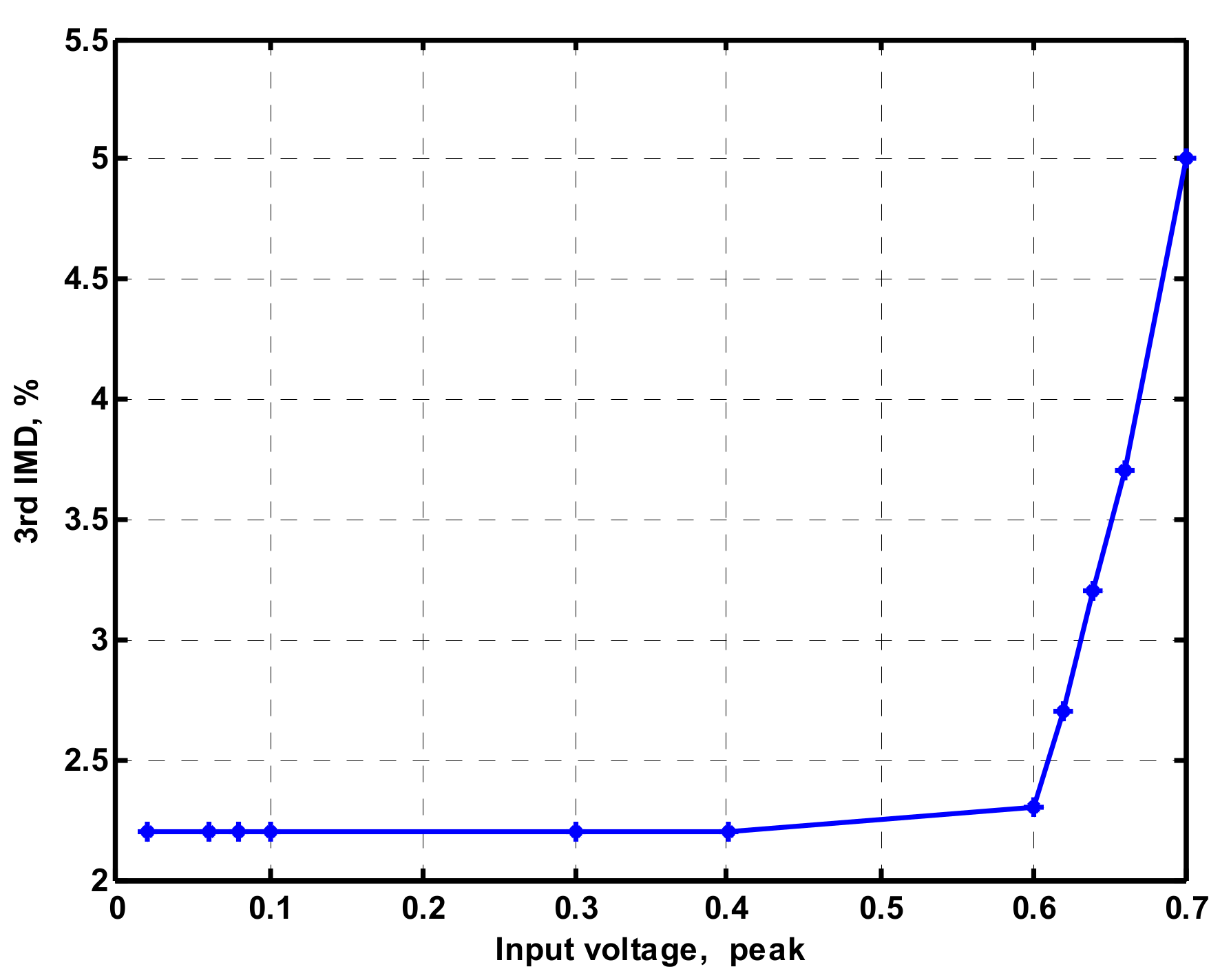
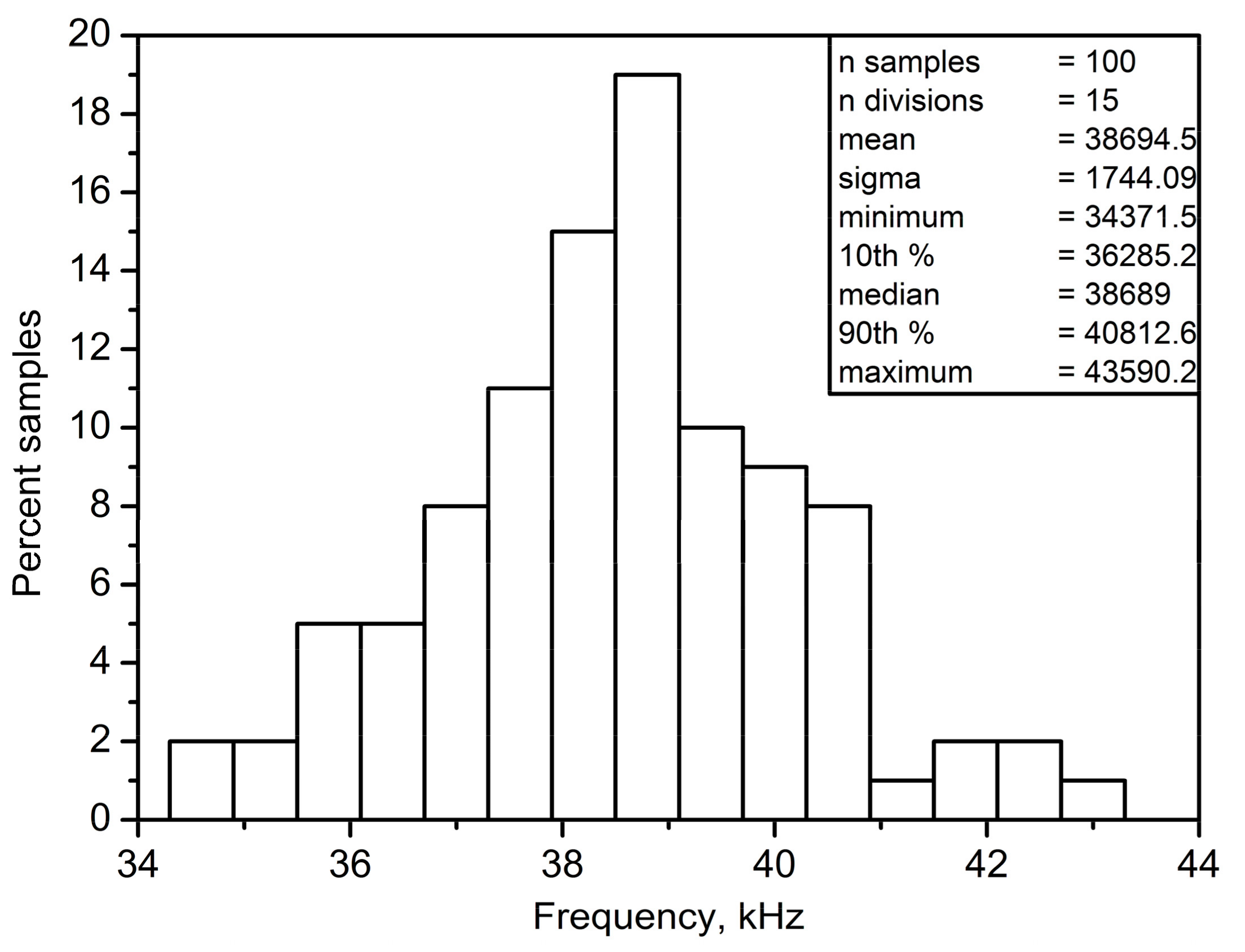
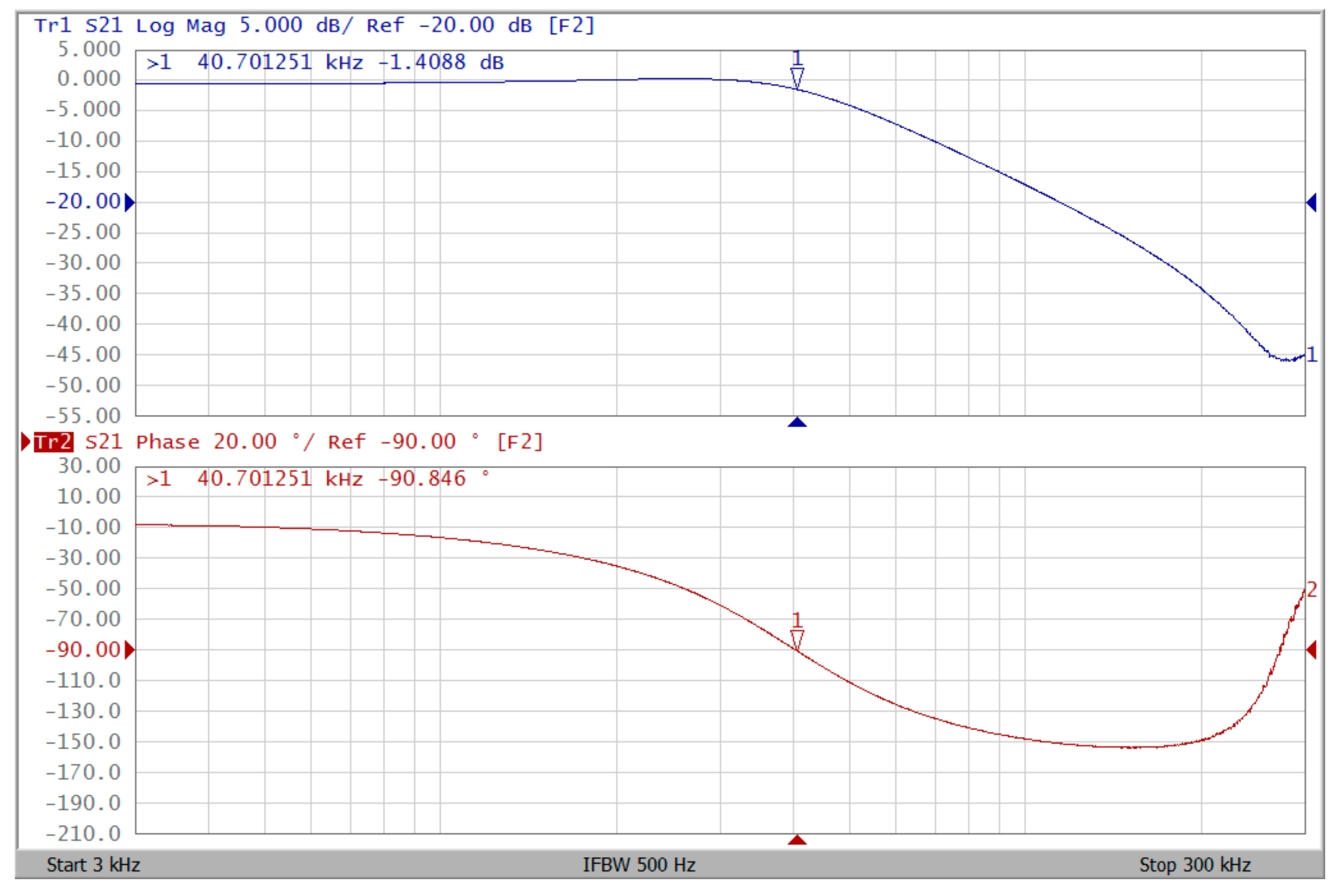
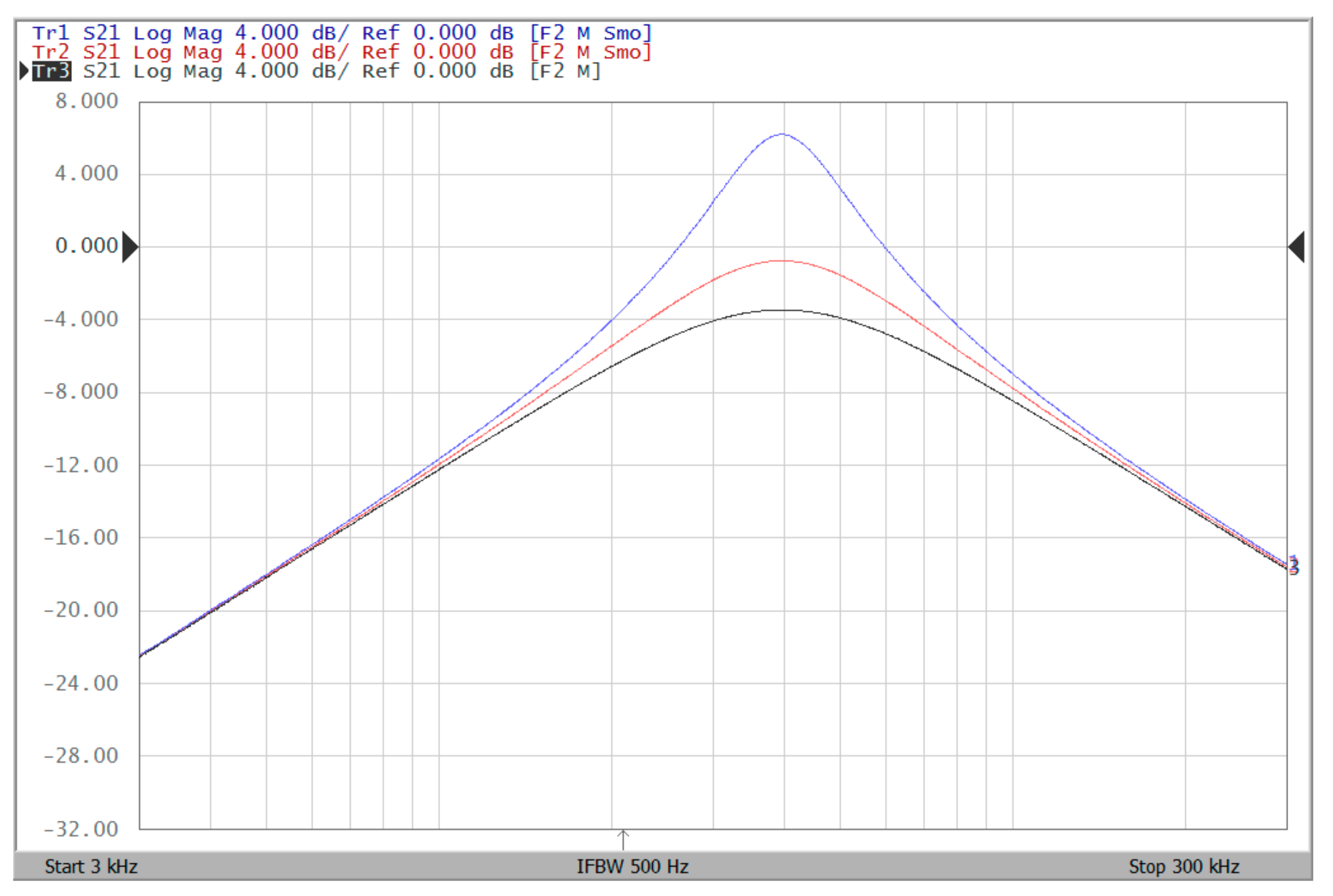
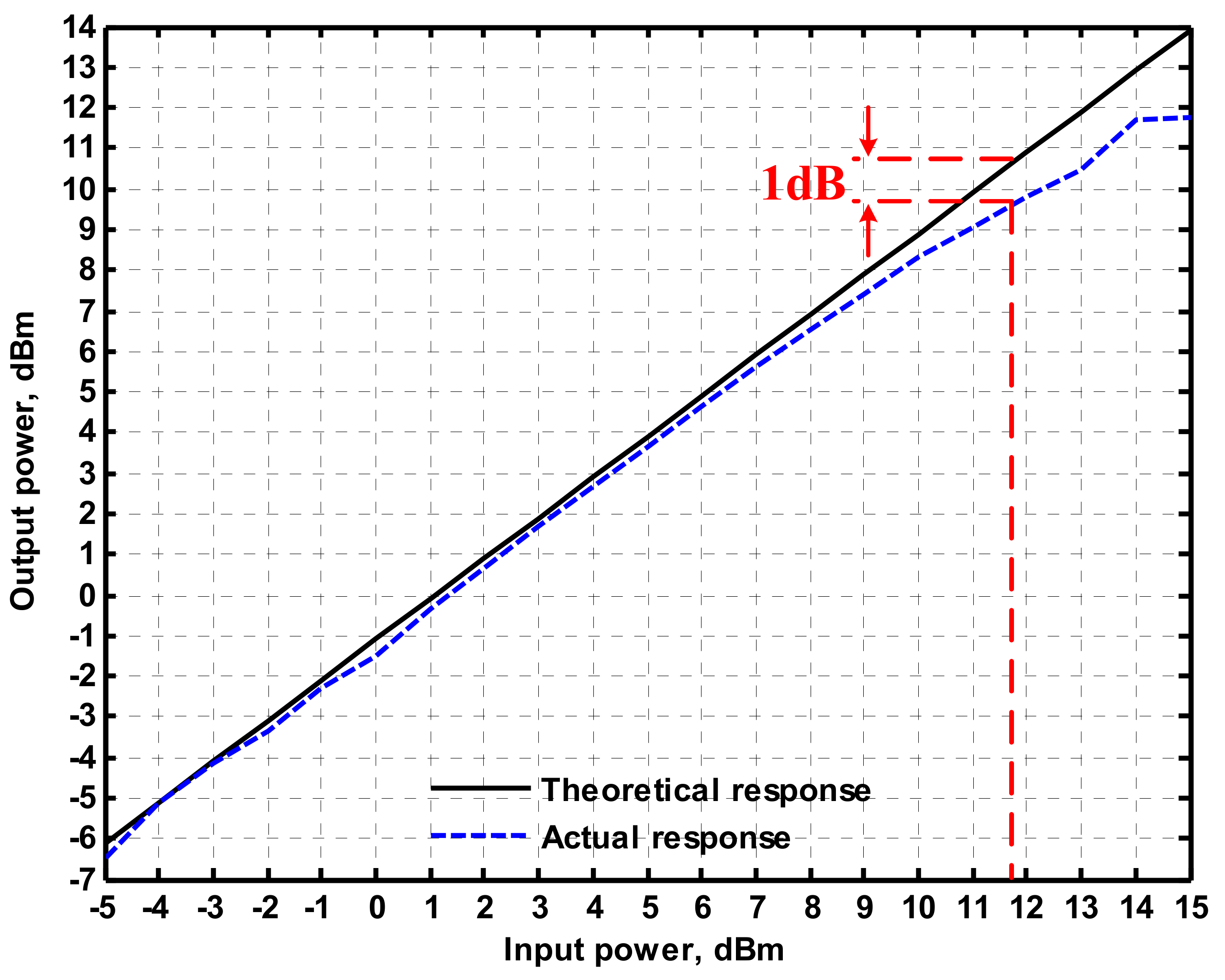
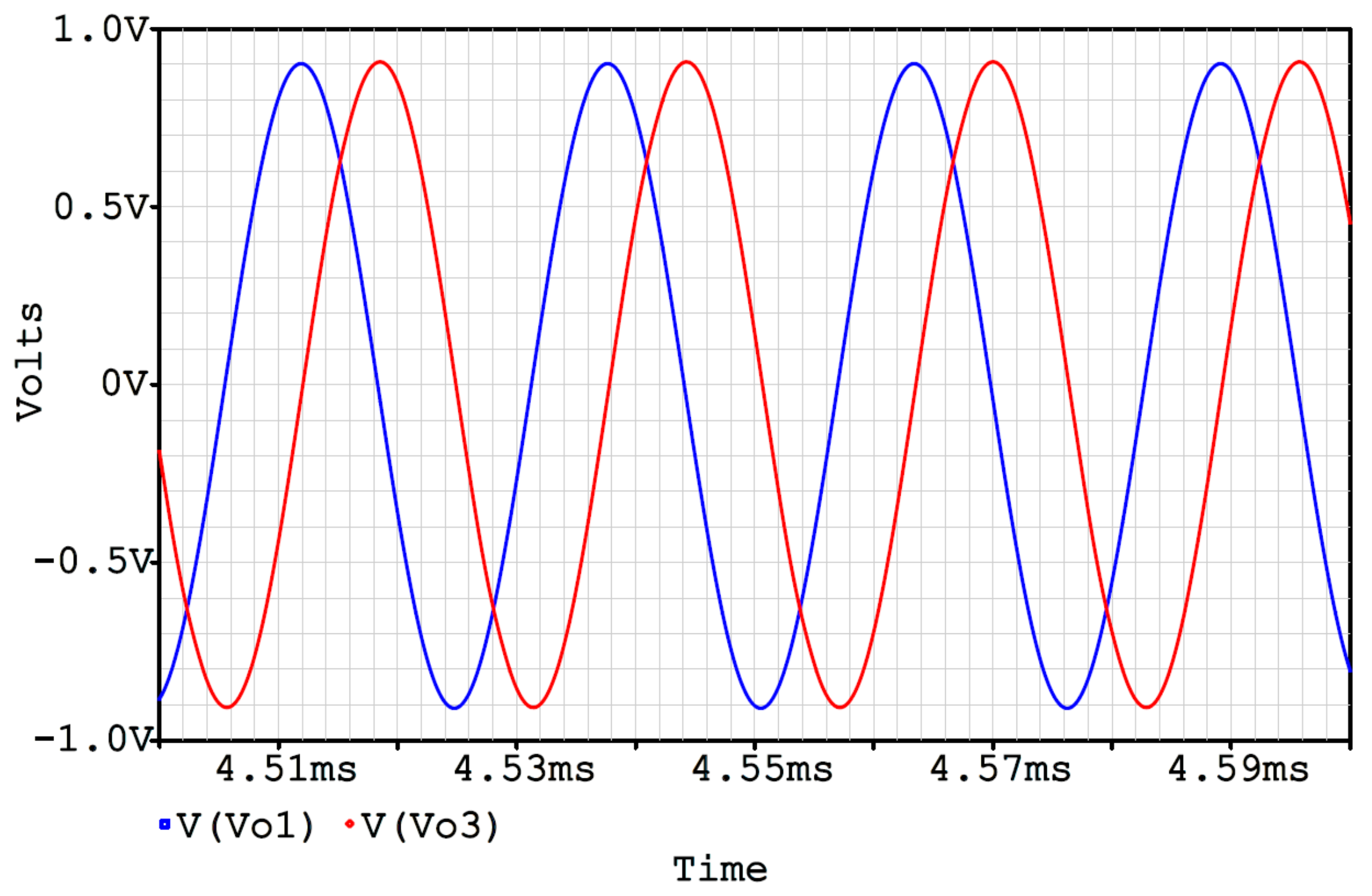
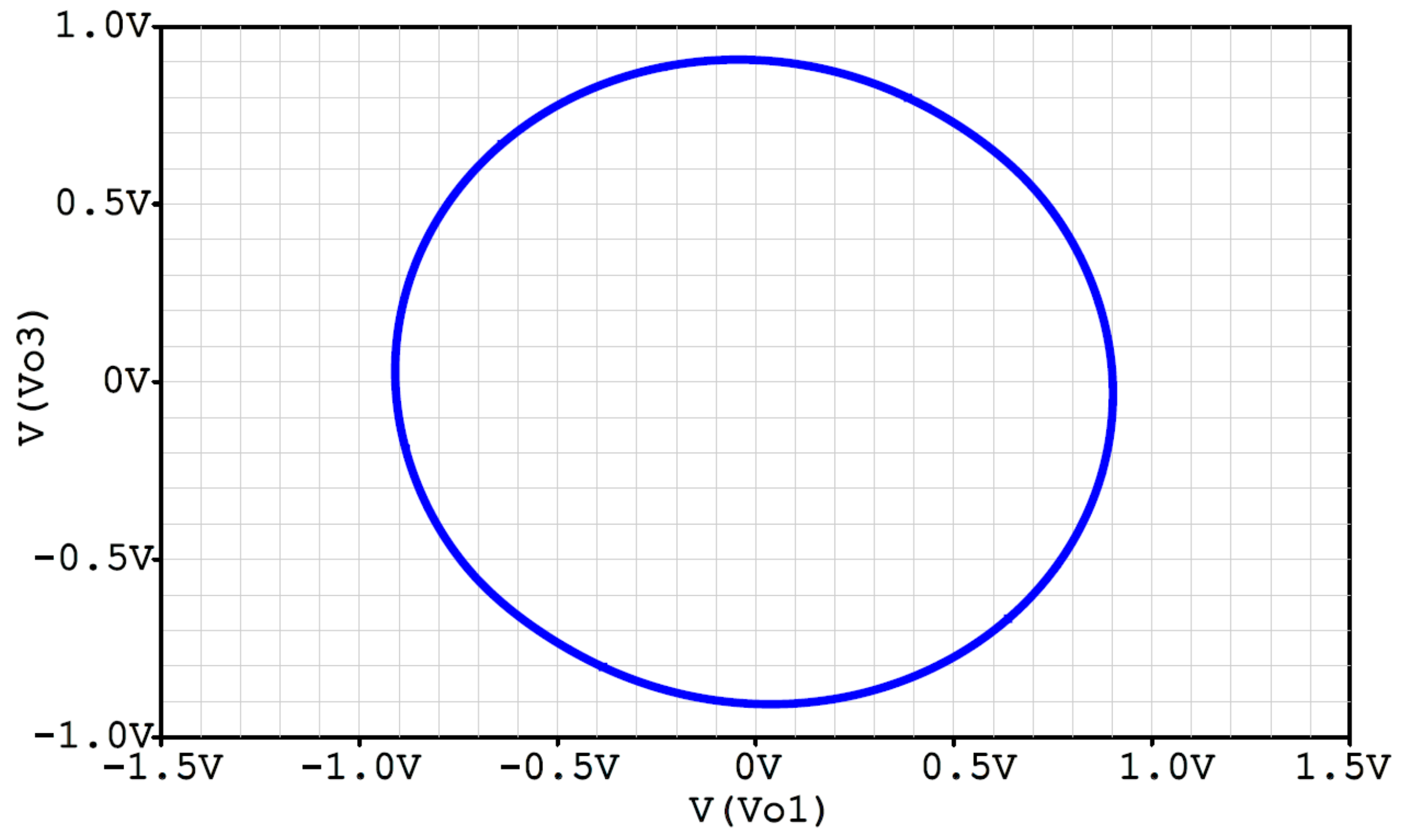
4. Simulation and Experimental Results
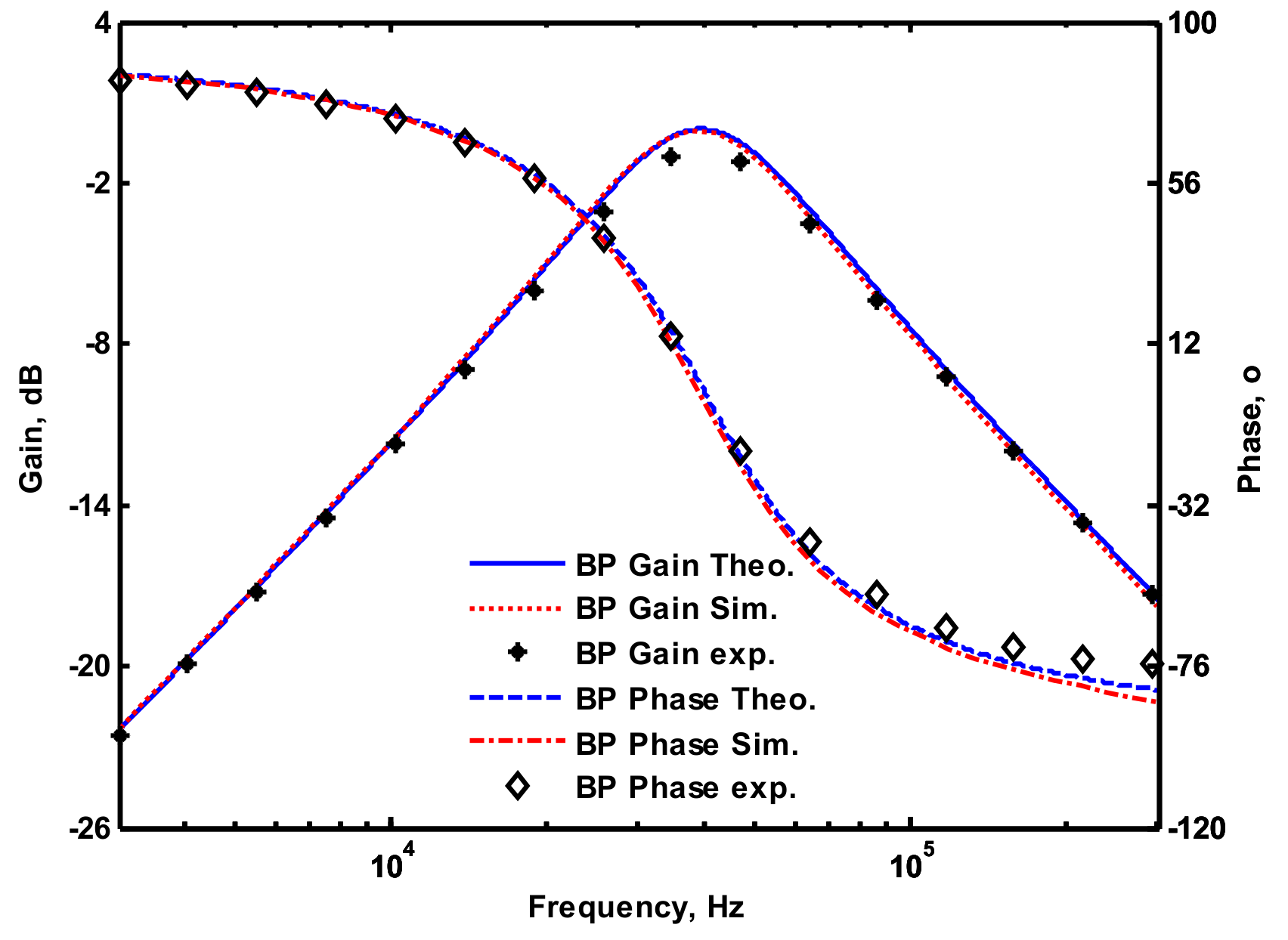
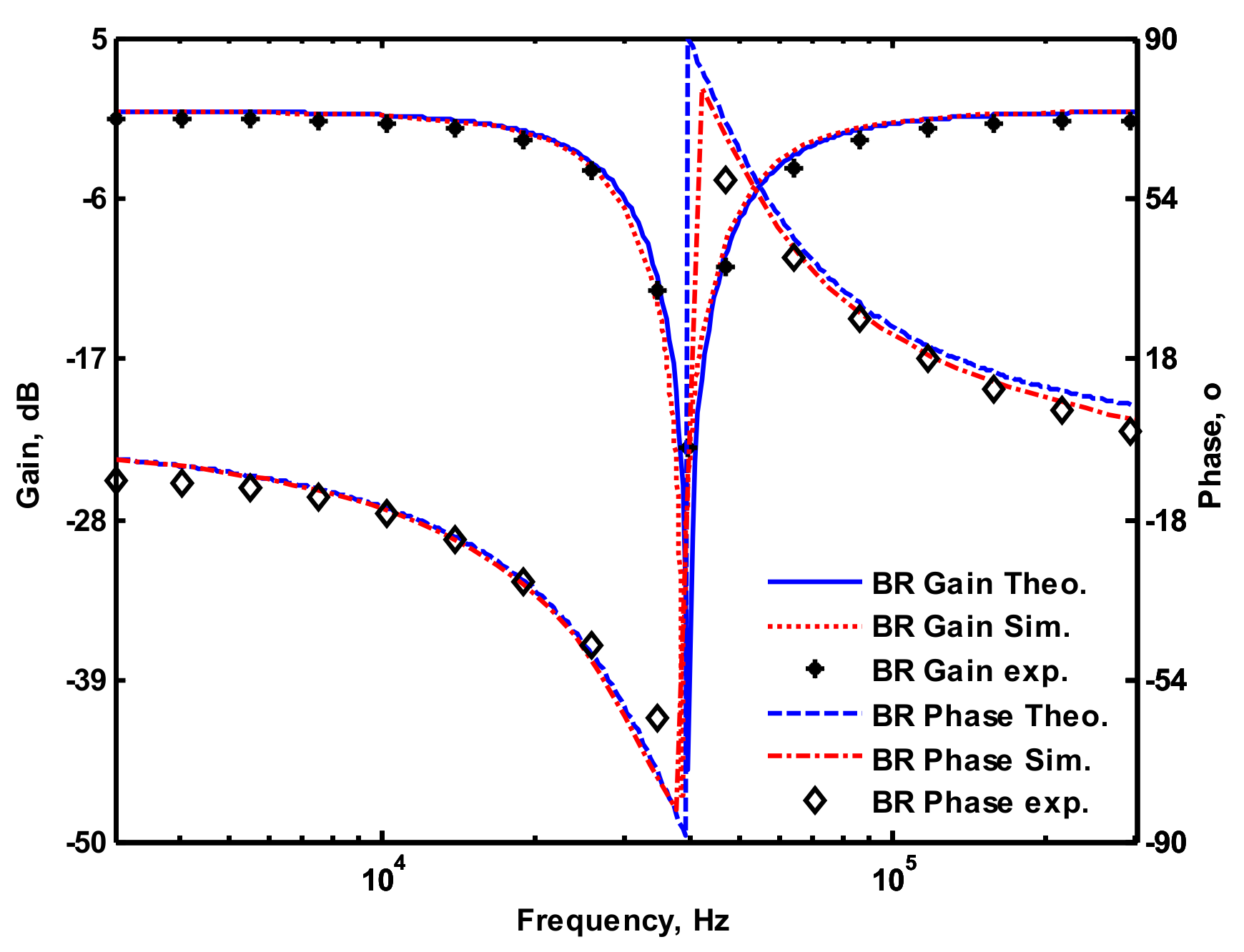
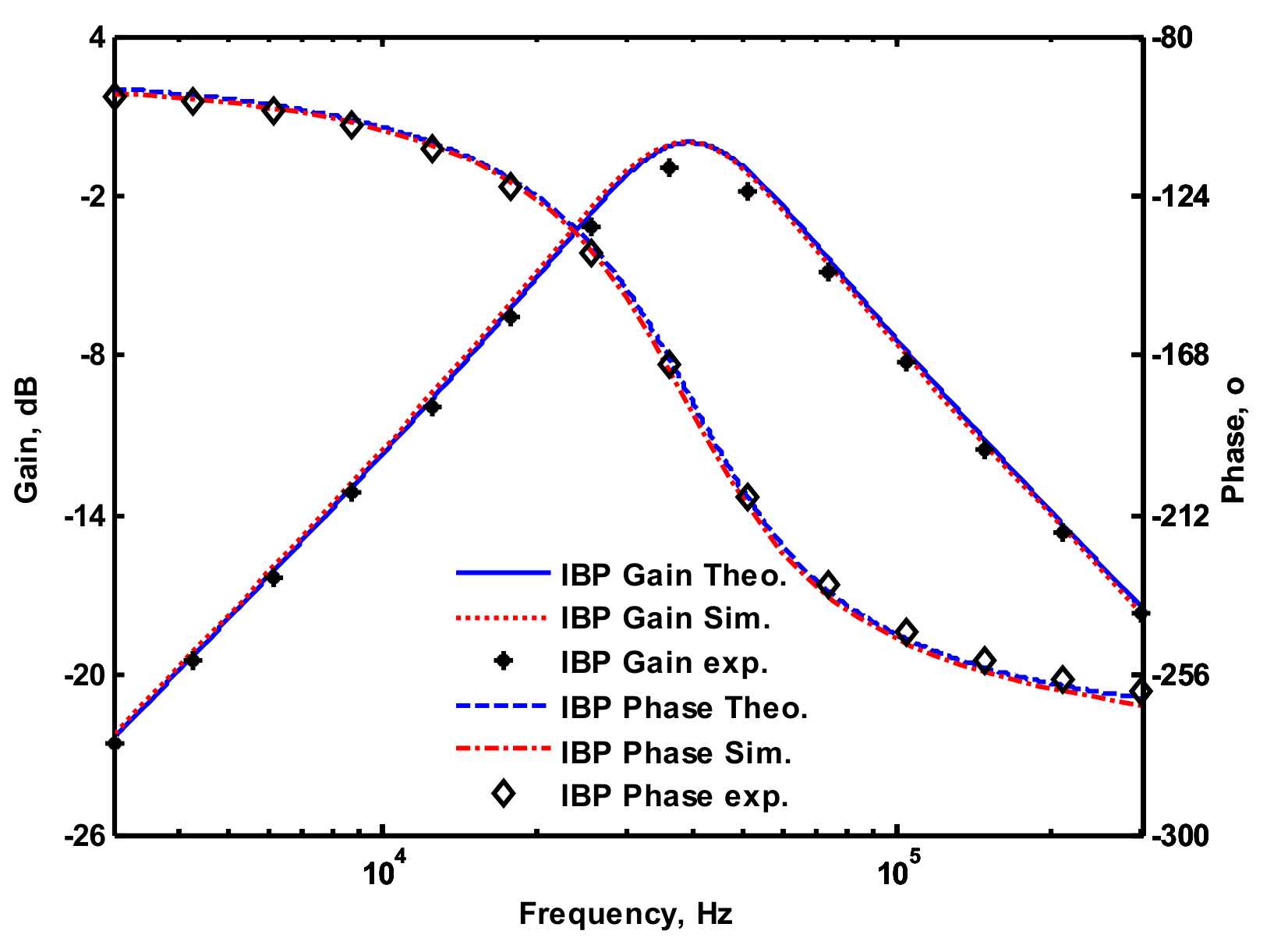
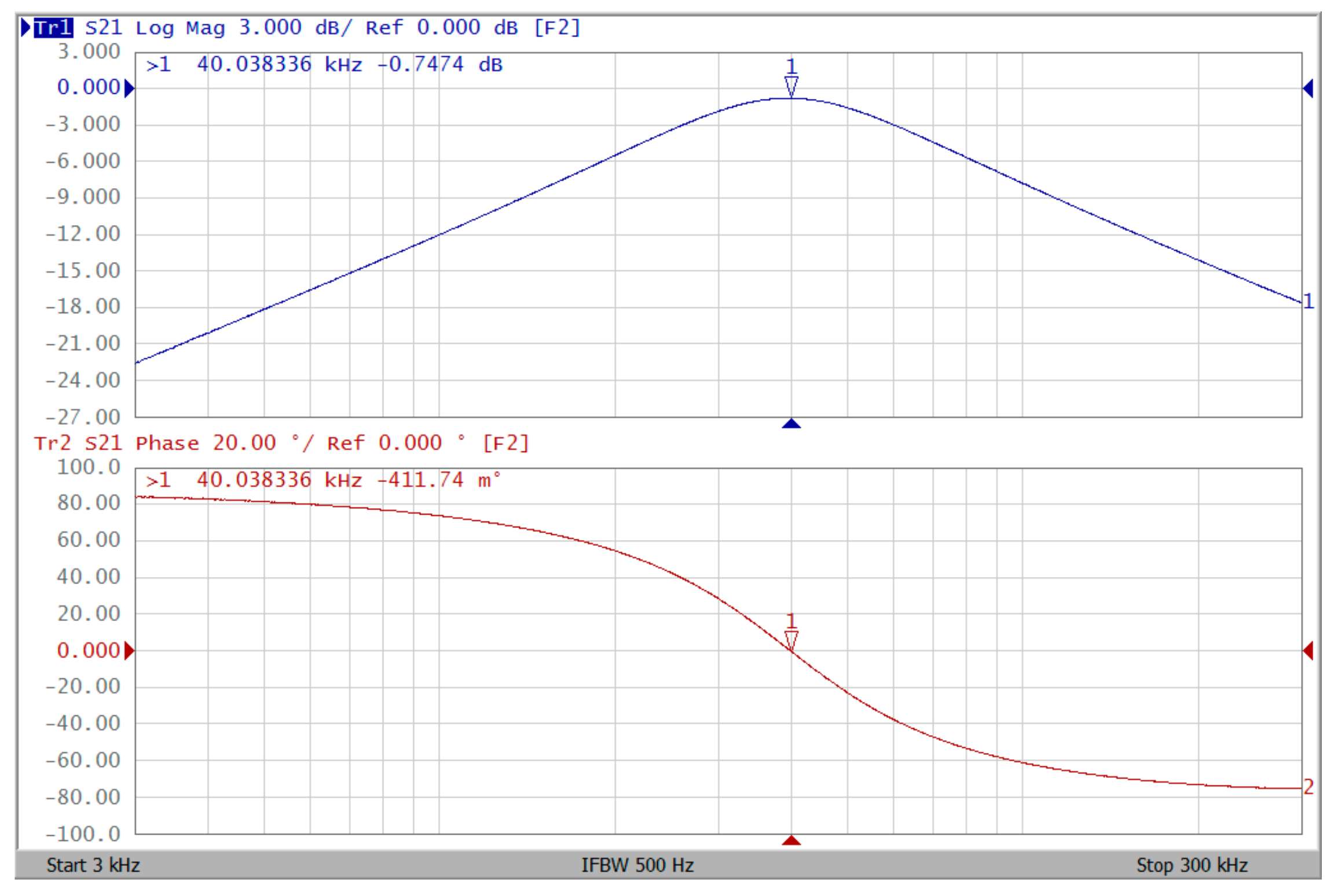
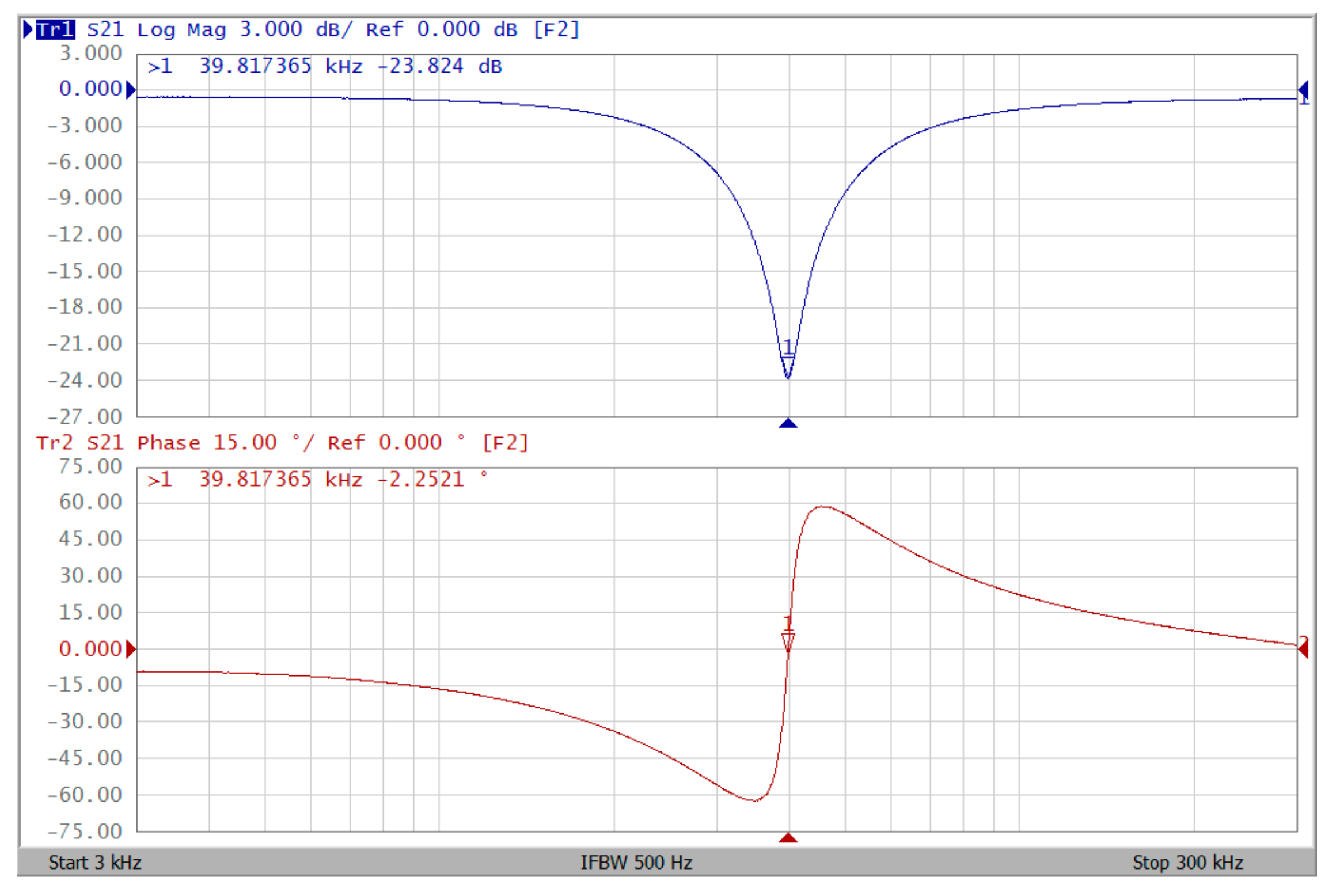
4.1. Voltage-Mode Multifunction Biquadratic Filter
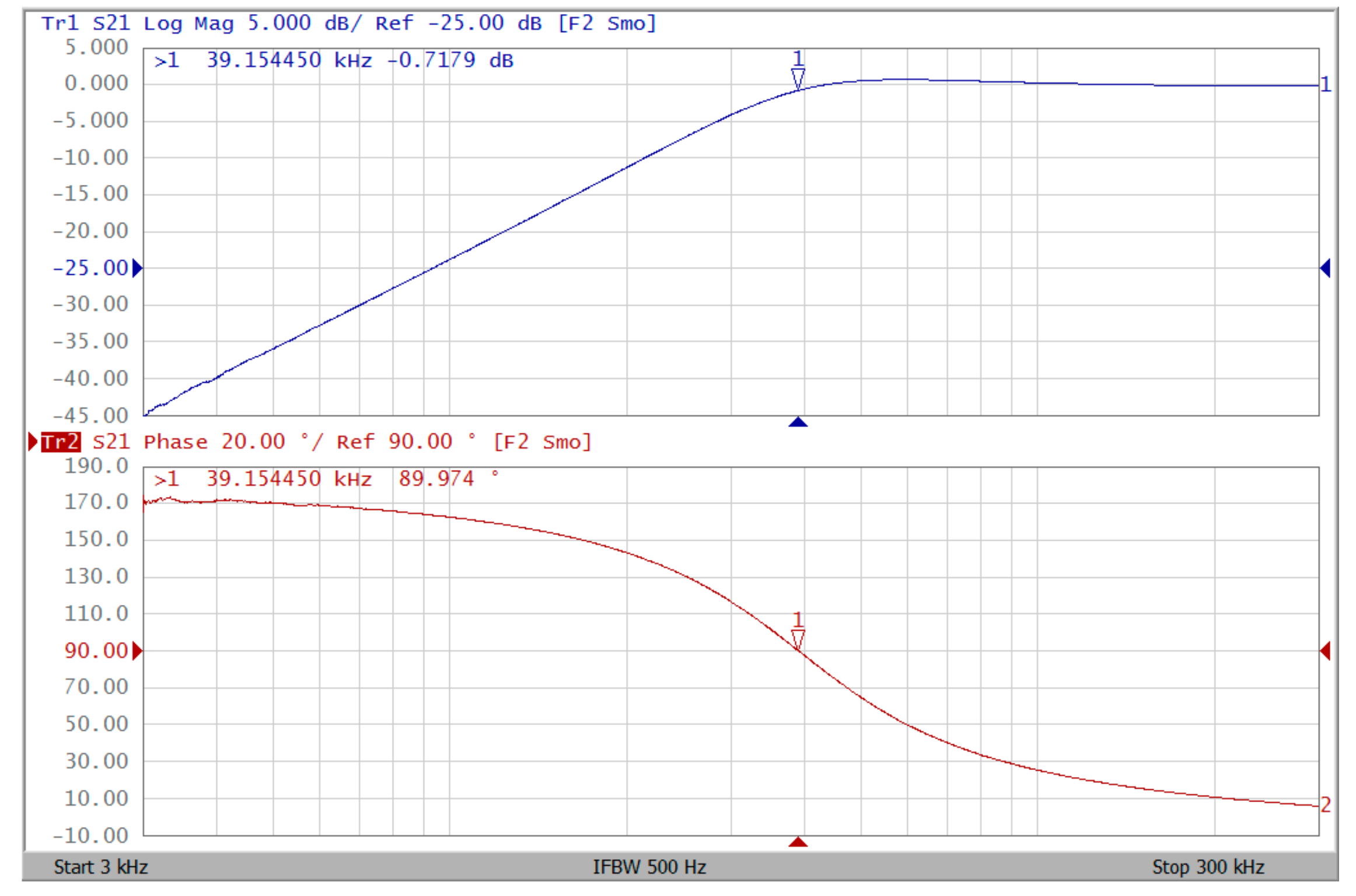
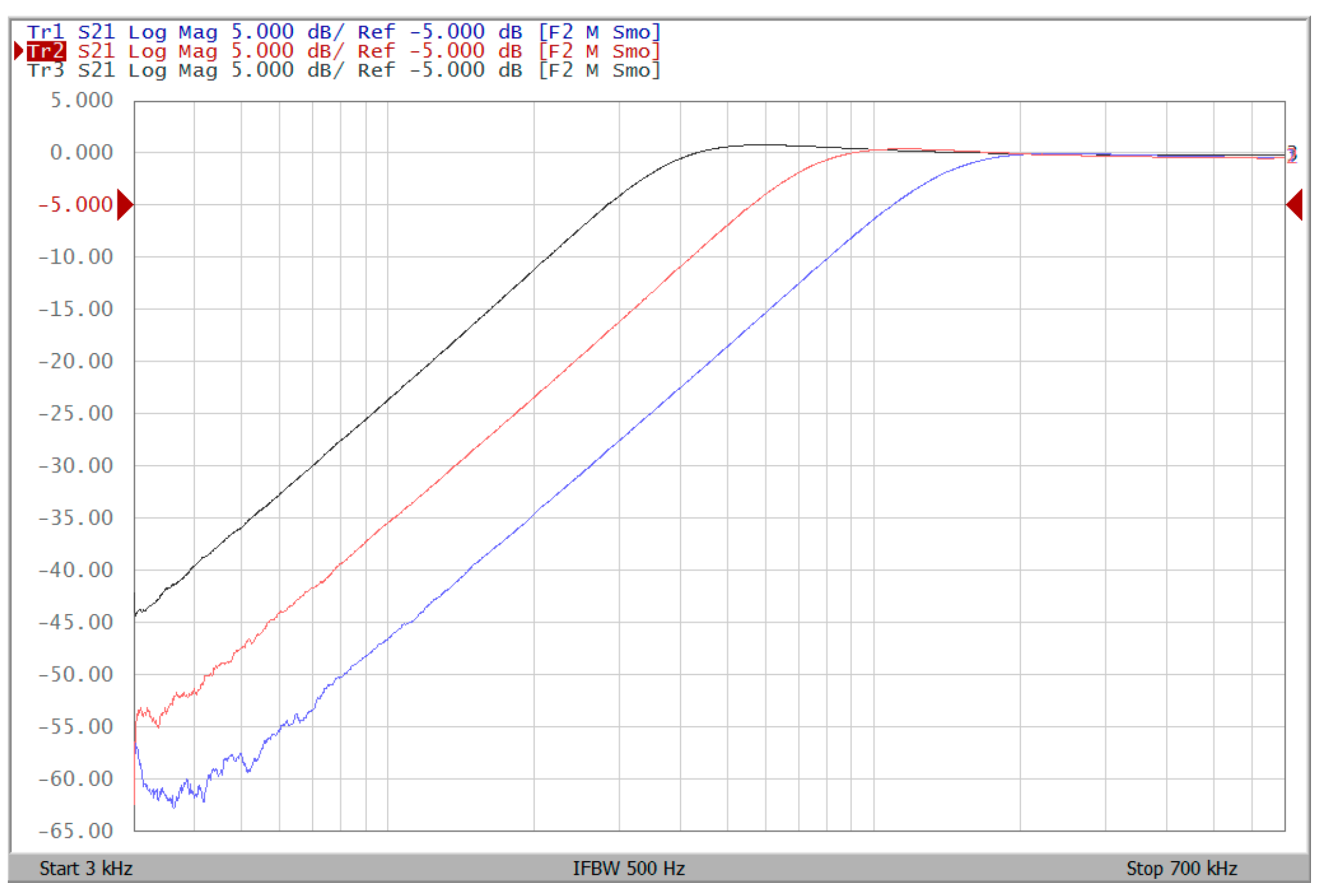
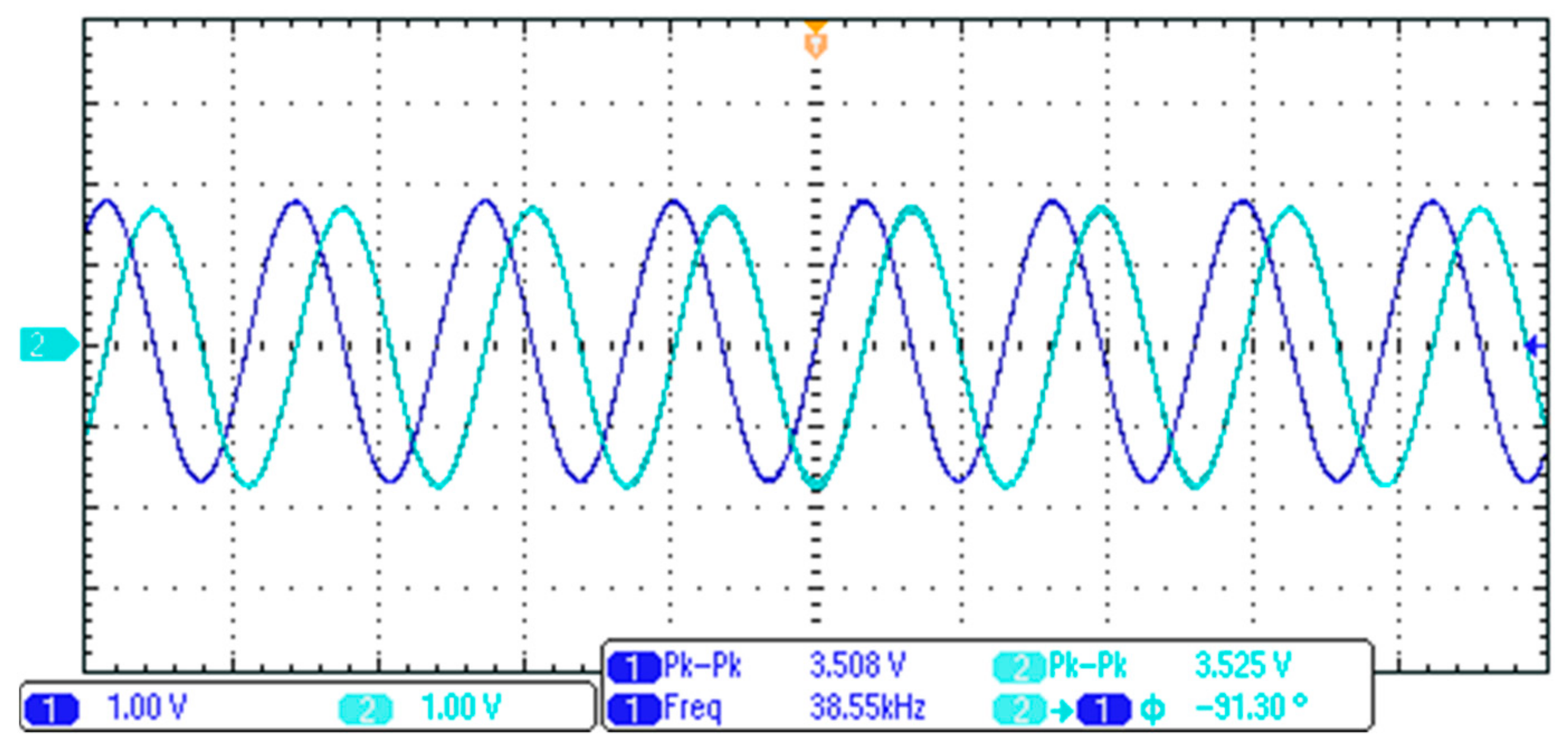
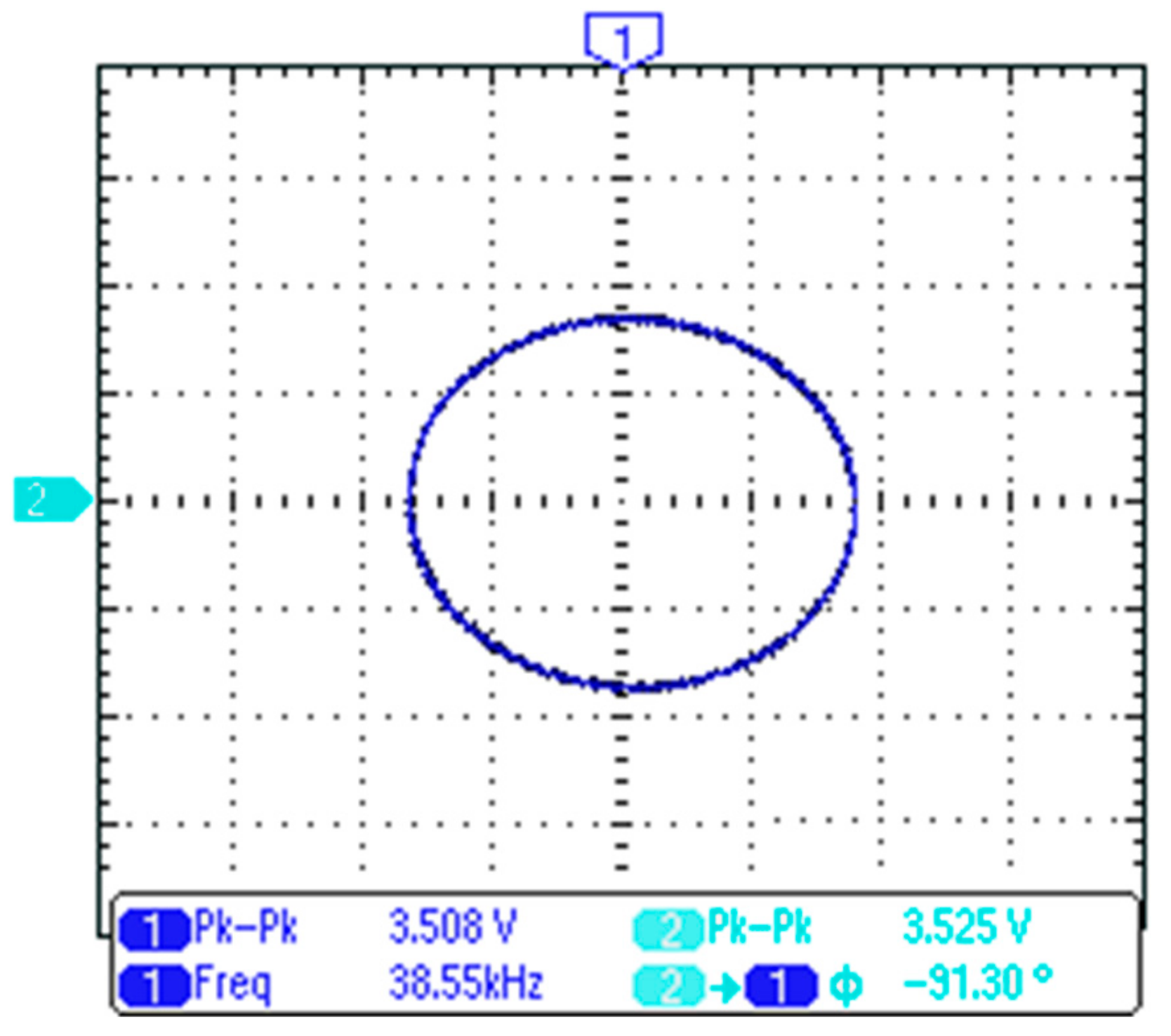
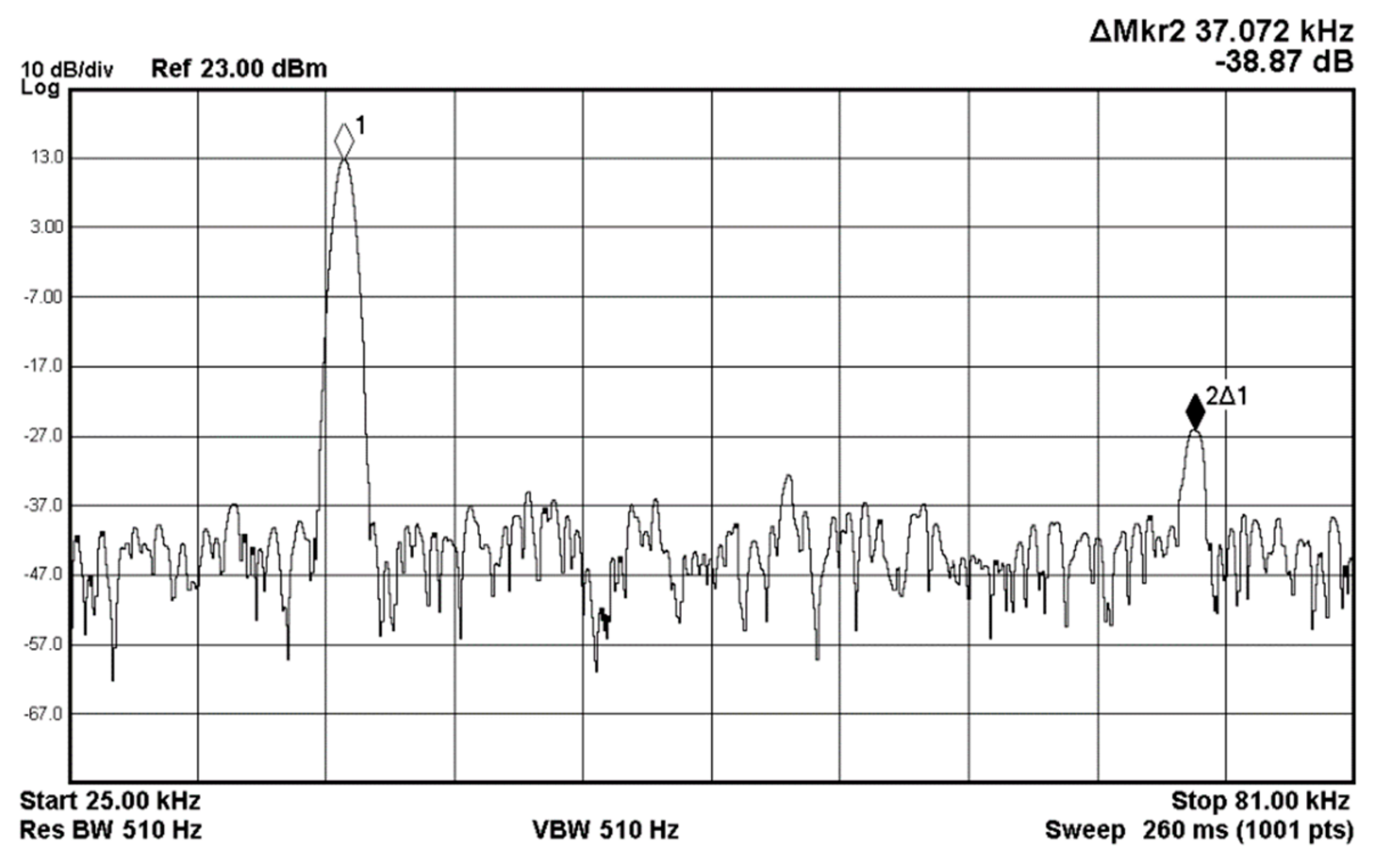
4.2. Voltage-Mode Quadrature Sinusoidal Oscillator
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, H.Y.; Tran, H.D.; Nguyen, Q.M.; Yin, L.T.; Liu, C.Y. Derivation of oscillators from biquadratic band pass filters using circuit transformations. Appl. Sci. 2014, 4, 482–492. [Google Scholar] [CrossRef]
- Tran, H.D.; Wang, H.Y.; Lin, M.C.; Nguyen, Q.M. Synthesis of cascadable DDCC-based universal filter using NAM. Appl. Sci. 2015, 5, 320–343. [Google Scholar] [CrossRef]
- Chen, H.P.; Hwang, Y.S.; Ku, Y.T. Voltage-mode and current-mode resistorless third-order quadrature oscillator. Appl. Sci. 2017, 7, 179. [Google Scholar] [CrossRef]
- Chen, H.P.; Yang, W.S. Electronically tunable current controlled current conveyor transconductance amplifier-based mixed-mode biquadratic filter with resistorless and grounded capacitors. Appl. Sci. 2017, 7, 244. [Google Scholar] [CrossRef]
- Herencsar, N.; Koton, J.; Hanak, P. Universal voltage conveyor and its novel dual-output fully-cascadable VM APF application. Appl. Sci. 2017, 7, 307. [Google Scholar] [CrossRef]
- Sotner, R.; Jerabek, J.; Langhammer, L.; Dvorak, J. Design and analysis of CCII-Based oscillator with amplitude stabilization employing optocouplers for linear voltage control of the output frequency. Electronics 2018, 7, 157. [Google Scholar] [CrossRef]
- Ullah, F.; Liu, Y.; Li, Z.; Wang, X.; Sarfraz, M.M.; Zhang, H. A bandwidth-enhanced differential LC-voltage controlled oscillator (LC-VCO) and superharmonic coupled quadrature VCO for K-band applications. Electronics 2018, 7, 127. [Google Scholar] [CrossRef]
- Abuelma’atti, M.T.; Farooqi, A.A.; Alshahrani, S.M. Novel RC oscillators using the current-feedback operational amplifier. IEEE Trans. Circuits Syst. I Fund. Theory Appl. 1996, 43, 155–157. [Google Scholar] [CrossRef]
- Senani, R.; Bhaskar, D.R.; Singh, A.K.; Singh, V.K. Current feedback operational amplifiers and their applications. In Analog Circuits and Signal Processing; Springer: New York, NY, USA, 2013. [Google Scholar]
- Wang, C.; Zhang, J.; Wang, L.; Shi, W.; Jing, D. A novel Nth-order voltage-mode universal filter based on CMOS CFOA. Opt. Int. J. Light Electron Opt. 2016, 127, 2226–2230. [Google Scholar] [CrossRef]
- Mahmoud, S.A.; Madian, A.H.; Soliman, A.M. Low-voltage CMOS current feedback operational amplifier and its application. ETRI J. 2007, 29, 212–218. [Google Scholar] [CrossRef]
- Chen, H.P.; Wang, S.F.; Ku, Y.T.; Hsieh, M.Y. Quadrature oscillators using two CFOAs and four passive components. IEICE Electron. Express 2015, 12, 1–8. [Google Scholar] [CrossRef]
- Lahiri, A.; Jaikla, W.; Siripruchyanun, M. First CFOA-based explicit-current-output quadrature sinusoidal oscillators using grounded capacitors. Int. J. Electron. 2013, 100, 259–273. [Google Scholar] [CrossRef]
- Horng, J.W. Voltage-mode multifunction filter using one current feedback amplifier and one voltage follower. Int. J. Electron. 2001, 88, 153–157. [Google Scholar] [CrossRef]
- Liu, S.I.; Wu, D.S. New current-feedback amplifier-based universal biquadratic filter. IEEE Trans. Instrum. Meas. 1995, 44, 915–917. [Google Scholar]
- Horng, J.W. New Configuration for realizing universal voltage-mode filter using two current-feedback amplifiers. IEEE Trans. Instrum. Meas. 2000, 49, 1043–1045. [Google Scholar] [CrossRef]
- Shan, N.A.; Rather, M.F.; Iqbal, S.Z. CFA-based three input and two outputs voltage-mode universal filter. Indian J. Pure Appl. Phys. 2005, 43, 636–639. [Google Scholar]
- Shah, N.A.; Iqbal, S.Z.; Rather, M.F. Versatile voltage-mode CFA-based universal filter. AEU Int. J. Electron. Commun. 2005, 59, 192–194. [Google Scholar] [CrossRef]
- Tangsrirat, W.; Surakampontorn, W. Single-resistance-controlled quadrature oscillator and universal biquad filter using CFOAs. AEU Int. J. Electron. Commun. 2009, 63, 1080–1086. [Google Scholar] [CrossRef]
- Horng, J.W. Voltage-mode universal biquad with five inputs and two outputs using two current feedback amplifiers. Indian J. Eng. Mater. Sci. 2013, 20, 87–91. [Google Scholar]
- Nikoloudis, S.; Psychalinos, C. Multiple input single output universal biquad filter with current feedback operational amplifiers. Circuits Syst. Signal Process. 2010, 29, 1167–1180. [Google Scholar] [CrossRef]
- Topaloglu, S.; Sagbas, M.; Anday, F. Three-input single-output second-order filters using current-feedback amplifiers. AEU Int. J. Electron. Commun. 2012, 66, 683–686. [Google Scholar] [CrossRef]
- Minaei, S.; Ibragun, M.A. A mixed-mode KHN-biquad using DVCC and grounded passive elements suitable for direct cascading. Int. J. Circuit Theory Appl. 2009, 37, 793–810. [Google Scholar] [CrossRef]
- Singh, V.K.; Singh, A.K.; Bhaskar, D.R.; Senani, R. New universal biquads employing CFOAs. IEEE Trans. Circuits Syst. II Express Briefs 2006, 53, 1299–1303. [Google Scholar] [CrossRef]
- Ibrahim, M.A.; Minaei, S.; Kuntman, H. A 22.5MHzcurrent-mode KHN biquad using differential voltage current conveyor and grounded passive element. AEU Int. J. Electron. Commun. 2005, 59, 311–318. [Google Scholar] [CrossRef]
- Chang, C.M.; Hwang, C.S.; Tu, S.H. Voltage-mode notch, lowpass and bandpass filter using current-feedback amplifiers. Electron. Lett. 1994, 30, 2002–2003. [Google Scholar] [CrossRef]
- Horng, J.W.; Lee, M.H. High input impedance voltage-mode lowpass, bandpass and highpass filter using current-feedback amplifiers. Electron. Lett. 1997, 33, 947–948. [Google Scholar] [CrossRef]
- Shan, N.A.; Malik, M.A. High input impedance voltage-mode lowpass, bandpass, highpass and notch filter using current feedback amplifiers. Indian J. Eng. Mater. Sci. 2005, 12, 278–280. [Google Scholar]
- Shan, N.A.; Malik, M.A. New high input impedance voltage-mode lowpass, bandpass and highpass filter using current feedback amplifiers. J. Circuits Syst. Comp. 2005, 14, 1037–1043. [Google Scholar]
- AD844: 60 MHz, 2000 V/μs, Monolithic Op Amp with Quad Low Noise Data Sheet (Rev. G). May 2017. Available online: www.linear.com. (accessed on 29 April 2019).





| Parameter | (i) | (ii) | (iii) | (iv) | (v) | (vi) | (vii) |
|---|---|---|---|---|---|---|---|
| Reference [26] | yes | no | no | yes | yes | yes | no |
| Reference [27] | no | no | yes | yes | yes | yes | no |
| Reference [28] | no | yes | yes | yes | yes | yes | no |
| Reference [29] | no | no | yes | no | no | yes | no |
| Proposed | yes | yes | yes | yes | yes | yes | yes |
| Input Conditions | Output Terminals | Filter Functions | Passband Gains |
|---|---|---|---|
| Only Vi1 as input signal | Vo1 | non-inverting low-pass | unity |
| Vo2 | non-inverting band-pass | ||
| Vo3 | non-inverting band-reject | unity | |
| Only Vi2 as input signal | Vo1 | inverting band-pass | |
| Vo2 | none | none | |
| Vo3 | non-inverting high-pass |
| Harmonic Number | Frequency (Hz) | Fourier Component | Normalized Component | Phase (Degree) | Normalized Phase (Degree) |
|---|---|---|---|---|---|
| 1 | 3.98 × 104 | 8.94 × 10−1 | 1.00 | 7.94 × 101 | 0 |
| 2 | 7.96 × 104 | 1.45 × 10−2 | 1.62 × 10−2 | 6.74 × 101 | −9.14 × 101 |
| 3 | 1.19 × 105 | 7.03 × 10−3 | 7.86 × 10−3 | 6.90 × 101 | −1.69 × 102 |
| 4 | 1.59 × 105 | 3.28 × 10−3 | 3.66 × 10−3 | 5.23 × 101 | −2.65 × 102 |
| 5 | 1.99 × 105 | 2.49 × 10−3 | 2.78 × 10−3 | 4.31 × 101 | −3.54 × 102 |
| 6 | 2.39 × 105 | 1.88 × 10−3 | 2.11 × 10−3 | 4.71 × 101 | −4.29 × 102 |
| 7 | 2.79 × 105 | 1.38 × 10−3 | 1.54 × 10−3 | 3.14 × 101 | −5.24 × 102 |
| 8 | 3.18 × 105 | 1.19 × 10−3 | 1.33 × 10−3 | 2.85 × 101 | −6.07 × 102 |
| 9 | 3.58 × 105 | 9.40 × 10−4 | 1.05 × 10−3 | 3.52 × 101 | −6.79 × 102 |
| DC component = −2.560956 × 10−2 | |||||
| Total harmonic distortion = 1.887184% | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.-F.; Chen, H.-P.; Ku, Y.; Chen, P.-Y. A CFOA-Based Voltage-Mode Multifunction Biquadratic Filter and a Quadrature Oscillator Using the CFOA-Based Biquadratic Filter. Appl. Sci. 2019, 9, 2304. https://doi.org/10.3390/app9112304
Wang S-F, Chen H-P, Ku Y, Chen P-Y. A CFOA-Based Voltage-Mode Multifunction Biquadratic Filter and a Quadrature Oscillator Using the CFOA-Based Biquadratic Filter. Applied Sciences. 2019; 9(11):2304. https://doi.org/10.3390/app9112304
Chicago/Turabian StyleWang, San-Fu, Hua-Pin Chen, Yitsen Ku, and Po-Yu Chen. 2019. "A CFOA-Based Voltage-Mode Multifunction Biquadratic Filter and a Quadrature Oscillator Using the CFOA-Based Biquadratic Filter" Applied Sciences 9, no. 11: 2304. https://doi.org/10.3390/app9112304
APA StyleWang, S.-F., Chen, H.-P., Ku, Y., & Chen, P.-Y. (2019). A CFOA-Based Voltage-Mode Multifunction Biquadratic Filter and a Quadrature Oscillator Using the CFOA-Based Biquadratic Filter. Applied Sciences, 9(11), 2304. https://doi.org/10.3390/app9112304







