A Simplified Approach to Design Jet-Grouted Bottom Sealing Barriers for Deep Excavations in Deep Aquifers
Abstract
:1. Introduction
2. Methodology
2.1. Problem Statement
2.2. Failure Mechanism
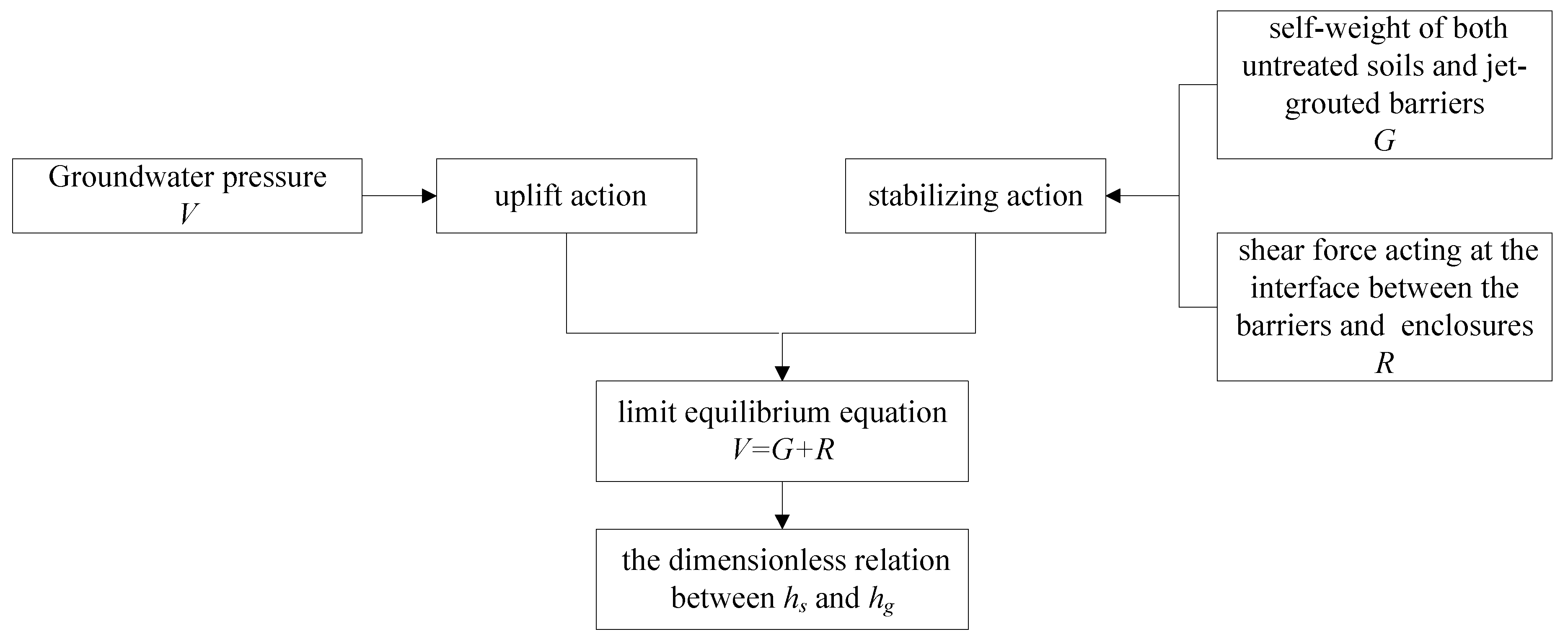
2.3. Calculation of Jet-Grouted Bottom Sealing Barriers Considering Instability Failure
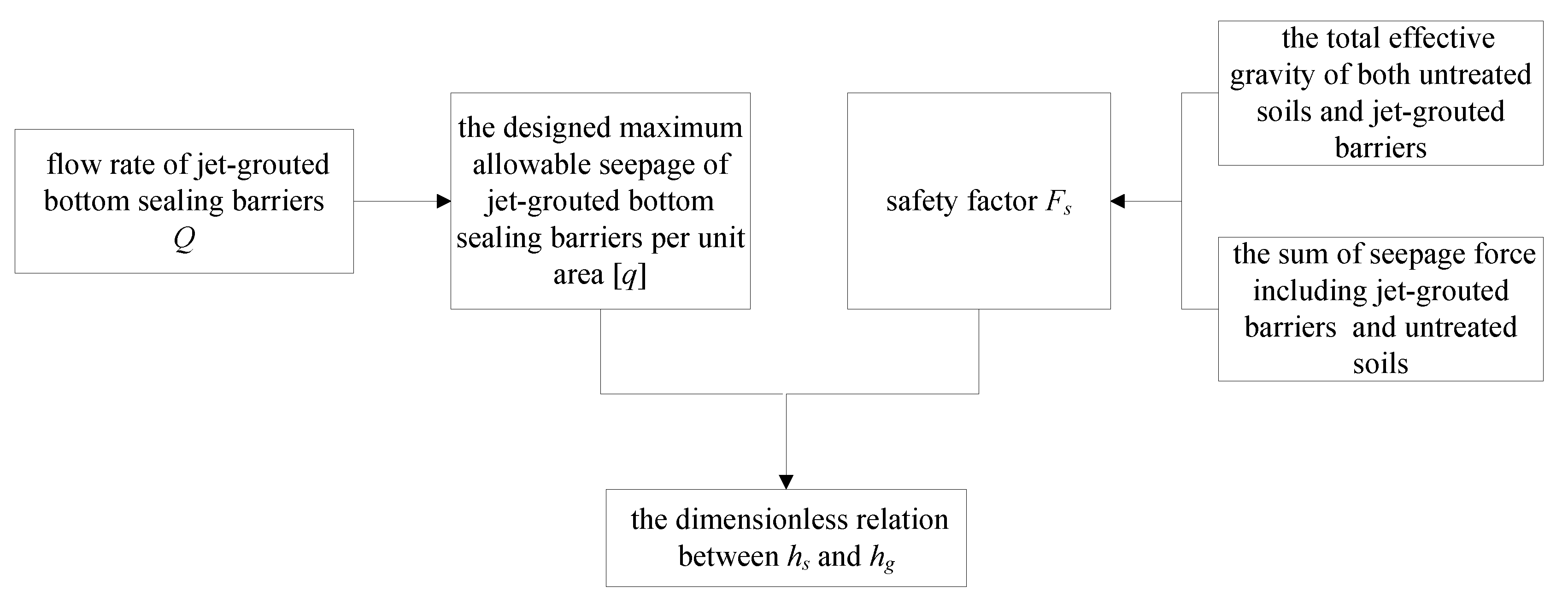
2.4. Calculation of Jet-Grouted Bottom Sealing Barriers Considering Seepage Failure
3. Parametric Analysis and Design Procedure
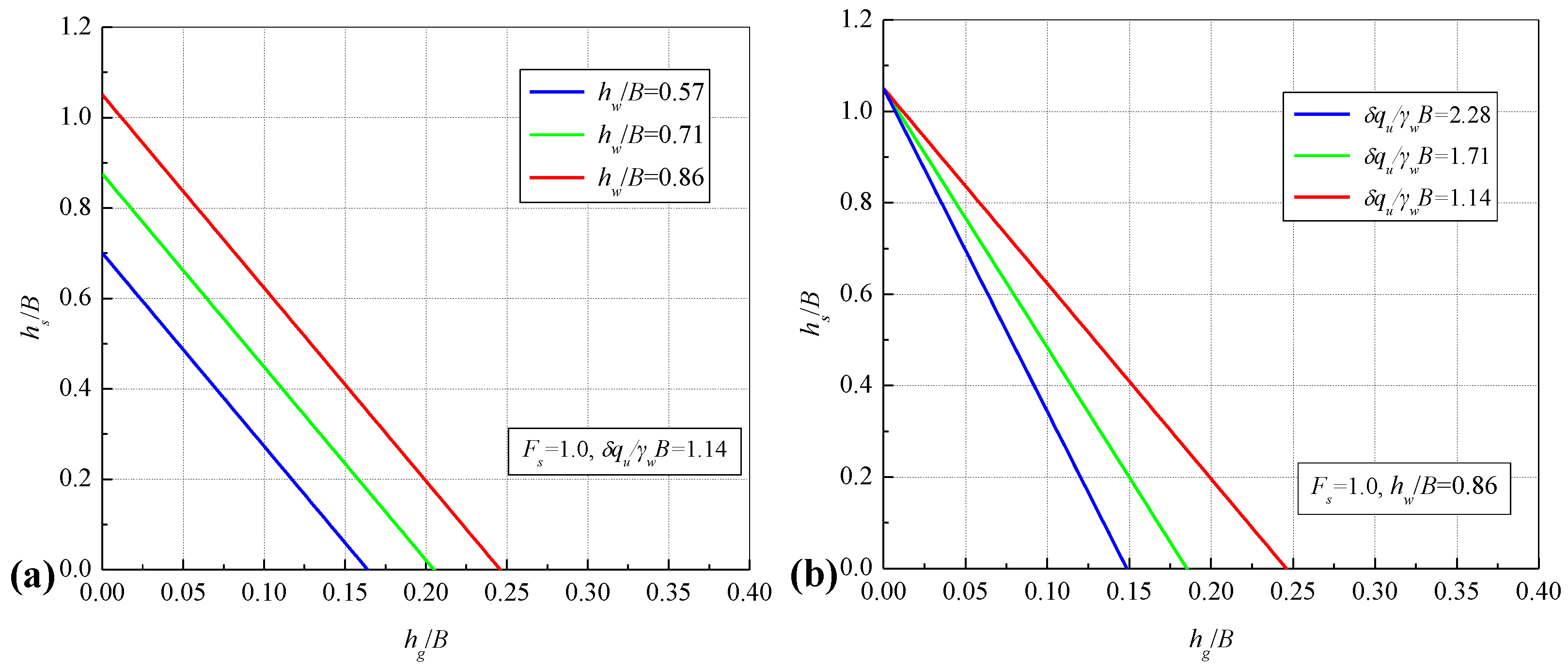
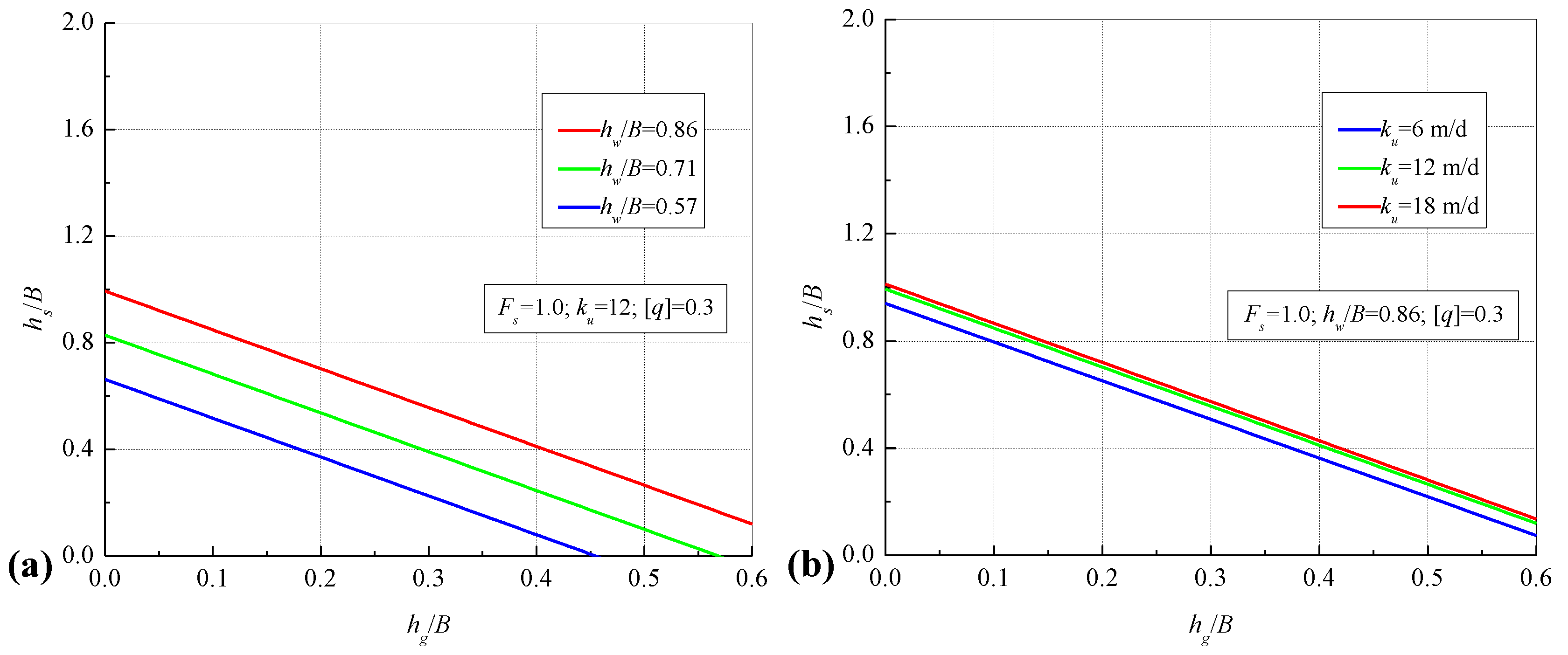
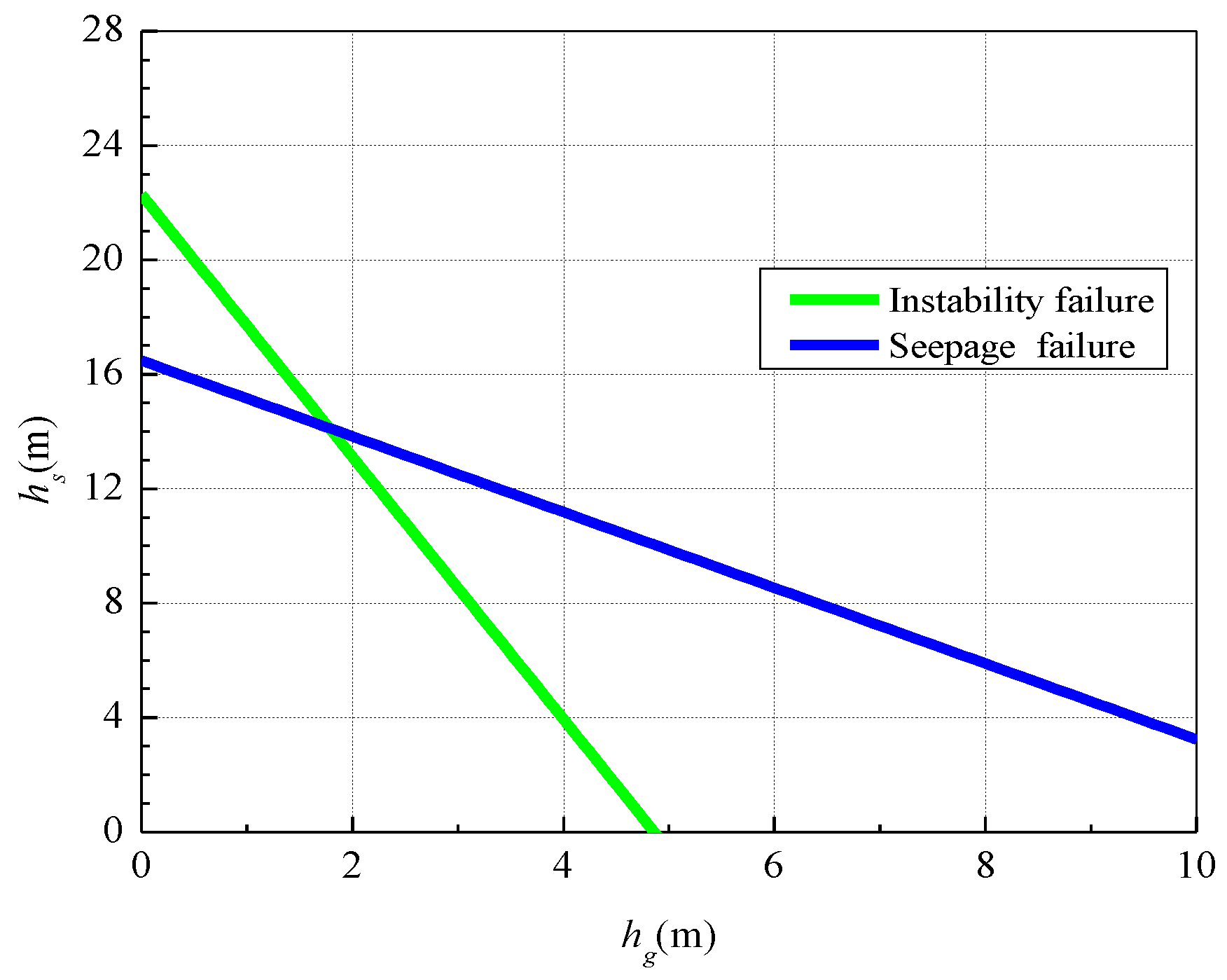
3.1. Parametric Analysis
3.2. Design Procedure
4. Application
4.1. Case Study
4.2. Design of Jet-Grouted Bottom Sealing Barriers
4.3. Pumping Test Results And Analyses
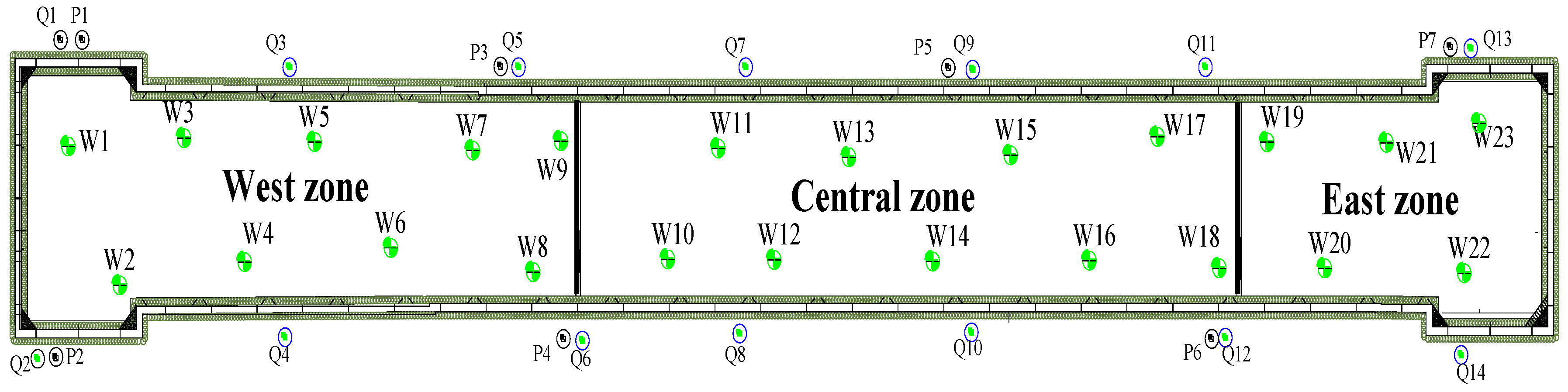
4.3.1. Pumping Test Scheme
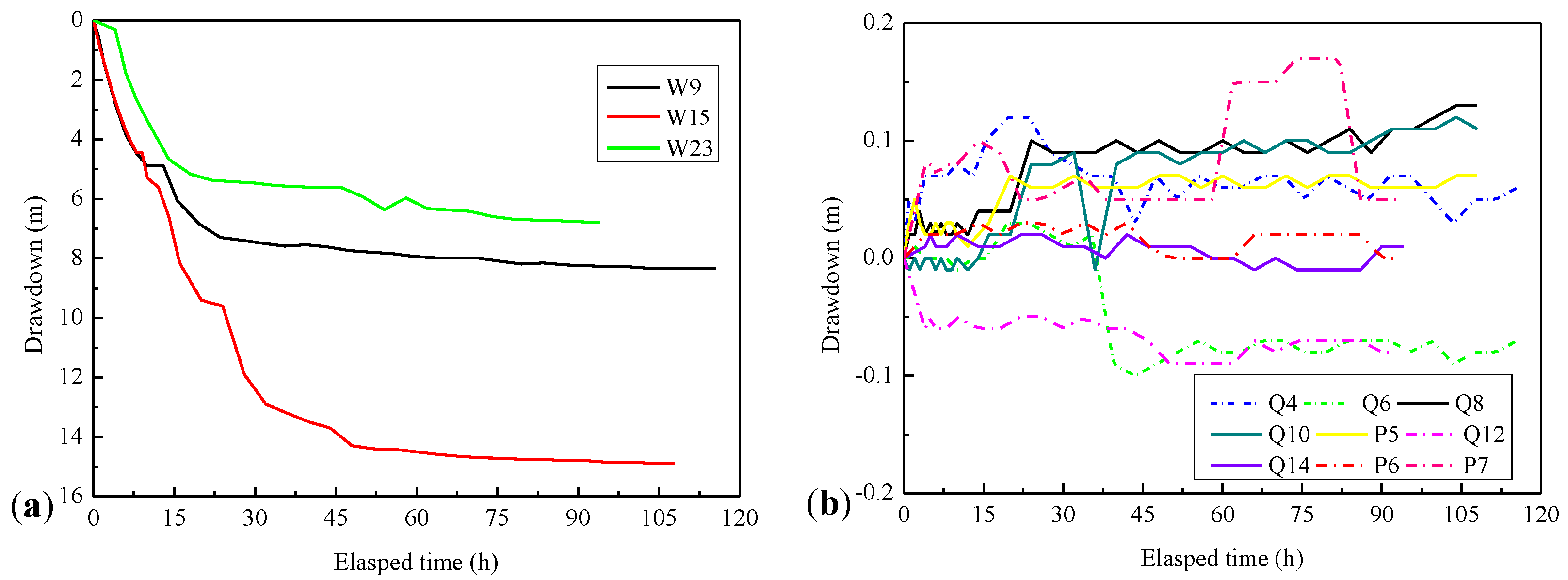
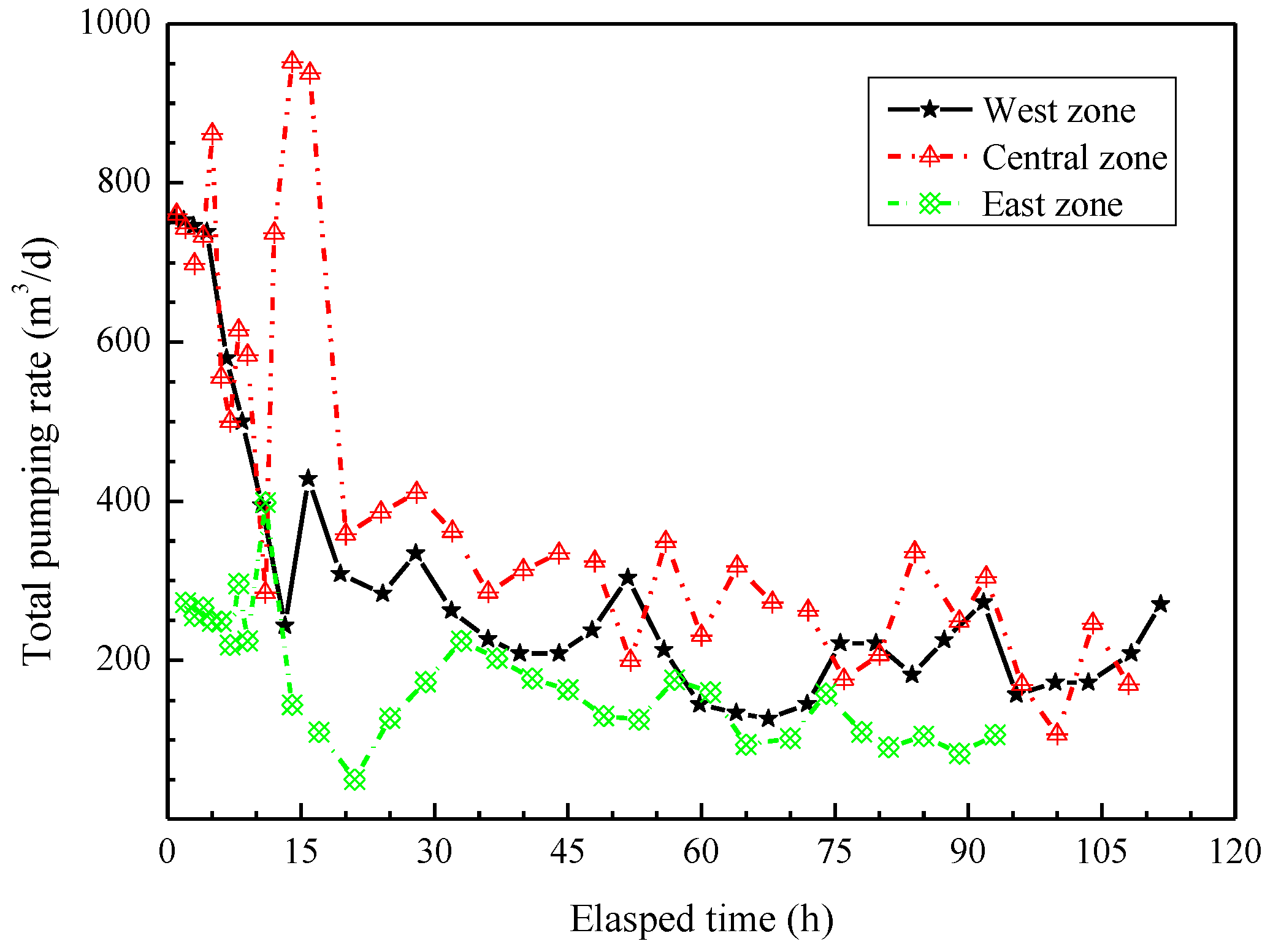
4.3.2. Pumping Test Results and Analyses
4.4. Discussion
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| L | length of rectangular excavation | B | width of rectangular excavation |
| p | perimeter of long rectangle excavation | Ap | area of jet-grouted bottom sealing barriers |
| hexc | depth of rectangular excavation | hw | groundwater head with regard to excavation bottom |
| hg | thickness of jet-grouted bottom-sealing barriers | hs | depth of untreated soils with regard to excavation bottom |
| hu | depth of enclosures embedded in the aquifers | γw | unit weight of water |
| γs | unit weight of natural soil | γg | unit weight of jet-grouted bottom sealing barriers |
| effective unit weight of untreated soils | effective unit weight of jet-grouted barriers | ||
| qu | unconfined compression strength of jet-grouted materials | cg | cohesion of jet-grouted materials |
| ki | hydraulic conductivity of each soil layer | Mi | the average thickness of each soil layer |
| ku | equivalent hydraulic conductivity of multi-layer soils | ks | effective hydraulic conductivity of untreated soils |
| kg | effective hydraulic conductivity of bottom sealing barriers | shear strength of jet-grouted materials | |
| h1 | hydraulic head at the top of the jet-grouted barriers | h2 | hydraulic head at the bottom of the jet-grouted barriers |
| h0 | hydraulic head of the excavation bottom | Q | flow rate of bottom sealing barriers |
| Jg | average hydraulic gradient of jet-grouted barriers | Js | average hydraulic gradient of and untreated soils |
| V | uplift action of the groundwater pressure | R | stabilizing action of the shear force |
| G | stabilizing action provided by self-weight of both untreated soils and jet-grouted barriers | ||
| [q] | designed allowable seepage of bottom sealing barriers per unit area |
References
- Chen, J.J.; Zhang, L.Y.; Zhang, J.F.; Zhu, Y.F.; Wang, J.H. Field tests, modification, and application of deep soil mixing method in soft clay. J. Geotech. Geoenviron. Eng. 2013, 139, 24–34. [Google Scholar] [CrossRef]
- Xu, Y.S.; Shen, S.L.; Ma, L.; Sun, W.J.; Yin, Z.Y. Evaluation of the blocking effect of retaining walls on groundwater seepage in aquifers with different insertion depths. Eng. Geol. 2014, 183, 254–264. [Google Scholar] [CrossRef]
- Wang, Z.F.; Shen, S.L.; Ho, C.E.; Kim, Y.H. Investigation of field-installation effects of horizontal twin-jet grouting in Shanghai soft soil deposits. Can. Geotech. J. 2013, 50, 288–297. [Google Scholar] [CrossRef]
- Kimura, M.; Inazumi, S.; Too, J.K.A.; Isobe, K.; Mitsuda, Y.; Nishiyama, Y. Development and application of H-joint steel pipe sheet piles in construction of foundation for structures. Soils Found. 2007, 47, 237–251. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, P.; Yu, S. A new method for deformation monitoring on H-pile in SMW based on BOTDA. Measurement 2015, 70, 156–168. [Google Scholar] [CrossRef]
- Zhou, N.; Vermeer, P.; Lou, R.; Tang, Y.; Jiang, S. Numerical simulation of deep foundation pit dewatering and optimization of controlling land subsidence. Eng. Geol. 2010, 114, 251–260. [Google Scholar] [CrossRef]
- Shi, C.; Cao, C.; Lei, M.; Peng, L.; Jiang, J. Optimal design and dynamic control of construction dewatering with the consideration of dewatering process. Ksce J. Civ. Eng. 2017, 21, 1161–1169. [Google Scholar] [CrossRef]
- Roy, D.; Robinson, K.E. Surface settlements at a soft soil site due to bedrock dewatering. Eng. Geol. 2009, 107, 109–117. [Google Scholar] [CrossRef]
- Forth, R.A. Groundwater and geotechnical aspects of deep excavations in Hong Kong. Eng. Geol. 2004, 72, 253–260. [Google Scholar] [CrossRef]
- Shen, S.L.; Wu, Y.X.; Misra, A. Calculation of head difference at two sides of a cut-off barrier during excavation dewatering. Comput. Geotech. 2017, 91, 192–202. [Google Scholar] [CrossRef]
- Wang, J.X.; Liu, X.T.; Wu, Y.B.; Liu, S.L.; Wu, L.G.; Lou, R.X.; Lu, J.S.; Yao, Y. Field experiment and numerical simulation of coupling non-Darcy flow caused by curtain and pumping well in foundation pit dewatering. J. Hydrol. 2017, 549, 277–293. [Google Scholar] [CrossRef]
- Wang, J.X.; Liu, X.T.; Liu, S.L.; Zhu, Y.F.; Pan, W.Q.; Zhou, J. Physical model test of transparent soil on coupling effect of cut-off wall and pumping wells during foundation pit dewatering. Acta Geotech. 2018, 14, 141–162. [Google Scholar] [CrossRef]
- Wu, Y.X.; Shen, S.L.; Xu, Y.S.; Yin, Z.Y. Characteristics of groundwater seepage with cutoff wall in gravel aquifer. I: field observations. Can. Geotech. J. 2015, 52, 1526–1538. [Google Scholar]
- Wu, Y.X.; Shen, S.L.; Yuan, D.J. Characteristics of dewatering induced drawdown curve under blocking effect of retaining wall in aquifer. J. Hydrol. 2016, 539, 554–566. [Google Scholar] [CrossRef]
- Wu, Y.X.; Shen, S.L.; Cheng, W.C.; Hino, T. Semi-analytical solution to pumping test data with barrier, wellbore storage, and partial penetration effects. Eng. Geol. 2017, 226, 44–51. [Google Scholar] [CrossRef]
- Zeng, C.F.; Xue, X.L.; Zheng, G.; Xue, T.Y.; Mei, G.X. Responses of retaining wall and surrounding ground to pre-excavation dewatering in an alternated multi-aquifer-aquitard system. J. Hydrol. 2018, 559, 609–626. [Google Scholar] [CrossRef]
- Croce, P.; Modoni, G. Design of jet-grouting cut-off. Ground Improv. 2007, 11, 11–19. [Google Scholar] [CrossRef]
- Pujades, E.; Carrera, J.; Vàzquez-Suñé, E.; Jurado, A.; Vilarrasa, V.; Mascuñano-Salvador, E. Hydraulic characterization of diaphragm walls for cut and cover tunnelling. Eng. Geol. 2012, 125, 1–10. [Google Scholar] [CrossRef]
- Pujades, E.; Jurado, A.; Carrera, J.; Vàzquez-Suñé, E.; Dassargues, A. Hydrogeological assessment of non-linear underground enclosures. Eng. Geol. 2016, 207, 91–102. [Google Scholar] [CrossRef]
- Vilarrasa, V.; Carrera, J.; Jurado, A.; Pujades, E.; Vazquez-Sune, E. A methodology for characterizing the hydraulic effectiveness of an annular low-permeability barrier. Eng. Geol. 2011, 120, 68–80. [Google Scholar] [CrossRef]
- Ochmański, M.; Modoni, G.; Bzòwka, J. Prediction of the diameter of jet grouting columns with artificial neural networks. Soils Found. 2015, 55, 425–436. [Google Scholar] [CrossRef] [Green Version]
- Van Tol, A.F. Lessons Learned from Jetgrouting at A Tunnel Project in the Haghe; Dhouib, A., Magnan, J.P., Mastat, P., Eds.; LCPC: Paris, France, 2004; pp. 321–331. [Google Scholar]
- Flora, A.; Lirer, S.; Lignola, G.P.; Modoni, G. Mechanical Analysis of jet-grouted supporting structures. In Proceedings of the 7th International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground, Taylor & Francis Group, Boca Raton, FL, USA, 15 May 2011. [Google Scholar]
- Modoni, G.; Croce, P.; Mongiovi, L. Theoretical modelling of jet grouting. Geotechnique 2006, 56, 335–347. [Google Scholar] [CrossRef]
- Shen, S.L.; Wang, Z.F.; Horpibulsuk, S.; Kim, Y.H. Jet grouting with a newly developed technology: The Twin-Jet method. Eng. Geol. 2013, 152, 87–95. [Google Scholar] [CrossRef]
- Shen, S.L.; Wang, Z.F.; Sun, W.J.; Wang, L.B.; Horpibulsuk, S. A field trial of horizontal jet grouting using the composite-pipe method in the soft deposit of Shanghai. Tunn. Undergr. Space Technol. 2013, 35, 142–151. [Google Scholar] [CrossRef]
- Croce, P.; Flora, A.; Modoni, G. Jet Grouting Technology, Design and Control; CRC: New York, NY, USA, 2014. [Google Scholar]
- Pujades, E.; Vàzquez-Suñé, E.; Carrera, J.; Vilarrasa, V.; De Simone, S.; Jurado, A.; Ledesma, A.; Ramos, G.; Lloret, A. Deep enclosures versus pumping to reduce settlements during shaft excavations. Eng. Geol. 2014, 169, 100–111. [Google Scholar] [CrossRef]





| Soil Layer | Average Thickness (m) | Hydraulic Conductivity | Void Ratio e | Unit Weight γ (kN/m3) | Compression Modulus Es (MPa) | |
|---|---|---|---|---|---|---|
| kh (m/d) | kv (m/d) | |||||
| miscellaneous fill | 2.8 | 8.64 × 10−2 | - | 18.5 | 4.0 | |
| silt | 4.2 | 0.00085 | 0.00046 | 1.71 | 15.6 | 1.6 |
| silt with sand | 4.3 | 0.13 | 1.60 | 15.9 | 4.0 | |
| fine-medium sand with silt | 10.0 | 8.5 | - | 18.5 | 6.0 | |
| silty clay | 3.0 | 0.004 | 0.003 | 0.71 | 19.2 | 7.0 |
| medium-coarse sand | 11.0 | 15 | - | 19.0 | 13.0 | |
| silt with sand | 2 | 0.13 | 1.1 | 17.4 | 3.5 | |
| gravel | 8.0 | 40 | - | 18.0 | 40.0 | |
| Variables | B (m) | γs (kN/m3) | γw (kN/m3) | γg (kN/m3) | ku (m/d) | hw (m) | hexc (m) | [q] (m/d) | cg (kPa) |
|---|---|---|---|---|---|---|---|---|---|
| Value | 18.1 | 19 | 10 | 22 | 11.5 | 13 | 16 | 0.25 | 200 |
| Properties | Grout | Water | Air | Rod Lifting Rate (cm/min) | Rod Rotation Rate (rpm) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Pressure (MPa) | Flow Rate (L/min) | Water-Cement Ratio by Weight | Pressure (MPa) | Flow Rate (L/min) | Pressure (MPa) | Flow Rate (m3/min) | |||
| Range value | 35 | 100 | 1:1 | 25–35 | 70 | 0.8 | 6 | 12 | 10 |
| Test | Subsection | Pumping Wells | Observation Wells | Pumping Time (d) | |
|---|---|---|---|---|---|
| Inside | Outside | ||||
| ① | West Zone | W1, W3, W4, W5, W6, W7, W8 | W9 | Q2, Q4, Q6, P2, P4 | 5 |
| ② | Central Zone | W10, W12, W13, W14, W16, W17 | W15 | Q6, Q8, Q10, Q12, P4, P5, P6 | 4.5 |
| ③ | East Zone | W18, W19, W20, W21, W22 | W23 | Q12, Q14, P6, P7 | 4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, C.; Shi, C.; Lei, M. A Simplified Approach to Design Jet-Grouted Bottom Sealing Barriers for Deep Excavations in Deep Aquifers. Appl. Sci. 2019, 9, 2307. https://doi.org/10.3390/app9112307
Cao C, Shi C, Lei M. A Simplified Approach to Design Jet-Grouted Bottom Sealing Barriers for Deep Excavations in Deep Aquifers. Applied Sciences. 2019; 9(11):2307. https://doi.org/10.3390/app9112307
Chicago/Turabian StyleCao, Chengyong, Chenghua Shi, and Mingfeng Lei. 2019. "A Simplified Approach to Design Jet-Grouted Bottom Sealing Barriers for Deep Excavations in Deep Aquifers" Applied Sciences 9, no. 11: 2307. https://doi.org/10.3390/app9112307





