Numerical Simulation of the Influence of Spur Dikes Spacing on Local Scour and Flow
Abstract
1. Introduction
2. Numerical Model
2.1. Sedimentation Scour Model
2.1.1. Bed-load Transport
2.1.2. Entrainment and Deposition
2.1.3. Suspended Load Transport
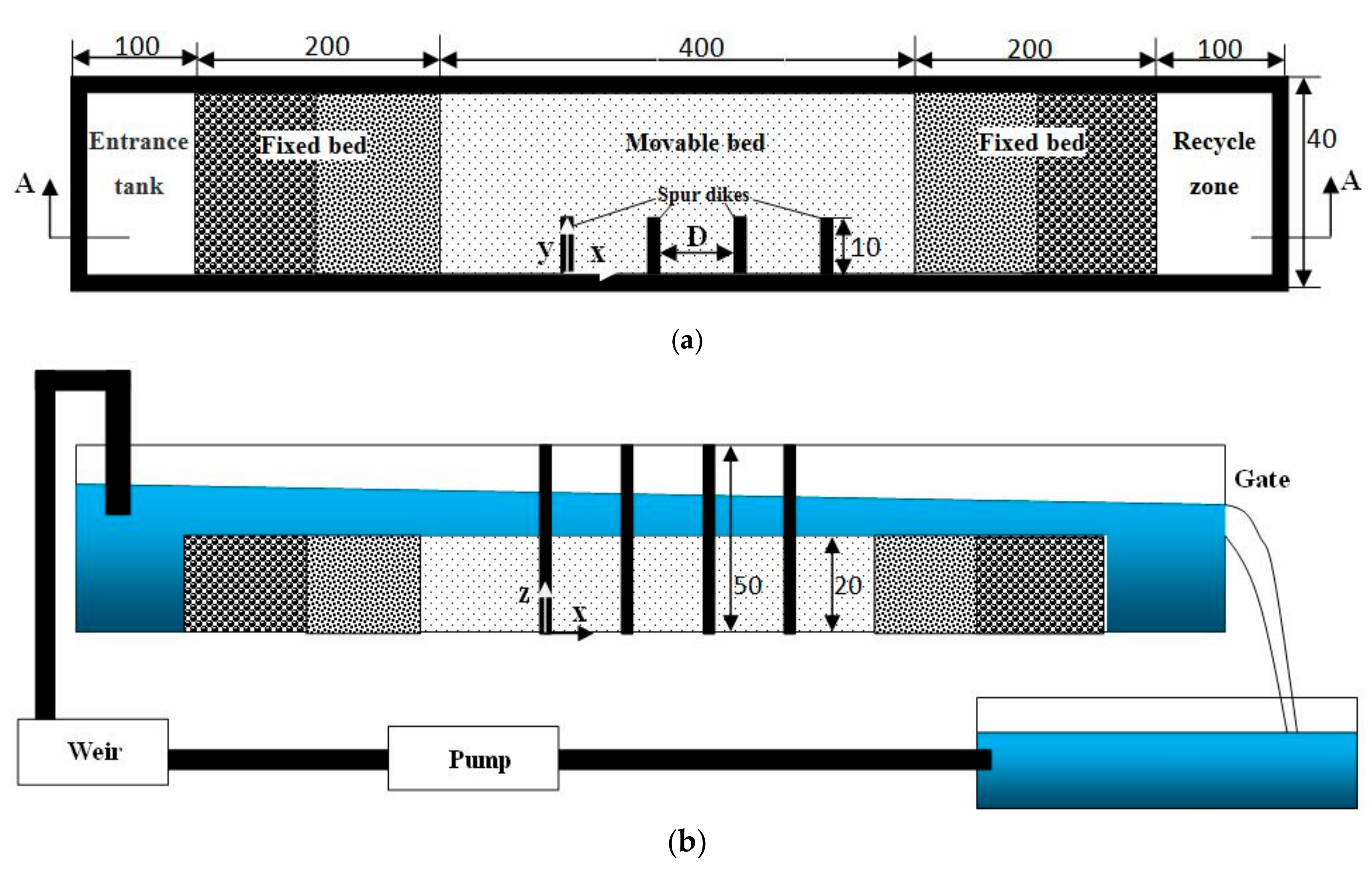
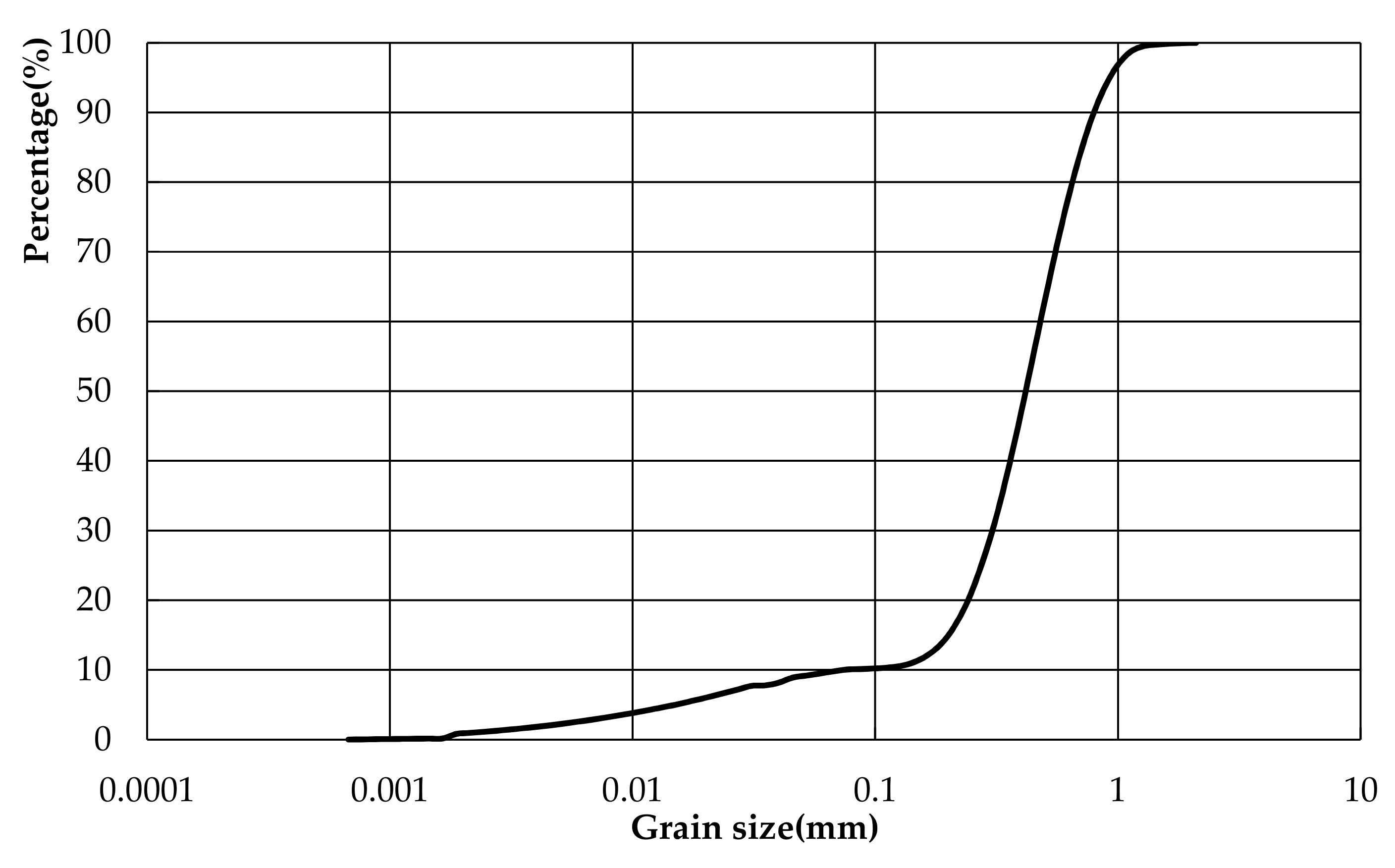
3. Laboratory Experiments
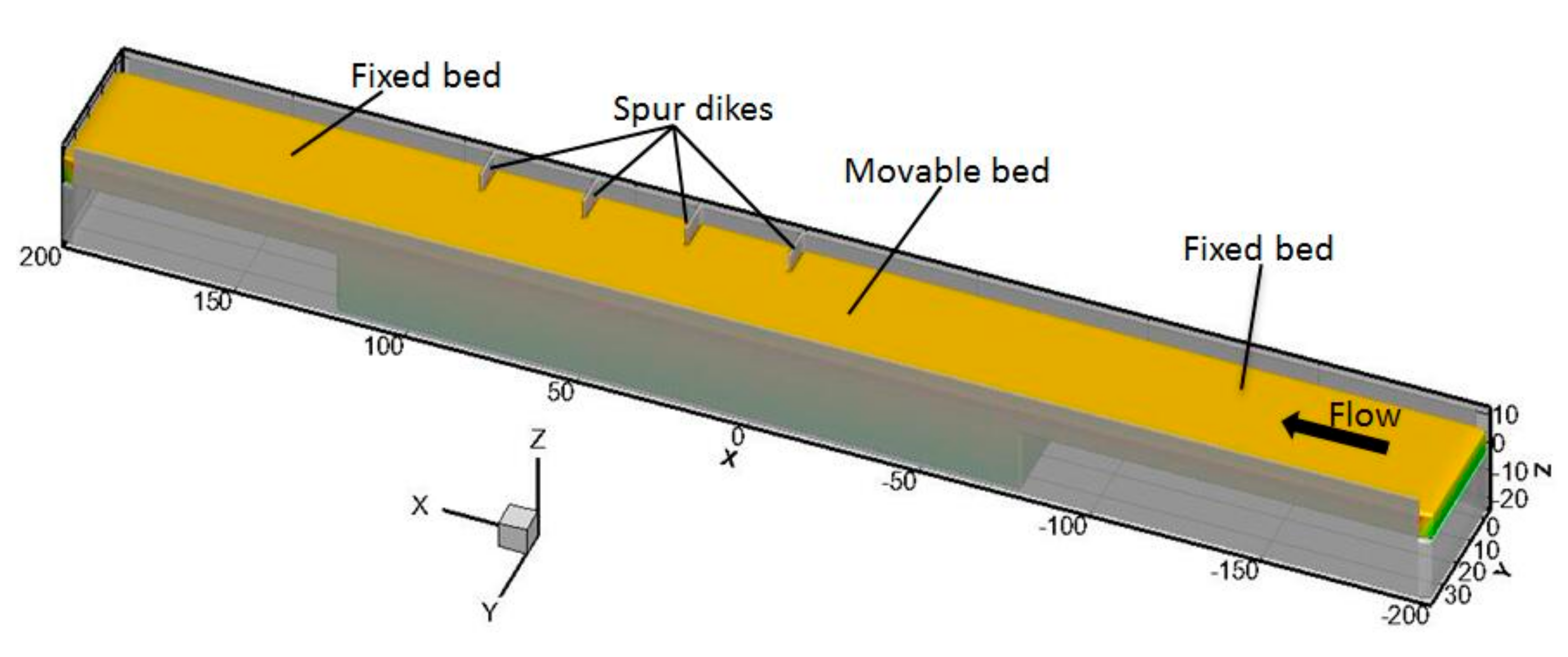
4. Computational Conditions
Grid Convergence Calculation
5. Results and Discussion
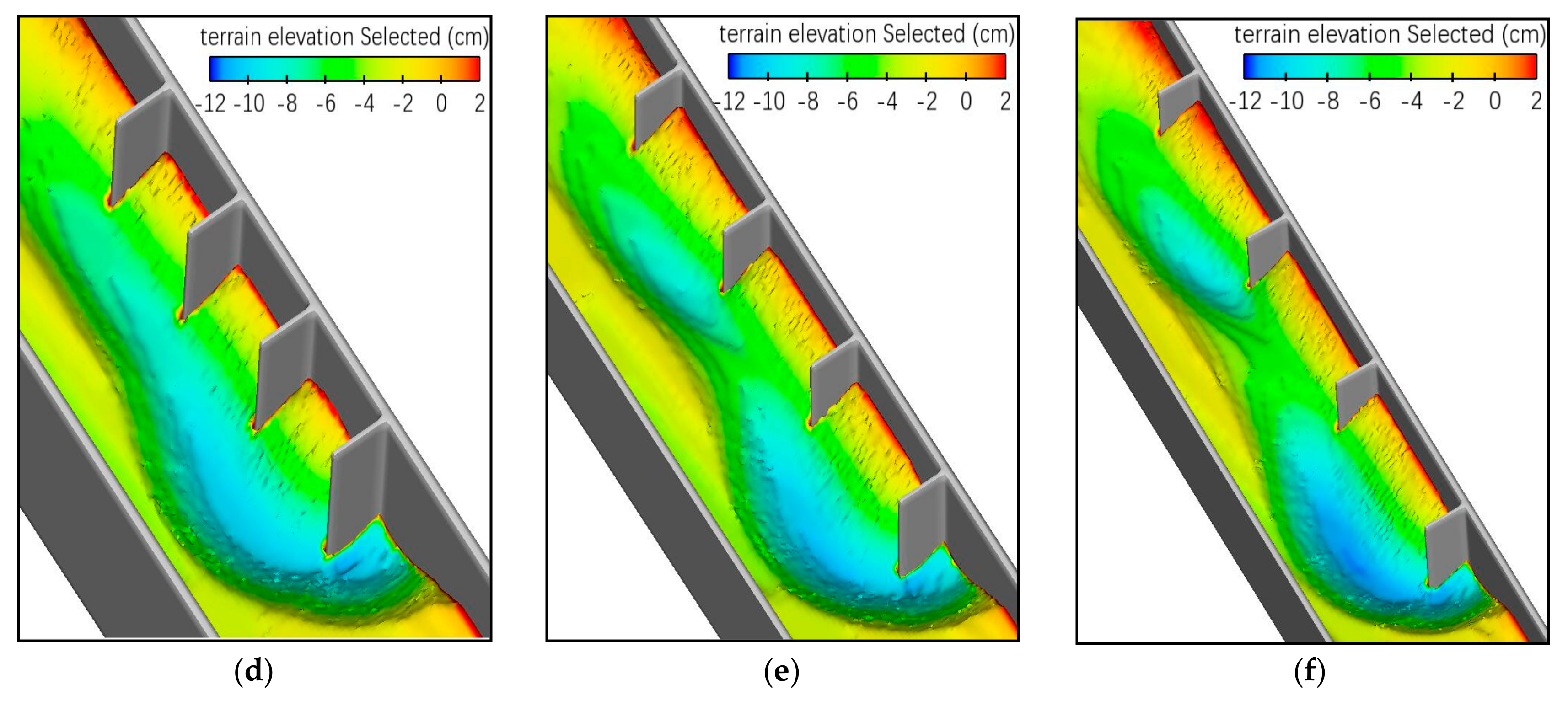
5.1. Local Scour and Bed Topographic Change
5.1.1. Qualitative Analysis
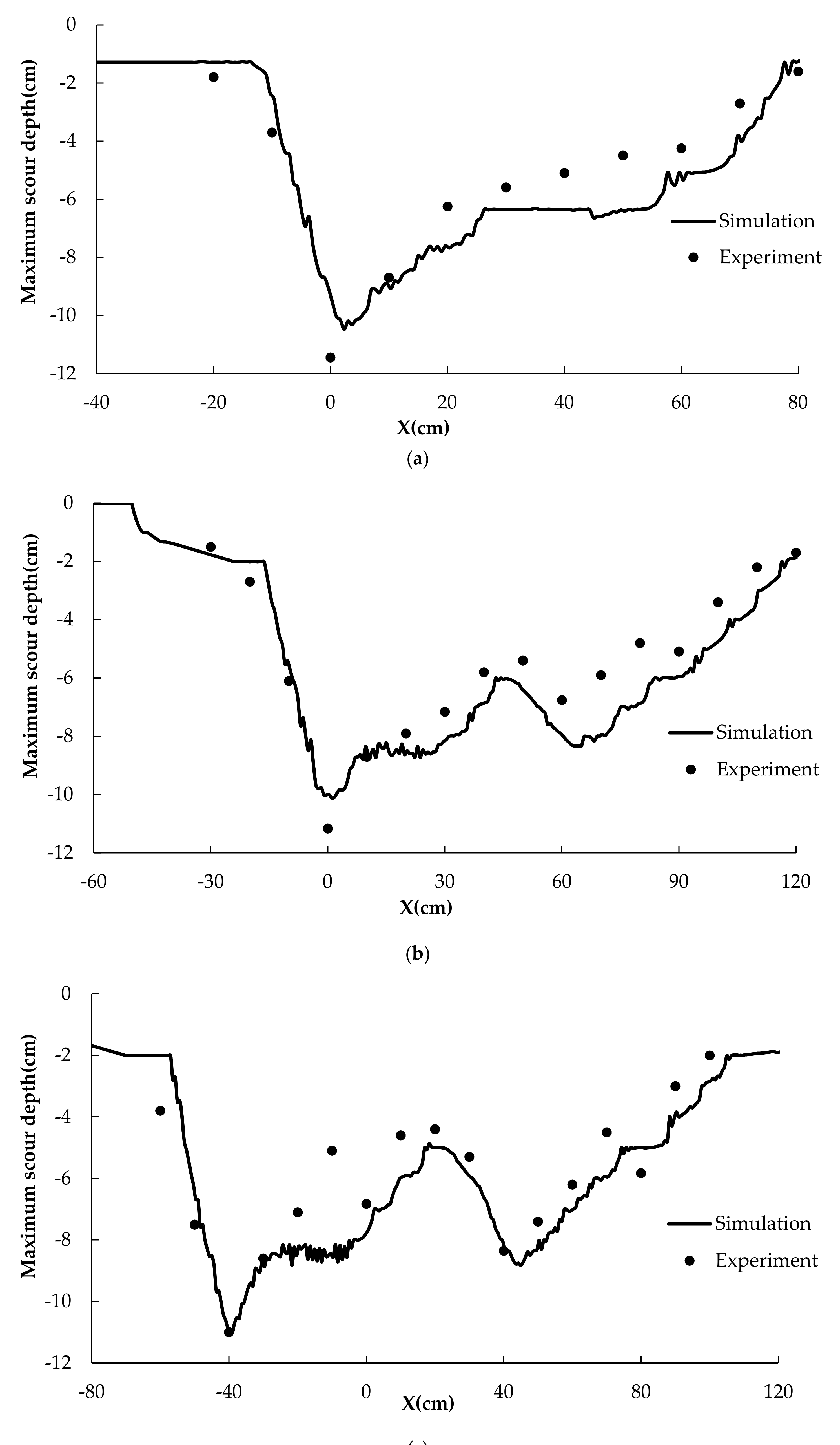
5.1.2. Quantitative Analysis
5.2. Flow Field Structure Analysis
5.2.1. Velocity Field and Streamlines Analysis
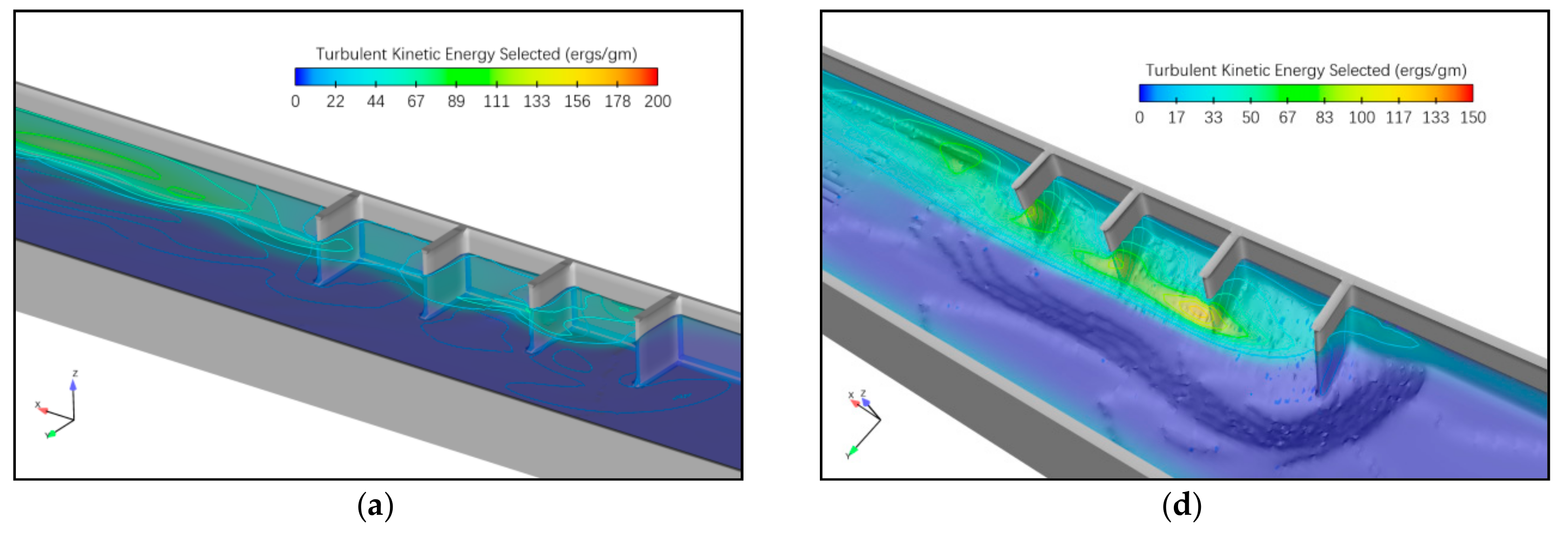
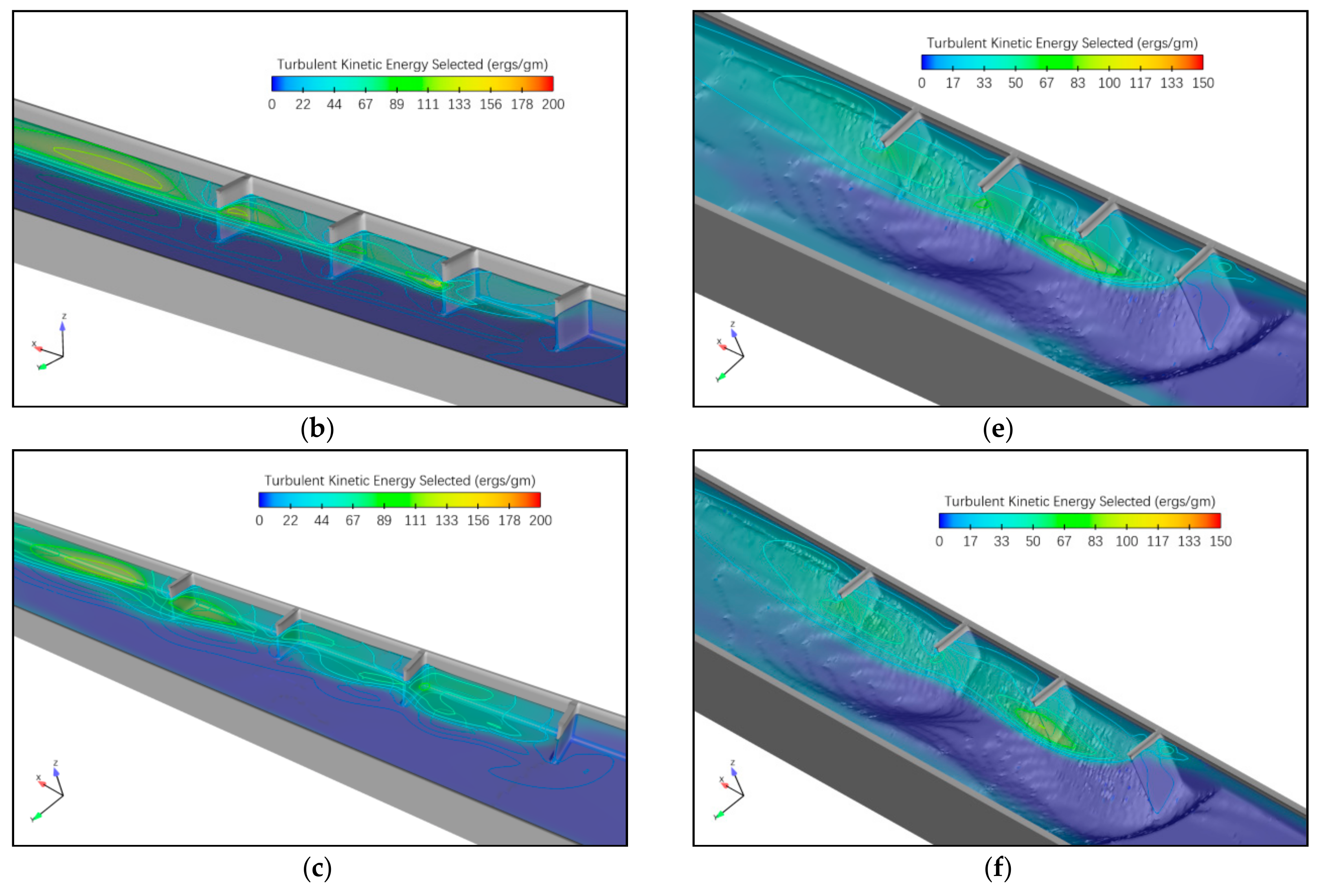
5.2.2. Turbulent Flow Field Analysis
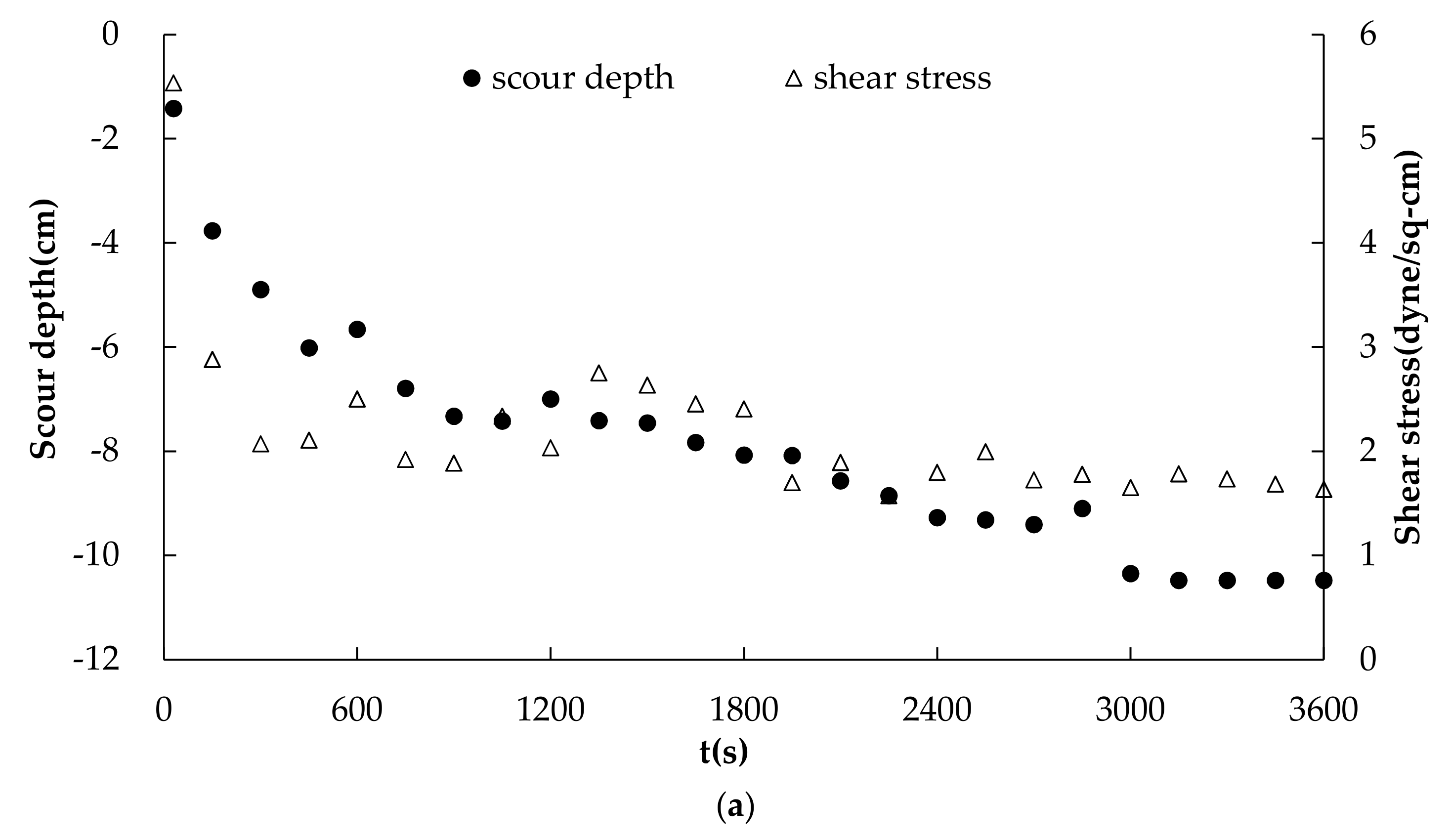
5.2.3. Bed Shear Stress Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barbhuiya, A.K.; Dey, S. Local scour at abutments: A review. Sadhana 2004, 29, 449–476. [Google Scholar] [CrossRef]
- Dey, S.; Barbhuiya, A.K. Time variation of scour at abutments. J. Hydraul. Eng. 2005, 131, 11–23. [Google Scholar] [CrossRef]
- Fukuoka, S.; Nakagawa, N.; Sumi, T.; Zhang, H. Advances in River Sediment Research; Taylor & Francis Group: London, UK, 2013. [Google Scholar]
- Pandey, M.; Ahmad, Z.; Sharma, P.K. Scour around impermeable spur dikes: A review. ISH J. Hydraul. Eng. 2017, 1–20. [Google Scholar] [CrossRef]
- Zhang, H.; Nakagawa, H.; Ishigaki, T.; Muto, Y. Prediction of 3D Flow Field and Local Scouring Around Spur Dikes. Proc. Hydraul. Eng. 2005, 49, 1003–1008. [Google Scholar] [CrossRef]
- Basser, H.; Karami, H.; Shamshirband, S.; Jahangirzadeh, A.; Akib, S.; Saboohi, H. Predicting optimum parameters of a protective spur dike using soft computing methodologies–A comparative study. Comput. Fluids 2014, 97, 168–176. [Google Scholar] [CrossRef]
- Pandey, M. Flow Pattern and Scour Around Multiple Spur-Dikes in Channels. Master’s Thesis, Indian Institute of Technology Roorkee, Roorkee, India, 2014. [Google Scholar]
- Tominaga, A.; Sadat, S.H. Combination of permeable and impermeable spur dikes to reduce local scour and to create diverse river bed. In River Sedimentation: Proceedings of the 13th International Symposium on River Sedimentation (Stuttgart, Germany, 19–22 September, 2016); CRC Press: Boca Raton, FL, USA, 2016; Volume 101, pp. 19–22. [Google Scholar]
- Nakagawa, K.; Kawahara, Y.; Tamai, N. Experimental study on hydraulic characteristics of flows in embayments. Proc. Hydraul. Eng. 1995, 39, 595–600. [Google Scholar] [CrossRef][Green Version]
- Muto, Y.; Imamoto, H.; Ishigaki, T. Turbulence characteristics of a shear flow in an embayment attached to a straight open channel. Adv. Hydro Sci. Eng. 2000, IV, 232–241. [Google Scholar]
- Choufu, L.; Abbasi, S.; Pourshahbaz, H.; Taghvaei, P.; Tfwala, S. Investigation of flow, erosion, and sedimentation pattern around varied groynes under different hydraulic and geometric conditions: A numerical study. Water 2019, 11, 235. [Google Scholar] [CrossRef]
- Duan, J.G. Mean Flow and Turbulence around a Laboratory Spur Dike. J. Hydraul. Eng. 2009, 135, 803–811. [Google Scholar] [CrossRef]
- Yaeger, M.A. Mean Flow and Turbulence around Two Series of Experimental Dikes; Department of Hydrology and Water Resources, The University of Arizona: Tucson, AZ, USA, 2009. [Google Scholar]
- Acharya, A. Experimental Study and Numerical Simulation of Flow and Sediment Transport around a Series of Spur Dikes; Department of Civil Engineering and Engineering Mechanics, The University of Arizona: Tucson, AZ, USA, 2011. [Google Scholar]
- Molinas, A.; Kheireldin, K.; Wu, B. Shear stress around vertical wall abutments. J. Hydraul. Eng. 1998, 124, 463–480. [Google Scholar] [CrossRef]
- Koken, M.; Gogus, M. Effect of spur dike length on the horseshoe vortex system and the bed shear stress distribution. J. Hydraul. Res. 2015, 53, 196–206. [Google Scholar] [CrossRef]
- Yakhot, V.; Orzag, S.A. Renormalization group analysis of turbulence: Basic theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Hirt, C.W.; Sicilian, J.M. A porosity technique for the definition of obstacles in rectangular cell meshes. In Proceedings of the 4th International Conference on Numerical Ship Hydrodynamics, Washington, DC, USA, 24–27 September 1985. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Wei, G.; Brethour, J.M.; Gruenzner, M.; Burnham, J. Sedimentation Scour Model; Flow Science Report 03-14; Flow Science, Inc.: Santa Fe, NM, USA, 2014. [Google Scholar]
- Winterwerp, J.C.; Bakker, W.T.; Mastbergen, D.R.; van Rossum, H. Hyperconcentrated sand-water mixture flows over erodible bed. J. Hydraul. Eng. 1992, 118, 1508–1525. [Google Scholar] [CrossRef]
- Soulsby, R. Dynamics of Marine Sands; Thomas Telford Publications: London, UK, 1997. [Google Scholar]
- Elsayed, K.; Lacor, C. Numerical modeling of the flow field and performance in cyclones of different cone-tip diameters. Comput. Fluids 2011, 51, 48–59. [Google Scholar] [CrossRef]





| Flow Discharge (l/s) | 9.62 |
|---|---|
| Channel slop | 1/1000 |
| Channel width (cm) | 40 |
| Flow depth (cm) | 9 |
| Flow velocity (m/s) | 0.267 |
| Sediment grain size D50 (mm) | 0.473 |
| Sediment density (g/cm³) | 1.9 |
| Reynolds number, | 16,585 |
| Froude number, | 0.28 |
| Grid Number | Grid Size (cm) | |||||
|---|---|---|---|---|---|---|
| p | h (cm) | Relative Error | GCI (%) | |||
| 520,800 | 1 | — | 1 | 10.75 | — | — |
| 1,223,768 | 0.75 | 1.33 | 1 | 10.45 | 0.028708 | 10.77 |
| 1,978,886 | 0.5 | 1.5 | 1 | 10.48 | 0.002863 | 0.72 |
| 2,864,400 | 0.4 | 1.25 | 1 | 10.5 | 0.001905 | 0.95 |
| Case | Spacing | Maximum Scour Depth (cm) | |||
|---|---|---|---|---|---|
| I | II | III | IV | ||
| Experiment | 2l | −11.45 | −6.25 | −5.1 | −4.25 |
| 3l | −11.16 | −7.16 | −6.76 | −5.09 | |
| 4l | −11.01 | −6.83 | −8.35 | −5.83 | |
| Simulation | 2l | −10.48 | −7.676 | −6.364 | −5.346 |
| 3l | −10.12 | −8.115 | −8.107 | −5.94 | |
| 4l | −11 | −7.828 | −8.313 | −5.01 | |
| Scour Depth/Shear Stress | Correlations | ||
|---|---|---|---|
| 2l | 3l | 4l | |
| Pearson Correlation | 0.789 | 0.863 | 0.968 |
| Sig. (2-tailed) | 0 | 0 | 0 |
| N | 25 | 25 | 25 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, J.; Li, G.; Li, S. Numerical Simulation of the Influence of Spur Dikes Spacing on Local Scour and Flow. Appl. Sci. 2019, 9, 2306. https://doi.org/10.3390/app9112306
Ning J, Li G, Li S. Numerical Simulation of the Influence of Spur Dikes Spacing on Local Scour and Flow. Applied Sciences. 2019; 9(11):2306. https://doi.org/10.3390/app9112306
Chicago/Turabian StyleNing, Jian, Guodong Li, and Shanshan Li. 2019. "Numerical Simulation of the Influence of Spur Dikes Spacing on Local Scour and Flow" Applied Sciences 9, no. 11: 2306. https://doi.org/10.3390/app9112306
APA StyleNing, J., Li, G., & Li, S. (2019). Numerical Simulation of the Influence of Spur Dikes Spacing on Local Scour and Flow. Applied Sciences, 9(11), 2306. https://doi.org/10.3390/app9112306





