Predicting Behavior of Grouted Dowel Connections Using Interfacial Cohesive Elements
Abstract
:1. Introduction and Background
2. Experimental Procedure and Results
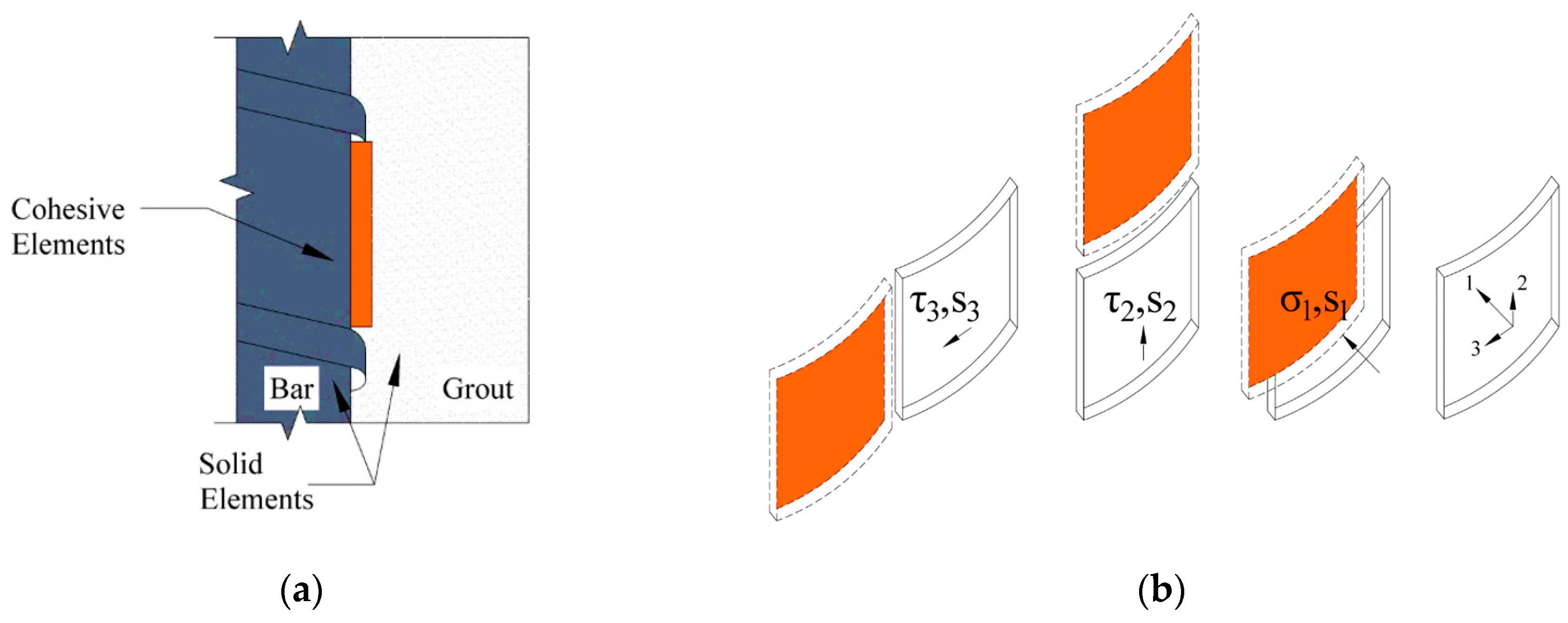
3. Interfacial Modeling
3.1. Bond–Slip Law
3.2. Normal Stress
3.3. Tangential Stress
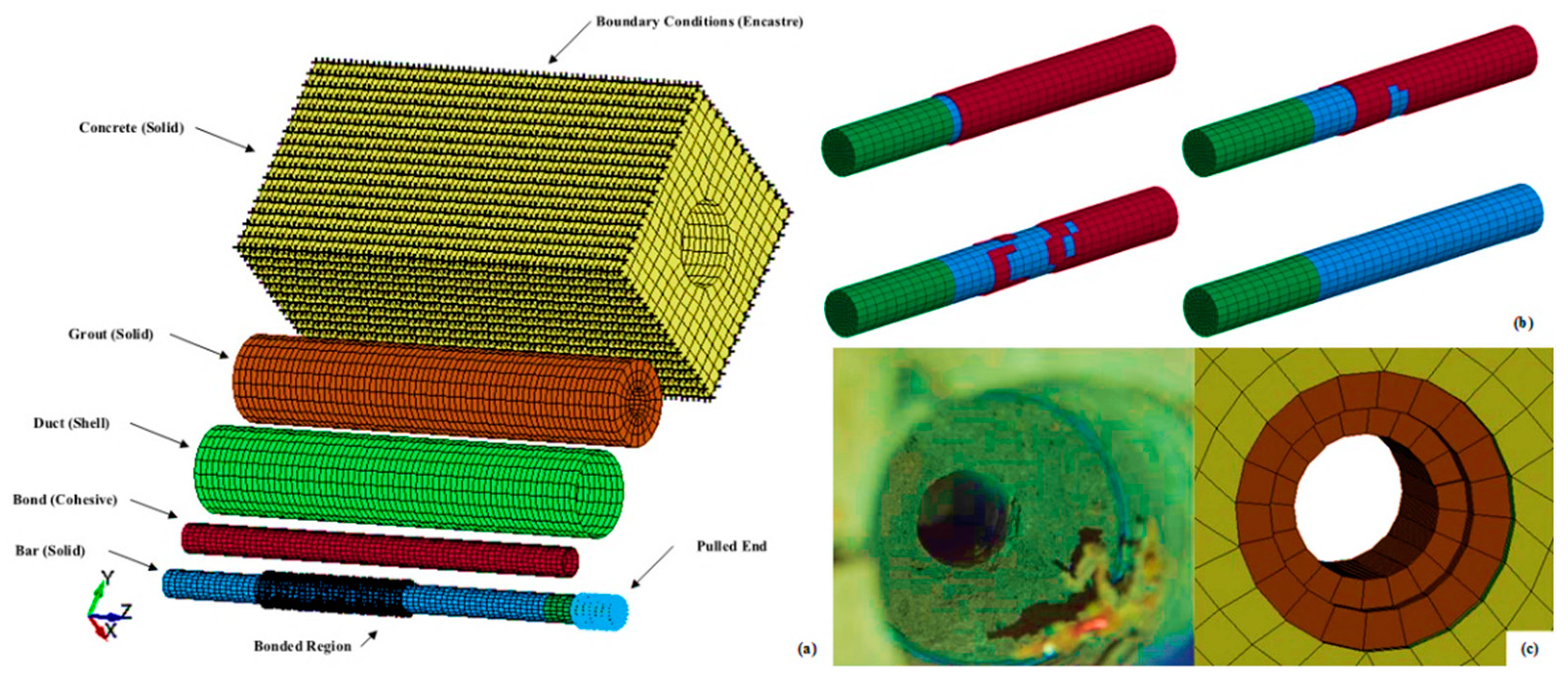
4. Implementation
4.1. Materials Constitutive Models
4.1.1. Metallic Elements
4.1.2. Concrete and Grout
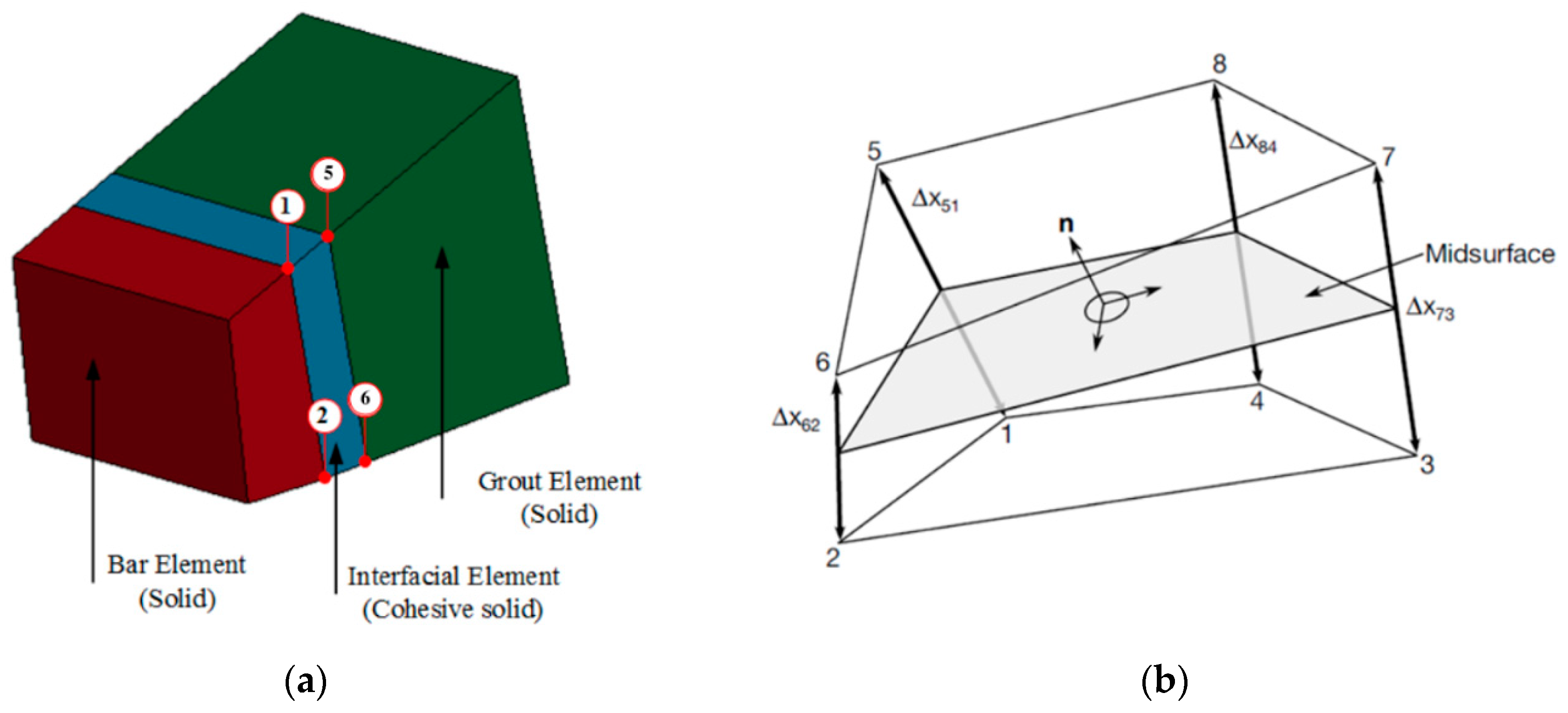
4.1.3. Cohesive Elements
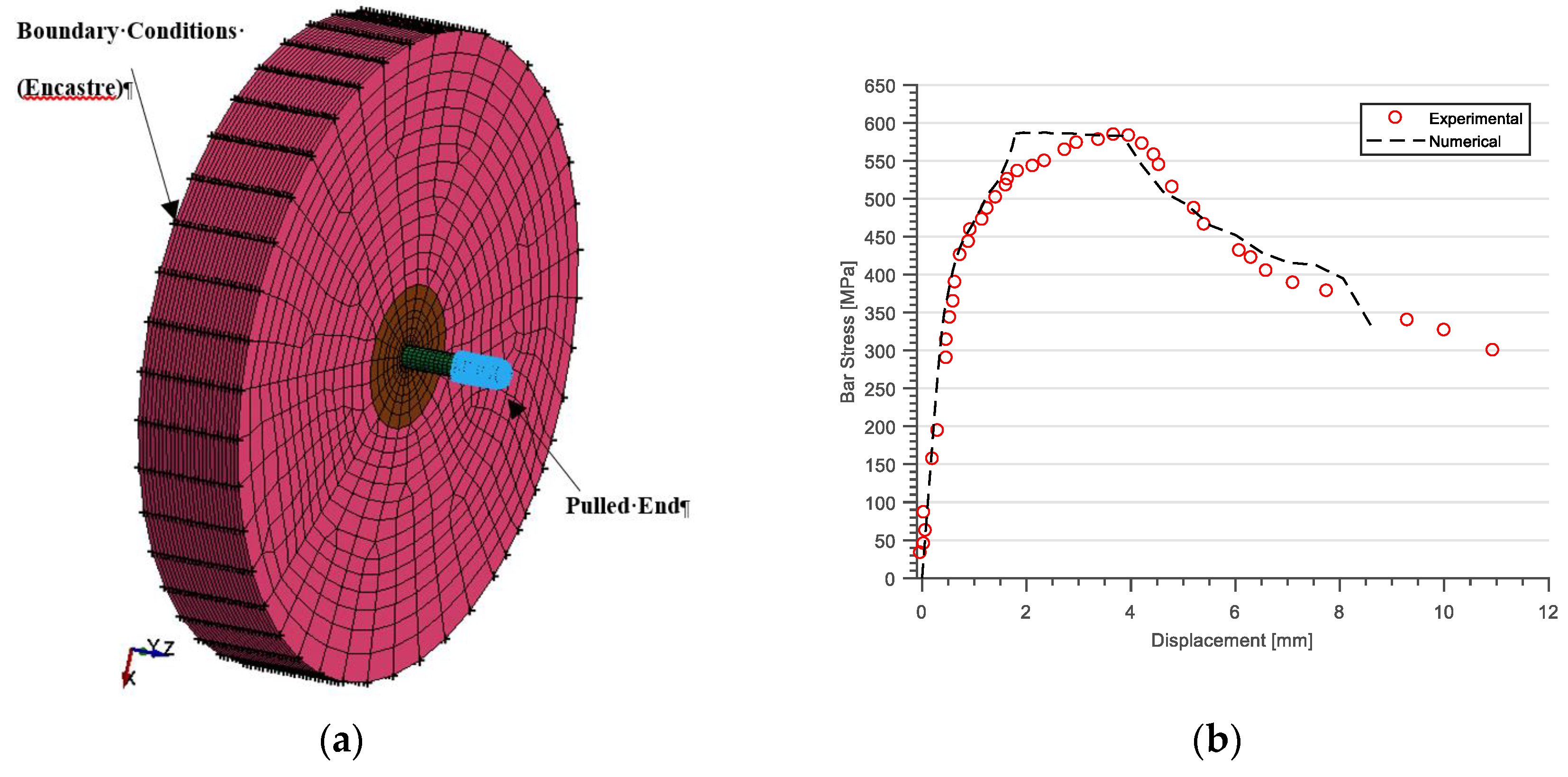
5. Model Validation
5.1. Validation Metric
5.2. Validation Examples
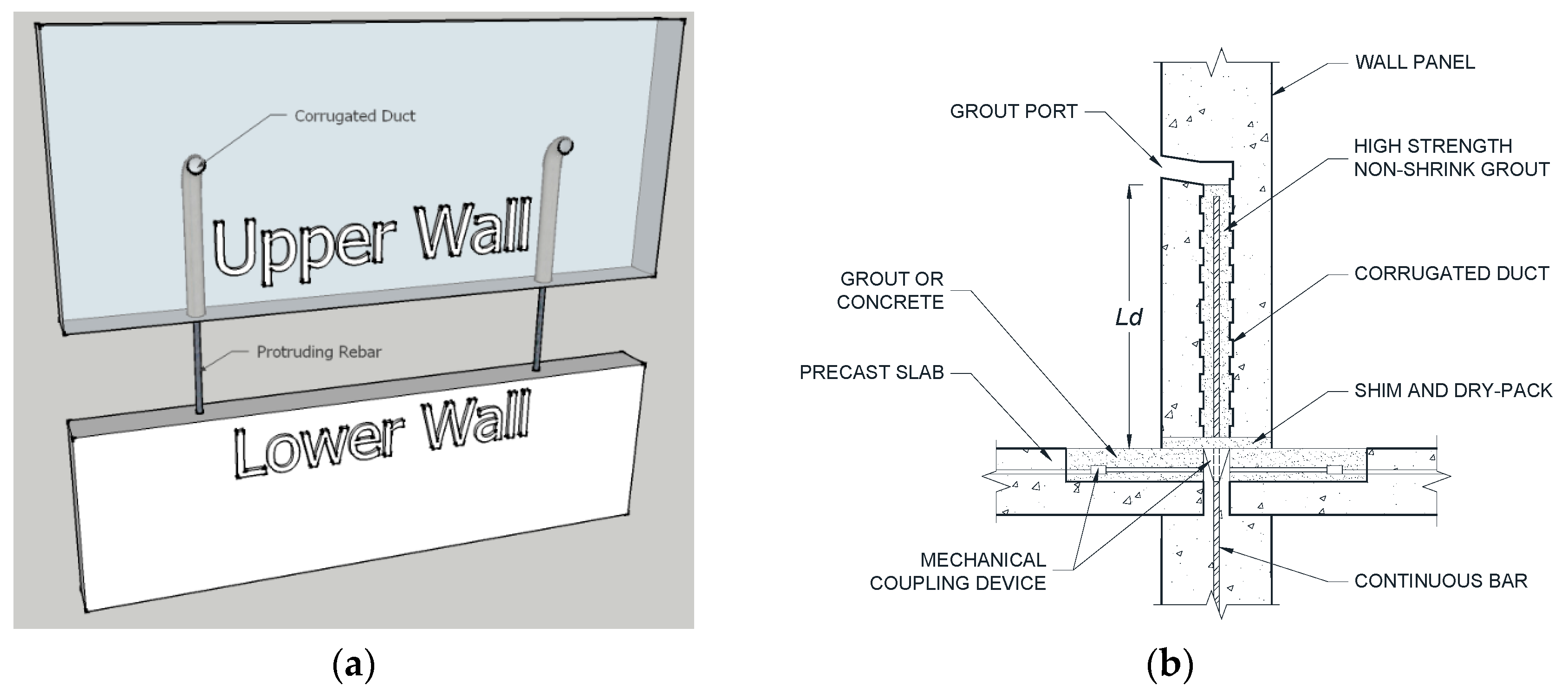
5.2.1. Grouted Ducts in Walls
5.2.2. Grouted Ducts for Segmental Bridges
5.2.3. Grouted Ducts for Bridge Bents
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- ACI Committee. Building Code Requirements for Structural Concrete and Commentary; ACI Committee: Farmingt Hills, MI, USA, 2014; pp. 1–519. [Google Scholar]
- Steuck, K.P.; Eberhard, M.O.; Stanton, J.F. Anchorage of Large-Diameter Reinforcing Bars in Ducts. ACI Struct. J. 2009, 106, 506–513. [Google Scholar]
- Nehdi, M.L.; Elsayed, M. Experimental and analytical study on grouted duct connections in precast concrete construction. Mater. Struct. 2017, 50, 1–15. [Google Scholar]
- Brenes, F.J.; Wood, S.L.; Kreger, M.E. Anchorage Requirements for Grouted Vertical-Duct Connectors in Precast Bent Cap Systems; Technical Report No. FHWA/TX-06-4176-1; Texas Department of Transportation: Austin, TX, USA, 2006; pp. 1–251.
- Tazarv, M.; Saiidi, M.S. UHPC-filled duct connections for accelerated bridge construction of RC columns in high seismic zones. Eng. Struct. 2015, 99, 413–422. [Google Scholar] [CrossRef]
- Hosseini, S.J.A.; Rahman, A.B.A.; Osman, M.H.; Saim, A.; Adnan, A. Bond behavior of spirally confined splice of deformed bars in grout. Constr. Build. Mater. 2015, 80, 180–194. [Google Scholar] [CrossRef]
- Provost-Smith, D.; Elsayed, M.; Nehdi, M. Effect of early-age subfreezing temperature on grouted dowel precast concrete wall connections. Constr. Build. Mater. 2017, 140, 385–394. [Google Scholar] [CrossRef]
- Elsayed, M.; Ghrib, F.; Nehdi, M. Experimental and analytical study on precast concrete dowel connections under quasi-static loading. Constr. Build. Mater. 2018, 168, 692–704. [Google Scholar] [CrossRef]
- Lu, Z.; Huang, J.; Li, Y.; Dai, S.; Peng, Z.; Liu, X.; Zhang, M. Mechanical behaviour of grouted sleeve splice under uniaxial tensile loading. Eng. Struct. 2019, 186, 421–435. [Google Scholar] [CrossRef] [Green Version]
- Raynor, D.J.; Dawn, E.L.; Stanton, J.F. Bond-Slip Response of Reinforcing Bars Grouted in Ducts. ACI Struct. J. 2002, 99, 568–576. [Google Scholar]
- Zhou, Y.; Ou, Y.C.; Lee, G.C. Bond-slip responses of stainless reinforcing bars in grouted ducts. Eng. Struct. 2017, 141, 651–665. [Google Scholar] [CrossRef]
- Ameli, M.J.; Pantelides, C.P. Seismic Analysis of Precast Concrete Bridge Columns Connected with Grouted Splice Sleeve Connectors. J. Struct. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Wang, Z.; Qu, H.; Li, T.; Wei, H.; Wang, H.; Duan, H.; Jiang, H. Quasi-static cyclic tests of precast bridge columns with different connection details for high seismic zones. Eng. Struct. 2018, 158, 13–27. [Google Scholar] [CrossRef]
- Kuang, Z.; Zheng, G. Computational and Experimental Mechanical Modelling of a Composite Grouted Splice Sleeve Connector System. Materials. 2018, 11, 1–12. [Google Scholar]
- Li, Y.; Bielak, J.; Hegger, J.; Chudoba, R. An incremental inverse analysis procedure for identification of bond-slip laws in composites applied to textile reinforced concrete. Compos. Part. B Eng. 2018, 137, 111–122. [Google Scholar] [CrossRef]
- Monti, G.; Spacone, E. Reinforced Concrete Fiber Beam Element with Bond-Slip. J. Struct. Eng. 2000, 126, 654–661. [Google Scholar] [CrossRef]
- Zhao, J.; Sritharan, S. Modelling of strain penetration effects in fibre-based analysis of reinforced concrete structures. ACI Struct. J. 2007, 104, 133–141. [Google Scholar]
- Cho, J.Y.; Pincheira, J.A. Inelastic Analysis of Reinforced Concrete Columns with Short Lap Splices Subjected to Reversed Cyclic Loads. ACI Struct. J. 2006, 103, 280–290. [Google Scholar]
- Salem, H.M.; Maekawa, K. Pre- and Postyield Finite Element Method Simulation of Bond of Ribbed Reinforcing Bars. J. Struct. Eng. 2004, 130, 671–680. [Google Scholar] [CrossRef]
- Gan, Y. Bond Stress and Slip Modeling in Nonlinear Finite Element Analysis of Reinforced Concrete Structures. M.Sc. Thesis, University of Toronto, Toronto, ON, Canada, 2000. [Google Scholar]
- Li, J. An Investigation of Behavior and Modeling of Bond for Reinforced Concrete. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2010. [Google Scholar]
- Cox, J.V.; Herrmann, L.R. Development of a plasticity bond model for steel reinforcement. Mech. Cohesive-Frict. Mater. 1998, 3, 155–180. [Google Scholar] [CrossRef]
- Cox, J.V.; Herrmann, L.R. Validation of a plasticity bond model for steel reinforcement. Mech. Cohesive-Frict. Mater. 1999, 4, 361–389. [Google Scholar] [CrossRef]
- Lundgren, K.; Magnusson, J. Three-Dimensional Modeling of Anchorage Zones in Reinforced Concrete. J. Eng. 2001, 127, 693–699. [Google Scholar] [CrossRef] [Green Version]
- Lowes, L.N.; Moehle, J.P.; Govindjee, S. Concrete-Steel Bond Model for Use in Finite Element Modeling of Reinforced Concrete Structures. ACI Struct. J. 2004, 101, 501–511. [Google Scholar]
- Murcia-Delso, J.; Shing, P.B. Bond-Slip Model for Detailed Finite-Element Analysis of Reinforced Concrete Structures. J. Struct. Eng. 2015, 141, 4014125. [Google Scholar] [CrossRef]
- Eligehausen, R.; Popov, E.P.; Bertero, V.V. Local Bond Stress-Slip Relationships of Deformed Bars under Generalized Excitations; NSF Rep. No. UCB/EERC-82/23; National Science Foundation: Berkeley, CA, USA, 1982; pp. 69–80.
- ASTM. Standard Specification for Deformed and Plain, Low-carbon, Chromium, Steel Bars for Concrete Reinforcement; ASTM: West Conshohocken, PA, USA, 2016; pp. 1–7. [Google Scholar]
- Tastani, S.P.; Pantazopoulou, S.J. Direct Tension Pullout Bond Test: Experimental Results. J. Struct. Eng. 2010, 136, 731–743. [Google Scholar] [CrossRef]
- Parks, J.E.; Papulak, T.; Pantelides, C.P. Acoustic emission monitoring of grouted splice sleeve connectors and reinforced precast concrete bridge assemblies. Constr. Build. Mater. 2016, 122, 537–547. [Google Scholar] [CrossRef]
- Shima, H.; Chou, L.L.; Okamura, H. Bond characteristics in post-yield range of deformed bars. Doboku Gakkai Ronbunshu. 1987, 6, 213–220. [Google Scholar] [CrossRef]
- Lutz, L.A.; Gergely, P. Mechanics of Bond and Slip of Deformed Bars in Concrete. ACI J. Proc. 1967, 64, 711–721. [Google Scholar]
- Cairns, J.; Jones, K. An evaluation of the bond-splitting action of ribbed bars. ACI Mater. J. 1996, 93, 10–19. [Google Scholar]
- Goto, Y. Cracks Formed in Concrete Around Deformed Tension Bars. ACI J. Proc. 1971, 68, 244–251. [Google Scholar]
- Grassl, P.; Xenos, D.; Nyström, U.; Rempling, R.; Gylltoft, K. CDPM2: A damage-plasticity approach to modelling the failure of concrete. Int. J. Solids Struct. 2013, 50, 3805–3816. [Google Scholar] [CrossRef] [Green Version]
- Menetrey, P.; Willam, K.J. Triaxial Failure Criterion for Concrete and its Generalization. ACI Struct. J. 1995, 92, 311–318. [Google Scholar]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Hognestad, E. A Study of Combined Bending and Axial Load in Reinforced Concrete Members. Bull. Ser. 1951, 399, 128. [Google Scholar]
- Esmaeeli, H.S.; Shishehbor, M.; Weiss, W.J.; Zavattieri, P.D. A two-step multiscale model to predict early age strength development of cementitious composites considering competing fracture mechanisms. Constr. Build. Mater. 2019, 208, 577–600. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Becq-Giraudon, E. Statistical prediction of fracture parameters of concrete and implications for choice of testing standard. Cem. Concr. Res. 2002, 32, 529–556. [Google Scholar] [CrossRef]
- Tvergaard, V.; Hutchinson, J.W. The relation between crack growth resistance and fracture process parameters in elastic-plastic solids. J. Mech. Phys. Solids. 1992, 40, 1377–1397. [Google Scholar] [CrossRef]
- Livermore Software Technology Corporation. LS-DYNA Keyword User’s Manual Volume I; Livermore Software Technology Corporation: Livermore, CA, USA, 2016. [Google Scholar]
- Coronado, C.A.; Lopez, M.M. Sensitivity analysis of reinforced concrete beams strengthened with FRP laminates. Cem. Concr. Compos. 2006, 28, 102–114. [Google Scholar] [CrossRef]
- Oberkampf, W.L.; Trucano, T.G. Verification and Validation in Computational Fluid Dynamics. Verif. Valid. Prog. Aerosp. Sci. 2002, 38, 209–272. [Google Scholar] [CrossRef]






| Material Parameters | Model Calibration Parameters | (1) Model Validation | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Study | Ld (db) | Steel | Concrete | Grout | Relative Error (%) | V | RMSE | MAPE (%) | |||||||
| db (mm) | fy (MPa) | fu (MPa) | fc’ (MPa) | ft (MPa) | fc’ (MPa) | ft (MPa) | (2)τmax (MPa) | smax (mm) | sr (mm) | ||||||
| Elsayed and Nehdi | 6.0 | 25.4 | 418.8 | 601.2 | 61.6 | 6.1 | 39.3 | 6.3 | 20.7 | 1.6 | 9.8 | 18.36 | 0.82 | 26.02 | 13.93 |
| 8.0 | 22.13 | 0.78 | 44.92 | 17.80 | |||||||||||
| 12.0 | − | − | − | − | |||||||||||
| Zhou et al. | 3.9 | 25.4 | 400.0 | 635.0 | 44.8 | 4.0 | 34.5 | 3.5 | 14.7 | 4.2 | 12.0 | 19.47 | 0.81 | 12.18 | 8.79 |
| 7.8 | 20.68 | 0.79 | 41.98 | 10.12 | |||||||||||
| Steuck et al. | 8.0 | 32.2 | 421.2 | 700.0 | 42.8 | 3.9 | 57.0 | 4.5 | 18.1 | 3.8 | 17.5 | 23.23 | 0.77 | 49.83 | 13.47 |
| Calculated as [43]. | |||||||||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elsayed, M.; Nehdi, M.L.; Ghrib, F. Predicting Behavior of Grouted Dowel Connections Using Interfacial Cohesive Elements. Appl. Sci. 2019, 9, 2344. https://doi.org/10.3390/app9112344
Elsayed M, Nehdi ML, Ghrib F. Predicting Behavior of Grouted Dowel Connections Using Interfacial Cohesive Elements. Applied Sciences. 2019; 9(11):2344. https://doi.org/10.3390/app9112344
Chicago/Turabian StyleElsayed, Mohamed, Moncef L. Nehdi, and Faouzi Ghrib. 2019. "Predicting Behavior of Grouted Dowel Connections Using Interfacial Cohesive Elements" Applied Sciences 9, no. 11: 2344. https://doi.org/10.3390/app9112344
APA StyleElsayed, M., Nehdi, M. L., & Ghrib, F. (2019). Predicting Behavior of Grouted Dowel Connections Using Interfacial Cohesive Elements. Applied Sciences, 9(11), 2344. https://doi.org/10.3390/app9112344






