Pneumatic Soft Actuator with Anisotropic Soft and Rigid Restraints for Pure in-Plane Bending Motion

Featured Application

2D-PSA can be applied to soft robots that work in environments with in-plane features, such as climbing robots moving on poles or surfaces, robotic hand/finger grasp or manipulation without twisting, planar soft arms, and so on.

Abstract

A variety of soft robots with prospective applications has been developed in recent years. As a key component of a soft robot, the soft actuator plays a critical role and hence must be designed carefully according to application requirements. The soft body may deform in undesired directions if no restraint is endued, due to the isotropy of the pure soft material. For some soft robots such as an inchworm-like biped climbing robot, the actuation direction must be constrained with the appropriate structure design of the soft actuator. This study proposes a pneumatic soft actuator (PSA) to achieve pure in-plane bending motion with anisotropic soft and rigid restraints. The in-plane bending pneumatic soft actuator (2D-PSA) is developed with a composite structure where a metal hinge belt is embedded into the soft material. The design method, material choice, and fabrication process are presented in detail in this paper. Tests are conducted to measure the actuating performance of 2D-PSA in terms of the relationship between the bending angle or force and the input air pressure. Dynamic response is also measured with a laser tracker. Furthermore, a comparative experiment is carried out between the presented 2D-PSA and a general PSA, with results verifying the effectiveness of the presented 2D-PSA. A robot consisting of two serially-connected 2D-PSAs and three pneumatic suckers, which can climb on a flat surface mimicking a snake’s locomotion, is developed as an application demo of the presented 2D-PSA. Its locomotion capability presents the in-plane performance and mobility of 2D-PSA.

1. Introduction

Soft robotics is a continuously-growing research field in which smart materials and advanced control methods are applied to develop novel robots to achieve target functions. For practical applications, the target motion of soft robots must meet application-specific requirements. Mechanical programming is a new method by which soft robots can achieve target motions using soft and rigid coupling structures [1,2,3,4,5]. Unlike the rigid materials in traditional robots, the Young’s modulus of soft materials varies from ${10}^2$–${10}^6$ kPa [1]. Thus, the soft robot moves with endless degrees of freedom (DOFs). However, target motions are generally anisotropic, which means that they are able to move freely in some DOFs and are restrained in others. Thus, both soft and rigid restraints are employed to design the structure.

Common soft actuators are constructed as monolithic structures from soft materials, such as silicone rubbers [2,3], electroactive polymers [6,7,8], shape memory alloys [9,10], elastomers [11,12], hydrogels [13], or composites [14,15]. Actuation methods include a variety of stimuli, such as electrical charges [6,7,8,9,10], chemical reactions [2,16,17], and pressurized air or fluids [12,18]. Although their size, structure, material, and stimuli generally differ, their actuation motion can be divided into three basic types: bending, extending/contracting, and twisting [19]. These actuators can be configured into soft robotic systems to fulfill designated applications. However, the majority of current soft robots are designed and fabricated for specific movements. The literature includes some exceptions, such as the application of a rapid mechanical programmable method to change the bending radius and bending axis by modifying the mechanical structure [20]. A bipolar network made of soft materials was studied both experimentally and numerically to evaluate the precise role of geometry [21]. However, these studies were able to achieve their target motions, but not address the design method to make them anisotropic rigorously. In other words, these robots were able to move as required, but were also able to be forced to deform passively by unexpected loads.

The problem related to variable stiffness design and control is regarded as the core challenge of soft robotics [22]. Two main approaches are summarized in this paper: the use of active actuators arranged in an antagonistic manner and the use of semi-active actuators that can change their elastic properties (Young’s modulus). Actuators with variable and controllable deformability and compliance have been successfully applied to develop many robot systems [23], like a medical robot [24,25] and a wearable robot [26], as well as to achieve robot manipulation [27] and locomotion [28,29]. The cited works have used active, active-passive, or semi-active solutions to achieve variable stiffness. However, variable stiffness usually needs complex and active control. For some special applications, it is necessary to constrain the deformation in some specific direction, but not necessary to vary stiffness in real time. For example, in-plane bending (e.g., in the author’s previous work [12]) is needed to achieve climbing on inclined surfaces or poles. The out-of-plane motion is limited, but it is not necessary to change its stiffness. This kind of target motion is categorized as uncontrollable passive stiffness motion, and it requires a new suitable design method. Current methods do not quite meet the requirements, when stiffness control is not included.

In this study, an in-plane pneumatic soft actuator (2D-PSA) with anisotropic soft and rigid restraints is proposed. In-plane bending is a target motion derived from some practical applications, such as soft climbing robots and grippers. Without in-plane motion restraints, many situations can lead to accidental distortion of a general PSA by external forces. For this reason, both anisotropic soft and rigid materials are included in the proposed design as soft and rigid restraints to achieve pure in-plane bending. Potential anisotropic soft materials include fiber, cloth, thin-gauge skin, nets, and so on. They are soft in most orientations, but rigid in others. Conversely, anisotropic rigid restraints are rigid in most orientations, but soft in others. The means of achieving rigidity include chains, linkages, etc. For 2D-PSA, anisotropic soft and rigid restraints are blended into a soft matrix, which is made of silicone rubber, gum, or other elastomers. In the geometrical layout, anisotropic soft and rigid restraints and the soft matrix are configured together to achieve pure in-plane bending. Herein, the design prototype and fabrication process are first introduced, followed by a description of the experimental platform setup used to measure the relationship between the bending angle or bending force and air pressure, as well as to assess the dynamic response. The 2D performance resulting from anti-extra passive distortion of 2D-PSA is evaluated using the measurements of the oscillation angles of the bending axis. A novel soft robot prototype named 2D-Dancer, which is configured by two serially-connected 2D-PSAs and three pneumatic suckers, can move forward smoothly on a flat board to mimic a snake’s locomotion. Its excellent locomotion capability also verifies 2D-PSA’s remarkable 2D performance and mobility.

2. Design, Material, and Fabrication

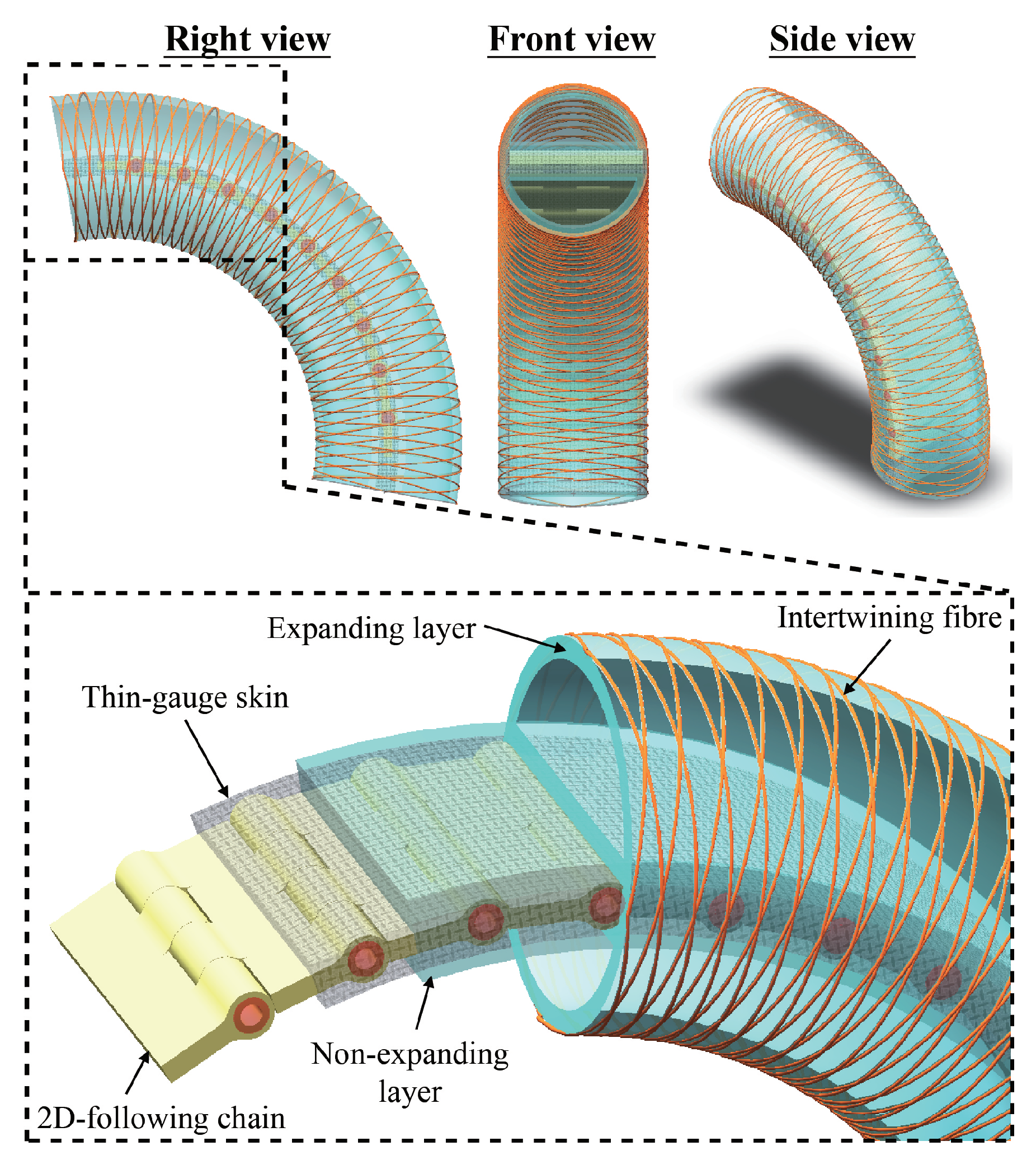
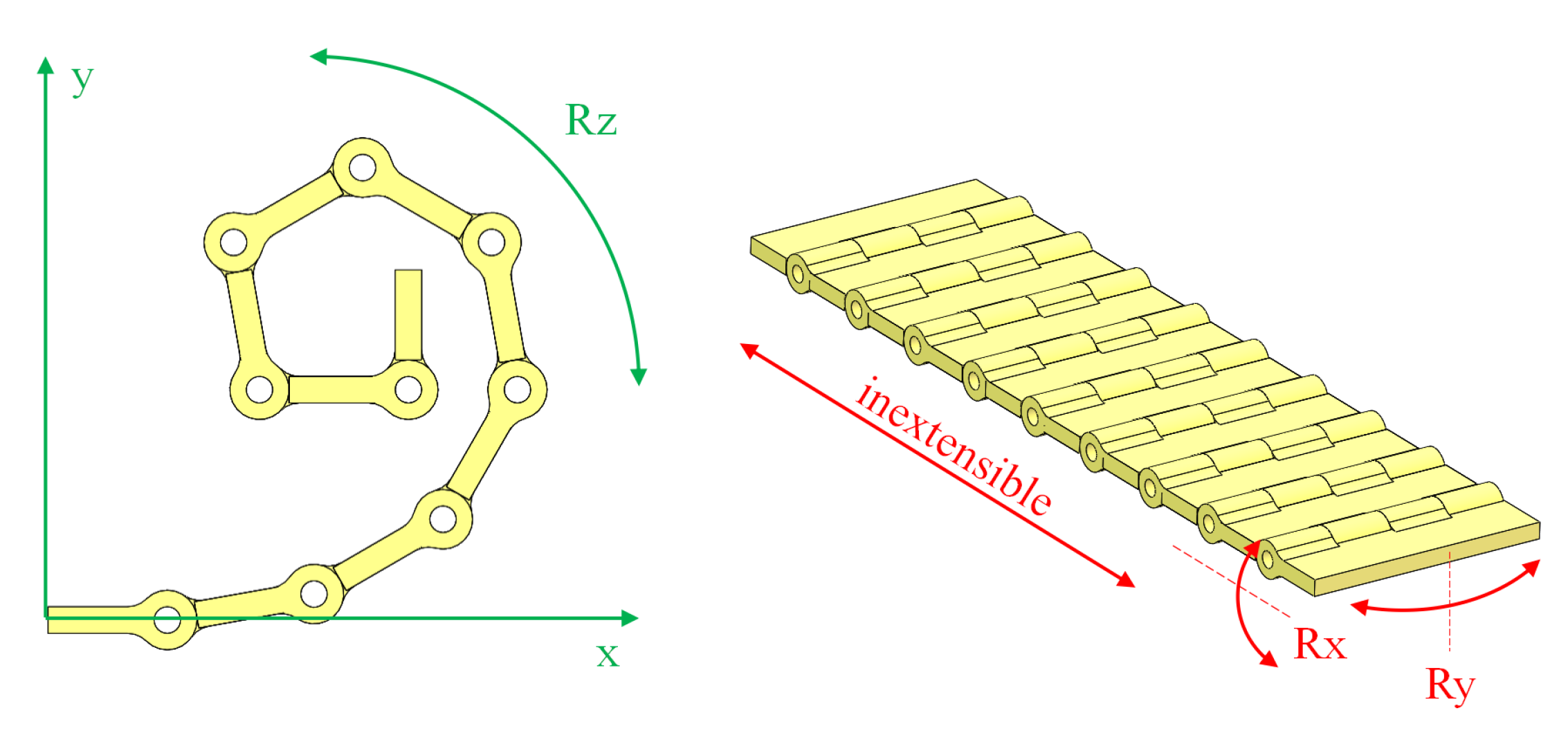
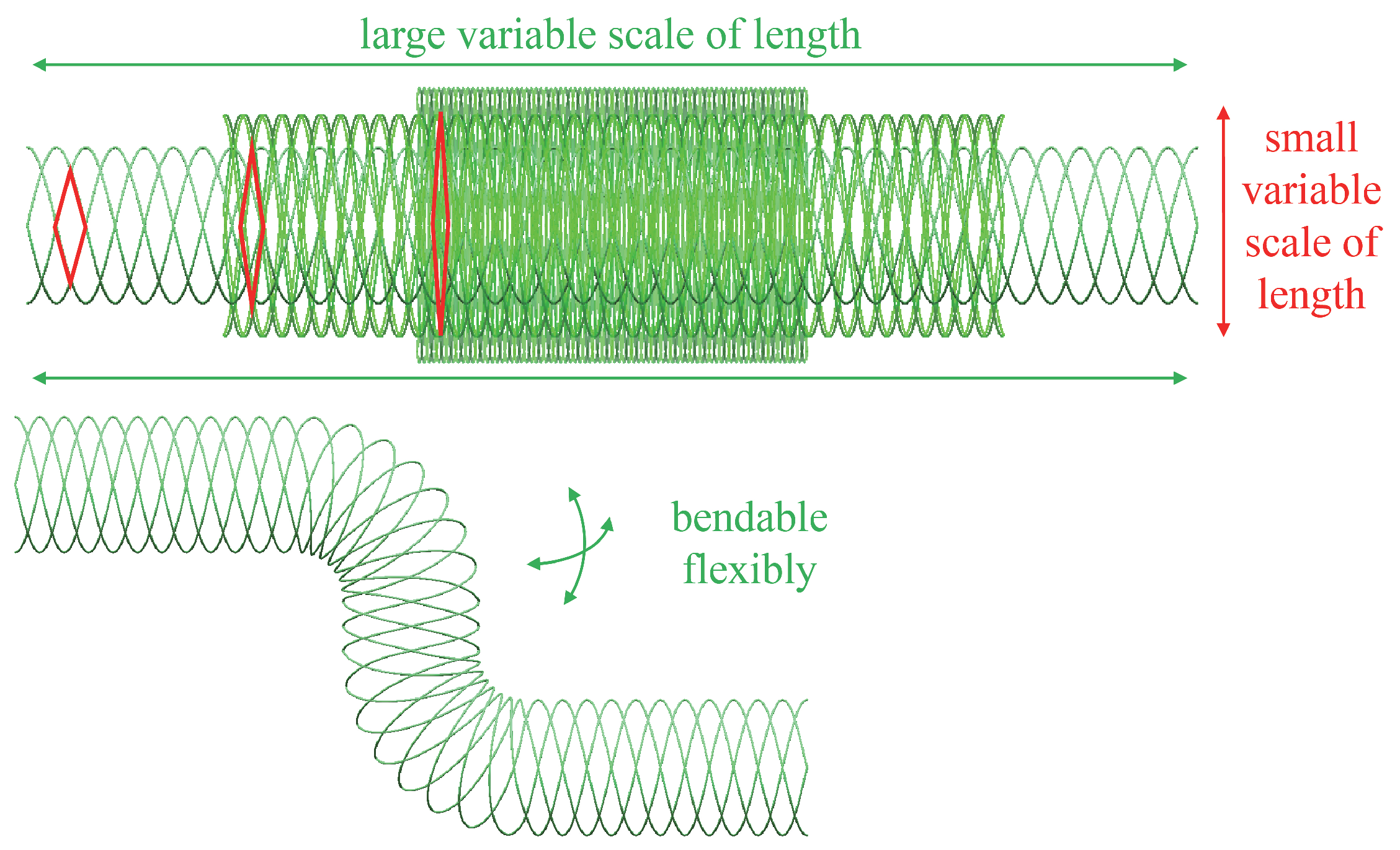
2.1. Structural Design and Analysis

The in-plane bending actuator with anisotropic soft and rigid restraints (2D-PSA) was composed of two parts, as shown in Figure 1. One part included the anisotropic soft and rigid restraints, which consisted of intertwining fiber and a 2D-following chain. The other part was the soft matrix, which was made of a rubber compound named Ecoflex 0030 (Smooth-On Inc., Macungie, PA, USA).

A soft matrix has an air cavity enveloped by expanding and non-expanding layers to fulfill the requirements for a common bending motion [12,19,20]. However, a common bending motion can be distorted when out-of-plane forces are applied. With the aim of achieving pure in-plane bending motion, a previously-published mechanical programming design method [20,21] is referenced and improved in this study.

First, the pure in-plane bending motion was specified by two norms.

Norm I: Pure in-plane bending without out-of-plane distortion external to the plane, such as twisting;

Norm II: Only axial, but non-radial inflation of the soft matrix is allowed.

To meet Norm I, a serial 2D-following chain, which consisted of a set of rigidly-connected hinges, was buried inside the non-expanding layer matrix. The 2D-following chain acted as a rigid restraint for 2D-PSA, as shown in Figure 2. Each section of the 2D-following chain had three degrees of freedom: translations along the x- and y-axes and rotation around the z-axis. In other words, translation along the z-axis and rotations around the x- and y-axes were restrained. The mechanism of the 2D-following chain reserved certain degrees of freedom for in-plane bending and restrained other degrees of freedom to avoid out-of-plane distortion. Furthermore, the inextensibility of the 2D-following chain restrained elongation of the soft matrix to form a non-expanding layer.

To meet Norm II, intertwining fiber was buried inside the expanding layer matrix. The intertwining fiber acted as a soft restraint for 2D-PSA. It was a 3D structure that was woven as an intertwining net, whose pattern was a compressed rhombus along the axial direction. Then, the intertwining net allowed the expanding layer to elongate in the axial direction, but restrained the expanding layer from enlarging in the radial direction. There was still some slight enlarging in the radial direction, but we neglected it. As shown in Figure 3, the structure of the intertwining fiber maintained all DOFs except for elongation in the tangent direction of the lines. The dense grids ensured that the matrix in the expanding layer did not easily burst when it was inflated. As a result, the actuator was able to tolerate higher air pressure so that a larger bending angle and greater force could be realized.

Two air cavities that were symmetrical with respect to the 2D-following chain were included in the design to achieve in-plane bidirectional bending. When one air cavity was inflated and the other was not, 2D-PSA was able to bend to one side. It bent to the other side when the second cavity was inflated and the first one was deflated.

Overall, because of the 2D-following chain, intertwining fiber, and symmetrical soft matrix, 2D-PSA gained an anisotropic structural feature (as shown in Figure 1) to achieve pure in-plane bending.

2.2. Material

The 2D smart soft actuator was fabricated with close-clearance metal hinges (Young’s modulus of about 200 GPa), a thin steel bar, thin-gauge chemical fabric, a polyethylene net, and Ecoflex 0030 silicone rubber (Young’s modulus of about 60,000 Pa). Serial hinges made of brass were used for the 2D-following chain and acted as rigid restraints. The thin steel bar (No. 45 steel, about 0.6 mm) connected the hinges rigidly without additive clearance (about 2–4${}^{\circ }$/cm), while the thin-gauge chemical fabric enveloped the 2D-following chain. As a soft restraint, the intertwining net was made of polyethylene fiber, and the intersection node was tied into a knot to preserve the net’s structural shape. It also reinforced the rubber matrix. Ecoflex 0030 rubber was the soft matrix, forming both the non-expanding layer and expanding layer. This rubber consisted of platinum-catalyzed silicone, which was a mixture of 1A and 1B by weight or volume. It must be cured at room temperature (23 ${}^{\circ }$C) with negligible shrinkage. The elastic modulus of Ecoflex rubber was low (60,000 Pa), so it could expand easily. It took approximately 2 h to cure Ecoflex rubber at room temperature.

2.3. Fabrication Process

The fabrication process of 2D-PSA was comprised of five steps, as shown in Figure 4. Firstly, 12 hinges were connected face to back, one after another, by winding the thin steel bar across the hinges’ mounting holes. This kind of connection is rigid. When straightened, the entire 2D-following chain was 140 mm in length, and it weighed 40 g. The 2D-following chain could move flexibly in its active plane. Before it was buried in the non-expanding layer, the 2D-following chain was enveloped with a thin-gauge chemical fabric, which served two functions. One was to cover all sharp corners of the 2D-following chain, and the other was to allow penetration of the liquid rubber for blending purposes; the latter function was provided by the thin-gauge skin. Moreover, the thin gauge was an extremely soft material and placed no additional restraints on the 2D-following chain’s degrees of freedom. The 2D-following chain was then placed inside a mold filled with liquid rubber (Ecoflex 0030). After about 2 h of curing at room temperature, a non-expanding layer was obtained. Note that the cured rubber matrix did not reduce the 2D-following chain’s degrees of freedom, but created a certain resistance. Then, two pieces of the expanding layer were poured into two molds for about 2 h of curing. After all the layers were cured, the non-expanding layer was placed between the two expanding layers and butt fused with the Ecoflex rubber again. After curing, the fabrication of the airtight in-plane bending actuator was finished. Finally, woven fiber with a diamond mesh was intertwined around the bare matrix. To prevent the intertwining fiber from becoming displaced, another layer of Ecoflex 0030 rubber was used to coat on the fiber and matrix. After another 2 h of curing, the fabrication of 2D-PSA was successfully complete. The entire fabrication process required approximately 10 h.

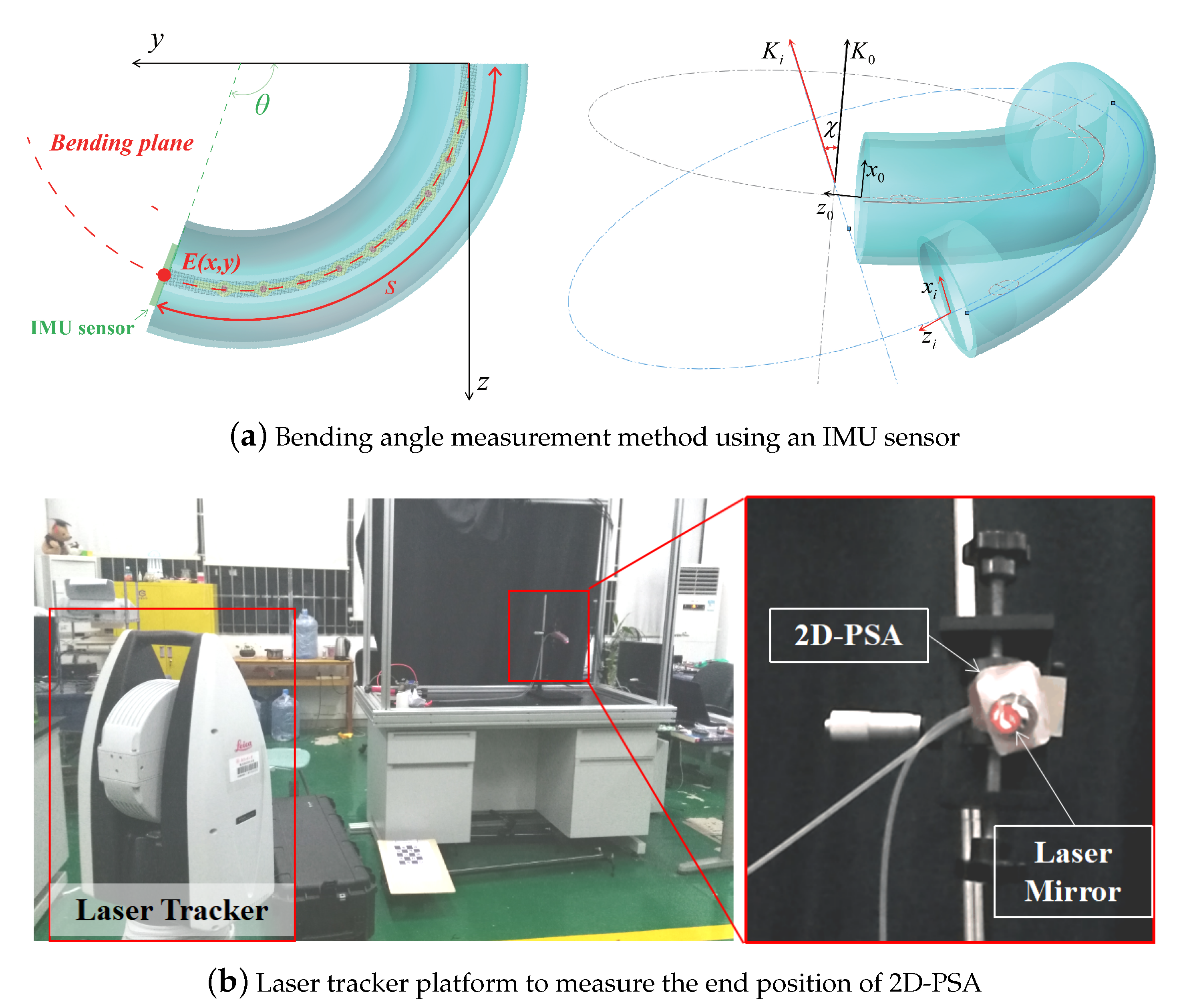
3. Experimental Setup and Test

Experiments were conducted to measure 2D-PSA’s bending angle–air pressure relationship and the bending force–air pressure relationship, as well as to assess its vibration abatement. The width, height, and length of 2D-PSA prototype were 30, 24, and 150 mm, respectively. Evaluation of the bending effects of 2D-PSA generally required measurement of the bending angle and bending force with respect to the unit length. The 2D performance of 2D-PSA was analyzed using a contrast experiment with a standard PSA. Furthermore, a soft robot named 2D-Dancer was developed to analyze the in-plane locomotion.

A digital force gauge (HP-5) was placed perpendicularly to the end of 2D-PSA in the bending plane, while the head of 2D-PSA was fixed using a supporting structure as a base, as shown in Figure 5. To show anisotropic stiffness based on composite restraints, the stiffness in different directions of 2D-PSA, that is $\overrightarrow{y}$ and $\overrightarrow{z}$ in Figure 2, was measured as shown in Figure 5a. The force F was defined as the winding force for 2D-PSA, being measured as shown in Figure 5b.

An inertial measurement unit (IMU) sensor and laser tracker were applied to measure the quasi-static and dynamic effects of 2D-PSA, as shown in Figure 6. We used a JY901 integrated module as the IMU sensor and a Leica Absolute Tracker AT960 as the laser tracker. Neither the IMU sensor nor the laser tracker can directly achieve a bending angle, so Euler angles and the end position were first measured instead. In Figure 6a, if we suppose that $\left\{{\alpha }_0,{\beta }_0,{\gamma }_0\right\}$ are Euler angles in the initial bending angle (0${}^{\circ }$) and that $\left\{\alpha ,\beta ,\gamma \right\}$ are Euler angles in a random bending angle ($\theta$), we can calculate the rotation matrix as:

$$R_K\left(\theta \right)=R{R}_0^{-1}$$

(1)

where R is the rotation matrix of $\left\{\alpha ,\beta ,\gamma \right\}$ and $R_0$ is the rotation matrix of $\left\{{\alpha }_0,{\beta }_0,{\gamma }_0\right\}$. Because 2D-PSA was an in-plane actuator, it bent at an angle $\theta$ around an equivalent axis K, which was perpendicular to the bending plane. We can calculate the bending angle as:

$$\theta =\arccos \left(\frac{r_{11}+r_{22}+r_{33}-1}{2}\right)$$

(2)

where $r_{ij}$ is an element of the rotation matrix $R_K\left(\theta \right)$. Here, a 2D in-plane criterion, $\chi$, named the axial oscillation angle, is defined to measure the performance level of 2D-PSA’s bending inside an initial plane:

$$\chi =〈K_0,K_i〉$$

(3)

where $K_0$ is the initial equivalent axis and $K_i$ is the equivalent axis in the ith bending angle. Alternatively, as shown in Figure 6b, the bending angle $\theta$ can be calculated according to the end position $\left\{y,z\right\}$ as:

$$\theta =2\arctan \frac{y}{z}$$

(4)

4. Results and Discussion

4.1. Comparative In-Plane and Out-Of-Plane Performance

Since the rigid restrained material (the 2D-following chain) played a major role in preserving 2D-PSA’s in-plane motion, we measured the anisotropic stiffness of 2D-PSA and compared 2D-PSA with a general PSA, which lacked a 2D-following chain (similar to that in [2,3]). As shown in Figure 7, force values were measured every increasing 5-mm deflection in the z- and y-directions separately. In the z-direction, the force value increased rapidly from the deflection of 0–15 mm. When the deflection reached 15 mm, the base could not fix the end of 2D-PSA stably any more. These verified that the stiffness in the z-direction, which was the hard direction of 2D-following chain, was high. However, the force value in the y-direction increased slowly from the deflection of 0–30 mm (even more deflection was possible actually). This meant that the flexibility in the y-direction of 2D-PSA was high. The curves showed inherent in-plane and out-of-plane performance of 2D-PSA without inflation.

All parts and the fabrication process of the general PSA were the same as those of 2D-PSA, but there was no 2D-following chain inside the latter (as shown in Figure 4). As shown in Figure 8, the unsupported section of 2D-PSA drooped a little, and the bending movement was almost in-plane. However, the general PSA could not resist gravity and drooped completely. Then, its movement was not in-plane at all. From the marked difference in 2D performance between 2D-PSA and general PSA, it can be inferred that the combination of rigid and soft restraints in this prototype was responsible for the pure bending motion.

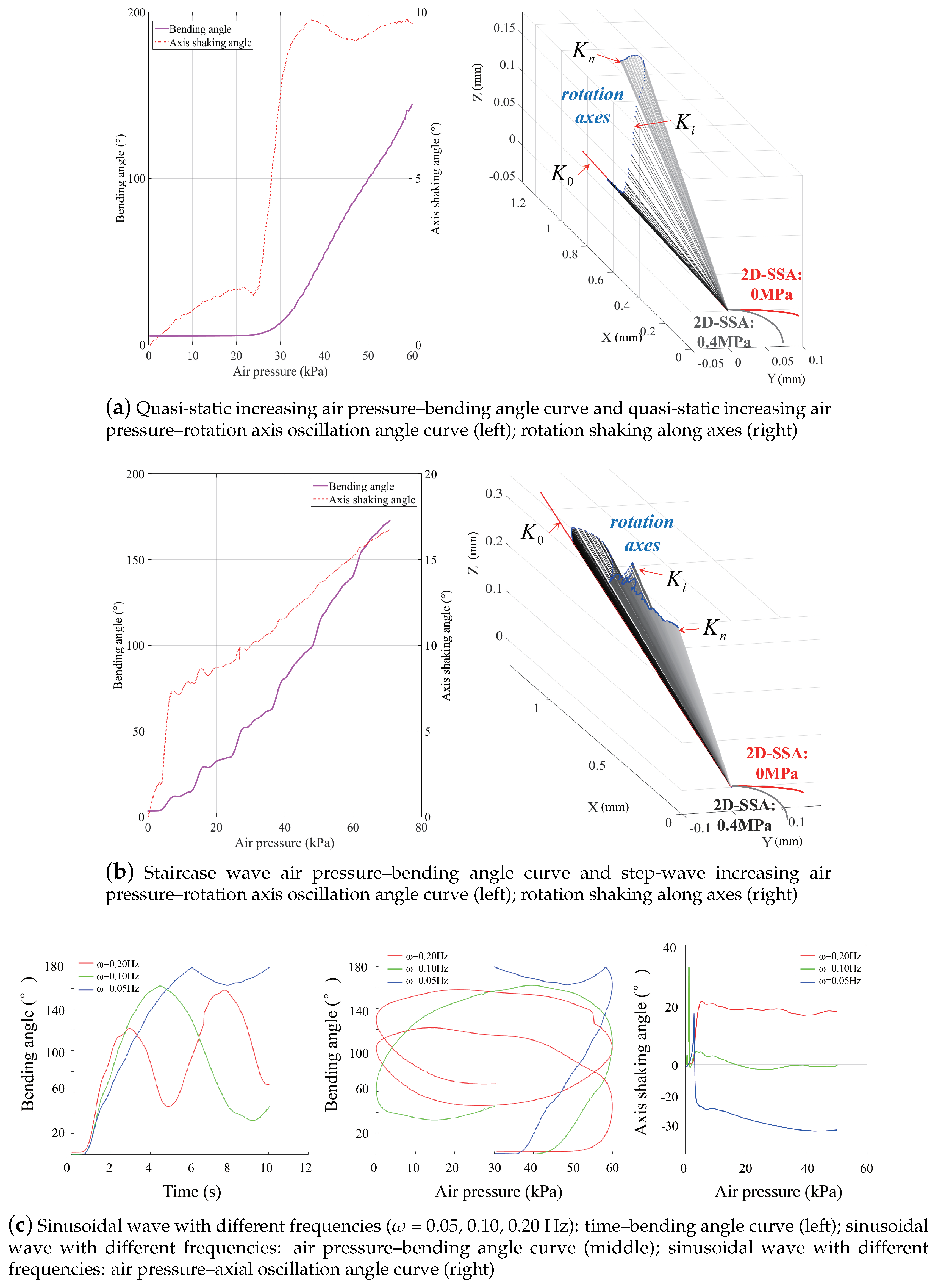
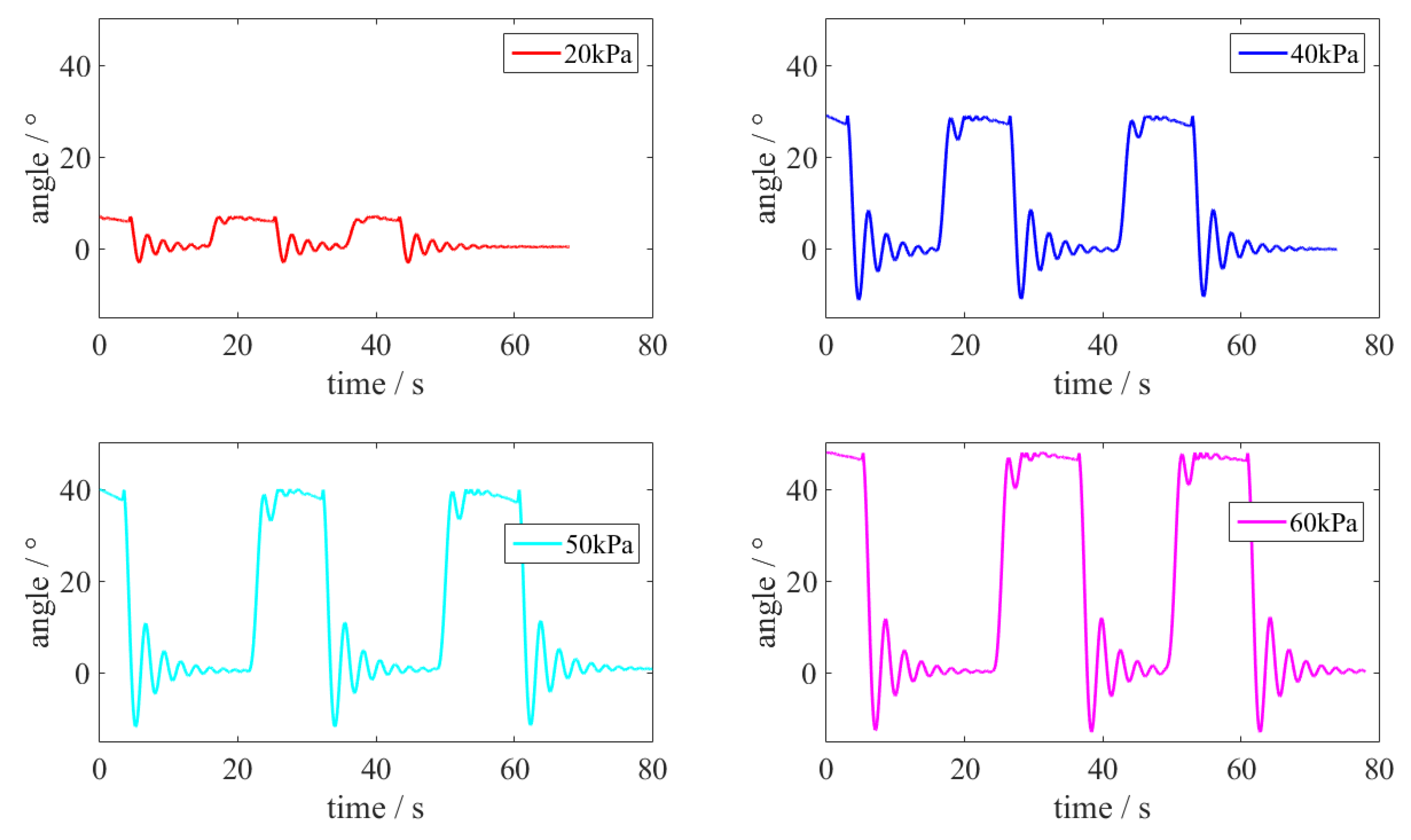
4.2. Pure Bending Motion

Figure 8 presented the intuitive 2D performance of 2D-PSA. When the air at a certain pressure entered one of 2D-PSA’s cavities, 2D-PSA would theoretically bend to a corresponding angle. At this time, the expansive force generated by the air pressure was balanced by the elastic force generated by the soft matrix. However, it was very difficult to establish an accurate model to describe the relationship between the bending angle and air pressure. Thus, we plotted the curve for bending angle vs. air pressure (Figure 9) by varying the air pressure and recording the quasi-static bending angle. In this part, the IMU sensor recorded the data. Three air-pressure input signals were used, namely quasi-static increasing air pressure, staircase wave air pressure, and sinusoidal waves with air pressure at different frequencies. When pure bending is studied, both the bending angle and the corresponding 2D in-plane criteria should be considered. Calculating the bending angle according to Formula (2) required the IMU sensor to obtain three Euler angles. Then, the 2D in-plane criterion, i.e., the axis oscillation angle (Figure 6a), could be calculated according to Formula (3). This resulted in bending angle curves and axis oscillation angle curves for the three designed air-pressure signals. The 2D performance was more intuitive if the equivalent axes were drawn with respect to the same starting point so that the shaking range was easy to recognize. In Figure 9, continuously-increasing air pressure was slowly fed into 2D-PSA (quasi-static). In Figure 9a, once the air pressure reached approximately 25 kPa, 2D-PSA started bending linearly at a rate of approximately 4.1${}^{\circ }$/kPa. All equivalent axes defined in Figure 6a are drawn to allow for the intuitive observation of the oscillation amplitude. The maximum axis oscillation angle was less than 10${}^{\circ }$, and the maximum end displacement of the unit length equivalent axes was less than 0.015 mm. In Figure 9b, a series of staircase wave air pressures (10, 20, 30, 40, 50, and 60 kPa) was fed step-by-step to 2D-PSA. The resulting bending angle–air pressure curve shape resembled a staircase wave with an increasing rate. The maximum axis oscillation angle was less than 18${}^{\circ }$, and the maximum end displacement of the unit length equivalent axes was less than 0.2 mm. In this case, the larger maximum axis oscillation angle was caused by the vibrations induced by the stepped inflating staircase wave air pressure. In Figure 9c, sinusoidal waves with different frequencies (0.05, 0.1, and 0.2 Hz) at a fixed air pressure amplitude (60 kPa) were fed to 2D-PSA. If low-frequency sinusoidal waves with air pressure were fed to 2D-PSA, the bending angle followed the variation in air pressure very well. However, a hysteresis effect emerged and became more pronounced with increasing sinusoidal frequency, as shown by the red curve for 4 Hz in the left-most plot, and the second peak of the sinusoidal-shaped bending angle curve was higher than the first peak. The maximum axis oscillation angle was approximately 20${}^{\circ }$ and was believed to be within an acceptable shaking range despite the vibration. A discontinuous break occurred at the beginning of the green oscillation angle–air pressure curve; however, this was an accidental error in the data.

When we concentrated on the dynamic response of 2D-PSA with compressed air, residual oscillation was quite obvious around the equilibrium position. The main reason was that the extremely low stiffness of the soft matrix permitted higher levels of oscillation. A laser tracker with a high sampling frequency was used to record the end position of 2D-PSA, and bending angles were calculated according to Formula (4). Hence, air with various step-air-pressure values was periodically fed into 2D-PSA’s cavity. The resulting real-time curves for bending angle versus air pressure are plotted in Figure 10, and the values of the step-air-pressure were 20, 40, 50, and 60 kPa. There were two types of residual oscillations in each cycle. Both positive and negative oscillations occurred when 2D-PSA returned to its initial position, whilst a secondary negative oscillation occurred when 2D-PSA reached its equilibrium position. The amplitude of the vibration near the initial position was larger than that near the equilibrium position. This was because the stiffness of 2D-PSA near the initial position was larger than that near the equilibrium position. It can be intuited from Figure 10 that 2D-PSA required approximately 10 s to reduce vibrations near the initial position, but needed only 4 s near the equilibrium position (peaks).

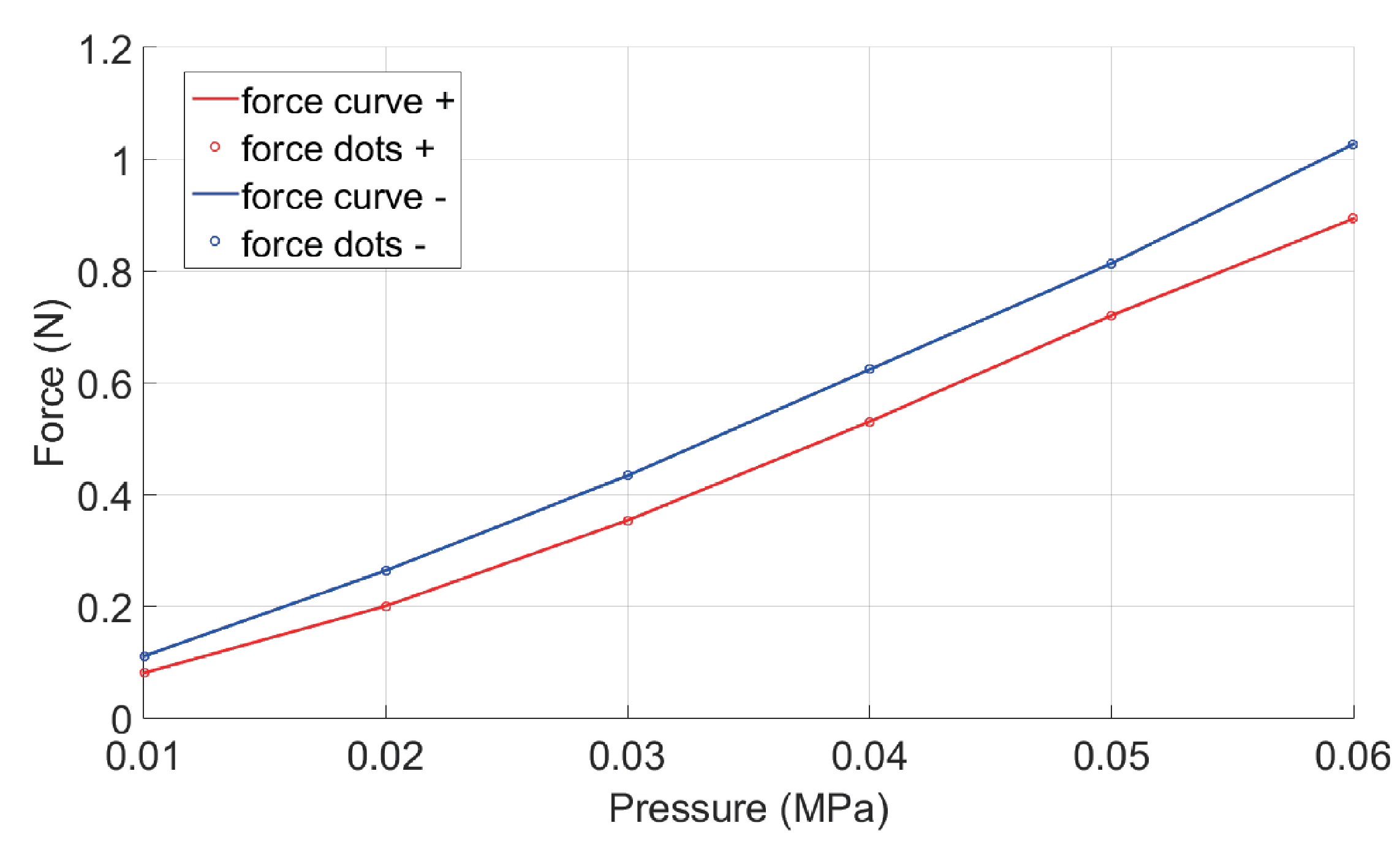
4.3. Winding Force

The winding force, another parameter of 2D-PSA’s performance, was measured using the setup in Figure 5. As shown in Figure 11, increasing air pressure was fed into the “+” cavity and the “−” cavity separately. The force was recorded by a force gauge. The force curve was essentially linear with an increasing rate of about 15 N/MPa, which was highly suitable for open-loop force control. However, the force curve “−” was universally slightly larger than the force curve “+”. This was because of a fabrication error between the “+” side and “−” side cavities.

5. Application

A pure in-plane bending actuation was achieved by combining a soft matrix and anisotropic soft and rigid restraints. The next required step was the verification of its in-plane application performance. Since 2D-PSA was an independent module that could mimic the muscular function of some animals with a musculoskeletal structure, a simple in-plane robot prototype, named 2D-Dancer, was designed. 2D-Dancer was configured by two (or more) serially-connected 2D-PSAs and three pneumatic suckers. It was capable of moving forward like a snake on a flat board as a result of 2D-PSA’s bending motions.

The 2D-Dancer robot with two serially-connected 2D-PSAs and three pneumatic suckers was developed and had the ability to move forward like a snake. In Figure 12, 2D-Dancer moved forward using a snake-like crawling locomotion, which was a longitudinally moving locomotion. When the head sucker was fixed, the middle and tail suckers moved forward by inflating two diagonally-opposite cavities. When the head and tail suckers were fixed at the same time, another two diagonally-opposite cavities were inflated, whilst the first two diagonally-opposite cavities were deflated. At this time, elastic potential energy was exerted within the body of 2D-PSA. When the head sucker was released and the tail sucker remained fixed, the head and middle suckers moved forward because the elastic potential energy was released. Afterward, another crawling cycle was repeated. The forward distance of this locomotion was approximately 40 mm, and the shortest period was 3 s.

The results indicated that 2D-Dancer, configured using two 2D-PSAs, achieved flexible, reasonable in-plane movement. According to the previous contrast experiment between 2D-PSA and general PSA, it was apparent that if 2D-Dancer were made of general PSAs, it could not successfully move on a flat board. The basis of the movement lied in the ability of the suckers to face the surface perpendicularly. If the sucker were unable to face the surface with sufficient perpendicularity, it would not move successfully. When PSA bent, the friction between the sucker and flat surface prevented the sucker from facing the surface with enough perpendicularity. The robot configured with 2D-PSAs was able to move in-plane, which counteracted the friction. Conversely, for the robot configured with general PSAs, the sucker could not typically face the surface with enough perpendicularity. Thus, this prototype was one potential application (but not the only one) of 2D-PSA, and it verified the design method of using soft actuation with anisotropic soft and rigid restraints.

6. Conclusions

For some soft robots such as an inchworm-like biped climbing robot or soft hand/finger grasp or manipulation without twisting, in-plane or 2D bending of the soft body is desired. In other words, the actuating deformation of the soft body must be constrained with the appropriate structure design of the soft actuator. To this end, a smart pneumatic soft actuator, called 2D-PSA, with anisotropic soft and rigid restraints for pure in-plane bending motion was proposed in this paper. The soft actuator was developed with a composite construct where a 2D free-bending chain (metal hinge chain) was embedded into the soft main body.

The design method, material choice and fabrication process of the soft actuator was presented in detail in this paper. The tests of the actuating performance and dynamic response of the soft actuator and a demo application in a climbing soft robot on a surface verified that the combination of soft and rigid restraints may achieve the target motion of pure in-plane bending. Our approach to design the anisotropic motion of a soft actuator by embedding a simple 2D free-bending chain into soft materials resulted in quite different stiffness in different directions without complex and active control.

Of course, the work was not perfect. The performance and effectiveness of the presented 2D-PSA is to be enhanced. 2D-PSA’s development is still open improvement; especially, the material choice and structure design of the embedded 2D free-bending chain need to be investigated further. We are trying to use the compliant mechanisms of plastic materials such as PLA to improve the effect of in-plane restraint, with a lighter weight and smaller size. With the new design, it was possible to achieve complex restrained actuation such as 3D twisting-like screwing motion for special purposes. Real applications in climbing soft robots will be performed once the performance of 2D-PSA and attachment parts is enhanced. Finally, theoretical modeling and mechanical analysis are challenging problems to be investigated.