Multi-Robot Path Planning Method Using Reinforcement Learning
Abstract
:1. Introduction
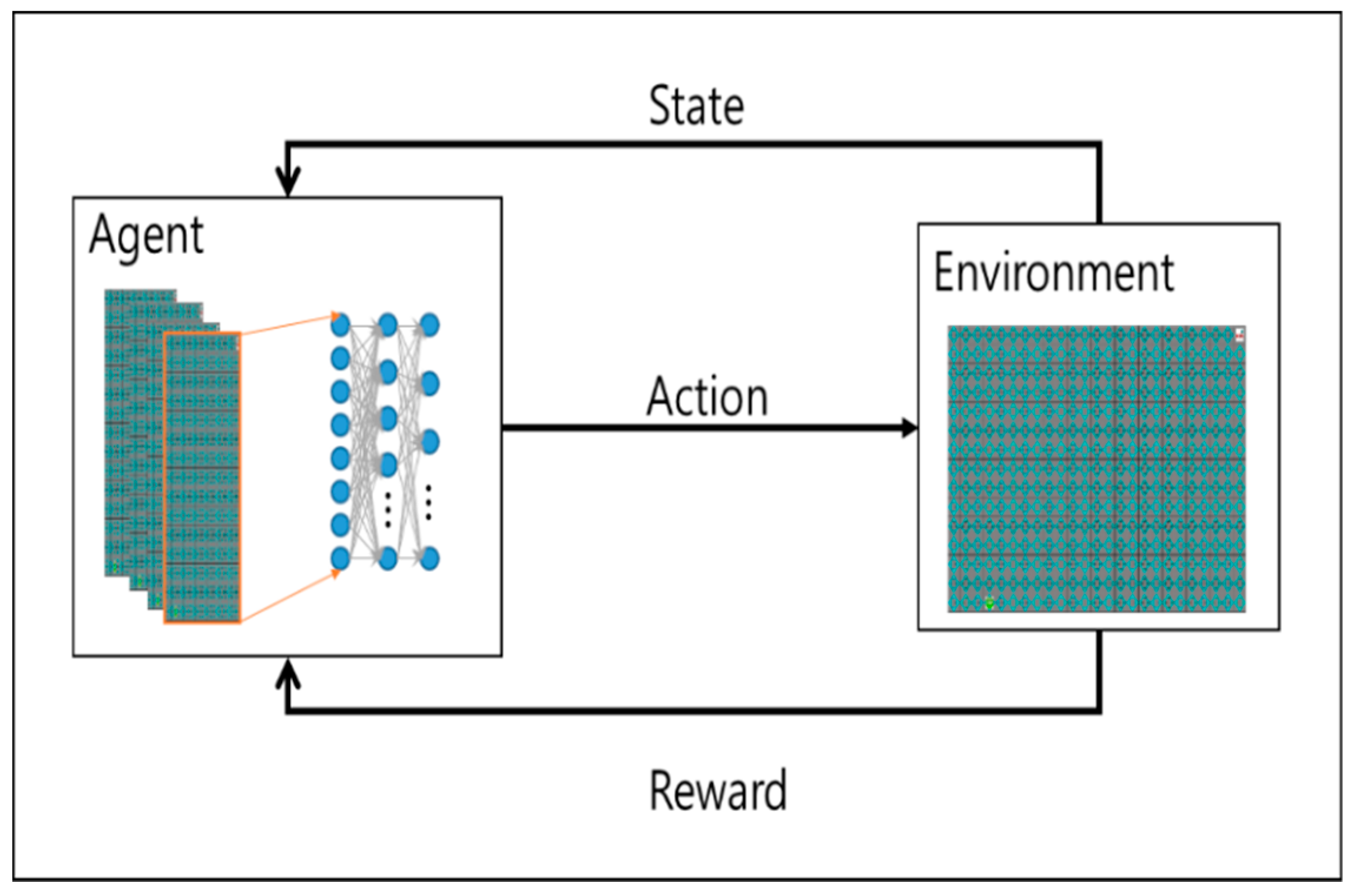
2. Reinforcement Learning
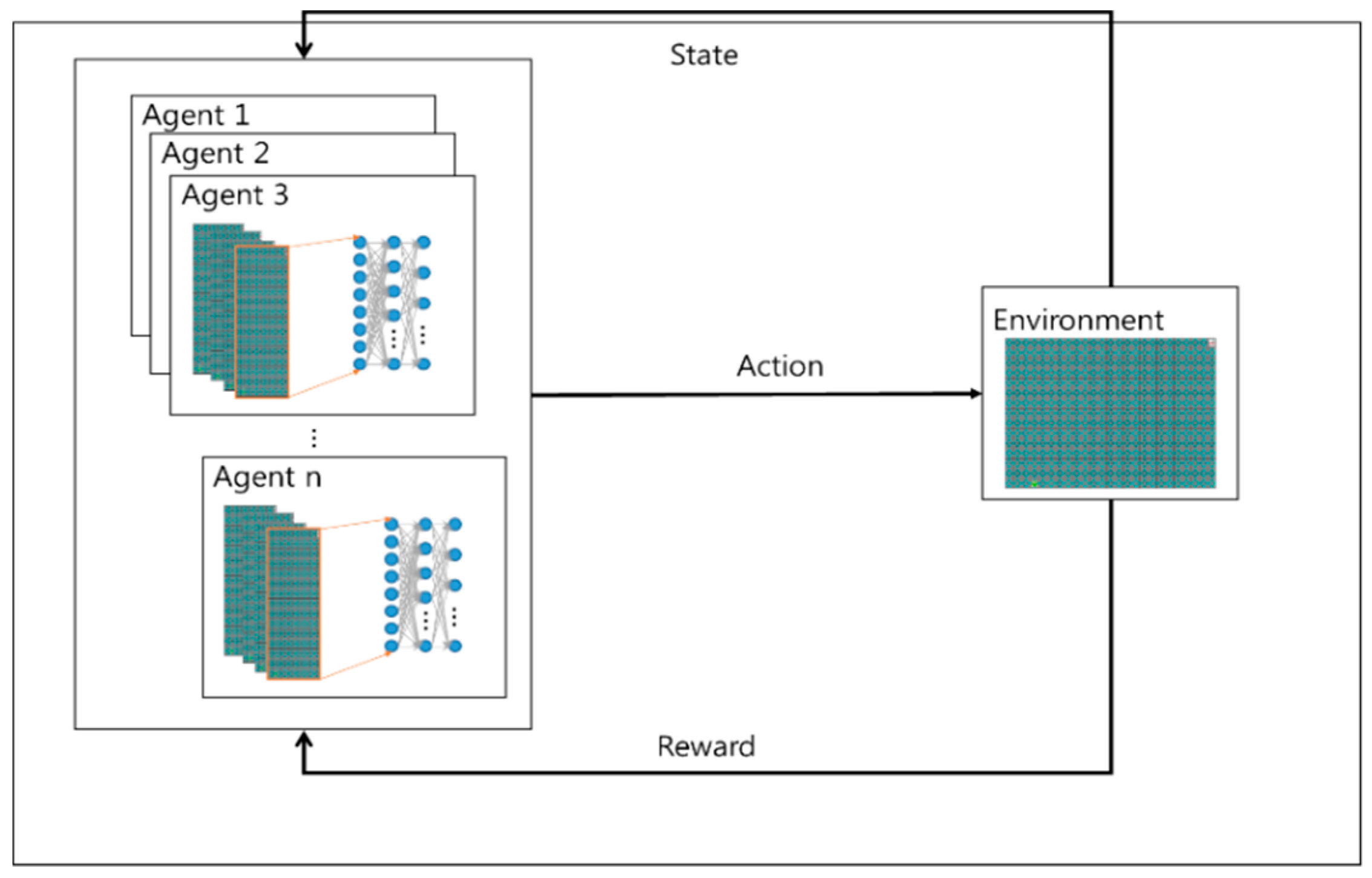
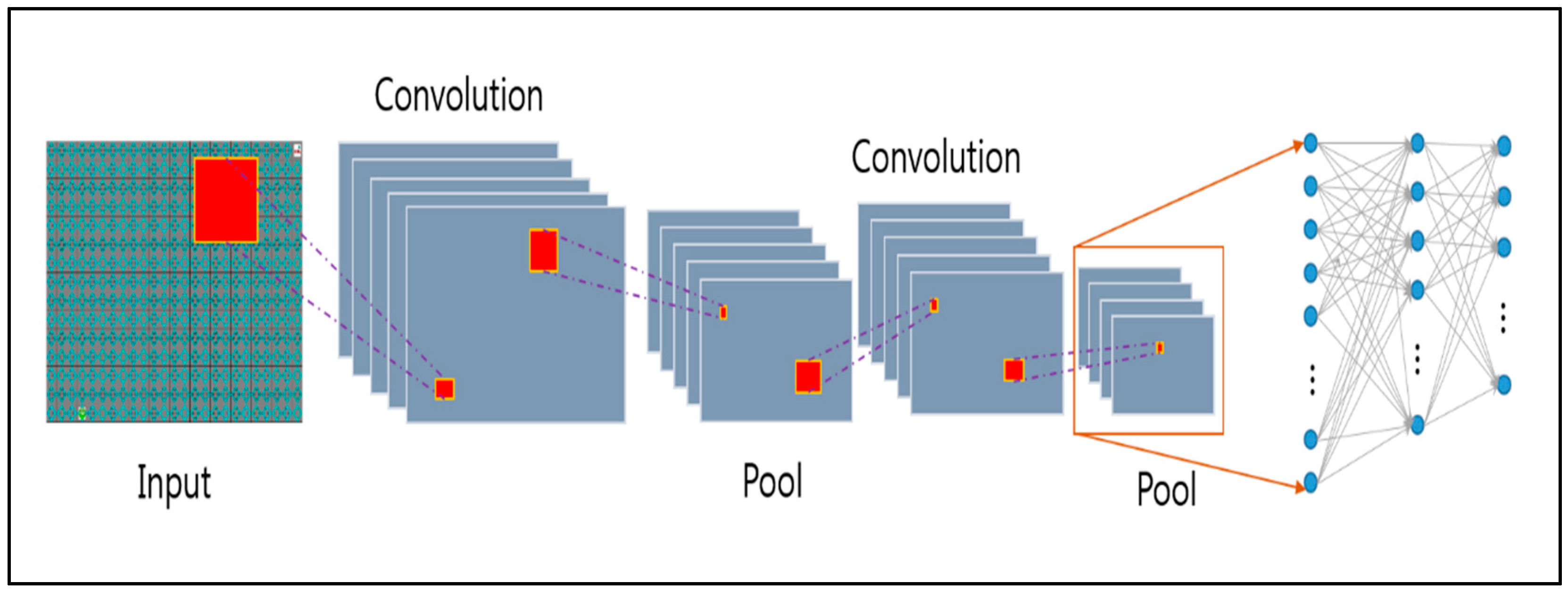
3. Proposed Algorithm
| Algorithm 1 Reward Function |
| if distancet−1 > distancet then reward = 0.2 else then reward = −0.2 if action == 0 then reward = reward + 0.1 else if action == 1 or action == 2 then reward = reward − 0.1 else if action == 3 or action == 4 then reward = reward − 0.2 if collision then reward = −10 else if goal then reward = 100 return reward |
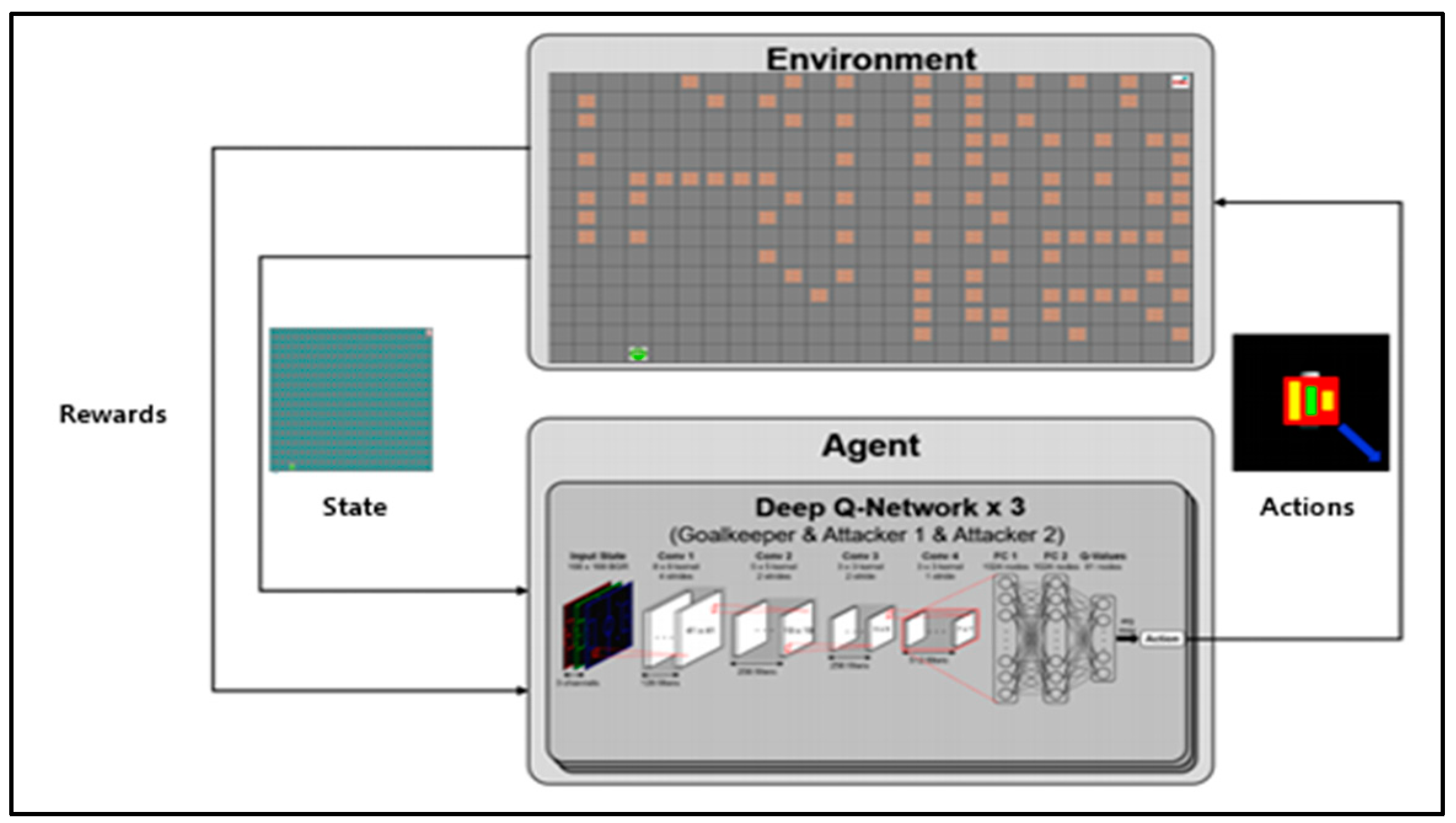
4. Experiment
4.1. Experiment Environment
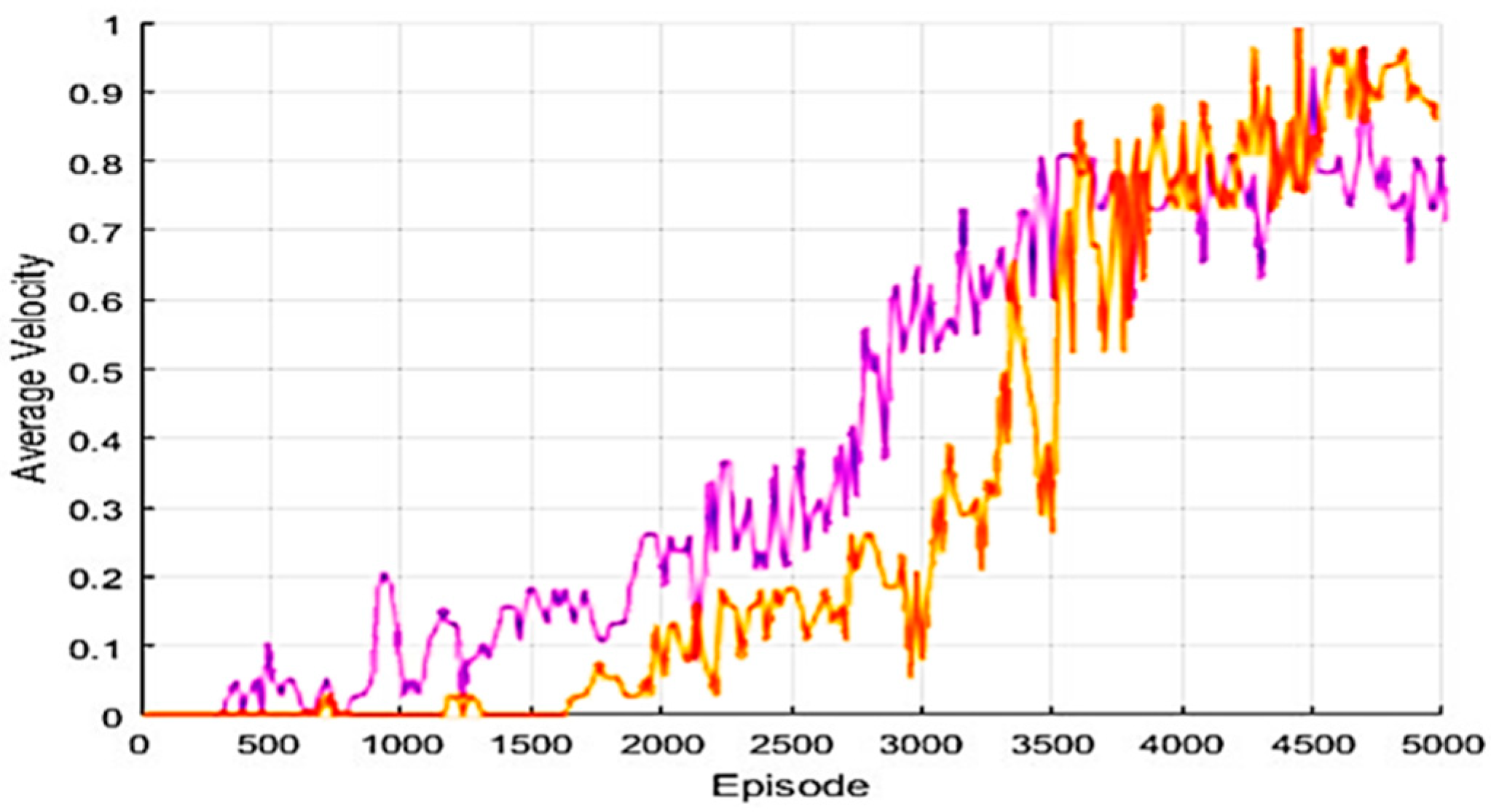
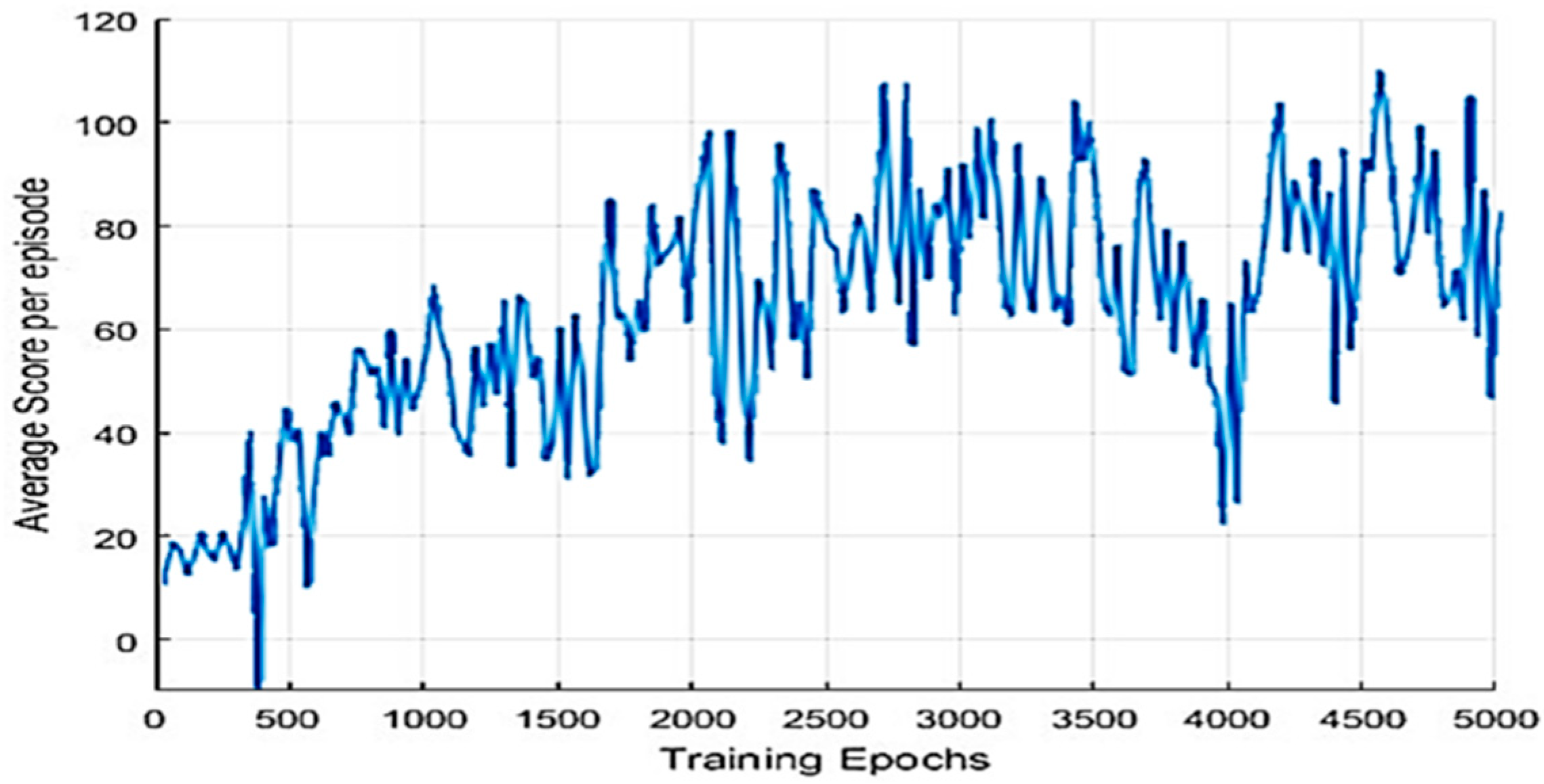
4.2. Learning Environment
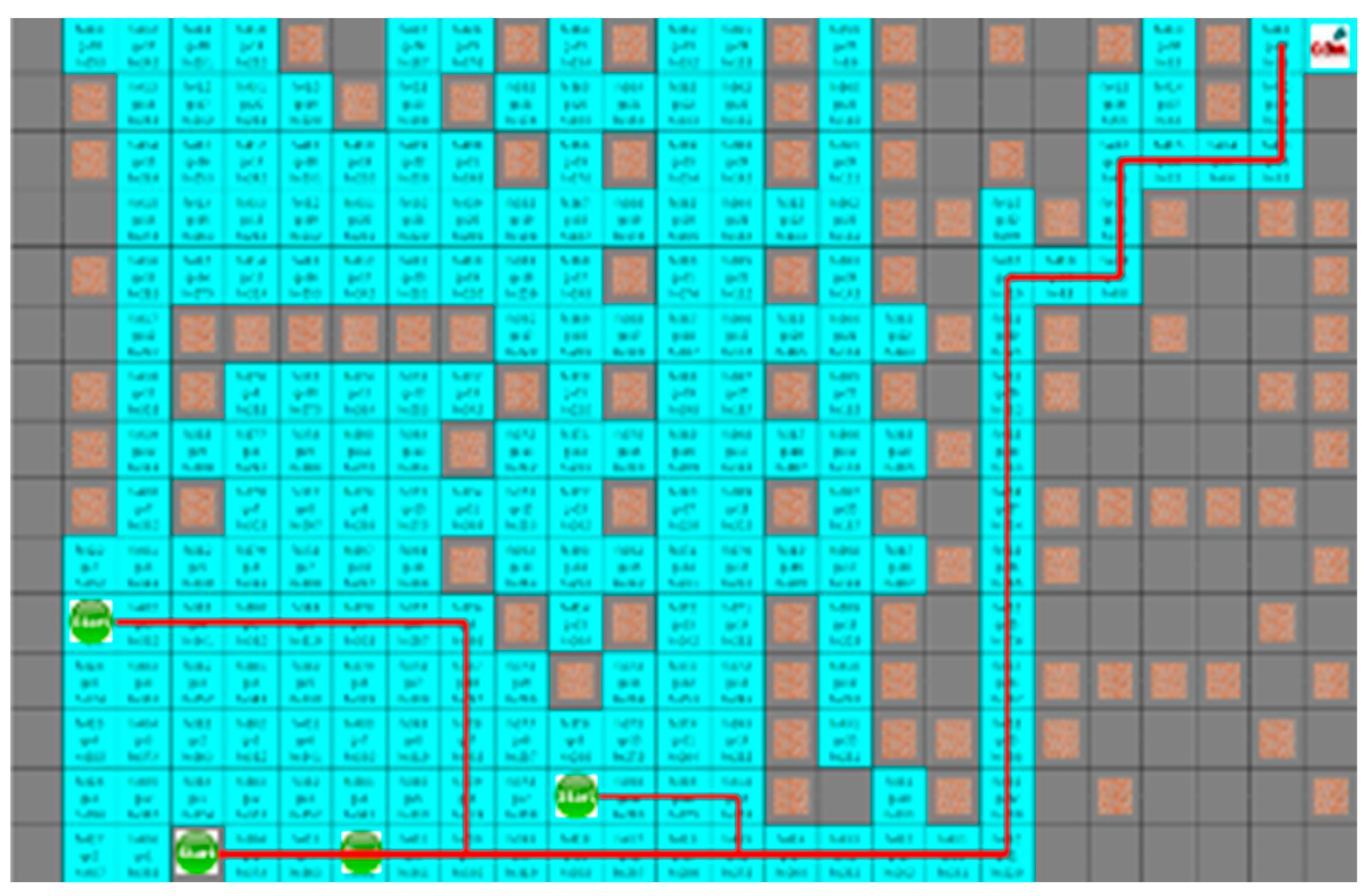
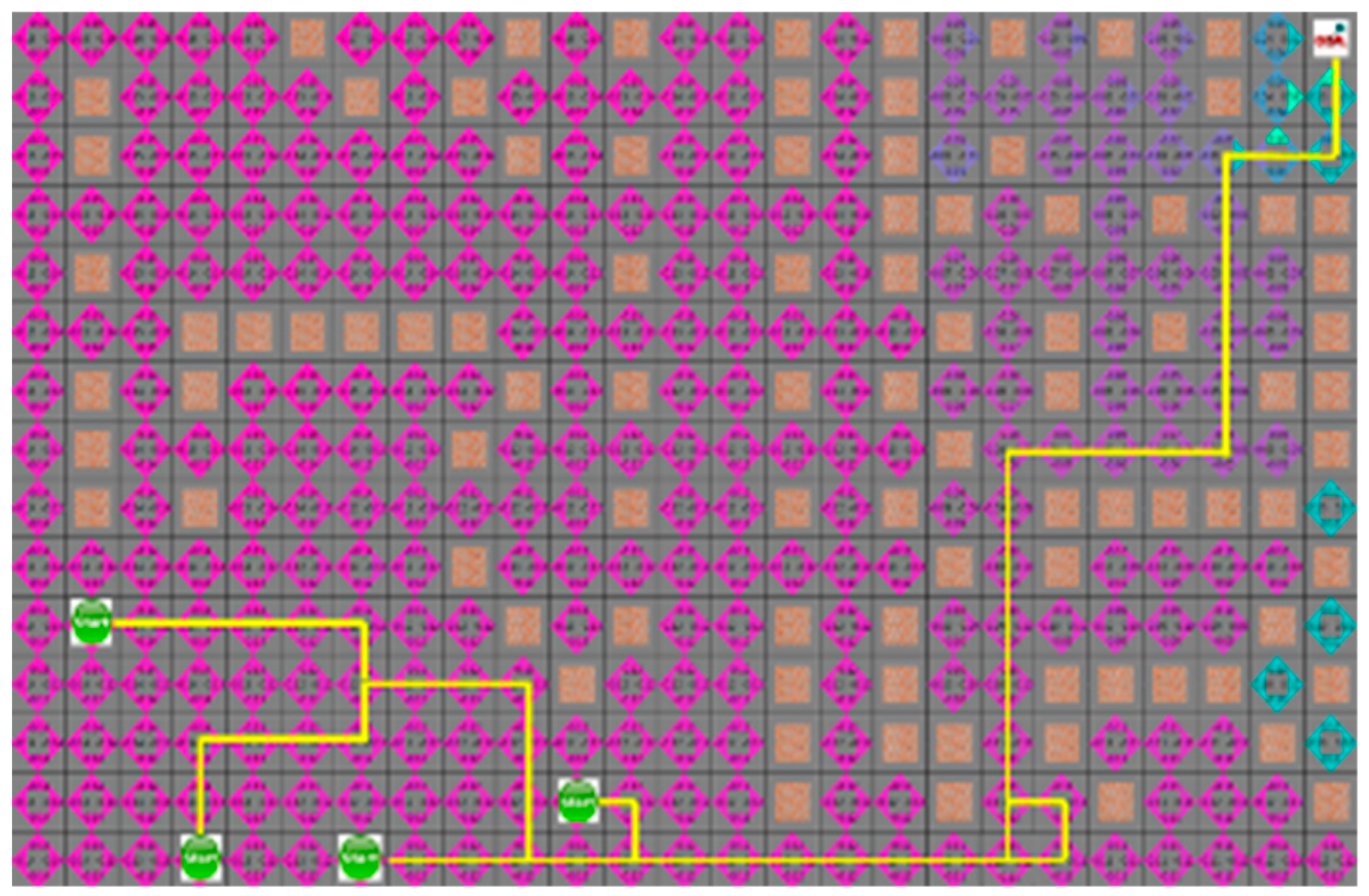
4.3. Experimental Results in a Static Environment
4.4. Experimental Results in a Dynamic Environment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nasser, M. Pattern Recognition and Machine Learning. J. Electron. Imaging 2007, 16, 4. [Google Scholar]
- Yu, D.; Li, D. Deep learning and its applications to signal and information processing [exploratory dsp]. IEEE Signal Process. Mag. 2010, 28, 145–154. [Google Scholar] [CrossRef]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.R.; Jaitly, N.; Kingsbury, B. Deep neural Networks for acoustic modeling in speech recognition. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Graves, A.; Abdel-rahman, M.; Geoffrey, H. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- Kumar, A. Ask me anything: Dynamic memory networks for natural language processing. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1378–1387. [Google Scholar]
- Machine Learning and Natural Language Processing. Available online: http://l2r.cs.uiuc.edu/~danr/Teaching/CS546-13/Papers/marquez-LNLP00.pdf (accessed on 11 July 2010).
- Manning, C. The Stanford CoreNLP natural language processing toolkit. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics: System Demonstrations, Baltimore, MD, USA, 22–27 June 2014; pp. 55–60. [Google Scholar]
- Collobert, R.; Jason, W. A unified architecture for natural language processing: Deep neural networks with multitask learning. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 160–167. [Google Scholar]
- Kononenko, I. Machine learning for medical diagnosis: History, state of the art and perspective. Artif. Intell. Med. 2001, 23, 89–109. [Google Scholar] [CrossRef]
- Shvets, A.A.; Rakhlin, A.; Kalinin, A.A.; Iglovikov, V.I. Automatic instrument segmentation in robot-assisted surgery using deep learning. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 624–628. [Google Scholar]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the COMPSTAT’2010, Paris, France, 22–27 August 2010; pp. 177–186. [Google Scholar]
- Peters, J.; Stefan, S. Natural actor-critic. Neurocomputing 2008, 71, 1180–1190. [Google Scholar] [CrossRef]
- Bhasin, S.; Kamalapurkar, R.; Johnson, M.; Vamvoudakis, K.G.; Lewis, F.L.; Dixon, W.E. A novel actor-identifier architecture for approximate optimal control of uncertain nonlinear systems. Automatica 2013, 49, 82–92. [Google Scholar] [CrossRef]
- Vamvoudakis Kyriakos, G.; Frank, L.L. Online actor-critic algorithm to solve the continuous-time infinite horizon optimal control problem. Automatica 2010, 46, 878–888. [Google Scholar] [CrossRef]
- Florensa, C.; Degrave, J.; Heess, N.; Springenberg, J.T.; Riedmiller, M. Self-supervised learning of image embedding for continuous control. arXiv 2019, arXiv:1901.00943. [Google Scholar]
- Lillicrap Timothy, P. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Watkins Christopher, J.; Peter, D. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Littman, M.L. Markov games as a framework for multi-agent-reinforcement learning. In Proceedings of the Eleventh International Conference on Machine Learning, New Brunswick, NJ, USA, 10–13 July 1994; Volume 157, pp. 157–163. [Google Scholar]
- Foster, D.; Peter, D. Structure in the space of value functions. Mach. Learn. 2002, 49, 325–346. [Google Scholar] [CrossRef]
- Kofinas, P.; Dounis, A.I.; Vouros, G.A. Fuzzy Q-Learning for multi-agent decentralized energy management in microgrids. Appl. Energy 2018, 219, 53–67. [Google Scholar] [CrossRef]
- Keselman, A.; Ten, S.; Ghazali, A.; Jubeh, M. Reinforcement Learning with A* and a Deep Heuristic. arXiv 2018, arXiv:1811.07745. [Google Scholar]
- Stentz, A. Optimal and efficient path planning for partially known environments. In Intelligent Unmanned Ground Vehicles; Springer: Boston, MA, USA, 1997; pp. 203–220. [Google Scholar]
- Ge, S.S.; Yan, J.C. New potential functions for mobile robot path planning. IEEE Trans. Robot. Autom. 2000, 16, 615–620. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Gong, D.-W.; Zhang, J.-H. Robot path planning in uncertain environment using multi-objective particle swarm optimization. Neurocomputing 2013, 103, 172–185. [Google Scholar] [CrossRef]
- Tharwat, A.; Elhoseny, M.; Hassanien, A.E.; Gabel, T.; Kumar, A. Intelligent Bézier curve-based path planning model using Chaotic Particle Swarm Optimization algorithm. Clust. Comput. 2018, 1–22. [Google Scholar] [CrossRef]
- Elhoseny, M.; Tharwat, A.; Hassanien, A.E. Bezier curve based path planning in a dynamic field using modified genetic algorithm. J. Comput. Sci. 2018, 25, 339–350. [Google Scholar] [CrossRef]
- Hu, X.; Chen, L.; Tang, B.; Cao, D.; He, H. Dynamic path planning for autonomous driving on various roads with avoidance of static and moving obstacles. Mech. Syst. Signal Process. 2018, 100, 482–500. [Google Scholar] [CrossRef]
- Alomari, A.; Comeau, F.; Phillips, W.; Aslam, N. New path planning model for mobile anchor-assisted localization in wireless sensor networks. Wirel. Netw. 2018, 24, 2589–2607. [Google Scholar] [CrossRef]
- Li, G.; Chou, W. Path planning for mobile robot using self-adaptive learning particle swarm optimization. Sci. China Inf. Sci. 2018, 61, 052204. [Google Scholar] [CrossRef]
- Thrun, S.; Wolfram, B.; Dieter, F. A real-time algorithm for mobile robot mapping with applications to multi-robot and 3D mapping. In Proceedings of the ICRA, San Francisco, CA, USA, 24–28 April 2000; Volume 1, pp. 321–328. [Google Scholar]
- Bruce, J.; Manuela, V. Real-time randomized path planning for robot navigation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Takamatsu, Japan, 31 October–5 November 2002; Volume 3, pp. 2383–2388. [Google Scholar]
- Indelman, V. Cooperative multi-robot belief space planning for autonomous navigation in unknown environments. Auton. Robot. 2018, 42, 353–373. [Google Scholar] [CrossRef]
- Fan, T.; Long, P.; Liu, W.; Pan, J. Fully distributed multi-robot collision avoidance via deep reinforcement learning for safe and efficient navigation in complex scenarios. arXiv 2018, arXiv:1808.03841. [Google Scholar]
- Van Den Berg, J.; Dave, F.; James, K. Anytime path planning and replanning in dynamic environments. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 2366–2371. [Google Scholar]
- Raja, P.; Sivagurunathan, P. Optimal path planning of mobile robots: A review. Int. J. Phys. Sci. 2012, 7, 1314–1320. [Google Scholar] [CrossRef]
- Van, H.; Hado, A.G.; David, S. Deep reinforcement learning with double q-learning. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Mnih, V. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Mnih, V. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Ren, S. Faster r-cnn: Towards real-time object detection with region proposal networks. In Proceedings of the Twenty-ninth Conference on Neural Information Processing Systems, Montréal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Kalchbrenner, N.; Edward, G.; Phil, B. A convolutional neural network for modelling sentences. arXiv 2014, arXiv:1404.2188. [Google Scholar]
- Abdel-Hamid, O. Convolutional neural networks for speech recognition. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 1533–1545. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Borboni, A.; Lancini, M. Commanded motion optimization to reduce residual vibration. J. Vib. Acoust. 2015, 137, 031016. [Google Scholar] [CrossRef]
- Alonso-Mora, J.; Montijano, E.; Nägeli, T.; Hilliges, O.; Schwager, M.; Rus, D. Distributed multi-robot formation control in dynamic environments. Auton. Robots 2019, 43, 1079–1100. [Google Scholar] [CrossRef]
- Yu, J.; Ji, J.; Miao, Z.; Zhou, J. Neural network-based region reaching formation control for multi-robot systems in obstacle environment. Neurocomputing 2019, 333, 11–21. [Google Scholar] [CrossRef]

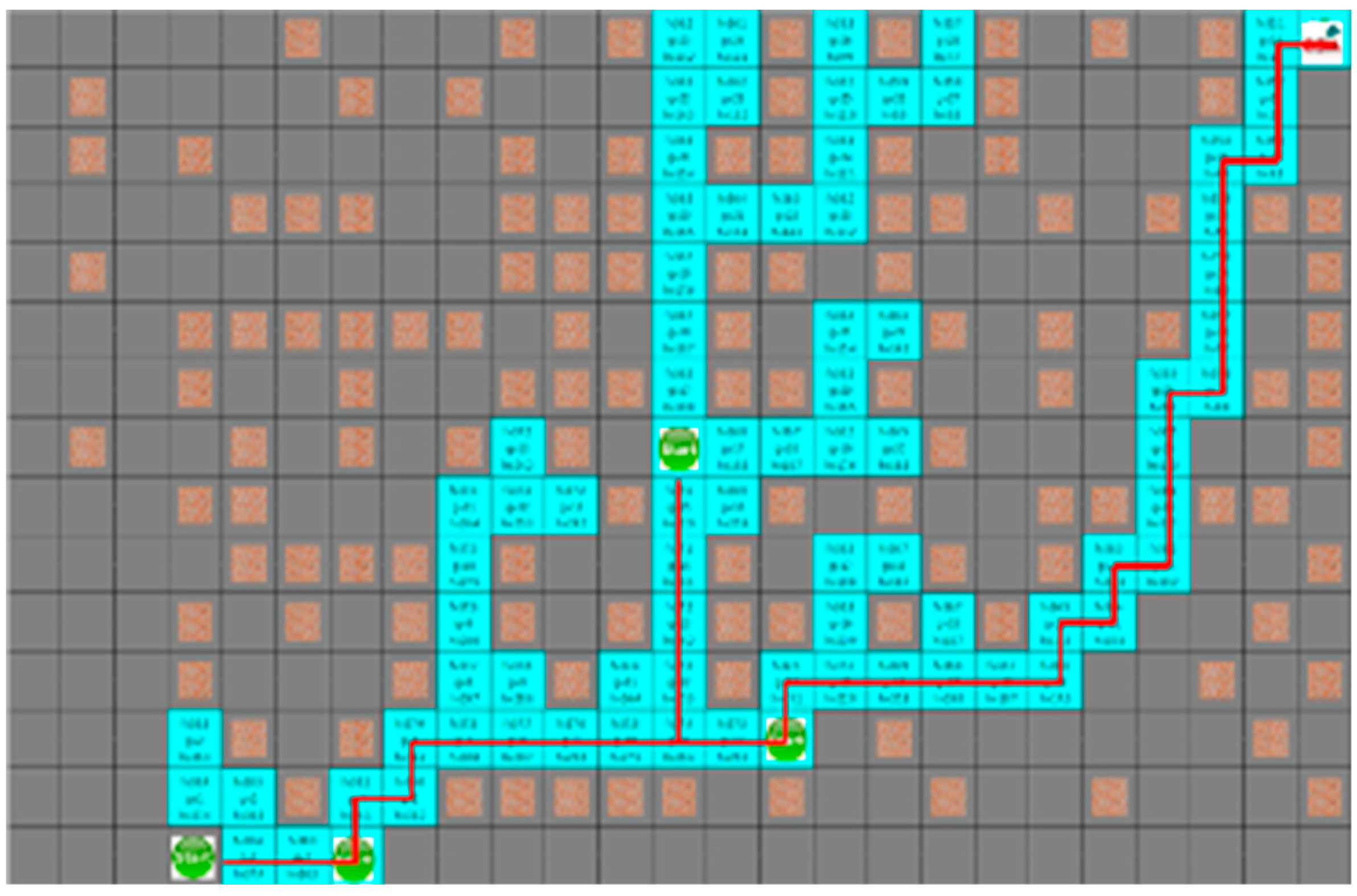
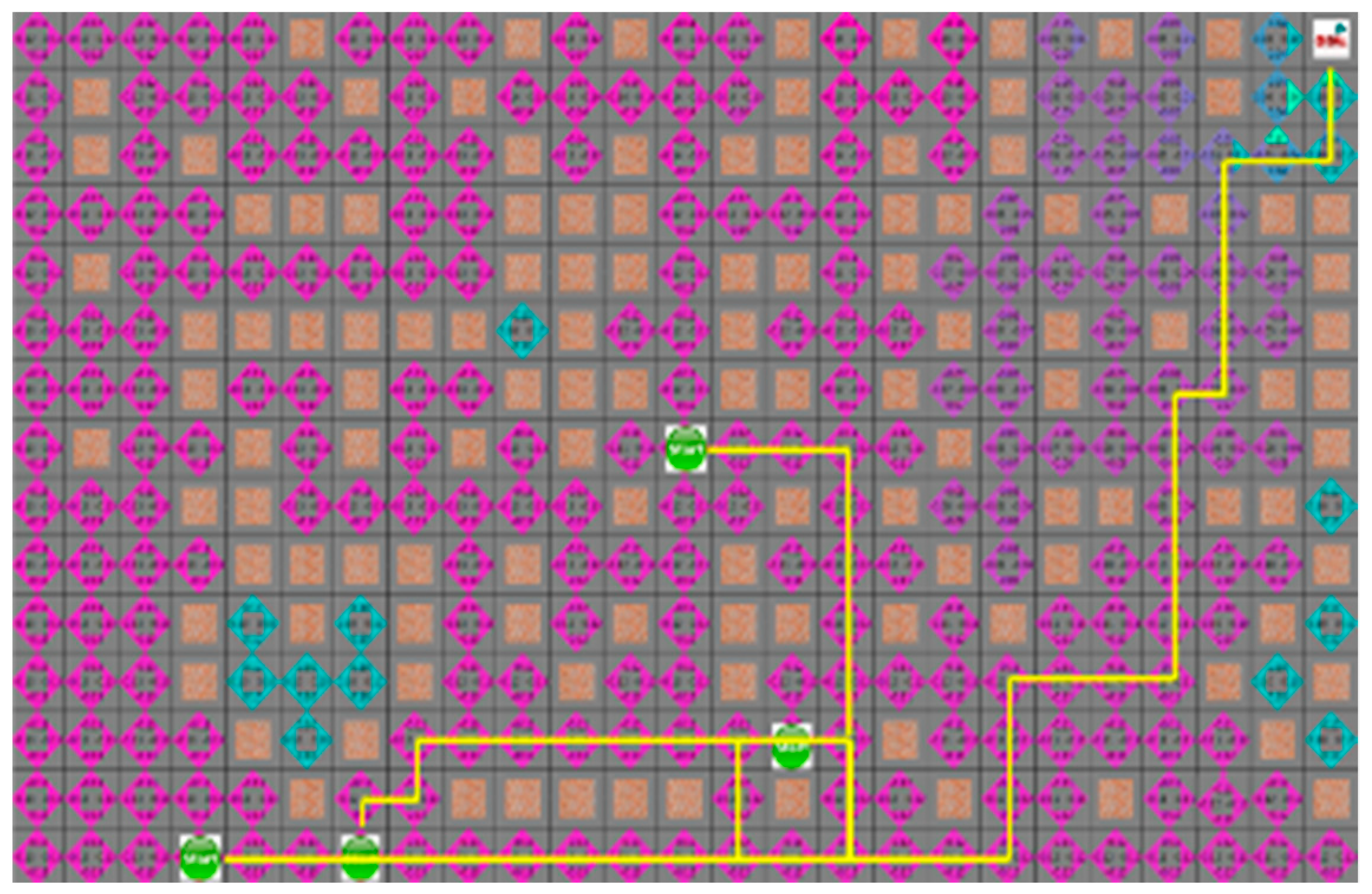

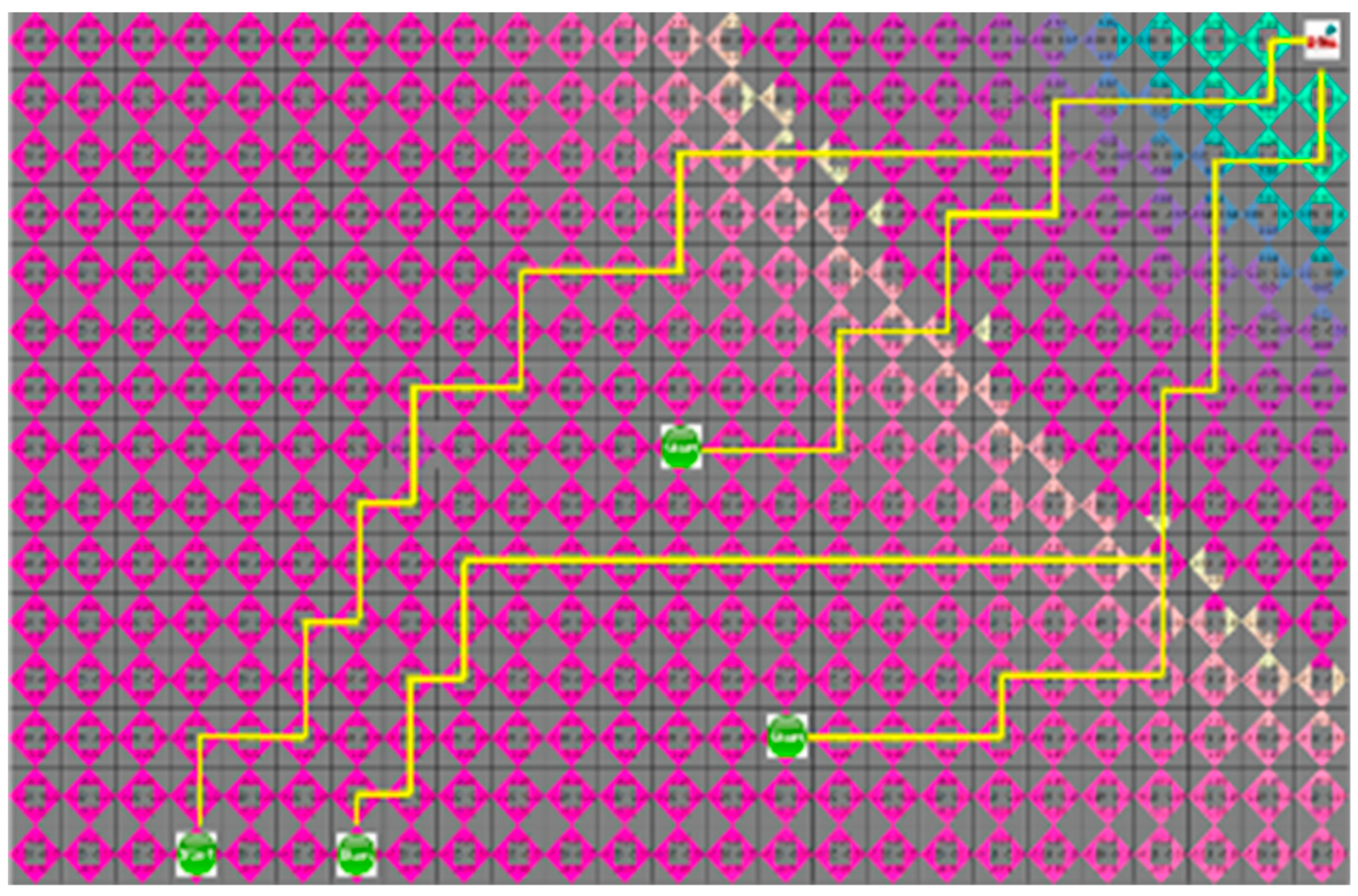
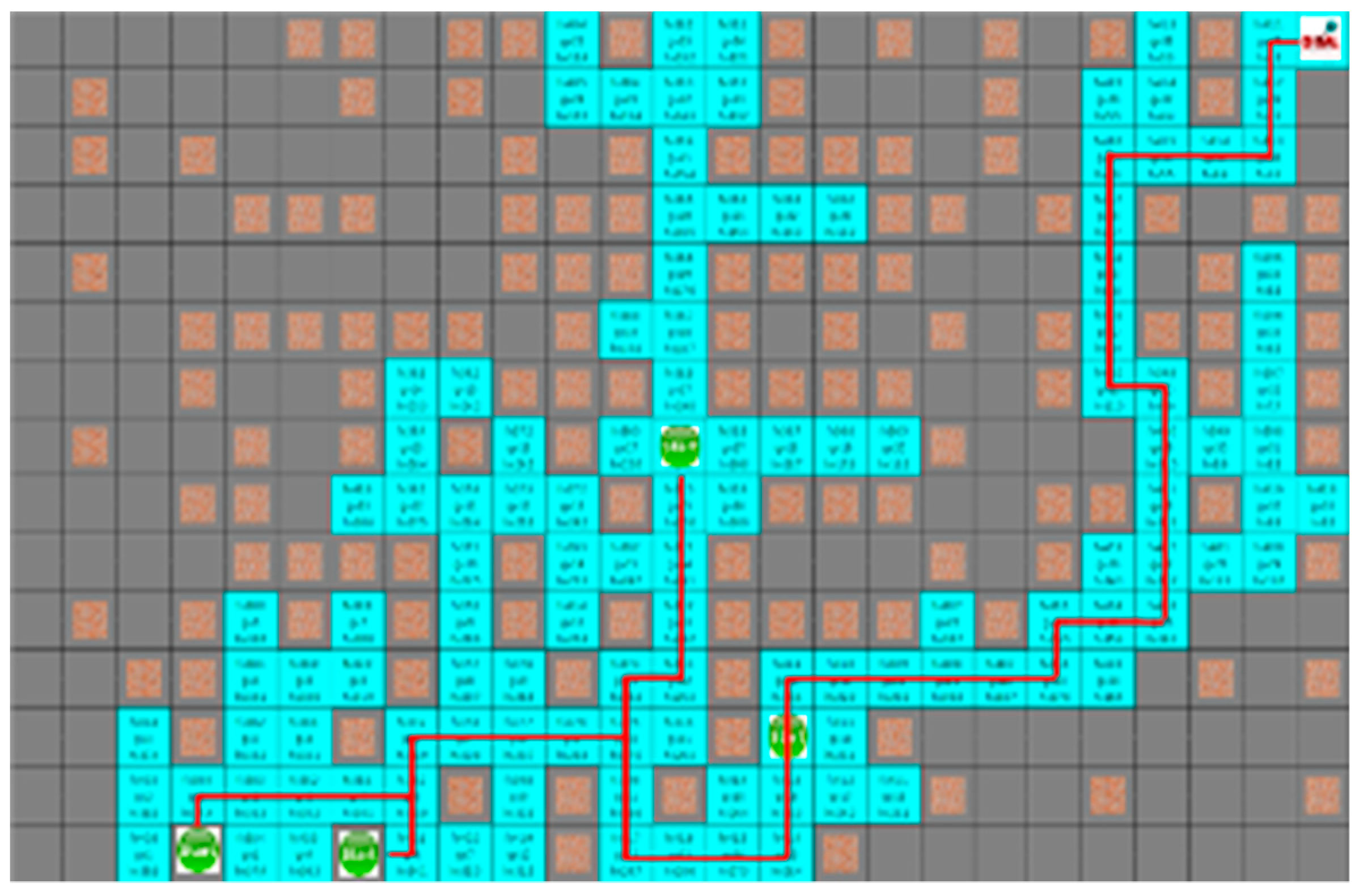
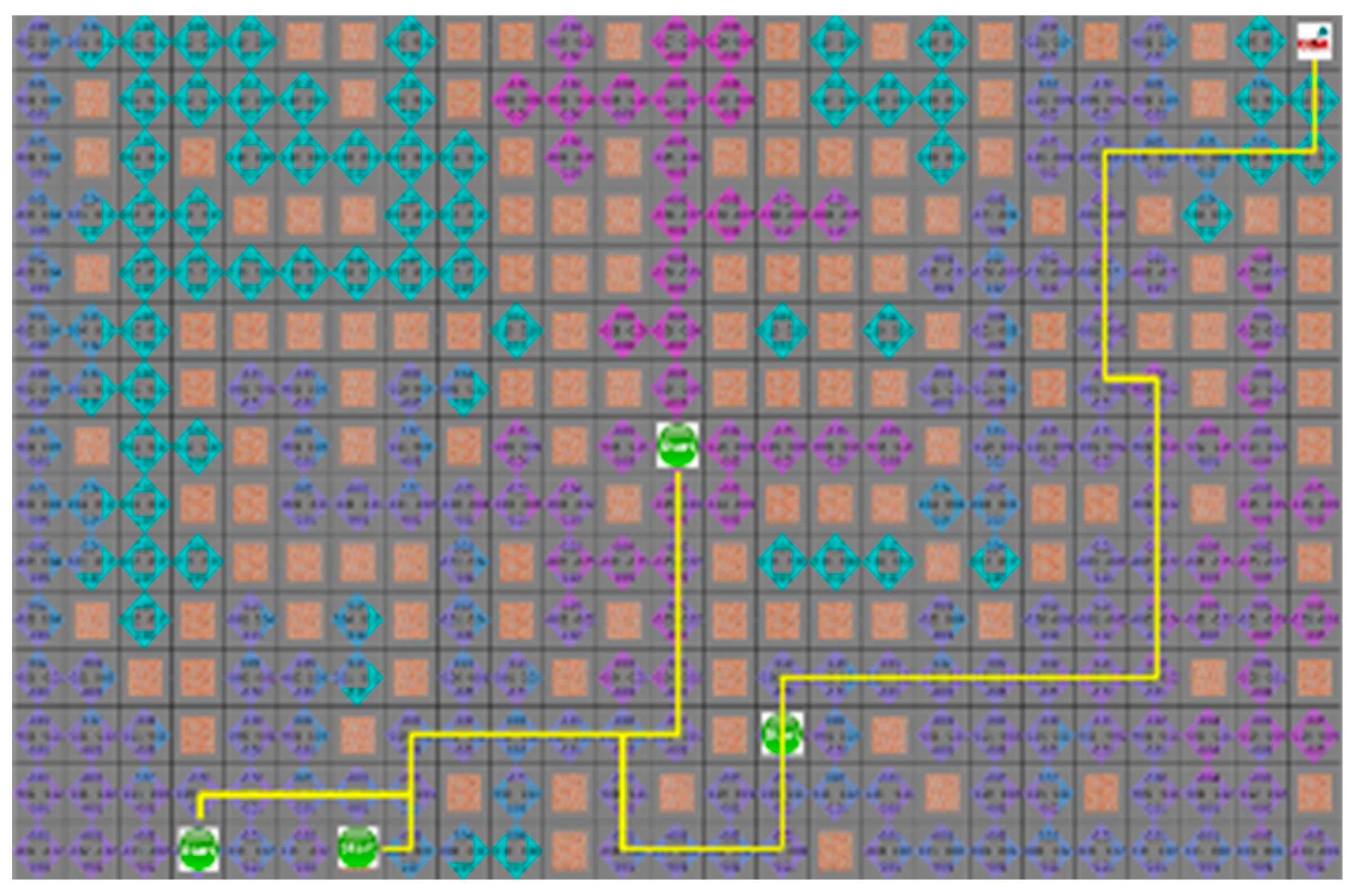
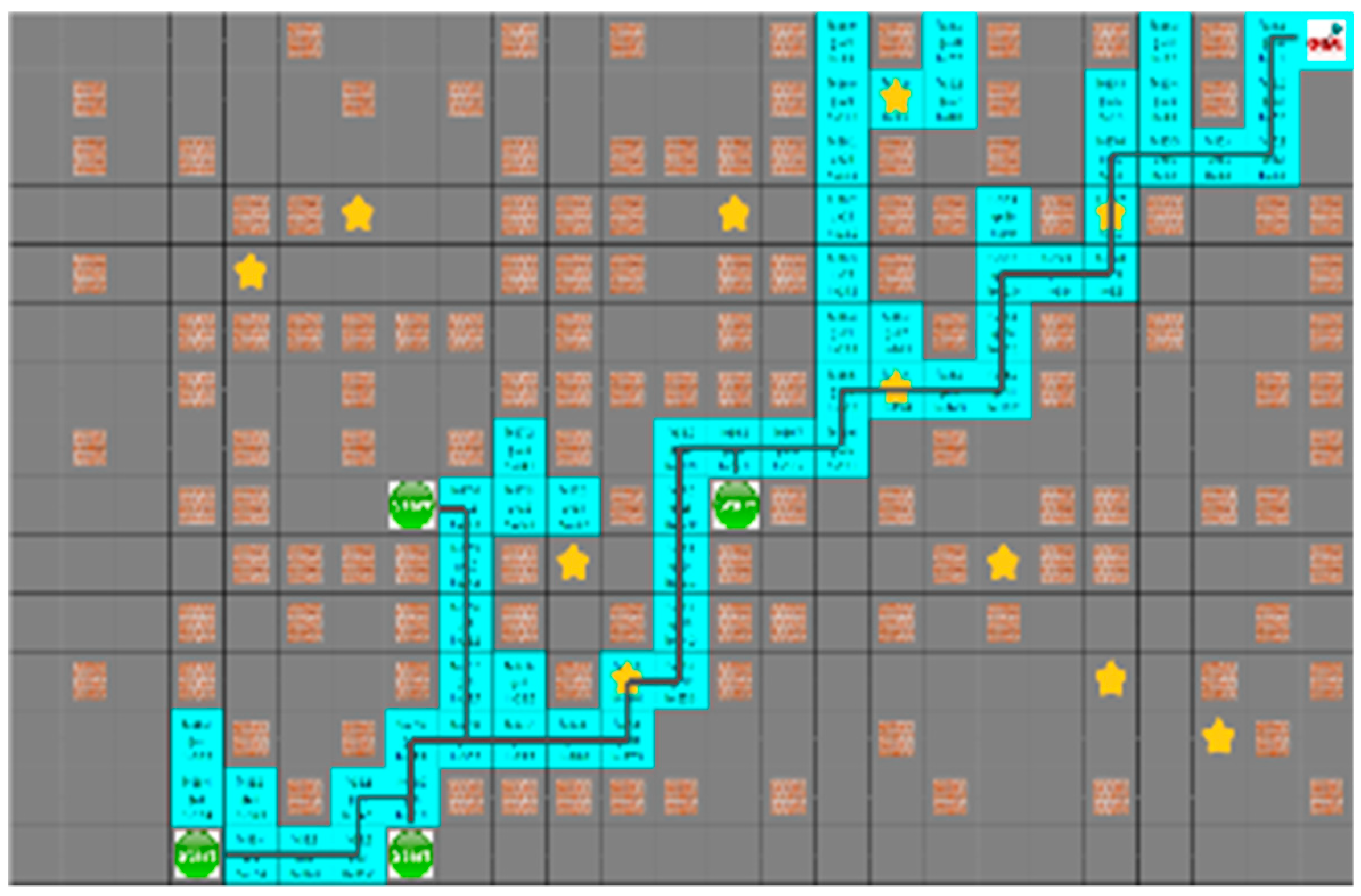
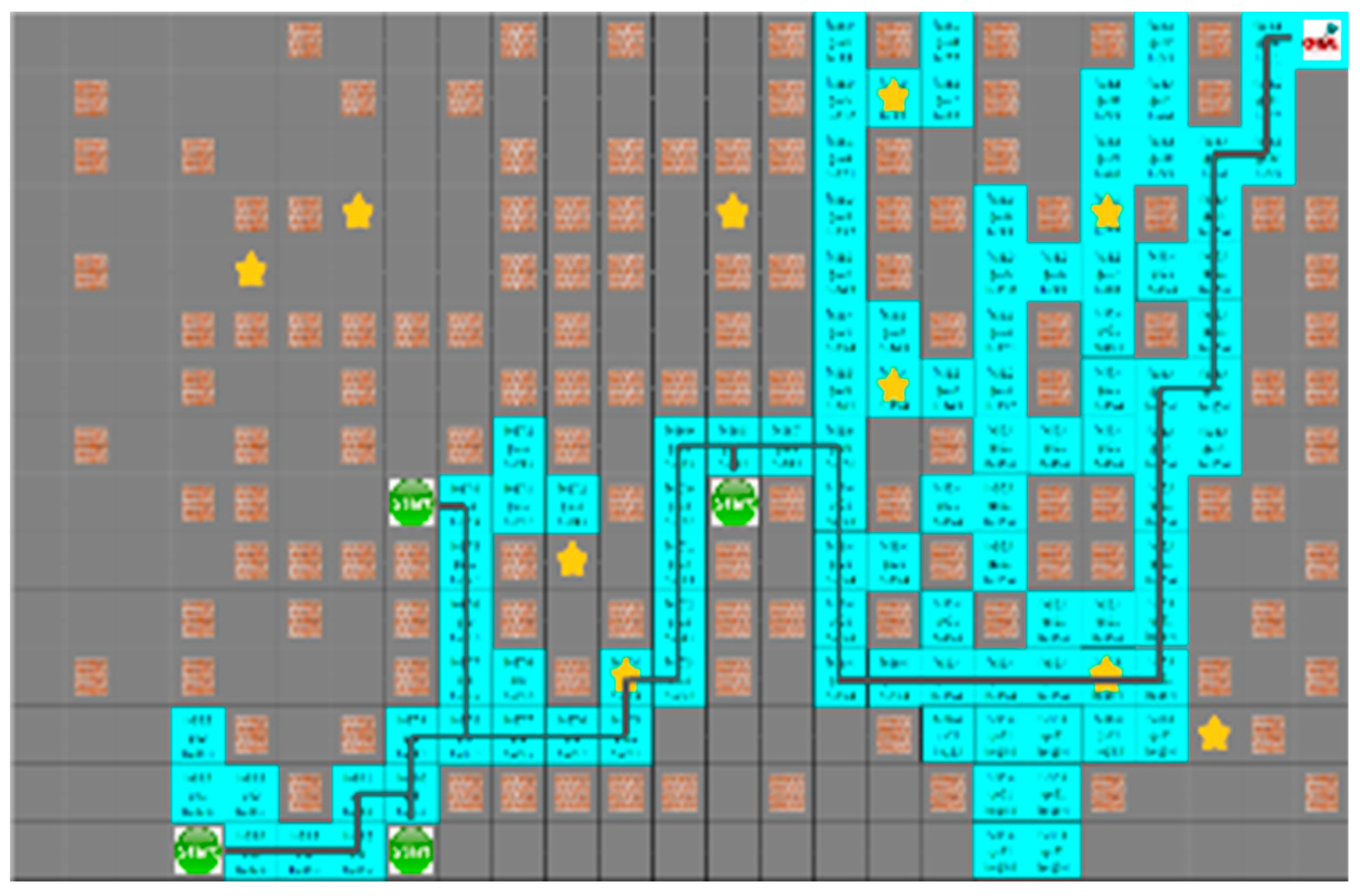

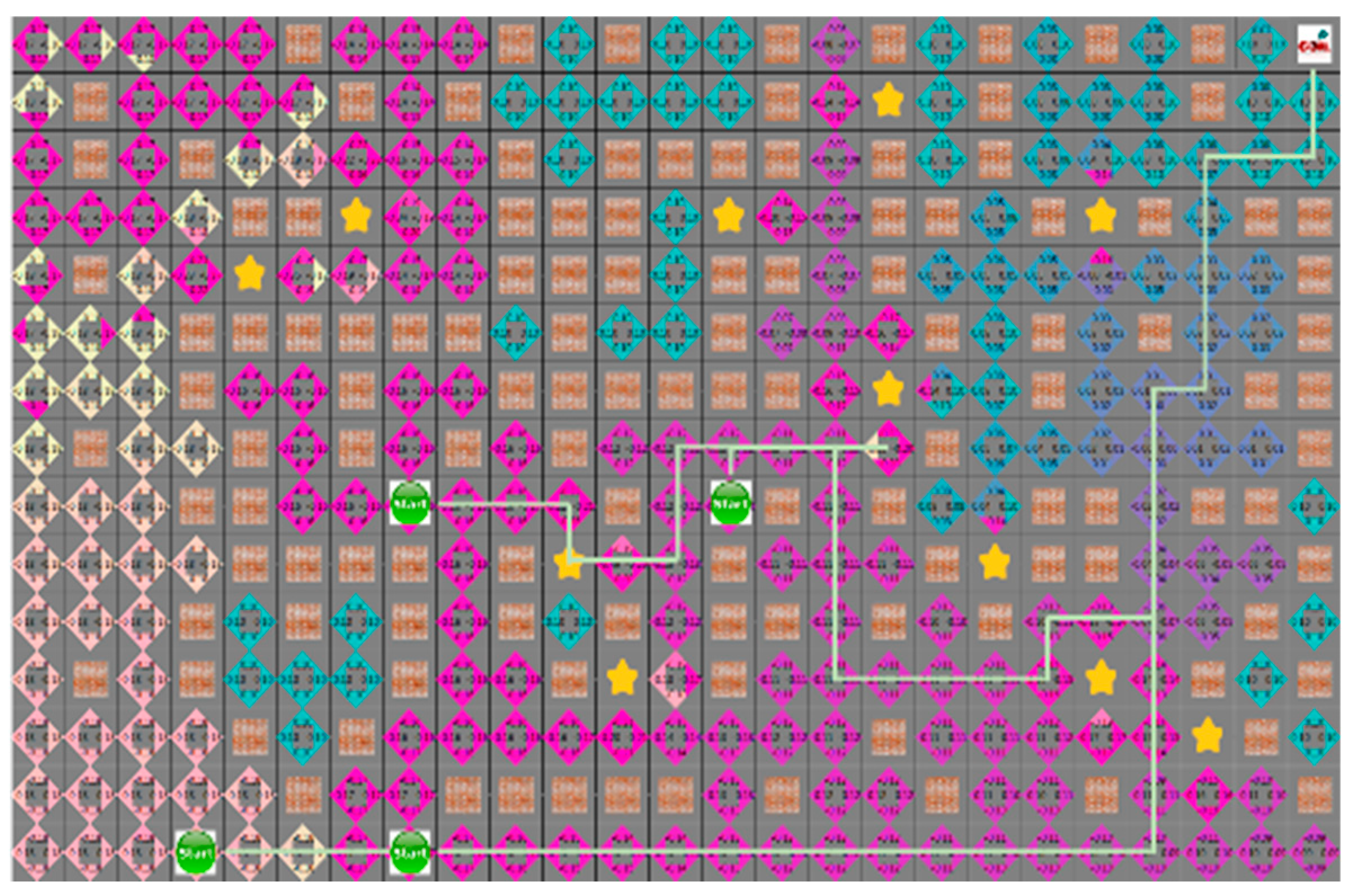
| Situation | A* Algorithm | Proposed Algorithm |
|---|---|---|
| Situation 1 | 258 | 155 |
| Situation 2 | 83 | 67 |
| Situation 3 | 69 | 69 |
| Situation 4 | 120 | 101 |
| Situation | A* Algorithm | Proposed Algorithm |
|---|---|---|
| Situation 1 | 35 | 36 |
| Situation 2 | 28 | 30 |
| Situation 3 | 30 | 31 |
| Situation 4 | 32 | 32 |
| Situation | Frequency of Occurrence |
|---|---|
| Situation 1 | 3262 |
| Situation 2 | 1556 |
| Situation 3 | 102 |
| Situation 4 | 80 |
| Situation | D* Algorithm | Proposed Algorithm |
|---|---|---|
| First bypass | 84 | 65 |
| Second bypass | 126 | 83 |
| Situation | D* Algorithm | Proposed Algorithm |
|---|---|---|
| Minimum Exploration Range | 66 | 66 |
| Maximum Exploration Range | 294 | 237 |
| Average Exploration Range | 188 | 141 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bae, H.; Kim, G.; Kim, J.; Qian, D.; Lee, S. Multi-Robot Path Planning Method Using Reinforcement Learning. Appl. Sci. 2019, 9, 3057. https://doi.org/10.3390/app9153057
Bae H, Kim G, Kim J, Qian D, Lee S. Multi-Robot Path Planning Method Using Reinforcement Learning. Applied Sciences. 2019; 9(15):3057. https://doi.org/10.3390/app9153057
Chicago/Turabian StyleBae, Hyansu, Gidong Kim, Jonguk Kim, Dianwei Qian, and Sukgyu Lee. 2019. "Multi-Robot Path Planning Method Using Reinforcement Learning" Applied Sciences 9, no. 15: 3057. https://doi.org/10.3390/app9153057
APA StyleBae, H., Kim, G., Kim, J., Qian, D., & Lee, S. (2019). Multi-Robot Path Planning Method Using Reinforcement Learning. Applied Sciences, 9(15), 3057. https://doi.org/10.3390/app9153057





