An Anti-Jamming Hierarchical Optimization Approach in Relay Communication System via Stackelberg Game
Abstract
:1. Introduction
- In relay communication scenario, considering the competitive relationship between the user and jammer, we formulate the anti-jamming joint optimization problem as a Stackelberg game, in which the user acts as leader and jammer acts as follower.
- We prove the existence of SE and propose a hierarchical joint optimization algorithm based on Q-learning and MAB method via Stackelberg game frame.
- Simulation results show the user’s strategy selection probability and jammer’s regret. Utility under the proposed algorithm is compared with random selection algorithm to verify the algorithm’s superiority. Moreover, the influence of feedback error and eavesdropping error on utility is analyzed.
2. System Model and Problem Formulation
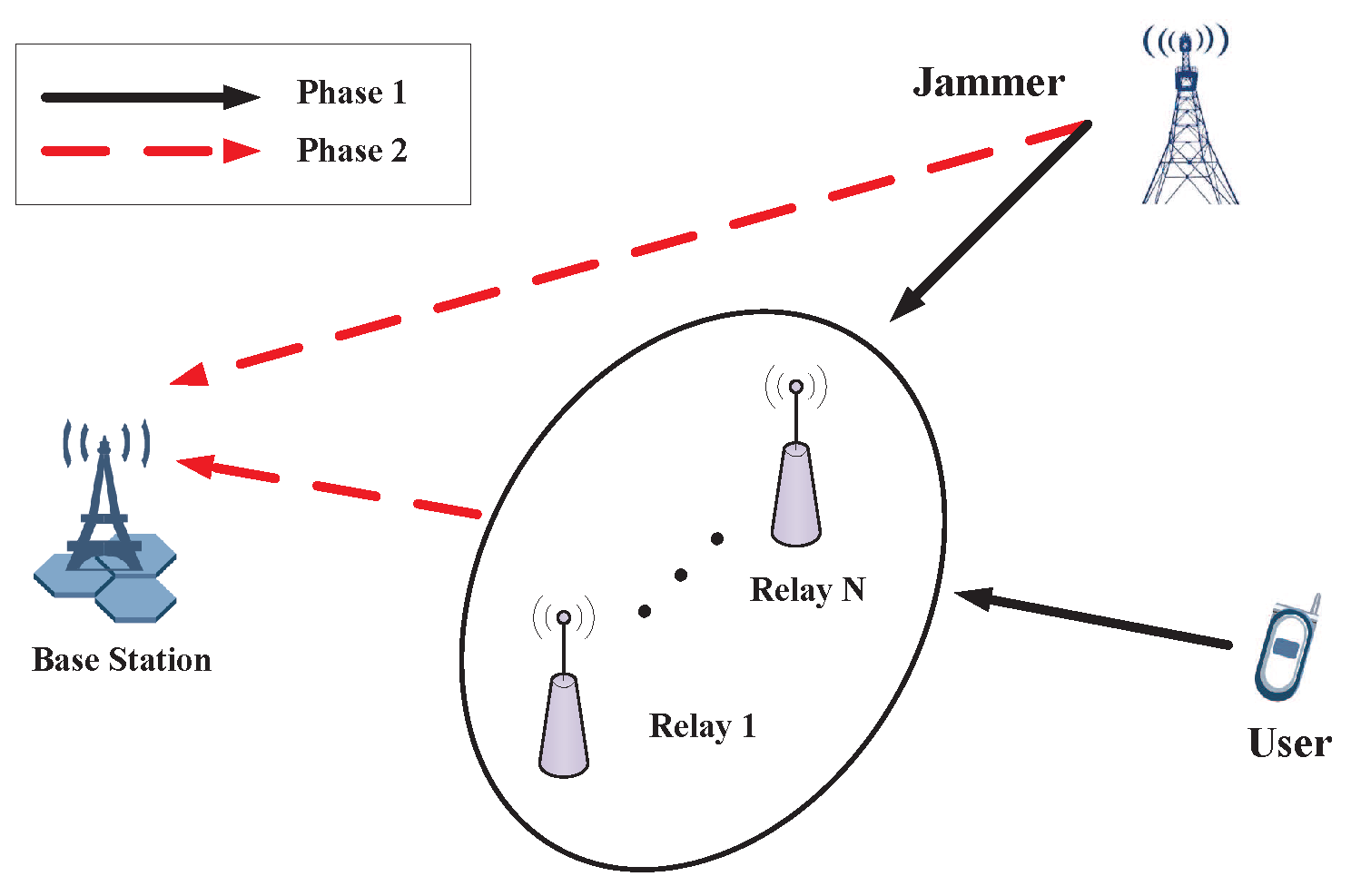
2.1. System Model
2.2. Problem Formulation
3. The Joint Relay Selection and Power Control Optimization Method via Stackelberg Game
3.1. Stackelberg Game Model
3.2. Existence of Stackelberg Equilibrium
3.3. Hierarchical Joint Optimization Algorithm
| Algorithm 1: Hierarchical joint optimization algorithm (HJOA). |
| Initialization: |
| The number T of time slots in one epoch, the number of all epochs. |
| User selects power P randomly, , . |
| Outer Iteration: |
| 1. Jammer selects the optimal arm according to Equation (21). |
| Inner Iteration: |
| (1) In the time slot, the user selects its joint relay and power strategy according to . |
| (2) Obtain the user’s utility through the feedback of SINR at the end of current time slot according to Equation (5). |
| (3) Update the user’s Q values according to Equation (14). |
| (4) Update the user’s mixed strategy according to Equation (15). |
| (5) Time slot . |
| (6) Return to (1) until . |
| End Inner Iteration. |
| 2. Obtain jammer’s utility through eavesdropping the feedback of SINR in the epoch according to Equation (6). |
| 3. Update and in turn. |
| 4. Epoch , . |
| 5. Return to 1 until . |
| End Outer Iteration. |
4. Simulation Results and Discussions
4.1. User’s Strategy Selection Probability and Jammer’s Regret
4.2. Utility Comparison under Different Algorithms with Feedback Error and Eavesdropping Error
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Meng, D.; Feng, Z.; Lu, M. Anti-jamming with adaptive arrays utilizing power inversion algorithm. Tsinghua Sci. Technol. 2008, 13, 796–799. [Google Scholar] [CrossRef]
- Yang, D.; Xue, G.; Zhang, J.; Richa, A.; Fang, X. Coping with a smart jammer in wireless networks: A Stackelberg game approach. IEEE Trans. Wirel. Commun. 2013, 12, 4038–4047. [Google Scholar] [CrossRef]
- Xiao, L.; Chen, T.; Liu, J.; Dai, H.; Anpalagan, A. Anti-jamming transmission Stackelberg game with observation errors. IEEE Commun. Lett. 2015, 19, 949–952. [Google Scholar] [CrossRef]
- Jia, L.; Yao, F.; Sun, Y.; Niu, Y.; Zhu, Y. Bayesian Stackelberg Game for Antijamming Transmission with Incomplete Information. IEEE Commun. Lett. 2016, 20, 1991–1994. [Google Scholar] [CrossRef]
- E1-Bardan, R.; Brahma, S.; Varshney, P.K. Strategic power allocation with incomplete information in the presence of jammer. IEEE Trans. Commun. 2016, 64, 3467–3479. [Google Scholar] [CrossRef]
- Chen, G.; Zhan, Y.; Chen, Y.; Xiao, L.; Wang, Y.; An, N. Reinforcement Learning Based Power Control for In-Body Sensors in WBANs Against Jamming. IEEE Access 2018, 6, 37403–37412. [Google Scholar] [CrossRef]
- Han, C.; Niu, Y. Cross-Layer Anti-Jamming Scheme: A Hierarchical Learning Approach. IEEE Access 2018, 6, 34874–34883. [Google Scholar] [CrossRef]
- Jia, L.; Yao, F.; Sun, Y.; Xu, Y.; Feng, S.; Anpalagan, A. A Hierarchical Learning Solution for Anti-Jamming Stackelberg Game with Discrete Power Strategies. IEEE Wirel. Commun. Lett. 2017, 6, 818–821. [Google Scholar] [CrossRef]
- Slimeni, F.; Nir, V.L.; Scheers, B.; Chtourou, Z.; Attia, R. Optimal power allocation over parallel Gaussian channels in cognitive radio and jammer games. IET Commun. 2016, 10, 980–986. [Google Scholar] [CrossRef] [Green Version]
- Jia, L.; Xu, Y.; Sun, Y.; Feng, S.; Anpalagan, A. Stackelberg game approaches for anti-jamming defence in wireless networks. IEEE Wirel. Commun. Mag. 2018, 25, 120–128. [Google Scholar] [CrossRef]
- Gao, Y.; Xiao, Y.; Wu, M.; Xiao, M.; Shao, J. Game Theory-Based Anti-Jamming Strategies for Frequency Hopping Wireless Communications. IEEE Trans. Wirel. Commun. 2018, 17, 5314–5326. [Google Scholar] [CrossRef]
- Xu, Y.; Anpalagan, A.; Wu, Q.; Shen, L.; Gao, Z.; Wang, J. Decision-theoretic distributed channel selection for opportunistic spectrum access: Strategies, challenges and solutions. IEEE Commun. Surv. Tutor. 2013, 15, 1689–1713. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Li, T. Anti-Jamming Message-Driven Frequency Hopping—Part I: System Design. IEEE Trans. Wirel. Commun. 2013, 12, 70–79. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, J.; Wu, Q.; Zheng, J.; Shen, L.; Anpalagan, A. Dynamic spectrum access in time-varying environment: Distributed learning beyond expectation optimization. IEEE Trans. Commun. 2017, 65, 5305–5318. [Google Scholar] [CrossRef]
- Shi, R.; Du, Y. Analysis on frequency diversity and anti-jamming characteristic of TDCS signal. In Proceedings of the 2017 IEEE 17th International Conference on Communication Technology (ICCT), Chengdu, China, 27–30 October 2017; pp. 27–30. [Google Scholar]
- Liu, X.; Xu, Y.; Jia, L.; Wu, Q.; Anpalagan, A. Anti-jamming communications using spectrum waterfall: A deep reinforcement learning approach. IEEE Commun. Lett. 2018, 22, 998–1001. [Google Scholar] [CrossRef]
- Zhu, Y.; Guo, C.; Wang, X. Throughput analysis of dynamic spectrum anti-jamming multiple-access in HF communication systems. China Commun. 2018, 15, 85–94. [Google Scholar] [CrossRef]
- Zhu, H.; Fang, C.; Liu, Y.; Chen, C.; Li, M.; Shen, X. You Can Jam But You Cannot Hide: Defending against Jamming Attacks for Geo-Location Database Driven Spectrum Sharing. IEEE J. Sel. Areas Commun. 2016, 34, 2723–2737. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, J.; Wu, Q.; Anpalagan, A.; Yao, Y. Opportunistic spectrum access in unknown dynamic environment: A game-theoretic stochastic learning solution. IEEE Trans. Wirel. Commun. 2012, 11, 1380–1391. [Google Scholar] [CrossRef]
- Salvatore, D.; Laura, G.; Giacomo, M.; Sergio, P.; Lin, C.; Fabio, M. Defeating Jamming with the Power of Silence: A Game-Theoretic Analysis. IEEE Trans. Wirel. Commun. 2015, 15, 2337–2352. [Google Scholar]
- He, H.; Zhang, X. Application of improve subspace projection technique in anti-jam of GNSS space-time receiver. In Proceedings of the 2012 5th International Congress on Image and Signal Processing, Chongqing, China, 16–18 October 2012. [Google Scholar]
- Du, Y.; Gao, Y.; Liu, J.; Xi, X. Frequency-Space Domain Anti-Jamming Algorithm Assisted with Probability Statistics. In Proceedings of the 2013 International Conference on Information Technology and Applications, Chengdu, China, 16–17 November 2013. [Google Scholar]
- Liu, Y.; Zhang, S.; Shi, D.; Shen, Y.; Gao, Y. Anti-jamming space-time processor with digital beamformer for satellite navigation. In Proceedings of the 2015 7th Asia-Pacific Conference on Environmental Electromagnetics (CEEM), Hangzhou, China, 4–7 November 2015; pp. 31–35. [Google Scholar]
- Wang, D.; Chen, Q. Reduced rank calculation of space-time anti-jamming for navigation receiver. In Proceedings of the 2013 International Conference on Mechatronic Sciences, Electric Engineering and Computer (MEC), Shenyang, China, 20–22 December 2013. [Google Scholar]
- Xiao, A.; Zhong, B. Design for a dual-system satellite navigation anti-jamming receiver. In Proceedings of the 2015 Chinese Automation Congress (CAC), Wuhan, China, 27–29 November 2015. [Google Scholar]
- Laneman, G.N.; Tse, D.N.C.; Wornell, G.W. Cooperative Diversity in Wireless Networks: Efficient Protocols and Outage Behavior. IEEE Commun. Mag. 2004, 50, 3062–3080. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, H.; Zhang, B.; Peng, J. Intelligent Anti-Jamming Relay Communication System Based on Reinforcement Learning. In Proceedings of the 2019 2nd International Conference on Communication Engineering and Technology (ICCET), Nagoya, Japan, 12–15 April 2019. [Google Scholar]
- Zhong, W.; Chen, G.; Jin, S.; Wong, K. Relay Selection and Discrete Power Control for Cognitive Relay Networks via Potential Game. IEEE Trans. Signal Process. 2014, 62, 5411–5424. [Google Scholar] [CrossRef]
- Gu, P.; Hua, C.; Khatoun, R.; Wu, Y.; Serhrouchni, A. Cooperative Anti-Jamming Relaying for Control Channel Jamming in Vehicular Networks. IEEE Trans. Veh. Technol. 2018, 67, 7033–7046. [Google Scholar] [CrossRef]
- Xiao, L.; Li, Y.; Liu, J.; Zhao, Y. Power control with reinforcement learning in cooperative cognitive radio networks against jamming. J. Supercomput. 2015, 71, 3237–3257. [Google Scholar] [CrossRef]
- Liu, W.; Tan, D.; Xu, G. Low complexity power allocation and joint relay-jammer selection in cooperative jamming DF relay wireless secure networks. In Proceedings of the 2013 International Conference on Anti-Counterfeiting, Security and Identification (ASID), Shanghai, China, 25–27 October 2013. [Google Scholar]
- Liu, K.J.R.; Wang, B. Cognitive Radio Networking and Security: A Game-Theoretic View; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Naveen, K.P.; Altman, E.; Kumar, A. Competitive Selection of Ephemeral Relays in Wireless Networks. IEEE J. Sel. Areas Commun. 2017, 35, 586–600. [Google Scholar] [CrossRef]
- Kuhestani, A.; Mohammadi, A.; Yeoh, P.L. Optimal Power Allocation and Secrecy Sum Rate in Two-Way Untrusted Relaying Networks With an External Jammer. IEEE Trans. Commun. 2018, 6, 2671–2684. [Google Scholar] [CrossRef]
- Mamaghani, M.T.; Kuhestani, A.; Wong, K. Secure Two-Way Transmission via Wireless-Powered Untrusted Relay and External Jammer. IEEE Trans. Veh. Technol. 2018, 67, 8451–8465. [Google Scholar] [CrossRef] [Green Version]
- Feng, Z.; Ren, G.; Chen, J.; Zhang, X.; Luo, Y.; Wang, M.; Xu, Y. Power Control in Relay-assisted Anti-jamming Systems: A Bayesian Three-layer Stackelberg Game Approach. IEEE Access 2019, 7, 14623–14636. [Google Scholar] [CrossRef]
- Garnaev, A.; Trappe, W.; Petropulu, A. Combating Jamming in Wireless Networks: A Bayesian Game with Jammer’s Channel Uncertainty. In Proceedings of the 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019. [Google Scholar]
- Garnaev, A.; Liu, Y.; Trappe, W. Anti-jamming Strategy Versus a Low-Power Jamming Attack When Intelligence of Adversary’s Attack Type is Unknown. IEEE Trans. Signal Inf. Process. Netw. 2016, 2, 49–56. [Google Scholar] [CrossRef]
- Li, M.; Koutsopoulos, I.; Poovendran, R. Optimal Jamming Attacks and Network Defense Policies in Wireless Sensor Networks. In Proceedings of the 26th IEEE International Conference on Computer Communications, Barcelona, Spain, 6–12 May 2007. [Google Scholar]
- Luo, Y.; Feng, Z.; Jiang, H.; Yang, Y.; Huang, Y.; Yao, J. Game-theoretic Learning Approaches for Secure D2D Communications Against Full-duplex Active Eavesdropper. IEEE Access 2019, 7, 41324–41335. [Google Scholar] [CrossRef]
- Tang, X.; Ren, P.; Wang, Y.; Hang, Z. Combating full-duplex active eavesdropper: A hierarchical game perspective. IEEE Trans. Commun. 2017, 65, 1379–1395. [Google Scholar] [CrossRef]
- Qu, J.; Cai, Y.; Zheng, J. Power allocation for device-to-device communication underlaying cellular networks under a probabilistic eavesdropping scenario. Ann. Telecommun. 2016, 71, 389–398. [Google Scholar] [CrossRef]
- Goldsmith, A. Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Chen, X.; Zhang, H.; Chen, T.; Lasanen, M. Improving energy efficiency in green femtocell networks: A hierarchical reinforcement learning framework. In Proceedings of the 2013 IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 2241–2245. [Google Scholar]
- Sun, Y.; Shao, H.; Liu, X.; Zhang, J.; Qiu, J.; Xu, Y. Traffic offloading in two-tier multi-mode small cell networks over unlicensed bands: A hierarchical learning framework. TIIS 2015, 9, 4291–4310. [Google Scholar]
- Han, Z.; Niyato, D.; Saad, W.; Başar, T.; Hjørungnes, A. Game Theory in Wireless and Communication Networks; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Watkins, C.J.C.H.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Auer, P.; Cesa-Bianchi, N.; Fischer, P. Finite-time analysis of the multiarmed bandit problem. Mach. Learn. 2002, 47, 235–256. [Google Scholar] [CrossRef]
- Lai, T.; Robbins, H. Asymptotically efficient adaptive allocation rules. Adv. Appl. Math. 1985, 6, 4–22. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, R. Sample mean based index policies with O(log n) regret for the multi-armed bandit problem. Adv. Appl. Probab. 1995, 27, 1054–1078. [Google Scholar] [CrossRef]







| Power set of the user and jammer | |
| Relay set and all relays’ power set | |
| Transmitting power of the user and jammer, i.e., | |
| The channel gain between the user, jammer and the relay | |
| The channel gain between the relay, jammer and BS | |
| The back noise power at the relay and BS | |
| The relay’s amplification factor | |
| The user’s, jammer’s and relay’s transmitted signal | |
| The relay’s and BS’s received signal | |
| , | The transmitting cost of the user and jammer |
| Feedback error and eavesdropping error | |
| The SINR received at BS | |
| The feedback SINR received by the user and eavesdropped by jammer |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.; Ren, G.; Chen, J.; Chen, C.; Yang, X.; Luo, Y.; Xu, K. An Anti-Jamming Hierarchical Optimization Approach in Relay Communication System via Stackelberg Game. Appl. Sci. 2019, 9, 3348. https://doi.org/10.3390/app9163348
Feng Z, Ren G, Chen J, Chen C, Yang X, Luo Y, Xu K. An Anti-Jamming Hierarchical Optimization Approach in Relay Communication System via Stackelberg Game. Applied Sciences. 2019; 9(16):3348. https://doi.org/10.3390/app9163348
Chicago/Turabian StyleFeng, Zhibin, Guochun Ren, Jin Chen, Chaohui Chen, Xiaoqin Yang, Yijie Luo, and Kun Xu. 2019. "An Anti-Jamming Hierarchical Optimization Approach in Relay Communication System via Stackelberg Game" Applied Sciences 9, no. 16: 3348. https://doi.org/10.3390/app9163348
APA StyleFeng, Z., Ren, G., Chen, J., Chen, C., Yang, X., Luo, Y., & Xu, K. (2019). An Anti-Jamming Hierarchical Optimization Approach in Relay Communication System via Stackelberg Game. Applied Sciences, 9(16), 3348. https://doi.org/10.3390/app9163348






