The Influence of the Damage of Mortise-Tenon Joint on the Cyclic Performance of the Traditional Chinese Timber Frame
Abstract
:1. Introduction
2. Finite Element (FE) Model and Verification
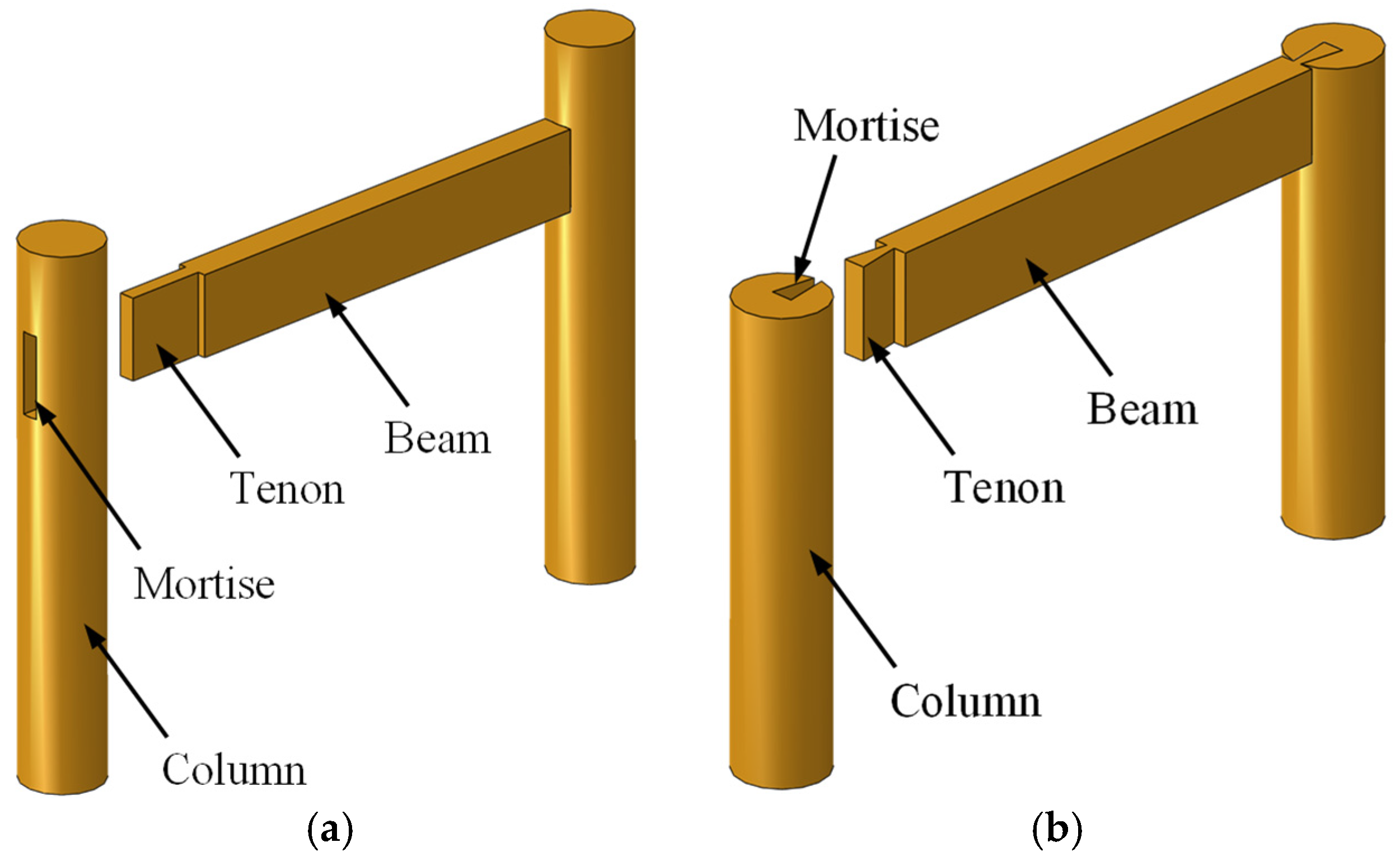
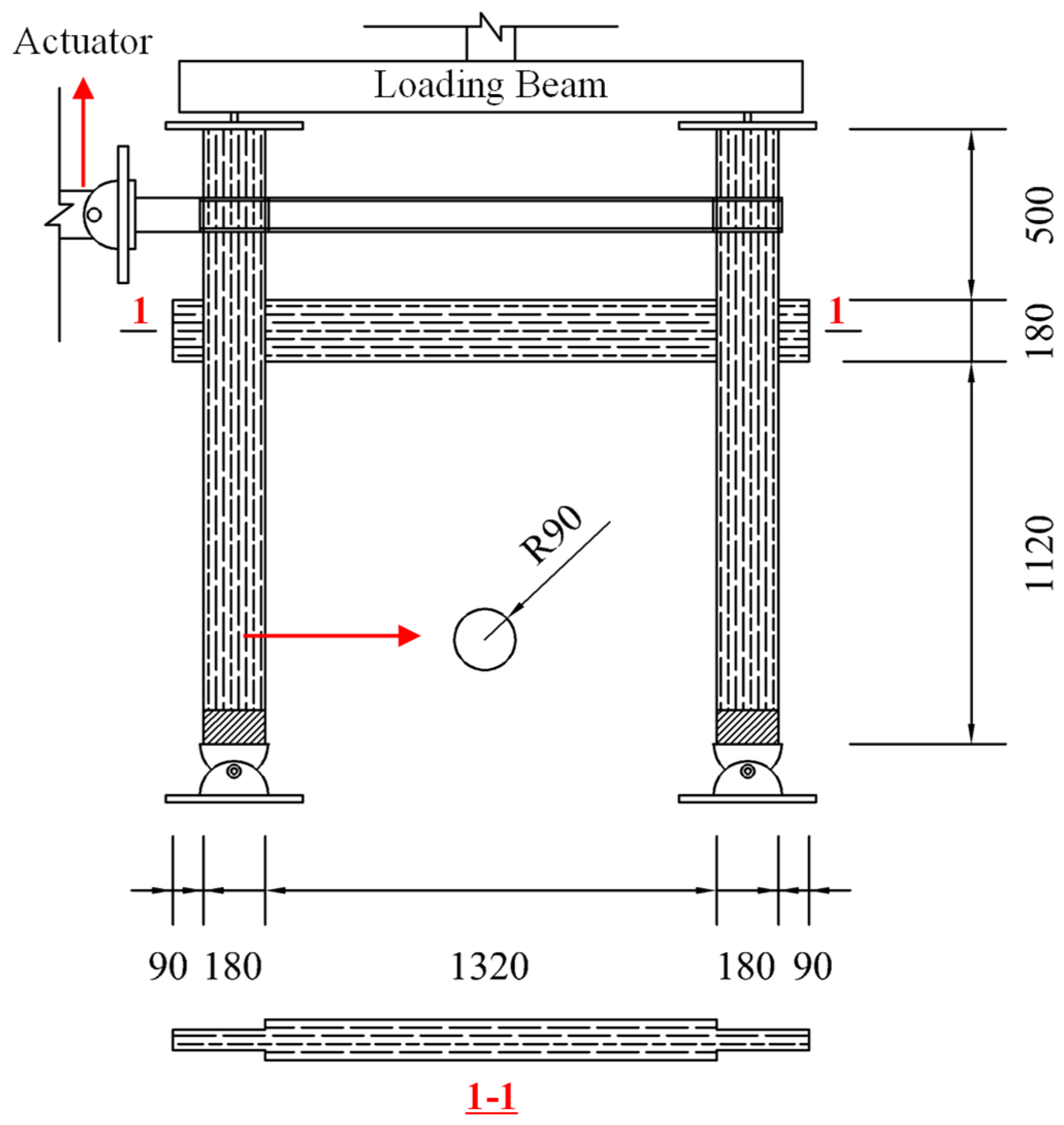
2.1. Test Model
2.2. FE Model
2.3. Verification
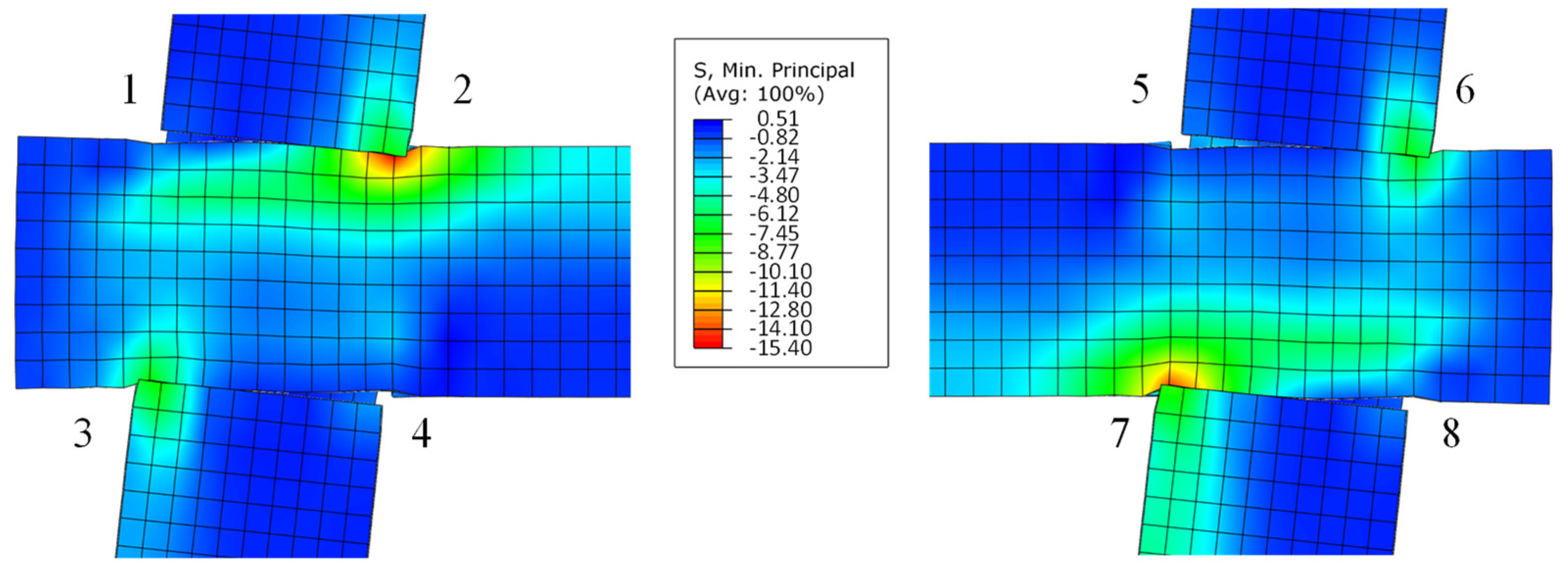
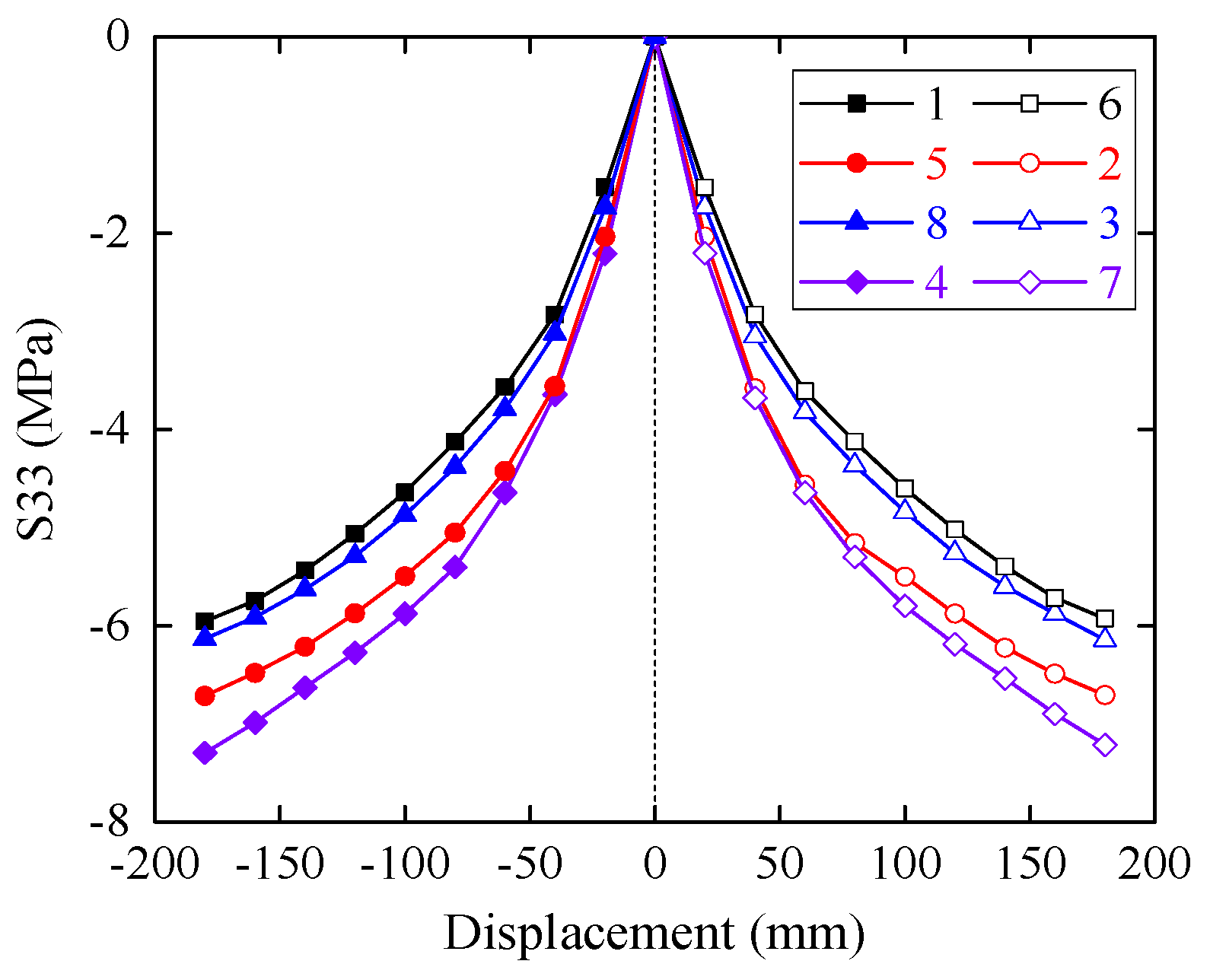
3. Stress Analysis
4. Damage of Mortise-Tenon Joint
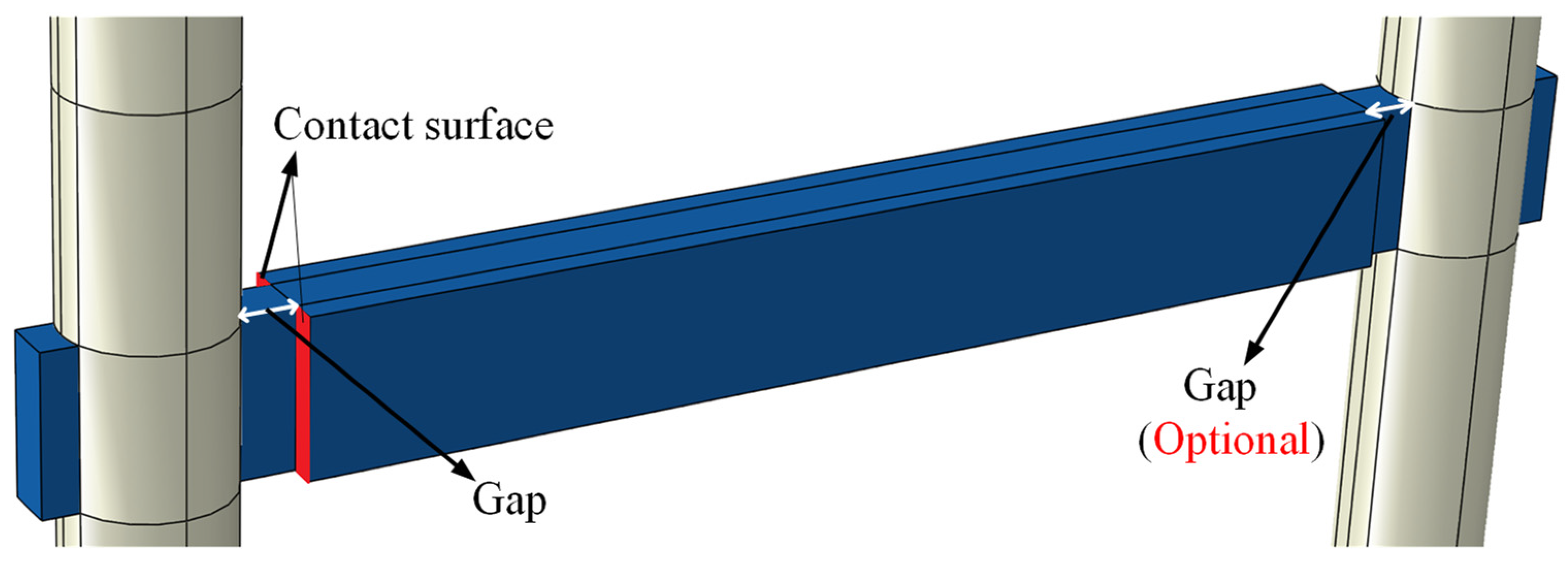
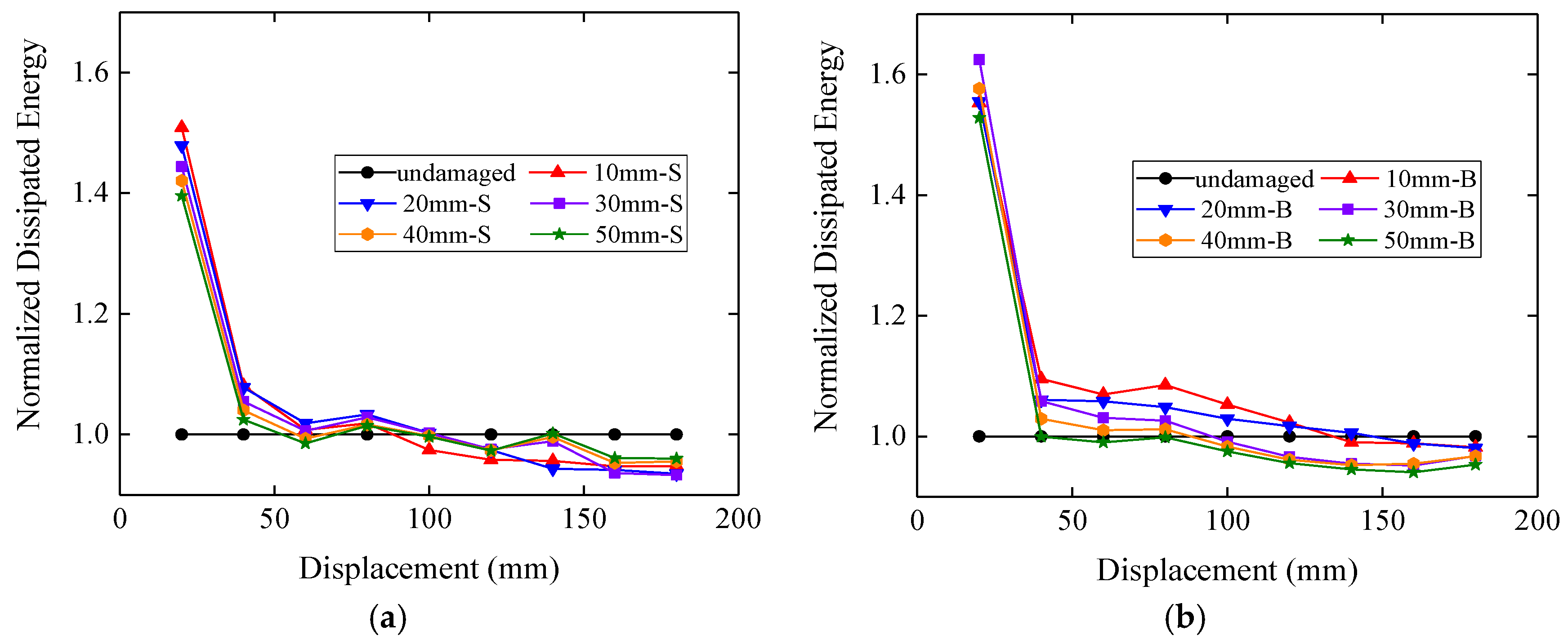
4.1. Gap between Mortise and Tenon
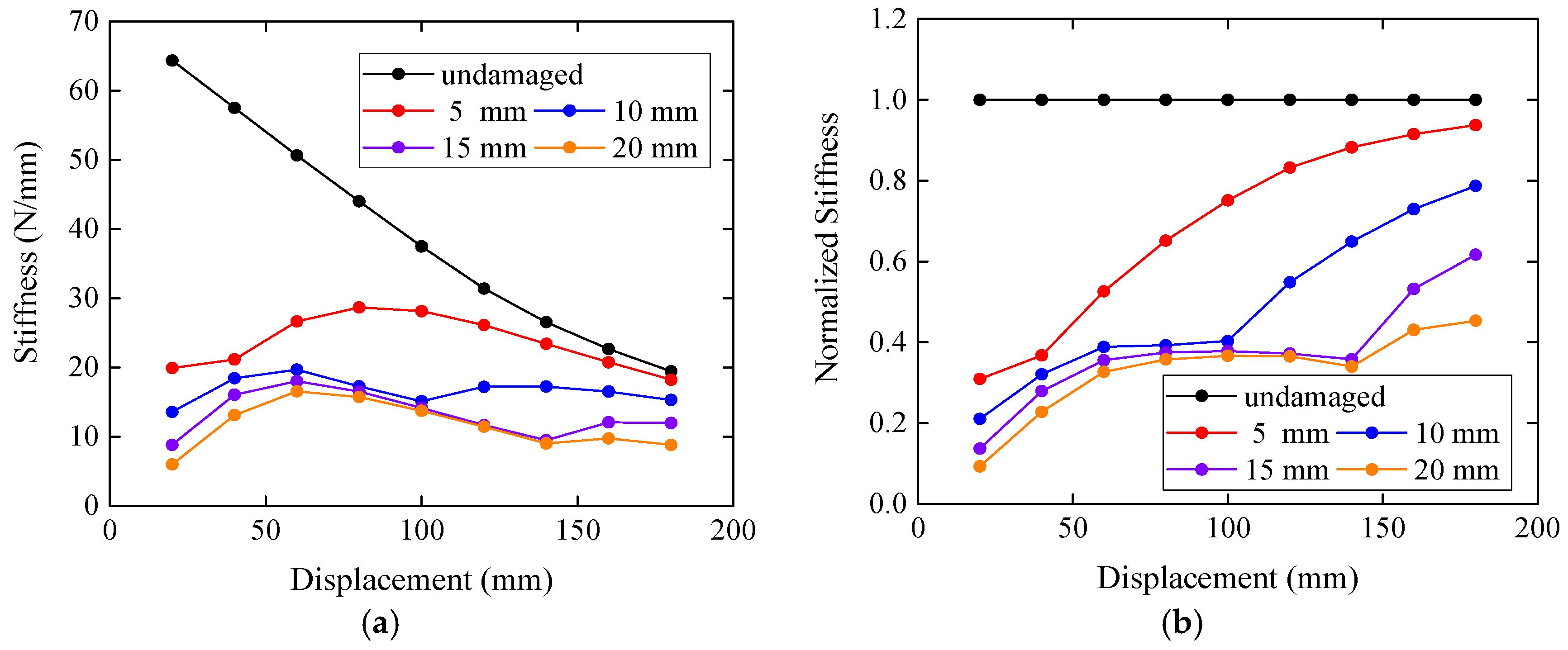
4.2. Damage in the Top of the Tenon
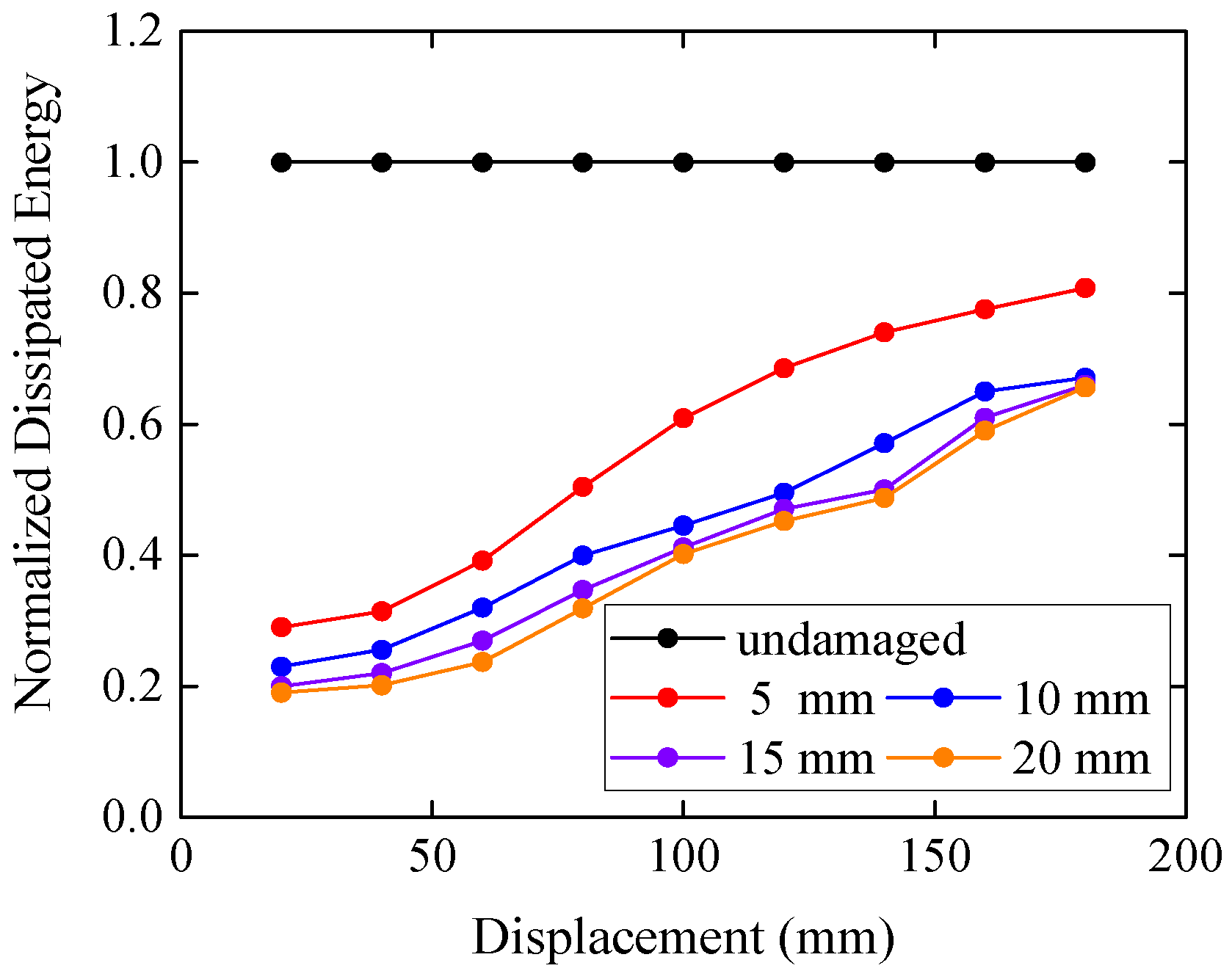
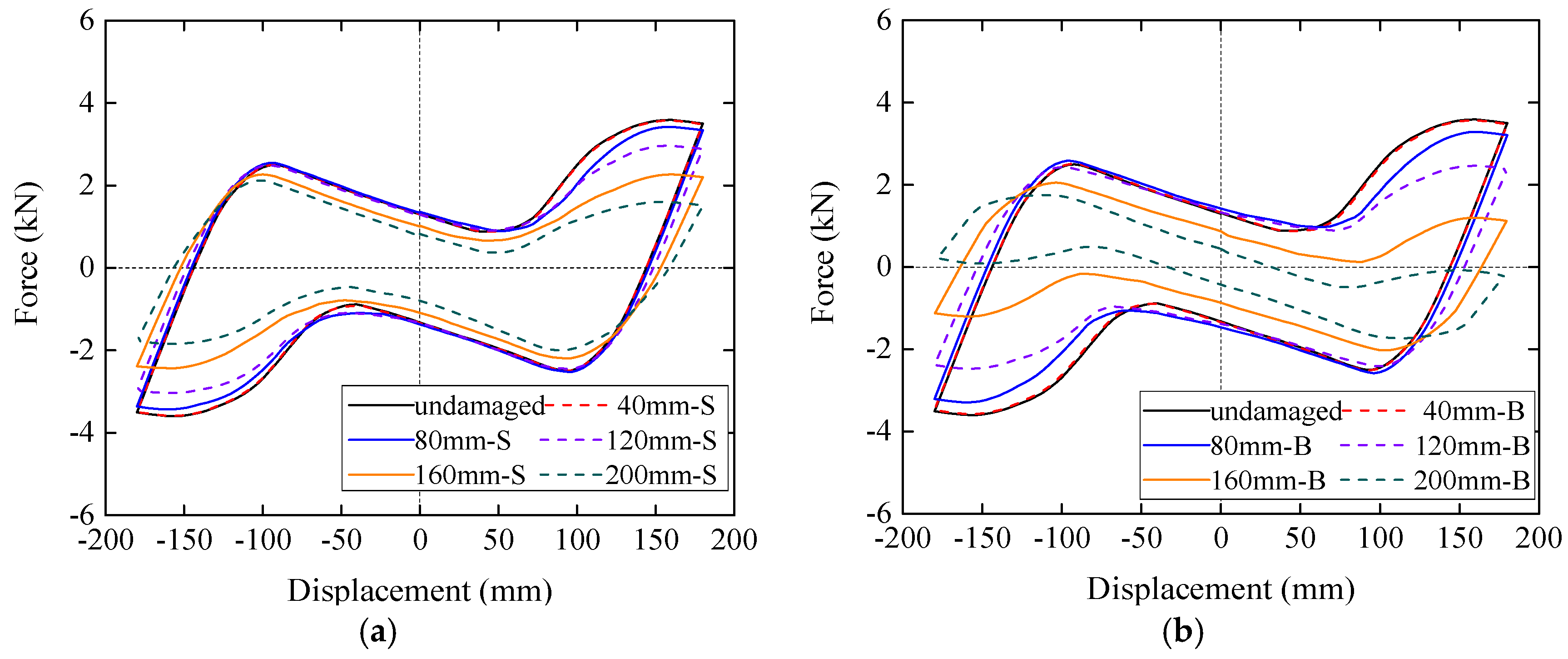
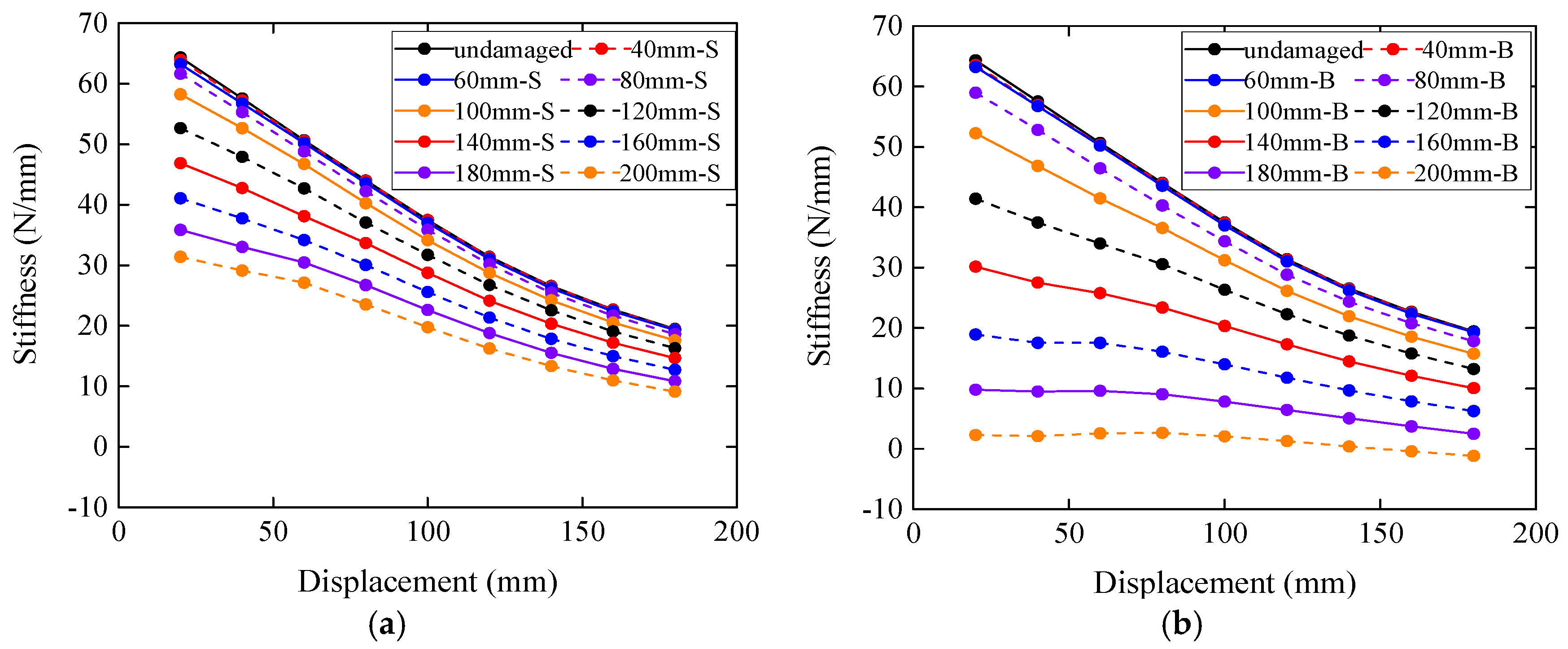
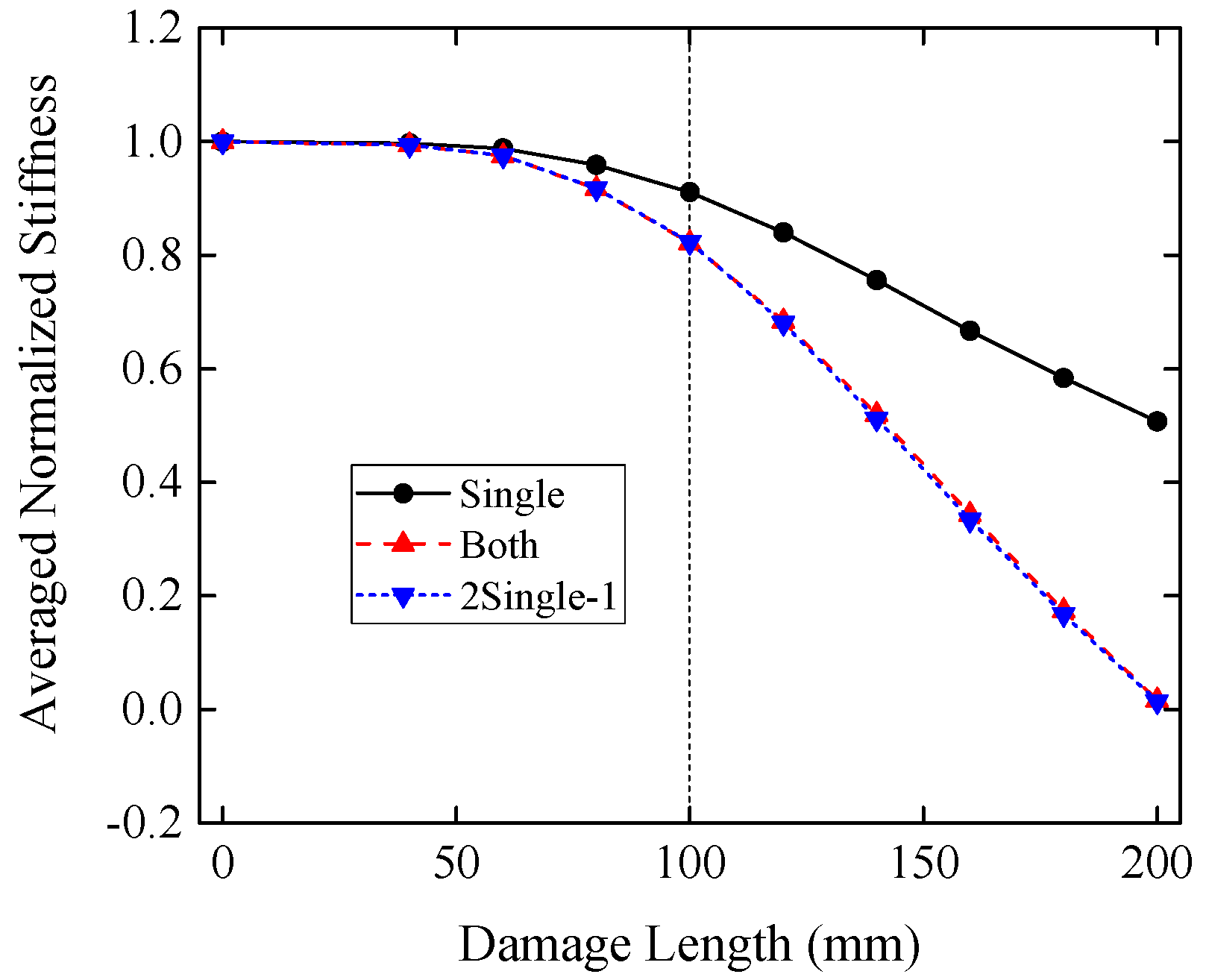
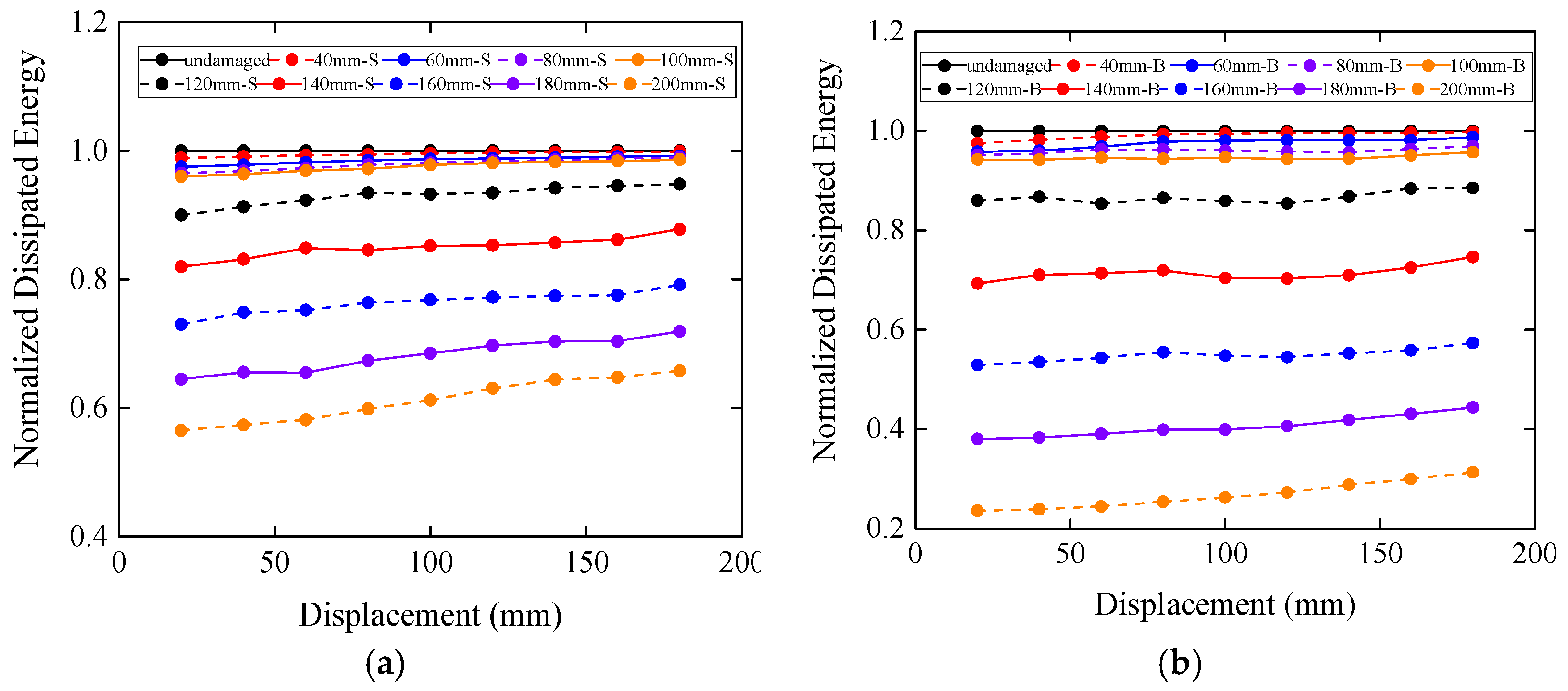
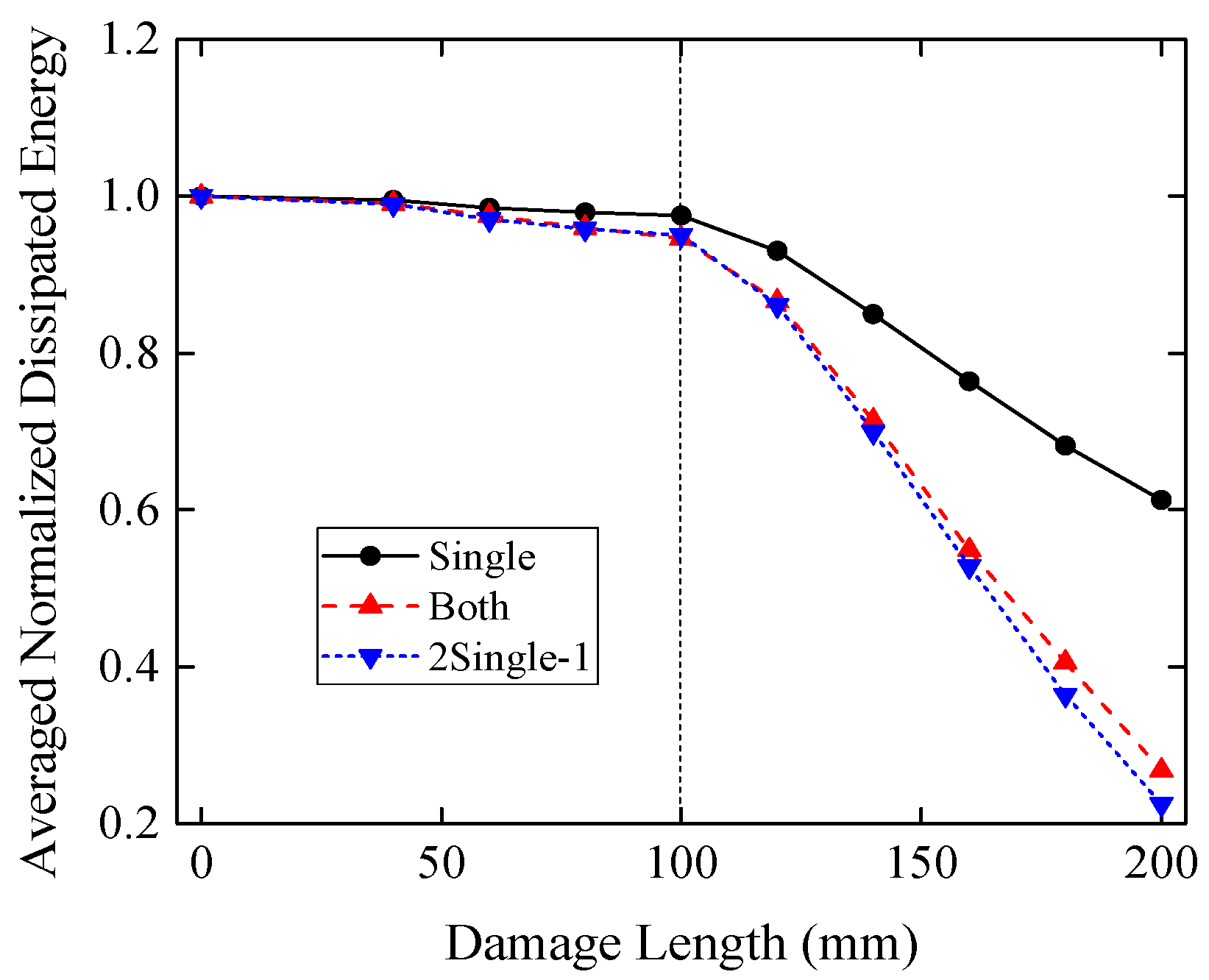
4.3. Damage in the End of the Tenon
5. Conclusions
- (1).
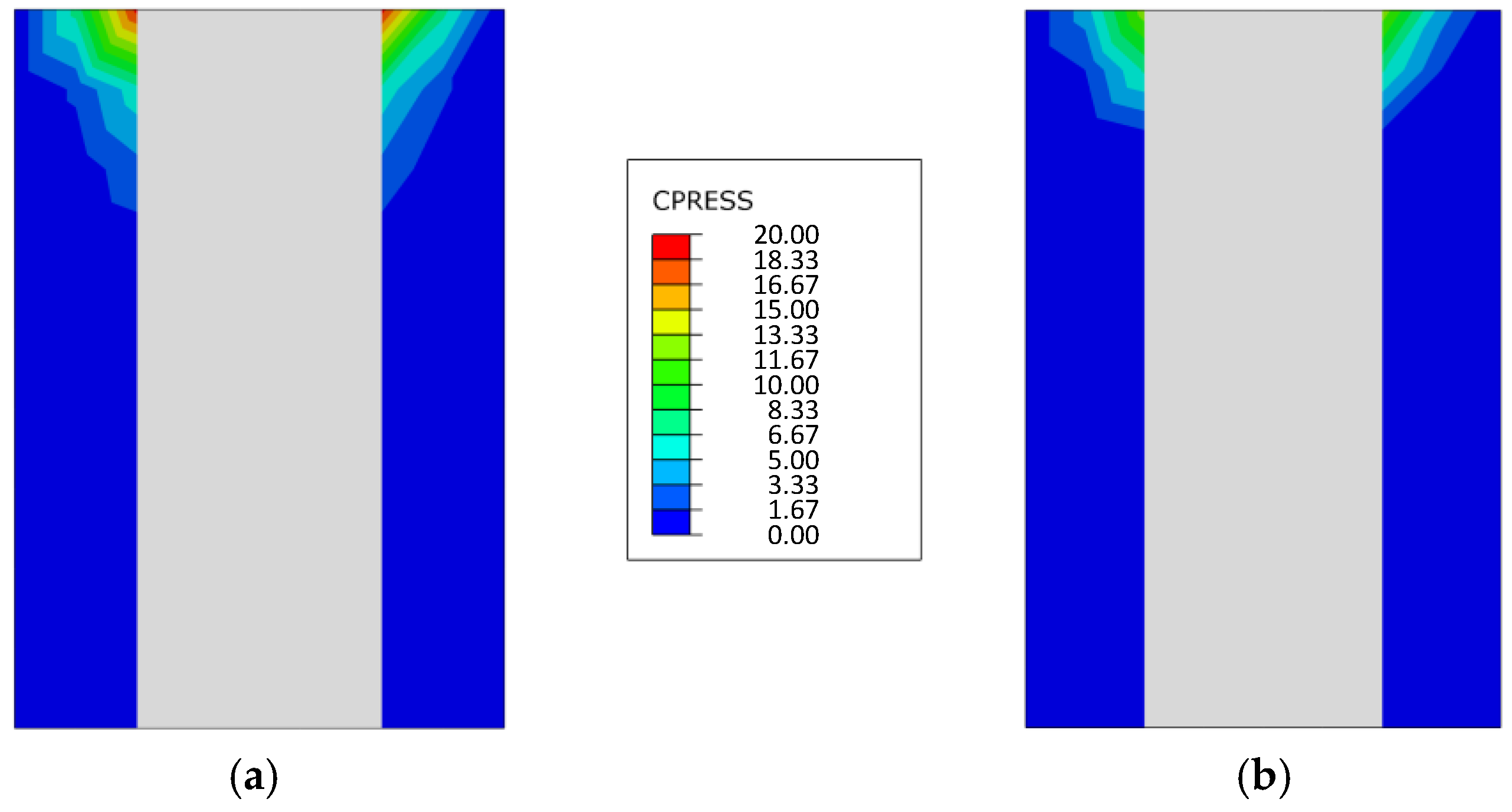
- The vertical compressive stress at the contact surface of the mortise-tenon joint is a reasonable variable that can represent the reaction force of the whole model. Larger value of this stress corresponds to more demand for the lateral loadings exerted on the columns.
- (2).
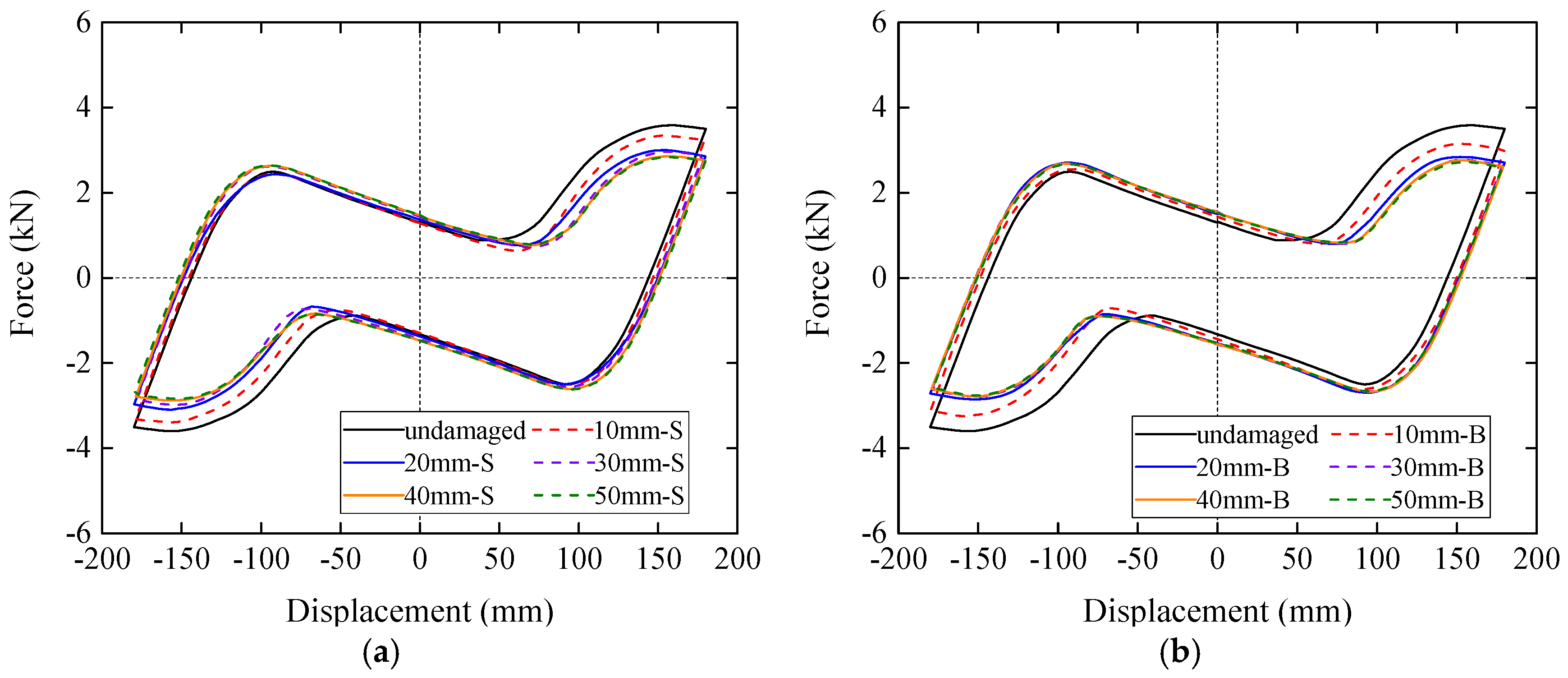
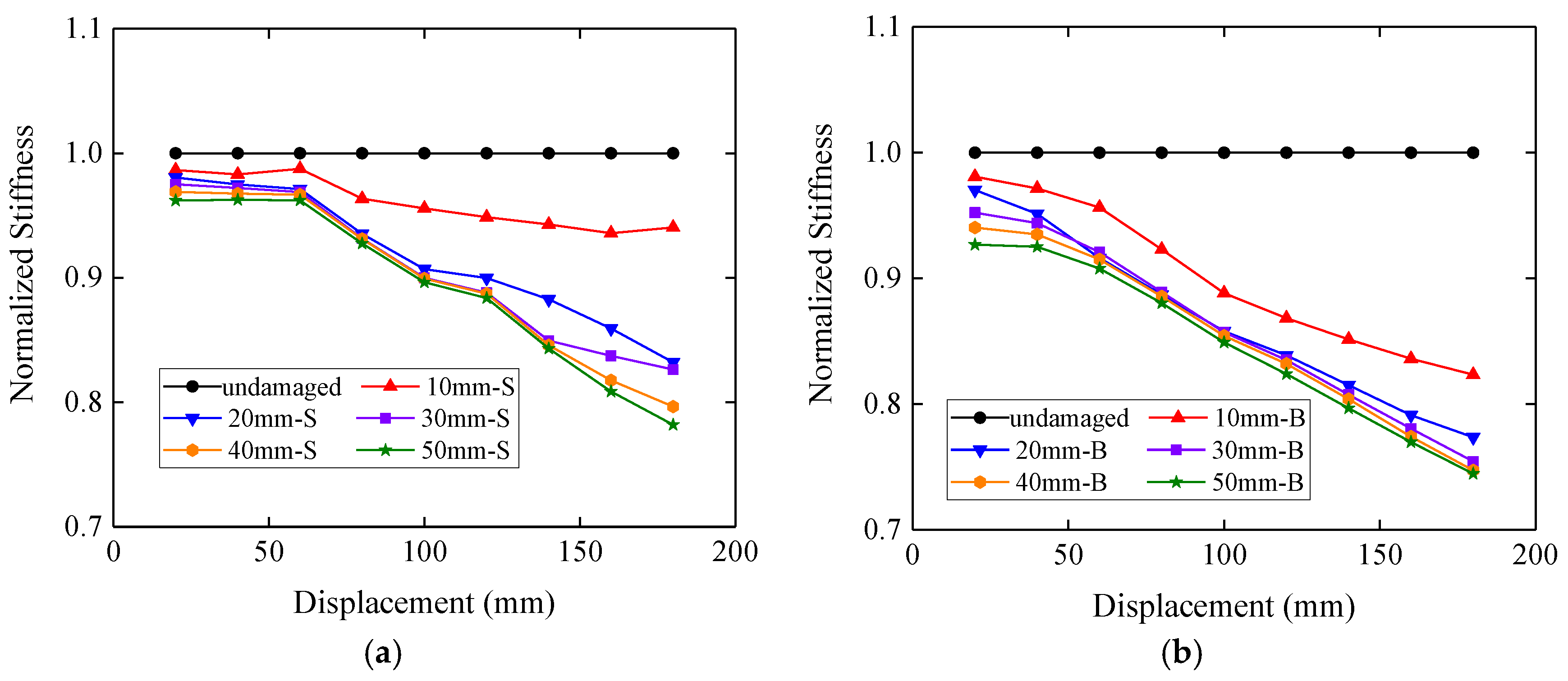
- The gap between the mortise and the tenon can reduce the stiffness of the timber frame because of the lack of contact between the external surface of the column and the vertical surface of the beam, while the dissipated energy remains almost unchanged. When the gap reaches a certain value, 20 mm in this study, the stiffness will become stable.
- (3).
- The damage in the top of the tenon can lead to the reduction in the maximum force and stiffness of the model followed by a sudden increase when some lateral displacement is reached. This certain lateral displacement can be derived from both the stiffness curves and the vertical compressive stresses at the contact surfaces.
- (4).
- Damage in the end of the tenon has two types of influences on the stiffness and dissipated energy of the model according to the length of the cutoff part. When the length is small, the stiffness and dissipated energy decrease slowly with the increase of the length. When this length is larger than 100 mm in this study, the stiffness and dissipated energy will decrease dramatically.
Author Contributions
Funding
Conflicts of Interest
References
- Fang, D.P.; Iwasaki, S.; Yu, M.H.; Shen, Q.P.; Miyamoto, Y.; Hikosaka, H. Ancient Chinese timber architecture. I: Experimental study. J. Struct. Eng. 2001, 127, 1348–1357. [Google Scholar] [CrossRef]
- Feio, A.O.; Lourenco, P.B.; Machado, J.S. Testing and modeling of a traditional timber mortise and tenon joint. Mater. Struct. 2014, 47, 213–225. [Google Scholar] [CrossRef]
- Xue, J.Y.; Xu, D.; Ren, G.Q.; Fu, C.W.; Yang, S.M. Earthquake simulation shaking table test of column-and-tie wooden structure dwellings. J. Build. Struct. 2019, 40, 123–132. (In Chinese) [Google Scholar]
- Xue, J.Y.; Wu, Z.J.; Zhang, F.L.; Zhao, H.T. Seismic damage evaluation model of Chinese ancient timber buildings. Adv. Struct. Eng. 2015, 18, 1671–1683. [Google Scholar] [CrossRef]
- Shi, X.W.; Chen, Y.F.; Chen, J.Y.; Yang, Q.S.; Li, T.Y. Experimental assessment on the hysteretic behavior of a full-scale traditional Chinese timber structure using a synchronous loading technique. Adv. Mater. Sci. Eng. 2018, 5729198. [Google Scholar] [CrossRef]
- Xie, Q.F.; Zhang, L.P.; Wang, L.; Zhou, W.J.; Zhou, T.G. Lateral performance of traditional Chinese timber frames: Experiments and analytical model. Eng. Struct. 2019, 186, 446–455. [Google Scholar] [CrossRef]
- Chun, Q.; Yue, Z.; Pan, J.W. Experimental study on seismic characteristics of typical mortise-tenon joints of Chinese southern traditional timber frame buildings. Sci. Chin. Technol. Sci. 2011, 54, 2404–2411. [Google Scholar] [CrossRef]
- Li, X.W.; Zhao, J.H.; Ma, G.W.; Chen, W. Experimental study on the seismic performance of a double-span traditional timber frame. Eng. Struct. 2015, 98, 141–150. [Google Scholar] [CrossRef]
- Li, X.W.; Zhao, J.H.; Ma, G.W.; Huang, S.H. Experimental study on the traditional timber mortise-tenon joints. Adv. Struct. Eng. 2015, 18, 2089–2102. [Google Scholar] [CrossRef]
- Seo, J.M.; Choi, I.K.; Lee, J.R. Static and cyclic behavior of wooden frames with tenon joints under lateral load. J. Struct. Eng. 1999, 125, 344–349. [Google Scholar] [CrossRef]
- Meng, X.J.; Li, T.Y.; Yang, Q.S. Experimental study on the seismic mechanism of a full-scale traditional Chinese timber structure. Eng. Struct. 2019, 180, 484–493. [Google Scholar] [CrossRef]
- Zhang, W.Z. The seismic and lateral resistance of column-and-tie wooden buildings based on mortise-tenon joint. Int. Wood Product J. 2019, 10, 86–91. [Google Scholar] [CrossRef]
- Jiang, S.F.; Wu, M.H.; Tang, W.J.; Liu, X.M. Multi-scale modeling method and seismic behavior analysis for ancient timber structures. J. Build. Struct. 2016, 37, 44–53. (In Chinese) [Google Scholar]
- Xiong, H.Y.; Tan, Z.R.; Zhang, R.H.; Zong, Z.J.; Luo, Z.P. Numerical calculation model performance analysis for aluminum alloy mortise-and-tenon structural joints used in electric vehicles. Compos. Part B Eng. 2019, 161, 77–86. [Google Scholar] [CrossRef]
- Sun, B.T.; Zhang, H.Y.; Yan, P.L. Earthquake damage and feature analysis of Chinese traditional timber frame structures subjected to the Lushan 7.0 earthquake. China Civ. Eng. J. 2014, 47, 1–11. [Google Scholar]
- Qu, Z.; Dutu, A.; Zhong, J.R.; Sun, J.J. Seismic damage to masonry-infilled timber houses in the 2013 M7.0 Lushan, China, earthquake. Earthq. Spectra 2015, 31, 1859–1874. [Google Scholar] [CrossRef]
- Xie, Q.F.; Wang, L.; Zheng, P.J.; Zhang, L.P.; Hu, W.B. Rotational behavior of degraded traditional mortise-tenon joints: Experimental tests and hysteretic model. Int. J. Archit. Herit. 2018, 12, 125–136. [Google Scholar] [CrossRef]
- King, W.S.; Yen, J.Y.R.; Yen, Y.N.A. Joint characteristics of traditional Chinese wooden frames. Eng. Struct. 1996, 18, 635–644. [Google Scholar] [CrossRef]
- Xue, J.Y.; Li, Y.Z.; Xia, H.L.; Sui, Y. Experimental study on seismic performance of dovetail joints with different loose degrees in ancient buildings. J. Build. Struct. 2016, 37, 73–79. (In Chinese) [Google Scholar]
- Xue, J.Y.; Guo, R.; Qi, L.J.; Xu, D. Experimental study on the seismic performance of traditional timber mortise-tenon joints with different looseness under low-cyclic reversed loading. Adv. Struct. Eng. 2019, 22, 1312–1328. [Google Scholar] [CrossRef]
- Li, S.C.; Jiang, Z.J.; Luo, H.Z.; Zhang, L. Seismic behavior of straight-tenon wood frames with column foot damage. Adv. Civ. Eng. 2019, 1–10. [Google Scholar] [CrossRef]
- Lin, M.Y. Experimental Research on Mechanical Property of Mortise-Tenon Joint of Chinese Ancient Timber Buildings. Master’s Thesis, Fuzhou University, Fuzhou, China, June 2014. (In Chinese). [Google Scholar]
- Li, J. Yingzaofashi; People’s Publishing House: Beijing, China, 2011. (In Chinese) [Google Scholar]
- Xie, Q.F.; Zhang, L.P.; Li, S.; Zhou, W.J.; Wang, L. Cyclic behavior of Chinese ancient wooden frame with mortise-tenon joints: Friction constitutive model and finite element modelling. J. Wood Sci. 2018, 64, 40–51. [Google Scholar] [CrossRef]















| E1/MPa | E2/MPa | E3/MPa | G12/MPa | G13/MPa | G23/MPa | υ12 | υ13 | υ23 |
|---|---|---|---|---|---|---|---|---|
| 4720 | 378 | 236 | 337 | 33.7 | 317 | 0.37 | 0.47 | 0.42 |
| Direction | 1 /MPa | 2 /MPa | 3 /MPa |
|---|---|---|---|
| 1 | 21 | 30 | 4.2 |
| 2 | 2.1 | 2.1 | 4.2 |
| 3 | 2.1 | 2.1 | 4.2 |
| Damage Length (mm) | 0 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ANS | Single | 1 | 0.997 | 0.988 | 0.959 | 0.911 | 0.840 | 0.756 | 0.667 | 0.584 | 0.507 |
| Both | 1 | 0.994 | 0.975 | 0.917 | 0.822 | 0.684 | 0.519 | 0.353 | 0.174 | 0.016 | |
| 2Single-1 1 | 1 | 0.994 | 0.976 | 0.917 | 0.823 | 0.680 | 0.512 | 0.334 | 0.167 | 0.014 | |
| Damage Length (mm) | 0 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ANDE | Single | 1 | 0.995 | 0.985 | 0.979 | 0.975 | 0.930 | 0.850 | 0.764 | 0.682 | 0.612 |
| Both | 1 | 0.991 | 0.975 | 0.960 | 0.946 | 0.866 | 0.714 | 0.549 | 0.406 | 0.268 | |
| 2Single-1 | 1 | 0.990 | 0.970 | 0.958 | 0.950 | 0.861 | 0.699 | 0.528 | 0.364 | 0.225 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sha, B.; Wang, H.; Li, A. The Influence of the Damage of Mortise-Tenon Joint on the Cyclic Performance of the Traditional Chinese Timber Frame. Appl. Sci. 2019, 9, 3429. https://doi.org/10.3390/app9163429
Sha B, Wang H, Li A. The Influence of the Damage of Mortise-Tenon Joint on the Cyclic Performance of the Traditional Chinese Timber Frame. Applied Sciences. 2019; 9(16):3429. https://doi.org/10.3390/app9163429
Chicago/Turabian StyleSha, Ben, Hao Wang, and Aiqun Li. 2019. "The Influence of the Damage of Mortise-Tenon Joint on the Cyclic Performance of the Traditional Chinese Timber Frame" Applied Sciences 9, no. 16: 3429. https://doi.org/10.3390/app9163429
APA StyleSha, B., Wang, H., & Li, A. (2019). The Influence of the Damage of Mortise-Tenon Joint on the Cyclic Performance of the Traditional Chinese Timber Frame. Applied Sciences, 9(16), 3429. https://doi.org/10.3390/app9163429






