Off-Resonance Control and All-Optical Switching: Expanded Dimensions in Nonlinear Optics
Abstract
1. Introduction
2. Conventional Nonlinear Optics
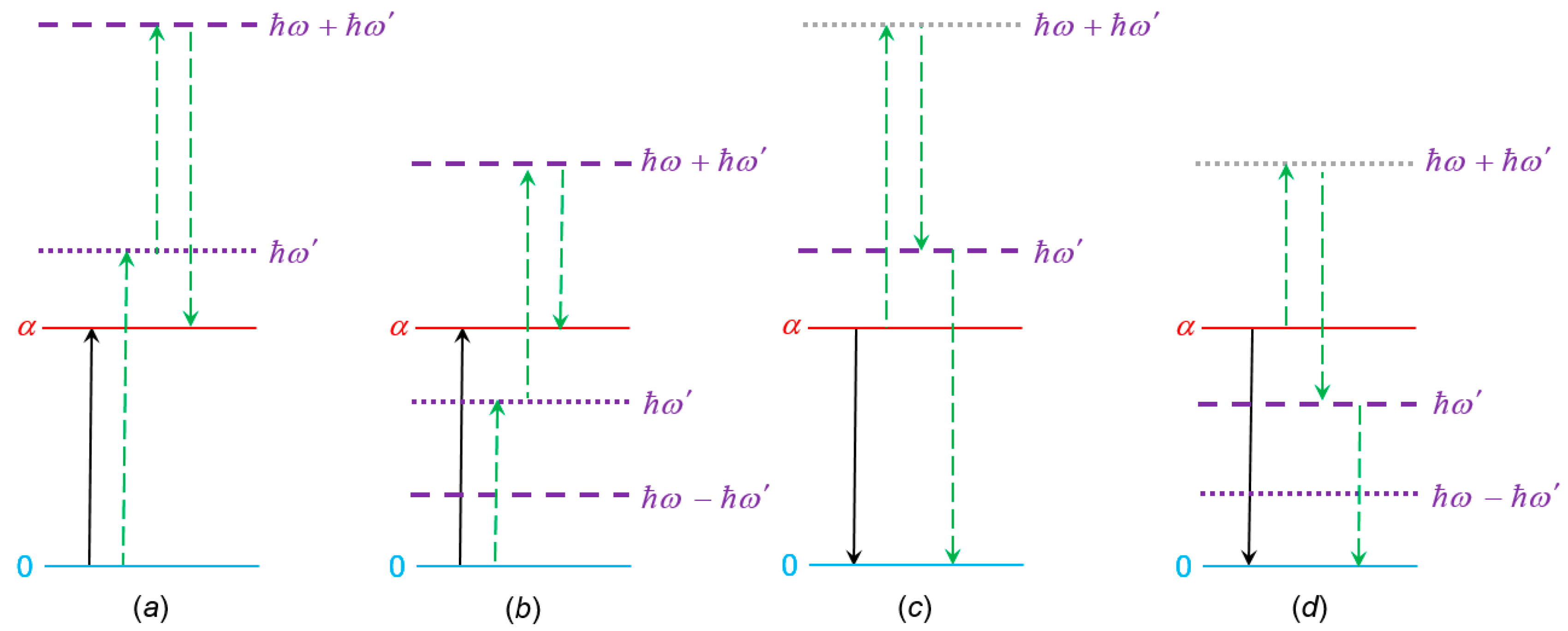
3. Laser-Modified Absorption
4. Laser-Modified Fluorescence
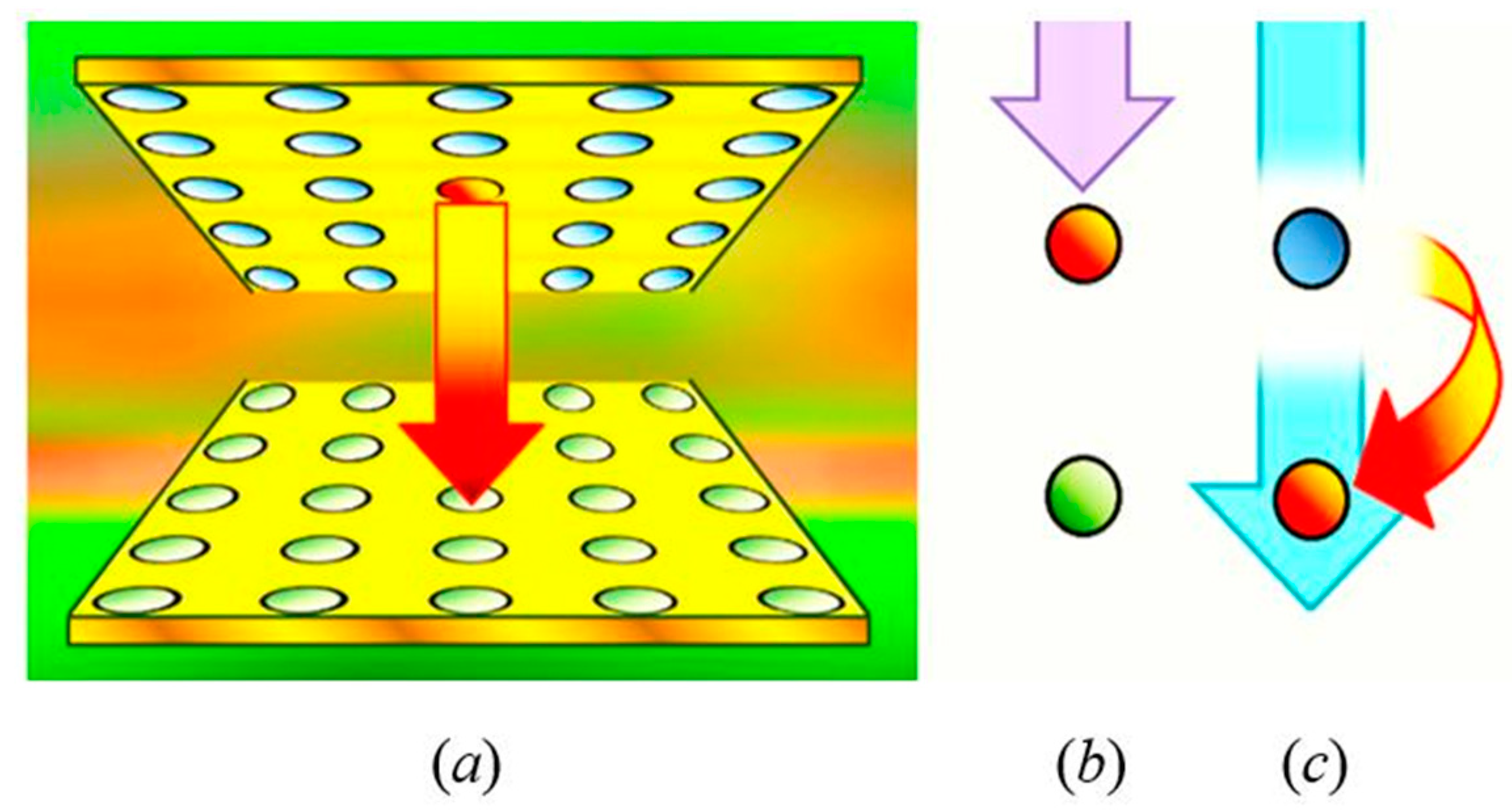
5. Optically Controlled Resonance Energy Transfer
6. All-Optical Switching
7. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bloembergen, N. Nonlinear Optics, 4th ed.; World Scientific: Singapore, 1996. [Google Scholar]
- Jha, S.S. Perspectives in Optoelectronics; World Scientific: Singapore, 1995. [Google Scholar]
- Sauter, E.G. Nonlinear Optics; Wiley: New York, NY, USA, 1996. [Google Scholar]
- He, G.; Liu, S.H. Physics of Nonlinear Optics; World Scientific: Singapore, 2000. [Google Scholar]
- Shen, Y.R. The Principles of Nonlinear Optics; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Sutherland, R.L. Handbook of Nonlinear Optics, 2nd ed.; Dekker: New York, NY, USA, 2003. [Google Scholar]
- Banerjee, P.P. Nonlinear Optics: Theory, Numerical Modeling, and Applications; Dekker: New York, NY, USA, 2003. [Google Scholar]
- Novotny, L.; Hecht, B. Principles of Nano-Optics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Boyd, R.W. Nonlinear Optics, 3rd ed.; Academic Press: New York, NY, USA, 2008. [Google Scholar]
- Lvovsky, A.I.; Mlynek, J. Quantum-optical catalysis: Generating nonclassical states of light by means of linear optics. Phys. Rev. Lett. 2002, 88, 250401. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.-Y.; Wu, J.-N.; Liao, Z.; Zubairy, M.S. Multiphoton catalysis with coherent state input: Nonclassicality and decoherence. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 175504. [Google Scholar] [CrossRef]
- Hu, L.; Liao, Z.; Zubairy, M.S. Continuous-variable entanglement via multiphoton catalysis. Phys. Rev. A 2017, 95, 012310. [Google Scholar] [CrossRef]
- Zhou, W.; Ye, W.; Liu, C.; Hu, L.; Liu, S. Entanglement improvement of entangled coherent state via multiphoton catalysis. Laser Phys. Lett. 2018, 15, 065203. [Google Scholar] [CrossRef]
- Ye, W.; Zhong, H.; Liao, Q.; Huang, D.; Hu, L.; Guo, Y. Improvement of self-referenced continuous-variable quantum key distribution with quantum photon catalysis. Opt. Express 2019, 27, 17186–17198. [Google Scholar] [CrossRef] [PubMed]
- Hilsabeck, K.I.; Meiser, J.L.; Sneha, M.; Harrison, J.A.; Zare, R.N. Nonresonant photons catalyze photodissociation of phenol. J. Am. Chem. Soc. 2019, 141, 1067–1073. [Google Scholar] [CrossRef] [PubMed]
- Cushing, S.K.; Li, J.; Meng, F.; Senty, T.R.; Suri, S.; Zhi, M.; Li, M.; Bristow, A.D.; Wu, N. Photocatalytic activity enhanced by plasmonic resonant energy transfer from metal to semiconductor. J. Am. Chem. Soc. 2012, 134, 15033–15041. [Google Scholar] [CrossRef] [PubMed]
- Gonzaga-Galeana, J.A.; Zurita-Sánchez, J.R. A revisitation of the Förster energy transfer near a metallic spherical nanoparticle: (1) Efficiency enhancement or reduction? (2) The control of the Förster radius of the unbounded medium. (3) The impact of the local density of states. J. Chem. Phys. 2013, 139, 244302. [Google Scholar] [CrossRef] [PubMed]
- Schleifenbaum, F.; Kern, A.M.; Konrad, A.; Meixner, A.J. Dynamic control of Förster energy transfer in a photonic environment. Phys. Chem. Chem. Phys. 2014, 16, 12812–12817. [Google Scholar] [CrossRef]
- Li, J.; Cushing, S.K.; Meng, F.; Senty, T.R.; Bristow, A.D.; Wu, N. Plasmon-induced resonance energy transfer for solar energy conversion. Nat. Photonics 2015, 9, 601. [Google Scholar] [CrossRef]
- Ghenuche, P.; Mivelle, M.; de Torres, J.; Moparthi, S.B.; Rigneault, H.; Van Hulst, N.F.; García-Parajó, M.F.; Wenger, J. Matching nanoantenna field confinement to FRET distances enhances Förster energy transfer rates. Nano Lett. 2015, 15, 6193–6201. [Google Scholar] [CrossRef] [PubMed]
- Konrad, A.; Metzger, M.; Kern, A.M.; Brecht, M.; Meixner, A.J. Controlling the dynamics of Förster resonance energy transfer inside a tunable sub-wavelength Fabry–Pérot-resonator. Nanoscale 2015, 7, 10204–10209. [Google Scholar] [CrossRef] [PubMed]
- Tumkur, T.U.; Kitur, J.K.; Bonner, C.E.; Poddubny, A.N.; Narimanov, E.E.; Noginov, M.A. Control of Förster energy transfer in the vicinity of metallic surfaces and hyperbolic metamaterials. Faraday Discuss. 2015, 178, 395–412. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bidault, S.; Devilez, A.; Ghenuche, P.; Stout, B.; Bonod, N.; Wenger, J. Competition between Förster resonance energy transfer and donor photodynamics in plasmonic dimer nanoantennas. ACS Photonics 2016, 3, 895–903. [Google Scholar] [CrossRef]
- de Torres, J.; Ferrand, P.; Colas des Francs, G.; Wenger, J. Coupling emitters and silver nanowires to achieve long-range plasmon-mediated fluorescence energy transfer. ACS Nano 2016, 10, 3968–3976. [Google Scholar] [CrossRef]
- Poudel, A.; Chen, X.; Ratner, M.A. Enhancement of resonant energy transfer due to an evanescent wave from the metal. J. Phys. Chem. Lett. 2016, 7, 955–960. [Google Scholar] [CrossRef]
- Marocico, C.A.; Zhang, X.; Bradley, A.L. A theoretical investigation of the influence of gold nanosphere size on the decay and energy transfer rates and efficiencies of quantum emitters. J. Chem. Phys. 2016, 144, 024108. [Google Scholar] [CrossRef]
- Wubs, M.; Vos, W.L. Förster resonance energy transfer rate in any dielectric nanophotonic medium with weak dispersion. New J. Phys. 2016, 18, 053037. [Google Scholar] [CrossRef]
- Higgins, L.J.; Marocico, C.A.; Karanikolas, V.D.; Bell, A.P.; Gough, J.J.; Murphy, G.P.; Parbrook, P.J.; Bradley, A.L. Influence of plasmonic array geometry on energy transfer from a quantum well to a quantum dot layer. Nanoscale 2016, 8, 18170–18179. [Google Scholar] [CrossRef]
- Bujak, Ł.; Ishii, T.; Sharma, D.K.; Hirata, S.; Vacha, M. Selective turn-on and modulation of resonant energy transfer in single plasmonic hybrid nanostructures. Nanoscale 2017, 9, 1511–1519. [Google Scholar] [CrossRef]
- Murphy, G.P.; Gough, J.J.; Higgins, L.J.; Karanikolas, V.D.; Wilson, K.M.; Garcia Coindreau, J.A.; Zubialevich, V.Z.; Parbrook, P.J.; Bradley, A.L. Ag colloids and arrays for plasmonic non-radiative energy transfer from quantum dots to a quantum well. Nanotechnology 2017, 28, 115401. [Google Scholar] [CrossRef] [PubMed]
- Steele, J.M.; Ramnarace, C.M.; Farner, W.R. Controlling FRET enhancement using plasmon modes on gold nanogratings. J. Phys. Chem. C 2017, 121, 22353–22360. [Google Scholar] [CrossRef]
- Akulov, K.; Bochman, D.; Golombek, A.; Schwartz, T. Long-distance resonant energy transfer mediated by hybrid plasmonic-photonic modes. J. Phys. Chem. C 2018, 122, 15853–15860. [Google Scholar] [CrossRef]
- Asgar, H.; Jacob, L.; Hoang, T.B. Fast spontaneous emission and high Förster resonance energy transfer rate in hybrid organic/inorganic plasmonic nanostructures. J. Appl. Phys. 2018, 124, 103105. [Google Scholar] [CrossRef]
- Eldabagh, N.; Micek, M.; DePrince, A.E.; Foley, J.J. Resonance energy transfer mediated by metal-dielectric composite nanostructures. J. Phys. Chem. C 2018, 122, 18256–18265. [Google Scholar] [CrossRef]
- Glaeske, M.; Juergensen, S.; Gabrielli, L.; Menna, E.; Mancin, F.; Gatti, T.; Setaro, A. PhysicaPlasmon-assisted energy transfer in hybrid nanosystems. Phys. Status Solidi Rapid Res. Lett. 2018, 12, 1800508. [Google Scholar] [CrossRef]
- Roth, D.J.; Nasir, M.E.; Ginzburg, P.; Wang, P.; Le Marois, A.; Suhling, K.; Richards, D.; Zayats, A.V. Förster resonance energy transfer inside hyperbolic metamaterials. ACS Photonics 2018, 5, 4594–4603. [Google Scholar] [CrossRef]
- Wu, J.-S.; Lin, Y.-C.; Sheu, Y.-L.; Hsu, L.-Y. Characteristic distance of resonance energy transfer coupled with surface plasmon polaritons. J. Phys. Chem. Lett. 2018, 9, 7032–7039. [Google Scholar] [CrossRef]
- Zurita-Sánchez, J.R.; Méndez-Villanueva, J. Förster energy transfer in the vicinity of two metallic nanospheres (dimer). Plasmonics 2018, 13, 873–883. [Google Scholar] [CrossRef]
- Olivo, J.; Zapata-Rodríguez, C.J.; Cuevas, M. Spatial modulation of the electromagnetic energy transfer by excitation of graphene waveguide surface plasmons. J. Opt. 2019, 21, 045002. [Google Scholar] [CrossRef]
- Bohlen, J.; Cuartero-González, Á.; Pibiri, E.; Ruhlandt, D.; Fernández-Domínguez, A.I.; Tinnefeld, P.; Acuna, G.P. Plasmon-assisted Förster resonance energy transfer at the single-molecule level in the moderate quenching regime. Nanoscale 2019, 11, 7674–7681. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, H.; Zhu, W.; He, F.; Huang, Y.; Chong, R.; Kou, D.; Zhang, W.; Meng, X.; Fang, X. Plasmon-mediated nonradiative energy transfer from a conjugated polymer to a plane of graphene-nanodot-supported silver nanoparticles: An insight into characteristic distance. Nanoscale 2019, 11, 6737–6746. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Glesk, I.; Chen, L.R. An integrated nonlinear optical loop mirror in silicon photonics for all-optical signal processing. APL Photon. 2018, 3, 026102. [Google Scholar] [CrossRef]
- Craig, D.P.; Thirunamachandran, T. Molecular Quantum Electrodynamics: An Introduction to Radiation-Molecule Interactions; Dover Publications: Mineola, NY, USA, 1998. [Google Scholar]
- Salam, A. Molecular Quantum Electrodynamics. Long-Range Intermolecular Interactions; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Grynberg, G.; Aspect, A.; Fabre, C. Introduction to Quantum Optics: From the Semi-Classical Approach to Quantized Light; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Andrews, D.L.; Allcock, P. Optical Harmonics in Molecular Systems; Wiley-VCH: Weinheim, Germany, 2002. [Google Scholar]
- Andrews, D.L.; Bradshaw, D.S. Introduction to Photon Science and Technology; SPIE Press: Bellingham, WA, USA, 2018. [Google Scholar]
- Andrews, D.L.; Jones, G.A.; Salam, A.; Woolley, R.G. Quantum Hamiltonians for optical interactions. J. Chem. Phys. 2018, 148, 040901. [Google Scholar] [CrossRef] [PubMed]
- Atkins, P.W.; Friedman, R.S. Molecular Quantum Mechanics; Oxford University Press: Oxford, 2011. [Google Scholar]
- Andrews, D.L.; Bradshaw, D.S.; Forbes, K.A.; Salam, A. A guide to quantum and semiclassical electrodynamics in modern optics. J. Opt. Soc. Am. B submitted 2019.
- Hollas, J.M. Modern Spectroscopy; Wiley: Chichester, UK, 2004. [Google Scholar]
- Bradshaw, D.S.; Andrews, D.L. Laser-modified one- and two-photon absorption: Expanding the scope of optical nonlinearity. Phys. Rev. A 2013, 88, 033807. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. Optically controlled resonance energy transfer: Mechanism and configuration for all-optical switching. J. Chem. Phys. 2008, 128, 144506. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. All-optical control of molecular fluorescence. Phys. Rev. A 2010, 81, 013424. [Google Scholar] [CrossRef]
- Andrews, D.L.; Bradshaw, D.S. Optically tailored access to metastable electronic states. Chem. Phys. Lett. 2013, 590, 235–238. [Google Scholar] [CrossRef][Green Version]
- Bradshaw, D.S.; Andrews, D.L. Mechanism for optical enhancement and suppression of fluorescence. J. Phys. Chem. A 2009, 113, 6537–6539. [Google Scholar] [CrossRef]
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy, 2nd ed.; Kluwer Academic: New York, NY, USA, 1999. [Google Scholar]
- Valeur, B.; Berberan-Santos, M.N. Molecular Fluorescence: Principles and Applications, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2013. [Google Scholar]
- Bradshaw, D.S.; Andrews, D.L. The control of near-field optics: Imposing direction through coupling with off-resonant laser light. Appl. Phys. B 2008, 93, 13–20. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. Laser conferral of a directed character to near-field energy transfer. Laser Phys. 2009, 19, 125–128. [Google Scholar] [CrossRef]
- Curto, A.G.; Volpe, G.; Taminiau, T.H.; Kreuzer, M.P.; Quidant, R.; van Hulst, N.F. Unidirectional emission of a quantum dot coupled to a nanoantenna. Science 2010, 329, 930–933. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Mueller, J.P.B.; Wang, Q.; Yuan, G.; Antoniou, N.; Yuan, X.-C.; Capasso, F. Polarization-controlled tnable directional coupling of surface plasmon polaritons. Science 2013, 340, 331–334. [Google Scholar] [CrossRef] [PubMed]
- Laux, F.; Bonod, N.; Gérard, D. Single emitter fluorescence enhancement with surface lattice resonances. J. Phys. Chem. C 2017, 121, 13280–13289. [Google Scholar] [CrossRef]
- Sun, Y.-Z.; Feng, L.-S.; Bachelot, R.; Blaize, S.; Ding, W. Full control of far-field radiation via photonic integrated circuits decorated with plasmonic nanoantennas. Opt. Express 2017, 25, 17417–17430. [Google Scholar] [CrossRef] [PubMed]
- van der Meer, B.W.; Coker, G.; Chen, S.Y.S. Resonance Energy Transfer: Theory and Data; VCH: New York, NY, USA, 1994. [Google Scholar]
- Andrews, D.L.; Demidov, A.A. Resonance Energy Transfer; Wiley: Chichester, UK, 1999. [Google Scholar]
- May, V. Charge and Energy Transfer Dynamics in Molecular Systems; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Medintz, I.; Hildebrandt, N. Förster Resonance Energy Transfer: From Theory to Applications; Wiley-VCH: Weinheim, Germany, 2013. [Google Scholar]
- Salam, A. The unified theory of resonance energy transfer according to molecular quantum electrodynamics. Atoms 2018, 6, 56. [Google Scholar] [CrossRef]
- Jones, G.A.; Bradshaw, D.S. Resonance energy transfer: From fundamental theory to recent applications. Front. Phys. 2019, 7, 100. [Google Scholar] [CrossRef]
- Andrews, D.L.; Bradshaw, D.S. The role of virtual photons in nanoscale photonics. Ann. Phys. 2014, 526, 173–186. [Google Scholar] [CrossRef]
- Allcock, P.; Jenkins, R.D.; Andrews, D.L. Laser assisted resonance energy transfer. Chem. Phys. Lett. 1999, 301, 228–234. [Google Scholar] [CrossRef][Green Version]
- Allcock, P.; Jenkins, R.D.; Andrews, D.L. Laser-assisted resonance-energy transfer. Phys. Rev. A 2000, 61, 023812. [Google Scholar] [CrossRef]
- Thirunamachandran, T. Intermolecular interactions in the presence of an intense radiation field. Mol. Phys. 1980, 40, 393–399. [Google Scholar] [CrossRef]
- Burns, M.M.; Fournier, J.-M.; Golovchenko, J.A. Optical binding. Phys. Rev. Lett. 1989, 63, 1233–1236. [Google Scholar] [CrossRef] [PubMed]
- Burns, M.M.; Fournier, J.-M.; Golovchenko, J.A. Optical matter: Crystallization and binding in intense optical fields. Science 1990, 249, 749–754. [Google Scholar] [CrossRef] [PubMed]
- Milonni, P.W.; Shih, M.L. Source theory of the Casimir force. Phys. Rev. A 1992, 45, 4241–4253. [Google Scholar] [CrossRef]
- Dapasse, F.; Vigoureux, J.M. Optical binding force between two Rayleigh particles. J. Phys. D Appl. Phys. 1994, 27, 914–919. [Google Scholar] [CrossRef]
- Milonni, P.W.; Smith, A. van der Waals dispersion forces in electromagnetic fields. Phys. Rev. A 1996, 53, 3484–3489. [Google Scholar] [CrossRef]
- Chaumet, P.C.; Nieto-Vesperinas, M. Optical binding of particles with or without the presence of a flat dielectric surface. Phys. Rev. B 2001, 64, 035422. [Google Scholar] [CrossRef]
- Nieto-Vesperinas, M.; Chaumet, P.C.; Rahmani, A. Near-field photonic forces. Philos. Trans. R. Soc. A 2004, 362, 719–737. [Google Scholar] [CrossRef]
- Mohanty, S.K.; Andrews, J.T.; Gupta, P.K. Optical binding between dielectric particles. Opt. Express 2004, 12, 2746–2753. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. Optically induced forces and torques: Interactions between nanoparticles in a laser beam. Phys. Rev. A 2005, 72, 033816. [Google Scholar] [CrossRef]
- Dholakia, K.; Zemanek, P. Gripped by light: Optical binding. Rev. Mod. Phys. 2010, 82, 1767–1791. [Google Scholar] [CrossRef]
- Bowman, R.W.; Padgett, M.J. Optical trapping and binding. Rep. Prog. Phys. 2013, 76, 026401. [Google Scholar] [CrossRef] [PubMed]
- Casimir, H.B.G.; Polder, D. The influence of retardation on the London-van der Waals forces. Phys. Rev. 1948, 73, 360–372. [Google Scholar] [CrossRef]
- Buhmann, S.Y.; Knöll, L.; Welsch, D.-G.; Dung, H.T. Casimir-Polder forces: A nonperturbative approach. Phys. Rev. A 2004, 70, 052117. [Google Scholar] [CrossRef]
- Przybytek, M.; Jeziorski, B.; Cencek, W.; Komasa, J.; Mehl, J.B.; Szalewicz, K. Onset of Casimir-Polder retardation in a long-range molecular quantum state. Phys. Rev. Lett. 2012, 108, 183201. [Google Scholar] [CrossRef] [PubMed]
- Salam, A. Non-Relativistic QED Theory of the van der Waals Dispersion Interaction; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Passante, R. Dispersion interactions between neutral atoms and the quantum electrodynamical vacuum. Symmetry 2018, 10, 735. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. Interparticle interactions: Energy potentials, energy transfer, and nanoscale mechanical motion in response to optical radiation. J. Phys. Chem. A 2013, 117, 75–82. [Google Scholar] [CrossRef]
- Forbes, K.A.; Bradshaw, D.S.; Andrews, D.L. Off-resonance nanophotonics: From optical binding and induced self-assembly to all-optical switching. Nanophoton 2019. submitted. [Google Scholar]
- Scholes, G.D.; Andrews, D.L. Damping and higher multipole effects in the quantum electrodynamical model for electronic energy transfer in the condensed phase. J. Chem. Phys. 1997, 107, 5374–5384. [Google Scholar] [CrossRef]
- Andrews, D.L.; Rodríguez, J. Resonance energy transfer: Spectral overlap, efficiency, and direction. J. Chem. Phys. 2007, 127, 084509. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. All-optical switching between quantum dot nanoarrays. Superlatt. Microstruct. 2010, 47, 308–313. [Google Scholar] [CrossRef]
- Andrews, D.L.; Bradshaw, D.S. Off-resonant activation of optical emission. Opt. Commun. 2010, 283, 4365–4367. [Google Scholar] [CrossRef]
- Taghinejad, M.; Cai, W. All-optical control of light in micro- and nanophotonics. ACS Photonics 2019, 6, 1082–1093. [Google Scholar] [CrossRef]
- Bajcsy, M.; Hofferberth, S.; Balic, V.; Peyronel, T.; Hafezi, M.; Zibrov, A.S.; Vuletic, V.; Lukin, M.D. Efficient all-optical switching using slow light within a hollow fiber. Phys. Rev. Lett. 2009, 102, 203902. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.-J.; Chen, Y.-H.; Wang, I.C.; Yu, I.A. EIT-based all-optical switching and cross-phase modulation under the influence of four-wave mixing. Opt. Express 2012, 20, 11057–11063. [Google Scholar] [CrossRef] [PubMed]
- Clader, B.D.; Hendrickson, S.M.; Camacho, R.M.; Jacobs, B.C. All-optical microdisk switch using EIT. Opt. Express 2013, 21, 6169–6179. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kumar, S.; Singh, L. Proposed new approach to design all optical AND gate using plasmonic based Mach-Zehnder interferometer for high speed communication. Proc. SPIE 2016, 9884, 98842D. [Google Scholar]
- Wang, B.; Xiong, L.; Zeng, Q.; Chen, Z.; Lv, H.; Ding, Y.; Du, J.; Yu, H. All-optical Mach–Zehnder interferometer switching based on the phase-shift multiplication effect of an analog on the electromagnetically induced transparency effect. Opt. Eng. 2016, 55, 067104. [Google Scholar] [CrossRef]
- Piccione, B.; Cho, C.-H.; van Vugt, L.K.; Agarwal, R. All-optical active switching in individual semiconductor nanowires. Nat. Nanotechnol. 2012, 7, 640. [Google Scholar] [CrossRef]
- Bajcsy, M.; Majumdar, A.; Englund, D.; Vučković, J. Ultra-low power all-optical switching with a single quantum dot in a photonic-crystal cavity. Proc. SPIE 2013, 8635, 863516. [Google Scholar]
- Born, B.; Geoffroy-Gagnon, S.; Krupa, J.D.A.; Hristovski, I.R.; Collier, C.M.; Holzman, J.F. Ultrafast all-optical switching via subdiffractional photonic nanojets and select semiconductor nanoparticles. ACS Photonics 2016, 3, 1095–1101. [Google Scholar] [CrossRef]
- Lu, H.; Liu, X.; Wang, L.; Gong, Y.; Mao, D. Ultrafast all-optical switching in nanoplasmonic waveguide with Kerr nonlinear resonator. Opt. Express 2011, 19, 2910–2915. [Google Scholar] [CrossRef] [PubMed]
- Foroutan, S.; Rostami, G.; Dolatyari, M.; Rostami, A. All-optical switching in metal nanoparticles plasmonic waveguide using EIT phenomenon. Optik 2017, 132, 291–298. [Google Scholar] [CrossRef]
- Neira, A.D.; Wurtz, G.A.; Zayats, A.V. All-optical switching in silicon photonic waveguides with an epsilon-near-zero resonant cavity. Photon. Res. 2018, 6, B1–B5. [Google Scholar] [CrossRef]
- Nurmohammadi, T.; Abbasian, K.; Yadipour, R. Ultra-fast all-optical plasmon induced transparency in a metal-insulator-metal waveguide containing two Kerr nonlinear ring resonators. J. Opt. 2018, 20, 055504. [Google Scholar] [CrossRef]
- Kabakova, I.V.; Corcoran, B.; Bolger, J.A.; de Sterke, C.M.; Eggleton, B.J. All-optical self-switching in optimized phase-shifted fiber Bragg grating. Opt. Express 2009, 17, 5083–5088. [Google Scholar] [CrossRef]
- Zang, Z.; Yang, W. The optical performance of all-optical switching based on fiber Bragg grating. Proc. SPIE 2011, 8040, 80400E. [Google Scholar]
- Scholtz, Ľ.; Solanská, M.; Ladányi, L.; Müllerová, J. Power requirements reducing of FBG based all-optical switching. Proc. SPIE 2017, 10603, 1060310. [Google Scholar]
- Nozaki, K.; Tanabe, T.; Shinya, A.; Matsuo, S.; Sato, T.; Taniyama, H.; Notomi, M. Sub-femtojoule all-optical switching using a photonic-crystal nanocavity. Nat. Photonics 2010, 4, 477. [Google Scholar] [CrossRef]
- Ghadrdan, M.; Mansouri-Birjandi, M.A. Low-threshold photonic crystal all-optical switch using plasmonic nanowires placed in nonlinear resonator structure. J. Nanophoton. 2017, 11, 036017. [Google Scholar] [CrossRef]
- Dawes, A.M.C.; Illing, L.; Clark, S.M.; Gauthier, D.J. All-optical switching in rubidium vapor. Science 2005, 308, 672–674. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, S.-T.; Zhao, Y. All-optical switching characteristics in bacteriorhodopsin and its applications in integrated optics. Opt. Express 2004, 12, 895–906. [Google Scholar] [CrossRef] [PubMed]
- Roy, S.; Sharma, P.; Dharmadhikari, A.K.; Mathur, D. All-optical switching with bacteriorhodopsin. Opt. Commun. 2004, 237, 251–256. [Google Scholar] [CrossRef][Green Version]
- Wada, O. Femtosecond all-optical devices for ultrafast communication and signal processing. New J. Phys. 2004, 6, 183. [Google Scholar] [CrossRef]
- Chai, Z.; Hu, X.; Wang, F.; Niu, X.; Xie, J.; Gong, Q. Ultrafast all-optical switching. Adv. Opt. Mater. 2017, 5, 1600665. [Google Scholar] [CrossRef]
- Georgiou, K.; Michetti, P.; Gai, L.; Cavazzini, M.; Shen, Z.; Lidzey, D.G. Control over energy transfer between fluorescent BODIPY dyes in a strongly coupled microcavity. ACS Photonics 2018, 5, 258–266. [Google Scholar] [CrossRef]
- Li, R.; Petit, L.; Franke, D.P.; Dehollain, J.P.; Helsen, J.; Steudtner, M.; Thomas, N.K.; Yoscovits, Z.R.; Singh, K.J.; Wehner, S.; et al. A crossbar network for silicon quantum dot qubits. Sci. Adv. 2018, 4, eaar3960. [Google Scholar] [CrossRef]
- Paul, N.; Metwalli, E.; Yao, Y.; Schwartzkopf, M.; Yu, S.; Roth, S.V.; Müller-Buschbaum, P.; Paul, A. Templating growth of gold nanostructures with a CdSe quantum dot array. Nanoscale 2015, 7, 9703–9714. [Google Scholar] [CrossRef]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bradshaw, D.S.; Forbes, K.A.; Andrews, D.L. Off-Resonance Control and All-Optical Switching: Expanded Dimensions in Nonlinear Optics. Appl. Sci. 2019, 9, 4252. https://doi.org/10.3390/app9204252
Bradshaw DS, Forbes KA, Andrews DL. Off-Resonance Control and All-Optical Switching: Expanded Dimensions in Nonlinear Optics. Applied Sciences. 2019; 9(20):4252. https://doi.org/10.3390/app9204252
Chicago/Turabian StyleBradshaw, David S., Kayn A. Forbes, and David L. Andrews. 2019. "Off-Resonance Control and All-Optical Switching: Expanded Dimensions in Nonlinear Optics" Applied Sciences 9, no. 20: 4252. https://doi.org/10.3390/app9204252
APA StyleBradshaw, D. S., Forbes, K. A., & Andrews, D. L. (2019). Off-Resonance Control and All-Optical Switching: Expanded Dimensions in Nonlinear Optics. Applied Sciences, 9(20), 4252. https://doi.org/10.3390/app9204252