Extension of an FFT-Based Beam Propagation Method to Plasmonic and Dielectric Waveguide Discontinuities and Junctions
Abstract
:1. Introduction
2. Reconsideration of TM Fields Difficulties:
3. Reconsideration of Reflected and Transmitted Fields:
4. Numerical Results:
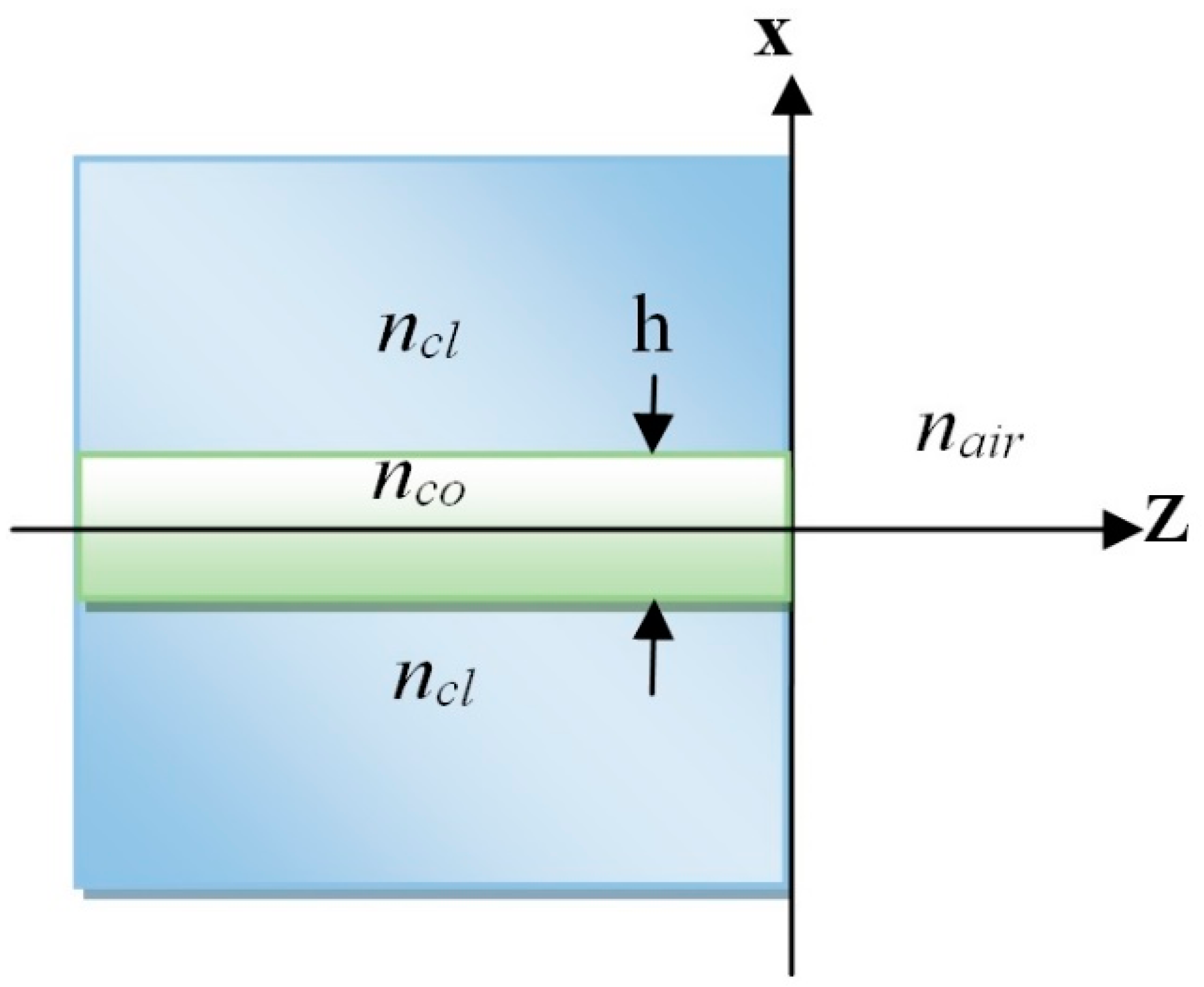
4.1. Dielectric Waveguide Facet
4.2. Butt-Coupling Between Plasmonic and Dielectric Waveguide
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Li, E.P.; Chu, H.S. Plasmonic Nanoelectronics and Sensing; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Kinsey, N.; Ferrera, M.; Shalaev, V.M.; Boltasseva, A. Examining nanophotonics for integrated hybrid systems: A review of plasmonic interconnects and modulators using traditional and alternative materials. JOSA B 2015, 32, 121–142. [Google Scholar] [CrossRef]
- Chen, J.; Badioli, M.; Alonso-González, P.; Thongrattanasiri, S.; Huth, F.; Osmond, J.; Spasenović, M.; Centeno, A.; Pesquera, A.; Godignon, P.; et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 2012, 487, 77–81. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ni, G.X.; Wang, L.; Goldflam, M.D.; Wagner, M.; Fei, Z.; McLeod, A.S.; Liu, M.K.; Keilmann, F.; Özyilmaz, B.; Neto, A.H.C.; et al. Ultrafast optical switching of infrared plasmon polaritons in high-mobility graphene. Nat. Photonics 2016, 10, 244–247. [Google Scholar] [CrossRef]
- Basov, D.N.; Fogler, M.M.; De Abajo, F.J.G.; Fogler, M. Polaritons in van der Waals materials. Science 2016, 354, aag1992. [Google Scholar] [CrossRef]
- Koppens, F.H.L.; Chang, D.E.; De Abajo, F.J.G. Graphene Plasmonics: A Platform for Strong Light–Matter Interactions. Nano Lett. 2011, 11, 3370–3377. [Google Scholar] [CrossRef]
- Chen, L.; Shakya, J.; Lipson, M. Subwavelength confinement in an integrated metal slot waveguide on silicon. Opt. Lett. 2006, 31, 2133–2135. [Google Scholar] [CrossRef]
- Tang, L.; Kocabas, S.E.; Latif, S.; Okyay, A.K.; Ly-Gagnon, D.-S.; Saraswat, K.C.; Miller, D.A.B. Nanometre-scale germanium photodetector enhanced by a near-infrared dipole antenna. Nat. Photonics 2008, 2, 226–229. [Google Scholar] [CrossRef]
- Garcia-Vidal, F.J. Solid-state physics: Light at the end of the channel. Nature 2006, 440, 431–433. [Google Scholar] [CrossRef]
- Gomaa, L.R.; Shaaban, A.; Hameed, M.F.O.; Obayya, S.S.A. Competitiveness of the BPM in studying the optical beams at critical incidence on dielectric interfaces. Opt. Quantum Electron. 2017, 49, 51. [Google Scholar] [CrossRef]
- Shaaban, A.; Sayed, M.; Hameed, M.F.O.; Saleh, H.I.; Gomaa, L.; Du, Y.-C.; Obayya, S.; Obayya, S.A. Fast parallel beam propagation method based on multi-core and many-core architectures. Optik 2019, 180, 484–491. [Google Scholar] [CrossRef]
- Kaczmarski, P.; Lagasse, P. Bidirectional beam propagation method. Electron. Lett. 1988, 24, 675–676. [Google Scholar] [CrossRef]
- Shaaban, A.; Lotfy, R.G.; Du, Y.C. Adaptability of Bidirectional FFT-Based Beam propagation Method to investigate Dielectric-Plasmonic waveguide coupler. 2019, submitted. 2019. submitted. [Google Scholar]
- Franssens, G.; Kaczmarski, P.; Baets, R.; Lagasse, P. Extension of bidirectional beam propagation method to TM polarisation and application to laser facet reflectivity. Electron. Lett. 1989, 25, 716–717. [Google Scholar] [CrossRef]
- Vassallo, C. Difficulty with vectorial BPM. Electron. Lett. 1997, 33, 61–62. [Google Scholar] [CrossRef]
- Hoekstra, H.J.W.M.; Lambeck, P.V.; Krijnen, G.J.; Ctvroky, J.; De Minicis, H.; Sibilia, C.; Conradi, O.; Helfert, S.; Pregla, R. A COST 240 benchmark test for beam propagation methods applied to an electrooptical modulator based on surface plasmons. J. Lightwave Technol. 1998, 16, 1921–1927. [Google Scholar] [CrossRef]
- Poladian, L.; Ladouceur, F. Unification of TE and TM beam propagation algorithms. IEEE Photonics Technol. Lett. 1998, 10, 105–107. [Google Scholar] [CrossRef]
- Yamauchi, J.; Shimada, N.; Nito, Y.; Nakano, H. Transverse-magnetic BPM analysis of a step-index slab waveguide expressed by a sigmoid function. IEEE Photonics Technol. Lett. 2009, 21, 149–151. [Google Scholar] [CrossRef]
- Smartt, C.; Benson, T.; Kendall, P. ‘Free space radiation mode’ method for the analysis of propagation in optical waveguide devices. IEE Proc. J Optoelectron. 1993, 140, 56–61. [Google Scholar] [CrossRef]
- Wu, S.; Xiao, J. A pseudospectral reflective beam propagation method for optical waveguides. IEEE Photonics Technol. Lett. 2017, 29, 435–438. [Google Scholar] [CrossRef]
- Manenkov, A.B.; Latsas, G.P.; Tigelis, I.G. Scattering of the transverse magnetic modes from an abruptly ended strongly asymmetrical slab waveguide by an accelerated integral equation technique. J. Opt. Soc. Am. A 2001, 18, 3110. [Google Scholar] [CrossRef]
- Vassallo, C. Reflectivity of multidielectric coatings deposited on the end facet of a weakly guiding dielectric slab waveguide. J. Opt. Soc. Am. A 1988, 5, 1918. [Google Scholar] [CrossRef]
- Smartt, C.; Benson, T.; Kendall, P. Exact analysis of waveguide discontinuities: Junctions and laser facets. Electron. Lett. 1993, 29, 1352–1353. [Google Scholar] [CrossRef]
- Nguyen, T.G.; Mitchell, A. Analysis of optical waveguides with multilayer dielectric coatings using plane wave expansion. J. Lightwave Technol. 2006, 24, 635–642. [Google Scholar] [CrossRef]
- Yamauchi, J.; Kanbara, H.; Nakano, H. Analysis of optical waveguides with high-reflection coatings using the FD-TD method. IEEE Photonics Technol. Lett. 1998, 10, 111–113. [Google Scholar] [CrossRef] [Green Version]
- Orfanidis, S.J. Electromagnetic Waves and Antennas; Rutgers University: Piscataway, NJ, USA, 2008. [Google Scholar]
- Veronis, G.; Fan, S. Theoretical investigation of compact couplers between dielectric slab waveguides and two-dimensional metal-dielectric-metal plasmonic waveguides. Opt. Express 2007, 15, 1211–1221. [Google Scholar] [CrossRef] [PubMed] [Green Version]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaaban, A.; Du, Y.-C.; Gomaa, L.R. Extension of an FFT-Based Beam Propagation Method to Plasmonic and Dielectric Waveguide Discontinuities and Junctions. Appl. Sci. 2019, 9, 4362. https://doi.org/10.3390/app9204362
Shaaban A, Du Y-C, Gomaa LR. Extension of an FFT-Based Beam Propagation Method to Plasmonic and Dielectric Waveguide Discontinuities and Junctions. Applied Sciences. 2019; 9(20):4362. https://doi.org/10.3390/app9204362
Chicago/Turabian StyleShaaban, Adel, Yi-Chun Du, and Lotfy Rabeh Gomaa. 2019. "Extension of an FFT-Based Beam Propagation Method to Plasmonic and Dielectric Waveguide Discontinuities and Junctions" Applied Sciences 9, no. 20: 4362. https://doi.org/10.3390/app9204362
APA StyleShaaban, A., Du, Y.-C., & Gomaa, L. R. (2019). Extension of an FFT-Based Beam Propagation Method to Plasmonic and Dielectric Waveguide Discontinuities and Junctions. Applied Sciences, 9(20), 4362. https://doi.org/10.3390/app9204362





