Shape Optimization of Single-Curvature Arch Dam Based on Sequential Kriging-Genetic Algorithm
Abstract
:1. Introduction
2. Methodology
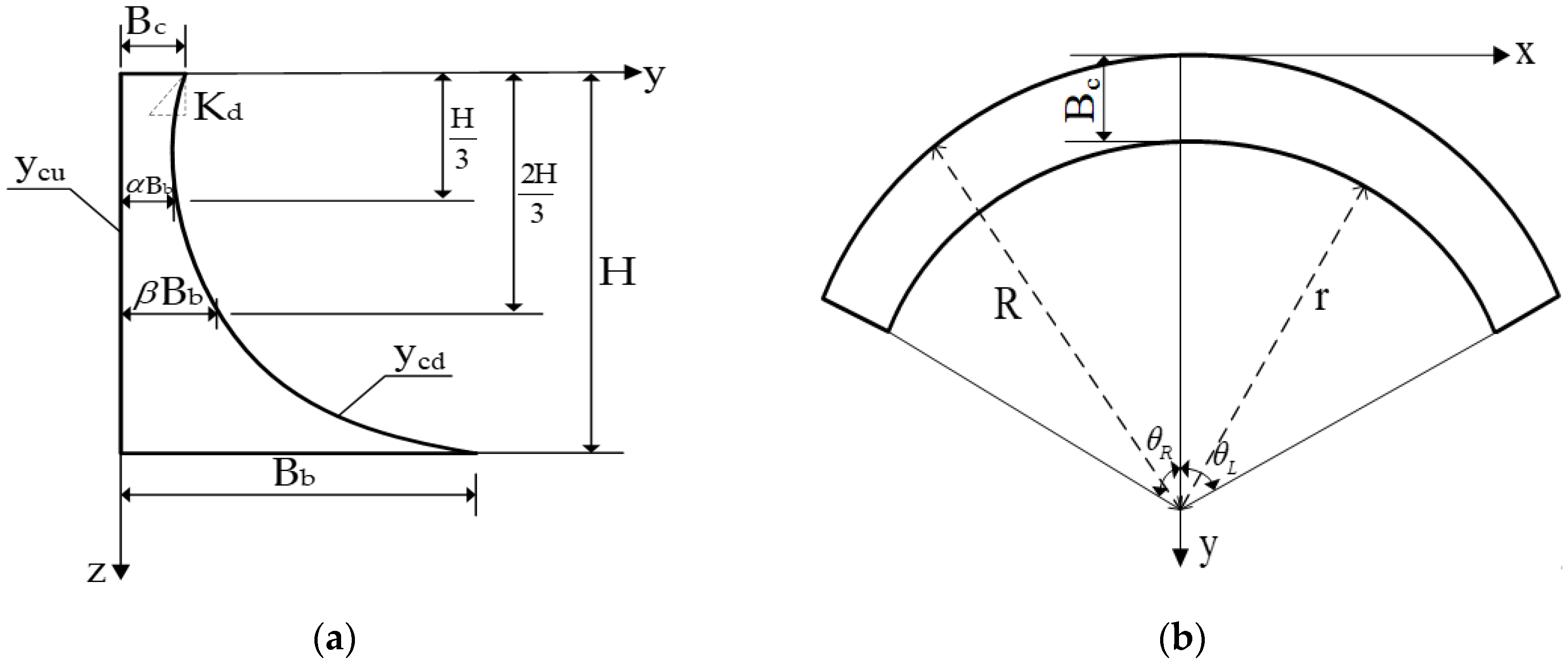
2.1. Geometric Model of a Single-Curvature Arch Dam
2.1.1. Arch Crown Cantilever
2.1.2. Horizontal Arch Ring
2.2. Construction of Mathematical Optimization Model
2.2.1. Design Variables and Objective Function
2.2.2. Constraints
2.3. Solution of Mathematical Optimization Model
2.3.1. Genetic Algorithm
2.3.2. Kriging Surrogate Model
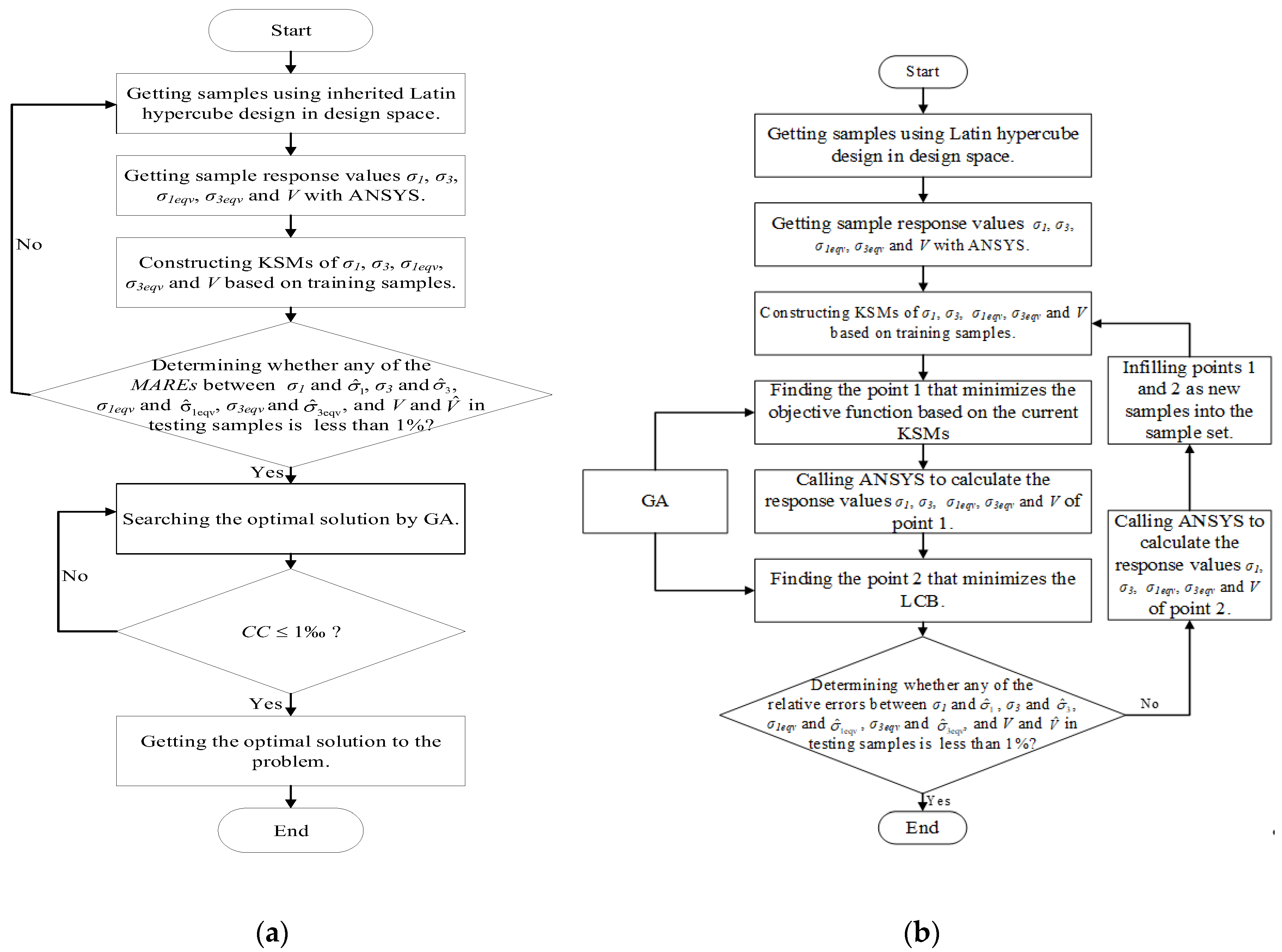
2.3.3. Sequential KSM
2.3.4. Optimization Procedure
3. Case Study
3.1. Basic Information of a Single-Curvature Arch Dam
3.2. Finite Element Model Establishing and Parameter Setting
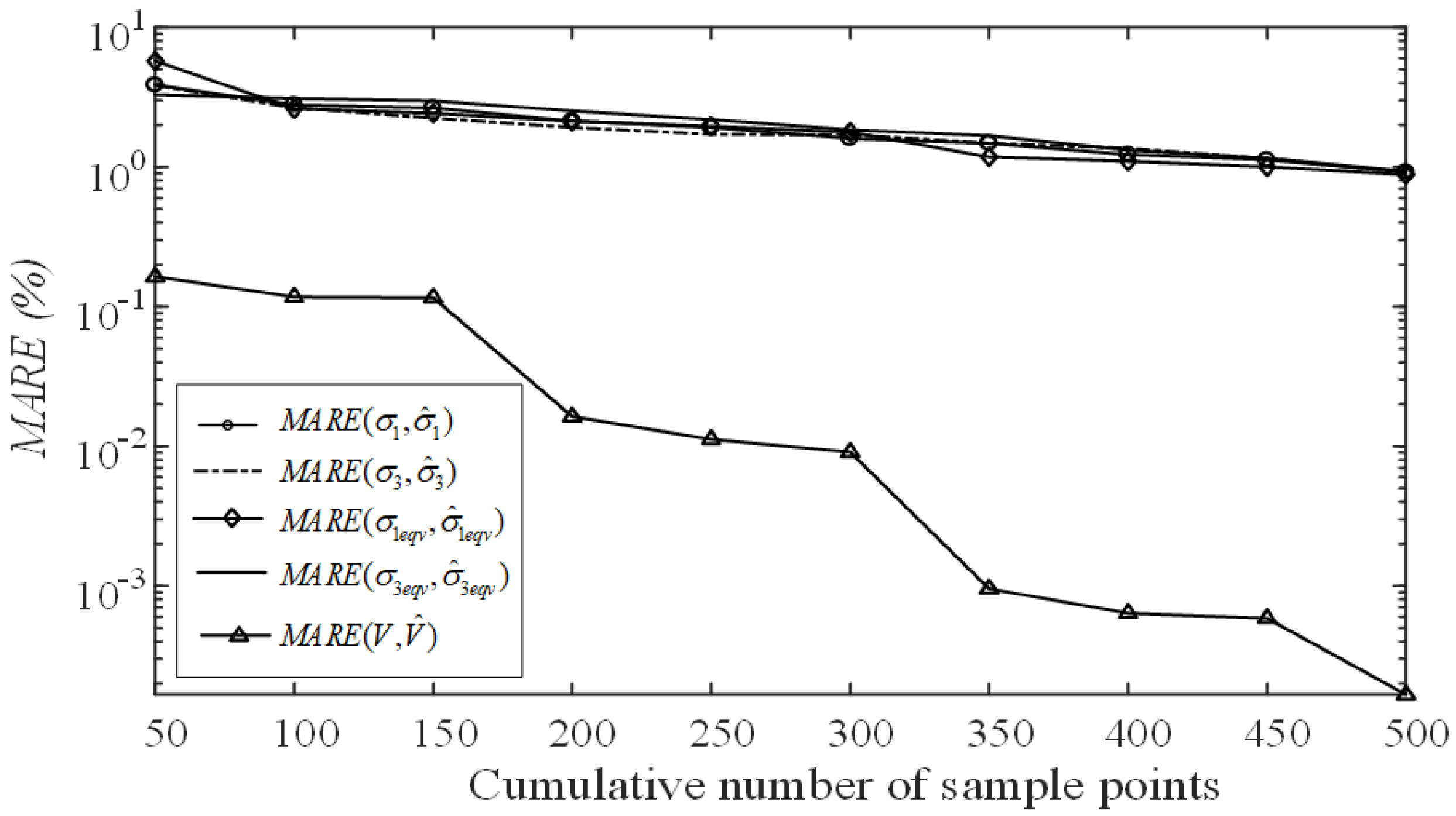
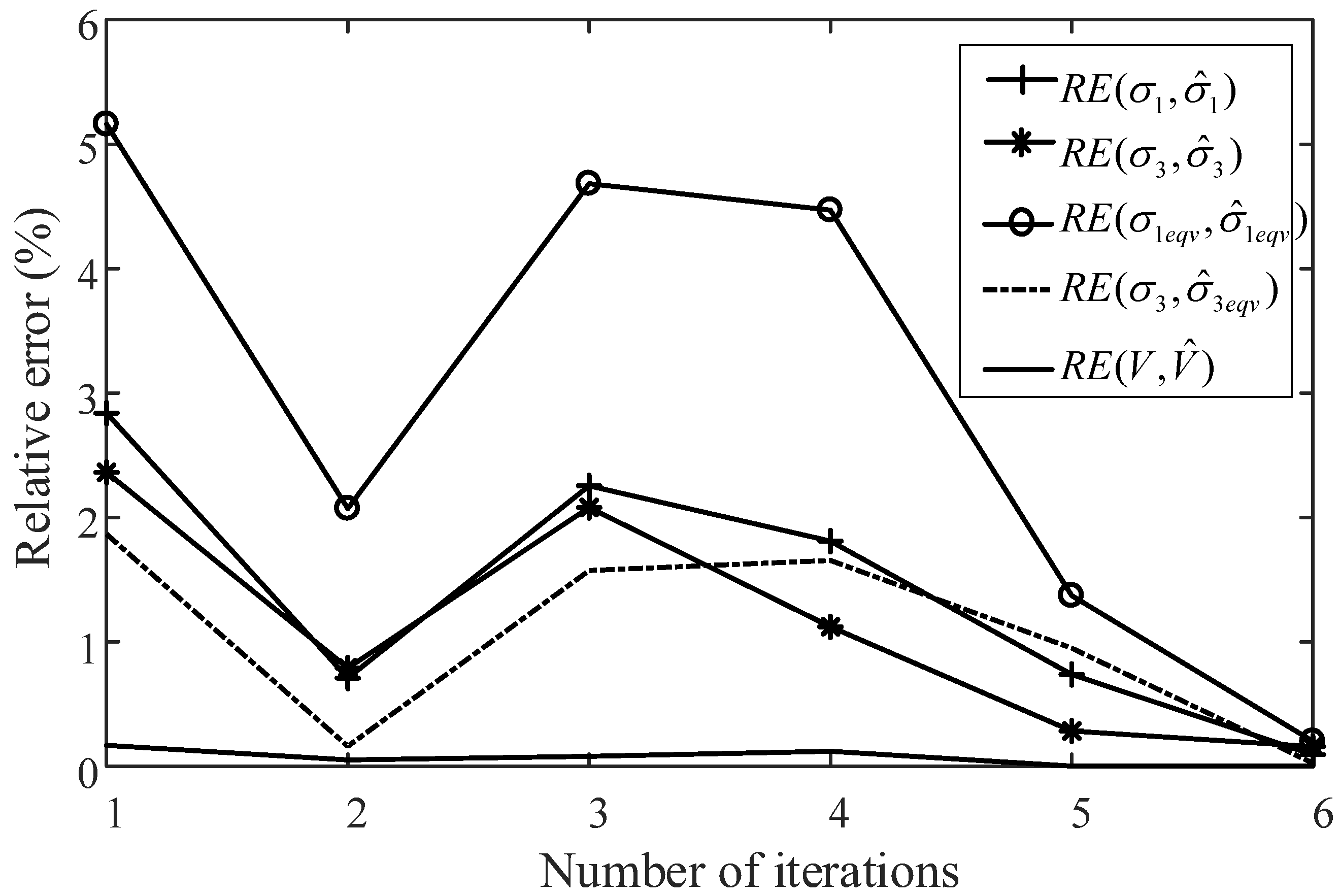
3.3. Optimization Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pourbakhshian, S.; Ghaemain, M. Shape Optimization of Arch Dams Using Sensitivity Analysis. KSCE J. Civ. Eng. 2016, 20, 1966–1976. [Google Scholar] [CrossRef]
- Rita, M.; Fairbairn, E.; Ribeiro, F.; Andrade, H.; Barbosa, H. Optimization of Mass Concrete Construction Using a Twofold Parallel Genetic Algorithm. Appl. Sci. 2018, 8, 399. [Google Scholar] [CrossRef]
- Tan, F.J.; Lahmer, T. Shape Optimization Based Design of Arch-Type Dams under Uncertainties. Eng. Optimiz. 2018, 50, 1470–1482. [Google Scholar]
- Sukkarak, R.; Jongpradist, P.; Pramthawee, P. A Modified Valley Shape Factor for the Estimation of Rockfill Dam Settlement. Comput. Geotech. 2019, 108, 244–256. [Google Scholar] [CrossRef]
- Wang, G.G.; Shan, S. Review of Metamodeling Techniques in Support of Engineering Design Optimization. J. Mech. Des. 2007, 129, 370–380. [Google Scholar] [CrossRef]
- Mahani, A.S.; Shojaee, S.; Salajegheh, E.; Khatibinia, M. Hybridizing Two-Stage Meta-Heuristic Optimization Model with Weighted Least Squares Support Vector Machine for Optimal Shape of Double-Arch Dams. Appl. Soft Comput. 2015, 27, 205–218. [Google Scholar] [CrossRef]
- Chang, C.M.; Lin, T.K.; Chang, C.W. Applications of Neural Network Models for Structural Health Monitoring Based on Derived Modal Properties. Measurement 2018, 129, 457–470. [Google Scholar] [CrossRef]
- Jamli, M.R.; Farid, N.M. The Sustainability of Neural Network Applications within Finite Element Analysis in Sheet Metal Forming: A Review. Measurement 2019, 138, 446–460. [Google Scholar] [CrossRef]
- Krige, D.G. A Statistical Approach to Some Basic Mine Valuation Problems on the Witwatersrand. J. South. Afr. Inst. Min. Metall. 1994, 94, 95–111. [Google Scholar]
- Putra, N.K.; Palar, P.S.; Anzai, H.; Shimoyama, K.; Ohta, M. Multiobjective Design Optimization of Stent Geometry with Wall Deformation for Triangular and Rectangular Struts. Med. Biol. Eng. Comput. 2019, 57, 15–26. [Google Scholar] [CrossRef]
- Gaspar, B.; Teixeira, A.P.; Soares, C.G. Assessment of the Efficiency of Kriging Surrogate Models for Structural Reliability Analysis. Probabilist. Eng. Mech. 2014, 37, 24–34. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Yang, H.T. An Approximate Solution for the Bimodular Plane Problem Based on Kriging Surrogate Model. Eng. Mech. 2013, 30, 23–27. [Google Scholar]
- Liu, Y.S.; Wang, X.J.; Wang, L. A Dynamic Evolution Scheme for Structures with Interval Uncertainties by Using Bidirectional Sequential Kriging Method. Comput. Methods Appl. Mech. Eng. 2019, 348, 712–729. [Google Scholar]
- Cheng, J.; Jiang, P.; Zhou, Q.; Hu, J.X.; Yu, T.; Shu, L.S.; Shao, X.Y. A Lower Confidence Bounding Approach Based on the Coefficient of Variation for Expensive Global Design Optimization. Eng. Comput. 2019, 36, 830–849. [Google Scholar] [CrossRef]
- Raponi, E.; Bujny, M.; Olhofer, M.; Aulig, N.; Boria, S.; Duddeck, F. Kriging-Assisted Topology Optimization of Crash Structures. Comput. Methods Appl. Mech. Eng. 2019, 348, 730–752. [Google Scholar] [CrossRef]
- Song, C.; Yang, X.D.; Song, W.P. Multi-Infill Strategy for Kriging Models Used in Variable Fidelity Optimization. Chin. J. Aeronaut. 2018, 31, 448–456. [Google Scholar] [CrossRef]
- Salmasi, F. Design of Gravity Dam by Genetic Algorithms. World Acad. Sci. Eng. Technol. 2011, 56, 864–869. [Google Scholar]
- Babbar-Sebens, M.; Minsker, B.S. Interactive Genetic Algorithm with Mixed Initiative Interaction for Multi-Criteria Ground Water Monitoring Design. Appl. Soft Comput. 2012, 12, 182–195. [Google Scholar] [CrossRef]
- Li, M.G.; Li, M.; Han, G.P.; Liu, N.; Zhang, Q.M.; Wang, Y. Optimization Analysis of the Energy Management Strategy of the New Energy Hybrid 100% Low-Floor Tramcar Using a Genetic Algorithm. Appl. Sci. 2018, 8, 1144. [Google Scholar] [CrossRef]
- Prasanchum, H.; Kangrang, A. Optimal Reservoir Rule Curves under Climatic and Land Use Changes for Lampao Dam Using Genetic Algorithm. KSCE J. Civ. Eng. 2018, 22, 351–364. [Google Scholar] [CrossRef]
- Yoo, J.W.; Ronzio, F.; Courtois, T. Road Noise Reduction of a Sport Utility Vehicle Via Panel Shape and Damper Optimization on the Floor Using Genetic Algorithm. Int. J. Automot. Technol. 2019, 20, 1043–1050. [Google Scholar] [CrossRef]
- Zhang, J.M.; Xie, L. Particle Swarm Optimization Algorithm for Constrained Problems. Asia Pac. J. Chem. Eng. 2009, 4, 437–442. [Google Scholar] [CrossRef]
- Kim, J.B.; Hwang, K.Y.; Kwon, B.I. Optimization of Two-Phase in-Wheel Ipmsm for Wide Speed Range by Using the Kriging Model Based on Latin Hypercube Sampling. IEEE. Trans. Magn. 2011, 47, 1078–1081. [Google Scholar] [CrossRef]
- Wang, G.G. Adaptive Response Surface Method Using Inherited Latin Hypercube Design Points. J. Mech. Des. 2003, 125, 210–220. [Google Scholar] [CrossRef]
- Parr, J.M.; Keane, A.J.; Forrester, A.I.J.; Holden, C.M.E. Infill Sampling Criteria for Surrogate-Based Optimization with Constraint Handling. Eng. Optimiz. 2012, 44, 1147–1166. [Google Scholar] [CrossRef]
- Yang, Z.B.; Zhou, J.Z.; Li, H.T.; Li, W.T.; Shi, X.W.; Wang, M. Design of Hexagonal Circularly Polarized Antenna Array Using Paralleled Dynamic Minimum Lower Confidence Bound. Int. J. RF Microw. Comput. Aided Eng. 2018, 28, e21184. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, Q.; Fernandez, F.; Gielen, G. Self-Adaptive Lower Confidence Bound: A New General and Effective Prescreening Method for Gaussian Process Surrogate Model Assisted Evolutionary Algorithms. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, Australia, 10–15 June 2012. [Google Scholar]

| Design Variable | α | β | Bc (m) | Bb (m) |
|---|---|---|---|---|
| Lower Bound | 0.2 | 0.5 | 4 | 15 |
| Upper Bound | 0.5 | 0.9 | 8 | 18 |
| Material | Linear Expansion Coefficient (10−6/°C) | Elastic Modulus (MPa) | Mass Density (Kg/m3) | Poisson’s Ratio | The Allowable Compressive Stress (MPa) | The Allowable Tensile Stress (MPa) |
|---|---|---|---|---|---|---|
| Dam body | 7 | 10 | 2300 | 0.25 | −5.0 | 1.5 |
| Foundation rock | 0 | 8 | 2600 | 0.21 | - | - |
| Method | α | β | Bc (m) | Bb (m) | V (m3) | NONS |
|---|---|---|---|---|---|---|
| GA-FEM | 0.31 | 0.61 | 4.21 | 15.37 | 36,450 | 1150 |
| GA-KSM | 0.32 | 0.60 | 5.72 | 15.12 | 35,579 | 500 |
| GA-SKSM | 0.31 | 0.63 | 5.80 | 15.10 | 35,435 | 62 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.-Q.; Zhao, R.-H.; Liu, Y.; Chen, Y.-Z.; Ma, X.-Y. Shape Optimization of Single-Curvature Arch Dam Based on Sequential Kriging-Genetic Algorithm. Appl. Sci. 2019, 9, 4366. https://doi.org/10.3390/app9204366
Wang Y-Q, Zhao R-H, Liu Y, Chen Y-Z, Ma X-Y. Shape Optimization of Single-Curvature Arch Dam Based on Sequential Kriging-Genetic Algorithm. Applied Sciences. 2019; 9(20):4366. https://doi.org/10.3390/app9204366
Chicago/Turabian StyleWang, Yong-Qiang, Rong-Heng Zhao, Ye Liu, Yi-Zheng Chen, and Xiao-Yi Ma. 2019. "Shape Optimization of Single-Curvature Arch Dam Based on Sequential Kriging-Genetic Algorithm" Applied Sciences 9, no. 20: 4366. https://doi.org/10.3390/app9204366
APA StyleWang, Y.-Q., Zhao, R.-H., Liu, Y., Chen, Y.-Z., & Ma, X.-Y. (2019). Shape Optimization of Single-Curvature Arch Dam Based on Sequential Kriging-Genetic Algorithm. Applied Sciences, 9(20), 4366. https://doi.org/10.3390/app9204366




