Earthquake-Induced Pounding of Medium-to-High-Rise Base-Isolated Buildings
Abstract
:1. Introduction
2. Materials and Methods
2.1. Analyzed Cases of Pounding between Buildings
2.2. Description of Buildings
2.3. Numerical Models
2.4. Modeling of Pounding
2.5. Details of Dynamic Analysis
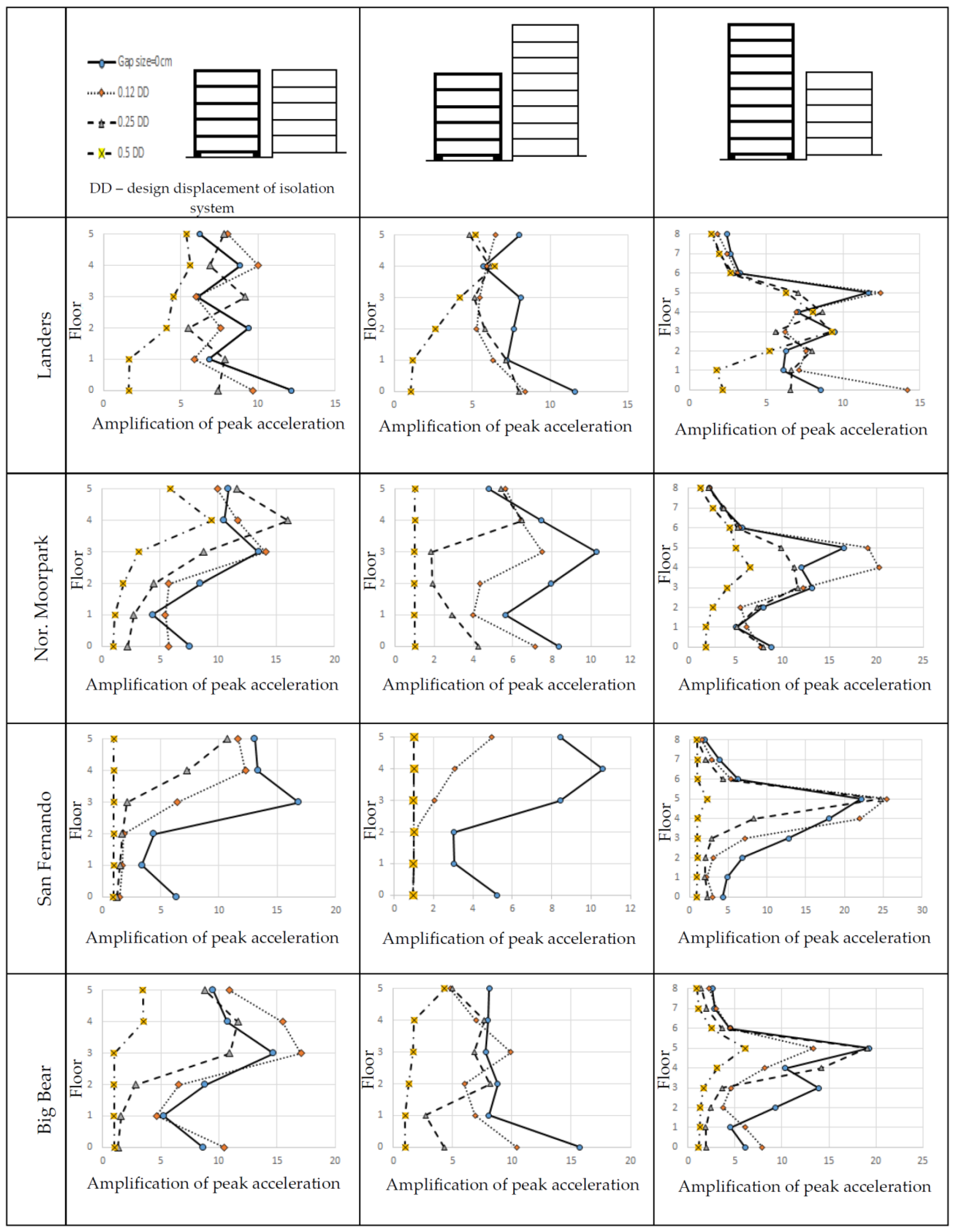
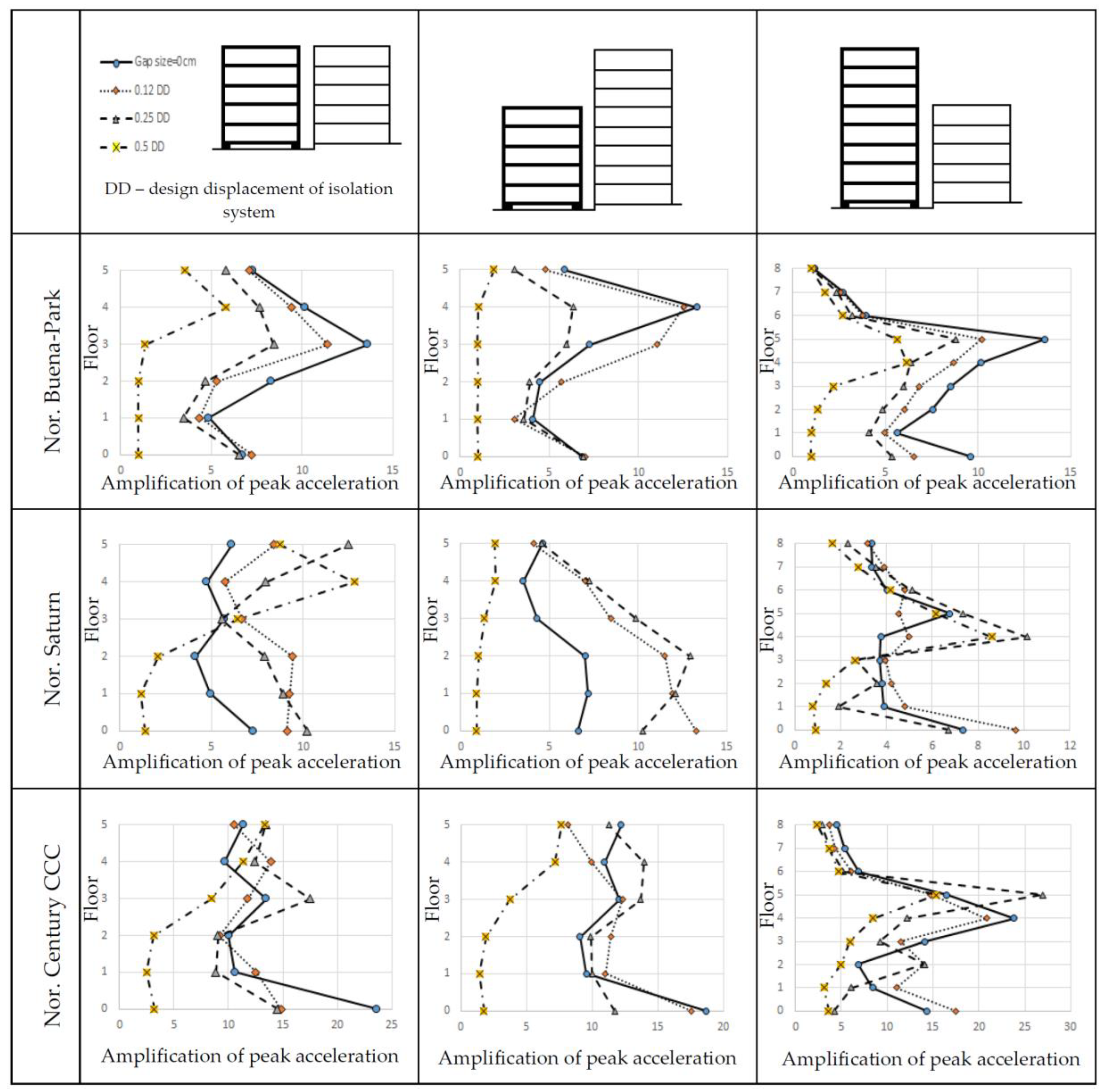
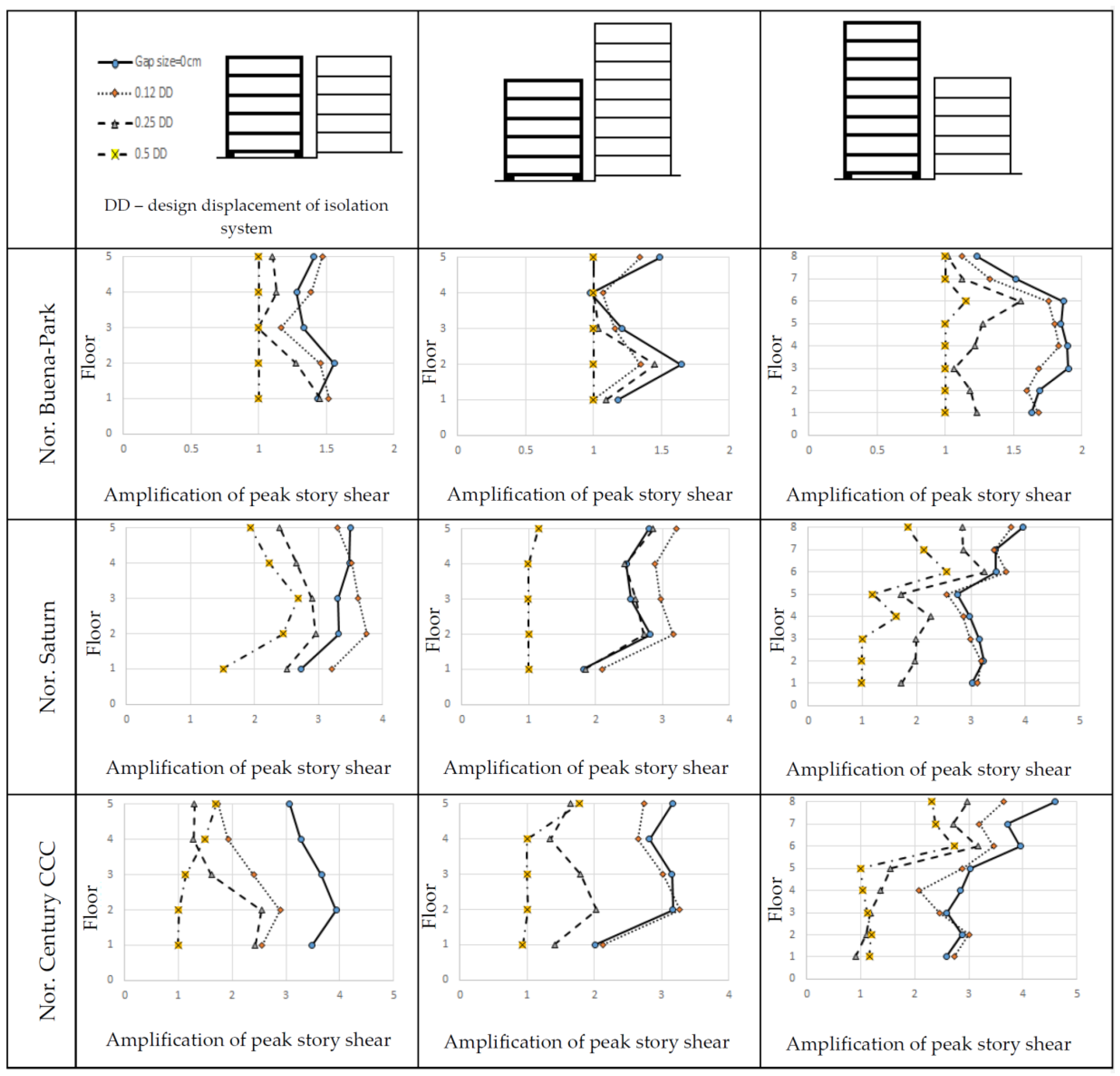
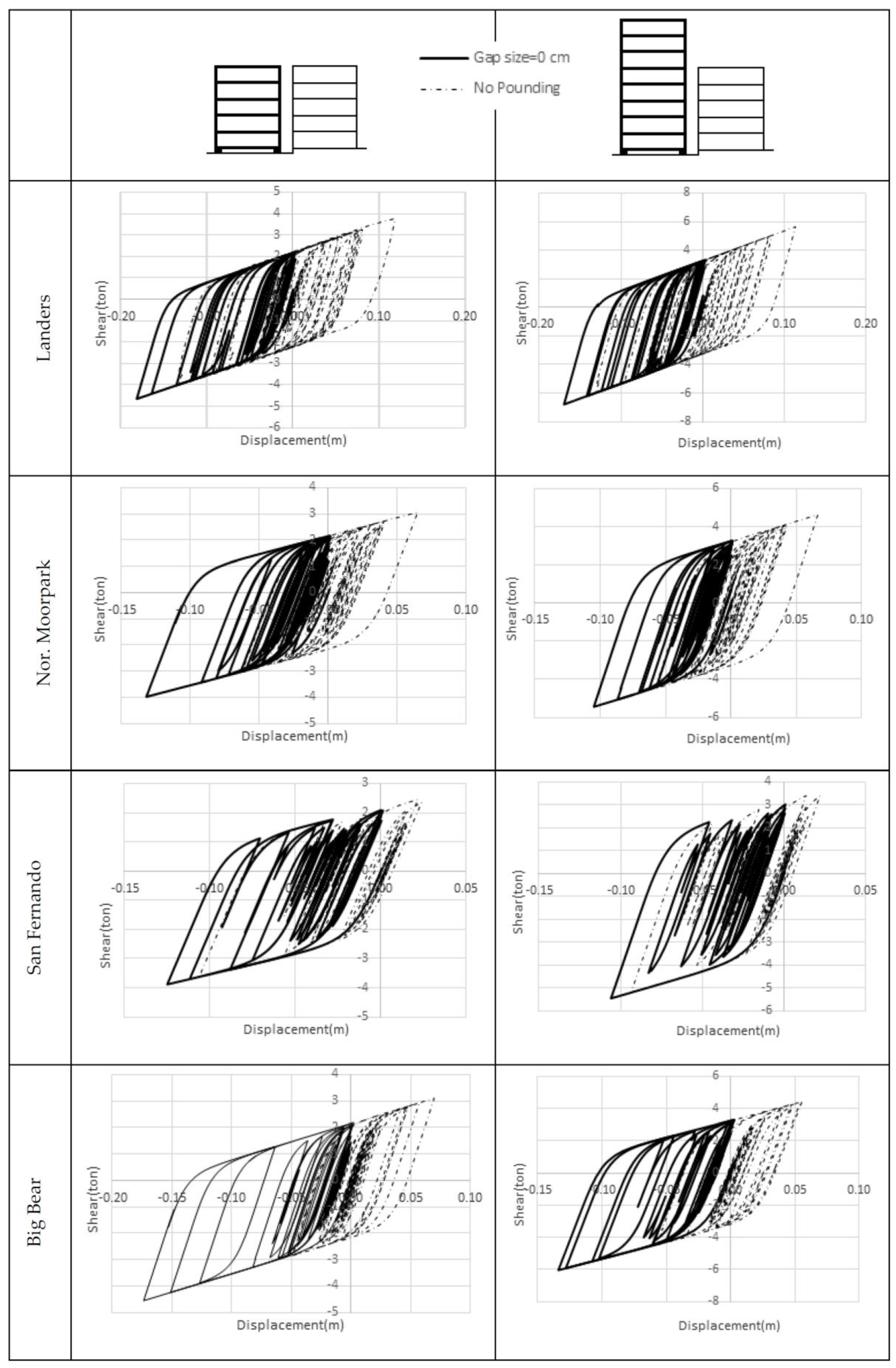
3. Results and Discussion
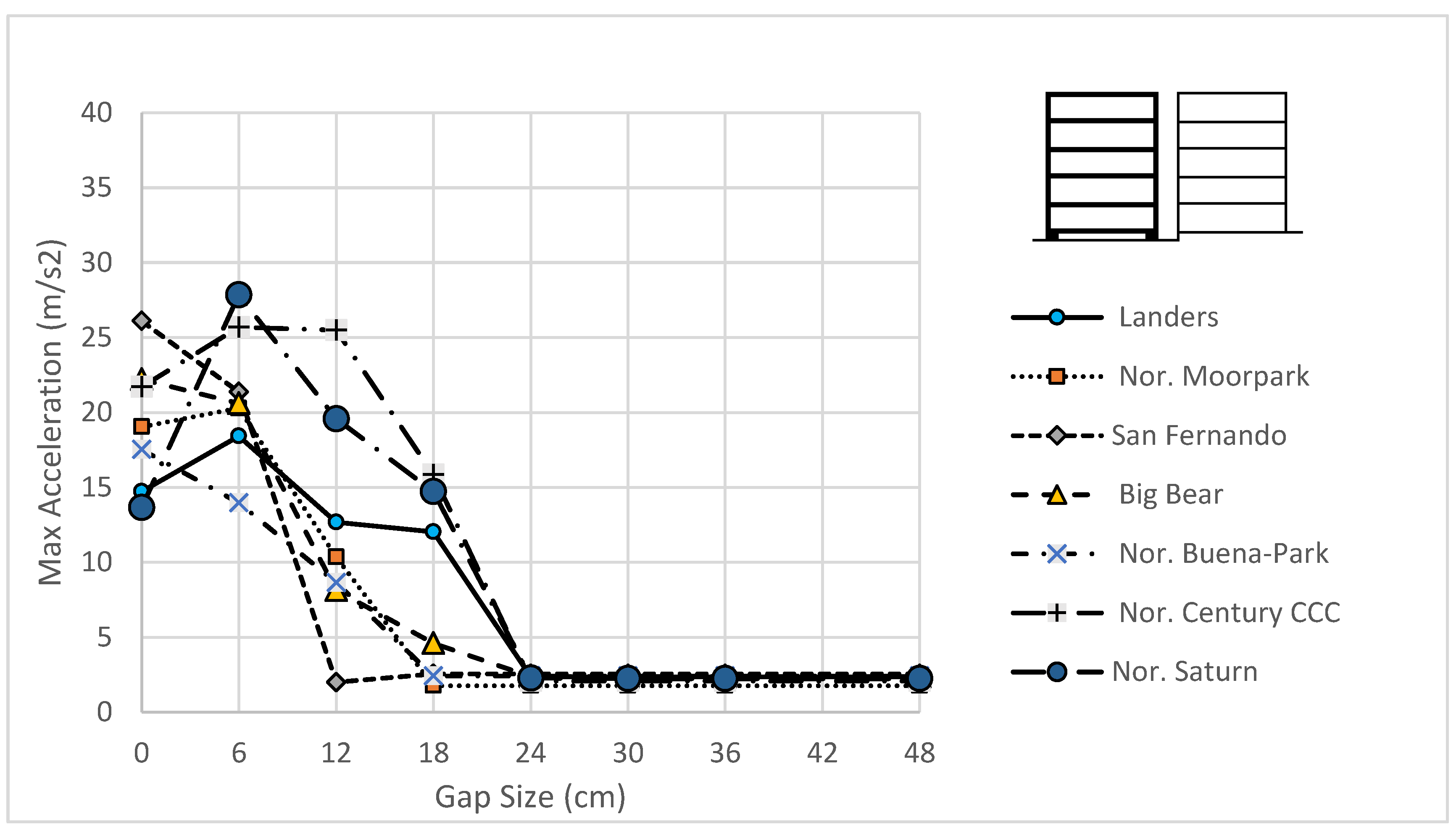
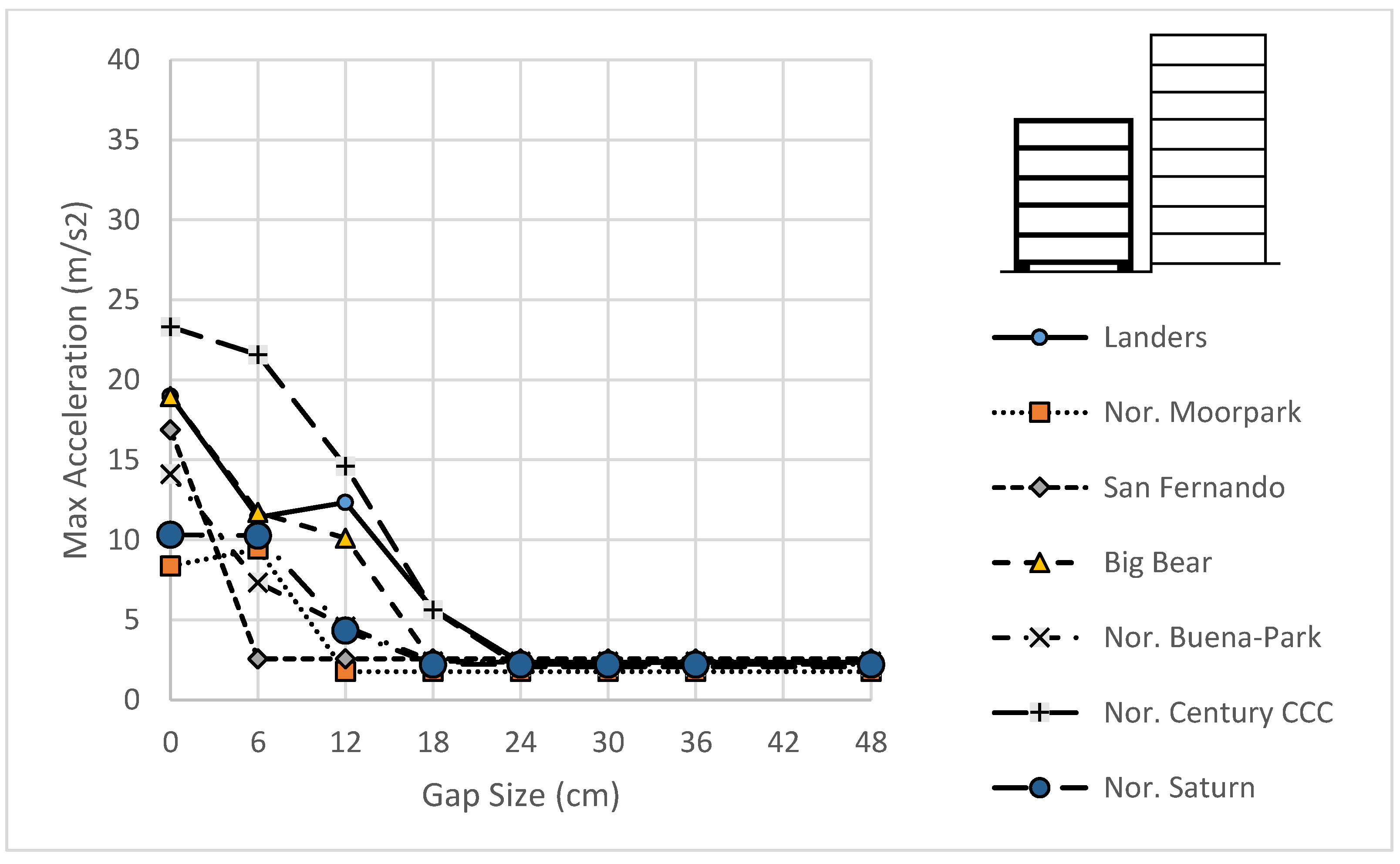
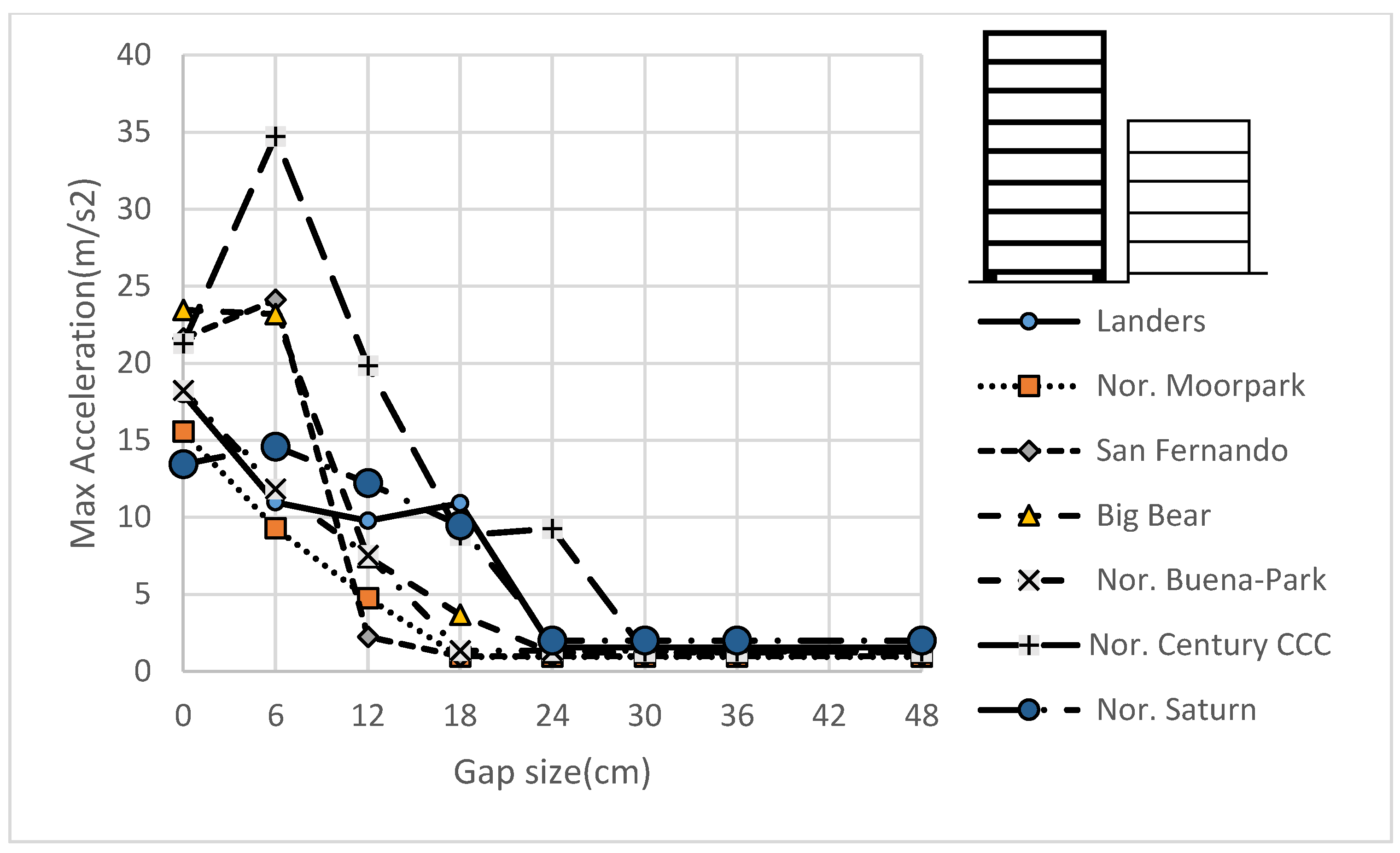
3.1. Response for Different Gap Sizes
3.2. Amplification Factors
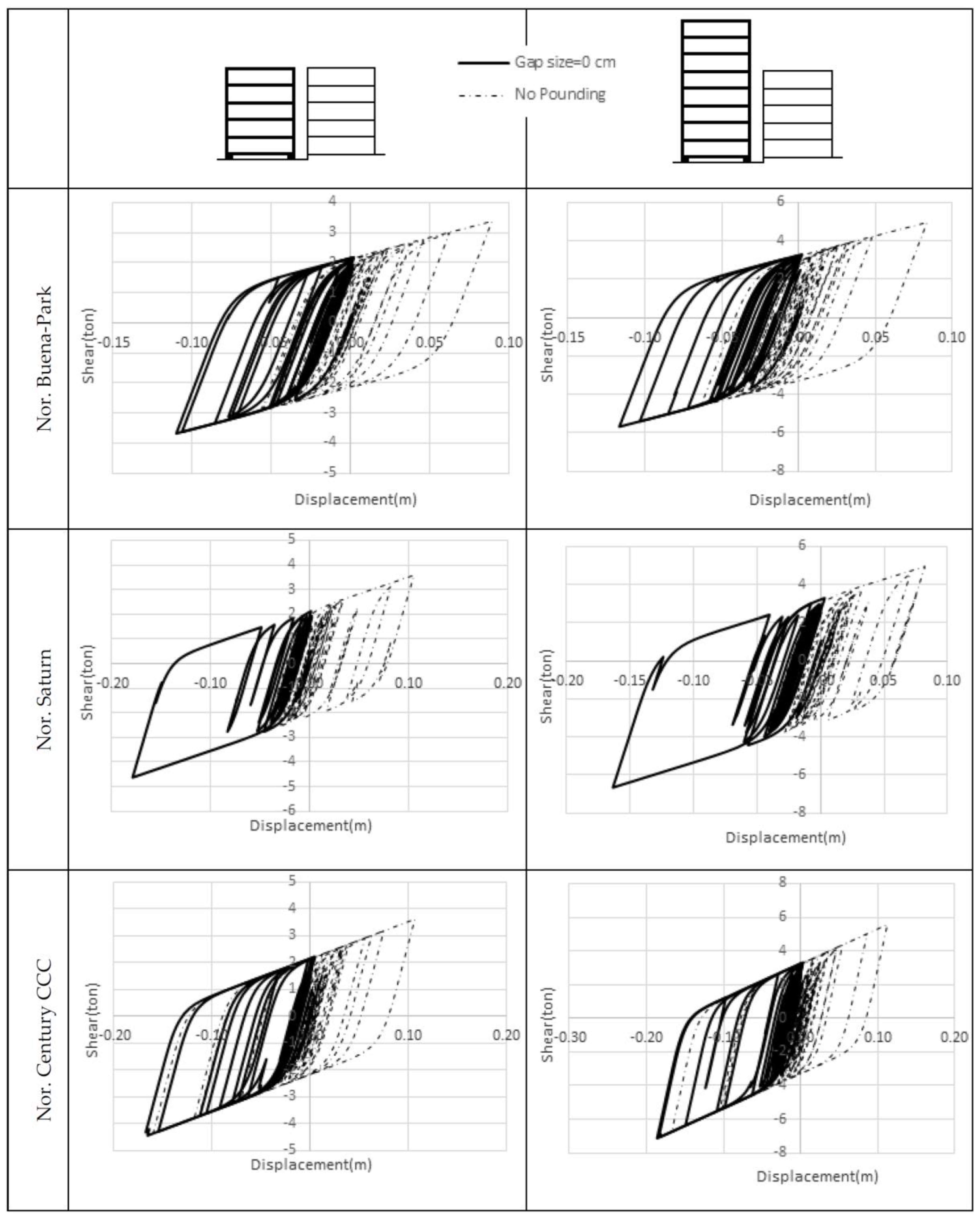
3.3. Hysteresis Curves
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Anagnostopoulos, S.A. Pounding of buildings in series during earthquakes. Earthq. Eng. Struct. Dyn. 1988, 16, 443–456. [Google Scholar] [CrossRef]
- Favvata, M.J.; Karayannis, C.G.; Liolios, A.A. Influence of exterior joint effect on the inter-story pounding interaction of structures. J. Struct. Eng. Mech. 2009, 33, 113–136. [Google Scholar] [CrossRef]
- Naderpour, H.; Khatami, S.M. A new model for calculating the impact force and the energy dissipation based on CR-factor and impact velocity. Sci. Iran. 2015, 22, 59–68. [Google Scholar]
- Sołtysik, B.; Jankowski, R. Non-linear strain rate analysis of earthquake-induced pounding between steel buildings. Int. J. Earth Sci. Eng. 2013, 6, 429–433. [Google Scholar]
- Elwardany, H.; Seleemah, A.; Jankowski, R. Seismic pounding behavior of multi-story buildings in series considering the effect of infill panels. Eng. Struct. 2017, 144, 139–150. [Google Scholar] [CrossRef]
- Khatami, S.M.; Naderpour, H.; Barros, R.C.; Jakubczyk-Gałczyńska, A.; Jankowski, R. Effective formula for impact damping ratio for simulation of earthquake-induced structural pounding. Geosciences 2019, 9, 347. [Google Scholar] [CrossRef]
- Rosenblueth, E.; Meli, R. The 1985 earthquake: Causes and effects in Mexico City. Concr. Int. 1986, 8, 23–34. [Google Scholar]
- Kasai, K.; Maison, B.F. Building pounding damage during the 1989 Loma Prieta earthquake. Eng. Struct. 1997, 19, 195–207. [Google Scholar] [CrossRef]
- Eurocode 8: Design Provisions for Earthquake Resistance of Structures; European Committee for Standardization: Brussels, Belgium, 1998.
- Jankowski, R.; Mahmoud, S. Linking of adjacent three-storey buildings for mitigation of structural pounding during earthquakes. Bull. Earthq. Eng. 2016, 14, 3075–3097. [Google Scholar] [CrossRef] [Green Version]
- Naeim, F.; Kelly, J.M. Design of Seismic Isolated Structures: From Theory to Practice; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1999. [Google Scholar]
- Falborski, T.; Jankowski, R. Experimental study on effectiveness of a prototype seismic isolation system made of polymeric bearings. Appl. Sci. 2017, 7, 808. [Google Scholar] [CrossRef]
- Falborski, T.; Jankowski, R.; Kwiecień, A. Experimental study on polymer mass used to repair damaged structures. Key Eng. Mater. 2012, 488, 347–350. [Google Scholar] [CrossRef]
- Naderpour, H.; Naji, N.; Burkacki, D.; Jankowski, R. Seismic response of high-rise buildings equipped with base isolation and non-traditional tuned mass dampers. Appl. Sci. 2019, 9, 1201. [Google Scholar] [CrossRef]
- Kelly, J.M. Earthquake-Resistant Design with Rubber; Springer: London, UK, 1993. [Google Scholar]
- Skinner, R.I.; Kelly, J.M.; Heine, A.J. Hysteretic dampers for earthquake-resistant structures. Earthq. Eng. Struct. Dyn. 1975, 3, 287–296. [Google Scholar] [CrossRef]
- Kumar, M.; Whittaker, A.S.; Constantinou, M.C. An advanced numerical model of elastomeric seismic isolation bearings. Earthq. Eng. Struct. Dyn. 2014, 43, 1955–1974. [Google Scholar] [CrossRef]
- Kumar, M.; Whittaker, A.S.; Constantinou, M.C. Characterizing friction in sliding isolation bearings. Earthq. Eng. Struct. Dyn. 2015, 44, 1409–1425. [Google Scholar] [CrossRef]
- Nagarajaiah, S.; Sun, X. Seismic performance of base-isolated buildings in the 1994 Northridge earthquake. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. paper no. 598. [Google Scholar]
- Das, S.; Gur, S.; Mishra, S.K.; Chakraborty, S. Optimal performance of base isolated building considering limitation on excessive isolator displacement. Struct. Infrastruct. Eng. 2015, 11, 904–917. [Google Scholar] [CrossRef]
- Fallah, N.; Zamiri, G. Multi-objective optimal design of sliding base isolation using genetic algorithm. Sci. Iran. 2013, 20, 87–96. [Google Scholar] [CrossRef]
- Jain, S.K.; Thakkar, S.K. Application of base isolation for flexible buildings. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. paper no. 1924. [Google Scholar]
- Zelleke, D.H.; Elias, S.; Matsagar, V.A.; Jain, A.K. Supplemental dampers in base-isolated buildings to mitigate large isolator displacement under earthquake excitations. Bull. N. Z. Soc. Earthq. Eng. 2015, 48, 100–117. [Google Scholar] [CrossRef] [Green Version]
- Fu, W.; Zhang, C.; Sun, L.; Askari, M.; Samali, B.; Chung, K.L.; Sharafi, P. Experimental investigation of a base isolation system incorporating MR dampers with the high-order single step control algorithm. Appl. Sci. 2017, 7, 344. [Google Scholar] [CrossRef]
- AlMusbahi, S.; Güngör, A. A composite building isolation system for earthquake protection. Eng. Sci. Technol. Int. J. 2019, 22, 399–404. [Google Scholar] [CrossRef]
- Nagarajaiah, S.; Sun, X. Base-isolated FCC building: Impact response in Northridge earthquake. J. Struct. Eng. 2001, 127, 1063–1075. [Google Scholar] [CrossRef]
- Tsai, H.C. Dynamic analysis of base-isolated shear beams bumping against stops. Earthq. Eng. Struct. Dyn. 1997, 26, 515–528. [Google Scholar] [CrossRef]
- Malhotra, P.K. Dynamics of seismic impacts in base-isolated buildings. Earthq. Eng. Struct. Dyn. 1997, 26, 797–813. [Google Scholar] [CrossRef]
- Dimova, S.L. Numerical problems in modelling of collision in sliding systems subjected to seismic excitations. Adv. Eng. Softw. 2000, 31, 467–471. [Google Scholar] [CrossRef]
- Matsagar, V.A.; Jangid, R.S. Seismic response of base-isolated structures during impact with adjacent structures. Eng. Struct. 2003, 25, 1311–1323. [Google Scholar] [CrossRef]
- Komodromos, P.; Polycarpou, P.C.; Papaloizou, L.; Phocas, M.C. Response of seismically isolated buildings considering poundings. Earthq. Eng. Struct. Dyn. 2007, 36, 1605–1622. [Google Scholar] [CrossRef]
- Komodromos, P. Simulation of the earthquake-induced pounding of seismically isolated buildings. Comput. Struct. 2008, 86, 618–626. [Google Scholar] [CrossRef]
- Agarwal, V.K.; Niedzwecki, J.M.; van de Lindt, J.W. Earthquake induced pounding in friction varying base isolated buildings. Eng. Struct. 2007, 29, 2825–2832. [Google Scholar] [CrossRef]
- Mahmoud, S.; Jankowski, R. Pounding-involved response of isolated and non-isolated buildings under earthquake excitation. Earthq. Struct. 2010, 1, 231–252. [Google Scholar] [CrossRef]
- Polycarpou, P.C.; Komodromos, P. Earthquake-induced poundings of a seismically isolated building with adjacent structures. Eng. Struct. 2010, 32, 1937–1951. [Google Scholar] [CrossRef]
- Bedon, C.; Morassi, A. Dynamic testing and parameter identification of a base-isolated bridge. Eng. Struct. 2014, 60, 85–99. [Google Scholar] [CrossRef]
- Vaseghi Amiri, J.; Jalali, S.G. Study of different contact elements in poundings of steel buildings. J. Model. Eng. 2011, 9, 1–20. [Google Scholar]
- Jankowski, R. Pounding between superstructure segments in multi-supported elevated bridge with three-span continuous deck under 3D non-uniform earthquake excitation. J. Earthq. Tsunami 2015, 9, 1550012. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]


| Isolator Characteristics | Building | |
|---|---|---|
| Five-Story | Eight-Story | |
| Effective stiffness, Keff (kN/m) | 208.6 | 313.81 |
| Effective damping, Ceff (kN·s/m) | 49.9 | 75.15 |
| Initial stiffness, K1 (kN/m) | 1351.85 | 2039.7 |
| Yield force, fy (kN) | 23.54 | 35.5 |
| Year of Occurrence | Earthquake | MW | Station | Duration (s) | PGA (g) | PGD (cm) |
|---|---|---|---|---|---|---|
| 1992 | Big Bear | 6.4 | Desert Hot Spr. (New Fire Stn.) | 60 | 0.23 | 4.53 |
| 1994 | Northridge | 6.7 | Century CCC | 60 | 0.26 | 7.85 |
| 1994 | Northridge | 6.7 | Saturn Street School | 32 | 0.43 | 23.04 |
| 1971 | San Fernando | 6.6 | Castaic, Old Ridge Route | 30 | 0.27 | 4.87 |
| 1994 | Northridge | 6.7 | Buena-Park | 35 | 0.14 | 1.62 |
| 1992 | Landers | 7.3 | Baker | 50 | 0.11 | 5.76 |
| 1994 | Northridge | 6.7 | Moorpark (Ventura Fire Stn.) | 60 | 0.29 | 5.48 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naderpour, H.; Danaeifard, P.; Burkacki, D.; Jankowski, R. Earthquake-Induced Pounding of Medium-to-High-Rise Base-Isolated Buildings. Appl. Sci. 2019, 9, 4681. https://doi.org/10.3390/app9214681
Naderpour H, Danaeifard P, Burkacki D, Jankowski R. Earthquake-Induced Pounding of Medium-to-High-Rise Base-Isolated Buildings. Applied Sciences. 2019; 9(21):4681. https://doi.org/10.3390/app9214681
Chicago/Turabian StyleNaderpour, Hosein, Payam Danaeifard, Daniel Burkacki, and Robert Jankowski. 2019. "Earthquake-Induced Pounding of Medium-to-High-Rise Base-Isolated Buildings" Applied Sciences 9, no. 21: 4681. https://doi.org/10.3390/app9214681





