Formation and Breakup of an Immiscible Compound Jet with Density or Viscosity Stratification
Abstract
:1. Introduction
2. Formulation
3. Numerical Method
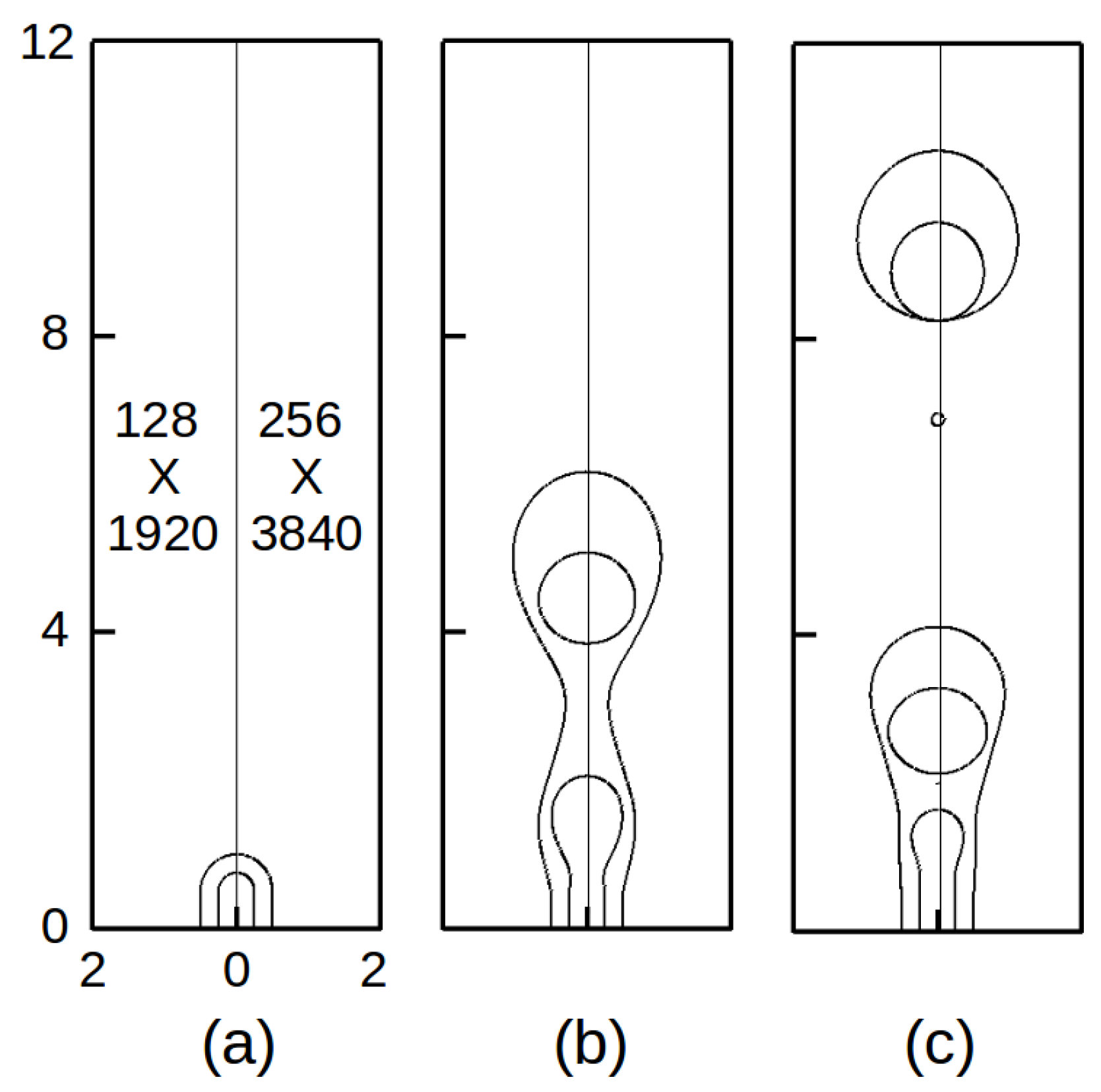
4. Results and Discussion
4.1. Baseline Case
4.2. Effect of Inner-to-Outer Density Ratio
4.3. Effect of Intermediate-to-Outer Density Ratio (
4.4. Effect of Inner-to-Outer Viscosity Ratio (
4.5. Effect of Intermediate-to-Outer Viscosity Ratio (
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abate, A.R.; Thiele, J.; Weitz, D.A. One-step formation of multiple emulsions in microfluidics. Lab Chip 2011, 11, 253–258. [Google Scholar] [CrossRef] [PubMed]
- Denn, M.M. Continuous Drawing of Liquids to form Fibers. Annu. Rev. Fluid Mech. 1980, 12, 365–387. [Google Scholar] [CrossRef]
- Hertz, C.H.; Hermanrud, B. A liquid compound jet. J. Fluid Mech. 1983, 131, 271. [Google Scholar] [CrossRef]
- Shen, J. Experiments on annular liquid jet breakup. At. Sprays 2001, 11, 18. [Google Scholar] [CrossRef]
- Mathiowitz, E.; Jacob, J.S.; Jong, Y.S. Biologically erodable microspheres as potential oral drug delivery systems. Nature 1997, 386, 410–414. [Google Scholar] [CrossRef]
- Herrada, M.A.; Montanero, J.M.; Ferrera, C.; Gañán-calvo, A.M. Analysis of the dripping–jetting transition in compound capillary jets. J. Fluid Mech. 2010, 649, 523. [Google Scholar] [CrossRef]
- Andreas, S.; Alexiou, C.; Bergemann, C. Clinical Applications of Magnetic Drug Targeting. J. Fluid Mech. 2001, 95, 200–206. [Google Scholar]
- Rayleigh, L. On the capillary phenomena of jets. Proc. R. Soc. Lond. 1879, 29, 71–97. [Google Scholar]
- Chauhan, A.; Maldarelli, C.; Papageorgiou, D.T.; Rumschitzki, D.S. Temporal instability of compound threads and jets. J. Fluid Mech. 2000, 420, 1–25. [Google Scholar] [CrossRef]
- Subramani, H.J.; Yeoh, H.K.; Suryo, R.; Xu, Q.; Ambravaneswaran, B.; Basaran, O.A. Simplicity and complexity in a dripping faucet. Phys. Fluids 2006, 18, 1–13. [Google Scholar] [CrossRef]
- Vu, T.V.; Homma, S.; Wells, J.C.; Takakura, H.; Tryggvason, G. Numerical simulation of formation and breakup of a three-fluid compound jet. J. Fluid Sci. Technol. 2011, 6, 252–263. [Google Scholar] [CrossRef]
- Vu, T.V.; Wells, J.C.; Takakura, H.; Homma, S.; Tryggvason, G. Numerical calculations of pattern formation of compound drops detaching from a compound jet in a coflowing immiscible fluid. J. Chem. Eng. Jpn. 2012, 45, 721–726. [Google Scholar] [CrossRef]
- Vu, T.V.; Homma, S.; Tryggvason, G.; Wells, J.C.; Takakura, H. Computations of breakup modes in laminar compound liquid jets in a coflowing fluid. Int. J. Multiph. Flow 2013, 49, 58–69. [Google Scholar] [CrossRef]
- Nadler, J.H.; Sanders, T.H., Jr.; Cochran, J.K. Aluminum hollow sphere processing. Mater. Sci. Forum 2000, 331, 495–500. [Google Scholar] [CrossRef]
- Lee, S.Y.; Snider, C.; Park, K.; Robinson, J.P. Compound jet instability in a microchannel for mononuclear compound drop formation. J. Micromech. Microeng. 2007, 17, 1558–1566. [Google Scholar] [CrossRef]
- Utada, A.S. Monodisperse double emulsions generated from a microcapillary device. Science 2005, 308, 537–541. [Google Scholar] [CrossRef]
- Kendall, J.M. Experiments on annular liquid jet instability and on the formation of liquid shells. Phys. Fluids 1986, 29, 2086. [Google Scholar] [CrossRef]
- Zhou, C.; Yue, P.; Feng, J.J. Formation of simple and compound drops in microfluidic devices. Phys. Fluids 2006, 18, 092105. [Google Scholar] [CrossRef]
- Suryo, R.; Doshi, P.; Basaran, O.A. Nonlinear dynamics and breakup of compound jets. Phys. Fluids 2006, 18, 082107. [Google Scholar] [CrossRef]
- Harlow, F.H.; Welch, J.E. Numerical calculation of time-dependent Viscous incompressible flow of fluid with free surface. Phys. Fluids 1965, 8, 2185–2189. [Google Scholar] [CrossRef]
- Tryggvason, G.; Bunner, B.; Esmaeeli, A.; Juric, D.; Al-Rawahi, N.; Tauber, W.; Han, J.; Nas, S.; Ja, Y.J. A front-tracking method for the computations of multiphase flow. J. Comput. Phys. 2001, 169, 708–759. [Google Scholar] [CrossRef]
- Homma, S.; Koga, J.; Matsumoto, S.; Song, M.; Tryggvason, G. Breakup Mode of an Axisymmetric Liquid Jet Injected into Another Immiscible Liquid. Chem. Eng. Sci. 2006, 61, 3986–3996. [Google Scholar] [CrossRef]
- Cramer, C.; Fischer, P.; Windhab, E.J. Drop formation in a co-flowing ambient fluid. Chem. Eng. Sci. 2004, 59, 3045–3058. [Google Scholar] [CrossRef]
- Pal, R. Rheological Constitutive Equation for Bubbly Suspensions. Ind. Eng. Chem. Res. 2004, 43, 5372–5379. [Google Scholar] [CrossRef]
- Scheele, G.F.; Meister, B.J. Drop formation at low velocities in liquid-liquid systems. AIChE J. 1968, 14, 9–15. [Google Scholar] [CrossRef]
- Rappa, B.E. Microfluidics: Modeling, Mechanics and Mathematics; Elsevier: Amsterdam, The Netherlands, 2017; pp. 745–754. [Google Scholar]
- Afzaal, M.F.; Uddin, J.; Alsharif, A.M.; Mohsin, M. Temporal and spatial instability of a compound jet in a surrounding gas. Phys. Fluids 2015, 27, 044106. [Google Scholar] [CrossRef]
- Homsy, G.M. Viscous Fingering in Porous Media. Annu. Rev. Fluid Mech. 1987, 19, 271–311. [Google Scholar] [CrossRef]
- Omocea, I.L.; Patrascu, C.; Turcanu, M.; Balan, C. Breakup of Liquid Jets. Energy Procedia 2016, 85, 383–389. [Google Scholar] [CrossRef]
- Zhang, D.F.; Stone, H.A. Drop formation in viscous flows at a vertical capillary tube. Phys. Fluids 1997, 9, 2234–2242. [Google Scholar] [CrossRef] [Green Version]











| 0.1–5 | 1–5 | 0.18–5 | 0.18–5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhagat, K.D.; Vu, T.V.; Wells, J.C. Formation and Breakup of an Immiscible Compound Jet with Density or Viscosity Stratification. Appl. Sci. 2019, 9, 4817. https://doi.org/10.3390/app9224817
Bhagat KD, Vu TV, Wells JC. Formation and Breakup of an Immiscible Compound Jet with Density or Viscosity Stratification. Applied Sciences. 2019; 9(22):4817. https://doi.org/10.3390/app9224817
Chicago/Turabian StyleBhagat, Kunal D., Truong V. Vu, and John C. Wells. 2019. "Formation and Breakup of an Immiscible Compound Jet with Density or Viscosity Stratification" Applied Sciences 9, no. 22: 4817. https://doi.org/10.3390/app9224817
APA StyleBhagat, K. D., Vu, T. V., & Wells, J. C. (2019). Formation and Breakup of an Immiscible Compound Jet with Density or Viscosity Stratification. Applied Sciences, 9(22), 4817. https://doi.org/10.3390/app9224817






