Stress Distribution of Pediatric Zirconia and Stainless Steel Crowns after Pulpotomy Procedure under Vertical Loading: A Patient-Specific Finite Element Analysis
Abstract
:1. Introduction
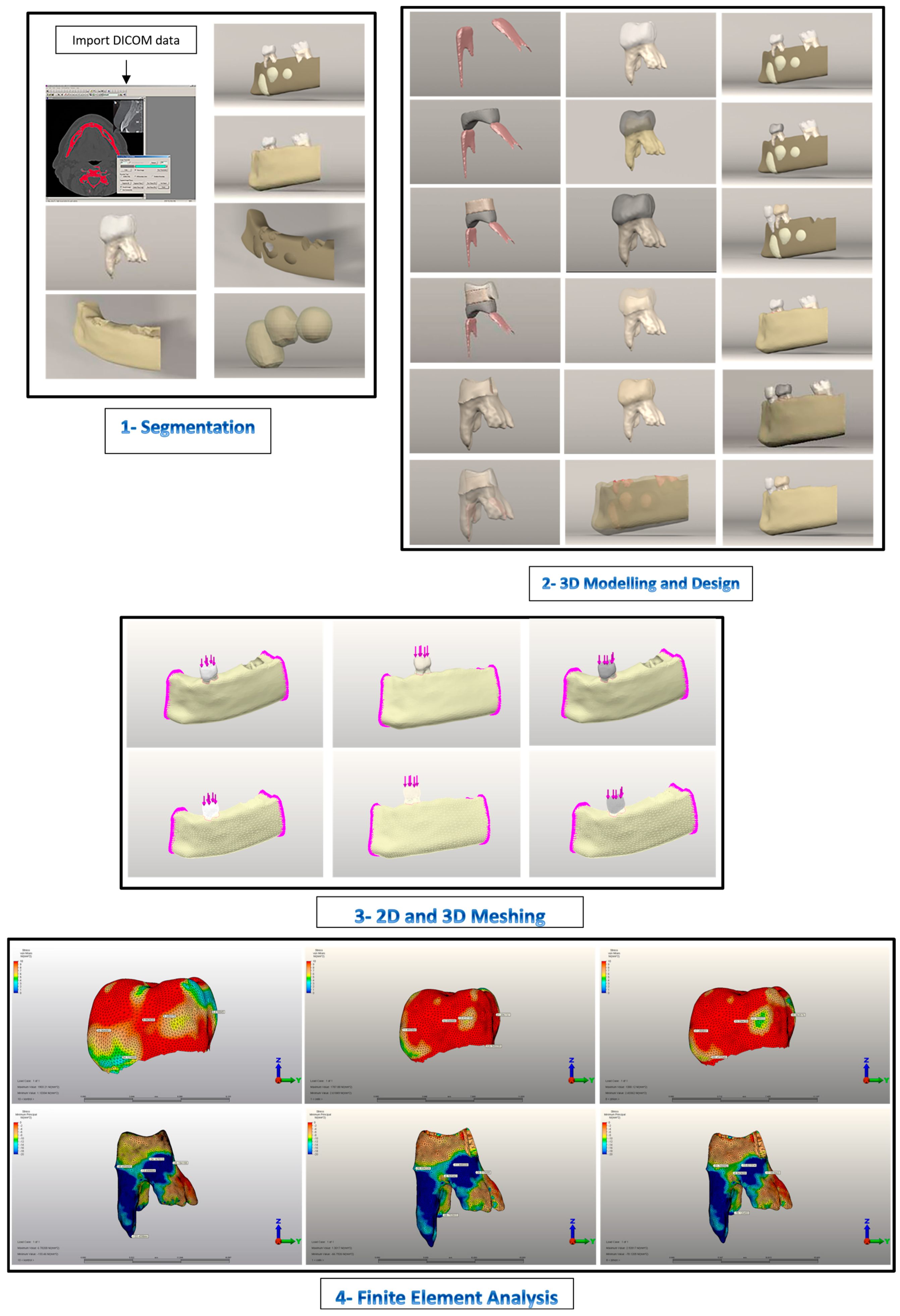
2. Materials and Methods
2.1. Model Generation
2.1.1. Boundary Conditions
2.1.2. Simulation of Force Loading and FEA
2.1.3. Statistical Analyses and Interpretation of Analysis Results
3. Results
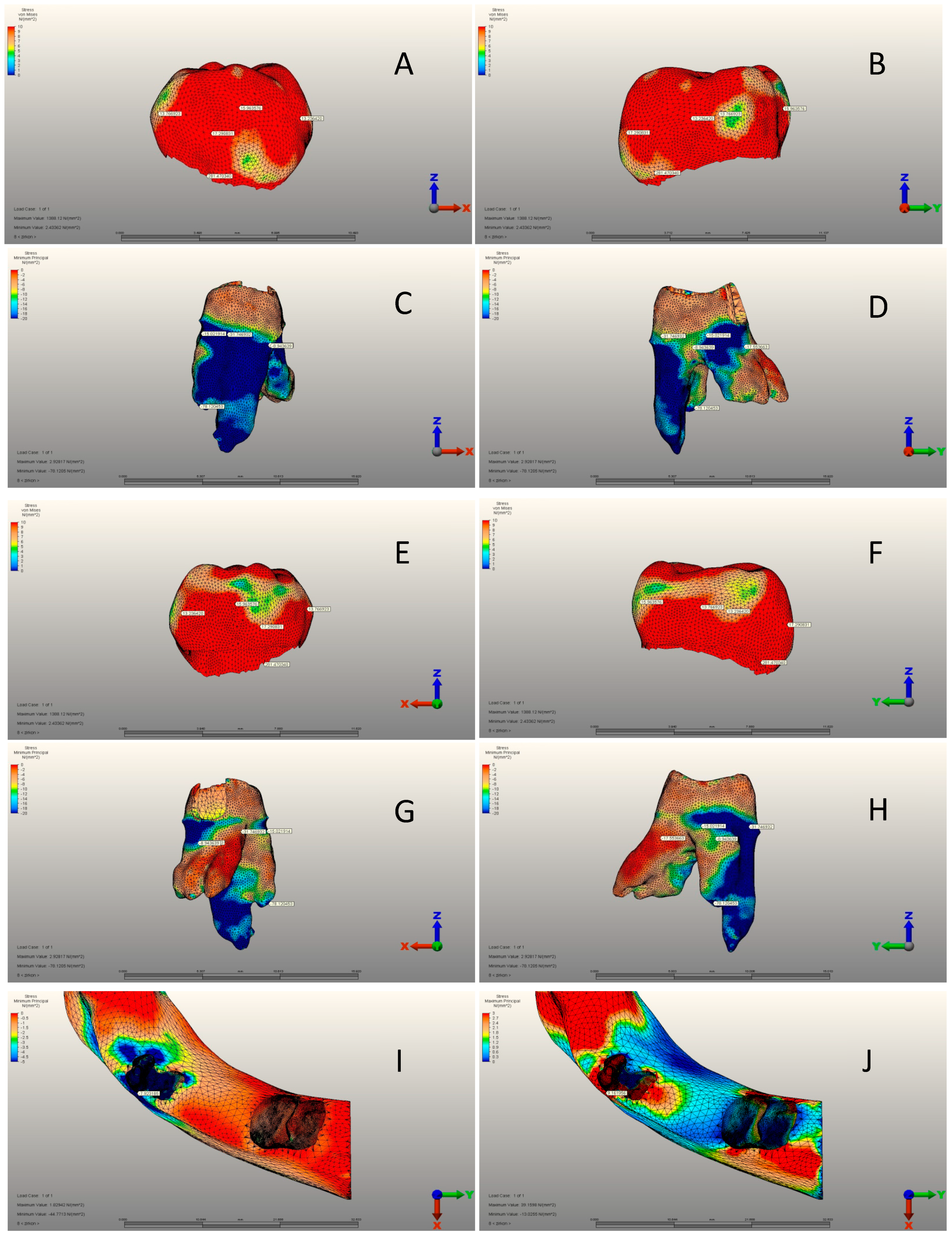
3.1. Pediatric Zirconia, Stainless Steel, and Control Group Crowns
3.2. Pediatric Zirconia, Stainless Steel, and Control Group Roots
3.3. Pediatric Zirconia, Stainless Steel, and Control Group Cement Layers
4. Discussion
5. Conclusions
- The von Mises stress values for SSCs are higher regardless of the cement used. Steel material’s flexibility and force-absorbing properties are likely to be responsible for this situation.
- Compressive stress values were highest in intact tooth root areas. Without intervention in the stress transmission mechanism, the intact tooth’s root area experiences higher stress values. This mechanism involves the use of restorative materials and cement. Consequently, they alter the stress transmission mechanism, causing stress to accumulate on them.
- In PZC crowns, the zirconia material’s rigidity leads to a higher transmission of von Mises stresses to the root area.
- Despite the same cement layer thickness in PZC and SSC crowns, SSC crowns achieved higher compressive values. It is believed that steel absorbs chewing stress, distributes it throughout the crown, and transmits it to the cement layer. Due to its rigid structure, zirconia seems to have a linear stress transmission mechanism in PZCs.
- In the mixed dentition, cortical and cancellous bones are not sensitive to chewing forces transmitted through crowns in full-coverage crown restorations. Cement or crown composition had no effect on this situation. Possibly, this is due to the periodontal ligament’s buffering capacity, which absorbs chewing force.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alamoudi, R.A.; Walia, T.; Debaybo, D. Evaluation of the Clinical Performance of NuSmile Pedodontics Zirconia Crowns in Pulp-Treated Primary Teeth—2 Years Follow-Up Study. Eur. J. Dent. 2022, 17, 82–90. [Google Scholar] [CrossRef] [PubMed]
- Walia, T.; Salami, A.A.; Bashiri, R.; Hamoodi, O.M.; Rashid, F. A randomised controlled trial of three aesthetic full-coronal restorations in primary maxillary teeth. Eur. J. Paediatr. Dent. 2014, 15, 113–118. [Google Scholar]
- Alrashdi, M.; Ardoin, J.; Liu, J.A. Zirconia crowns for children: A systematic review. Int. J. Paediatr. Dent. 2021, 32, 66–81. [Google Scholar] [CrossRef]
- Patnana, A.K.; Chugh, V.K.; Chugh, A.; Vanga, N.R.V.; Kumar, P. Effectiveness of zirconia crowns compared with stainless steel crowns in primary posterior teeth rehabilitation. J. Am. Dent. Assoc. 2022, 153, 158–166.e5. [Google Scholar] [CrossRef] [PubMed]
- Chowdhary, R.; Ajayakumar, L.P.; Chowdhary, N.; Reddy, V.R. Use of Restorative Full Crowns Made with Zirconia in Children: A Systematic Review. Int. J. Clin. Pediatr. Dent. 2020, 13, 551–558. [Google Scholar] [CrossRef]
- Larsson, C.; Wennerberg, A. The Clinical Success of Zirconia-Based Crowns: A Systematic Review. Int. J. Prosthodont. 2014, 27, 33–43. [Google Scholar] [CrossRef] [PubMed]
- Dogan, O.; Dogan, S.S.A. Arm design of band and loop space maintainer affects its longevity: A patient-specific finite element study. J. Clin. Pediatr. Dent. 2024, 48, 171–183. [Google Scholar] [CrossRef] [PubMed]
- Doğan, S.S.A.; Doğan, Ö.; Doğan, Ö.; Başkurt, N.A. Protective potential of different mouthguard thicknesses against perianaesthetic dental specific-finite element study. Comput. Methods Biomech. Biomed. Eng. 2023, 27, 1346–1356. [Google Scholar] [CrossRef]
- Tribst, J.P.M.; Piva, A.M.d.O.D.; Bottino, M.A.; Kleverlaan, C.J.; Koolstra, J.H. Mouthguard use and TMJ injury prevention with different occlusions: A three-dimensional finite element analysis. Dent. Traumatol. 2020, 36, 662–669. [Google Scholar] [CrossRef]
- de Bragança, G.F.; Vilela, A.B.F.; Soares, P.B.F.; Tantbirojn, D.; Versluis, A.; Soares, C.J. Influence of ceramic veneer thickness and antagonist on impact stresses during dental trauma with and without a mouthguard assessed with finite element analysis. Dent. Traumatol. 2020, 37, 215–222. [Google Scholar] [CrossRef]
- Seale, N.S.; Randall, R. The use of stainless steel crowns: A systematic literature review. Pediatr. Dent. 2015, 37, 145–160. [Google Scholar] [PubMed]
- Geduk, N.; Ozdemir, M.; Unverdi, G.E.; Ballikaya, E.; Cehreli, Z.C. Clinical and radiographic performance of preformed zirconia crowns and stainless-steel crowns in permanent first molars: 18-month results of a prospective, randomized trial. BMC Oral Health 2023, 23, 828. [Google Scholar] [CrossRef] [PubMed]
- Mathew, M.G.; Roopa, K.B.; Soni, A.J.; Khan, M.; Kauser, A. Evaluation of clinical success, parental and child satisfaction of stainless steel crowns and zirconia crowns in primary molars. J. Fam. Med. Prim. Care 2020, 9, 1418–1423. [Google Scholar] [CrossRef]
- Pei, S.-L.; Chen, M.-H. Comparison of periodontal health of primary teeth restored with zirconia and stainless steel crowns: A systemic review and meta-analysis. J. Formos. Med. Assoc. 2023, 122, 148–156. [Google Scholar] [CrossRef]
- American Academy of Pediatric Dentistry. Clinical Affairs Committee—Restorative Dentistry Subcommittee. Guideline on pediatric restorative dentistry. Pediatr. Dent. 2012, 34, 173–180. [Google Scholar]
- Kindelan, S.A.; Day, P.; Nichol, R.; Willmott, N.; Fayle, S.A. UK National Clinical Guidelines in Paediatric Dentistry: Stainless steel preformed crowns for primary molars. Int. J. Paediatr. Dent. 2008, 18, 20–28. [Google Scholar] [CrossRef]
- Conway, F. Primary pulpotomies—What should we be using? Evid. Based Dent. 2022, 23, 150–151. [Google Scholar] [CrossRef] [PubMed]
- Canoglu, E.; Gungor, H.C.; Uysal, S. Direct Pulp Capping of Primary Molars with Calcium Hydroxide or MTA Following Hemorrhage Control with Different Medicaments: Randomized Clinical Trial. Pediatr. Dent. 2022, 44, 167–173. [Google Scholar]
- El Karim, I.A.; Duncan, H.F.; Fouad, A.F.; Taha, N.A.; Yu, V.; Saber, S.; Ballal, V.; Chompu-Inwai, P.; Ahmed, H.M.A.; Gomes, B.P.F.A.; et al. Effectiveness of full Pulpotomy compared with Root canal treatment in managing teeth with signs and symptOms indicative of irreversible pulpitis: A protocol for prospectiVE meta-analysis of individual participant data of linked randomised clinical trials (PROVE). Trials 2023, 24, 807. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Changiz, S.; Makarem, A.; Ahrari, F. Clinical and radiographic effectiveness of mineral trioxide aggregate (MTA) partial pulpotomy with low power or high power diode laser irradiation in deciduous molars: A randomized clinical trial. Lasers Med. Sci. 2022, 37, 2293–2303. [Google Scholar] [CrossRef]
- Saket, P.; Gandhi, S.; Anandan, V.; Inbanathan, J.; Krishnamoorthy, V.; Chandrababu, V.K. Assessment of Clinical and Radiographic Success Rate of Formocresol-based Pulpotomy versus Collagen-based Pulpotomy: An In Vivo Study. J. Contemp. Dent. Pract. 2021, 22, 680–685. [Google Scholar] [CrossRef]
- Demirel, A.; Bezgin, T.; Sarı, Ş. Effects of Root Maturation and Thickness Variation in Coronal Mineral Trioxide Aggregate Plugs Under Traumatic Load on Stress Distribution in Regenerative Endodontic Procedures: A 3-dimensional Finite Element Analysis Study. J. Endod. 2020, 47, 492–499.e4. [Google Scholar] [CrossRef] [PubMed]
- Demirel, A.; Sarı, Ş. Are Increased Masticatory Forces Risk for Primary 2nd Molars without Successors? A 3D FEA Study. J. Clin. Pediatr. Dent. 2019, 43, 64–68. [Google Scholar] [CrossRef] [PubMed]
- Firmiano, T.C.; de Oliveira, A.A.; Costa, P.V.d.M.; Cardoso, L.S.; Pereira, R.D.; Veríssimo, C. Influence of different ethylene-vinyl acetate brands used for custom-fitted mouthguard fabrication on the stress and strain during an impact. Dent. Traumatol. 2022, 38, 431–438. [Google Scholar] [CrossRef]
- Otani, T.; Kobayashi, M.; Nozaki, K.; Gonda, T.; Maeda, Y.; Tanaka, M. Influence of mouthguards and their palatal design on the stress-state of tooth-periodontal ligament-bone complex under static loading. Dent. Traumatol. 2018, 34, 208–213. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, A.; Prabhakar, A.R.; Nadig, B.; Yavagal, C. Finite element stress analysis of restored primary teeth: A comparative evaluation between stainless steel crowns and preformed zirconia crowns. Int. J. Oral Health Sci. 2017, 7, 10. [Google Scholar] [CrossRef]
- Belli, S.; Eraslan, O.; Eskitascioglu, G. Effect of Root Filling on Stress Distribution in Premolars with Endodontic-Periodontal Lesion: A Finite Elemental Analysis Study. J. Endod. 2016, 42, 150–155. [Google Scholar] [CrossRef]
- Guler, M.S.; Guler, C.; Kara, N.B.; Odabasi, D.; Bekci, M.L. The stress distribution of a primary molar tooth restored with stainless steel crown using different luting cements. BMC Oral Health 2024, 24, 269. [Google Scholar] [CrossRef]
- Chung, S.-Y.; Lee, H.; Chae, Y.K.; Jung, Y.S.; Jo, S.-S.; Lee, K.E.; Choi, S.C.; Nam, O.H. Stress distribution in pediatric zirconia crowns depending on different tooth preparation and cement type: A finite element analysis. BMC Oral Health 2022, 22, 550. [Google Scholar] [CrossRef]
- Öksüzer, M.Ç.; Çıkman, A.Ş. Evaluation of Fracture Strength after Repair of Cervical External Resorption Cavities with Different Materials. J. Endod. 2024, 50, 85–95. [Google Scholar] [CrossRef]
- NuSmile® Pre Contoured SSC Instruction for Use. Available online: https://www.flipsnack.com/6C989CDD75E/ifu-35-nusmile-ssc-instructions-for-use-multi-lang-rev-5/full-view.html (accessed on 2 September 2024).
- Clark, L.; Wells, M.H.; Harris, E.F.; Lou, J. Comparison of Amount of Primary Tooth Reduction Required for Anterior and Posterior Zirconia and Stainless Steel Crowns. Pediatr. Dent. 2016, 38, 42–46. [Google Scholar] [PubMed]
- NuSmile® Zirconia Instructions for Use and General Information. Available online: https://www.flipsnack.com/6C989CDD75E/ifu-05-zr-technical-guide-eng-rev-13/full-view.html (accessed on 2 September 2024).
- Sagsoz, N.; Yanıkoglu, N. Evaluation of the fracture resistance of computer-aided design/computer-aided manufacturing monolithic crowns prepared in different cement thicknesses. Niger. J. Clin. Pract. 2018, 21, 417–422. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Jo, M.; Sailer, I.; Noh, G. Effects of implant diameter, implant-abutment connection type, and bone density on the biomechanical stability of implant components and bone: A finite element analysis study. J. Prosthet. Dent. 2021, 128, 716–728. [Google Scholar] [CrossRef]
- Karimizadeh, Z.; Sabeti, A.K.; Rafatjou, R. Maximum equivalent stress induced and the displacement of the developing permanent first molars after the premature loss of primary second molars: A finite element analysis. Dent. Med. Probl. 2020, 57, 401–409. [Google Scholar] [CrossRef]
- Guduk, O.F.; Sivrikaya, E.C.; Yilmaz, N.; Baygin, O.; Tuzuner, T. Is zirconium or stainless steel the most suitable crown material for less dentin stress in endodontically treated teeth? Technol. Health Care 2022, 30, 1199–1207. [Google Scholar] [CrossRef] [PubMed]
- Hollanders, A.; Kuper, N.; Huysmans, M.; Versluis, A. The effect of occlusal loading on cervical gap deformation: A 3D finite element analysis. Dent. Mater. 2020, 36, 681–686. [Google Scholar] [CrossRef] [PubMed]
- Owais, A.I.; Shaweesh, M.; Abu Alhaija, E.S.J. Maximum occusal bite force for children in different dentition stages. Eur. J. Orthod. 2012, 35, 427–433. [Google Scholar] [CrossRef]
- Waly, A.S.; Souror, Y.R.; Yousief, S.A.; Alqahtani, W.M.; El-Anwar, M.I. Pediatric Stainless-Steel Crown Cementation Finite Element Study. Eur. J. Dent. 2020, 15, 077–083. [Google Scholar] [CrossRef]
- Bramanti, E.; Cervino, G.; Lauritano, F.; Fiorillo, L.; D’amico, C.; Sambataro, S.; Denaro, D.; Famà, F.; Ierardo, G.; Polimeni, A.; et al. FEM and Von Mises Analysis on Prosthetic Crowns Structural Elements: Evaluation of Different Applied Materials. Sci. World J. 2017, 2017, 1029574. [Google Scholar] [CrossRef]
- Amend, S.; Boutsiouki, C.; Bekes, K.; Kloukos, D.; Gizani, S.; Lygidakis, N.N.; Frankenberger, R.; Krämer, N. Clinical effectiveness of restorative materials for the restoration of carious lesions in pulp treated primary teeth: A systematic review. Eur. Arch. Paediatr. Dent. 2022, 23, 761–776. [Google Scholar] [CrossRef]
- Stanley, J.N. AMM. Wheeler’s Dental Anatomy, Physiology and Occlusion; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Erdemci, Z.Y.; Cehreli, S.B.; Tirali, R.E. Hall versus conventional stainless steel crown techniques: In vitro investigation of marginal fit and microleakage using three different luting agents. Pediatr. Dent. 2014, 36, 286–290. [Google Scholar] [PubMed]
- Rentes, A.M.; Gavião, M.B.D.; Amaral, J.R. Bite force determination in children with primary dentition. J. Oral Rehabil. 2002, 29, 1174–1180. [Google Scholar] [CrossRef] [PubMed]
- Prabhakar, A.R.; Yavagal, C.M.; Chakraborty, A.; Sugandhan, S. Finite Element Stress Analysis of Stainless Steel Crowns. Saudi J. Kidney Dis. Transplant. 2015, 33, 183–191. [Google Scholar] [CrossRef] [PubMed]
- European Commission. Medical Radiation Exposure of the European Population; Publications Office of the European Union: Luxembourg, 2015; Available online: https://data.europa.eu/doi/10.2833/708119 (accessed on 2 September 2024).
- Abduljabar, A.H.; Iskander, A.W.; Elfezary, M.T.; Wakwak, M.A.A.; Bathabt, W.A.; Souror, Y.R. Endocrown Feasibility for Primary Molars: A Finite Element Study. Eur. J. Dent. 2023, 18, 208–213. [Google Scholar] [CrossRef]
- Jing, L.; Chen, J.-W.; Roggenkamp, C.; Suprono, M.S. Effect of Crown Preparation Height on Retention of a Prefabricated Primary Posterior Zirconia Crown. Pediatr. Dent. 2019, 41, 229–233. Available online: http://www.ncbi.nlm.nih.gov/pubmed/31171076. (accessed on 2 September 2024).



| Part | Hounsfield Unit | |
|---|---|---|
| Min | Max | |
| Cortical bone | 662 | 1988 |
| Cancellous bone | 148 | 661 |
| Enamel | 1553 | 2850 |
| Dentin | 1200 | 1552 |
| Groups | Number of Nodes | Number of Elements |
|---|---|---|
| Control | 129,863 | 600,043 |
| Pediatric zirconia group | 156,290 | 708,986 |
| Stainless steel group | 156,678 | 709,751 |
| Materials | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|
| Primary teeth enamel | 80,349 | 0.33 [26] |
| Primary teeth dentine | 19,890 | 0.31 [26] |
| Pulp | 30 | 0.45 [8] |
| Periodontal ligament | 50 | 0.49 [27] |
| Stainless steel crown | 200,000 | 0.33 [28] |
| Pediatric zirconia crown | 205,000 | 0.19 [29] |
| Mineral trioxide aggregate | 11,700 | 0.31 [30] |
| Cortical bone | 13,700 | 0.30 [8] |
| Cancellous bone | 1400 | 0.30 [8] |
| Resin-modified glass ionomer cement | 3700 | 0.30 [28] |
| Glass ionomer cement | 10,800 | 0.25 [30] |
| Crown Variables | Control Group | Stainless Steel Crown | Pediatric Zirconia Crown | p-Value | |
|---|---|---|---|---|---|
| Mesial view (MPa) | Mean ± SD | 5.24 ± 2.01 | 13.01 ± 4.02 | 13.76 ± 3.56 | <0.001 a |
| Median (min–max) | 4.88 (2.09–9.05) | 13.17 (5.95–19.13) | 13.75 (8.39–22.18) | ||
| Buccal view (MPa) | Mean ± SD | 14.96 ± 2.91 | 11.98 ± 3.05 | 17.29 ± 2.73 | <0.001 a |
| Median (min–max) | 15.98 (7.57–20.87) | 12.64 (5.82–17.15) | 17.82 (12.38–22.82) | ||
| Distal view (MPa) | Mean ± SD | 9.94 ± 1.92 | 14.03 ± 2.79 | 13.23 ± 2.46 | <0.001 a |
| Median (min–max) | 9.97 (6.57–13.34) | 13.74 (10.88–21.10) | 13.37 (9.84–17.63) | ||
| Lingual view (MPa) | Mean ± SD | 6.61 ± 1.76 | 21.39 ± 4.06 | 15.96 ± 2.97 | <0.001 a |
| Median (min–max) | 6.71 (4.33–9.53) | 22.06 (14.50–27.45) | 17.02 (10.78–20.41) | ||
| Max. von Mises stress (MPa) | Mean ± SD | 54.12 ± 10.98 | 326.54 ± 24. 84 | 281.47 ± 27.76 | <0.001 a |
| Median (min–max) | 54.22 (34.47–73.13) | 330.10 (271.50–359.29) | 280.26 (238.81–317.58) | ||
| Root Structure Variables | Control Group | Stainless Steel Crown | Pediatric Zirconia Crown | p-Value | ||
|---|---|---|---|---|---|---|
| Mesial view (MPa) | Maximum principal stresses | Mean ± SD | 0.89 ± 0.08 | 0.21 ± 0.06 | 0.05 ± 0.01 | <0.001 a |
| Median (min–max) | 0.89 (0.78–1.13) | 0.21 (0.11–0.30) | 0.05 (0.03–0.07) | |||
| Minimum principal stresses | Mean ± SD | 35.65 ± 6.92 | 30.93 ± 6.25 | 31.74 ± 6.24 | 0.056 a | |
| Median (min–max) | 34.29 (26.26–48.97) | 31.22 (17.37–40.83) | 30.53 (22.38–42.61) | |||
| Buccal view (MPa) | Maximum principal stresses | Mean ± SD | 0.06 ± 0.02 | 0.12 ± 0.03 | 0.01 ± 0.01 | <0.001 b |
| Median (min–max) | 0.06 (0.03–0.11) | 0.12 (0.07–0.18) | 0.01 (0.00–0.02) | |||
| Minimum principal stresses | Mean ± SD | 13.69 ± 2.30 | 8.76 ± 2.96 | 8.95 ± 2.00 | <0.001 a | |
| Median (min–max) | 13.38 (9.70–17.47) | 9.19 (4.31–13.75) | 8.48 (4.69–12.96) | |||
| Distal view (MPa) | Maximum principal stresses | Mean ± SD | 0.25 ± 0.06 | 0.90 ± 0.16 | 0.08 ± 0.02 | <0.001 a |
| Median (min–max) | 0.25 (0.13–0.37) | 0.92 (0.53–1.13) | 0.08 (0.05–0.13) | |||
| Minimum principal stresses | Mean ± SD | 20.15 ± 4.20 | 26.51 ± 3.61 | 17.55 ± 3.58 | <0.001 b | |
| Median (min–max) | 19.52 (13.86–26.80) | 27.49 (20.13–31.69) | 17.58 (11.94–25.27) | |||
| Lingual view (MPa) | Maximum principal stresses | Mean ± SD | 1.92 ± 0.33 | 0.42 ± 0.13 | 0.45 ± 0.09 | <0.001 a |
| Median (min–max) | 1.91 (1.42–2.64) | 0.45 (0.21–0.59) | 0.47 (0.28–0.61) | |||
| Minimum principal stresses | Mean ± SD | 24.15 ± 4.63 | 11.94 ± 2.73 | 15.02 ± 2.88 | <0.001 a | |
| Median (min–max) | 24.77 (14.35–32.52) | 12.03 (5.54–17.51) | 15.29 (8.41–21.90) | |||
| The highest principal stress (MPa) | Maximum principal stresses | Mean ± SD | 53.71 ± 12.20 | 37.24 ± 9.36 | 43.48 ± 9.20 | <0.001 a |
| Median (min–max) | 50.58 (35.64–75.60) | 37.65 (17.78–55.69) | 41.23 (26.16–57.78) | |||
| Minimum principal stresses | Mean ± SD | 133.44 ± 19.67 | 66.79 ± 11.39 | 78.12 ± 11.98 | <0.001 a | |
| Median (min–max) | 130.83 (101.20–174.26) | 65.08 (41.15–91.45) | 78.41 (59.45–95.38) | |||
| Cement Layer | Stainless Steel Crown | Pediatric Zirconia Crown | p-Value | |
|---|---|---|---|---|
| Mesial view (MPa) | Mean ± SD | 1.23 ± 0.25 | 1.49 ± 0.32 | 0.007 a |
| Median (min–max) | 1.24 (0.86–1.62) | 1.46 (0.79–2.13) | ||
| Buccal view (MPa) | Mean ± SD | 1.45 ± 0.43 | 1.63 ± 0.58 | 0.270 a |
| Median (min–max) | 1.51 (0.69–2.11) | 1.65 (0.83–2.93) | ||
| Distal view (MPa) | Mean ± SD | 1.46 ± 0.37 | 1.29 ± 0.28 | 0.110 a |
| Median (min–max) | 1.46 (0.56–2.11) | 1.35 (0.70–1.79) | ||
| Lingual view (MPa) | Mean ± SD | 1.56 ± 0.40 | 1.29 ± 0.34 | 0.027 a |
| Median (min–max) | 1.61 (0.87–2.22) | 1.38 (0.63–1.87) | ||
| Max. von Mises stress (MPa) | Mean ± SD | 16.61 ± 3.64 | 13.58 ± 2.01 | 0.003 b |
| Median (min–max) | 16.82 (10.47–23.76) | 13.95 (10.38–16.55) | ||
| Alveolar Bone Structures | Control Group | Stainless Steel Crown | Pediatric Zirkonia Crown | p-Value | ||
|---|---|---|---|---|---|---|
| Cortical bones (MPa) | Maximum principal stresses | Mean ± SD | 9.02 ± 1.85 | 9.74 ± 2.11 | 9.16 ± 1.99 | 0.477 a |
| Median (min–max) | 8.60 (6.16–13.19) | 9.76 (6.36–13.63) | 9.25 (6.36–13.24) | |||
| Minimum principal stresses | Mean ± SD | 7.19 ± 1.94 | 8.08 ± 1.88 | 7.92 ± 1.98 | 0.306 a | |
| Median (min–max) | 7.27 (3.48–10.02) | 8.07 (4.14–12.43) | 8.34 (4.51–10.82) | |||
| Cancellous bone (MPa) | Maximum principal stresses | Mean ± SD | 1.22 ± 0.20 | 1.24 ± 0.22 | 1.30 ± 0.26 | 0.493 b |
| Median (min–max) | 1.23 (0.77–1.58) | 1.17 (0.84–1.76) | 1.33 (0.75–1.74) | |||
| Minimum principal stresses | Mean ± SD | 4.22 ± 1.10 | 4.34 ± 1.63 | 4.22 ± 1.03 | 0.950 a | |
| Median (min–max) | 4.07 (2.53–6.74) | 4.58 (1.91–6.97) | 3.96 (2.79–6.12) | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doğan, Ö. Stress Distribution of Pediatric Zirconia and Stainless Steel Crowns after Pulpotomy Procedure under Vertical Loading: A Patient-Specific Finite Element Analysis. J. Funct. Biomater. 2024, 15, 268. https://doi.org/10.3390/jfb15090268
Doğan Ö. Stress Distribution of Pediatric Zirconia and Stainless Steel Crowns after Pulpotomy Procedure under Vertical Loading: A Patient-Specific Finite Element Analysis. Journal of Functional Biomaterials. 2024; 15(9):268. https://doi.org/10.3390/jfb15090268
Chicago/Turabian StyleDoğan, Özgür. 2024. "Stress Distribution of Pediatric Zirconia and Stainless Steel Crowns after Pulpotomy Procedure under Vertical Loading: A Patient-Specific Finite Element Analysis" Journal of Functional Biomaterials 15, no. 9: 268. https://doi.org/10.3390/jfb15090268
APA StyleDoğan, Ö. (2024). Stress Distribution of Pediatric Zirconia and Stainless Steel Crowns after Pulpotomy Procedure under Vertical Loading: A Patient-Specific Finite Element Analysis. Journal of Functional Biomaterials, 15(9), 268. https://doi.org/10.3390/jfb15090268






