Improved Design of Slope-Shaped Hole-Blocking Layer and Electron-Blocking Layer in AlGaN-Based Near-Ultraviolet Laser Diodes
Abstract
:1. Introduction
2. Laser Structure and Simulation Parameters
2.1. Laser Structure
2.2. Simulation Parameters
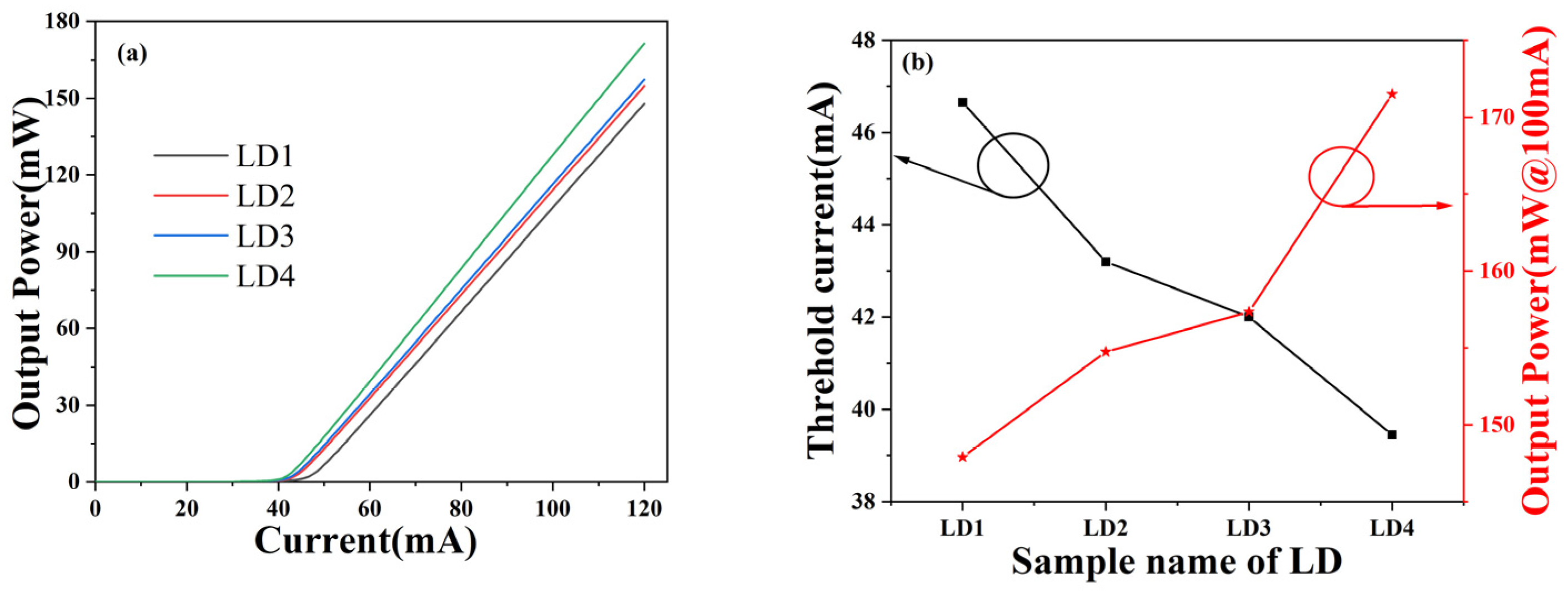
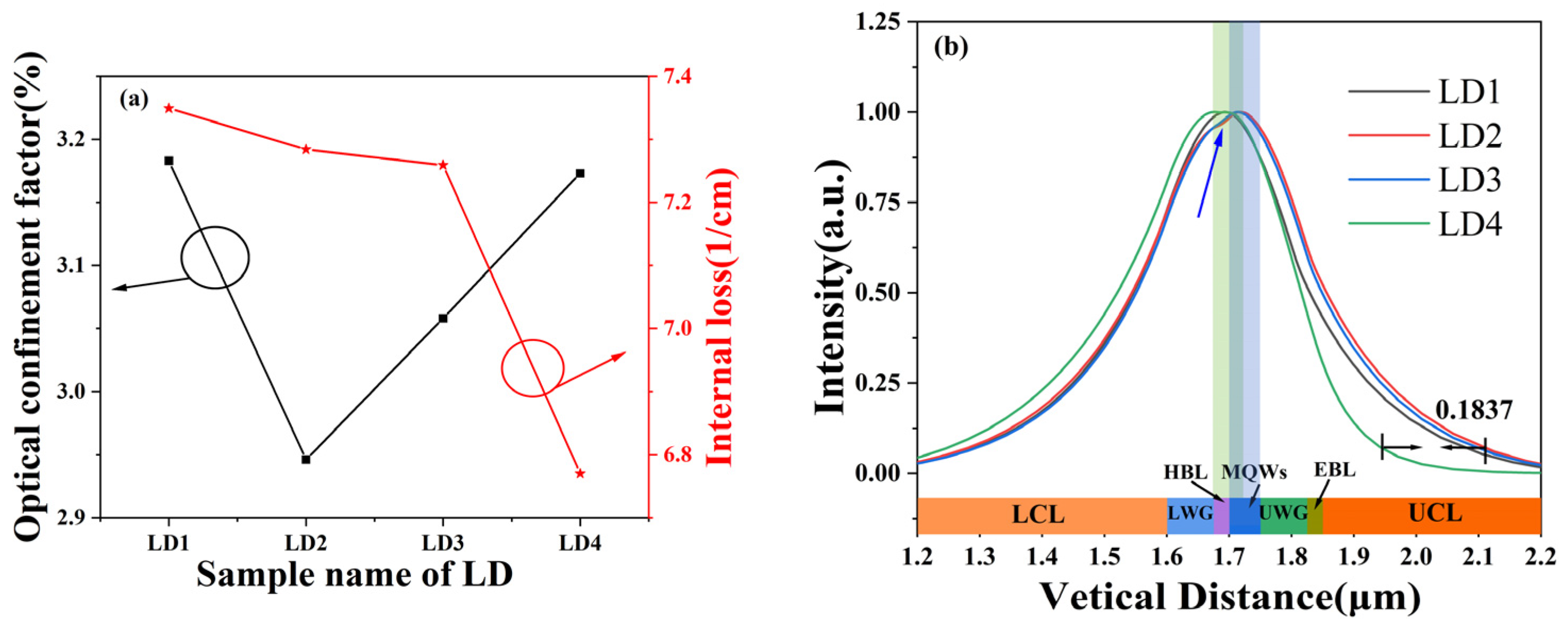
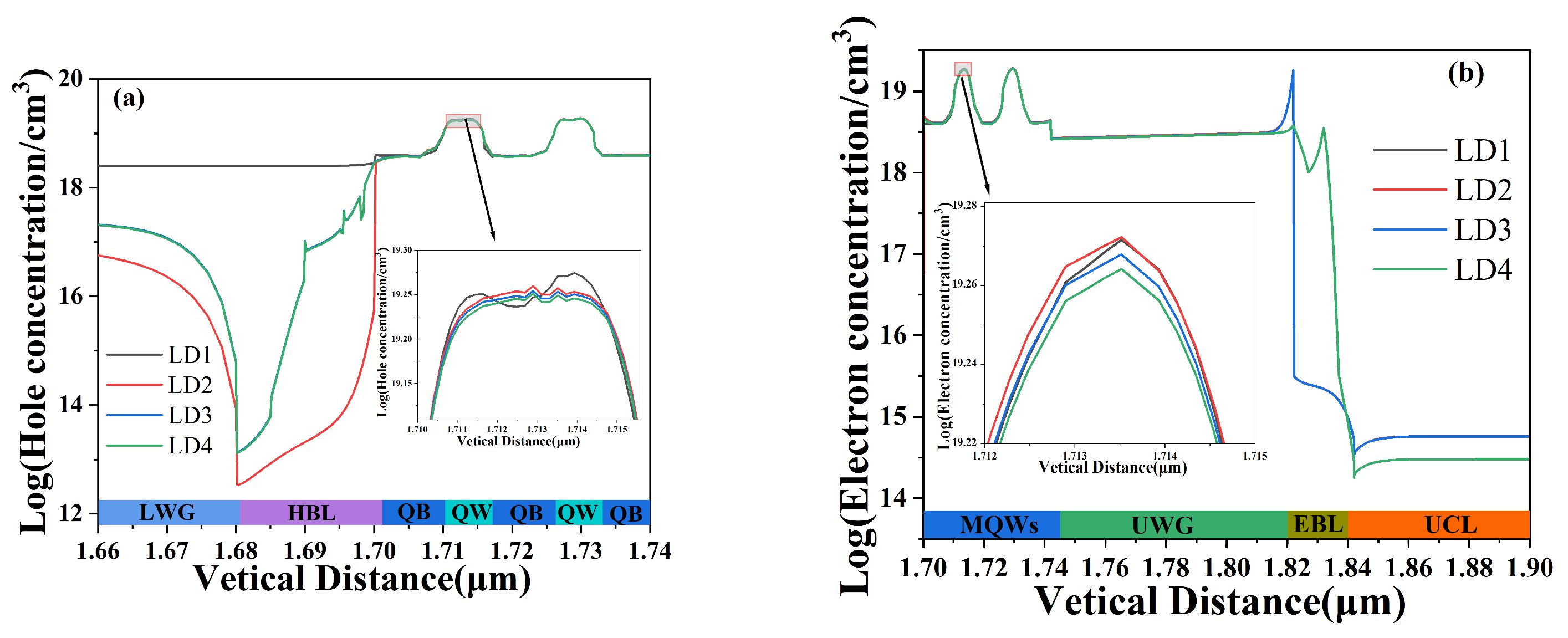
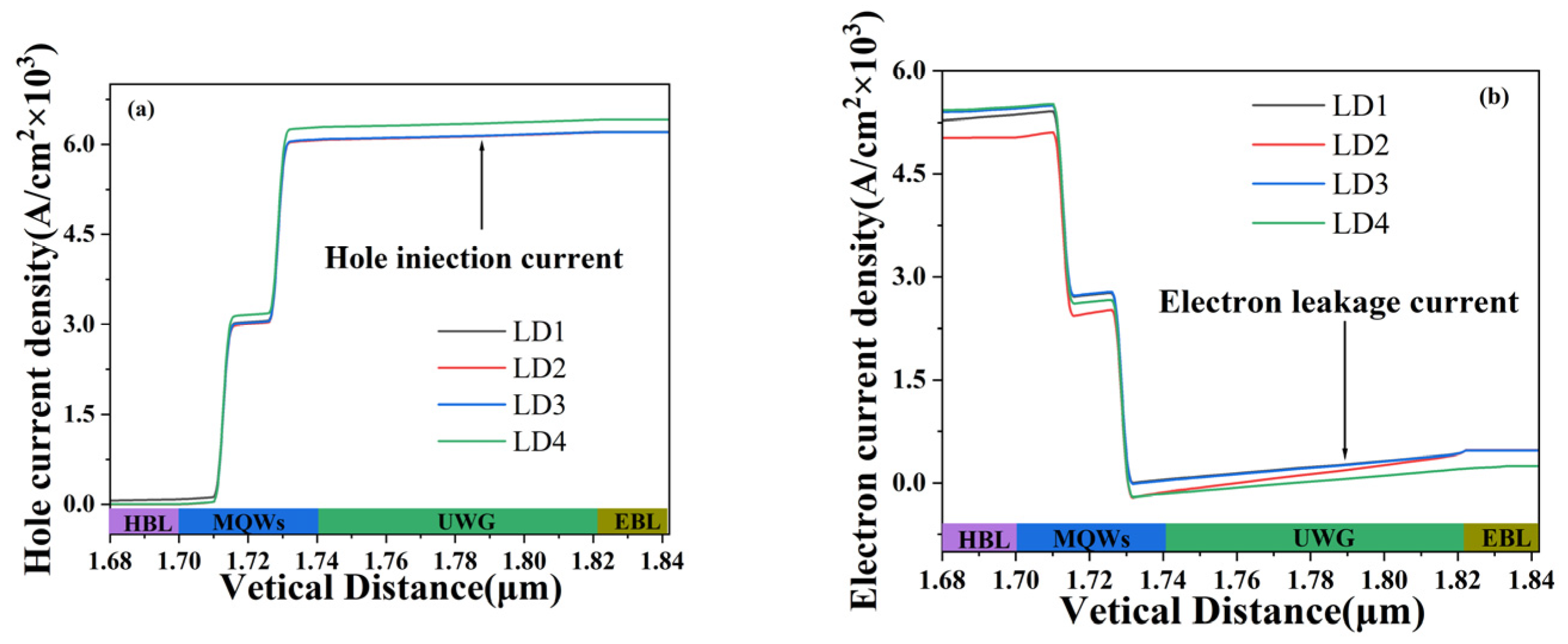
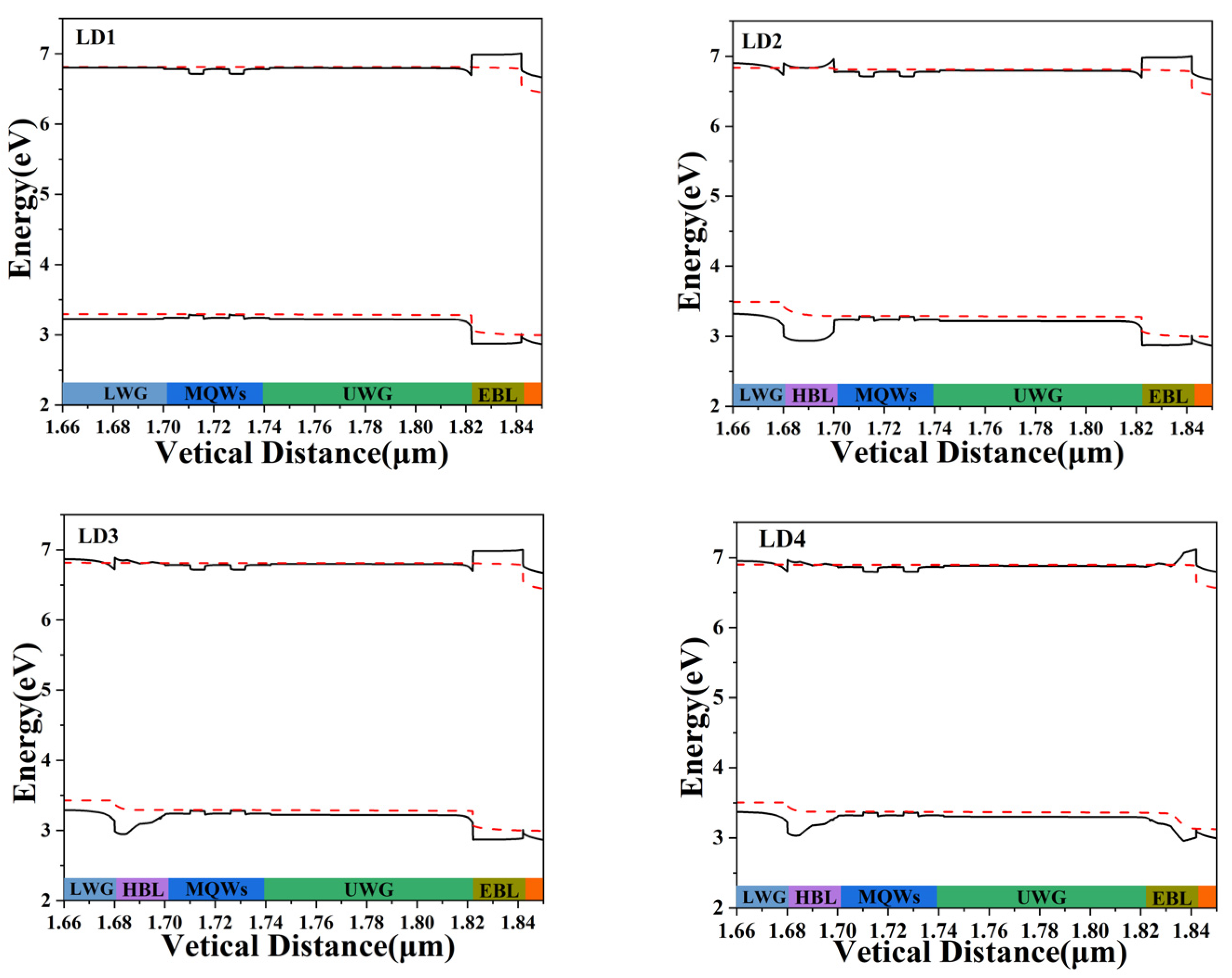
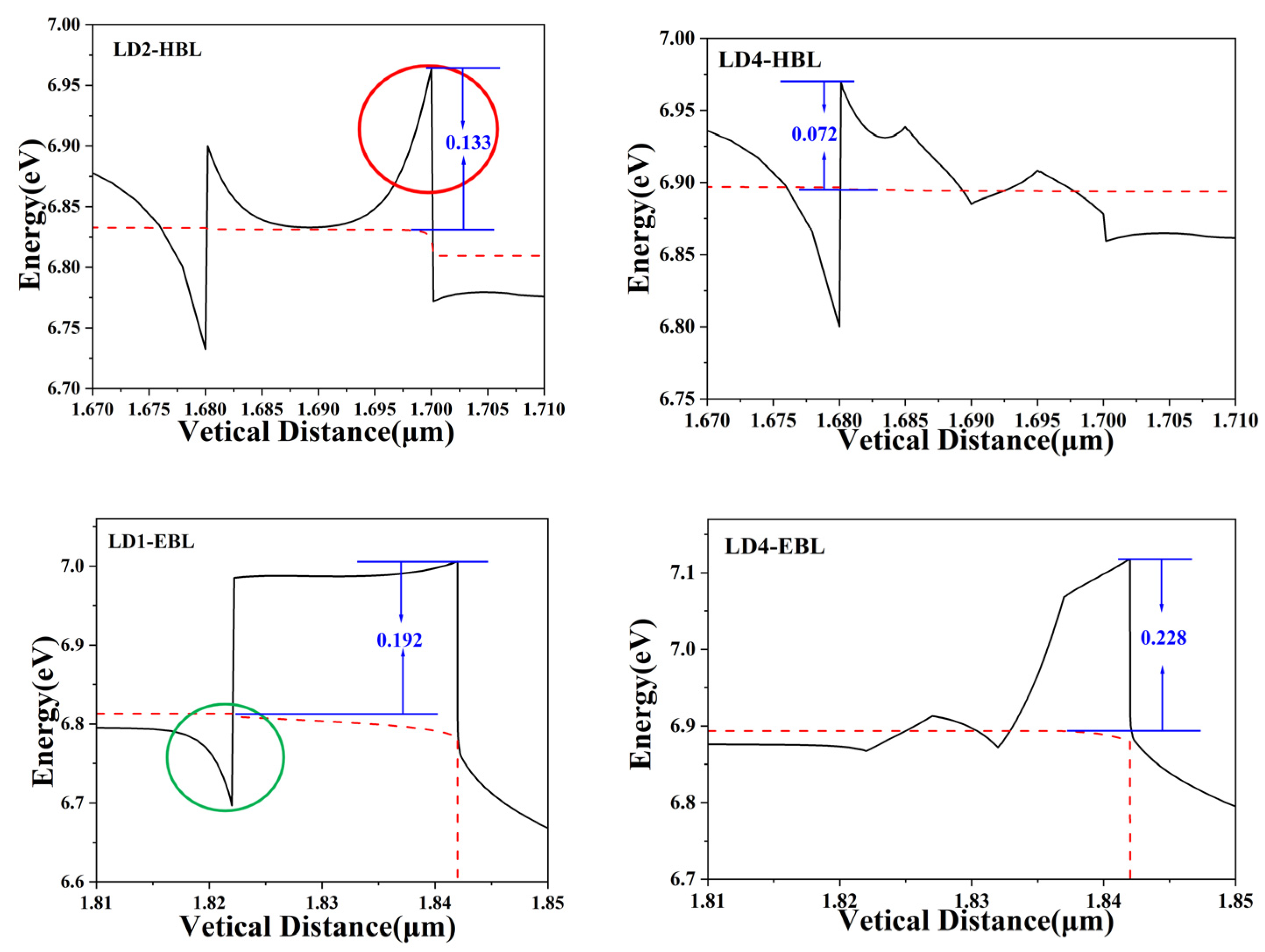
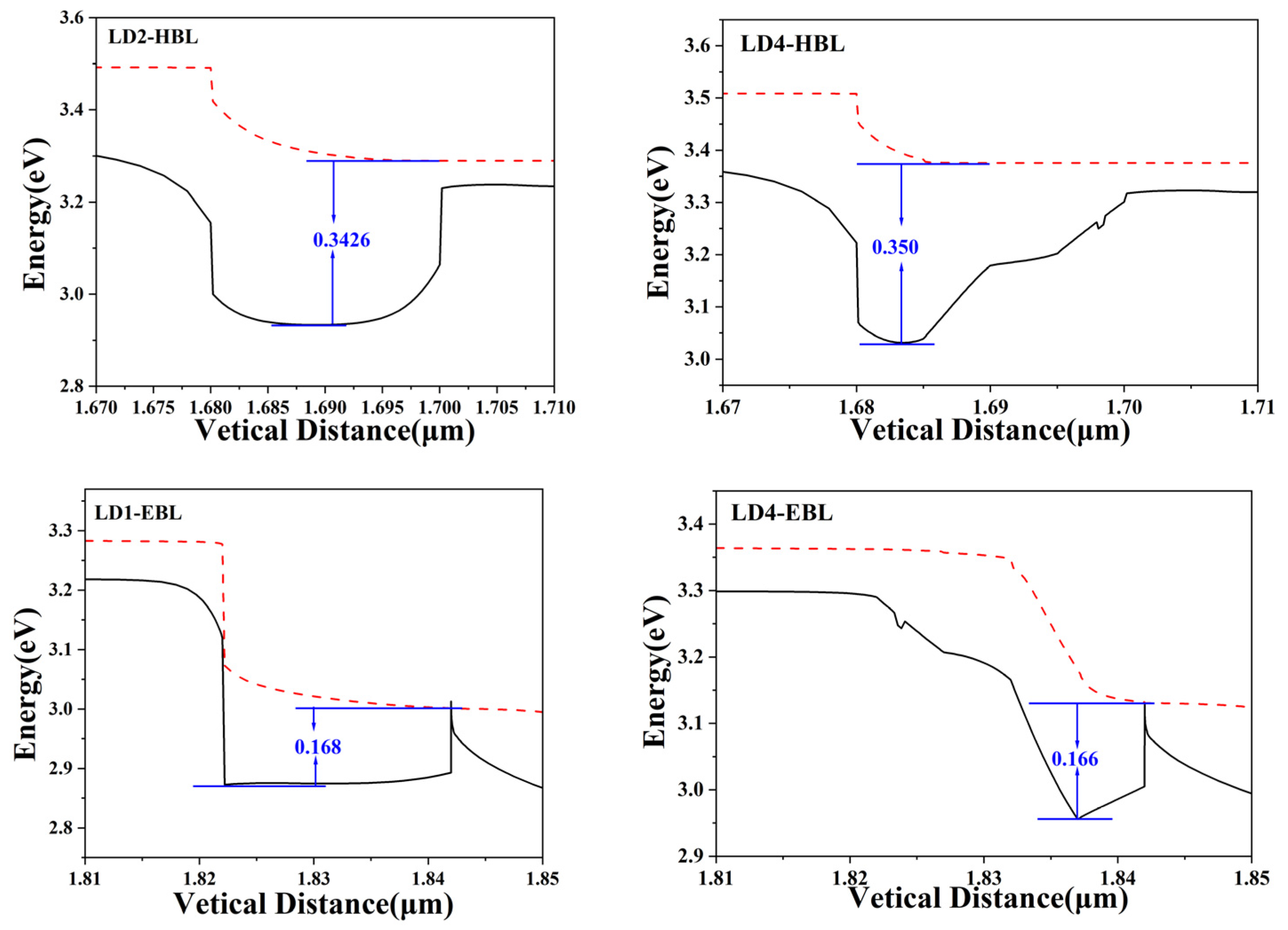
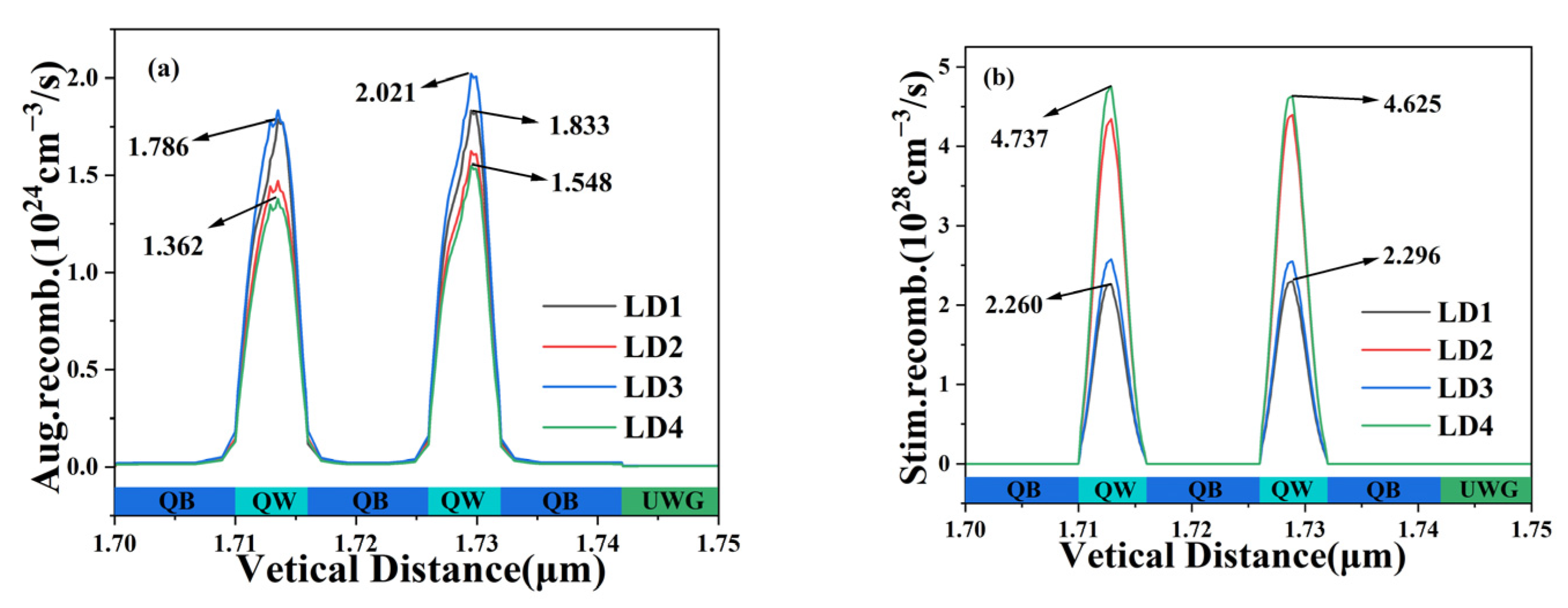
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sfuncia, G.; Nicotra, G.; Giannazzo, F.; Pécz, B.; Gueorguiev, G.K.; Kakanakova-Georgieva, A. 2D graphitic-like gallium nitride and other structural selectivity in confinement at the graphene/SiC interface. CrystEngComm 2023, 25, 5810–5817. [Google Scholar] [CrossRef]
- Filho, M.A.M.; Hsiao, C.-L.; dos Santos, R.B.; Hultman, L.; Birch, J.; Gueorguiev, G.K. Self-Induced Core–Shell InAlN Nanorods: Formation and Stability Unraveled by Ab Initio Simulations. ACS Nanosci. Au 2022, 3, 84–93. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Balakrishnan, K.; Katona, T. Ultraviolet light-emitting diodes based on group three nitrides. Nat. Photonics 2008, 2, 77–84. [Google Scholar] [CrossRef]
- Mishra, U.K.; Parikh, P.; Wu, Y.F. AlGaN/GaN HEMTs-an overview of device operation and applications. Proc. IEEE 2002, 90, 1022–1031. [Google Scholar] [CrossRef]
- Zhao, D.; Yang, J.; Liu, Z.; Chen, P.; Zhu, J.; Jiang, D.; Shi, Y.; Wang, H.; Duan, L.; Zhang, L.; et al. Fabrication of room temperature continuous-wave operation GaN-based ultraviolet laser diodes. J. Semicond. 2017, 38, 051001. [Google Scholar] [CrossRef]
- Sun, Q.; Yan, W.; Feng, M.; Li, Z.; Feng, B.; Zhao, H.; Yang, H. GaN-on-Si blue/white LEDs: Epitaxy, chip, and package. J. Semicond. 2016, 37, 044006. [Google Scholar] [CrossRef]
- Fujita, S. Wide-bandgap semiconductor materials: For their full bloom. Jpn. J. Appl. Phys. 2015, 54, 030101. [Google Scholar] [CrossRef]
- Kuo, Y.K.; Chen, Y.H.; Chang, J.Y.; Tsai, M.C. Numerical analysis on the effects of bandgap energy and polarization of electron blocking layer in near-ultraviolet light-emitting diodes. Appl. Phys. Lett. 2012, 100, 043513. [Google Scholar] [CrossRef]
- Lee, S.N.; Cho, S.Y.; Ryu, H.Y.; Son, J.K.; Paek, H.S.; Sakong, T.; Jang, T.; Choi, K.K.; Ha, K.H.; Yang, M.H.; et al. High-power GaN-based blue-violet laser diodes with AlGaN∕ GaN multiquantum barriers. Appl. Phys. Lett. 2006, 88, 111101. [Google Scholar] [CrossRef]
- Cho, J.; Schubert, E.F.; Kim, J.K. Efficiency droop in light-emitting diodes: Challenges and countermeasures. Laser Photonics Rev. 2013, 7, 408–421. [Google Scholar] [CrossRef]
- Zhang, A.; Wang, Y.; Wang, M.; Wei, S.; Wang, F.; Liu, Y. Performance optimization of AlGaN-based deep ultraviolet laser diode with M-shaped hole barrier structure. Chin. J. Quantum Electron. 2022, 39, 583. [Google Scholar]
- Xu, Y.; Yin, M.; Zhang, P.; Zhang, A.; Wang, W.; Liou, J.J.; Liu, Y. Deep-ultraviolet Laser Diode Characterization Improvement by Inverted Trapezoidal Hole Blocking Layer. In Proceedings of the 2022 19th China International Forum on Solid State Lighting & 2022 8th International Forum on Wide Bandgap Semiconductors (SSLCHINA: IFWS), Suzhou, China, 7–10 February 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 167–169. [Google Scholar]
- Shih, Y.H.; Chang, J.Y.; Sheu, J.K.; Kuo, Y.K.; Chen, F.M.; Lee, M.L.; Lai, W.C. Design of hole-blocking and electron-blocking layers in Al x Ga 1–x N-based UV light-emitting diodes. IEEE Trans. Electron Devices 2016, 63, 1141–1147. [Google Scholar] [CrossRef]
- Wang, L.; He, W.; Zheng, T.; Chen, Z.; Zheng, S. Enhanced optical performance of AlGaN-based deep-ultraviolet light-emitting diode with m-shaped hole blocking layer and w-shaped electron blocking layer. Superlattices Microstruct. 2019, 133, 106188. [Google Scholar] [CrossRef]
- Zhang, A.; Jia, L.; Zhang, P.; Xing, Z.; Wang, F.; Liu, Y. Optimization of AlGaN-Based Deep Ultraviolet Laser Diodes with Graded Rectangular Superlattice Electron Blocking Layer and Graded Trapezoidal Superlattice Hole Blocking Layer. J. Russ. Laser Res. 2022, 43, 489–496. [Google Scholar] [CrossRef]
- Shi, H.; Gu, H.; Li, J.; Yang, X.; Zhang, J.; Yuan, R.; Chen, X.; Liu, N. Performance improvements of AlGaN-based deep-ultraviolet light-emitting diodes with specifically designed irregular sawtooth hole and electron blocking layers. Opt. Commun. 2019, 441, 149–154. [Google Scholar] [CrossRef]
- Jia, L.; Zhang, P.; Yin, M.; Wang, W.; Liou, J.J.; Liu, Y. Performance optimization of deep ultraviolet laser diodes with superlattice hole blocking layer. In Proceedings of the 2022 19th China International Forum on Solid State Lighting & 2022 8th International Forum on Wide Bandgap Semiconductors (SSLCHINA: IFWS), Suzhou, China, 7–10 February 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 164–166. [Google Scholar]
- Yi, X.; Sun, H.; Li, Z.; Sun, J.; Liu, T.; Wang, X.; Zhang, X.; Guo, Z. Special AlGaN graded superlattice hole and electron blocking layers improved performance of AlGaN-based ultraviolet light-emitting diodes. Opt. Laser Technol. 2018, 106, 469–473. [Google Scholar] [CrossRef]
- Piprek, J. Semiconductor Optoelectronic Devices: Introduction to Physics and Simulation; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Zhang, A.; Ren, B.; Wang, F.; Liou, J.J.; Liu, Y. Study of AlGaN-based deep ultraviolet laser diodes using one-way step-shaped quantum barriers and symmetrical step-shaped electron and hole blocking layers. Opt. Eng. 2022, 61, 106101. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J.; Zhao, D.; Liang, F.; Chen, P.; Liu, Z. Theoretical Optical Output Power Improvement of InGaN-Based Violet Laser Diode Using AlGaN/GaN Composite Last Quantum Barrier. Nanomaterials 2022, 12, 3990. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Zhao, D.; Chen, P.; Liang, F.; Liu, Z.; Yang, J. Stepped upper waveguide layer for higher hole injection efficiency in GaN-based laser diodes. Opt. Express 2021, 29, 33992–34001. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J.; Liang, F.; Chen, P.; Liu, Z.; Zhao, D. Low threshold current density and high power InGaN-based blue-violet laser diode with an asymmetric waveguide structure. Opt. Express 2023, 31, 7839–7849. [Google Scholar] [CrossRef]
- Laws, G.M.; Larkins, E.C.; Harrison, I.; Molloy, C.; Somerford, D. Improved refractive index formulas for the Alx Ga1 − xN and Iny Ga1 − yN alloys. J. Appl. Phys. 2001, 89, 1108–1115. [Google Scholar] [CrossRef]
- Fiorentini, V.; Bernardini, F.; Ambacher, O. Evidence for nonlinear macroscopic polarization in III–V nitride alloy heterostructures. Appl. Phys. Lett. 2002, 80, 1204–1206. [Google Scholar] [CrossRef]
- Wang, C.; Li, C.; Wang, Z. Analysis of optical and thermal properties of 940-nm vertical-cavity surface-emitting lasers. Opt. Quantum Electron. 2022, 54, 438. [Google Scholar] [CrossRef]
- Pan, Z.; Li, W.; Jiagang, L.; Chang, J.; Wang, Z.; Liu, S.; Zhong, L.; Ma, X. Reflection Characteristics Analysis of DBR in 940 nm VCSEL. Chin. J. Lasers 2023, 50, 0701007. [Google Scholar]
- Huang, X.D.; Huang, L.R.; Hong, W. Semiconductor Optoelectronics, 3rd ed.; Publishing House of Electronics Industry: Beijing, China, 2018; pp. 12–124. [Google Scholar]
- Huang, C.Y.; Lin, Y.D.; Tyagi, A. Optical waveguide simulations for the optimization of InGaN-based green laser diodes. J. Appl. Phys. 2010, 107, 023101. [Google Scholar] [CrossRef]
- Götz, W.; Johnson, N.M.; Walker, J.; Bour, D.P. Activation of acceptors in Mg-doped, p-type GaN. MRS Online Proc. Libr. 1996, 423, 595. [Google Scholar] [CrossRef]
- Yu, J.Z. Semiconductor Photonics; Science Press: Beijing, China, 2015; pp. 154–376. [Google Scholar]
- Sin, Y.; Hsieh, K.Y.; Lee, J.H. Surface and bulk leakage currents in transverse junction stripe lasers. J. Appl. Phys. 1991, 69, 1081–1090. [Google Scholar] [CrossRef]
- Bin, Y.; Guo, Z.-Y.; Nan, X.; Zhang, P.-J.; Li, J.; Li, F.-Z.; Lin, H.; Zheng, H.; Cai, J.-X. A GaN–AlGaN–InGaN last quantum barrier in an InGaN/GaN multiple-quantum-well blue LED. Chin. Physics. B 2014, 23, 048502. [Google Scholar]
- Brendel, M.; Kruse, A.; Jönen, H.; Hoffmann, L.; Bremers, H.; Rossow, U.; Hangleiter, A. Auger recombination in GaInN/GaN quantum well laser structures. Appl. Phys. Lett. 2011, 99, 031106. [Google Scholar] [CrossRef]
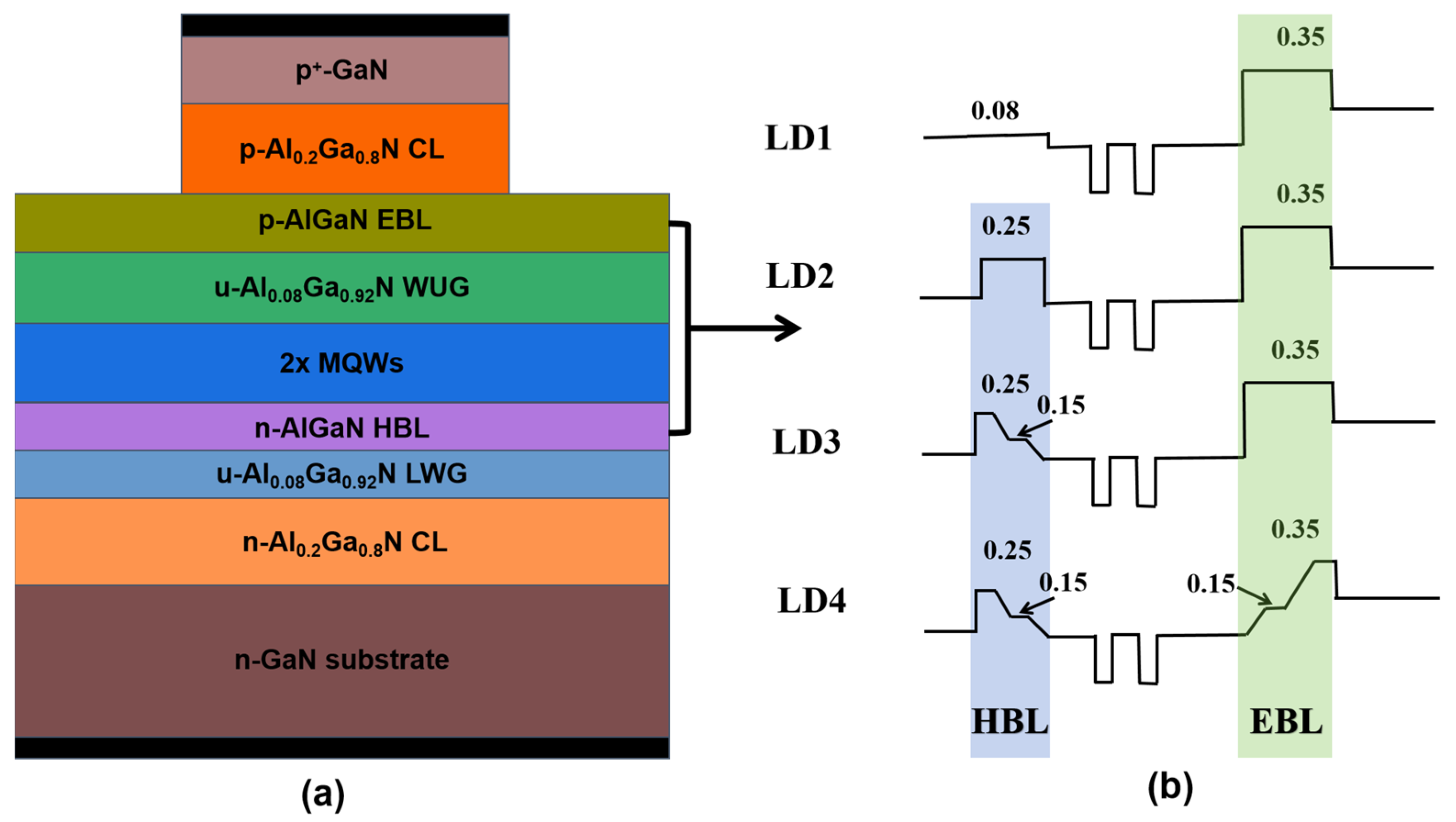
| The Names of the Laser | HBL of Al Composition (%) | HBL of Layer Thickness (nm) | EBL of Al Composition (%) | EBL of Layer Thickness (nm) |
|---|---|---|---|---|
| LD1 | 0 | 0 | 35 | 20 |
| LD2 | 25 | 20 | 35 | 20 |
| LD3 | 25 | 5 | 35 | 20 |
| 25 → 15 | 5 | |||
| 15 | 5 | |||
| 15 → 7 | 5 | |||
| LD4 | 25 | 5 | 7 → 15 | 5 |
| 25 → 15 | 5 | 15 | 5 | |
| 15 | 5 | 15 → 35 | 5 | |
| 15 → 7 | 5 | 35 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Yang, J.; Jia, W.; Zhao, D.; Zhai, G.; Dong, H.; Xu, B. Improved Design of Slope-Shaped Hole-Blocking Layer and Electron-Blocking Layer in AlGaN-Based Near-Ultraviolet Laser Diodes. Nanomaterials 2024, 14, 649. https://doi.org/10.3390/nano14070649
Gao M, Yang J, Jia W, Zhao D, Zhai G, Dong H, Xu B. Improved Design of Slope-Shaped Hole-Blocking Layer and Electron-Blocking Layer in AlGaN-Based Near-Ultraviolet Laser Diodes. Nanomaterials. 2024; 14(7):649. https://doi.org/10.3390/nano14070649
Chicago/Turabian StyleGao, Maolin, Jing Yang, Wei Jia, Degang Zhao, Guangmei Zhai, Hailiang Dong, and Bingshe Xu. 2024. "Improved Design of Slope-Shaped Hole-Blocking Layer and Electron-Blocking Layer in AlGaN-Based Near-Ultraviolet Laser Diodes" Nanomaterials 14, no. 7: 649. https://doi.org/10.3390/nano14070649
APA StyleGao, M., Yang, J., Jia, W., Zhao, D., Zhai, G., Dong, H., & Xu, B. (2024). Improved Design of Slope-Shaped Hole-Blocking Layer and Electron-Blocking Layer in AlGaN-Based Near-Ultraviolet Laser Diodes. Nanomaterials, 14(7), 649. https://doi.org/10.3390/nano14070649






