RETRACTED: The Effect of Structural Phase Transitions on Electronic and Optical Properties of CsPbI3 Pure Inorganic Perovskites
Abstract
:1. Introduction
2. Computational Details
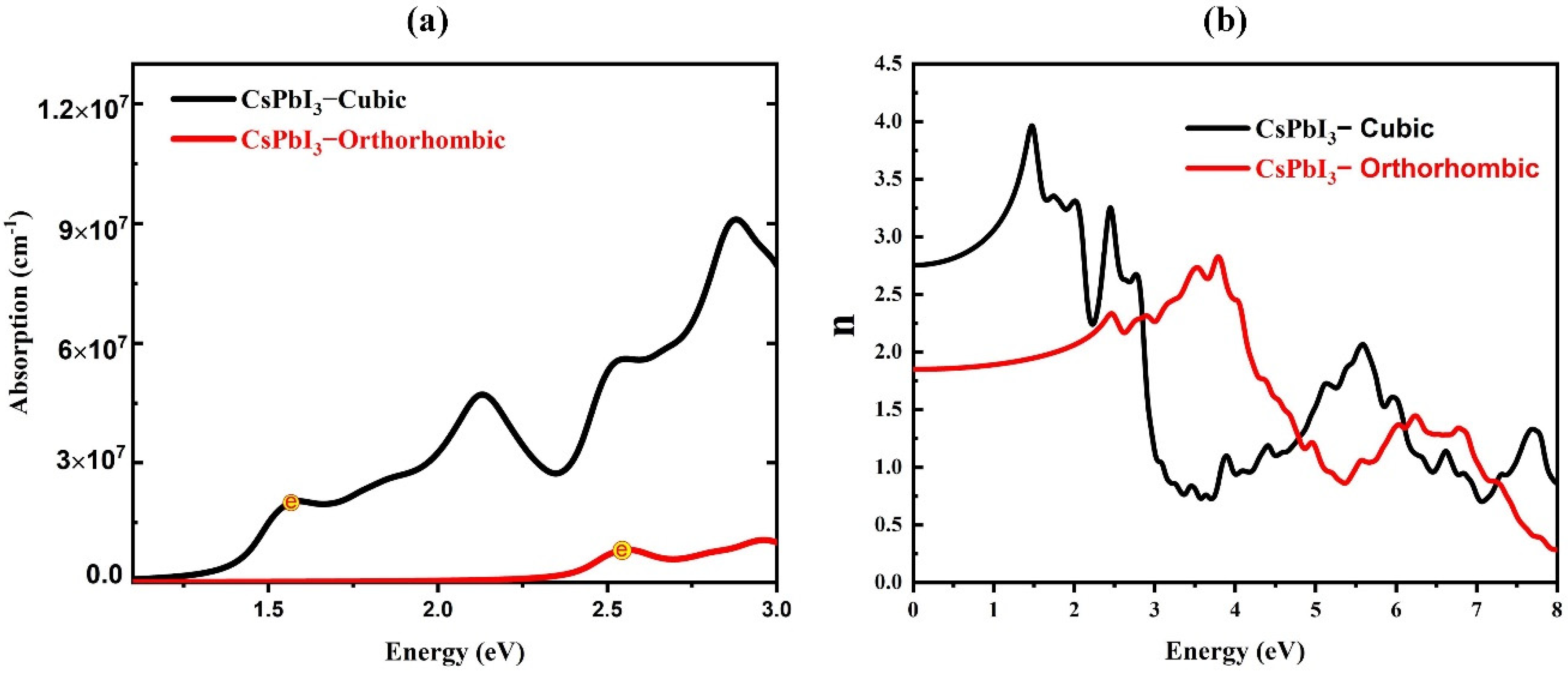
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Z.; Qin, J.; Xiang, X.; Tan, Y.; Liu, Q.; Xiong, N.N. News text topic clustering optimized method based on TF-IDF algorithm on spark. Comput. Mater. Contin. 2020, 62, 217–231. [Google Scholar] [CrossRef]
- Tian, L.; Li, J.; Zhang, L.; Sun, Y.; Yang, S. TCPW BR: A wireless congestion control scheme base on RTT. Comput. Mater. Contin. 2020, 62, 233–244. [Google Scholar] [CrossRef]
- Huang, Z.; Nie, Y.; Li, Y.; Ma, B.; Dui, G.; Yang, S.; Xin, L. Microstructural modeling and multiscale mechanical properties analysis of cancellous bone. Comput. Mater. Contin. 2020, 62, 245–265. [Google Scholar] [CrossRef]
- Chen, H.; Heidari, A.A.; Chen, H.; Wang, M.; Pan, Z.; Gandomi, A.H. Multi-population differential evolution-assisted Harris hawks optimization: Framework and case studies. Futur. Gener. Comput. Syst. 2020, 111, 175–198. [Google Scholar] [CrossRef]
- Wang, M.; Chen, H. Chaotic multi-swarm whale optimizer boosted support vector machine for medical diagnosis. Appl. Soft Comput. 2020, 88, 105946. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, H.; Luo, J.; Zhang, Q.; Jiao, S.; Zhang, X. Enhanced Moth-flame optimizer with mutation strategy for global optimization. Inf. Sci. 2019, 492, 181–203. [Google Scholar] [CrossRef]
- Lee, B.; Lee, Y. Distinction between real faces and photos by analysis of face data. Intell. Autom. Soft Comput. 2020, 26, 133–139. [Google Scholar] [CrossRef]
- Kim, M.; Kim, J.; Shin, M. Word embedding based knowledge representation with extracting relationship between scientific terminologies. Intell. Autom. Soft Comput. 2020, 26, 141–147. [Google Scholar] [CrossRef]
- Park, J.-S.; Kim, S.-H. Noise cancellation based on voice activity detection using spectral variation for speech recognition in smart home devices. Intell. Autom. Soft Comput. 2020, 26, 149–159. [Google Scholar] [CrossRef]
- Deng, J.; Chen, J.; Wang, D. Mechanism design and mechanical analysis of multi-suction sliding cleaning robot used in glass curtain wall. Comput. Syst. Sci. Eng. 2019, 34, 201–206. [Google Scholar] [CrossRef]
- Nie, X.; Zou, X.; Zhu, D. Modeling and Simulation of entrepreneur individual based on dynamic and complex system computing. Comput. Syst. Sci. Eng. 2019, 34, 207–214. [Google Scholar] [CrossRef]
- Hua, R.; Bao, Y.; Chen, S.; Zhuang, Z. Optimization of the dynamic measure of spillover effect based on knowledge graph. Comput. Syst. Sci. Eng. 2019, 34, 215–223. [Google Scholar] [CrossRef]
- Yang, Z.; Surrente, A.; Galkowski, K.; Miyata, A.; Portugall, O.; Sutton, R.; Haghighirad, A.; Snaith, H.; Maude, D.; Plochocka, P. Impact of the halide cage on the electronic properties of fully inorganic cesium lead halide perovskites. ACS Energy Lett. 2017, 2, 1621–1627. [Google Scholar] [CrossRef]
- Hu, Y.; Bai, F.; Liu, X.; Ji, Q.; Miao, X.; Qiu, T.; Zhang, S. Bismuth incorporation stabilized α-CsPbI3 for fully inorganic perovskite solar cells. ACS Energy Lett. 2017, 2, 2219–2227. [Google Scholar] [CrossRef]
- Nam, J.K.; Chai, S.U.; Cha, W.; Choi, Y.J.; Kim, W.; Jung, M.S.; Kwon, J.; Kim, D.; Park, J.H. Potassium incorporation for enhanced performance and stability of fully inorganic cesium lead halide perovskite solar cells. Nano Lett. 2017, 17, 2028–2033. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Zhang, X.; Cai, Z.; Tian, X.; Wang, X.; Huang, Y.; Chen, H.; Hu, L. Chaos enhanced grey wolf optimization wrapped ELM for diagnosis of paraquat-poisoned patients. Comput. Biol. Chem. 2019, 78, 481–490. [Google Scholar] [CrossRef]
- Li, C.; Hou, L.; Sharma, B.Y.; Li, H.; Chen, C.; Li, Y.; Zhao, X.; Huang, H.; Cai, Z.; Chen, H. Developing a new intelligent system for the diagnosis of tuberculous pleural effusion. Comput. Methods Programs Biomed. 2018, 153, 211–225. [Google Scholar] [CrossRef]
- Wang, M.; Chen, H.; Yang, B.; Zhao, X.; Hu, L.; Cai, Z.; Huang, H.; Tong, C. Toward an optimal kernel extreme learning machine using a chaotic moth-flame optimization strategy with applications in medical diagnoses. Neurocomputing 2017, 267, 69–84. [Google Scholar] [CrossRef]
- Bansal, S.; Chiu, M. Atmospherically processed and stable Cs-Pb based perovskite solar cells. MRS Adv. 2017, 2, 3083–3090. [Google Scholar] [CrossRef]
- Davarpanah, A.; Shirmohammadi, R.; Mirshekari, B.; Aslani, A. Analysis of hydraulic fracturing techniques: Hybrid fuzzy approaches. Arab. J. Geosci. 2019, 12, 1–8. [Google Scholar] [CrossRef]
- Swarnkar, A.; Marshall, A.R.; Sanehira, E.M.; Chernomordik, B.D.; Moore, D.T.; Christians, J.A.; Chakrabarti, T.; Luther, J.M. Quantum dot–induced phase stabilization of α-CsPbI3 perovskite for high-efficiency photovoltaics. Science 2016, 354, 92–95. [Google Scholar] [CrossRef]
- Duan, M.; Li, K.; Ouyang, A.; Win, K.N.; Li, K.; Tian, Q. EGroupNet: A feature-enhanced Network for age estimation with novel age group schemes. ACM Trans. Multim. Comput. Commun. Appl. 2020, 16, 1–23. [Google Scholar] [CrossRef]
- Yang, W.; Li, K.; Li, K. A pipeline computing method of SpTV for three-order tensors on CPU and GPU. ACM Trans. Knowl. Discov. Data 2019, 13, 1–27. [Google Scholar] [CrossRef]
- Zhou, X.; Li, K.; Yang, Z.; Xiao, G.; Li, K. Progressive approaches for pareto optimal groups computation. IEEE Trans. Knowl. Data Eng. 2019, 31, 521–534. [Google Scholar] [CrossRef]
- Jing, M.; Li, K.; Tong, Z.; Li, Q.; Li, K. Profit maximization for cloud brokers in cloud computing. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 190–203. [Google Scholar]
- Chen, Y.; Li, K.; Yang, W.; Xiao, G.; Xie, X.; Li, T. Performance-aware model for sparse matrix-matrix multiplication on the sunway taihulight supercomputer. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 923–938. [Google Scholar]
- Jianguo, C.; Kenli, L.; Kashif, B.; Xu, Z.; Keqin, L.; Philip, S.Y. A Bi-layered parallel training architecture for large-scale convolutional neural Networks. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 965–976. [Google Scholar]
- Eperon, G.E.; Paternò, G.M.; Sutton, R.J.; Zampetti, A.; Haghighirad, A.A.; Cacialli, F.; Snaith, H.J. Inorganic caesium lead iodide perovskite solar cells. J. Mater. Chem. A 2015, 3, 19688–19695. [Google Scholar] [CrossRef]
- Swarnkar, A.; Mir, W.J.; Nag, A. Can B-site doping or alloying improve thermal-and phase-stability of all-inorganic CsPbX3 (X= Cl, Br, I) perovskites? ACS Energy Lett. 2018, 3, 286–289. [Google Scholar] [CrossRef]
- Xia, J.; Chen, H.; Li, Q.; Zhou, M.; Chen, L.; Cai, Z.; Fang, Y.; Zhou, H. Ultrasound-based differentiation of malignant and benign thyroid Nodules: An extreme learning machine approach. Comput. Methods Programs Biomed. 2017, 147, 37–49. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Wang, G.; Ma, C.; Cai, Z.-N.; Liu, W.-B.; Wang, S.-J. An efficient hybrid kernel extreme learning machine approach for early diagnosis of Parkinson’s disease. Neurocomputing 2016, 184, 131–144. [Google Scholar] [CrossRef]
- Shen, L.; Chen, H.; Yu, Z.; Kang, W.; Zhang, B.; Li, H.; Yang, B.; Liu, D. Evolving support vector machines using fruit fly optimization for medical data classification. Knowledge-Based Syst. 2016, 96, 61–75. [Google Scholar] [CrossRef]
- Mir, W.J.; Mahor, Y.; Lohar, A.; Jagadeeswararao, M.; Das, S.; Mahamuni, S.; Nag, A. Postsynthesis doping of Mn and Yb into CsPbX3 (X= Cl, Br, or I) perovskite nanocrystals for downconversion emission. Chem. Mater. 2018, 30, 8170–8178. [Google Scholar] [CrossRef]
- Zhu, W.; Deng, M.; Chen, D.; Zhang, Z.; Chai, W.; Chen, D.; Xi, H.; Zhang, J.; Zhang, C.; Hao, Y. Dual-phase CsPbCl3–Cs4PbCl6 perovskite films for self-powered, visible-blind UV photodetectors with fast response. ACS Appl. Mater. Interfaces 2020, 12, 32961–32969. [Google Scholar] [CrossRef] [PubMed]
- Lau, C.F.J.; Deng, X.; Zheng, J.; Kim, J.; Zhang, Z.; Zhang, M.; Bing, J.; Wilkinson, B.; Hu, L.; Patterson, R. Enhanced performance via partial lead replacement with calcium for a CsPbI3 perovskite solar cell exceeding 13% power conversion efficiency. J. Mater. Chem. A 2018, 6, 5580–5586. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y.; Fu, L.; Yu, T.; Zhou, S.; Zhang, L.; Yin, L. Surface passivation engineering strategy to fully-inorganic cubic CsPbI3 perovskites for high-performance solar cells. Nat. Commun. 2018, 9, 1–8. [Google Scholar] [CrossRef]
- Lin, J.; Lai, M.; Dou, L.; Kley, C.S.; Chen, H.; Peng, F.; Sun, J.; Lu, D.; Hawks, S.A.; Xie, C. Thermochromic halide perovskite solar cells. Nat. Mater. 2018, 17, 261–267. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Li, J.; Niu, G.; Yuan, J.-H.; Xue, K.-H.; Xia, M.; Pan, W.; Yang, X.; Zhu, B.; Tang, J. Lead halide perovskite for efficient optoacoustic conversion and application toward high-resolution ultrasound imaging. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Yuan, J.; Ni, Y.; Yang, J.; Wang, Y.; Jiu, T.; Yuan, M.; Chen, J. Reduced-dimensional α-CsPbX3 perovskites for efficient and stable photovoltaics. Joule 2018, 2, 1356–1368. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, X.; Li, F.; Sangaiah, A.K.; Ding, X. Seam-carved image tampering detection based on the cooccurrence of adjacent LBPs. Secur. Commun. Netw. 2020, 2020, 1–12. [Google Scholar]
- Song, Y.; Zhang, D.; Tang, Q.; Tang, S.; Yang, K. Local and nonlocal constraints for compressed sensing video and multi-view image recovery. Neurocomputing 2020, 406, 34–48. [Google Scholar] [CrossRef]
- Zhou, S.; Qiu, J. Enhanced SSD with interactive multi-scale attention features for object detection. Multimed. Tools Appl. 2021, 80, 11539–11556. [Google Scholar] [CrossRef]
- Davarpanah, A. Parametric study of polymer-nanoparticles-assisted injectivity performance for axisymmetric two-phase flow in EOR processes. Nanomaterials 2020, 10, 1818. [Google Scholar] [CrossRef]
- Valizadeh, K.; Farahbakhsh, S.; Bateni, A.; Zargarian, A.; Davarpanah, A.; Alizadeh, A.; Zarei, M. A parametric study to simulate the non—Newtonian turbulent flow in spiral tubes. Energy Sci. Eng. 2020, 8, 134–149. [Google Scholar] [CrossRef]
- Tang, Q.; Wang, K.; Yang, K.; Luo, Y.-S. Congestion-balanced and welfare-maximized charging strategies for electric vehicles. IEEE Trans. Parallel Distrib. Syst. 2020, 31, 2882–2895. [Google Scholar] [CrossRef]
- Hu, L.; Hong, G.; Ma, J.; Wang, X.; Chen, H. An efficient machine learning approach for diagnosis of paraquat-poisoned patients. Comput. Biol. Med. 2015, 59, 116–124. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Chen, H.-L. Adaptive computational chemotaxis based on field in bacterial foraging optimization. Soft Comput. 2014, 18, 797–807. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, R.; Wang, X.; Chen, H.; Li, C. Boosted binary Harris hawks optimizer and feature selection. Eng. Comput. 2020, 15, 1–30. [Google Scholar] [CrossRef]
- Wang, J.; Chen, W.; Ren, Y.; Alfarraj, O.; Wang, L. Blockchain based data storage mechanism in cyber physical system. J. Internet Technol. 2020, 21, 1681–1689. [Google Scholar]
- Song, Y.; Li, J.; Chen, X.; Zhang, D.; Tang, Q.; Yang, K. An efficient tensor completion method via truncated nuclear norm. J. Vis. Commun. Image Represent. 2020, 70, 102791. [Google Scholar] [CrossRef]
- Wang, J.; Wu, W.; Liao, Z.; Jung, Y.W.; Kim, J.U. An Enhanced promot algorithm with D2D and robust for mobile edge computing. J. Internet Technol. 2020, 21, 1437–1445. [Google Scholar]
- Zhang, D.; Wang, S.; Li, F.; Tian, S.; Wang, J.; Ding, X.; Gong, R. An efficient ECG denoising method based on empirical mode decomposition, sample entropy, and improved threshold function. Wirel. Commun. Mob. Comput. 2020, 2020, 1–11. [Google Scholar]
- Tang, Q.; Wang, K.; Song, Y.; Li, F.; Park, J.H. Waiting time minimized charging and discharging strategy based on mobile edge computing supported by software-defined Network. IEEE Internet Things J. 2019, 7, 6088–6101. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, K.; Xiang, L.; Luo, Y.; Xiong, B.; Tang, Q. A self-adaptive regression-based multivariate data compression scheme with error bound in wireless sensor Networks. Int. J. Distrib. Sens. Netw. 2013, 9, 913497. [Google Scholar] [CrossRef]
- Møller, C.K. Crystal structure and photoconductivity of caesium plumbohalides. Nature 1958, 182, 1436. [Google Scholar] [CrossRef]
- Filip, M.R.; Verdi, C.; Giustino, F. GW band structures and carrier effective masses of CH3NH3PbI3 and hypothetical perovskites of the type APbI3: A= NH4, PH4, AsH4, and SbH4. J. Phys. Chem. C. 2015, 119, 25209–25219. [Google Scholar] [CrossRef]
- Davies, C.L.; Filip, M.R.; Patel, J.B.; Crothers, T.W.; Verdi, C.; Wright, A.D.; Milot, R.L.; Giustino, F.; Johnston, M.B.; Herz, L.M. Bimolecular recombination in methylammonium lead triiodide perovskite is an inverse absorption process. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef]
- Filip, M.R.; Eperon, G.E.; Snaith, H.J.; Giustino, F. Steric engineering of metal-halide perovskites with tunable optical band gaps. Nat. Commun. 2014, 5, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Sun, J.; Wang, J.; Yue, X.-G. Visual object tracking based on residual network and cascaded correlation filters. J. Ambient. Intell. Humaniz. Comput. 2020, 12, 1–14. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, R.; Heidari, A.A.; Wang, X.; Chen, Y.; Wang, M.; Chen, H. Towards augmented kernel extreme learning models for bankruptcy prediction: Algorithmic behavior and comprehensive analysis. Neurocomputing 2020, 430, 185–212. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, L.; Yu, F.; Heidari, A.A.; Wang, M.; Liang, G.; Muhammad, K.; Chen, H. Chaotic random spare ant colony optimization for multi-threshold image segmentation of 2D Kapur entropy. Knowledge-Based Syst. 2020, 216, 106510. [Google Scholar] [CrossRef]
- Tu, J.; Chen, H.; Liu, J.; Heidari, A.A.; Zhang, X.; Wang, M.; Ruby, R.; Pham, Q.-V. Evolutionary biogeography-based whale optimization methods with communication structure: Towards measuring the balance. Knowledge-Based Syst. 2020, 212, 106642. [Google Scholar] [CrossRef]
- Gu, K.; Wang, Y.; Wen, S. Traceable threshold proxy signature. J. Inf. Sci. Eng. 2017, 33, 63–79. [Google Scholar]
- Li, W.; Ding, Y.; Yang, Y.; Sherratt, R.S.; Park, J.H.; Wang, J. Parameterized algorithms of fundamental NP-hard problems: A survey. Hum. -Cent. Comput. Inf. Sci. 2020, 10, 1–24. [Google Scholar] [CrossRef]
- Gu, K.; Yang, L.; Wang, Y.; Wen, S. Traceable identity-based group signature. RAIRO-Theor. Inform. Appl. 2016, 50, 193–226. [Google Scholar] [CrossRef]
- Yin, B.; Zhou, S.; Lin, Y.; Liu, Y.; Hu, Y. Efficient distributed skyline computation using dependency-based data partitioning. J. Syst. Softw. 2014, 93, 69–83. [Google Scholar] [CrossRef]
- Long, M.; Xiao, X. Outage performance of double-relay cooperative transmission network with energy harvesting. Phys. Commun. 2018, 29, 261–267. [Google Scholar] [CrossRef]
- Xu, Z.; Liang, W.; Li, K.-C.; Xu, J.; Jin, H. A blockchain-based Roadside Unit-assisted authentication and key agreement protocol for Internet of Vehicles. J. Parallel Distrib. Comput. 2021, 149, 29–39. [Google Scholar] [CrossRef]
- Wang, W.; Yang, Y.; Li, J.; Hu, Y.; Luo, Y.; Wang, X. Woodland labeling in chenzhou, China, via deep learning approach. Int. J. Comput. Intell. Syst. 2020, 13, 1393–1403. [Google Scholar] [CrossRef]
- Ehyaei, M.A.; Ahmadi, A.; Rosen, M.A.; Davarpanah, A. Thermodynamic optimization of a geothermal power plant with a genetic algorithm in two stages. Processes 2020, 8, 1277. [Google Scholar] [CrossRef]
- Stoumpos, C.C.; Kanatzidis, M.G. The renaissance of halide perovskites and their evolution as emerging semiconductors. Acc. Chem. Res. 2015, 48, 2791–2802. [Google Scholar] [CrossRef] [PubMed]
- Marronnier, A.; Roma, G.; Boyer-Richard, S.; Pedesseau, L.; Jancu, J.-M.; Bonnassieux, Y.; Katan, C.; Stoumpos, C.C.; Kanatzidis, M.G.; Even, J. Anharmonicity and disorder in the black phases of cesium lead iodide used for stable inorganic perovskite solar cells. ACS Nano 2018, 12, 3477–3486. [Google Scholar] [CrossRef]
- Hu, X.; Xie, J.; Cai, W.; Wang, R.; Davarpanah, A. Thermodynamic effects of cycling carbon dioxide injectivity in shale reservoirs. J. Pet. Sci. Eng. 2020, 195, 107717. [Google Scholar] [CrossRef]
- Davarpanah, A.; Mirshekari, B. Experimental investigation and mathematical modeling of gas diffusivity by carbon dioxide and methane kinetic adsorption. Ind. Eng. Chem. Res. 2019, 58, 12392–12400. [Google Scholar] [CrossRef]
- Fu, Y.; Zhu, H.; Stoumpos, C.C.; Ding, Q.; Wang, J.; Kanatzidis, M.G.; Zhu, X.; Jin, S. Broad wavelength tunable robust lasing from single-crystal nanowires of cesium lead halide perovskites (CsPbX3, X= Cl, Br, I). ACS Nano 2016, 10, 7963–7972. [Google Scholar] [CrossRef]
- Shan, W.; Qiao, Z.; Heidari, A.A.; Chen, H.; Turabieh, H.; Teng, Y. Double adaptive weights for stabilization of moth flame optimizer: Balance analysis, engineering cases, and medical diagnosis. Knowledge-Based Syst. 2014, 214, 106728. [Google Scholar] [CrossRef]
- Yu, C.; Chen, M.; Cheng, K.; Zhao, X.; Ma, C.; Kuang, F.; Chen, H. SGOA: Annealing-behaved grasshopper optimizer for global tasks. Eng. Comput. 2021, 1–28. [Google Scholar] [CrossRef]
- Hu, J.; Chen, H.; Heidari, A.A.; Wang, M.; Zhang, X.; Chen, Y.; Pan, Z. Orthogonal learning covariance matrix for defects of grey wolf optimizer: Insights, balance, diversity, and feature selection. Knowledge-Based Syst. 2021, 213, 106684. [Google Scholar] [CrossRef]
- Zhao, X.; Li, D.; Yang, B.; Ma, C.; Zhu, Y.; Chen, H. Feature selection based on improved ant colony optimization for online detection of foreign fiber in cotton. Appl. Soft Comput. 2014, 24, 585–596. [Google Scholar] [CrossRef]
- Yu, H.; Li, W.; Chen, C.; Liang, J.; Gui, W.; Wang, M.; Chen, H. Dynamic Gaussian bare-bones fruit fly optimizers with abandonment mechanism: Method and analysis. Eng. Comput. 2020, 1–29. [Google Scholar] [CrossRef]
- Frolova, L.A.; Anokhin, D.V.; Piryazev, A.A.; Luchkin, S.Y.; Dremova, N.N.; Stevenson, K.J.; Troshin, P.A. Highly efficient all-inorganic planar heterojunction perovskite solar cells produced by thermal coevaporation of CsI and PbI2. J. Phys. Chem. Lett. 2017, 8, 67–72. [Google Scholar] [CrossRef]
- Lai, M.; Kong, Q.; Bischak, C.G.; Yu, Y.; Dou, L.; Eaton, S.W.; Ginsberg, N.S.; Yang, P. Structural, optical, and electrical properties of phase-controlled cesium lead iodide nanowires. Nano Res. 2017, 10, 1107–1114. [Google Scholar] [CrossRef]
- Paul, T.; Chatterjee, B.; Maiti, S.; Sarkar, S.; Besra, N.; Das, B.; Panigrahi, K.; Thakur, S.; Ghorai, U.; Chattopadhyay, K. Tunable cathodoluminescence over the entire visible window from all-inorganic perovskite CsPbX3 1D architecture. J. Mater. Chem. C 2018, 6, 3322–3333. [Google Scholar] [CrossRef]
- Fu, Y.; Rea, M.T.; Chen, J.; Morrow, D.J.; Hautzinger, M.P.; Zhao, Y.; Pan, D.; Manger, L.H.; Wright, J.C.; Goldsmith, R.H. Selective stabilization and photophysical properties of metastable perovskite polymorphs of CsPbI3 in thin films. Chem. Mater. 2017, 29, 8385–8394. [Google Scholar] [CrossRef]
- Bertolotti, F.; Protesescu, L.; Kovalenko, M.V.; Yakunin, S.; Cervellino, A.; Billinge, S.J.; Terban, M.W.; Pedersen, J.S.; Masciocchi, N.; Guagliardi, A. Coherent nanotwins and dynamic disorder in cesium lead halide perovskite nanocrystals. ACS Nano 2017, 11, 3819–3831. [Google Scholar] [CrossRef]
- Hybertsen, M.S.; Louie, S.G. Electron correlation in semiconductors and insulators: Band gaps and quasiparticle energies. Phys. Rev. B 1986, 34, 5390. [Google Scholar] [CrossRef] [PubMed]
- Linaburg, M.R.; McClure, E.T.; Majher, J.D.; Woodward, P.M. Cs1–xRbxPbCl3 and Cs1–xRbxPbBr3 solid solutions: Understanding octahedral tilting in lead halide perovskites. Chem. Mater. 2017, 29, 3507–3514. [Google Scholar] [CrossRef]
- Yamada, K.; Funabiki, S.; Horimoto, H.; Matsui, T.; Okuda, T.; Ichiba, S. Structural phase transitions of the polymorphs of CsSnI3 by means of rietveld analysis of the X-ray diffraction. Chem. Lett. 1991, 20, 801–804. [Google Scholar] [CrossRef]
- Chung, I.; Song, J.-H.; Im, J.; Androulakis, J.; Malliakas, C.D.; Li, H.; Freeman, A.J.; Kenney, J.T.; Kanatzidis, M.G. CsSnI3: Semiconductor or metal? High electrical conductivity and strong near-infrared photoluminescence from a single material. High hole mobility and phase-transitions. J. Am. Chem. Soc. 2012, 134, 8579–8587. [Google Scholar] [CrossRef]
- Hutter, E.M.; Sutton, R.J.; Chandrashekar, S.; Abdi-Jalebi, M.; Stranks, S.D.; Snaith, H.J.; Savenije, T.J. Vapour-deposited cesium lead iodide perovskites: Microsecond charge carrier lifetimes and enhanced photovoltaic performance. ACS Energy Lett. 2017, 2, 1901–1908. [Google Scholar] [CrossRef]
- Shahiduzzaman, M.; Yonezawa, K.; Yamamoto, K.; Ripolles, T.S.; Karakawa, M.; Kuwabara, T.; Takahashi, K.; Hayase, S.; Taima, T. Improved reproducibility and intercalation control of efficient planar inorganic perovskite solar cells by simple alternate vacuum deposition of PbI2 and CsI. ACS Omega 2017, 2, 4464–4469. [Google Scholar] [CrossRef]
- Yang, L.; Dai, Q.; Liu, L.; Shao, D.; Luo, K.; Jamil, S.; Liu, H.; Luo, Z.; Chang, B.; Wang, X. Rapid sintering method for highly conductive Li7La3Zr2O12 ceramic electrolyte. Ceram. Int. 2020, 46, 10917–10924. [Google Scholar] [CrossRef]
- Li, X.; Feng, Y.; Liu, B.; Yi, D.; Yang, X.; Zhang, W.; Chen, G.; Liu, Y.; Bai, P. Influence of NbC particles on microstructure and mechanical properties of AlCoCrFeNi high-entropy alloy coatings prepared by laser cladding. J. Alloy. Compd. 2019, 788, 485–494. [Google Scholar] [CrossRef]
- Chen, X.; Wang, D.; Wang, T.; Yang, Z.; Zou, X.; Wang, P.; Luo, W.; Li, Q.; Liao, L.; Hu, W. Enhanced photoresponsivity of a GaAs nanowire metal-semiconductor-metal photodetector by adjusting the fermi level. ACS Appl. Mater. Interfaces 2019, 11, 33188–33193. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Tang, J.; Kang, Y.; Zhao, H.; Fang, D.; Fang, X.; Chen, R.; Wei, Z. Optical properties of quasi-type-II structure in GaAs/GaAsSb/GaAs coaxial single quantum-well nanowires. Appl. Phys. Lett. 2018, 113, 233104. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, X.; Shaheen, S.M.; Rinklebe, J.; Bolan, N.S.; Ali, E.F.; Li, G.; Tsang, D.C. Effects of microorganism-mediated inoculants on humification processes and phosphorus dynamics during the aerobic composting of swine manure. J. Hazard. Mater. 2021, 416, 125738. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Tang, Y.; Zhang, F.; Lee, C.S. A novel aluminum-graphite dual—ion battery. Adv. Energy Mater. 2016, 6, 1502588. [Google Scholar] [CrossRef]
- Sheng, M.; Zhang, F.; Ji, B.; Tong, X.; Tang, Y. A novel tin-graphite dual—ion battery based on sodium—ion electrolyte with high energy density. Adv. Energy Mater. 2017, 7, 1601963. [Google Scholar] [CrossRef]
- Wang, M.; Jiang, C.; Zhang, S.; Song, X.; Tang, Y.; Cheng, H.-M. Reversible calcium alloying enables a practical room-temperature rechargeable calcium-ion battery with a high discharge voltage. Nat. Chem. 2018, 10, 667–672. [Google Scholar] [CrossRef]
- Li, X.; Sheng, X.; Guo, Y.; Lu, X.; Wu, H.; Chen, Y.; Zhang, L.; Gu, J. Multifunctional HDPE/CNTs/PW composite phase change materials with excellent thermal and electrical conductivities. J. Mater. Sci. Technol. 2021, 86, 171–179. [Google Scholar] [CrossRef]
- Niu, Z.; Zhang, B.; Li, D.; Ji, D.; Liu, Y.; Feng, Y.; Zhou, T.; Zhang, Y.; Fan, Y.; Niu, A.Z. A mechanical reliability study of 3-dB waveguide hybrid couplers in submillimeter and terahertz bands. Front. Inf. Technol. Electron. Eng. 2021, 22, 1104–1113. [Google Scholar] [CrossRef]
- Woodward, P.M. Octahedral tilting in perovskites. I. Geometrical considerations. Acta Crystallogr. Sect. B Struct. Sci. 1997, 53, 32–43. [Google Scholar] [CrossRef]
- Woodward, P.M. Octahedral tilting in perovskites. II. Structure stabilizing forces. Acta Crystallogr. Sect. B Struct. Sci. 1997, 53, 44–66. [Google Scholar] [CrossRef]
- Glazer, A.M. The classification of tilted octahedra in perovskites. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1972, 28, 3384–3392. [Google Scholar] [CrossRef]
- Nam, J.K.; Jung, M.S.; Chai, S.U.; Choi, Y.J.; Kim, D.; Park, J.H. Unveiling the crystal formation of cesium lead mixed-halide perovskites for efficient and stable solar cells. J. Phys. Chem. Lett. 2017, 8, 2936–2940. [Google Scholar] [CrossRef] [PubMed]
- Ripolles, T.S.; Nishinaka, K.; Ogomi, Y.; Miyata, Y.; Hayase, S. Efficiency enhancement by changing perovskite crystal phase and adding a charge extraction interlayer in organic amine free-perovskite solar cells based on cesium. Sol. Energy Mater. Sol. Cells 2016, 144, 532–536. [Google Scholar] [CrossRef]
- Luo, P.; Xia, W.; Zhou, S.; Sun, L.; Cheng, J.; Xu, C.; Lu, Y. Solvent engineering for ambient-air-processed, phase-stable CsPbI3 in perovskite solar cells. J. Phys. Chem. Lett. 2016, 7, 3603–3608. [Google Scholar] [CrossRef]
- Li, H.; Xu, P.; Liu, D.; He, J.; Zu, H.; Song, J.; Zhang, J.; Tian, F.; Yun, M.; Wang, F. Low-voltage and fast-response SnO2 nanotubes/perovskite heterostructure photodetector. Nanotechnology 2021, 32, 375202. [Google Scholar] [CrossRef]
- Li, F.; Ma, C.; Wang, H.; Hu, W.; Yu, W.; Sheikh, A.D.; Wu, T. Ambipolar solution-processed hybrid perovskite phototransistors. Nat. Commun. 2015, 6, 1–8. [Google Scholar] [CrossRef]
- Eperon, G.E.; Stranks, S.D.; Menelaou, C.; Johnston, M.B.; Herz, L.M.; Snaith, H.J. Formamidinium lead trihalide: A broadly tunable perovskite for efficient planar heterojunction solar cells. Energy Environ. Sci. 2014, 7, 982–988. [Google Scholar] [CrossRef]
- Swarnkar, A.; Chulliyil, R.; Ravi, V.K.; Irfanullah, M.; Chowdhury, A.; Nag, A. Colloidal CsPbBr3 perovskite nanocrystals: Luminescence beyond traditional quantum dots. Angew. Chem. 2015, 127, 15644–15648. [Google Scholar] [CrossRef]
- Zarei, M.; Davarpanah, A.; Mokhtarian, N.; Farahbod, F. Integrated feasibility experimental investigation of hydrodynamic, geometrical and, operational characterization of methanol conversion to formaldehyde. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 42, 89–103. [Google Scholar] [CrossRef]
- Ananthakumar, S.; Kumar, J.R.; Babu, S.M. Cesium lead halide (CsPbX3, X= Cl, Br, I) perovskite quantum dots-synthesis, properties, and applications: A review of their present status. J. Photonics Energy 2016, 6, 042001. [Google Scholar] [CrossRef]
- Tang, X.; Hu, Z.; Chen, W.; Xing, X.; Zang, Z.; Hu, W.; Qiu, J.; Du, J.; Leng, Y.; Jiang, X. Room temperature single-photon emission and lasing for all-inorganic colloidal perovskite quantum dots. Nano Energy 2016, 28, 462–468. [Google Scholar] [CrossRef]
- Somma, F.; Nikl, M.; Nitsch, K.; Fabeni, P.; Pazzi, G. Excitons in CsPbX3 (X= Cl, Br, I) ternary nanocrystallites in thin film matrices. J. Lumin. 2001, 94, 169–172. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Pack, J.D.; Monkhorst, H.J. “Special points for Brillouin-zone integrations”—A reply. Phys. Rev. B 1977, 16, 1748. [Google Scholar] [CrossRef]
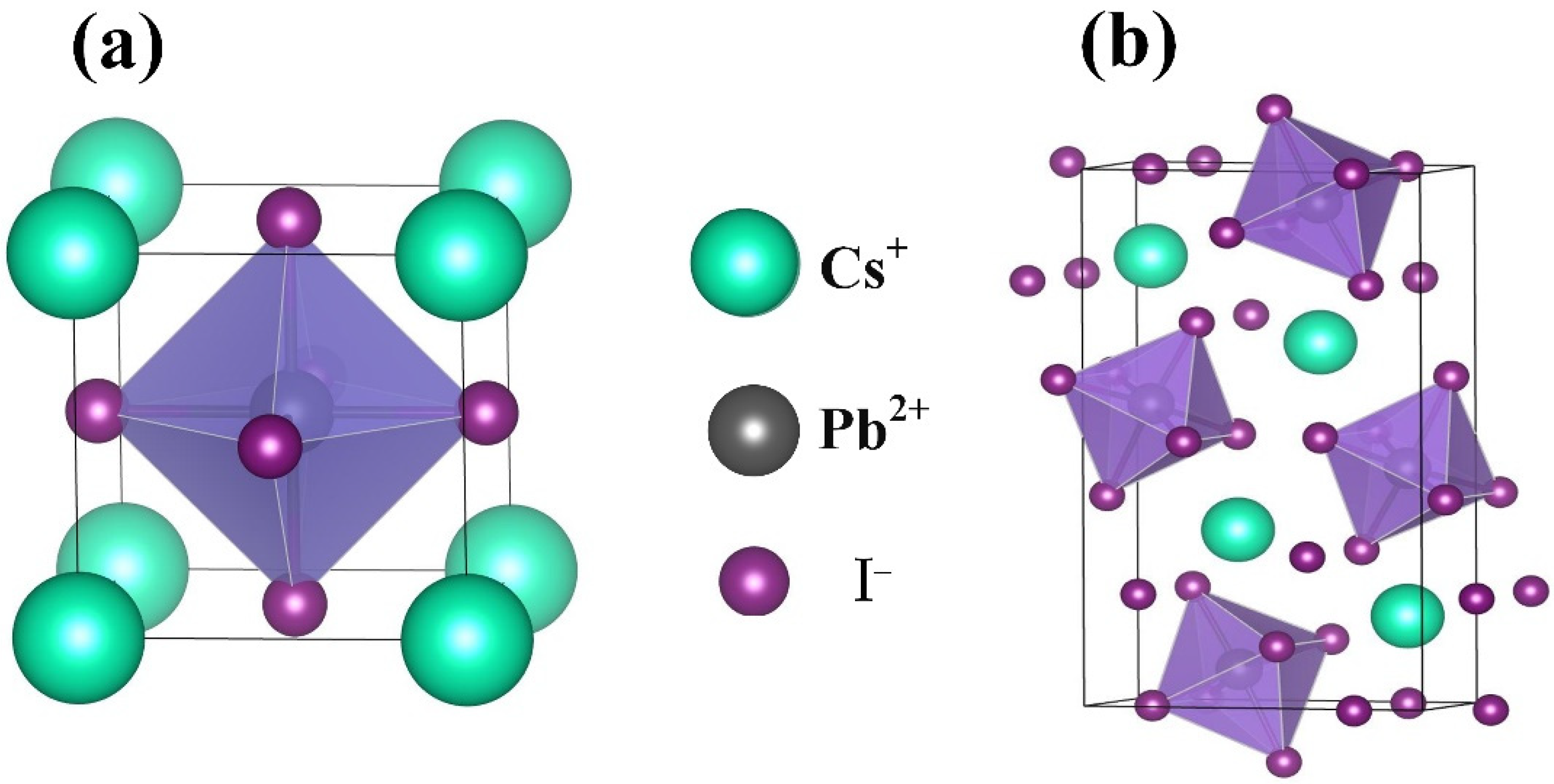

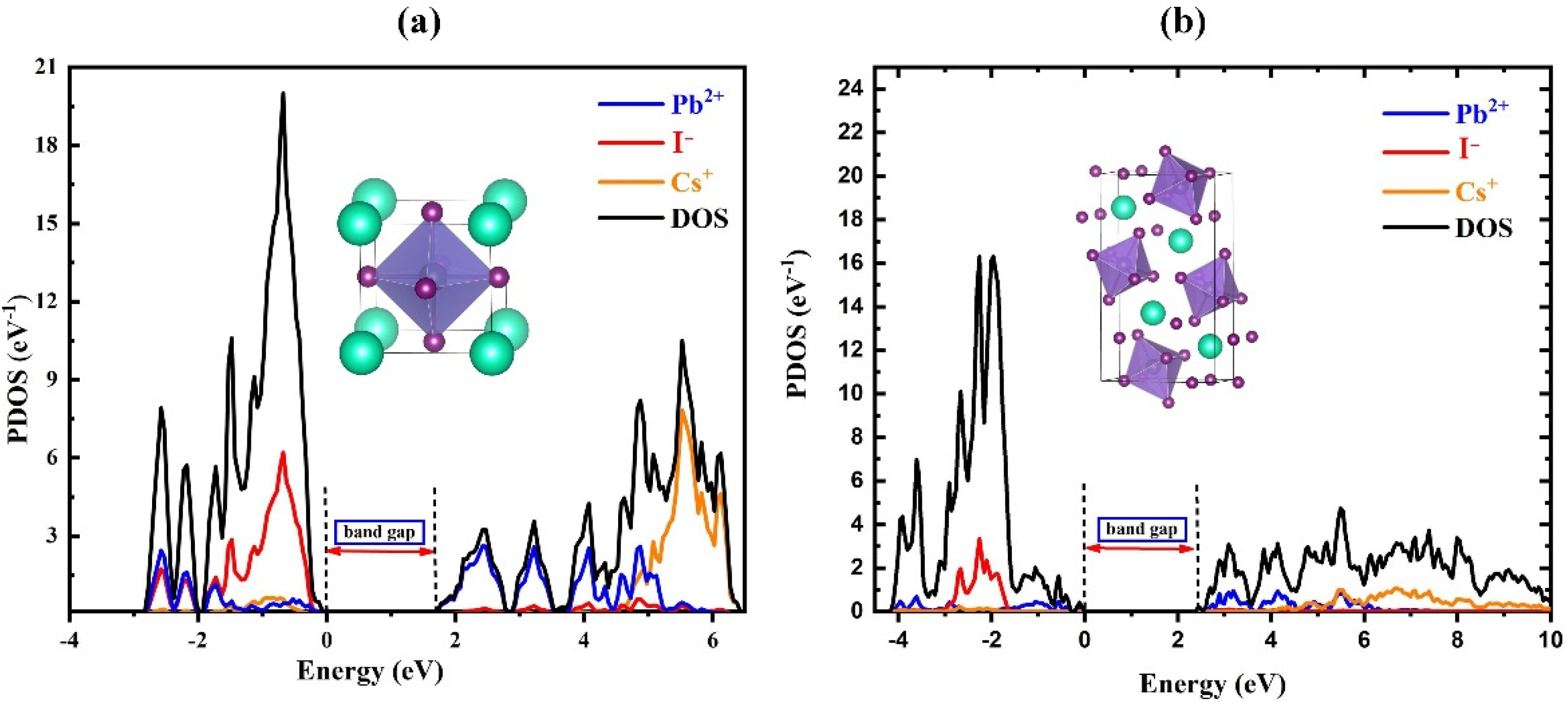
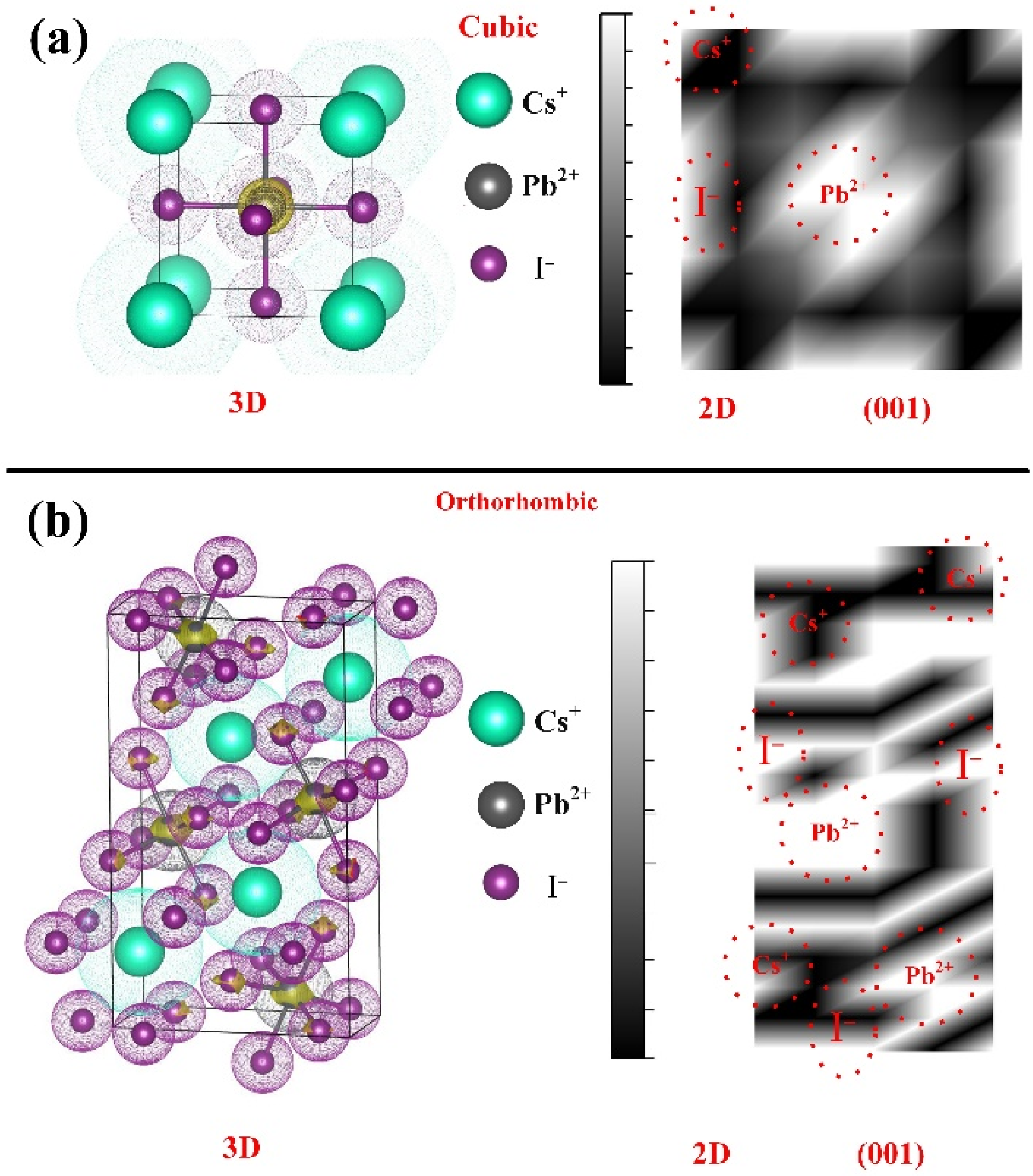

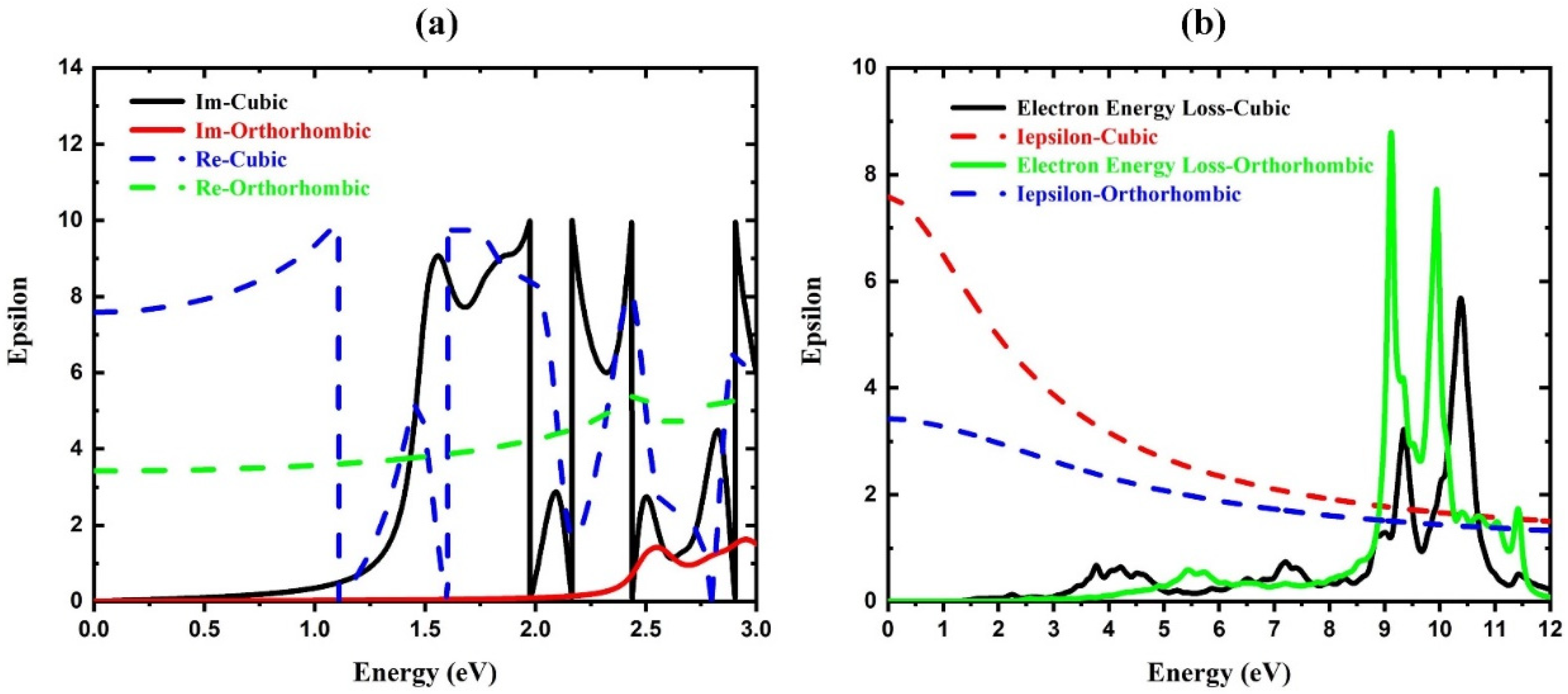
| Component | Lattice Parameter (Å) | Band Gap (eV) | Volume (Å)3 | Optimization Energy (eV) |
|---|---|---|---|---|
| CsPbI3−Cubic | a = b = c = 6.40 | 1.62 | 262.97 | −5265.40 |
| CsPbI3−Orthorhombic | a = 10.53, b = 4.87, c = 18.07 | 2.45 | 927.092 | −4223.486 |
| Atom Name | Ionic Radius (Å) | Atomic Radius (Å) | Van der Waals Radius (Å) | Atomic Mass |
|---|---|---|---|---|
| I | 2.2 | 1.33 | 1.98 | 126.90 |
| Pb | 1.19 | 1.75 | 2.16 | 207.20 |
| Cs | 1.74 | 2.72 | 3.31 | 132.90 |
| Cubic Phase | Orthorhomic Phase | ||||||
|---|---|---|---|---|---|---|---|
| Atom Name | I (Å) | Pb (Å) | Cs (Å) | Atom Name | I (Å) | Pb (Å) | Cs (Å) |
| I | 4.53 | 3.20 | 4.53 | I | 4.87 | 3.10 | 3.52 |
| Pb | 3.20 | 0 | 5.60 | Pb | 3.10 | 7.84 | 5.44 |
| Cs | 4.53 | 5.60 | 6.40 | Cs | 3.93 | 5.44 | 5.97 |
| Component | Distortion Index (Å) | Bond Angle Variance (deg2) | Volume (Å3) |
|---|---|---|---|
| CsPbI3−Cubic | 0 | 0 | 43.82 |
| CsPbI3−Orthorhombic | 0.01817 | 19.306 | 46.25 |
| Perovskite Structures | |
|---|---|
| CsPbI3−Cubic | 7.58 |
| CsPbI3−Orthorhombic | 3.42 |
| Perovskite Structures | n0 | α (nm) |
|---|---|---|
| CsPbI3−Cubic | 2.75 | 779 |
| CsPbI3−Orthorhombic | 1.82 | 506 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Syah, R.; Davarpanah, A.; Nasution, M.K.M.; Wali, Q.; Ramdan, D.; Albaqami, M.D.; Ouladsmane, M.; Noori, S.M. RETRACTED: The Effect of Structural Phase Transitions on Electronic and Optical Properties of CsPbI3 Pure Inorganic Perovskites. Coatings 2021, 11, 1173. https://doi.org/10.3390/coatings11101173
Syah R, Davarpanah A, Nasution MKM, Wali Q, Ramdan D, Albaqami MD, Ouladsmane M, Noori SM. RETRACTED: The Effect of Structural Phase Transitions on Electronic and Optical Properties of CsPbI3 Pure Inorganic Perovskites. Coatings. 2021; 11(10):1173. https://doi.org/10.3390/coatings11101173
Chicago/Turabian StyleSyah, Rahmad, Afshin Davarpanah, Mahyuddin K. M. Nasution, Qamar Wali, Dadan Ramdan, Munirah D. Albaqami, Mohamed Ouladsmane, and Saja Mohammed Noori. 2021. "RETRACTED: The Effect of Structural Phase Transitions on Electronic and Optical Properties of CsPbI3 Pure Inorganic Perovskites" Coatings 11, no. 10: 1173. https://doi.org/10.3390/coatings11101173
APA StyleSyah, R., Davarpanah, A., Nasution, M. K. M., Wali, Q., Ramdan, D., Albaqami, M. D., Ouladsmane, M., & Noori, S. M. (2021). RETRACTED: The Effect of Structural Phase Transitions on Electronic and Optical Properties of CsPbI3 Pure Inorganic Perovskites. Coatings, 11(10), 1173. https://doi.org/10.3390/coatings11101173








