Optimization of Substrate Sizes for In Situ Stress Measurement in Electrodeposits Relying on Nonlinear Effects
Abstract
1. Introduction
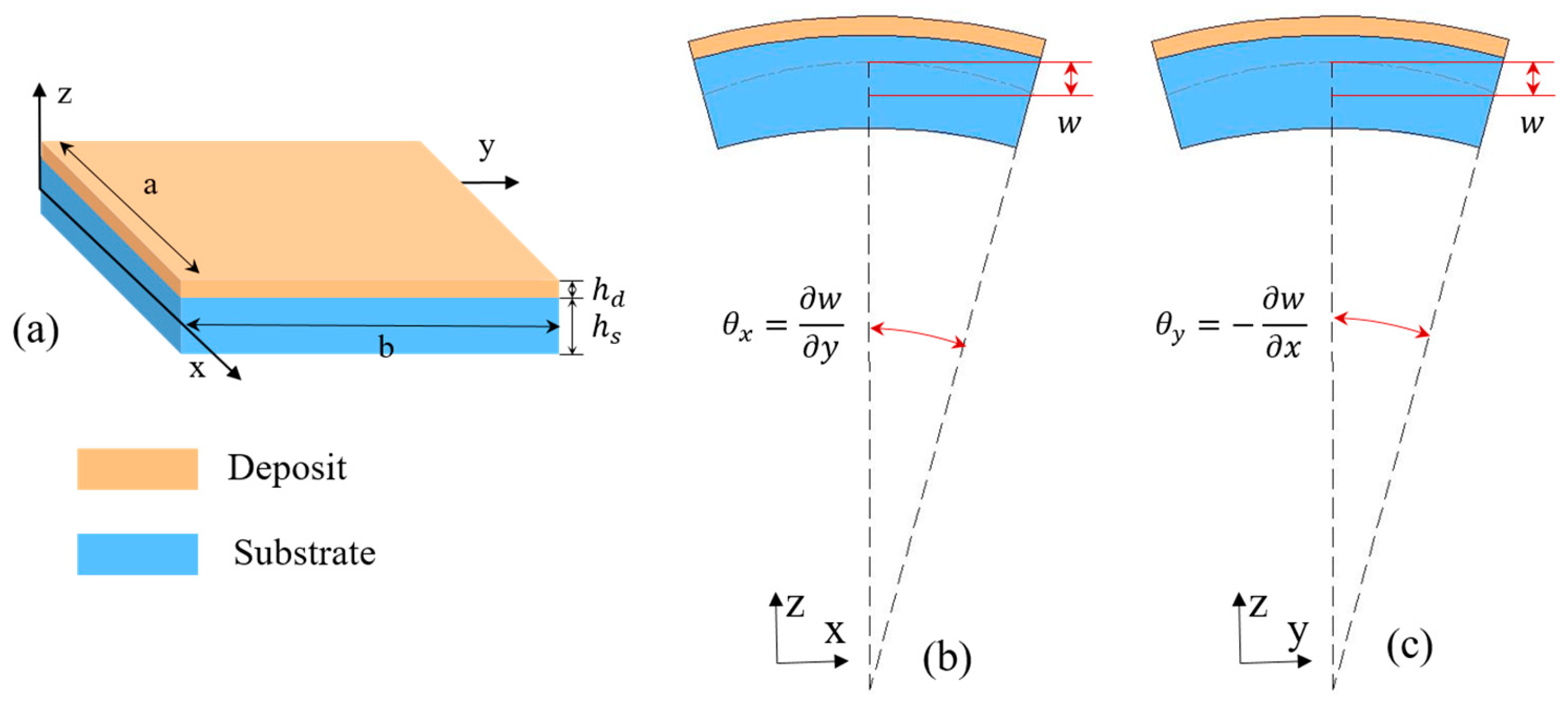
2. Materials and Methods
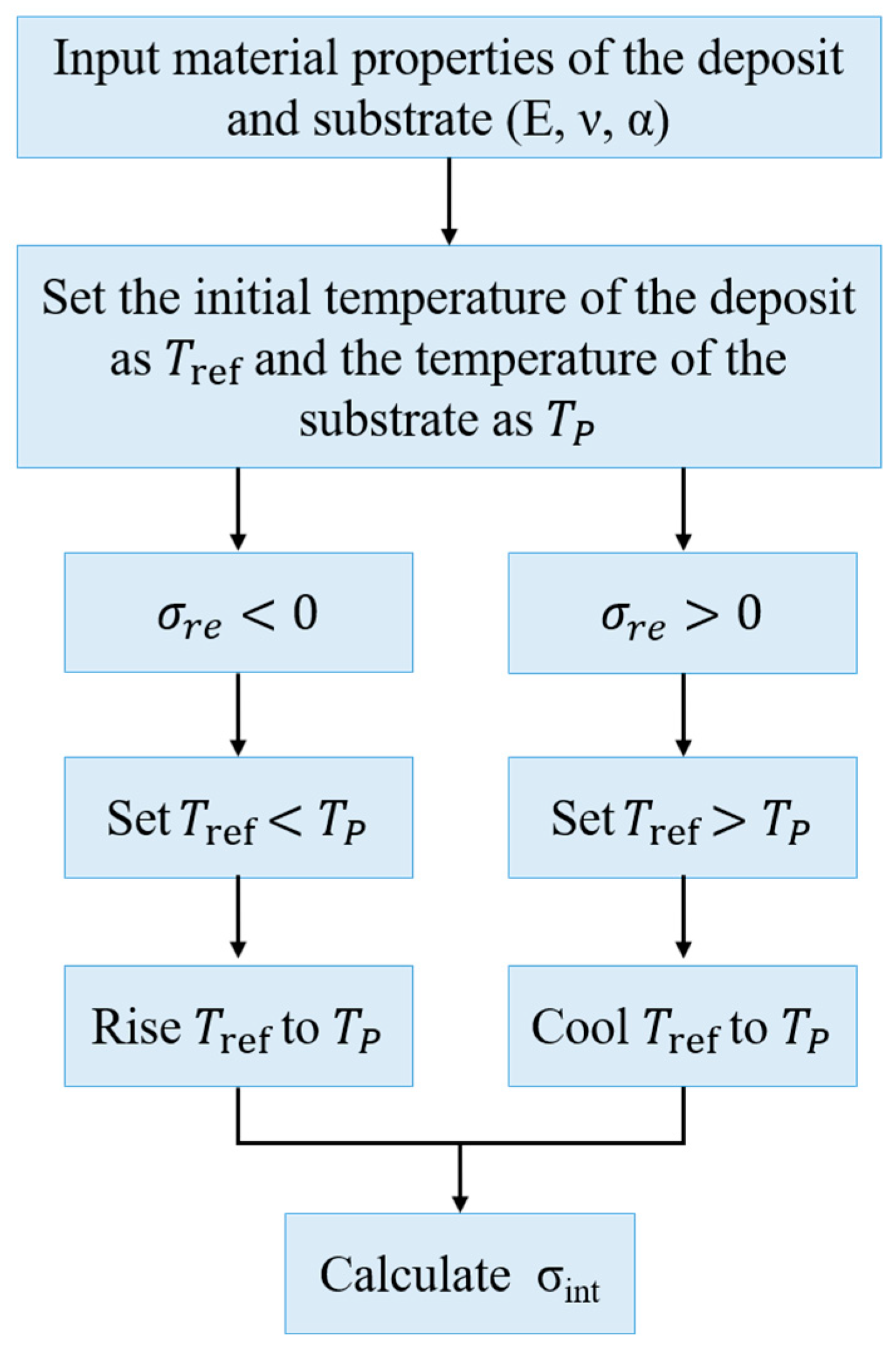
2.1. The Equivalent Reference Temperature Method
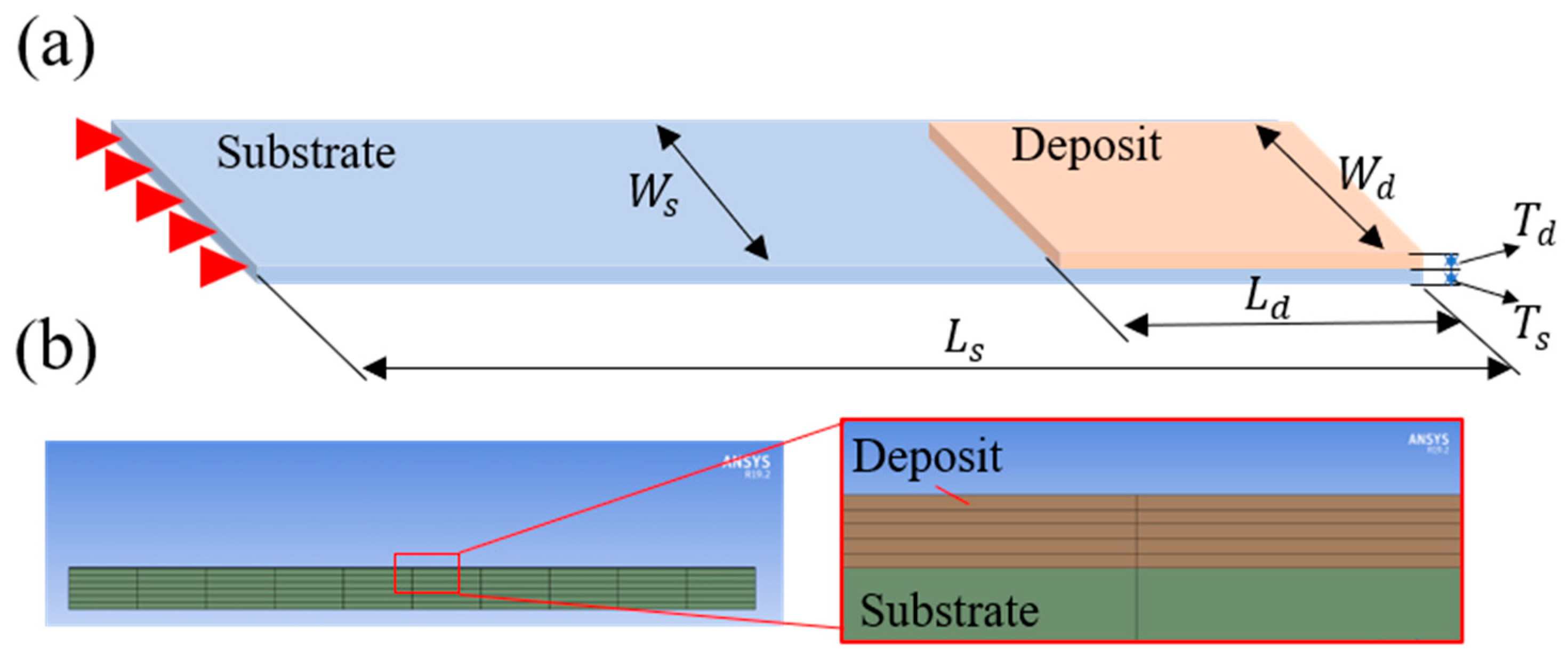
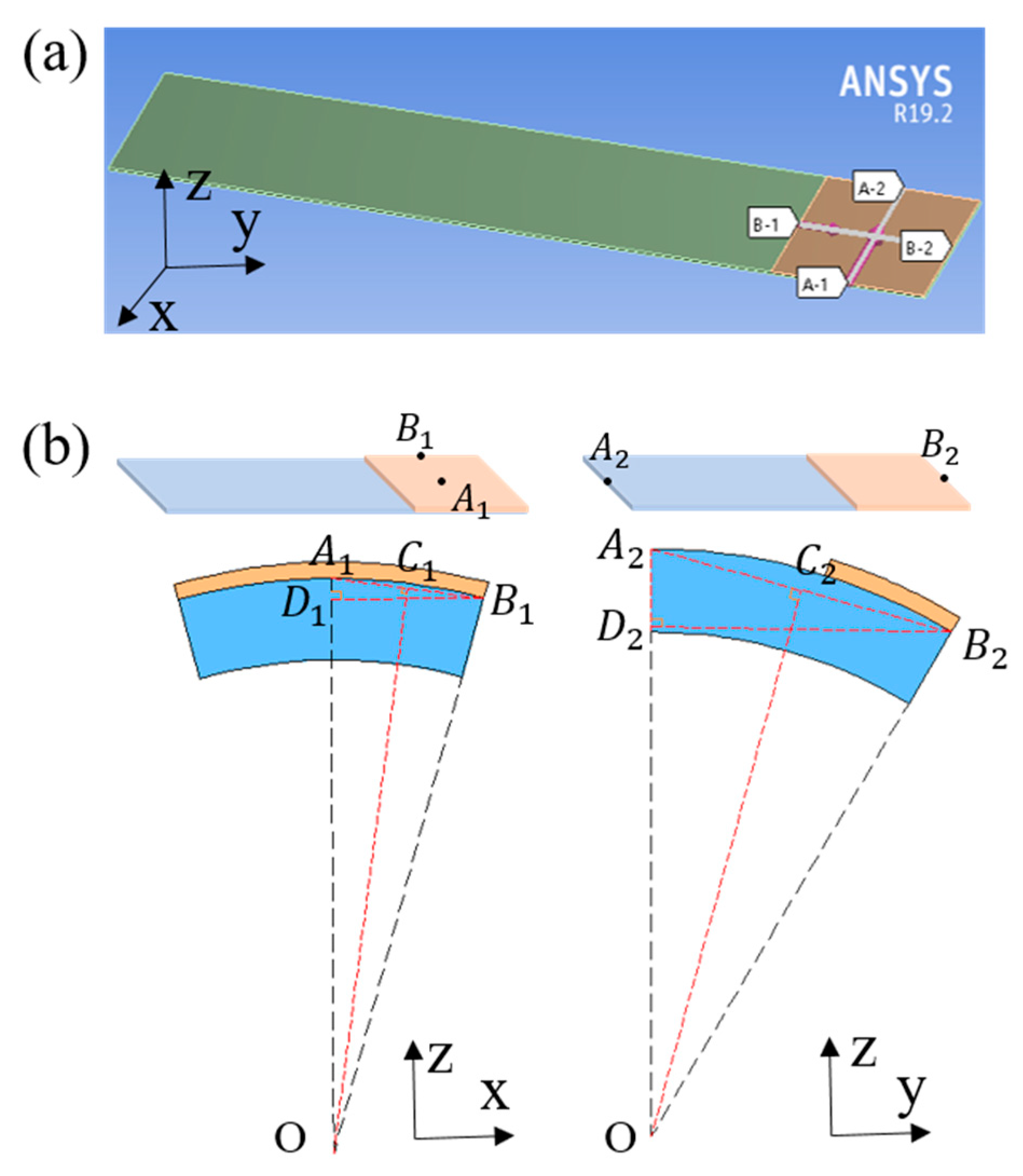
2.2. The Curvature Radius of a Substrate-Deposit System in the Simulation
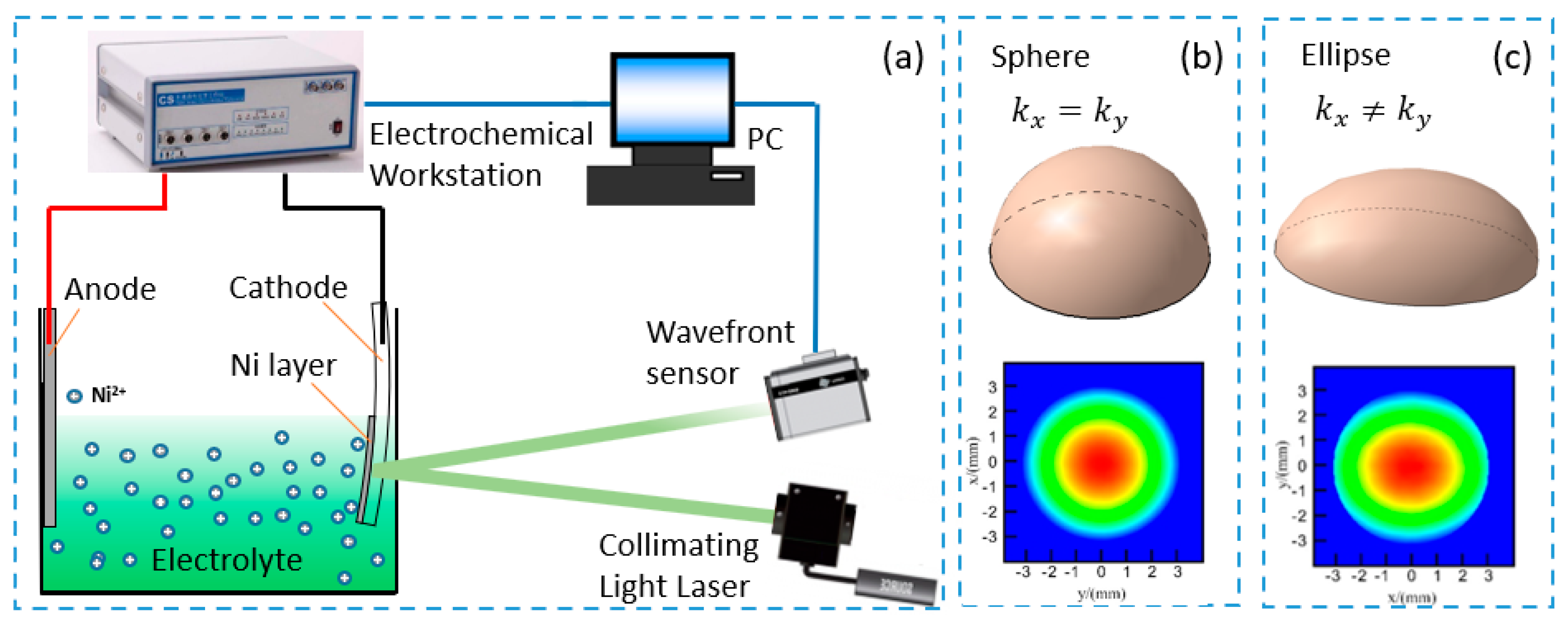
2.3. In Situ Stress Measurement of Ni Electrodeposition
3. Results and Discussion
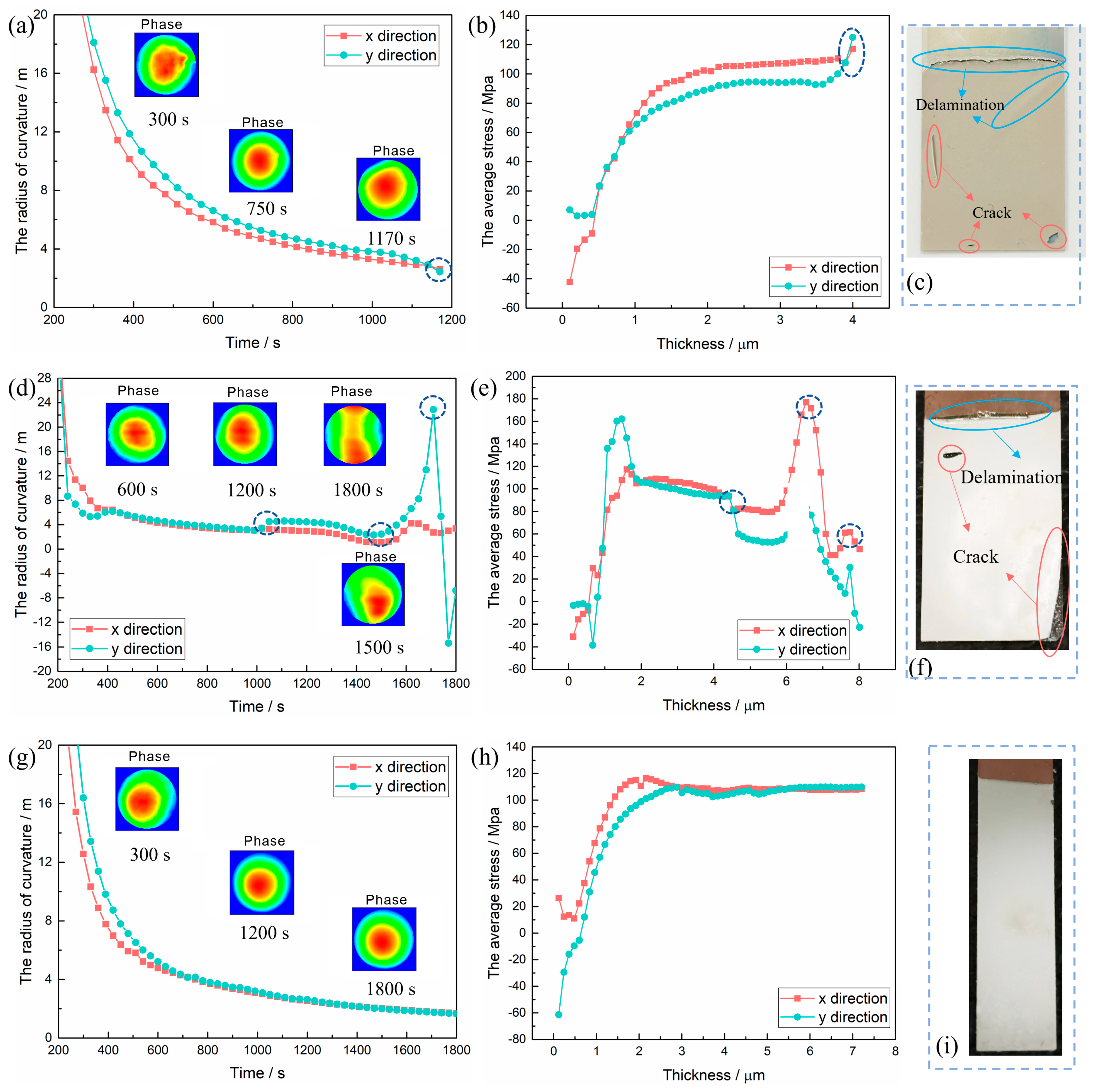
3.1. Effect of Substrate Width on the Curvature Radius and the Internal Stress of Nickel Deposits in Experiments
3.2. Effect of Substrate Width on the Curvature Radius of the Deposit in the Simulation
3.3. Effect of Substrate Width on the Internal Stress of the Deposit in the Simulation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Bending Stiffness Formula Considering Base Geometry

References
- Chason, E. Stress Measurement in Thin Films Using Wafer Curvature: Principles and Applications. In Handbook of Mechanics of Materials; Springer: Singapore, 2018; pp. 1–33. [Google Scholar]
- Pureza, J.; Lacerda, M.; De Oliveira, A.; Fragalli, J.; Zanon, R. Enhancing accuracy to Stoney equation. Appl. Surf. Sci. 2009, 255, 6426–6428. [Google Scholar] [CrossRef]
- Stoney, G.G. The Tension of Metallic Films deposited by Electrolysis. Proc. R. Soc. Lond. 1909, 82, 172–175. [Google Scholar]
- Hearne, S.J.; Floro, J.A. Mechanisms inducing compressive stress during electrodeposition of Ni. J. Appl. Phys. 2005, 97, 014901. [Google Scholar] [CrossRef]
- Takehiro Kume, S.E. Hidekazu Mimura, Development of internal stress measurement technique for Ni electroforming using Shack–Hartmann sensor. Int. J. Electr. Mach. 2016, 21, 25–30. [Google Scholar] [CrossRef][Green Version]
- Kume, T.; Egawa, S.; Yamaguchi, G.; Mimura, H. Influence of Residual Stress of Electrodeposited Layer on Shape Replication Accuracy in Ni Electroforming. Procedia CIRP 2016, 42, 783–787. [Google Scholar] [CrossRef]
- Qiang, J.; Luo, K.; Dong, Y.; Jiang, B.; Drummer, D.; Roth, B. In Situ Stress Measurement of Ni Electrodeposition Using Lateral Shearing Interferometry. J. Electrochem. Soc. 2020, 167, 162504. [Google Scholar] [CrossRef]
- Besnard, A.; Ardigo, M.R.; Imhoff, L.; Jacquet, P. Curvature radius measurement by optical profiler and determination of the residual stress in thin films. Appl. Surf. Sci. 2019, 487, 356–361. [Google Scholar] [CrossRef]
- Mezin, A. Coating internal stress measurement through the curvature method: A geometry-based criterion delimiting the relevance of Stoney’s formula. Surf. Coat. Technol. 2006, 200, 5259–5267. [Google Scholar] [CrossRef]
- Abadias, G.; Daniel, R. Stress in physical vapor deposited thin films: Measurement methods and selected examples. In Handbook of Modern Coating Technologies; Elsevier: Amsterdam, The Netherlands, 2021; pp. 359–436. [Google Scholar]
- Freund, L.; Floro, J.; Chason, E. Extensions of the Stoney formula for substrate curvature to configurations with thin substrates or large deformations. Appl. Phys. Lett. 1999, 74, 1987–1989. [Google Scholar] [CrossRef]
- Shiri, S.; Ashtijoo, P.; Odeshi, A.; Yang, Q. Evaluation of Stoney equation for determining the internal stress of DLC thin films using an optical profiler. Surf. Coat. Technol. 2016, 308, 98–100. [Google Scholar] [CrossRef]
- Guyot, N.; Harmand, Y.; Mezin, A. The role of the sample shape and size on the internal stress induced curvature of thin-film substrate systems. Int. J. Solids Struct. 2004, 41, 5143–5154. [Google Scholar] [CrossRef]
- Graciano, V.; Bertocci, U.; Stafford, G. In-Situ Stress Measurements during Cobalt Electrodeposition. J. Electrochem. Soc. 2019, 166, 3246–3253. [Google Scholar] [CrossRef]
- Fayette, M.; Bertocci, U.; Stafford, G. In Situ Stress Measurements during Cobalt Electrodeposition on (111)-Textured Au. J. Electrochem. Soc. 2016, 163, D146–D153. [Google Scholar] [CrossRef]
- Yu, H.; Thompson, C. Grain growth and complex stress evolution during Volmer-Weber growth of polycrystalline thin films. Acta Mater. 2014, 67, 189–198. [Google Scholar] [CrossRef]
- Song, C.; Du, L.; Li, X.; Li, Y.; Qi, L.; Li, Y. Residual stress modeling and analysis for micro electroforming layer. Microsyst. Technol. 2017, 23, 4709–4716. [Google Scholar] [CrossRef]
- Song, C.; Du, L.; Zhao, W.; Zhu, H.; Zhao, W.; Wang, W. Effectiveness of stress release geometries on reducing residual stress in electroforming metal microstructure. J. Micromechan. Microeng. 2018, 28, 045010. [Google Scholar] [CrossRef]
- Chen, H.; Huang, C.; Cheng, P. Stress mechanisms of SiO2 and Nb2O5 thin films sputtered on flexible substrates investigated by finite element method. Surf. Coat. Technol. 2018, 344, 449–457. [Google Scholar] [CrossRef]
- Nejhad, M.; Pan, C.; Feng, H. Intrinsic strain modeling and residual stress analysis for thin-film processing of layered structures. J. Electron. Packag. 2003, 125, 4–17. [Google Scholar] [CrossRef]
- Song, C.; Du, L.; Qi, L.; Li, Y.; Li, X.; Li, Y. Residual stress measurement in a metal microdevice by micro Raman spectroscopy. J. Micromechan. Microeng. 2017, 27, 7. [Google Scholar] [CrossRef]
- Floro, J.; Chason, E.; Cammarata, R.; Srolovitz, D. Physical origins of intrinsic stresses in Volmer-Weber thin films. MRS Bull. 2002, 27, 19–25. [Google Scholar] [CrossRef]
- Abadias, G.; Simonot, L.; Colin, J.; Michel, A.; Camelio, S.; Babonneau, D. Volmer-Weber growth stages of polycrystalline metal films probed by in situ and real-time optical diagnostics. Appl. Phys. Lett. 2015, 107, 183105. [Google Scholar] [CrossRef]
- Freund, L.B. Substrate curvature due to thin ®lm mismatch strain in the nonlinear deformation range. J. Mech. Phys. Solids 2000, 48, 1159–1174. [Google Scholar] [CrossRef]
- Huang, Y.; Rosakis, A. Extension of Stoney’s formula to nonuniform temperature distributions in thin film/substrate systems. J. Mech. Phys. Solids 2005, 53, 2483–2500. [Google Scholar] [CrossRef]
- Feng, X.; Huang, Y.; Rosakis, A.J. Stresses in a multilayer thin film/substrate system subjected to nonuniform temperature. J. Appl. Mech. Trans. Asme 2008, 75, 021022. [Google Scholar] [CrossRef]
- Blech, I.; Blech, I.; Finot, M. Determination of thin-film stresses on round substrates. J. Appl. Phys. 2005, 97, 113525. [Google Scholar] [CrossRef]
- Finot, M.; Blech, I.; Suresh, S.; Fujimoto, H. Large deformation and geometric instability of substrates with thin-film deposits. J. Appl. Phys. 1997, 81, 3457–3464. [Google Scholar] [CrossRef]
- Freund, L.; Suresh, S. Thin Film Materials: Stress, Defect Formation, and Surface Evolution; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Shield, T.; Kim, K. Beam theory models for thin film segments cohesively bonded to an elastic half space. Int. J. Solids Struct. 1992, 29, 1085–1103. [Google Scholar] [CrossRef]
- Hutchinson, J.; Suo, Z. Mixed Mode Cracking in Layered Materials. In Advances in Applied Mechanics; Hutchinson, J.W., Wu, T.Y., Eds.; Elsevier: Amsterdam, The Netherlands, 1991; pp. 63–191. [Google Scholar]
- Zhang, Y. Extended Stoney’s formula for a film-substrate bilayer with the effect of interfacial slip. J. Appl. Mech. Trans. Asme 2008, 75, 011008. [Google Scholar] [CrossRef]



| Materials | Elastic Modulus/GPa | Poisson Ratio | Coefficient of Thermal Expansion/°C−1 |
|---|---|---|---|
| Nickel | 210 | 0.31 | 1.33 × 10−5 |
| Quartz glass | 55 | 0.25 | 5.5 × 10−7 |
| Deposits | Substrates | ||||
|---|---|---|---|---|---|
| Length ) | Width ) | Thickness ) | Length ) | Width ) | Thickness ) |
| 15 | 5 | 0.01 | 80 | 5 | 0.3 |
| 10 | 10 | ||||
| 15 | 15 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiang, J.; Peng, T. Optimization of Substrate Sizes for In Situ Stress Measurement in Electrodeposits Relying on Nonlinear Effects. Coatings 2023, 13, 2031. https://doi.org/10.3390/coatings13122031
Qiang J, Peng T. Optimization of Substrate Sizes for In Situ Stress Measurement in Electrodeposits Relying on Nonlinear Effects. Coatings. 2023; 13(12):2031. https://doi.org/10.3390/coatings13122031
Chicago/Turabian StyleQiang, Jun, and Tao Peng. 2023. "Optimization of Substrate Sizes for In Situ Stress Measurement in Electrodeposits Relying on Nonlinear Effects" Coatings 13, no. 12: 2031. https://doi.org/10.3390/coatings13122031
APA StyleQiang, J., & Peng, T. (2023). Optimization of Substrate Sizes for In Situ Stress Measurement in Electrodeposits Relying on Nonlinear Effects. Coatings, 13(12), 2031. https://doi.org/10.3390/coatings13122031





