Study on the Multi-Physical Field Simulation of the Double-Glow Plasma Alloying Process Parameters
Abstract
1. Introduction
2. Model Building
2.1. Mathematical Model
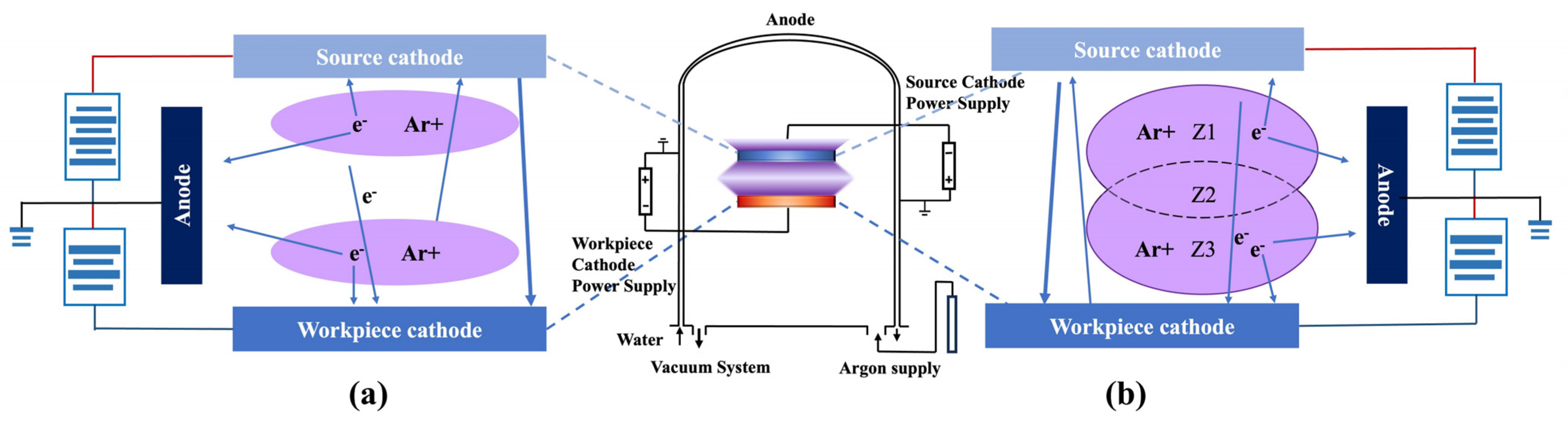
2.2. Double-Glow Physical Model in Simulation
- (1)
- Assuming the simplified furnace–body model is a two-dimensional axisymmetric geometric body, a cathode is set in the horizontal direction. A cylindrical rotating body is constructed with the center line as the axis; due to the axial symmetry of the discharge structure, the three-dimensional discharge structure can be simplified into a two-dimensional structure in the simulation.
- (2)
- Preliminary study on transient calculations of double-glow plasma and assuming local thermodynamic equilibrium.
- (3)
- In this simulation, the drift and transport of heavy matter in the electrode material were not considered, and only the generation of argon plasma in the furnace was considered.
- (4)
- The main research object is the discharge area between the two electrode plates. Therefore, when setting grid control edges, select areas close to the cathode and source plates to refine the grid of the main research area.
- (5)
- Glow intensity reflects the brightness and darkness of a glow, which is the most intuitive physical phenomenon. The main source of glow is excited argon ions, so the number density of excited argon ions is used to characterize glow intensity.
| Simulation Parameters | Specific Values |
|---|---|
| Anode voltage/V | 0 |
| Source voltage/V | −800 |
| Cathode voltage/V | −400 |
| Initial electron average energy/eV | 4 |
| /Pa | 20 |
| Cathode secondary electron emission coefficient | 0.25 |
| Source secondary electron emission coefficient | 0.25 |
| Heavy matter initial temperature T/K | 300 |
2.3. Boundary Conditions of Plasma Field Model
- (1)
- Anode boundary conditions: When electrons and ions touch the reaction chamber’s inner wall, they will be adsorbed. Following that
- (2)
- Cathode boundary condition: The surface of the cathode experiences secondary emission when it is bombarded by positive ions:
- (3)
- Reaction cavity wall boundary conditions: When electrons and ions move to the wall of the reaction cavity, charge builds up on it and creates an electrostatic field that reacts with the charged particles within the cavity. Therefore, the current density in the normal direction at the wall boundary should meet:
3. Results and Discussion
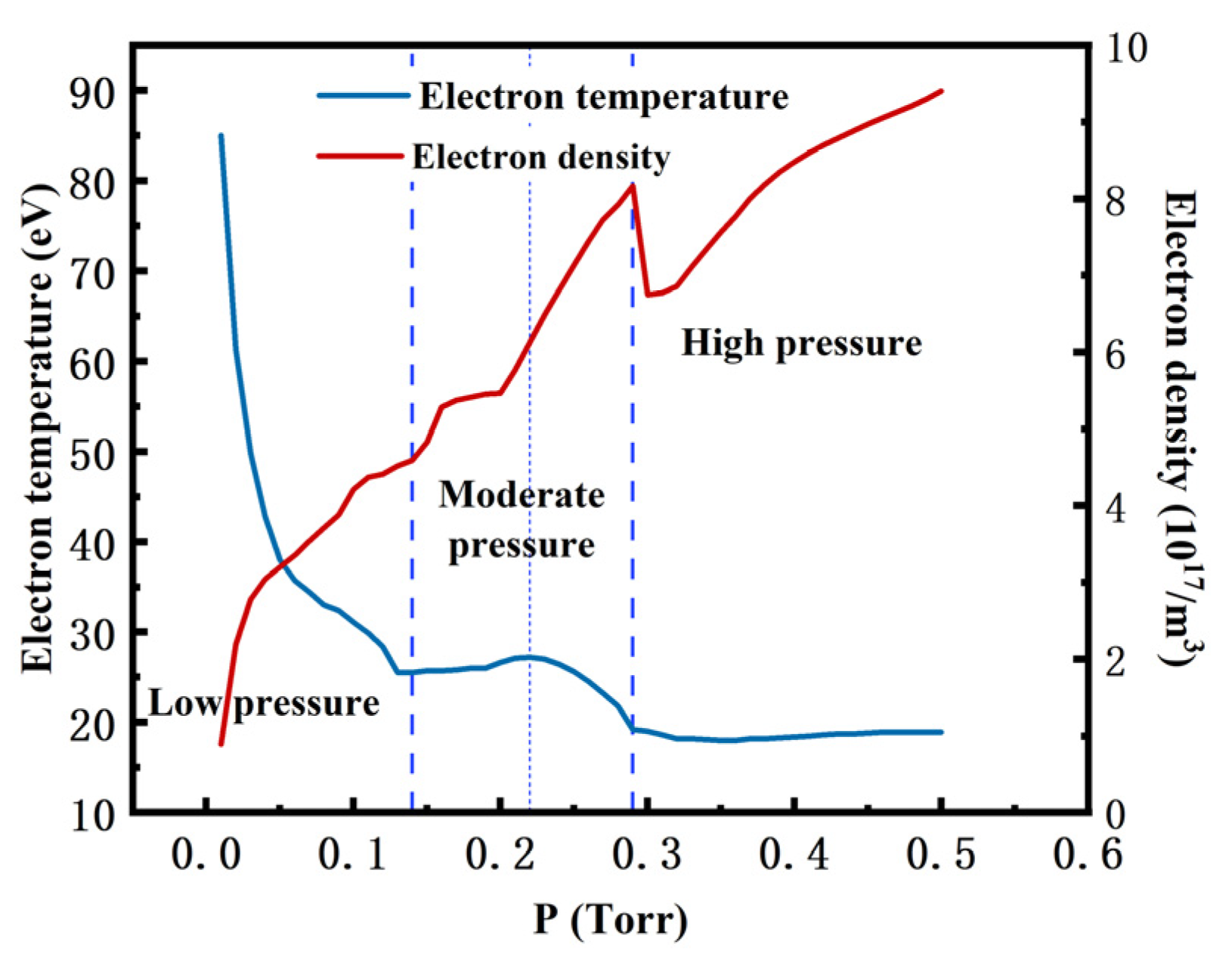
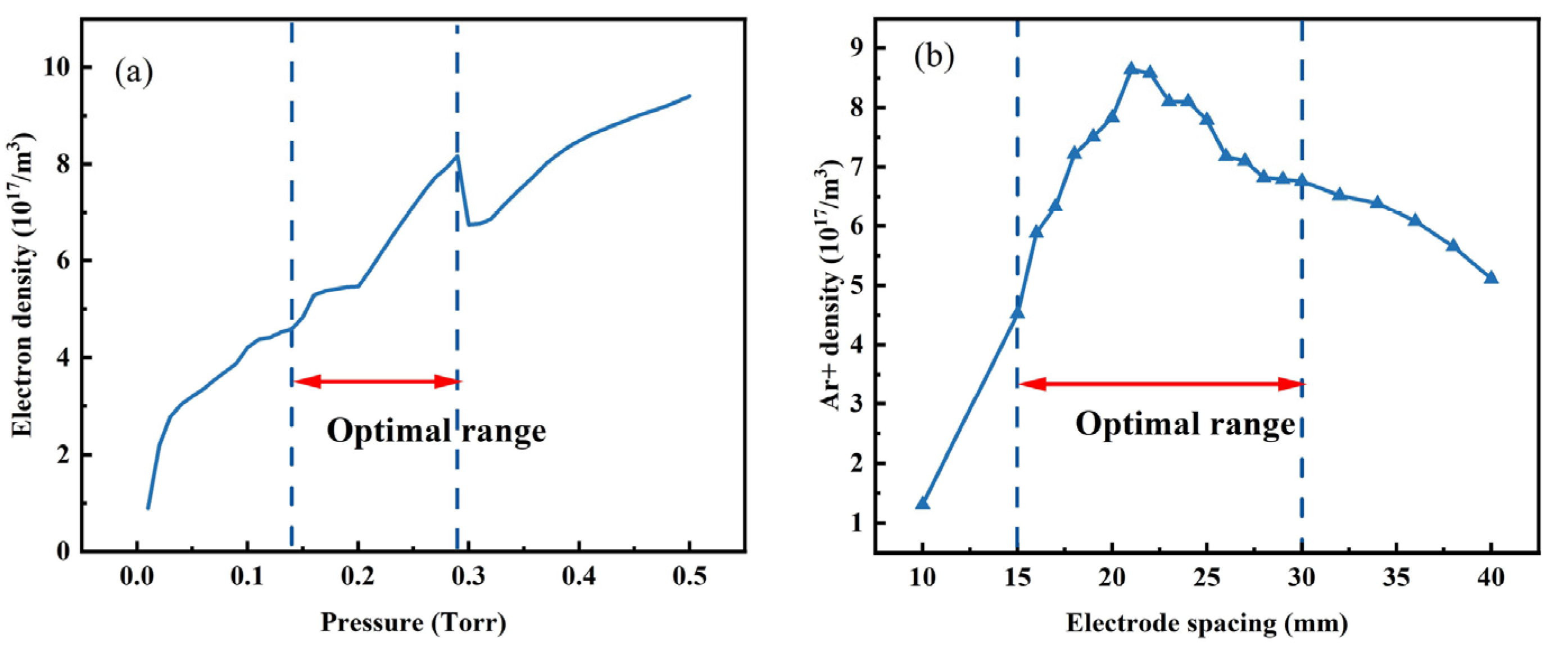
3.1. Effect of Working Pressure on Plasma Parameters
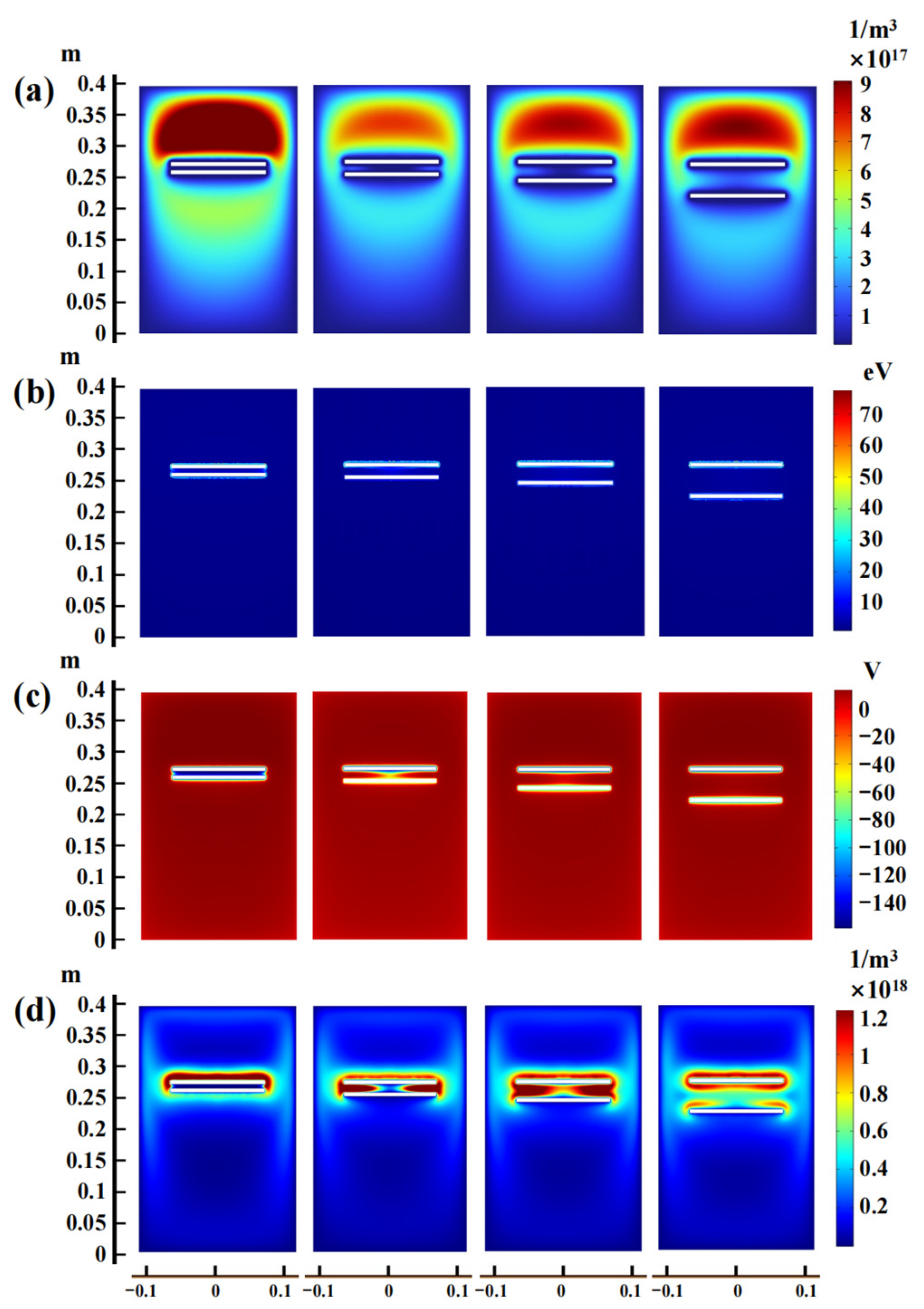
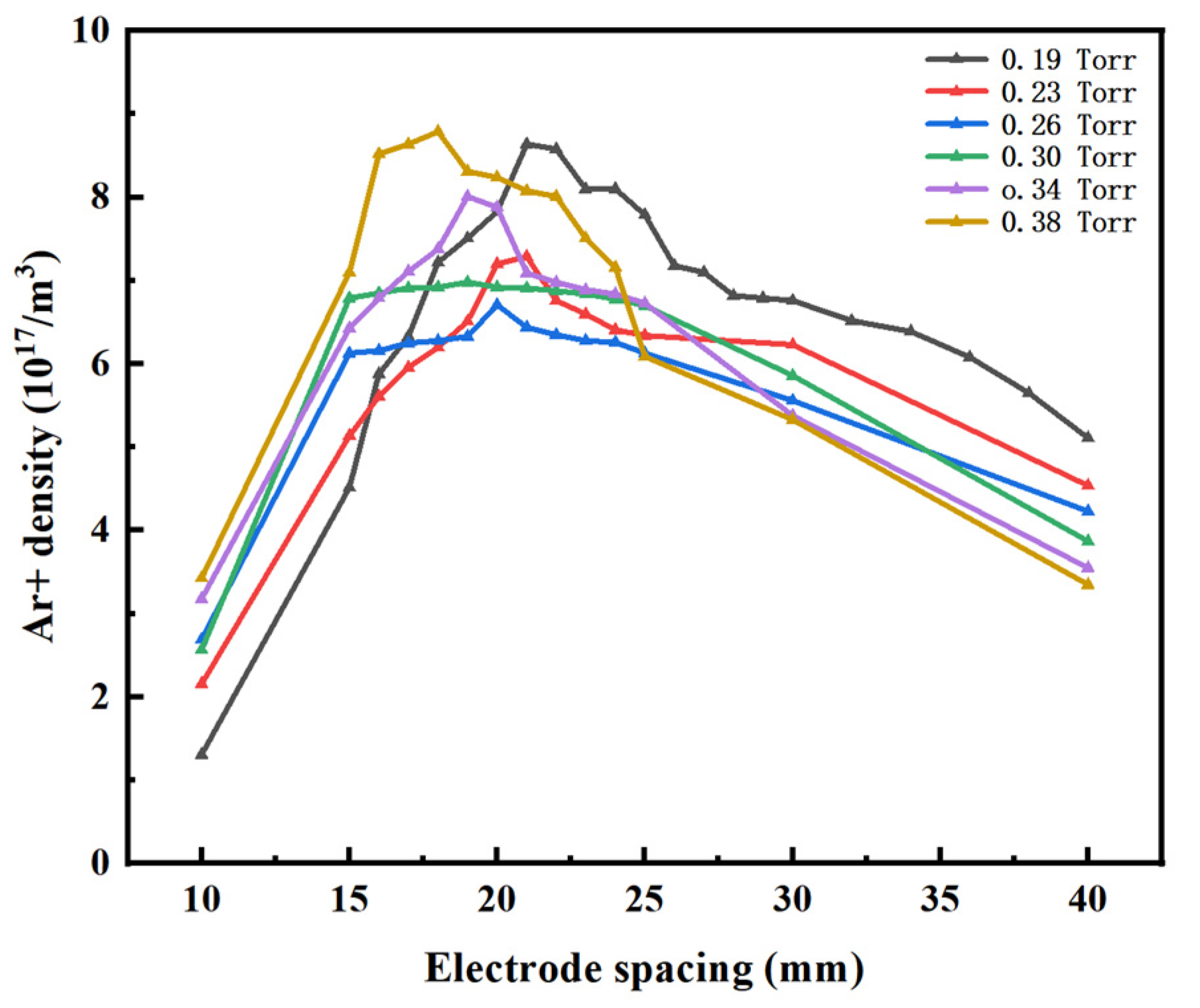
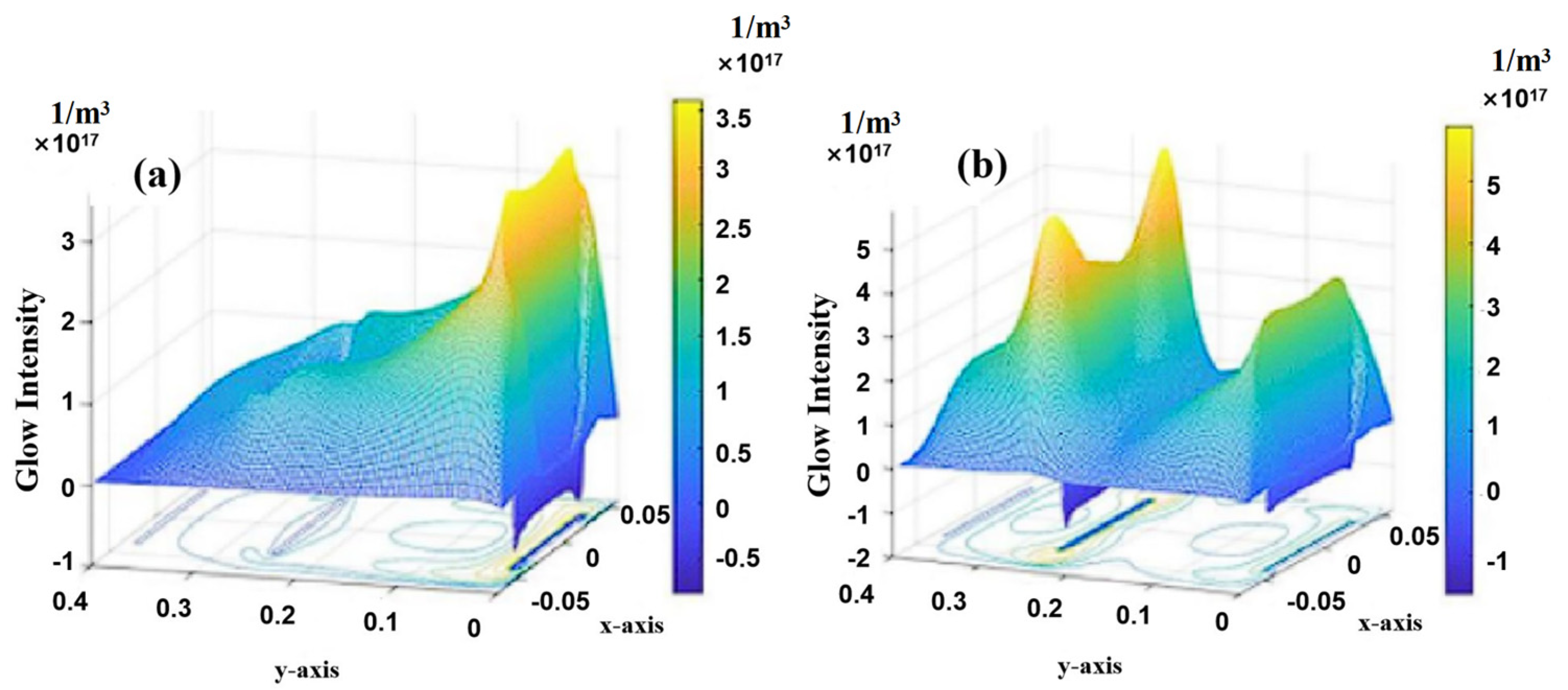
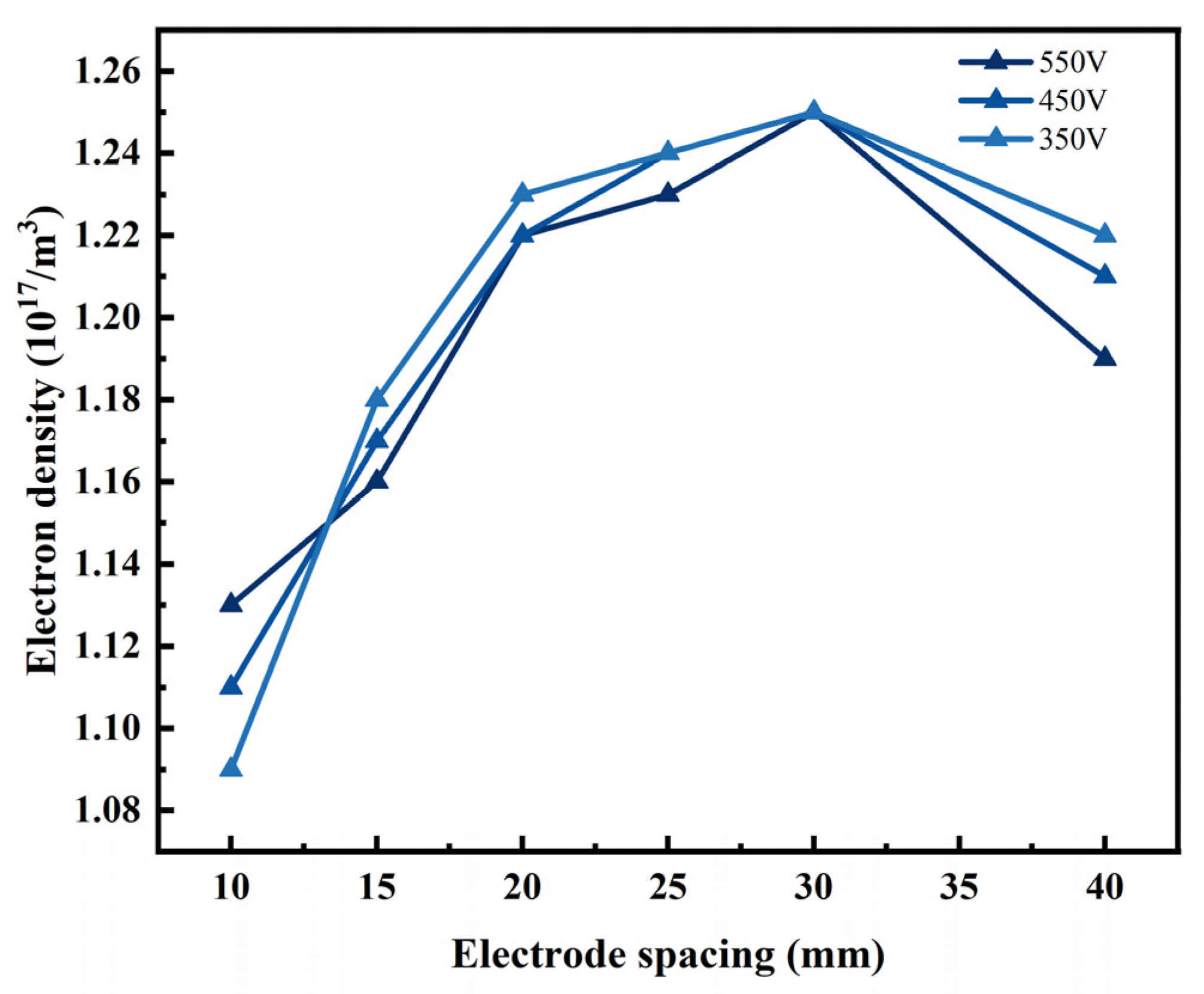
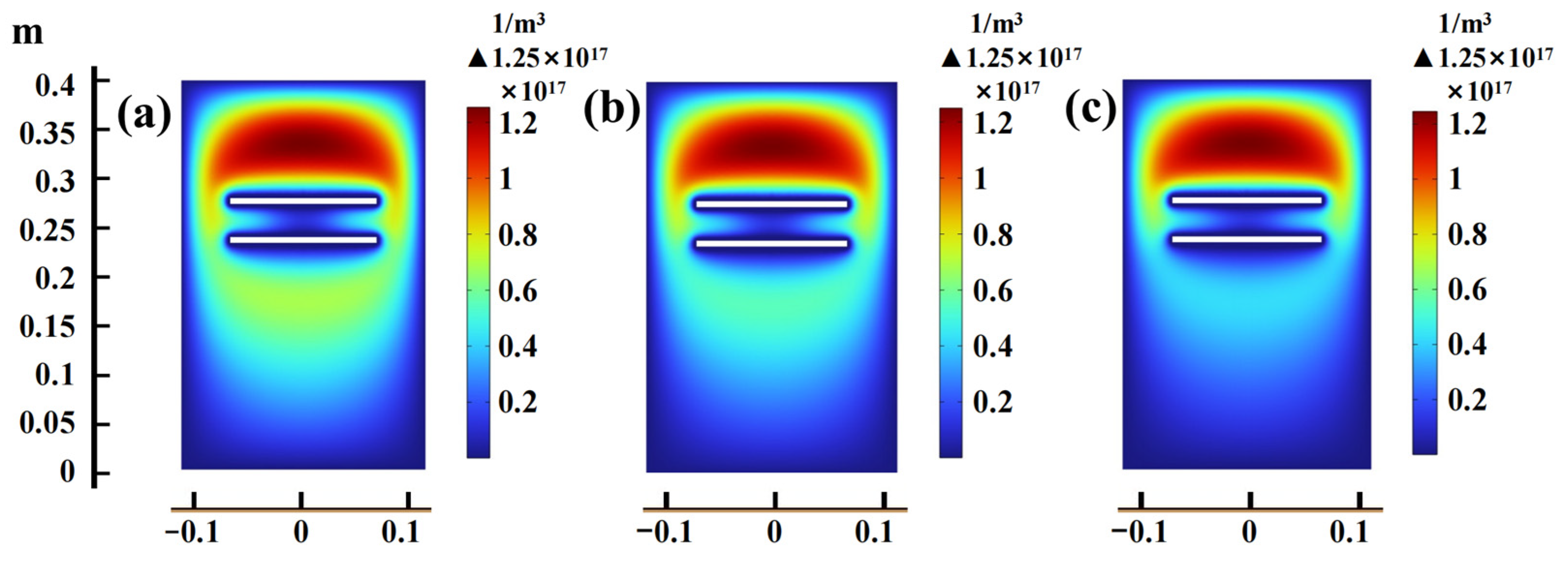
3.2. Electrode Spacing’s Impact on the Plasma Parameters
3.3. Effect of Voltage on Plasma Parameters
3.3.1. Impact of Cathode/Source Voltage
3.3.2. Impact of Negative/Source Voltage Difference
4. Comparison between the Theoretical and Experimental
5. Conclusions
- (1)
- Based on the double-glow plasma discharge model, we studied the plasma field’s physical characteristics, including the working pressure, electrode spacing and voltage difference. The result showed that as the working pressure increases, the electron density, temperature, potential and excited argon ion number density near the source electrode plate gradually increase, while it is less effective near the cathode electrode plate. As the electrode spacing increases, the above electron-field parameters significantly decrease at the beginning stage and then increase. However, due to the occurrence and disappearance of the glow crosslinking between the two electrode plates, the change in the number density of excited argon ions shows an opposite trend. The variation in voltage between the cathode and source electrodes significantly influences the electron field distribution across the electrode plates.
- (2)
- The relationship between the process parameters and physical field discharge characteristics has also been studied. The results revealed that the optimal working pressure range is between 0.14 Torr and 0.29 Torr. The electron temperature during the working pressure range has a maximum value, which can improve the diffusion efficiency of the sputtering elements. The optimal electrode-spacing range is between 15 mm and 30 mm. In this interval, the optimal value has a decreasing tendency with the increase in working pressure, which affects the distribution of the number density of excited argon ions, which can be beneficial for forming a uniform coating.
- (3)
- The results of the theory and experiment verify the consistency of the double-glow plasma discharge simulation. It has been confirmed that the model can guide the acquisition of optimized process parameters for the double-glow discharge and improve the predictability of dual glow surface metallurgy technology.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aung, L.M.; Renn, T.; Lin, J.C.; Salamanca, E.; Wu, Y.; Pan, Y.; Teng, N.; Huang, H.; Sun, Y.; Chang, W. Improving osteogenic properties of zirconia ceramic via glow discharge plasma-enhanced deposition of amine organic compound. J. Dent. Sci. 2024, in press. [Google Scholar] [CrossRef]
- Yang, Z.; Yu, T.; Hu, S.; Feng, Y.; Zhao, Y.; Chen, Y. Structural evolution, wear and corrosion failure mechanisms of CrN coating synthesized by applying gradient voltage and arc-enhanced glow discharge. Mater. Today Commun. 2024, 40, 109361. [Google Scholar] [CrossRef]
- Guo, R.; Yu, T.; Zhou, X.; Wang, G.; Chen, M. Chip geometry modeling in micro-milling of glow discharge polymer by a single-edge diamond tool considering tool inclination. J. Mater. Process Technol. 2023, 320, 118109. [Google Scholar] [CrossRef]
- Li, J.; Lei, B.; Wang, J.; Xu, B.; Ran, S.; Wang, Y.; Zhang, T.; Tang, J.; Zhao, W.; Duan, Y. Atmospheric diffuse plasma jet formation from positive-pseudo-streamer and negative pulseless glow discharges. Commun. Phys. 2021, 4, 64. [Google Scholar] [CrossRef]
- Yu, H.; Liang, W.; Miao, Q.; Yin, M.; Xue, L.; Yi, J.; Qi, Y. Improvement of plasma carbonitriding modified layer on TA15 surface by RASP-assisted DGPSA treatment. Vacuum 2022, 206, 111499. [Google Scholar] [CrossRef]
- Dong, C.; Huang, J.; Cui, A.; Luo, J.; Zhou, Z.; Cheng, H.; Wen, Z.; Xu, J. Microstructure and high-temperature oxidation behavior of Al2O3/Cr composite coating on Inconel 718 alloy. J. Mater. Res. Technol. 2024, 28, 4498–4507. [Google Scholar] [CrossRef]
- La, L.; Wang, L.; Liang, F.; Zhang, J.; Liang, G.; Wang, Z.; Lin, Q. High-temperature oxidation and tribological behaviors of WTaVCr alloy coating prepared by double glow plasma surface alloying technology. Surf. Coat. Technol. 2023, 464, 129429. [Google Scholar] [CrossRef]
- Lei, X.; Lin, N.; Yuan, S.; Lei, C.; Nouri, M.; Liu, Z.; Yu, Y.; Zeng, Q.; Ma, G.; Li, D.; et al. Combining laser surface texturing and double glow plasma surface chromizing to improve tribological performance of Ti6Al4V alloy. Surf. Coat. Technol. 2024, 478, 130418. [Google Scholar] [CrossRef]
- He, S.; Wang, P.; Ha, J.; Zhang, B.; Zhang, Z.; Li, Q. Effects of Discharge Parameters on the Micro-hollow Cathode Sustained Glow Discharge. Spectrosc. Spect. Anal. 2019, 39, 3377–3382. [Google Scholar] [CrossRef]
- Olejníček, J.; Šmíd, J.; Perekrestov, R.; Kšírová, P.; Rathouský, J.; Kohout, M.; Dvořáková, M.; Kment, Š.; Jurek, K.; Čada, M.; et al. Co3O4 thin films prepared by hollow cathode discharge. Surf. Coat. Technol. 2019, 366, 303–310. [Google Scholar] [CrossRef]
- Hsieh, J.H.; Huang, Y.; Huang, P.; Li, Y. Investigation of anode diameter and keeper geometry influence on open-end emitter heaterless hollow cathode discharge. Vacuum 2024, 113504. [Google Scholar] [CrossRef]
- Sorokin, I.A.; Kolodko, D.V. Planar hollow cathode sputtering with asymmetrical voltage supply. Vacuum 2023, 207, 111570. [Google Scholar] [CrossRef]
- Korolev, Y.D.; Koval, N.N. Low-pressure discharges with hollow cathode and hollow anode and their applications. J. Phys. D Appl. Phys. 2018, 51, 323001. [Google Scholar] [CrossRef]
- Bayki, S.; Mujumdar, S. A 1D model for prediction of dry electrical discharge machining (dry-EDM) plasma characteristics. J. Manuf. Process. 2023, 102, 417–428. [Google Scholar] [CrossRef]
- Yu, Y.; Kang, Z. Oscillation suppression for pulsed arc electrohydraulic discharges based on plasma impedance model. J. Electrostat. 2024, 129, 103923. [Google Scholar] [CrossRef]
- Yücel, H.H.; Utaş, S.; Ongun, E. The Study of DC-and AC-Driven GaAs-Coupled Gas Discharge Micro Plasma Systems: Modeling and Simulation. J. Electron. Mater. 2024, 53, 3792–3808. [Google Scholar] [CrossRef]
- Qiu, Y.; Yu, L.; Zhou, J.; Zhu, H.; Yang, D.; Yu, L.; Chen, R.; Zhang, C.; Ni, R.; Li, Q.; et al. Study of plasma characteristics of hollow cathode in glow discharge. J. Phys. D Appl. Phys. 2023, 56, 485201. [Google Scholar] [CrossRef]
- Liang, Y.; Yuan, C.; Gao, R.; Jia, J.; Kirsanov, G.; Bekasov, V.; Marin, A.; Kudryavtsev, A.; Eliseev, S.; Zhou, Z. Investigation of low-pressure glow discharge in a coaxial gridded hollow cathode. IEEE Trans. Plasma Sci. 2016, 44, 2965–2972. [Google Scholar] [CrossRef]
- Jiang, X.X.; He, F.; Chen, Q.; Ge, T.; Ouyang, J.T. Numerical simulation of the sustaining discharge in radio frequency hollow cathode discharge in argon. Phys. Plasmas 2014, 21, 033508. [Google Scholar] [CrossRef]
- Hagelaar, G.J.M.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Trans. 2005, 14, 722. [Google Scholar] [CrossRef]
- COMSOL. Available online: https://cn.comsol.com/model/dc-glow-discharge-8640 (accessed on 1 September 2024).
- Hojo, H.; Mase, A. Electromagnetic-wave transmittance characteristics in one-dimensional plasma photonic crystals. J. Plasma Fusion Res. Ser. 2009, 8, 477–479. [Google Scholar]
- Rafatov, I.; Bogdanov, E.A.; Kudryavtsev, A.A. On the accuracy and reliability of different fluid models of the direct current glow discharge. Phys. Plasmas 2012, 19, 033502. [Google Scholar] [CrossRef]
- Eliseev, S.I.; Kudryavtsev, A.A.; Liu, H.; Ning, Z.; Yu, D.; Chirtsov, A.S. Transition from glow microdischarge to arc discharge with thermionic cathode in argon at atmospheric pressure. IEEE Trans. Plasma Sci. 2016, 44, 2536–2544. [Google Scholar] [CrossRef]
- Arshadi, A.; Brinkmann, R.P. Analytical investigation of microwave resonances of a curling probe for low and high-pressure plasma diagnostics. Plasma Sources Sci Trans. 2016, 26, 015011. [Google Scholar] [CrossRef]
- Bormashenko, E.; Whyman, G.; Multanen, V.; Shulzinger, E.; Chaniel, G. Physical mechanisms of interaction of cold plasma with polymer surfaces. J. Colloid Interface Sci. 2015, 448, 175–179. [Google Scholar] [CrossRef]
- Zhang, Y.; Qu, Y.; Zhao, K.; He, S.; Zhao, X.; Li, Q. Discharge Characteristics in Hollow Cathode Filled with Helium/Argon Mixture: A Simulation Study. Chin. J. Vac. Sci. Technol. 2019, 39, 8. [Google Scholar]
- Ferreira, C.M.; Loureiro, J.; Ricard, A. Modelling of Stepwise Ionisation Effects in a Low-Pressure Argon Positive Column. In Phenomena in Ionized Gases, Proceedings of the XVI International Conference, Düsseldorf, Germany, 29 August–2 September 1983; Bötticher, W., Wenk, H., Schultz-Gulde, E., Eds.; Organizing Committee ICPIG-XVI: Düsseldorf, Germany, 1983; Volume 1, p. 598. [Google Scholar]
- Che, X.; Shao, T.; Nie, W.; Yan, P. Numerical simulation on a nanosecond-pulse surface dielectric barrier discharge actuator in near space. J. Phys. D Appl. Phys. 2012, 45, 145201. [Google Scholar] [CrossRef]
- Nakao, Y.; Tsukida, K.; Voronchev, V.T. Realistic neutron energy spectrum and a possible enhancement of reaction rates in the early Universe plasma. Phys. Rev. D 2011, 84, 063016. [Google Scholar] [CrossRef]
- Hopwood, J. Review of inductively coupled plasmas for plasma processing. Plasma Sources Sci. Trans. 1992, 1, 109. [Google Scholar] [CrossRef]
- Alakoski, E.; Tiainen, V.M. Energy dependence of the carbon plasma beam on the arc voltage and the anode–cathode distance in the pulsed arc discharge method. Diam. Relat. Mater. 2005, 14, 1451–1454. [Google Scholar] [CrossRef]
- Katoh, R.; Nonaka, K.; Sumiyama, K.; Peng, D.L.; Hihara, T. Morphology and magnetic properties of Fe and Al nanocomposites prepared with single and double-glow-discharge sources. Mater. Trans. 2008, 49, 1830–1835. [Google Scholar] [CrossRef]
- Ha, J.; Liu, L.; He, S. Influential Mechanism of Electrode Spacing on the Self-pulsing Discharge in Cavity Cathode Discharge. High Volt. Eng. 2021, 47, 796–804. [Google Scholar]
- Gu, X. Study on Processes and Properties of Fe-Al Alloy Layer of 45 Steel by Double-Glow Plasma Alloying. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2008. [Google Scholar]




| Serial Number | Reaction Expressions | Reaction Rate Constant |
|---|---|---|
| R 1 | e + Ar => e + Ar | Based on collision cross-section |
| R 2 | e + Ar => e + Ar* | Based on collision cross-section |
| R 3 | e + Ar* => e + Ar | Based on collision cross-section |
| R 4 | e + Ar => 2e+ Ar+ | Based on collision cross-section |
| R 5 | e + Ar* => 2e + Ar+ | Based on collision cross-section |
| R 6 | Ar* + Ar* => e + Ar + Ar+ | 3.734 × 108 m3/(s·mol) |
| R 7 | Ar* + Ar => Ar + Ar | 1 × 107 m3/(s·mol) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Wen, Y.; Zhou, J.; Qiu, Y.; Yang, D.; Dai, H.; Zhu, H.; Hu, Z.; Liu, G.; Khan, A.M.; et al. Study on the Multi-Physical Field Simulation of the Double-Glow Plasma Alloying Process Parameters. Coatings 2024, 14, 1175. https://doi.org/10.3390/coatings14091175
Yu L, Wen Y, Zhou J, Qiu Y, Yang D, Dai H, Zhu H, Hu Z, Liu G, Khan AM, et al. Study on the Multi-Physical Field Simulation of the Double-Glow Plasma Alloying Process Parameters. Coatings. 2024; 14(9):1175. https://doi.org/10.3390/coatings14091175
Chicago/Turabian StyleYu, Lu, Yiming Wen, Jindong Zhou, Yanzhao Qiu, Danning Yang, Hao Dai, Huilong Zhu, Zhiyuan Hu, Gongtao Liu, Aqib Mashood Khan, and et al. 2024. "Study on the Multi-Physical Field Simulation of the Double-Glow Plasma Alloying Process Parameters" Coatings 14, no. 9: 1175. https://doi.org/10.3390/coatings14091175
APA StyleYu, L., Wen, Y., Zhou, J., Qiu, Y., Yang, D., Dai, H., Zhu, H., Hu, Z., Liu, G., Khan, A. M., & Wu, H. (2024). Study on the Multi-Physical Field Simulation of the Double-Glow Plasma Alloying Process Parameters. Coatings, 14(9), 1175. https://doi.org/10.3390/coatings14091175







