Spin–Orbit Coupling Free Nonlinear Spin Hall Effect in a Triangle-Unit Collinear Antiferromagnet with Magnetic Toroidal Dipole
Abstract
1. Introduction
2. Model
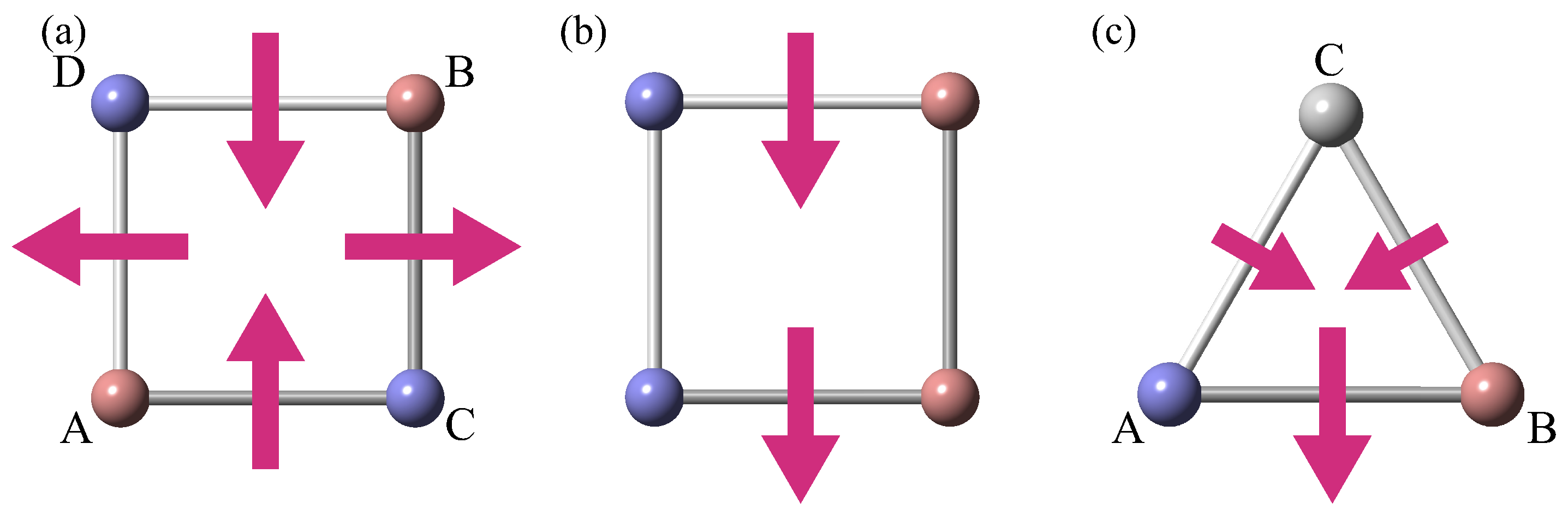
2.1. Magnetic Toroidal Multipoles in a Cluster
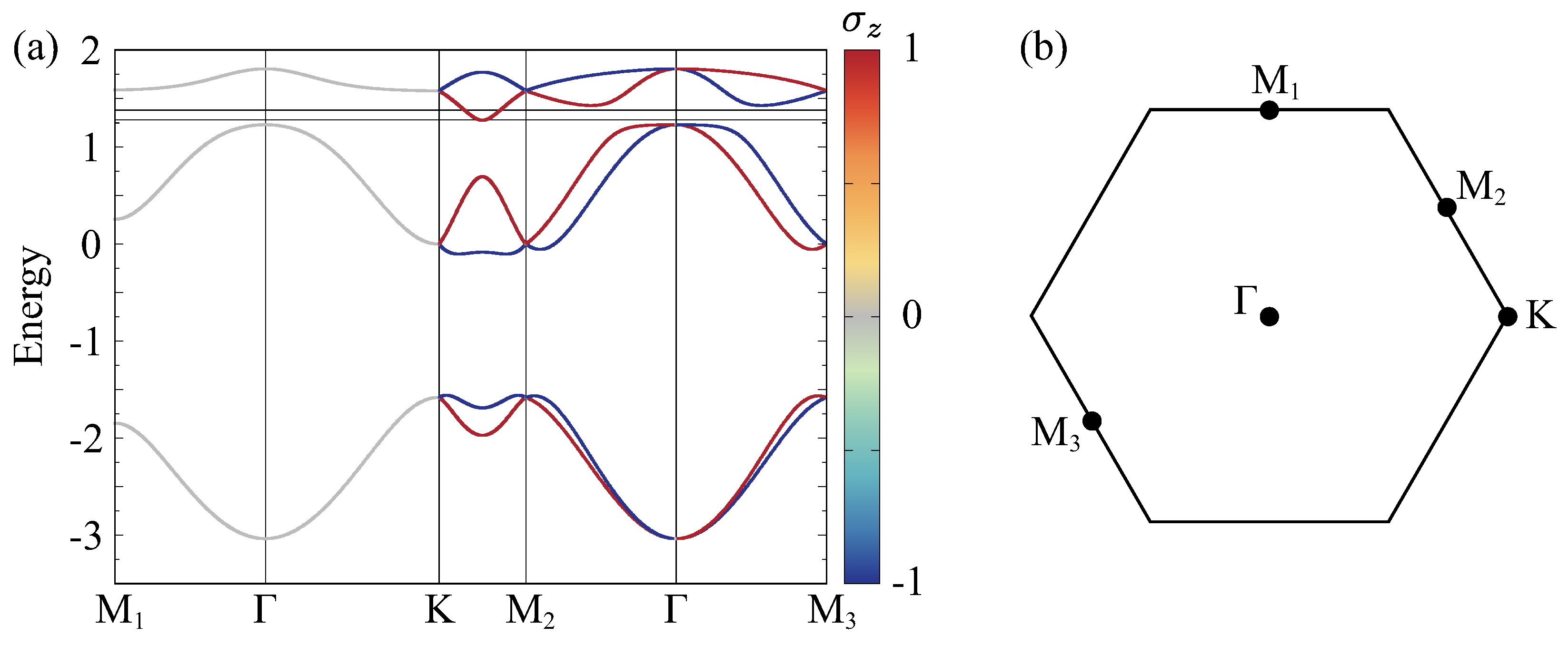
2.2. Breathing Kagome Model
3. Results
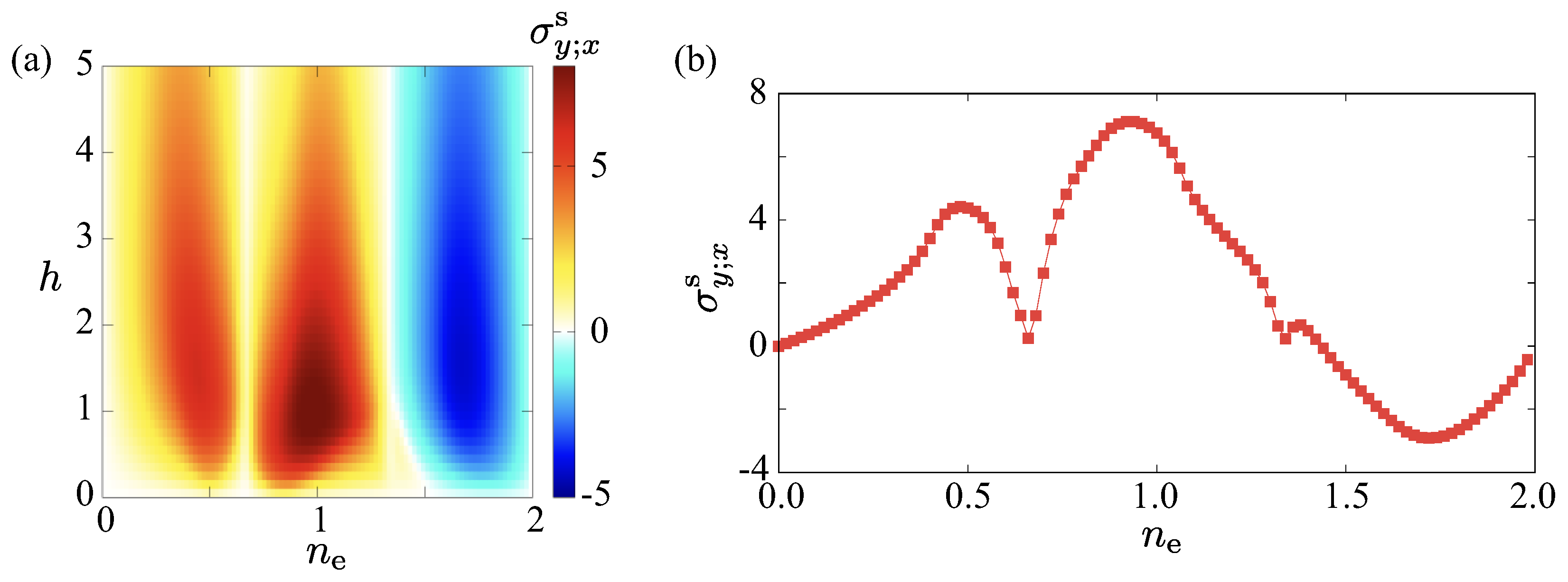
3.1. Linear Spin Conductivity
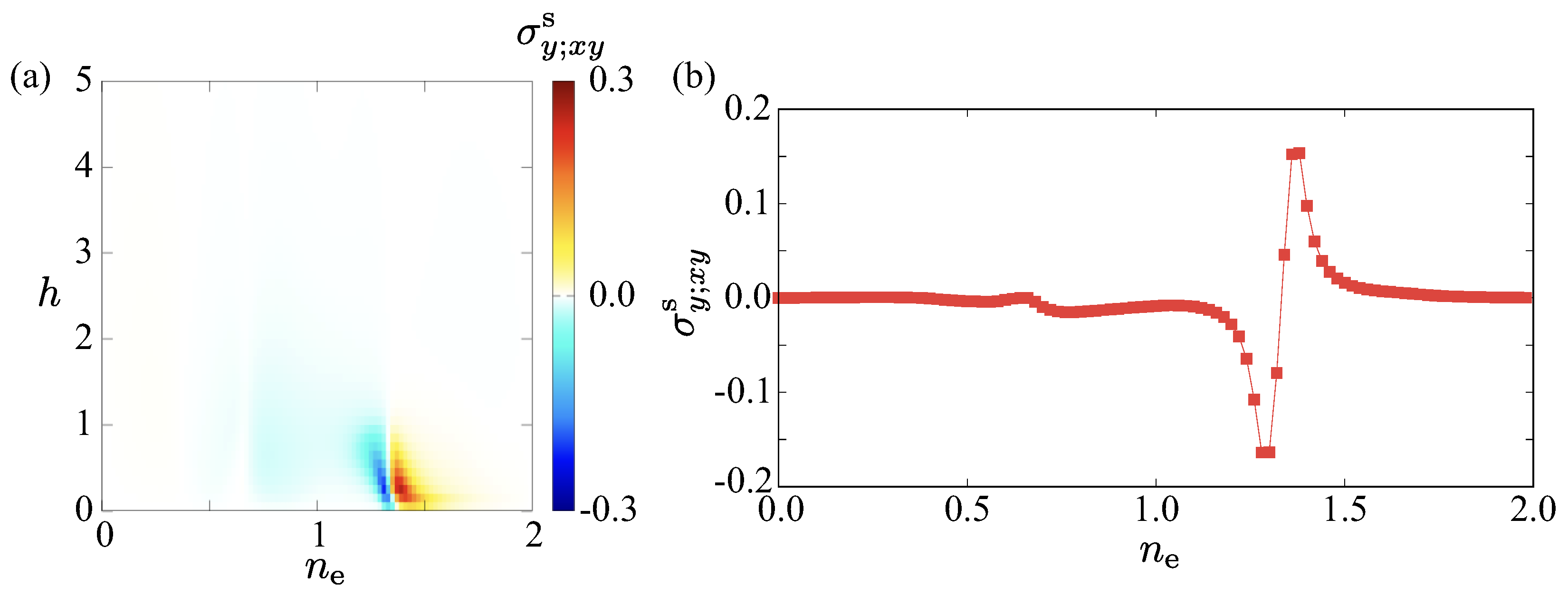
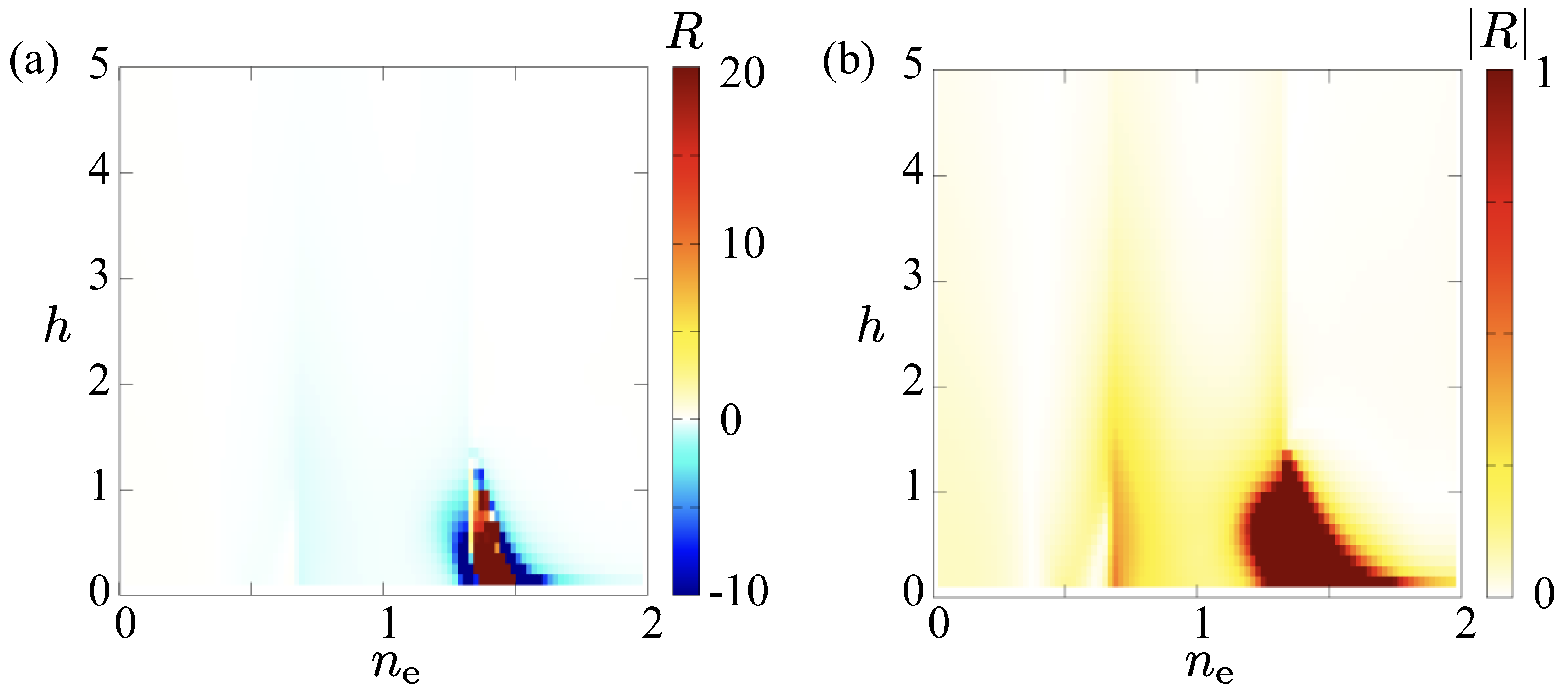
3.2. Nonlinear Spin Hall Conductivity
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Diep, H.T. Frustrated Spin Systems; World Scientific: Singapore, 2004. [Google Scholar]
- Lacroix, C.; Mendels, P.; Mila, F. (Eds.) Introduction to Frustrated Magnetism: Materials, Experiments, Theory; Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Bulaevskii, L.N.; Batista, C.D.; Mostovoy, M.V.; Khomskii, D.I. Electronic orbital currents and polarization in Mott insulators. Phys. Rev. B 2008, 78, 024402. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Unified Description of Electronic Orderings and Cross Correlations by Complete Multipole Representation. J. Phys. Soc. Jpn. 2024, 93, 072001. [Google Scholar] [CrossRef]
- Kimura, T.; Goto, T.; Shintani, H.; Ishizaka, K.; Arima, T.; Tokura, Y. Magnetic control of ferroelectric polarization. Nature 2003, 426, 55–58. [Google Scholar] [CrossRef] [PubMed]
- Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D Appl. Phys. 2005, 38, R123. [Google Scholar] [CrossRef]
- Spaldin, N.A.; Fiebig, M. The renaissance of magnetoelectric multiferroics. Science 2005, 309, 391–392. [Google Scholar] [CrossRef] [PubMed]
- Ramesh, R.; Spaldin, N.A. Multiferroics: Progress and prospects in thin films. Nat. Mater. 2007, 6, 21. [Google Scholar] [CrossRef]
- Khomskii, D. Classifying multiferroics: Mechanisms and effects. Physics 2009, 2, 20. [Google Scholar] [CrossRef]
- Tokura, Y.; Seki, S.; Nagaosa, N. Multiferroics of spin origin. Rep. Prog. Phys. 2014, 77, 076501. [Google Scholar] [CrossRef]
- Fiebig, M.; Lottermoser, T.; Meier, D.; Trassin, M. The evolution of multiferroics. Nat. Rev. Mater. 2016, 1, 16046. [Google Scholar] [CrossRef]
- Ohgushi, K.; Murakami, S.; Nagaosa, N. Spin anisotropy and quantum Hall effect in the kagomé lattice: Chiral spin state based on a ferromagnet. Phys. Rev. B 2000, 62, R6065–R6068. [Google Scholar] [CrossRef]
- Shindou, R.; Nagaosa, N. Orbital Ferromagnetism and Anomalous Hall Effect in Antiferromagnets on the Distorted fcc Lattice. Phys. Rev. Lett. 2001, 87, 116801. [Google Scholar] [CrossRef] [PubMed]
- Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef] [PubMed]
- Nagaosa, N.; Sinova, J.; Onoda, S.; MacDonald, A.H.; Ong, N.P. Anomalous Hall effect. Rev. Mod. Phys. 2010, 82, 1539–1592. [Google Scholar] [CrossRef]
- Xiao, D.; Chang, M.C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959–2007. [Google Scholar] [CrossRef]
- Chen, H.; Niu, Q.; MacDonald, A.H. Anomalous Hall Effect Arising from Noncollinear Antiferromagnetism. Phys. Rev. Lett. 2014, 112, 017205. [Google Scholar] [CrossRef]
- Nakatsuji, S.; Kiyohara, N.; Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 2015, 527, 212. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, M.T.; Koretsune, T.; Ochi, M.; Arita, R. Cluster multipole theory for anomalous Hall effect in antiferromagnets. Phys. Rev. B 2017, 95, 094406. [Google Scholar] [CrossRef]
- Chen, H.; Wang, T.C.; Xiao, D.; Guo, G.Y.; Niu, Q.; MacDonald, A.H. Manipulating anomalous Hall antiferromagnets with magnetic fields. Phys. Rev. B 2020, 101, 104418. [Google Scholar] [CrossRef]
- Feng, W.; Hanke, J.P.; Zhou, X.; Guo, G.Y.; Blügel, S.; Mokrousov, Y.; Yao, Y. Topological magneto-optical effects and their quantization in noncoplanar antiferromagnets. Nat. Commun. 2020, 11, 118. [Google Scholar] [CrossRef]
- Yanase, Y. Magneto-Electric Effect in Three-Dimensional Coupled Zigzag Chains. J. Phys. Soc. Jpn. 2014, 83, 014703. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous Multipole Ordering by Local Parity Mixing. J. Phys. Soc. Jpn. 2015, 84, 064717. [Google Scholar] [CrossRef]
- Sumita, S.; Yanase, Y. Superconductivity in magnetic multipole states. Phys. Rev. B 2016, 93, 224507. [Google Scholar] [CrossRef]
- Matsumura, T.; Yamamoto, T.; Tanida, H.; Sera, M. Temperature-Dependent Cycloidal Magnetic Structure in GdRu2Al10 Studied by Resonant X-ray Diffraction. J. Phys. Soc. Jpn. 2017, 86, 094709. [Google Scholar] [CrossRef]
- Cysne, T.P.; Guimarães, F.S.M.; Canonico, L.M.; Rappoport, T.G.; Muniz, R.B. Orbital magnetoelectric effect in zigzag nanoribbons of p-band systems. Phys. Rev. B 2021, 104, 165403. [Google Scholar] [CrossRef]
- Yatsushiro, M.; Oiwa, R.; Kusunose, H.; Hayami, S. Analysis of model-parameter dependences on the second-order nonlinear conductivity in PT-symmetric collinear antiferromagnetic metals with magnetic toroidal moment on zigzag chains. Phys. Rev. B 2022, 105, 155157. [Google Scholar] [CrossRef]
- Suzuki, Y. Tunneling spin current in systems with spin degeneracy. Phys. Rev. B 2022, 105, 075201. [Google Scholar] [CrossRef]
- Li, D.X.; Honda, F.; Miyake, A.; Homma, Y.; Haga, Y.; Nakamura, A.; Shimizu, Y.; Maurya, A.; Sato, Y.J.; Tokunaga, M.; et al. Magnetic and electrical properties of the ternary compound U2Ir3Si5 with one-dimensional uranium zigzag chains. Phys. Rev. B 2019, 99, 054408. [Google Scholar] [CrossRef]
- Li, X.; Cao, T.; Niu, Q.; Shi, J.; Feng, J. Coupling the valley degree of freedom to antiferromagnetic order. Proc. Natl. Acad. Sci. USA 2013, 110, 3738–3742. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous parity breaking in spin-orbital coupled systems. Phys. Rev. B 2014, 90, 081115. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent spin-valley-orbital physics by spontaneous parity breaking. J. Phys. Condens. Matter 2016, 28, 395601. [Google Scholar] [CrossRef]
- Yanagi, Y.; Kusunose, H. Optical Selection Rules in Spin–Orbit Coupled Systems on Honeycomb Lattice. J. Phys. Soc. Jpn. 2017, 86, 083703. [Google Scholar] [CrossRef]
- Oishi, R.; Umeo, K.; Shimura, Y.; Onimaru, T.; Strydom, A.M.; Takabatake, T. Antiferromagnetic order in the honeycomb Kondo lattice CePt6Al3 induced by Pd substitution. Phys. Rev. B 2021, 104, 104411. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent odd-parity multipoles and magnetoelectric effects on a diamond structure: Implication for the 5d transition metal oxides AOsO4(A=K, Rb, and Cs). Phys. Rev. B 2018, 97, 024414. [Google Scholar] [CrossRef]
- Ishitobi, T.; Hattori, K. Magnetoelectric Effects and Charge-Imbalanced Solenoids: Antiferro Quadrupole Orders in a Diamond Structure. J. Phys. Soc. Jpn. 2019, 88, 063708. [Google Scholar] [CrossRef]
- Yamaura, J.i.; Hiroi, Z. Crystal structure and magnetic properties of the 5d transition metal oxides AOsO4(A=K, Rb, Cs). Phys. Rev. B 2019, 99, 155113. [Google Scholar] [CrossRef]
- Paramekanti, A.; Maharaj, D.D.; Gaulin, B.D. Octupolar order in d-orbital Mott insulators. Phys. Rev. B 2020, 101, 054439. [Google Scholar] [CrossRef]
- Maharaj, D.D.; Sala, G.; Stone, M.B.; Kermarrec, E.; Ritter, C.; Fauth, F.; Marjerrison, C.A.; Greedan, J.E.; Paramekanti, A.; Gaulin, B.D. Octupolar versus Néel Order in Cubic 5d2 Double Perovskites. Phys. Rev. Lett. 2020, 124, 087206. [Google Scholar] [CrossRef]
- Winkler, R.; Zülicke, U. Theory of electric, magnetic, and toroidal polarizations in crystalline solids with applications to hexagonal lonsdaleite and cubic diamond. Phys. Rev. B 2023, 107, 155201. [Google Scholar] [CrossRef]
- Solovyev, I.V. Magneto-optical effect in the weak ferromagnets LaMO3 (M= Cr, Mn, and Fe). Phys. Rev. B 1997, 55, 8060–8063. [Google Scholar] [CrossRef]
- Sivadas, N.; Okamoto, S.; Xiao, D. Gate-Controllable Magneto-optic Kerr Effect in Layered Collinear Antiferromagnets. Phys. Rev. Lett. 2016, 117, 267203. [Google Scholar] [CrossRef]
- Yamasaki, Y.; Nakao, H.; Arima, T.h. Augmented Magnetic Octupole in Kagomé 120-degree Antiferromagnets Detectable via X-ray Magnetic Circular Dichroism. J. Phys. Soc. Jpn. 2020, 89, 083703. [Google Scholar] [CrossRef]
- Šmejkal, L.; González-Hernández, R.; Jungwirth, T.; Sinova, J. Crystal time-reversal symmetry breaking and spontaneous Hall effect in collinear antiferromagnets. Sci. Adv. 2020, 6, eaaz8809. [Google Scholar] [CrossRef] [PubMed]
- Naka, M.; Hayami, S.; Kusunose, H.; Yanagi, Y.; Motome, Y.; Seo, H. Anomalous Hall effect in κ-type organic antiferromagnets. Phys. Rev. B 2020, 102, 075112. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Essential role of the anisotropic magnetic dipole in the anomalous Hall effect. Phys. Rev. B 2021, 103, L180407. [Google Scholar] [CrossRef]
- Kimata, M.; Sasabe, N.; Kurita, K.; Yamasaki, Y.; Tabata, C.; Yokoyama, Y.; Kotani, Y.; Ikhlas, M.; Tomita, T.; Amemiya, K.; et al. X-ray study of ferroic octupole order producing anomalous Hall effect. Nat. Commun. 2021, 12, 5582. [Google Scholar] [CrossRef] [PubMed]
- Chen, H. Electronic chiralization as an indicator of the anomalous Hall effect in unconventional magnetic systems. Phys. Rev. B 2022, 106, 024421. [Google Scholar] [CrossRef]
- Sasabe, N.; Kimata, M.; Nakamura, T. Presence of X-Ray Magnetic Circular Dichroism Signal for Zero-Magnetization Antiferromagnetic State. Phys. Rev. Lett. 2021, 126, 157402. [Google Scholar] [CrossRef]
- Noda, Y.; Ohno, K.; Nakamura, S. Momentum-dependent band spin splitting in semiconducting MnO 2: A density functional calculation. Phys. Chem. Chem. Phys. 2016, 18, 13294–13303. [Google Scholar] [CrossRef] [PubMed]
- Okugawa, T.; Ohno, K.; Noda, Y.; Nakamura, S. Weakly spin-dependent band structures of antiferromagnetic perovskite LaMO3 (M= Cr, Mn, Fe). J. Phys. Condens. Matter 2018, 30, 075502. [Google Scholar] [CrossRef]
- Ahn, K.H.; Hariki, A.; Lee, K.W.; Kuneš, J. Antiferromagnetism in RuO2 as d-wave Pomeranchuk instability. Phys. Rev. B 2019, 99, 184432. [Google Scholar] [CrossRef]
- Naka, M.; Hayami, S.; Kusunose, H.; Yanagi, Y.; Motome, Y.; Seo, H. Spin current generation in organic antiferromagnets. Nat. Commun. 2019, 10, 4305. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Yanagi, Y.; Kusunose, H. Momentum-Dependent Spin Splitting by Collinear Antiferromagnetic Ordering. J. Phys. Soc. Jpn. 2019, 88, 123702. [Google Scholar] [CrossRef]
- Hayami, S.; Yanagi, Y.; Kusunose, H. Spontaneous antisymmetric spin splitting in noncollinear antiferromagnets without spin-orbit coupling. Phys. Rev. B 2020, 101, 220403(R). [Google Scholar] [CrossRef]
- Hayami, S.; Yanagi, Y.; Kusunose, H. Bottom-up design of spin-split and reshaped electronic band structures in antiferromagnets without spin-orbit coupling: Procedure on the basis of augmented multipoles. Phys. Rev. B 2020, 102, 144441. [Google Scholar] [CrossRef]
- Yuan, L.D.; Wang, Z.; Luo, J.W.; Rashba, E.I.; Zunger, A. Giant momentum-dependent spin splitting in centrosymmetric low-Z antiferromagnets. Phys. Rev. B 2020, 102, 014422. [Google Scholar] [CrossRef]
- Egorov, S.A.; Evarestov, R.A. Colossal Spin Splitting in the Monolayer of the Collinear Antiferromagnet MnF2. J. Phys. Chem. Lett. 2021, 12, 2363–2369. [Google Scholar] [CrossRef]
- Yuan, L.D.; Wang, Z.; Luo, J.W.; Zunger, A. Strong influence of nonmagnetic ligands on the momentum-dependent spin splitting in antiferromagnets. Phys. Rev. B 2021, 103, 224410. [Google Scholar] [CrossRef]
- Yuan, L.D.; Wang, Z.; Luo, J.W.; Zunger, A. Prediction of low-Z collinear and noncollinear antiferromagnetic compounds having momentum-dependent spin splitting even without spin-orbit coupling. Phys. Rev. Mater. 2021, 5, 014409. [Google Scholar] [CrossRef]
- Mazin, I.I. Altermagnetism in MnTe: Origin, predicted manifestations, and routes to detwinning. Phys. Rev. B 2023, 107, L100418. [Google Scholar] [CrossRef]
- Lovesey, S.W.; Khalyavin, D.D.; van der Laan, G. Templates for magnetic symmetry and altermagnetism in hexagonal MnTe. Phys. Rev. B 2023, 108, 174437. [Google Scholar] [CrossRef]
- Yuan, L.D.; Zunger, A. Degeneracy Removal of Spin Bands in Collinear Antiferromagnets with Non-Interconvertible Spin-Structure Motif Pair. Adv. Mater. 2023, 35, 2211966. [Google Scholar] [CrossRef] [PubMed]
- Yuan, L.D.; Zhang, X.; Acosta, C.M.; Zunger, A. Uncovering spin-orbit coupling-independent hidden spin polarization of energy bands in antiferromagnets. Nat. Commun. 2023, 14, 5301. [Google Scholar] [CrossRef]
- Gonzalez Betancourt, R.D.; Zubáč, J.; Gonzalez-Hernandez, R.; Geishendorf, K.; Šobáň, Z.; Springholz, G.; Olejník, K.; Šmejkal, L.; Sinova, J.; Jungwirth, T.; et al. Spontaneous Anomalous Hall Effect Arising from an Unconventional Compensated Magnetic Phase in a Semiconductor. Phys. Rev. Lett. 2023, 130, 036702. [Google Scholar] [CrossRef] [PubMed]
- Ouassou, J.A.; Brataas, A.; Linder, J. dc Josephson Effect in Altermagnets. Phys. Rev. Lett. 2023, 131, 076003. [Google Scholar] [CrossRef]
- Cui, Q.; Zeng, B.; Cui, P.; Yu, T.; Yang, H. Efficient spin Seebeck and spin Nernst effects of magnons in altermagnets. Phys. Rev. B 2023, 108, L180401. [Google Scholar] [CrossRef]
- Brekke, B.; Brataas, A.; Sudbø, A. Two-dimensional altermagnets: Superconductivity in a minimal microscopic model. Phys. Rev. B 2023, 108, 224421. [Google Scholar] [CrossRef]
- Aoyama, T.; Ohgushi, K. Piezomagnetic properties in altermagnetic MnTe. Phys. Rev. Mater. 2024, 8, L041402. [Google Scholar] [CrossRef]
- Hariki, A.; Takahashi, Y.; Kuneš, J. X-ray magnetic circular dichroism in RuO2. Phys. Rev. B 2024, 109, 094413. [Google Scholar] [CrossRef]
- Osumi, T.; Souma, S.; Aoyama, T.; Yamauchi, K.; Honma, A.; Nakayama, K.; Takahashi, T.; Ohgushi, K.; Sato, T. Observation of a giant band splitting in altermagnetic MnTe. Phys. Rev. B 2024, 109, 115102. [Google Scholar] [CrossRef]
- Hariki, A.; Dal Din, A.; Amin, O.J.; Yamaguchi, T.; Badura, A.; Kriegner, D.; Edmonds, K.W.; Campion, R.P.; Wadley, P.; Backes, D.; et al. X-Ray Magnetic Circular Dichroism in Altermagnetic α-MnTe. Phys. Rev. Lett. 2024, 132, 176701. [Google Scholar] [CrossRef]
- Šmejkal, L.; Sinova, J.; Jungwirth, T. Beyond Conventional Ferromagnetism and Antiferromagnetism: A Phase with Nonrelativistic Spin and Crystal Rotation Symmetry. Phys. Rev. X 2022, 12, 031042. [Google Scholar] [CrossRef]
- Šmejkal, L.; Sinova, J.; Jungwirth, T. Emerging Research Landscape of Altermagnetism. Phys. Rev. X 2022, 12, 040501. [Google Scholar] [CrossRef]
- Shao, D.F.; Zhang, S.H.; Li, M.; Eom, C.B.; Tsymbal, E.Y. Spin-neutral currents for spintronics. Nat. Commun. 2021, 12, 7061. [Google Scholar] [CrossRef] [PubMed]
- González-Hernández, R.; Šmejkal, L.; Výborný, K.; Yahagi, Y.; Sinova, J.; Jungwirth, T.; Železný, J. Efficient Electrical Spin Splitter Based on Nonrelativistic Collinear Antiferromagnetism. Phys. Rev. Lett. 2021, 126, 127701. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Yatsushiro, M. Spin Conductivity Based on Magnetic Toroidal Quadrupole Hidden in Antiferromagnets. J. Phys. Soc. Jpn. 2022, 91, 063702. [Google Scholar] [CrossRef]
- Bai, H.; Zhang, Y.C.; Zhou, Y.J.; Chen, P.; Wan, C.H.; Han, L.; Zhu, W.X.; Liang, S.X.; Su, Y.C.; Han, X.F.; et al. Efficient Spin-to-Charge Conversion via Altermagnetic Spin Splitting Effect in Antiferromagnet RuO2. Phys. Rev. Lett. 2023, 130, 216701. [Google Scholar] [CrossRef] [PubMed]
- Spaldin, N.A.; Fiebig, M.; Mostovoy, M. The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect. J. Phys. Condens. Matter 2008, 20, 434203. [Google Scholar] [CrossRef]
- Kopaev, Y.V. Toroidal ordering in crystals. Physics-Uspekhi 2009, 52, 1111–1125. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Microscopic Description of Electric and Magnetic Toroidal Multipoles in Hybrid Orbitals. J. Phys. Soc. Jpn. 2018, 87, 033709. [Google Scholar] [CrossRef]
- Suzuki, M.T.; Nomoto, T.; Arita, R.; Yanagi, Y.; Hayami, S.; Kusunose, H. Multipole expansion for magnetic structures: A generation scheme for a symmetry-adapted orthonormal basis set in the crystallographic point group. Phys. Rev. B 2019, 99, 174407. [Google Scholar] [CrossRef]
- Popov, Y.F.; Kadomtseva, A.; Belov, D.; Vorob’ev, G.; Zvezdin, A. Magnetic-field-induced toroidal moment in the magnetoelectric Cr2O3. J. Exp. Theor. Phys. Lett. 1999, 69, 330–335. [Google Scholar] [CrossRef]
- Schmid, H. On ferrotoroidics and electrotoroidic, magnetotoroidic and piezotoroidic effects*. Ferroelectrics 2001, 252, 41–50. [Google Scholar] [CrossRef]
- Ederer, C.; Spaldin, N.A. Towards a microscopic theory of toroidal moments in bulk periodic crystals. Phys. Rev. B 2007, 76, 214404. [Google Scholar] [CrossRef]
- Thöle, F.; Spaldin, N.A. Magnetoelectric multipoles in metals. Philos. Trans. R. Soc. A 2018, 376, 20170450. [Google Scholar] [CrossRef] [PubMed]
- Sawada, K.; Nagaosa, N. Optical Magnetoelectric Effect in Multiferroic Materials: Evidence for a Lorentz Force Acting on a Ray of Light. Phys. Rev. Lett. 2005, 95, 237402. [Google Scholar] [CrossRef]
- Miyahara, S.; Furukawa, N. Nonreciprocal Directional Dichroism and Toroidalmagnons in Helical Magnets. J. Phys. Soc. Jpn. 2012, 81, 023712. [Google Scholar] [CrossRef]
- Miyahara, S.; Furukawa, N. Theory of magneto-optical effects in helical multiferroic materials via toroidal magnon excitation. Phys. Rev. B 2014, 89, 195145. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Asymmetric Magnon Excitation by Spontaneous Toroidal Ordering. J. Phys. Soc. Jpn. 2016, 85, 053705. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M.; Kusunose, H. Nonlinear spin Hall effect in PT-symmetric collinear magnets. Phys. Rev. B 2022, 106, 024405. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M.; Yanagi, Y.; Kusunose, H. Classification of atomic-scale multipoles under crystallographic point groups and application to linear response tensors. Phys. Rev. B 2018, 98, 165110. [Google Scholar] [CrossRef]
- Yatsushiro, M.; Kusunose, H.; Hayami, S. Multipole classification in 122 magnetic point groups for unified understanding of multiferroic responses and transport phenomena. Phys. Rev. B 2021, 104, 054412. [Google Scholar] [CrossRef]
- Mook, A.; Neumann, R.R.; Johansson, A.; Henk, J.; Mertig, I. Origin of the magnetic spin Hall effect: Spin current vorticity in the Fermi sea. Phys. Rev. Res. 2020, 2, 023065. [Google Scholar] [CrossRef]
- Sodemann, I.; Fu, L. Quantum Nonlinear Hall Effect Induced by Berry Curvature Dipole in Time-Reversal Invariant Materials. Phys. Rev. Lett. 2015, 115, 216806. [Google Scholar] [CrossRef] [PubMed]
- Kondo, H.; Akagi, Y. Nonlinear magnon spin Nernst effect in antiferromagnets and strain-tunable pure spin current. Phys. Rev. Res. 2022, 4, 013186. [Google Scholar] [CrossRef]
- Yu, H.; Wu, Y.; Liu, G.B.; Xu, X.; Yao, W. Nonlinear Valley and Spin Currents from Fermi Pocket Anisotropy in 2D Crystals. Phys. Rev. Lett. 2014, 113, 156603. [Google Scholar] [CrossRef]
- Hamamoto, K.; Ezawa, M.; Kim, K.W.; Morimoto, T.; Nagaosa, N. Nonlinear spin current generation in noncentrosymmetric spin-orbit coupled systems. Phys. Rev. B 2017, 95, 224430. [Google Scholar] [CrossRef]
- Araki, Y. Strain-induced nonlinear spin Hall effect in topological Dirac semimetal. Sci. Rep. 2018, 8, 15236. [Google Scholar] [CrossRef]
- Pan, A.; Marinescu, D.C. Nonlinear spin-current generation in quantum wells with arbitrary Rashba-Dresselhaus spin-orbit interactions. Phys. Rev. B 2019, 99, 245204. [Google Scholar] [CrossRef]
- Zhang, Z.F.; Zhu, Z.G.; Su, G. Theory of nonlinear response for charge and spin currents. Phys. Rev. B 2021, 104, 115140. [Google Scholar] [CrossRef]

| PG | Irrep. | MPG | MT Multipole | SS | NSHC | |
|---|---|---|---|---|---|---|
| square | ✓ | – | ||||
| square | – | ✓ | ||||
| triangle | , | ✓ | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayami, S. Spin–Orbit Coupling Free Nonlinear Spin Hall Effect in a Triangle-Unit Collinear Antiferromagnet with Magnetic Toroidal Dipole. J. Low Power Electron. Appl. 2024, 14, 35. https://doi.org/10.3390/jlpea14030035
Hayami S. Spin–Orbit Coupling Free Nonlinear Spin Hall Effect in a Triangle-Unit Collinear Antiferromagnet with Magnetic Toroidal Dipole. Journal of Low Power Electronics and Applications. 2024; 14(3):35. https://doi.org/10.3390/jlpea14030035
Chicago/Turabian StyleHayami, Satoru. 2024. "Spin–Orbit Coupling Free Nonlinear Spin Hall Effect in a Triangle-Unit Collinear Antiferromagnet with Magnetic Toroidal Dipole" Journal of Low Power Electronics and Applications 14, no. 3: 35. https://doi.org/10.3390/jlpea14030035
APA StyleHayami, S. (2024). Spin–Orbit Coupling Free Nonlinear Spin Hall Effect in a Triangle-Unit Collinear Antiferromagnet with Magnetic Toroidal Dipole. Journal of Low Power Electronics and Applications, 14(3), 35. https://doi.org/10.3390/jlpea14030035






