An Industrial Quadrotor UAV Control Method Based on Fuzzy Adaptive Linear Active Disturbance Rejection Control
Abstract
:1. Introduction
2. Dynamics Model of Quadrotor UAV
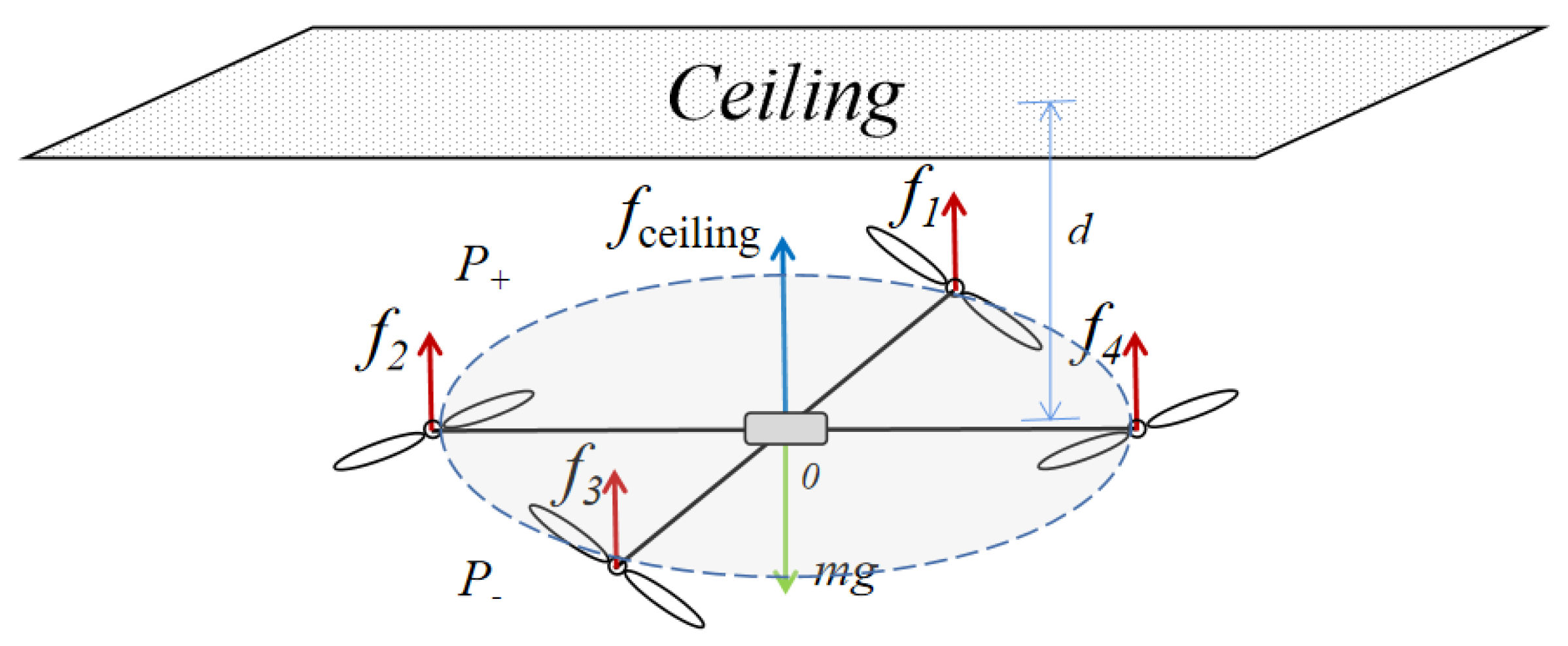
2.1. Thrust and Torque
2.2. UAV Dynamic Model
3. Design of Fuzzy-LADRC
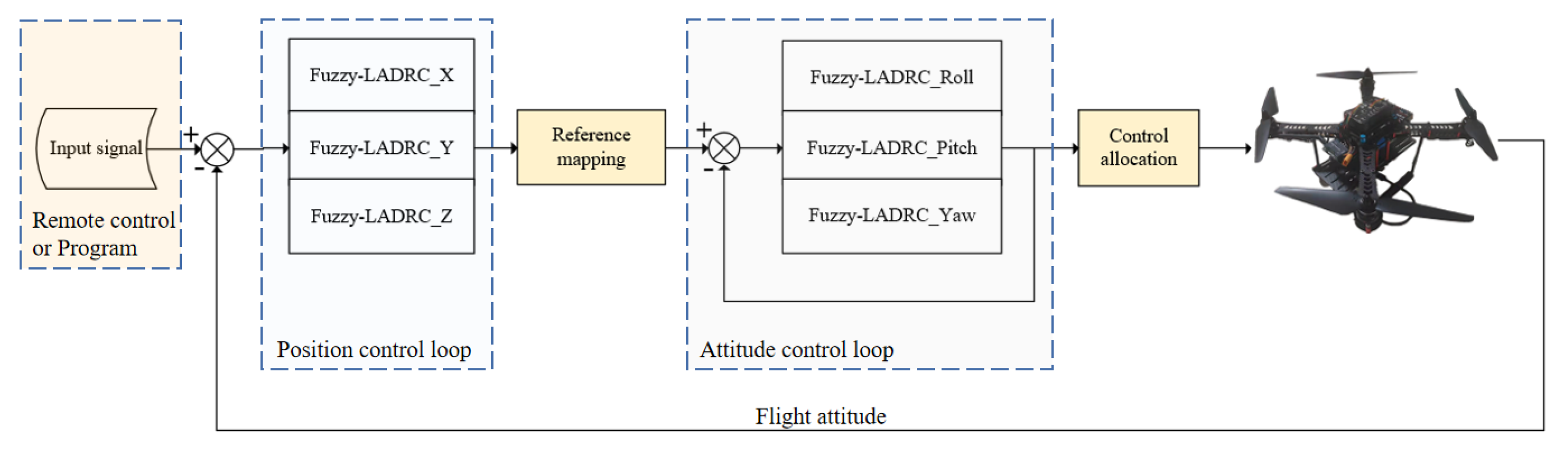
3.1. Control Scheme of Quadrotor UAV
3.2. The Principle of LADRC
3.3. Design of Fuzzy-LADRC
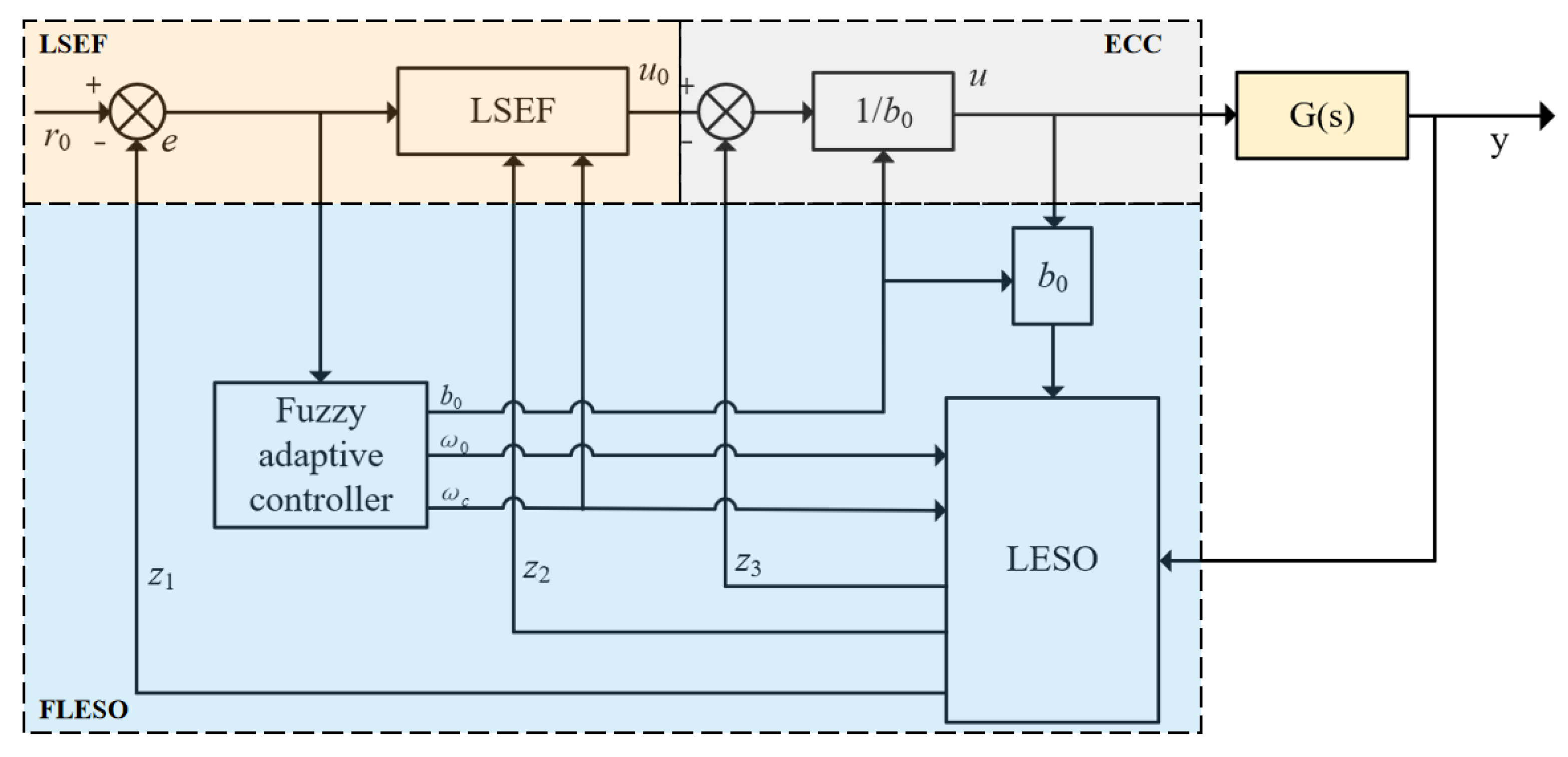
3.3.1. The Structure of Fuzzy-LADRC
3.3.2. Design of Fuzzy Adaptive Controller
3.3.3. Design of Fuzzy Linear Extended State Observer
3.3.4. Error Control Method
3.4. Frequency Domain Stability Analysis
4. Simulation and Discussion
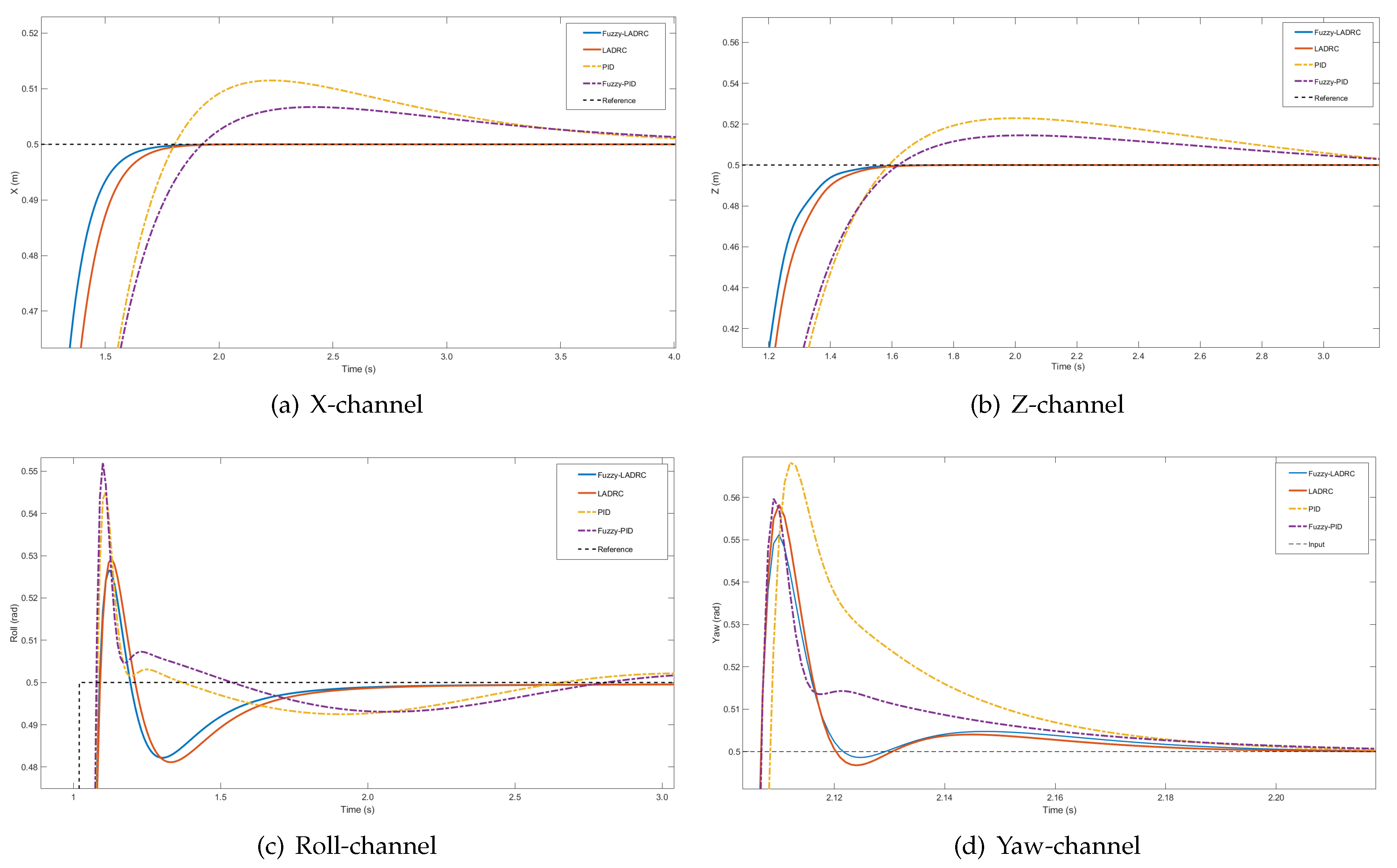
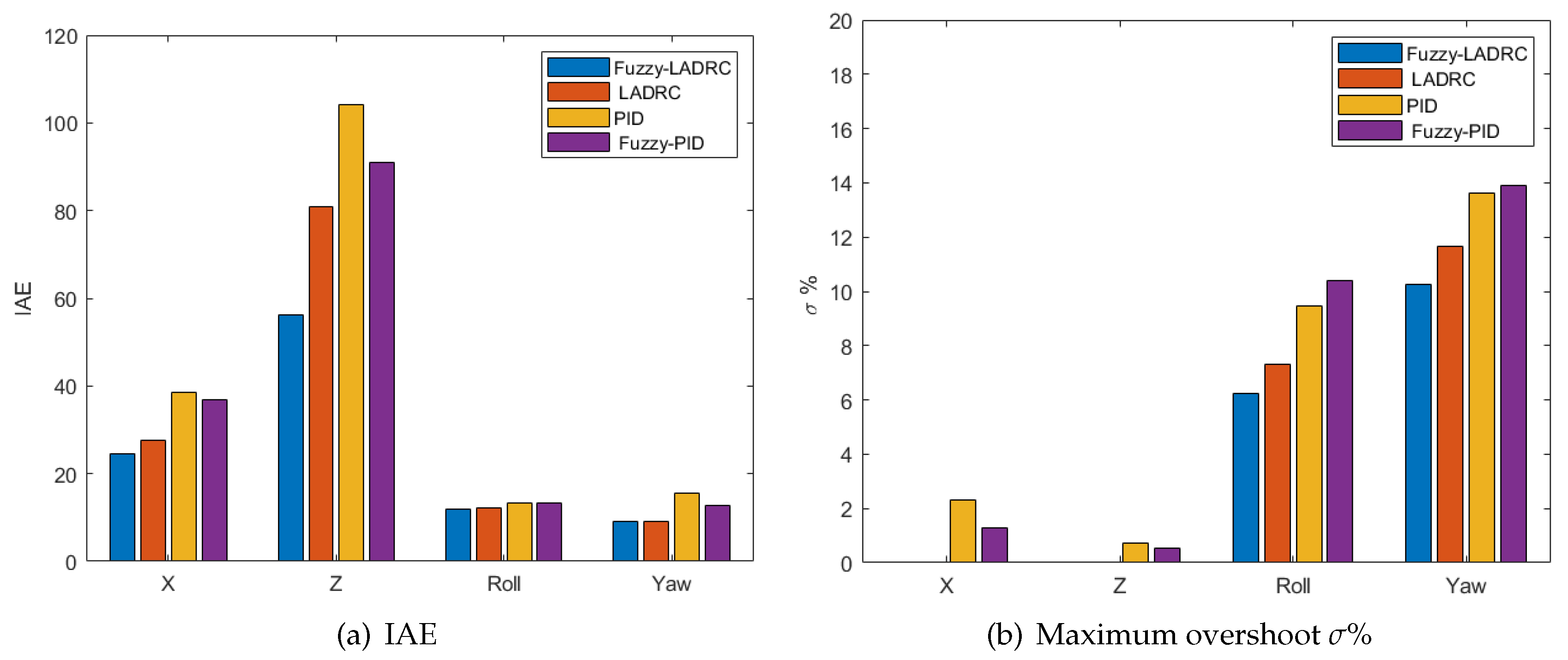
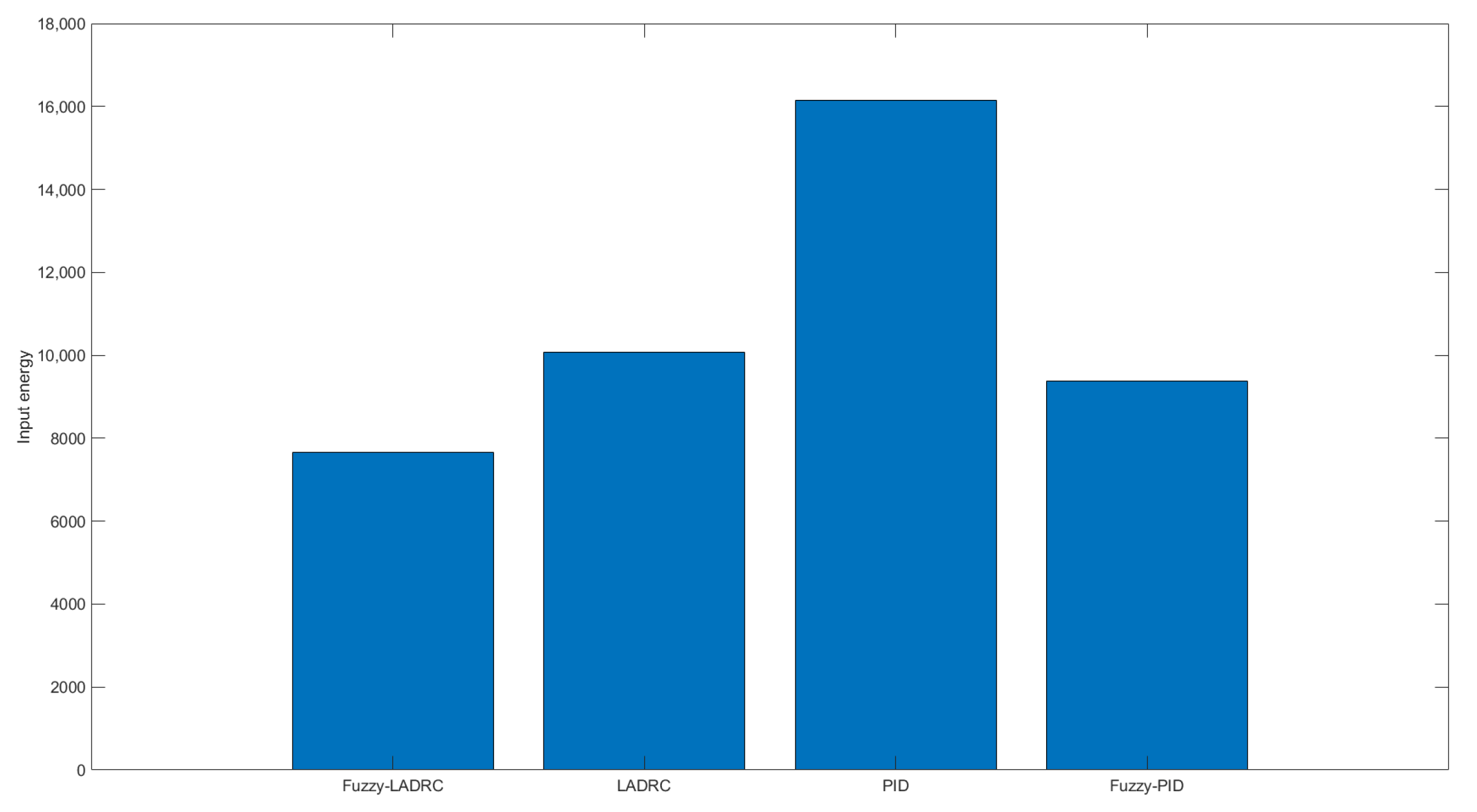
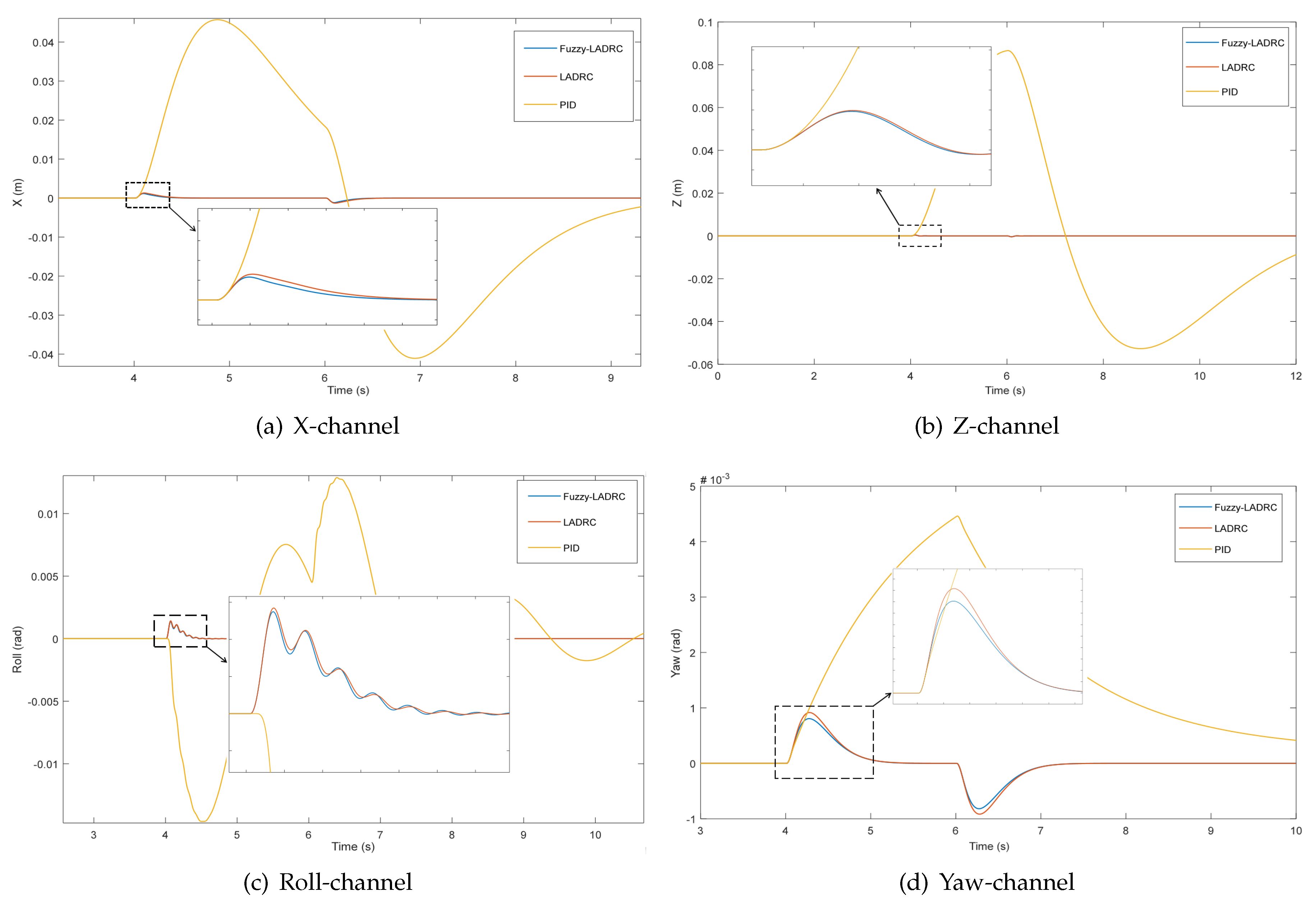
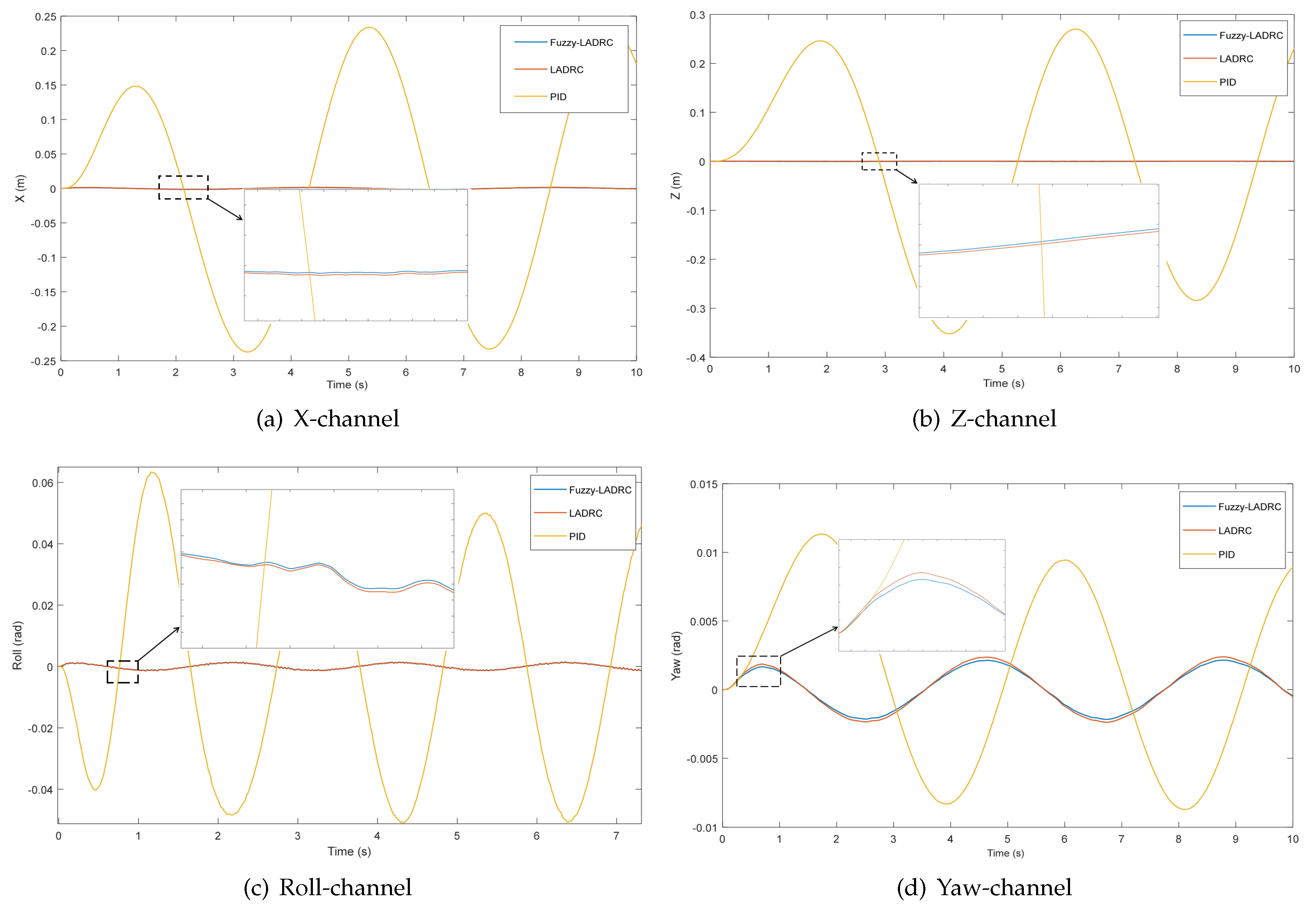
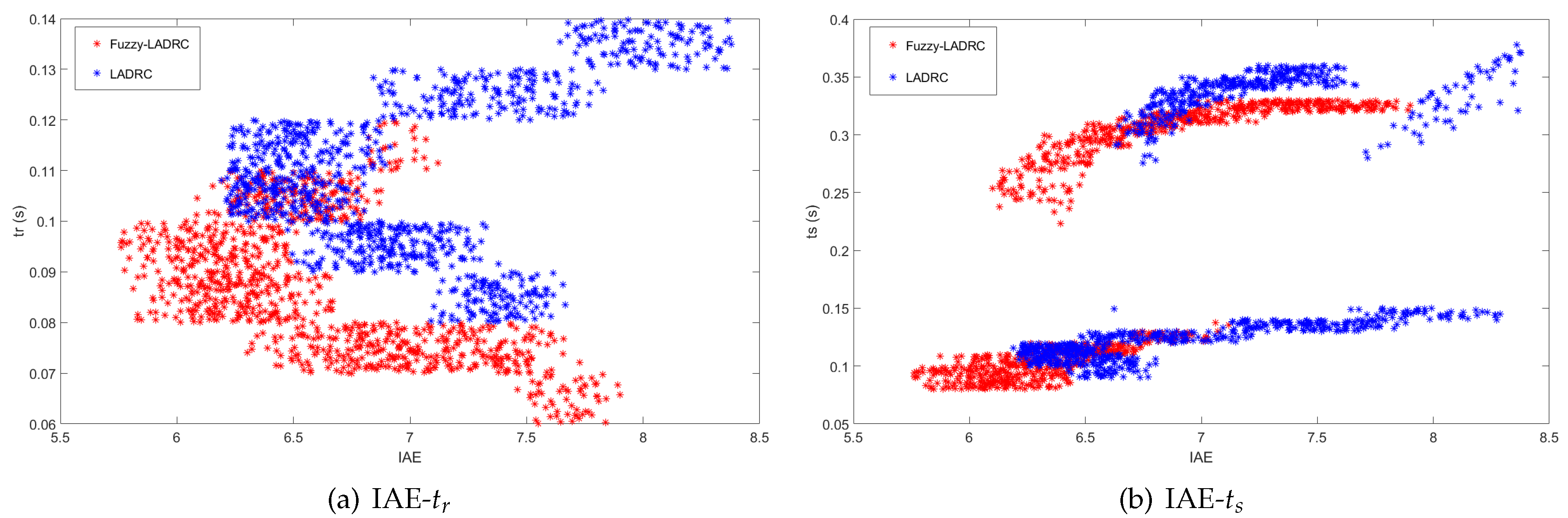
4.1. Tracking Experiment and Input Energy
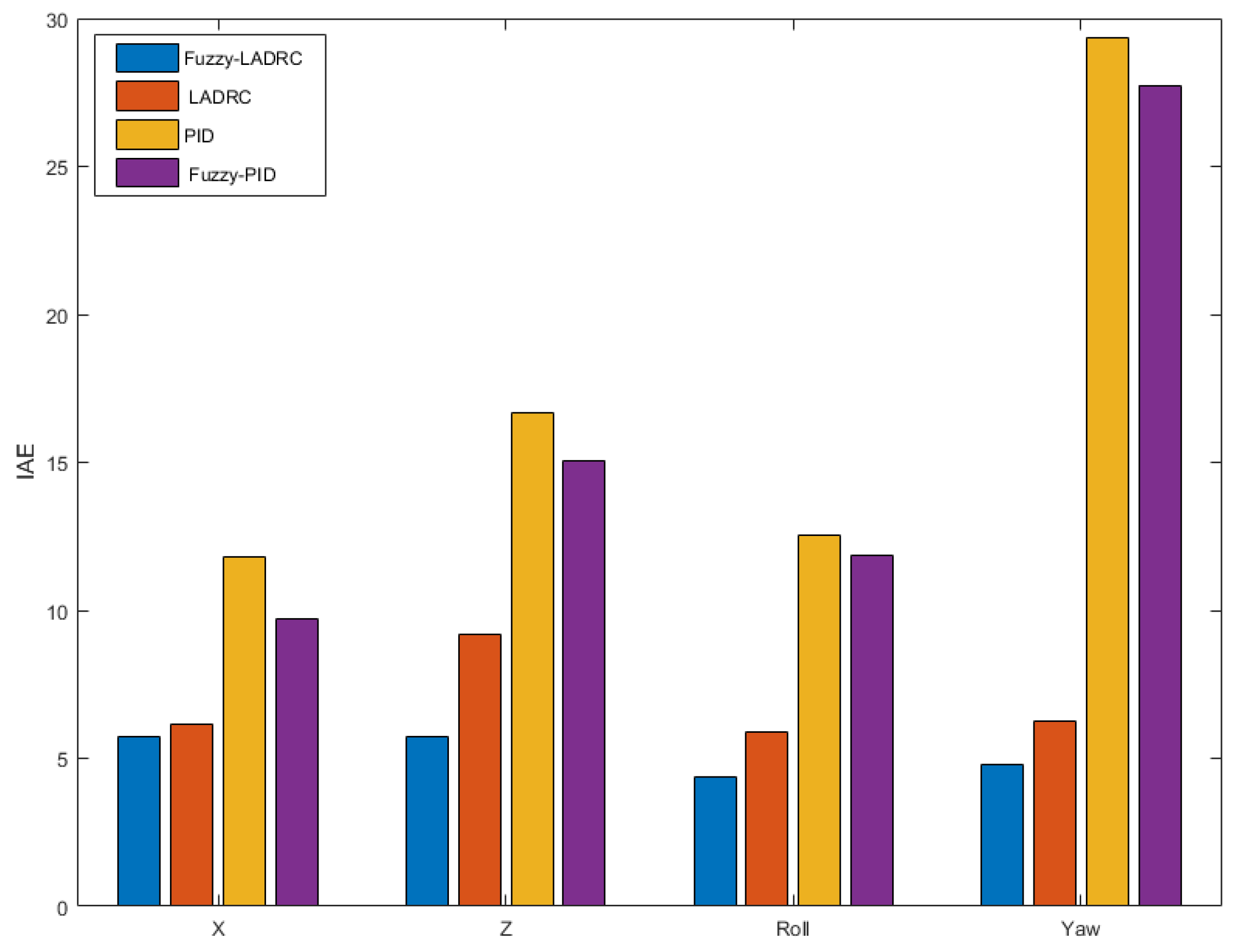
4.2. Disturbance Experiment
4.3. Robustness Experiment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Car, M.; Markovic, L.; Ivanovic, A.; Orsag, M.; Bogdan, S. Autonomous Wind-Turbine Blade Inspection Using LiDAR-Equipped Unmanned Aerial Vehicle. IEEE Access 2020, 8, 131380–131387. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.; Liu, Y. Application of Unmanned Aerial Vehicle Hangar in Transmission Tower Inspection Considering the Risk Probabilities of Steel Towers. IEEE Access 2019, 7, 159048–159057. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, C.; Xu, C.; Xiong, F.; Zhang, Y.; Umer, T. Energy-Efficient Industrial Internet of UAVs for Power Line Inspection in Smart Grid. IEEE Trans. Ind. Informatics 2018, 14, 2705–2714. [Google Scholar] [CrossRef] [Green Version]
- Gallardo-Saavedra, S.; Hernández-Callejo, L.; Duque-Perez, O. Image Resolution Influence in Aerial Thermographic Inspections of Photovoltaic Plants. IEEE Trans. Ind. Informatics 2018, 14, 5678–5686. [Google Scholar] [CrossRef]
- Kim, S.; Kim, D.; Jeong, S.; Ham, J.W.; Lee, J.K.; Oh, K.Y. Fault Diagnosis of Power Transmission Lines Using a UAV-Mounted Smart Inspection System. IEEE Access 2020, 8, 149999–150009. [Google Scholar] [CrossRef]
- Fang, S.; Haiyang, C.; Sheng, L.; Xiaoyu, W. A Framework of Power Pylon Detection for UAV-based Power Line Inspection. In Proceedings of the 2020 IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 12–14 June 2020; pp. 350–357. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, L.; Wang, B.; Chen, X.; Wang, Q.; Zheng, T. High Speed Automatic Power Line Detection and Tracking for a UAV-Based Inspection. In Proceedings of the 2012 International Conference on Industrial Control and Electronics Engineering, Xi’an, China, 23–25 August 2012; pp. 266–269. [Google Scholar] [CrossRef]
- Cao, P.; Liu, Y.; Yang, C.; Xie, S.; Xie, K. MEC-Driven UAV-Enabled Routine Inspection Scheme in Wind Farm Under Wind Influence. IEEE Access 2019, 7, 179252–179265. [Google Scholar] [CrossRef]
- Li, J.; Lei, G.; Xian, Y.; Wang, X. Research on Ground Effect of Shipborne Flying-Wing UAV. In Proceedings of the 2014 Tenth International Conference on Computational Intelligence and Security, Kunming, China, 15–16 November 2014; pp. 685–688. [Google Scholar] [CrossRef]
- Sanchez-Cuevas, P.; Heredia, G.; Ollero, A. Characterization of the Aerodynamic Ground Effect and Its Influence in Multirotor Control. Int. J. Aerosp. Eng. 2017, 2017, 1823056. [Google Scholar] [CrossRef]
- Kocer, B.B.; Tiryaki, M.E.; Pratama, M.; Tjahjowidodo, T.; Seet, G.G.L. Aerial Robot Control in Close Proximity to Ceiling: A Force Estimation-based Nonlinear MPC. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 2813–2819. [Google Scholar] [CrossRef] [Green Version]
- Kocer, B.B.; Tjahjowidodo, T.; Seet, G.G.L. Centralized predictive ceiling interaction control of quadrotor VTOL UAV. Aerosp. Sci. Technol. 2018, 76, 455–465. [Google Scholar] [CrossRef]
- Sanchez-Cuevas, P.J.; Heredia, G.; Ollero, A. Multirotor UAS for bridge inspection by contact using the ceiling effect. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 767–774. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Zhang, J.; Yu, H. Review of modeling and control in UAV autonomous maneuvering flight. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 1920–1925. [Google Scholar] [CrossRef]
- Poksawat, P.; Wang, L.; Mohamed, A. Gain Scheduled Attitude Control of Fixed-Wing UAV with Automatic Controller Tuning. IEEE Trans. Control Syst. Technol. 2018, 26, 1192–1203. [Google Scholar] [CrossRef]
- Vieira Lima, G.; Monteiro Jorge Alves de Souza, R.; Silva de Morais, A.; Oliveira-Lopes, L.C.; Mara Vieira Ladeira, G. Stabilization and Path Tracking of a Mini Quadrotor Helicopter: Experimental Results. IEEE Lat. Am. Trans. 2019, 17, 485–492. [Google Scholar] [CrossRef]
- Noordin, A.; Basri, M.A.M.; Mohamed, Z.; Lazim, I.M. Adaptive PID Controller Using Sliding Mode Control Approaches for Quadrotor UAV Attitude and Position Stabilization. Arab. J. Sci. Eng. 2020. [Google Scholar] [CrossRef]
- Rosales, C.; Tosetti, S.; Soria, C.; Rossomando, F. Neural Adaptive PID Control of a Quadrotor using EFK. IEEE Lat. Am. Trans. 2018, 16, 2722–2730. [Google Scholar] [CrossRef]
- Zhu, Z.; Cao, S. Back-stepping sliding mode control method for quadrotor UAV with actuator failure. J. Eng. 2019, 2019, 8374–8377. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Q.; Dong, C. Asynchronous H∞ control for unmanned aerial vehicles: Switched polytopic system approach. IEEE/CAA J. Autom. Sin. 2015, 2, 207–216. [Google Scholar] [CrossRef]
- Al Younes, Y.; Drak, A.; Noura, H.; Rabhi, A.; El Hajjaji, A. Robust Model-Free Control Applied to a Quadrotor UAV. J. Intell. Robot. Syst. 2016, 84, 37–52. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, Z.; Zhen, Z. Adaptive neural network finite time control for quadrotor UAV with unknown input saturation. Nonlinear Dyn. 2019, 98, 1973–1998. [Google Scholar] [CrossRef]
- Lopez, B.T.; Slotine, J.E.; How, J.P. Dynamic Tube MPC for Nonlinear Systems. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 1655–1662. [Google Scholar] [CrossRef] [Green Version]
- Feng, S.; Sun, H.; Zhang, Y.; Zheng, J.; Liu, H.X.; Li, L. Tube-Based Discrete Controller Design for Vehicle Platoons Subject to Disturbances and Saturation Constraints. IEEE Trans. Control Syst. Technol. 2020, 28, 1066–1073. [Google Scholar] [CrossRef]
- Mayne, D. Robust and stochastic model predictive control: Are we going in the right direction? Annu. Rev. Control 2016, 41, 184–192. [Google Scholar] [CrossRef]
- Peng-ya, X.; Yun-jie, W.; Jing-xing, Z.; Ling, C. Longitudinal attitude control of UAV based on fuzzy PID. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, H. Backstepping Fuzzy Sliding Mode Control for the Antiskid Braking System of Unmanned Aerial Vehicles. Electronics 2020, 9, 1731. [Google Scholar] [CrossRef]
- Li, K.; Wei, Y.; Wang, C.; Deng, H. Longitudinal Attitude Control Decoupling Algorithm Based on the Fuzzy Sliding Mode of a Coaxial-Rotor UAV. Electronics 2019, 8, 107. [Google Scholar] [CrossRef] [Green Version]
- Han, J. Active Disturbance Rejection Control Technology; National Defense Industry Press: Beijing, China, 2008. [Google Scholar]
- Wang, J.; Wang, X.; Luo, Z.; Assadian, F. Active disturbance rejection control of differential drive assist steering for electric vehicles. Energies 2020, 13, 2647. [Google Scholar] [CrossRef]
- Humaidi, A.J.; Ibraheem, I.K. Speed control of permanent magnet dC motor with friction and measurement noise using novel nonlinear extended state observer-based anti-disturbance control. Energies 2019, 12, 1651. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Chen, Z.; Zhang, X.; Sun, Q.; Sun, M. A novel control scheme for quadrotor UAV based upon active disturbance rejection control. Aerosp. Ence Technol. 2018, 79, 601–609. [Google Scholar] [CrossRef]
- Lotufo, M.A.; Colangelo, L.; Perez-Montenegro, C.; Canuto, E.; Novara, C. UAV quadrotor attitude control: An ADRC-EMC combined approach. Control Eng. Pract. 2019, 84, 13–22. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Sun, M. Trajectory tracking control for a quadrotor unmanned aerial vehicle based on dynamic surface active disturbance rejection control. Trans. Inst. Meas. Control 2020. [Google Scholar] [CrossRef]
- Niu, T.; Xiong, H.; Zhao, S. Based on ADRC UAV longitudinal pitching Angle control research. In Proceedings of the 2016 IEEE Information Technology, Networking, Electronic and Automation Control Conference, Chongqing, China, 20–22 May 2016; pp. 21–25. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 6, pp. 4989–4996. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, C.; Ma, Y. Vector speed regulation of an asynchronous motor based on improved first-order linear active disturbance rejection technology. Energies 2020, 13, 2168. [Google Scholar] [CrossRef]
- Li, H.; Li, S.; Lu, J.; Qu, Y.; Guo, C. A Novel Strategy Based on Linear Active Disturbance Rejection Control for Harmonic Detection and Compensation in Low Voltage AC Microgrid. Energies 2019, 12, 3982. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Wang, H.; Su, Z.; Shao, X. UAV broken-line path following under disturbance conditions. J. Aerosp. Eng. 2018, 31. [Google Scholar] [CrossRef]
- Liang, X.; Li, J.; Zhao, F. Attitude Control of Quadrotor UAV Based on LADRC Method. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 1924–1929. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, W.; Zuo, Z.; Zhong, Y. Robust Control for Quadrotors with Multiple Time-Varying Uncertainties and Delays. IEEE Trans. Ind. Electron. 2017, 64, 1303–1312. [Google Scholar] [CrossRef]






| Parameter | Unit | Value |
|---|---|---|
| m | kg | 1.5 |
| l | m | 0.4 |
| Ns | ||
| Nms | ||
| Kgm | ||
| Kgm | ||
| Kgm |
| NB | NM | NS | ZO | PS | PM | PB | ||
|---|---|---|---|---|---|---|---|---|
| e | NB | NB | NB | NM | NM | NS | ZO | ZO |
| NM | NB | NB | NM | NM | NS | ZO | ZO | |
| NS | NM | NM | NS | NS | ZO | ZO | PS | |
| ZO | NM | NS | NS | ZO | PS | PS | PM | |
| PS | NS | NS | ZO | PS | PM | PM | PB | |
| PM | ZO | ZO | PS | PM | PM | PB | PB | |
| PB | ZO | PS | PM | PM | PB | PB | PB | |
| NB | NM | NS | ZO | PS | PM | PB | ||
|---|---|---|---|---|---|---|---|---|
| e | NB | PB | PB | PM | PM | PS | ZO | ZO |
| NM | PB | PB | PM | PM | PS | ZO | ZO | |
| NS | PM | PM | PS | PS | PS | PS | NS | |
| ZO | PM | PS | PS | NB | NB | NB | NS | |
| PS | NS | NS | NS | NS | NS | NM | NM | |
| PM | PM | PM | PB | PB | PB | PB | PB | |
| PB | PB | PB | PB | PB | PB | PB | PB | |
| NB | NM | NS | ZO | PS | PM | PB | ||
|---|---|---|---|---|---|---|---|---|
| e | NB | PB | PB | PM | PM | PS | ZO | ZO |
| NM | PB | PB | PM | PM | PS | ZO | ZO | |
| NS | PM | PM | PS | PS | ZO | ZO | NS | |
| ZO | PM | PS | PS | ZO | NS | NS | NM | |
| PS | PS | ZO | ZO | NS | NM | NM | NM | |
| PM | ZO | ZO | NS | NM | NM | NB | NB | |
| PB | ZO | NS | NM | NM | NB | NB | NB | |
| Channel | Fuzzy-LADRC | LADRC | PID | Fuzzy-PID |
|---|---|---|---|---|
| X | 240.806 | 283.164 | 443.399 | 458.699 |
| Z | 446.113 | 655.948 | 1050.423 | 938.950 |
| Roll | 43.824 | 45.014 | 40.839 | 33.953 |
| Yaw | 35.896 | 36.128 | 45.169 | 32.990 |
| IAE | Disturbance (1) | Disturbance (2) | ||||||
|---|---|---|---|---|---|---|---|---|
| X | Z | Roll | Yaw | X | Z | Roll | Yaw | |
| Fuzzy-LADRC | 0.4507 | 0.0798 | 0.4229 | 0.7435 | 7.2666 | 1.0446 | 11.7110 | 12.7429 |
| LADRC | 0.5901 | 0.0827 | 0.4908 | 0.9297 | 9.4654 | 1.1963 | 12.4671 | 14.0729 |
| PID | 128.1835 | 274.6368 | 34.1867 | 11.6689 | 1373.3657 | 1695.544 | 480.7782 | 57.9432 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Liu, M.; Liu, C.; Feng, X.; Wu, H. An Industrial Quadrotor UAV Control Method Based on Fuzzy Adaptive Linear Active Disturbance Rejection Control. Electronics 2021, 10, 376. https://doi.org/10.3390/electronics10040376
Sun C, Liu M, Liu C, Feng X, Wu H. An Industrial Quadrotor UAV Control Method Based on Fuzzy Adaptive Linear Active Disturbance Rejection Control. Electronics. 2021; 10(4):376. https://doi.org/10.3390/electronics10040376
Chicago/Turabian StyleSun, Changhao, Mengqi Liu, Chang’an Liu, Xueling Feng, and Hua Wu. 2021. "An Industrial Quadrotor UAV Control Method Based on Fuzzy Adaptive Linear Active Disturbance Rejection Control" Electronics 10, no. 4: 376. https://doi.org/10.3390/electronics10040376
APA StyleSun, C., Liu, M., Liu, C., Feng, X., & Wu, H. (2021). An Industrial Quadrotor UAV Control Method Based on Fuzzy Adaptive Linear Active Disturbance Rejection Control. Electronics, 10(4), 376. https://doi.org/10.3390/electronics10040376






