The Prescribed-Time Sliding Mode Control for Underactuated Bridge Crane
Abstract
:1. Introduction
- (1)
- The two-dimensional bridge crane model was transformed into a chain system by linearizing the crane model and constructing auxiliary variables, simplifying the design difficulty of the underactuated bridge crane system’s prescribed-time positioning and anti-swing controller.
- (2)
- A new type of prescribed-time convergence rate was proposed herein. At the same time, the continuous prescribed-time convergence rate eliminates the chattering problem inherent in the switching term of the sliding mode control.
- (3)
- A new type of prescribed-time sliding surface has been proposed to ensure that the position of the trolley and the pendulum angle of the load converge to the desired position on the sliding surface within the prescribed time.
2. Problem Description
3. Bridge Crane Model
4. Controller Design
5. Stability Analysis
6. Simulation and Analysis
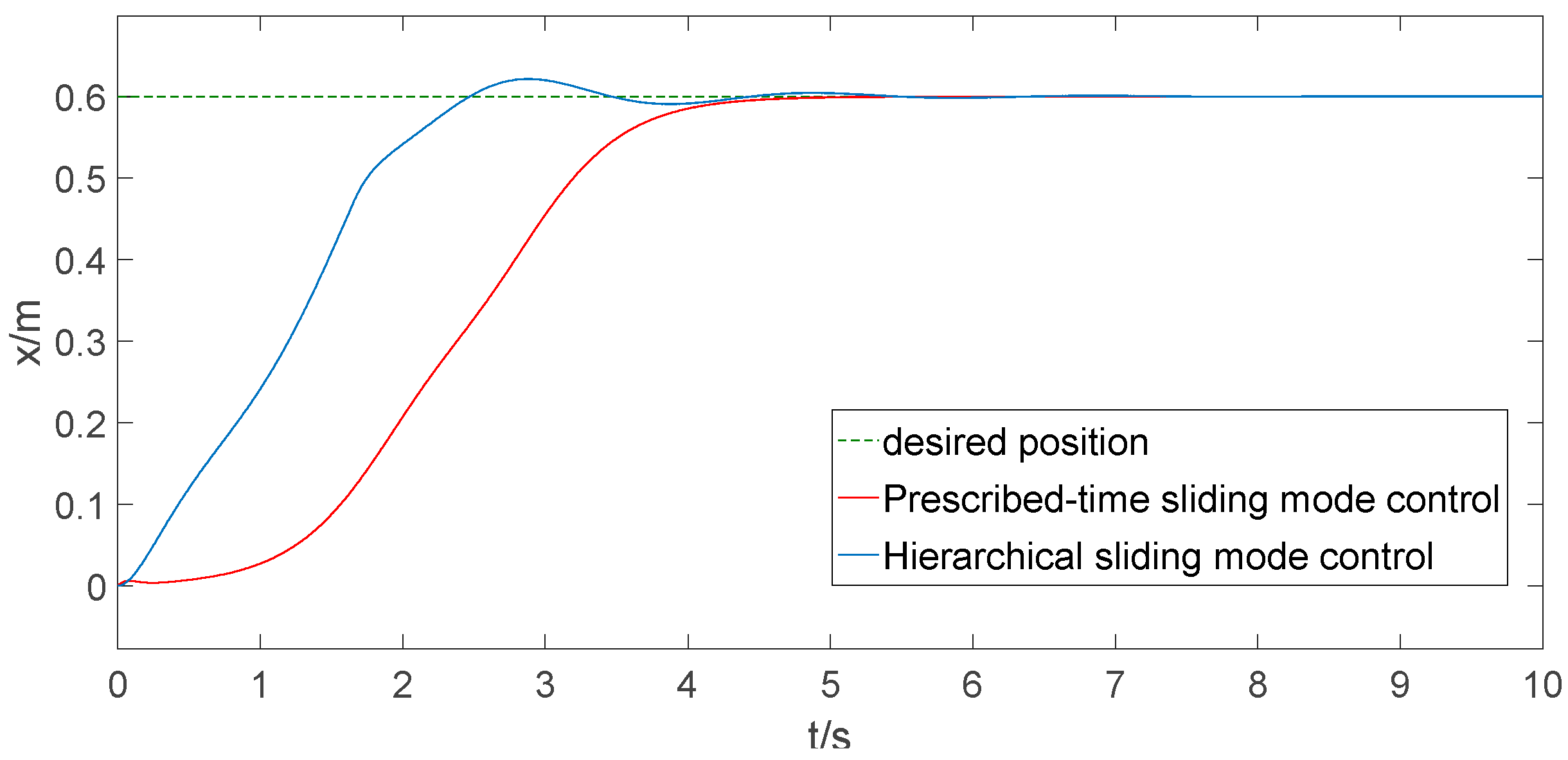
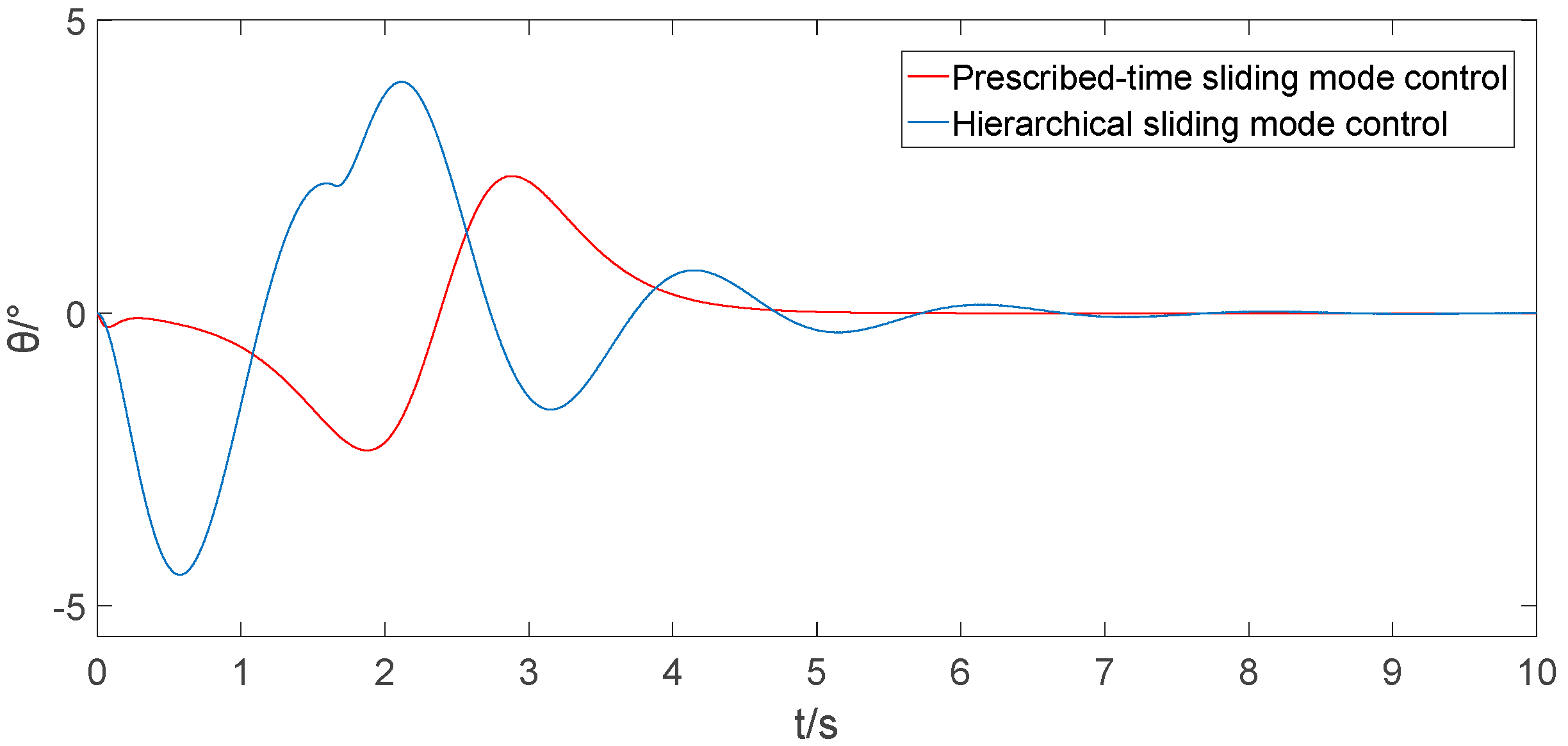
6.1. Contrast Simulation
6.2. Simulation under Different Prescribed Time
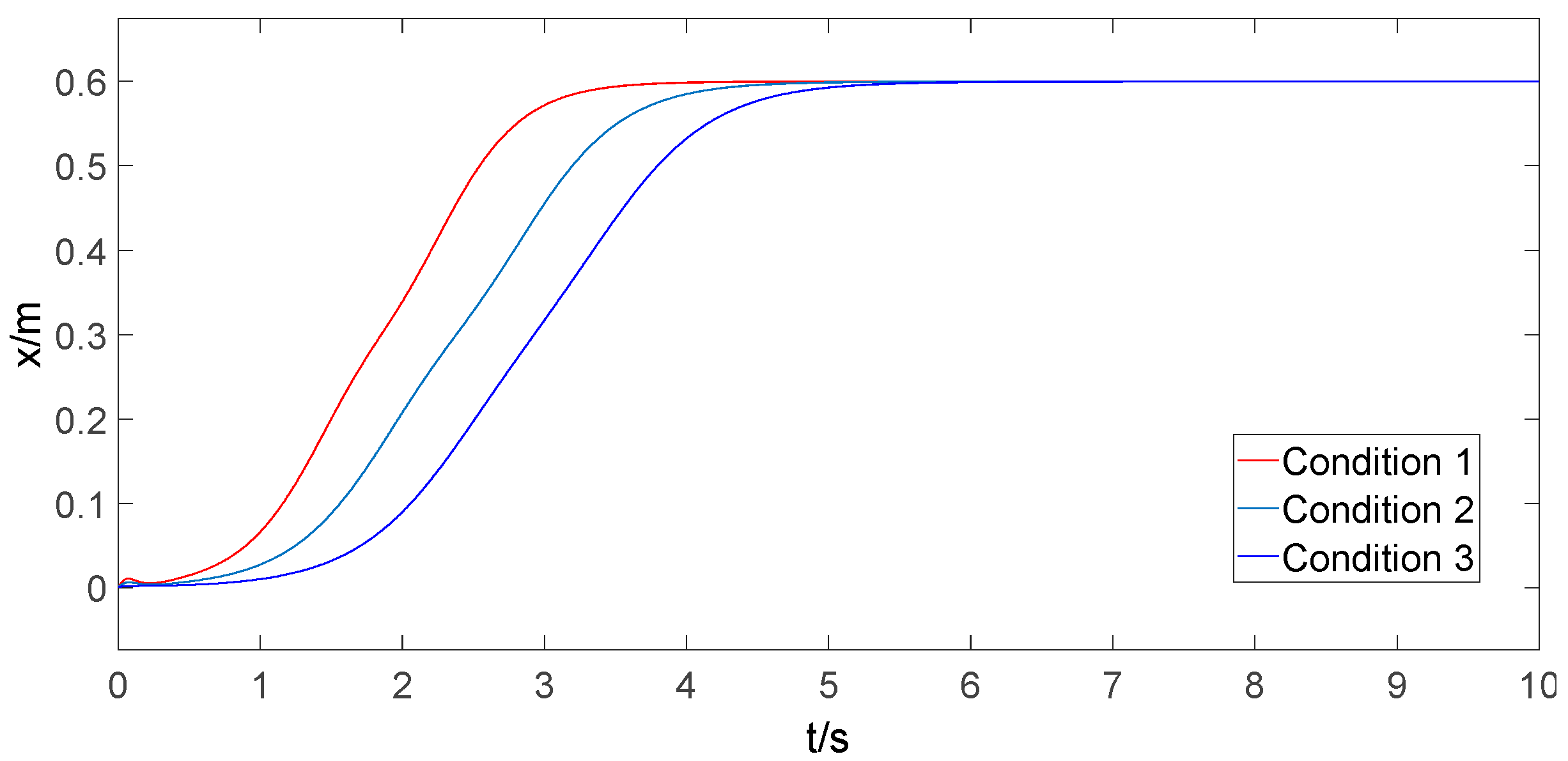
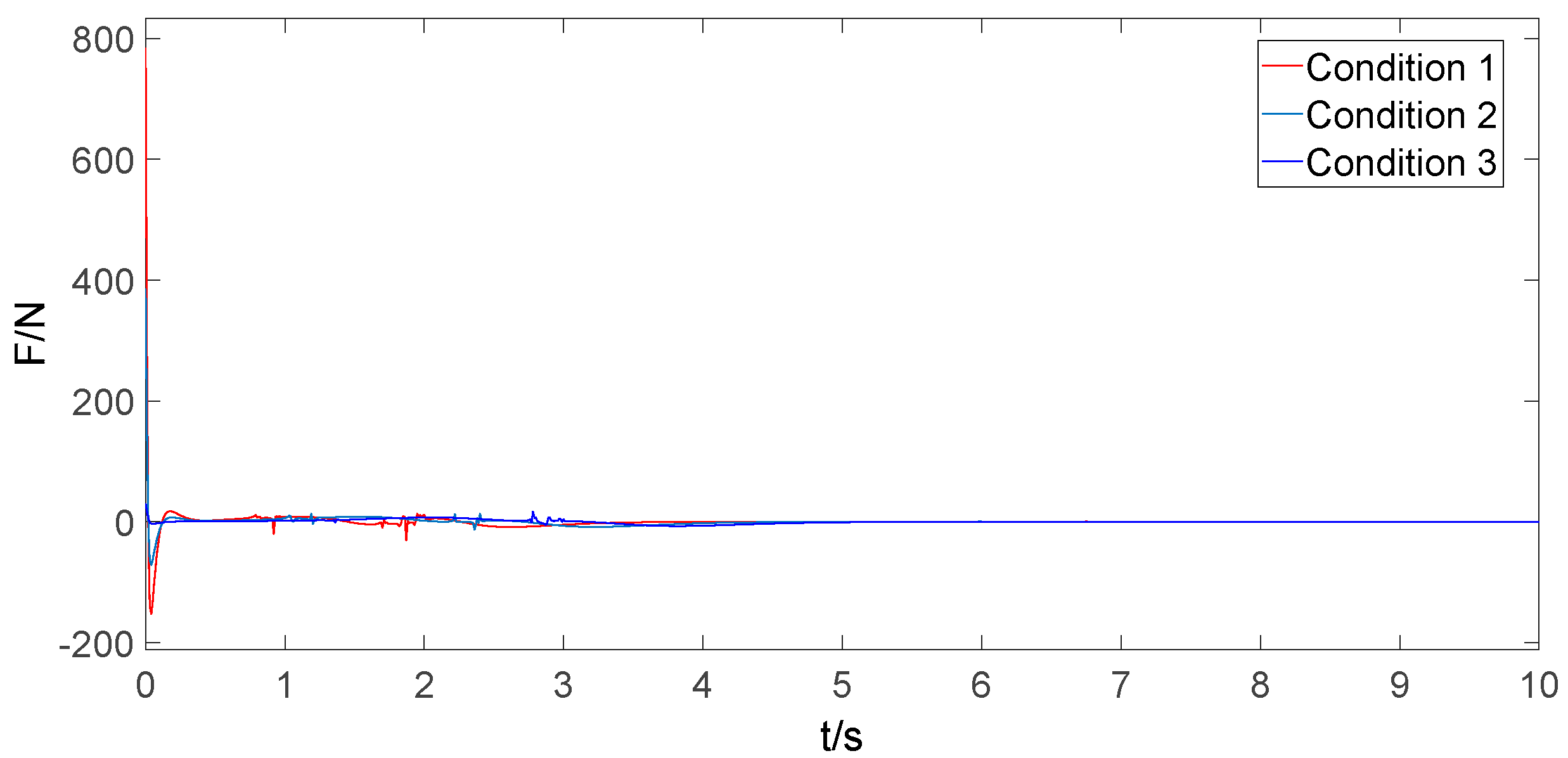
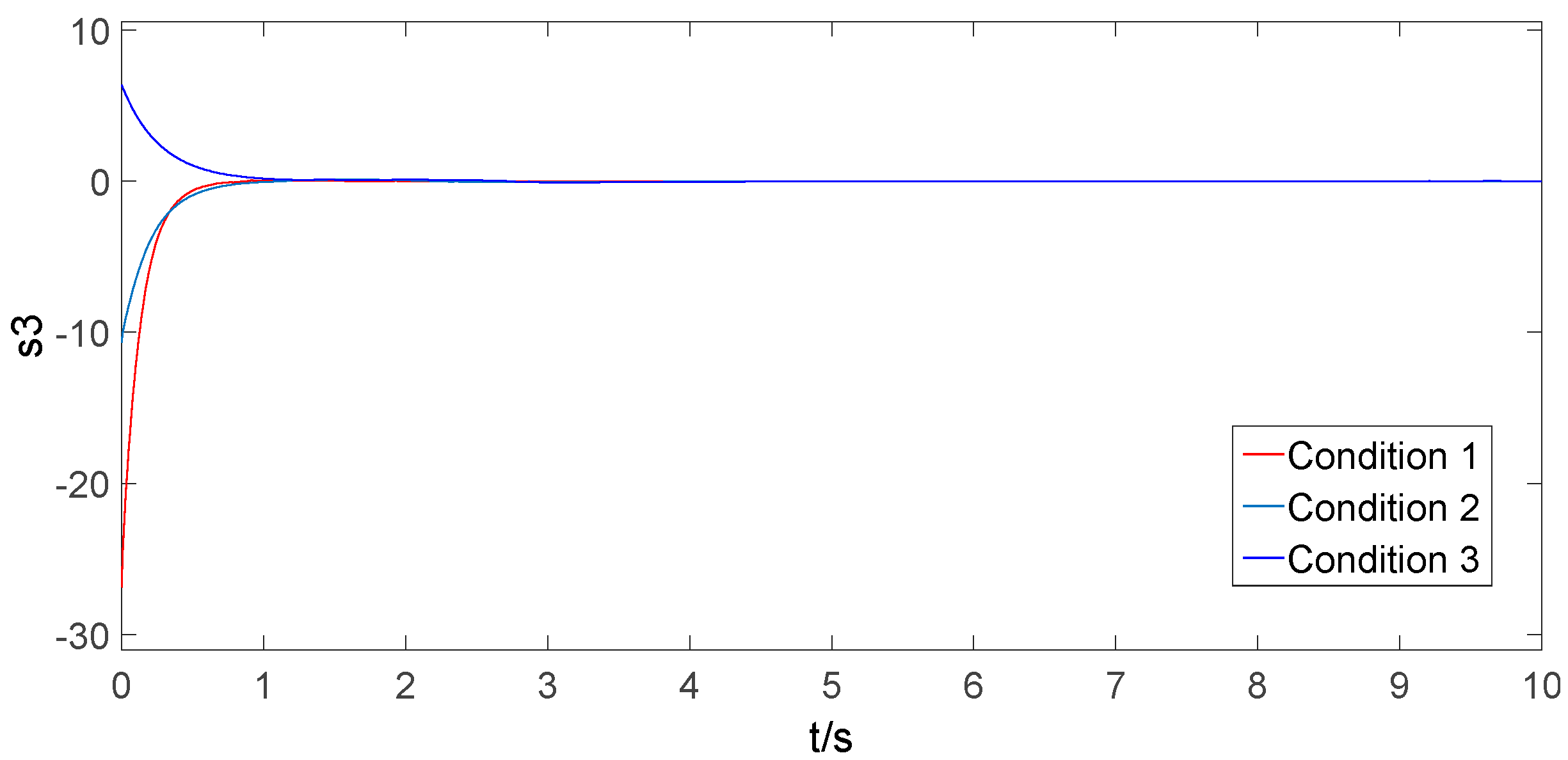
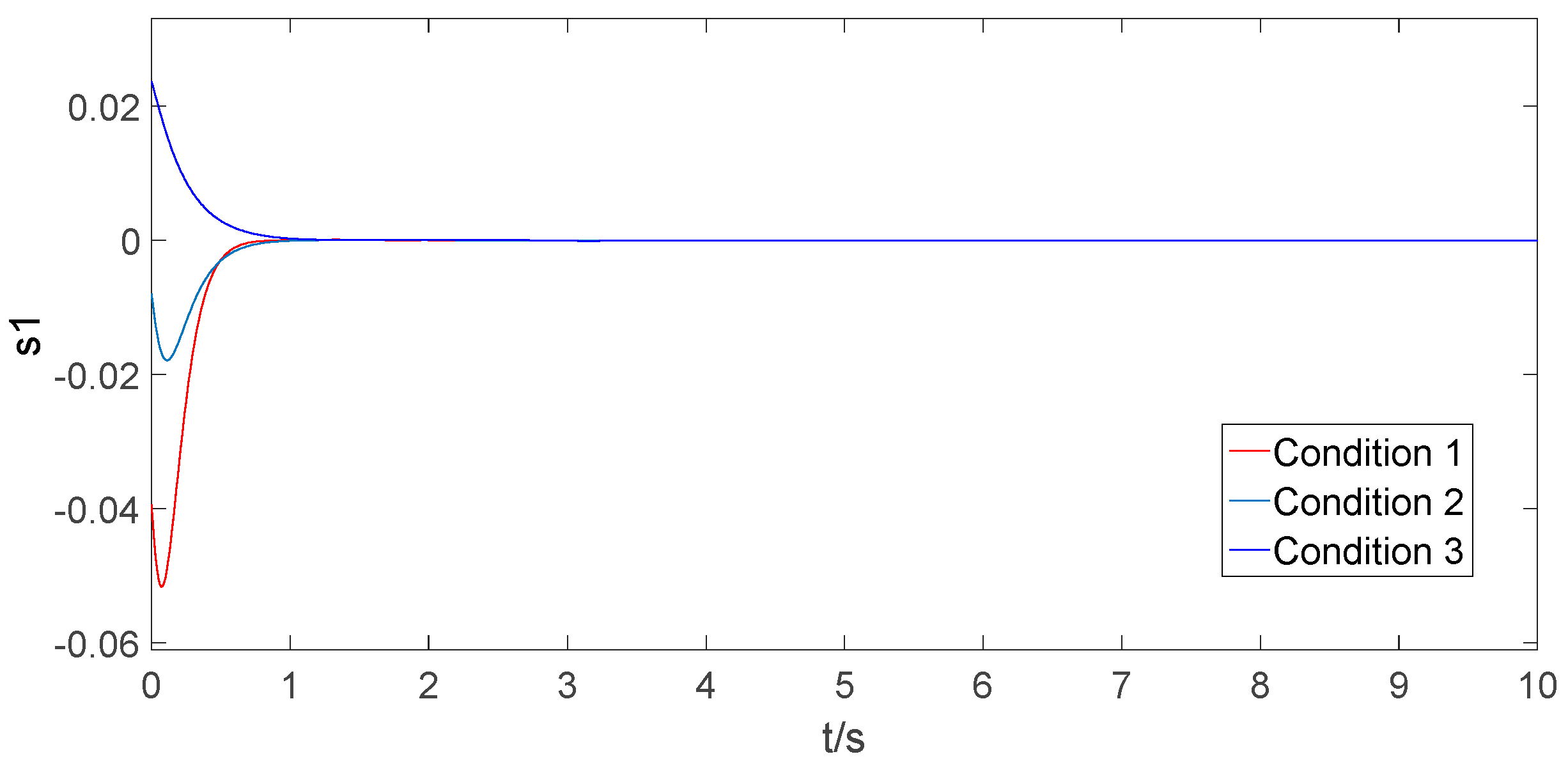
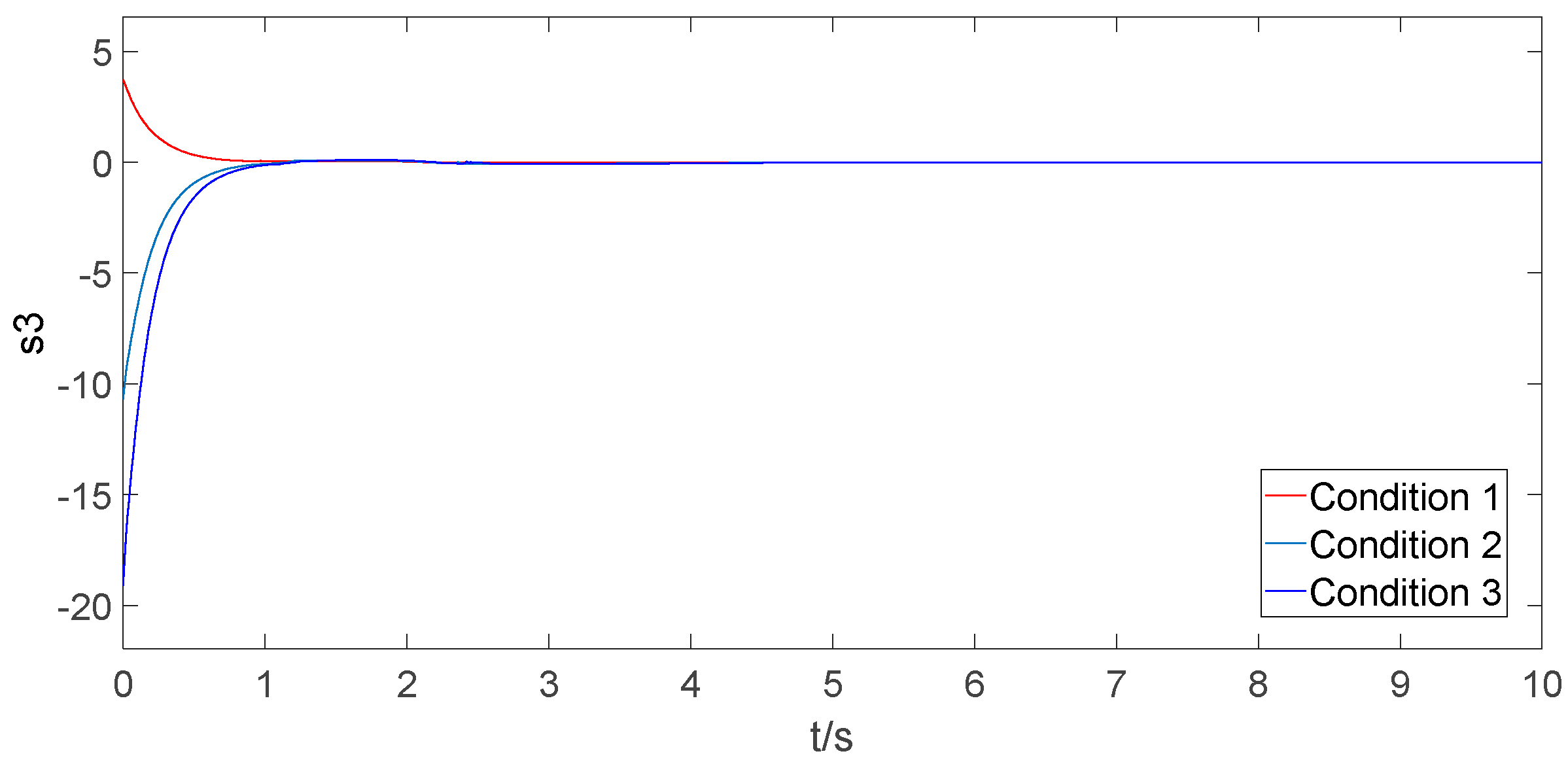
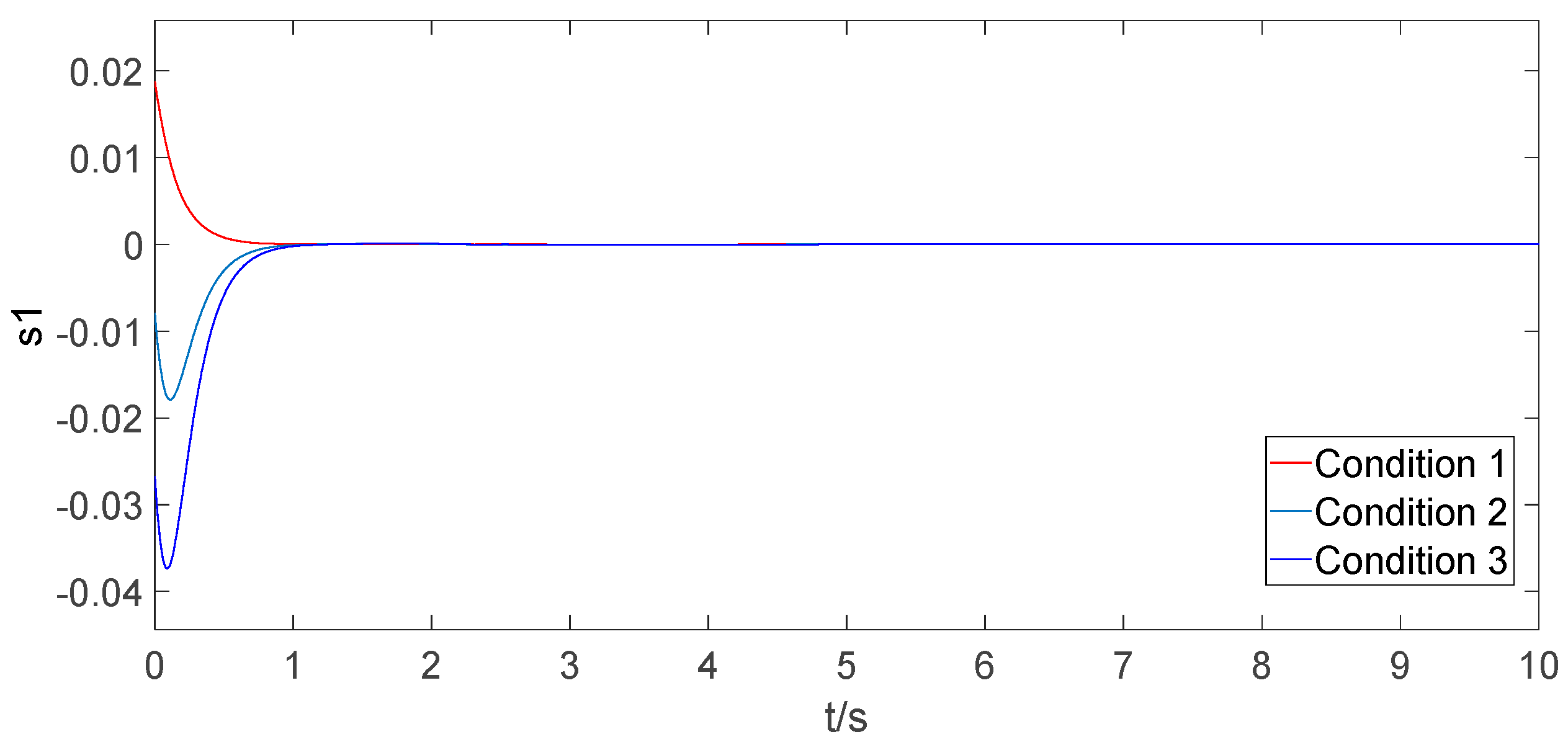
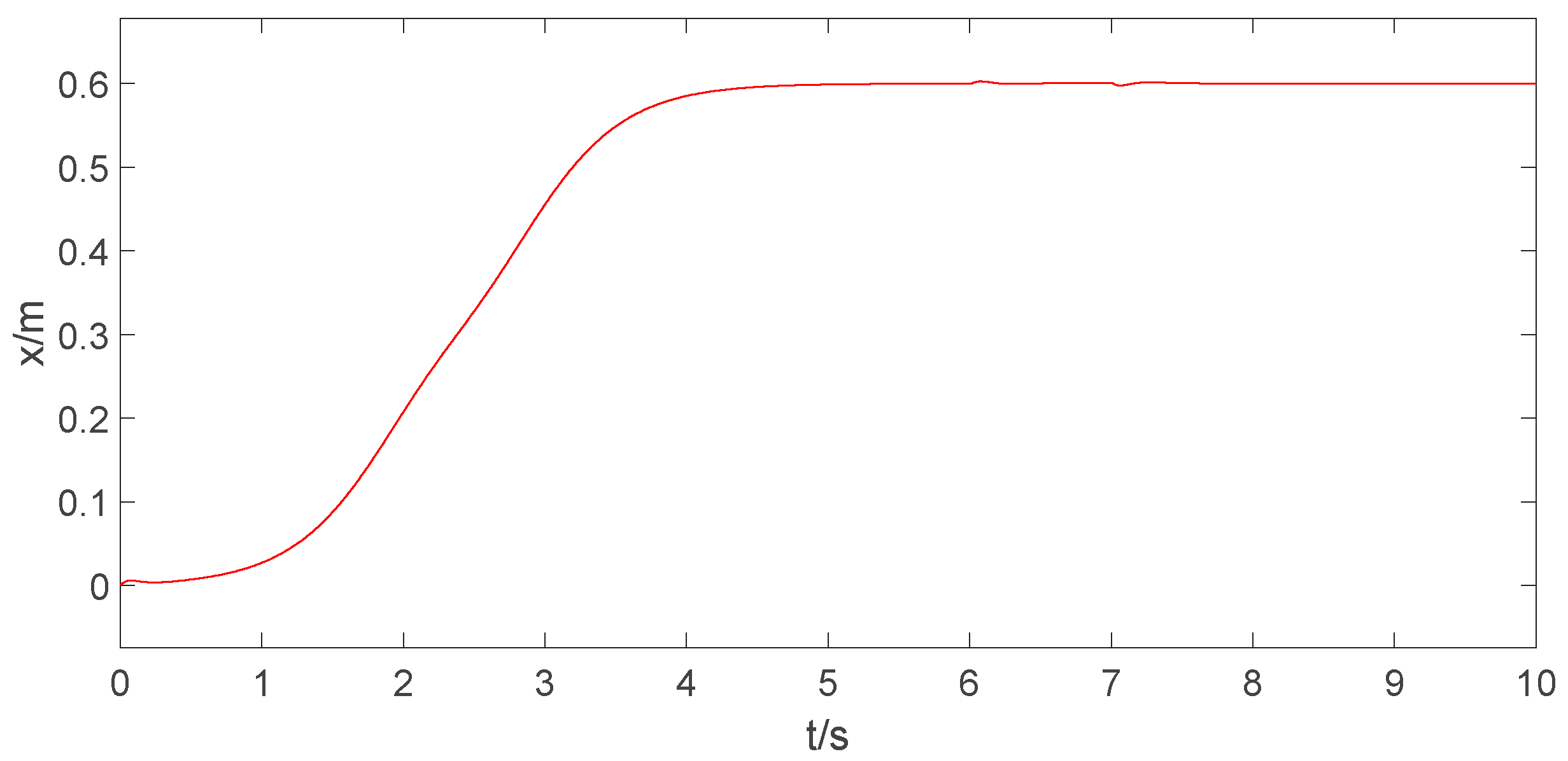
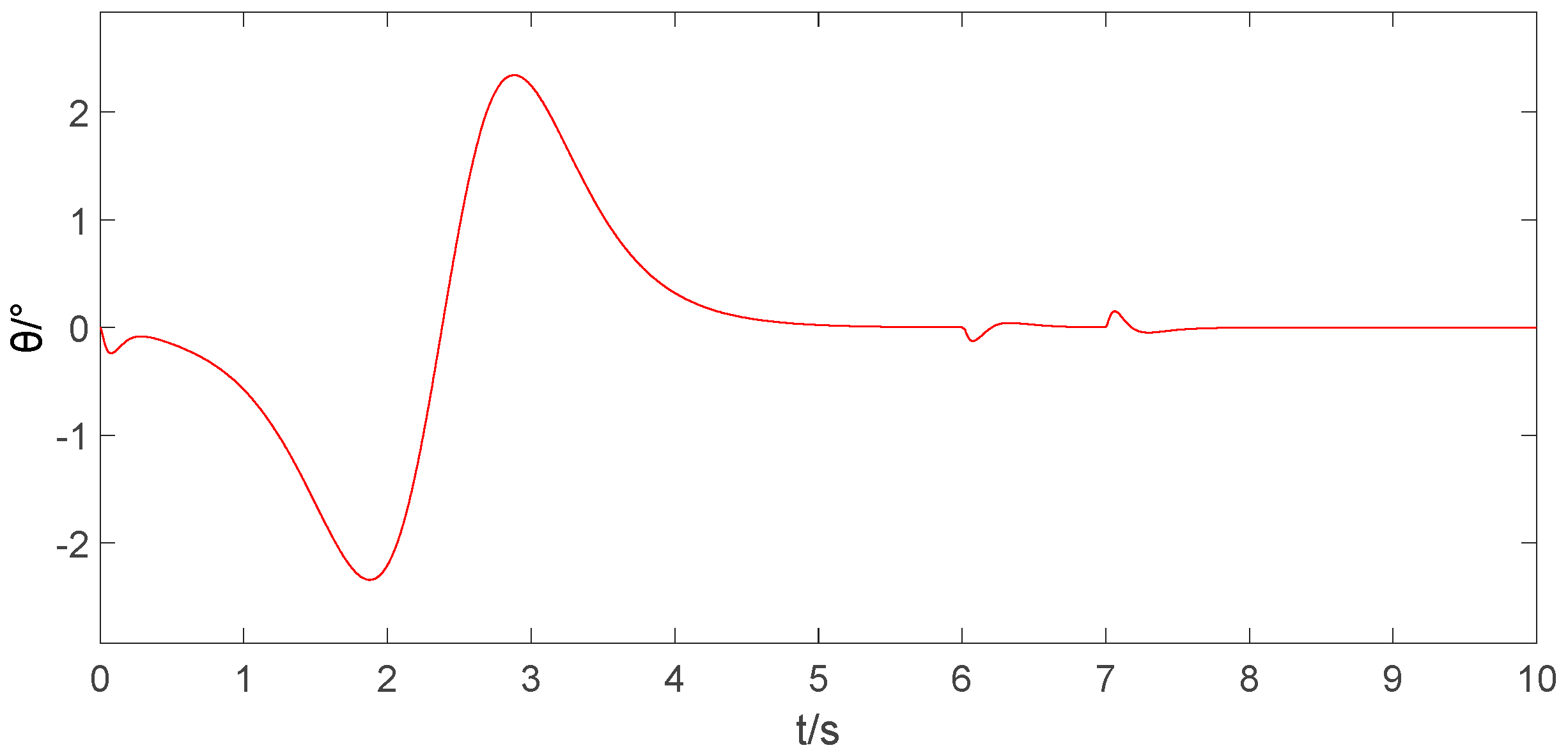
6.3. Simulation under Different Initial Conditions
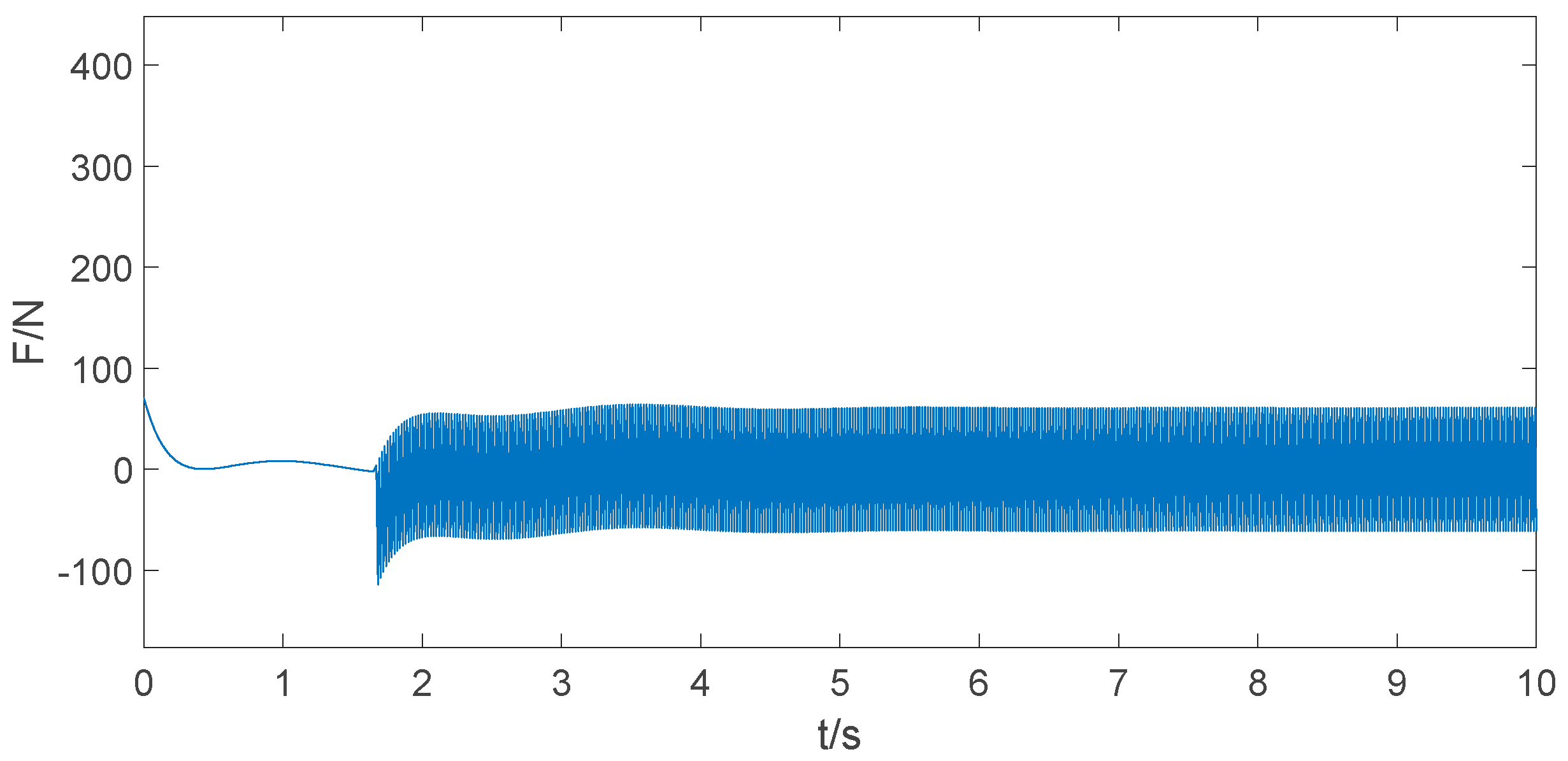
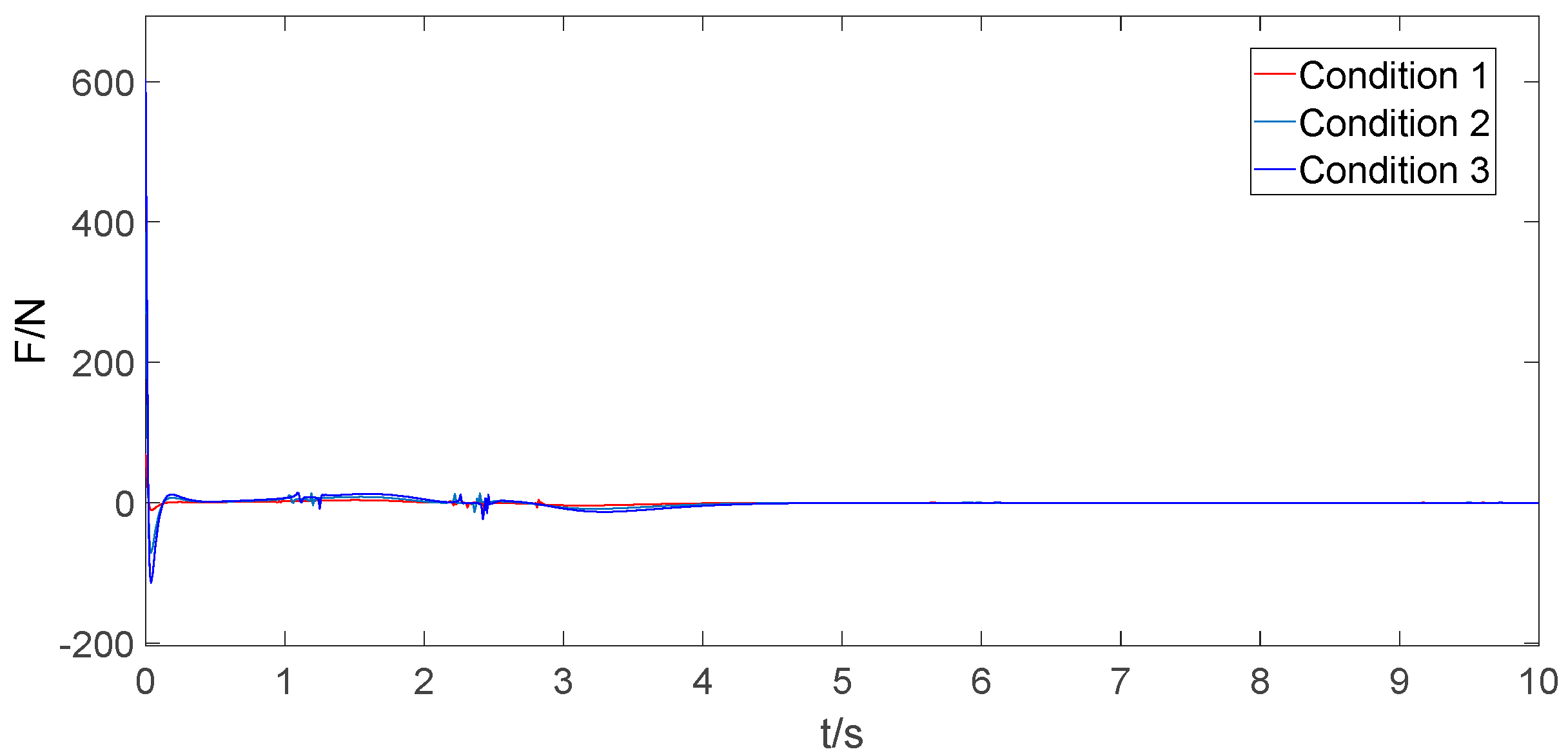
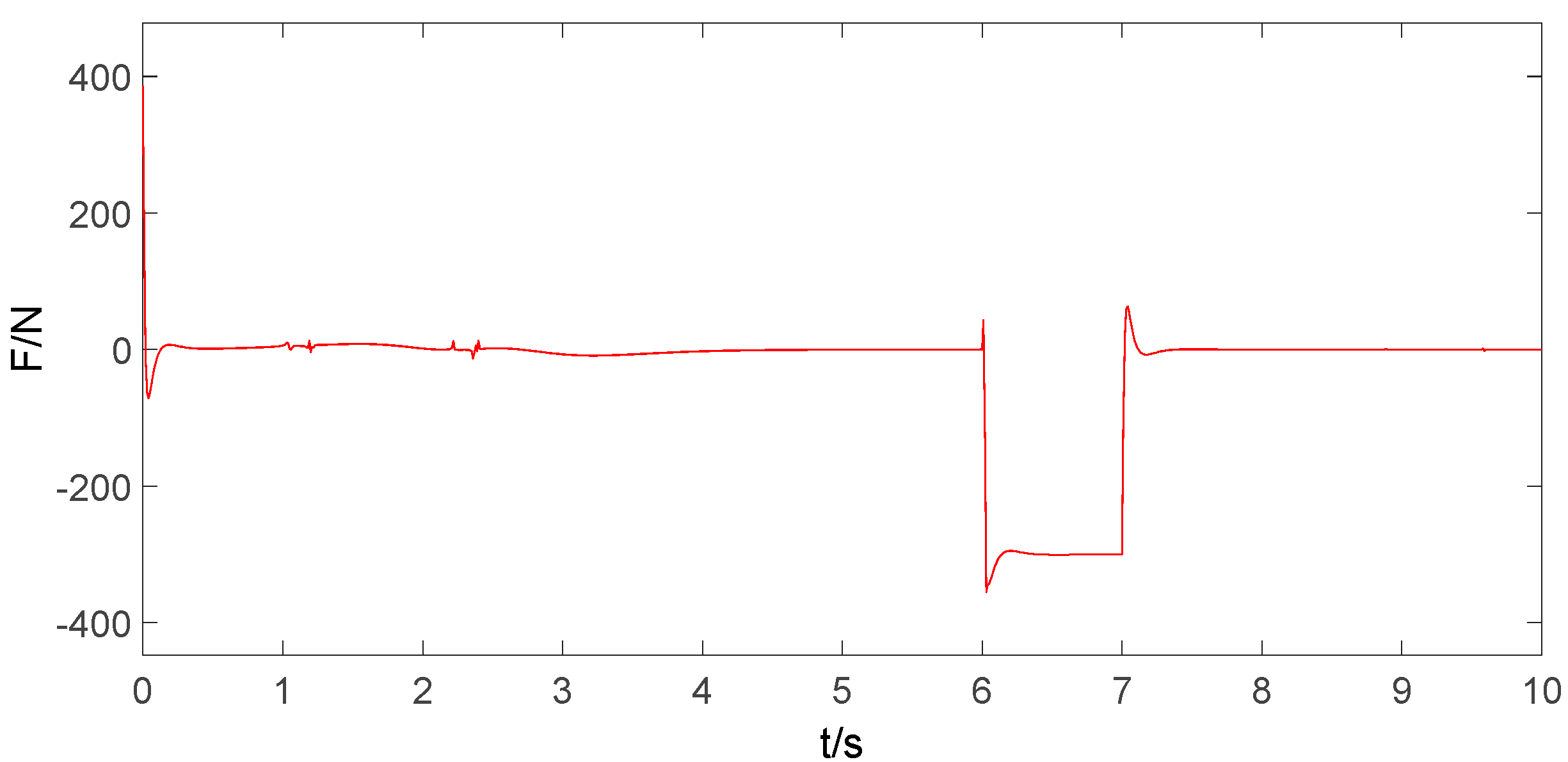
6.4. Robustness Test
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wahrburg, A.; Jurvanen, J.; Niemelä, M.; Holmberg, M. On reference trajectory generation for overhead crane travel movements. at-Automatisierungstechnik 2022, 70, 300–311. [Google Scholar] [CrossRef]
- Li, G.; Ma, X.; Li, Z.; Li, Y. Optimal trajectory planning strategy for underactuated overhead crane with pendulum-sloshing dynamics and full-state constraints. Nonlinear Dyn. 2022, 109, 815–835. [Google Scholar] [CrossRef]
- Wu, Q.; Sun, N.; Wang, X. Equivalent Rope Length-Based Trajectory Planning for Double Pendulum Bridge Cranes with Distributed Mass Payloads. Actuators 2022, 11, 25. [Google Scholar] [CrossRef]
- Li, H.; Hui, Y.; Ma, J.; Wang, Q.; Zhou, Y.; Wang, H. Research on Variable Universe Fuzzy Multi-Parameter Self-Tuning PID Control of Bridge Crane. Appl. Sci. 2023, 13, 4830. [Google Scholar] [CrossRef]
- Li, H.; Hui, Y.B.; Wang, Q.; Wang, H.-X.; Wang, L.-J. Design of Anti-Swing PID Controller for Bridge Crane Based on PSO and SA Algorithm. Electronics 2022, 11, 3143. [Google Scholar] [CrossRef]
- Yu, Z.; Niu, W. Flatness-Based Backstepping Antisway Control of Underactuated Crane Systems under Wind Disturbance. Electronics 2023, 12, 244. [Google Scholar] [CrossRef]
- Le, H.X.; Kim, T.D.; Hoang, Q.D.; Van Pham, M.; Van Nguyen, T.; Van Pham, H.; Do, D.M. Adaptive fuzzy backstepping hierarchical sliding mode control for six degrees of freedom overhead crane. Int. J. Dyn. Control 2022, 10, 2174–2192. [Google Scholar] [CrossRef]
- Pham, H.V.; Hoang, Q.D.; Pham, M.V.; Do, D.M.; Phi, N.H.; Hoang, D. An Efficient Adaptive Fuzzy Hierarchical Sliding Mode Control Strategy for 6 Degrees of Freedom Overhead Crane. Electronics 2022, 11, 713. [Google Scholar] [CrossRef]
- Zhu, X.; Xu, W. Nonlinear time-varying sliding mode synchronous control of double-lift overhead cranes under unknown disturbances. Trans. Inst. Meas. Control 2023, 45, 181–194. [Google Scholar] [CrossRef]
- Guo, Q.; Chai, L.; Liu, H. Anti-swing sliding mode control of three-dimensional double pendulum overhead cranes based on extended state observer. Nonlinear Dyn. 2022, 111, 391–410. [Google Scholar] [CrossRef]
- Wang, T.L.; Tan, N.L.; Zhang, X.W.; Li, G.; Su, S.; Zhou, J.; Qiu, J.; Wu, Z.; Zhai, Y.; Labati, R.D.; et al. A Time-Varying Sliding Mode Control Method for Distributed-Mass Double Pendulum Bridge Crane with Variable Parameters. IEEE Access 2021, 9, 75981–75992. [Google Scholar] [CrossRef]
- Wen, T.C.; Fang, Y.C.; Lu, B. Neural network-based adaptive sliding mode control for underactuated dual overhead cranes suffering from matched and unmatched disturbances. Auton. Intell. Syst. 2022, 2, 1. [Google Scholar] [CrossRef]
- Wang, L.Q.; Wu, X.Q.; Lei, M.Z. Feedforward-control-based nonlinear control for overhead cranes with matched and unmatched disturbances. J. Mech. Eng. Sci. 2022, 236, 5785–5795. [Google Scholar] [CrossRef]
- Chen, Q.R.; Cheng, W.M.; Liu, J.H.; Du, R. Partial state feedback sliding mode control for double-pendulum overhead cranes with unknown disturbances. J. Mech. Eng. Sci. 2022, 236, 3902–3911. [Google Scholar] [CrossRef]
- Le, H.X.; Le, A.V.; Nguyen, L. Adaptive fuzzy observer based hierarchical sliding mode control for uncertain 2D overhead cranes. Cyber-Phys. Syst. 2019, 5, 191–208. [Google Scholar] [CrossRef]
- Wang, T.L.; Zhou, J.; Wu, Z.Q.; Liu, R.J.; Zhang, J.L.; Liang, Y.Y. A Time-Varying PD Sliding Mode Control Method for the Container Crane Based on a Radial-Spring Damper. Electronics 2022, 11, 3543. [Google Scholar] [CrossRef]
- Yang, W.L.; Chen, J.Y.; Xu, D.Z.; Yan, X. Hierarchical global fast terminal sliding-mode control for a bridge travelling crane system. IET Control Theory Appl. 2021, 15, 814–828. [Google Scholar] [CrossRef]
- Xin, W.; Liu, C.T.; He, Z.X. A Parameters Adaptive Non-Singular Terminal Sliding Mode Control Method for Overhead Crane System. Int. J. Front. Eng. Technol. 2022, 4, 42–48. [Google Scholar]
- Nguyen, V.T.; Yang, C.H.; Du, C.L.; Liao, L. Design and implementation of finite time sliding mode controller for fuzzy overhead crane system. ISA Trans. 2019, 124, 374–385. [Google Scholar] [CrossRef]
- Gu, X.T.; Zhou, H.; Hong, M.Q.; Guo, Y. Adaptive hierarchical sliding mode controller for tower cranes based on finite time disturbance observer. Int. J. Adapt. Control Signal Process. 2022, 36, 2319–2340. [Google Scholar] [CrossRef]
- Wu, X.Q.; Xu, K.X.; He, X.X. Disturbance-observer-based nonlinear control for overhead cranes subject to uncertain disturbances. Mech. Syst. Signal Process. 2020, 139, 106631. [Google Scholar] [CrossRef]
- Zhang, M.H. Finite-time model-free trajectory tracking control for overhead cranes subject to model uncertainties, parameter variations and external disturbances. Trans. Inst. Meas. Control 2019, 41, 3516–3525. [Google Scholar] [CrossRef]
- Zhang, M.H.; Zhang, Y.F.; Cheng, X.G. Finite-Time Trajectory Tracking Control for Overhead Crane Systems Subject to Unknown Disturbances. IEEE Access 2019, 7, 55974–55982. [Google Scholar] [CrossRef]
- Wu, X.F.; Qian, J.Y. Fixed-time Tracking Control of Underactuated Overhead Cranes. In Proceedings of the 30th Chinese Control and Decision Conference, Shenyang, China, 9–11 June 2018; pp. 852–857. [Google Scholar]
- Khanzadeh, A.; Pourgholi, M. A novel continuous time-varying sliding mode controller for robustly synchronizing non-identical fractional-order chaotic systems precisely at any arbitrary pre-specified time. Nonlinear Dyn. 2016, 86, 543–558. [Google Scholar] [CrossRef]
- Liu, Y.F.; Zhao, Y.; Shi, Z.K.; Wei, D. Specified-time containment control of multi-agent systems over directed topologies. IET Control Theory Appl. 2017, 11, 576–585. [Google Scholar] [CrossRef]
- Wei, C.S.; Luo, J.J.; Yin, Z.Y.; Yuan, J. Leader-following consensus of second-order multi-agent systems with arbitrarily appointed-time prescribed performance. IET Control Theory Appl. 2018, 12, 2276–2286. [Google Scholar] [CrossRef]
- Wang, J.G.; Luo, X.Y.; Li, X.L.; Guan, X. Specified-Time Bearing-Based Formation Control of Multi-Agent Systems via a Dynamic Gain Approach. J. Frankl. Inst. 2018, 355, 8619–8641. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Y.F.; Wen, G.H.; Ren, W.; Chen, G. Designing Distributed Specified-Time Consensus Protocols for Linear Multiagent Systems Over Directed Graphs. IEEE Trans. Automat. Control 2019, 64, 2945–2952. [Google Scholar] [CrossRef]
- Liu, M.M.; Shao, X.D.; Ma, G.F. Appointed-time fault-tolerant attitude tracking control of spacecraft with double-level guaranteed performance bounds. Aerosp. Sci. Technol. 2019, 92, 337–346. [Google Scholar] [CrossRef]
- Wu, X.J.; Zheng, W.Y.; Zhou, X.X.; Shao, S. Adaptive dynamic surface and sliding mode tracking control for uncertain QUAV with time-varying load and appointed-time prescribed performance. J. Frankl. Inst. 2021, 358, 4178–4208. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, J.F.; Cui, N.G. Backstepping control for a two-link manipulator with appointed-time convergence. ISA Trans. 2021, 128, 208–219. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.T.; Yi, J.Q.; Zhao, D.B.; Wang, W. Adaptive sliding mode fuzzy control for a two-dimensional overhead crane. Mechatronics 2005, 15, 505–522. [Google Scholar] [CrossRef]
- Fang, Y.; Ma, B.; Wang, P.; Zhang, X. A Motion Planning-Based Adaptive Control Method for an Underactuated Crane System. IEEE Trans. Control Syst. Technol. 2012, 20, 241–248. [Google Scholar] [CrossRef]










| Symbols | Physical Meaning | Unit |
|---|---|---|
| Trolley mass | kg | |
| Load mass | kg | |
| Cable length | m | |
| Trolley position | m | |
| Load swing angle | rad | |
| Driving force | N | |
| Gravitational acceleration |
| Condition | Load Mass | Cable Length | Transit Distance |
|---|---|---|---|
| Condition 1 | 5 kg | 1 m | 0.3 m |
| Condition 2 | 8 kg | 1.2 m | 0.6 m |
| Condition 3 | 10 kg | 0.9 m | 0.9 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Zhang, H.; Gu, C. The Prescribed-Time Sliding Mode Control for Underactuated Bridge Crane. Electronics 2024, 13, 219. https://doi.org/10.3390/electronics13010219
Feng Y, Zhang H, Gu C. The Prescribed-Time Sliding Mode Control for Underactuated Bridge Crane. Electronics. 2024; 13(1):219. https://doi.org/10.3390/electronics13010219
Chicago/Turabian StyleFeng, Yin’an, Hao Zhang, and Chan Gu. 2024. "The Prescribed-Time Sliding Mode Control for Underactuated Bridge Crane" Electronics 13, no. 1: 219. https://doi.org/10.3390/electronics13010219




