Nonlinear Control System for Flat Plate Structures Considering Interference Based on Operator Theory and Optimization Method
Abstract
:1. Introduction
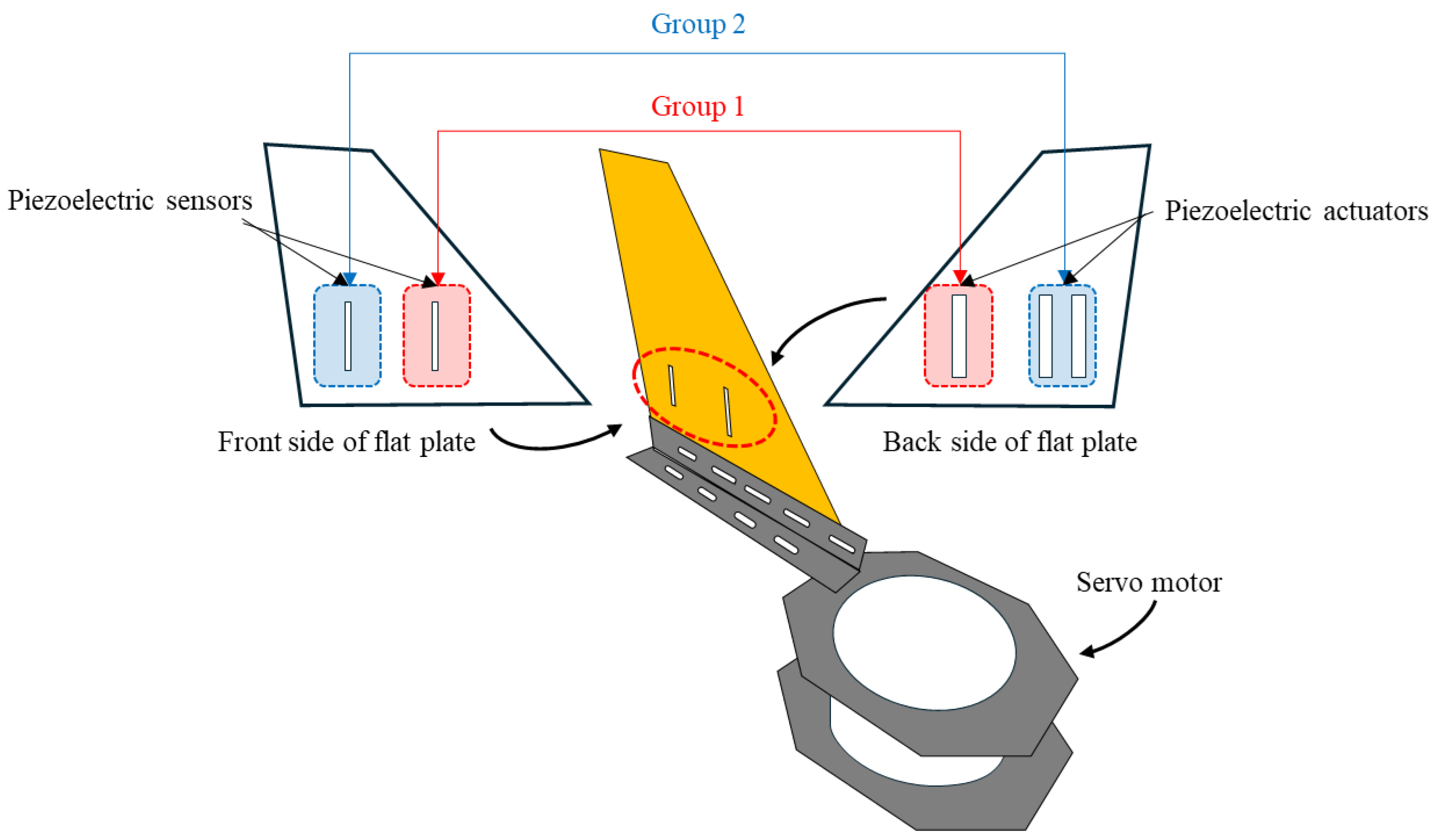
2. Modeling
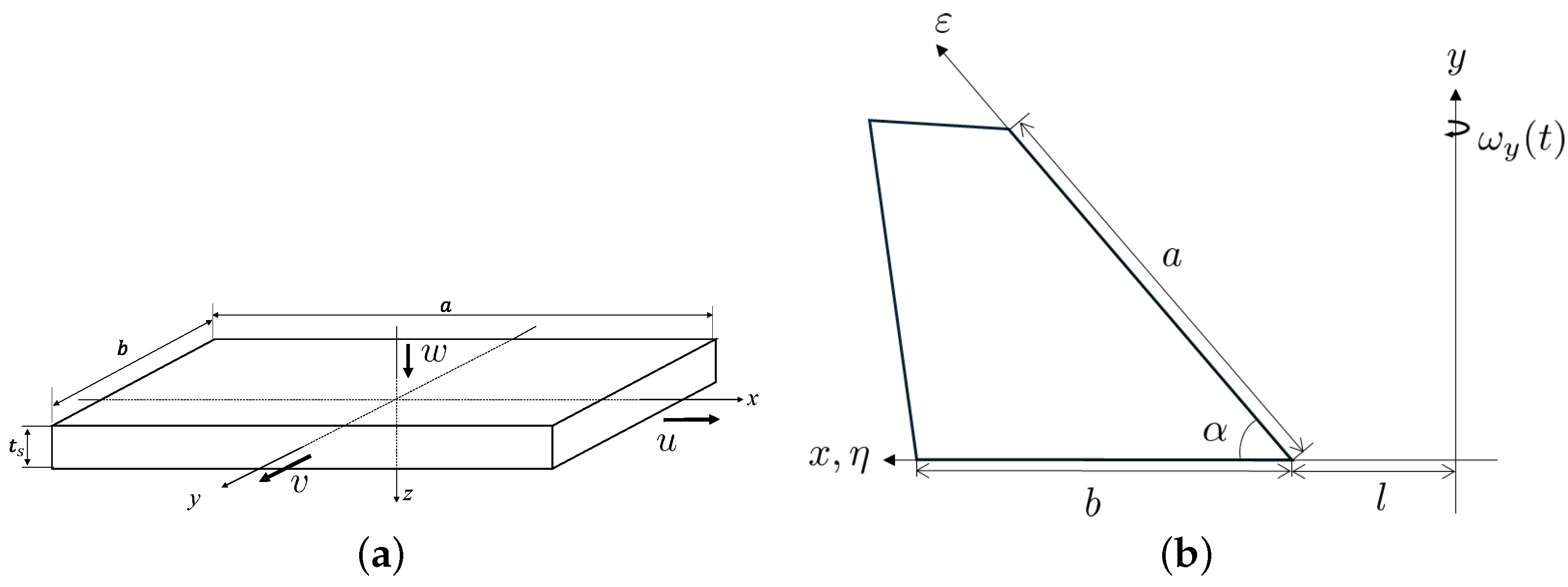
2.1. Modeling of Flat Plate
- The thickness of the plate remains constant.
- Shear deformation acting in the direction perpendicular to the surface is neglected.
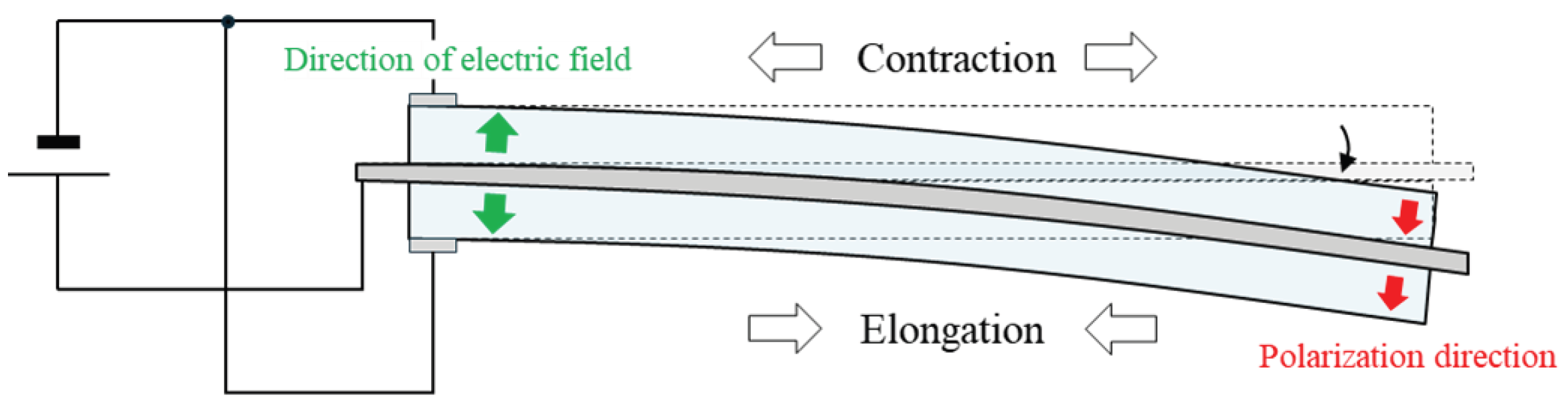
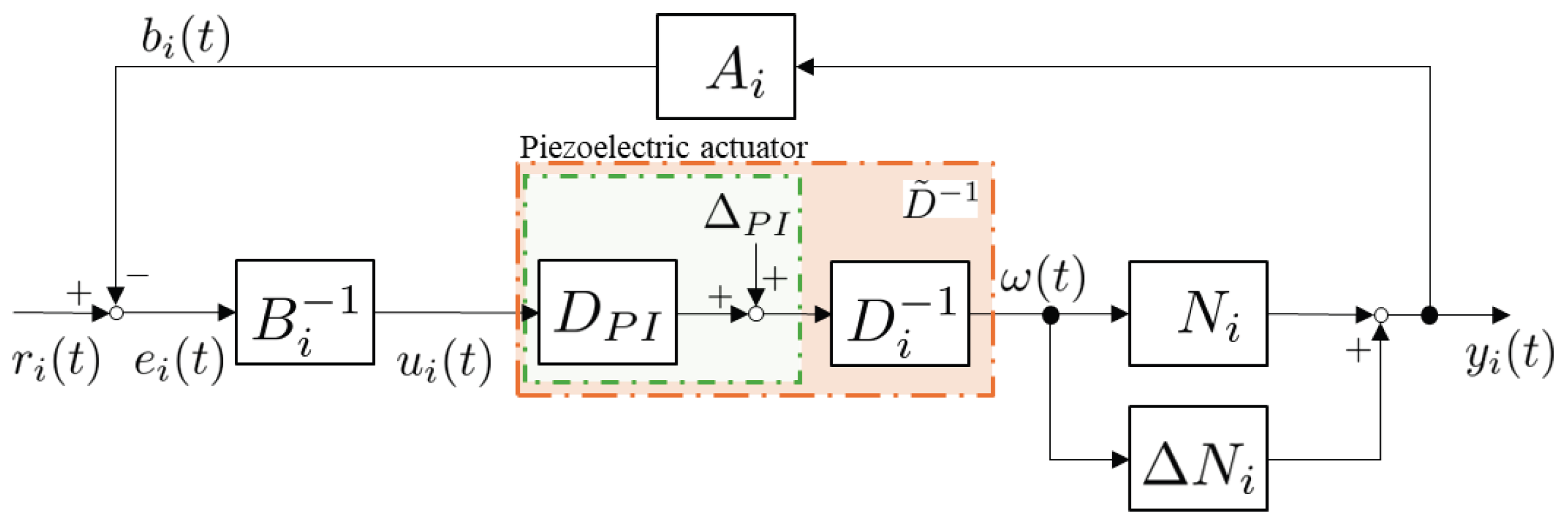
2.2. Modeling of Piezoelectric Actuator
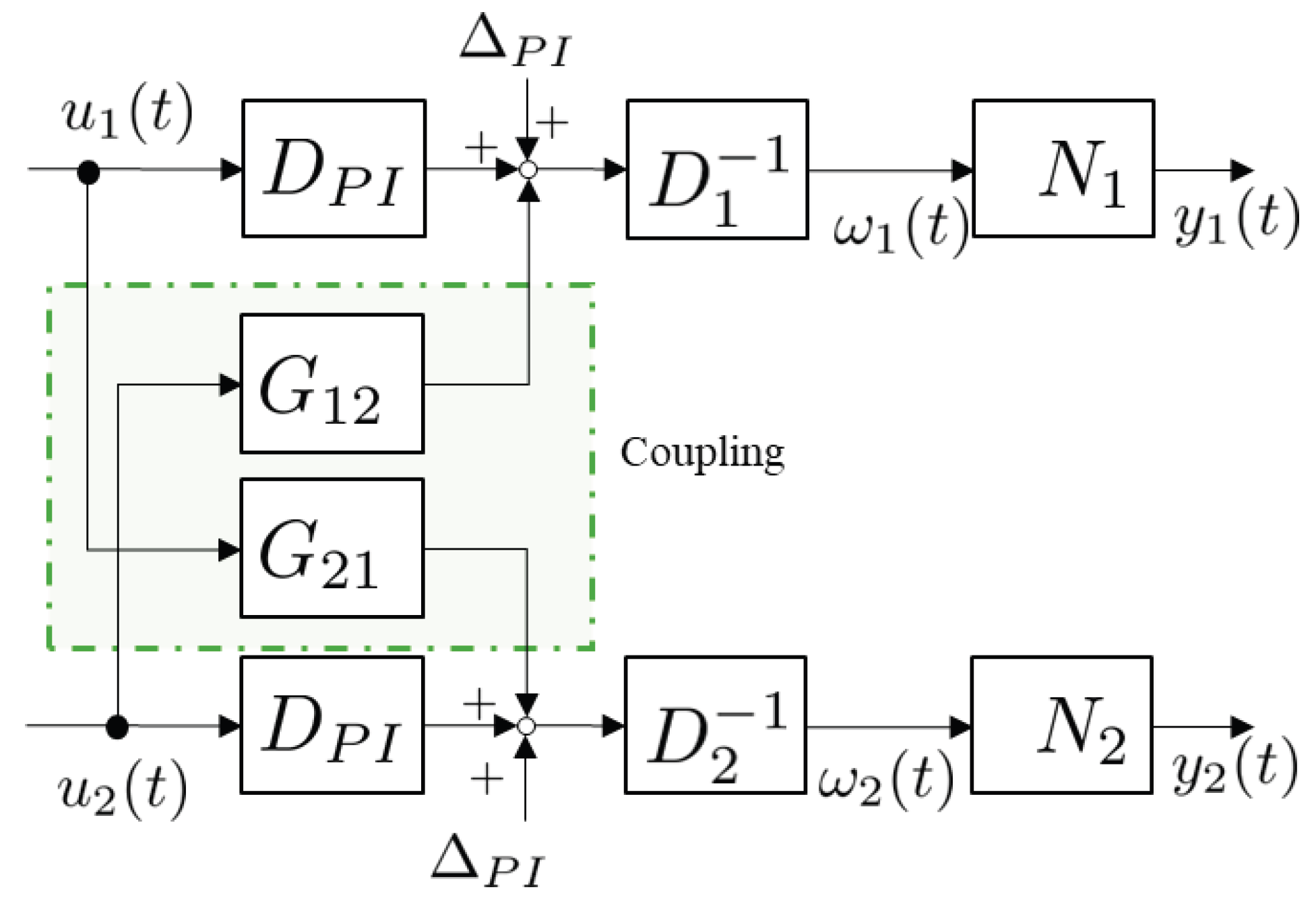
2.3. Problem Statement
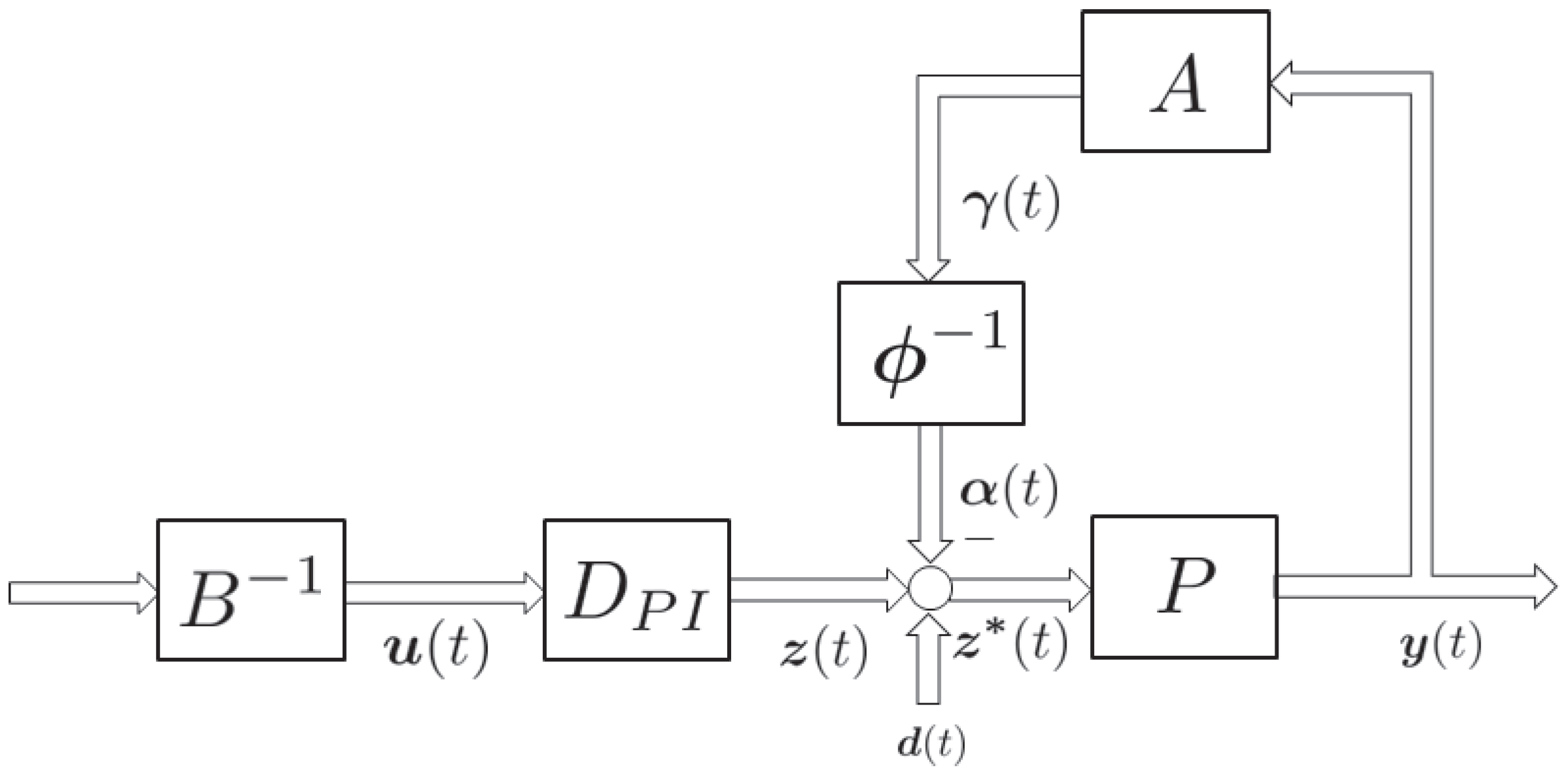
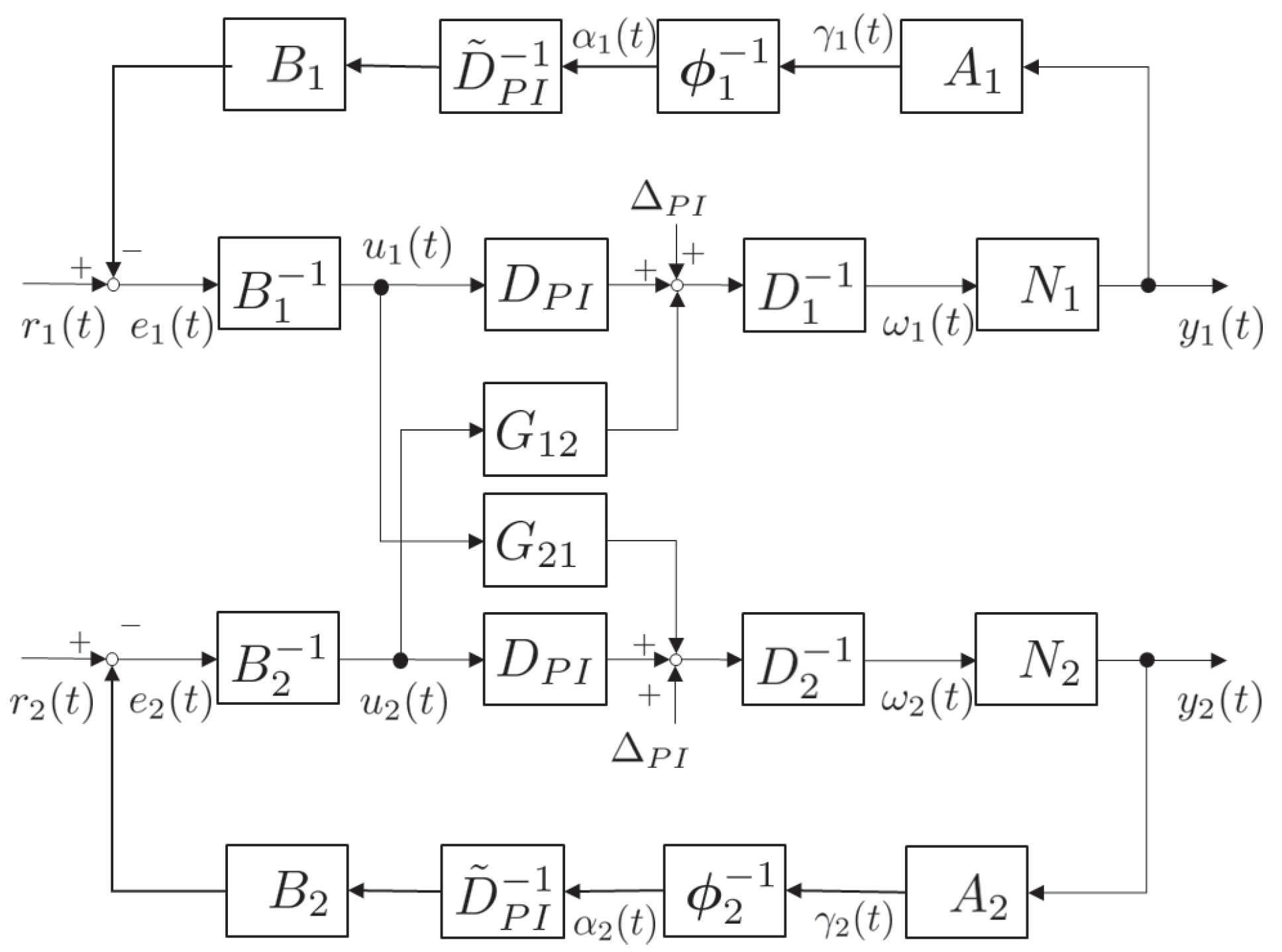
3. Control System Design
Design of the Operator
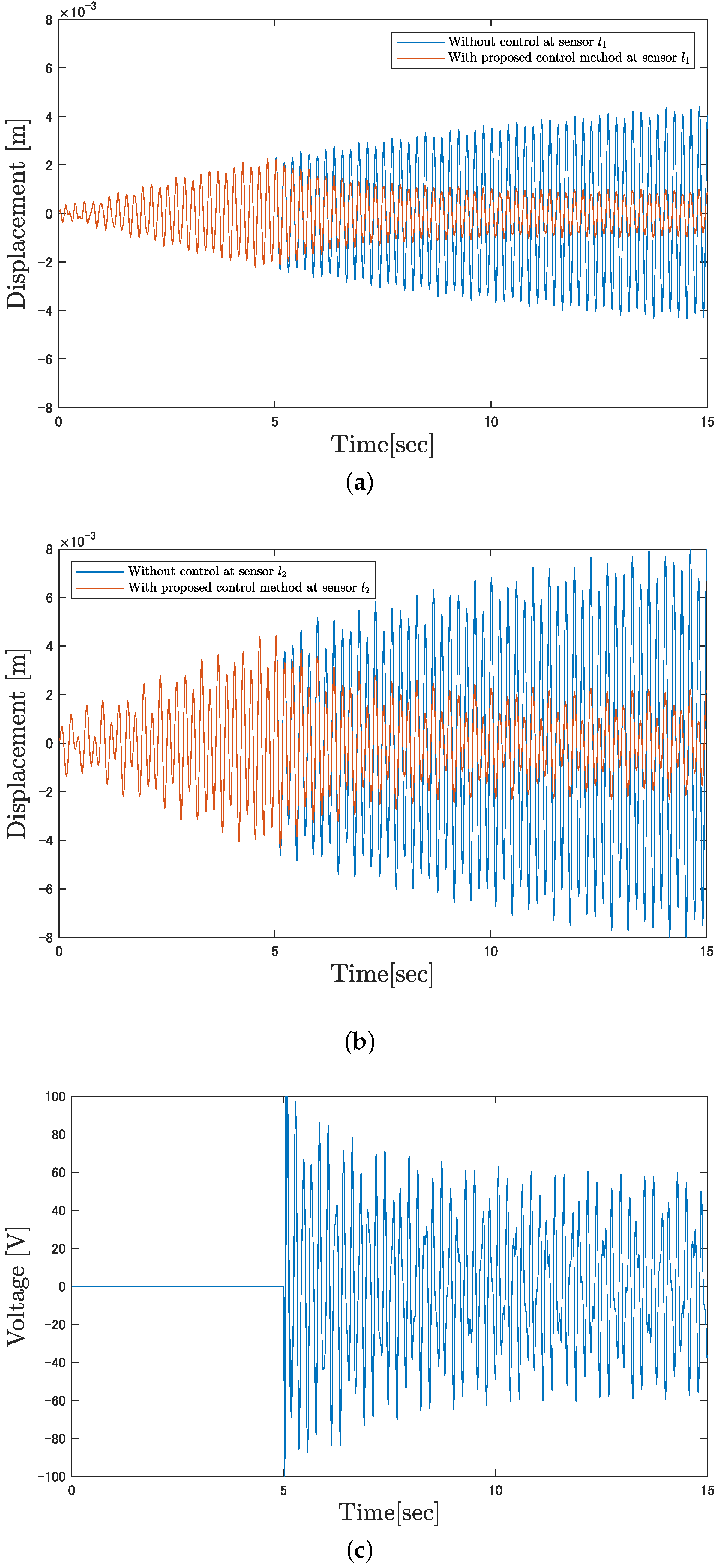
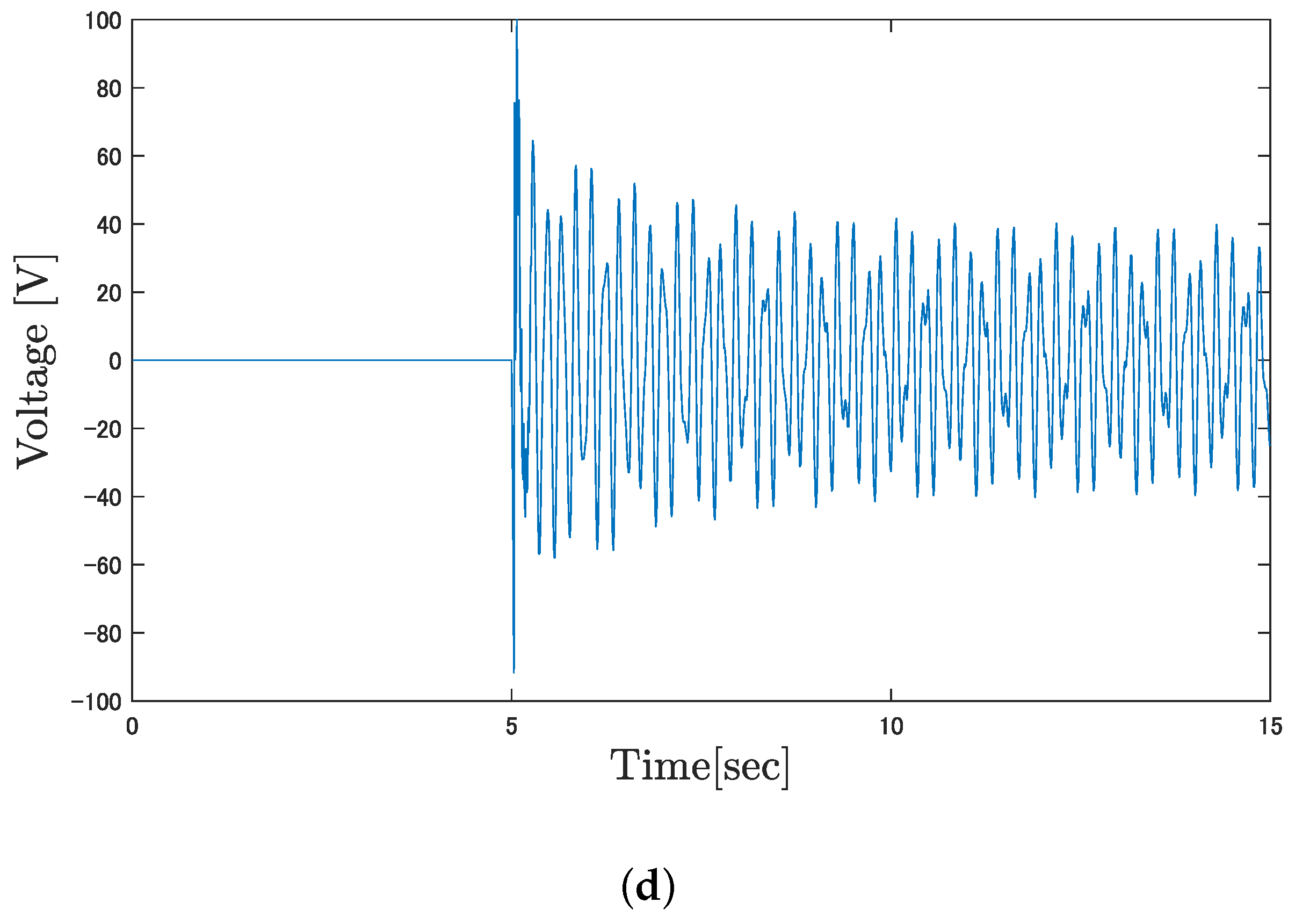
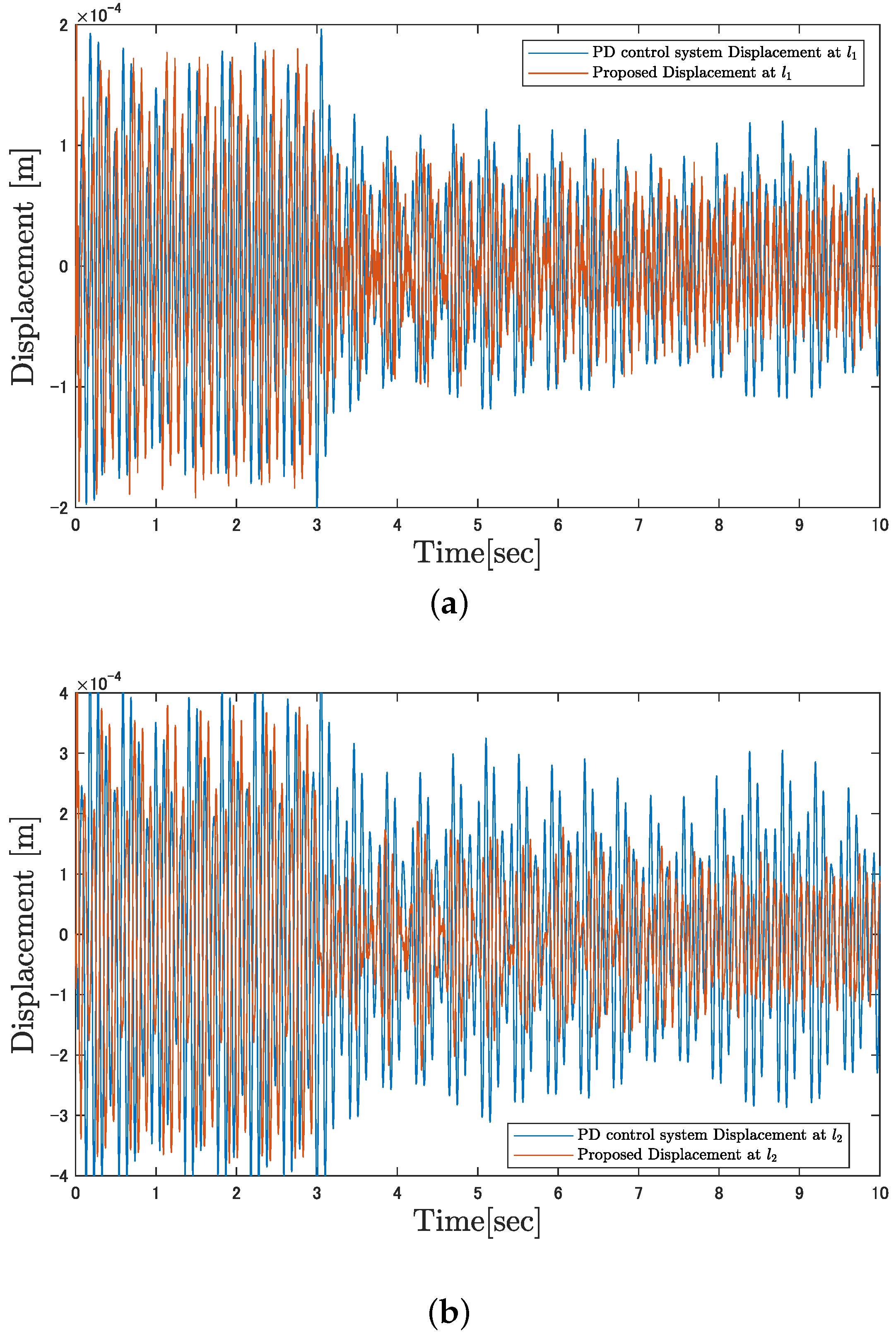
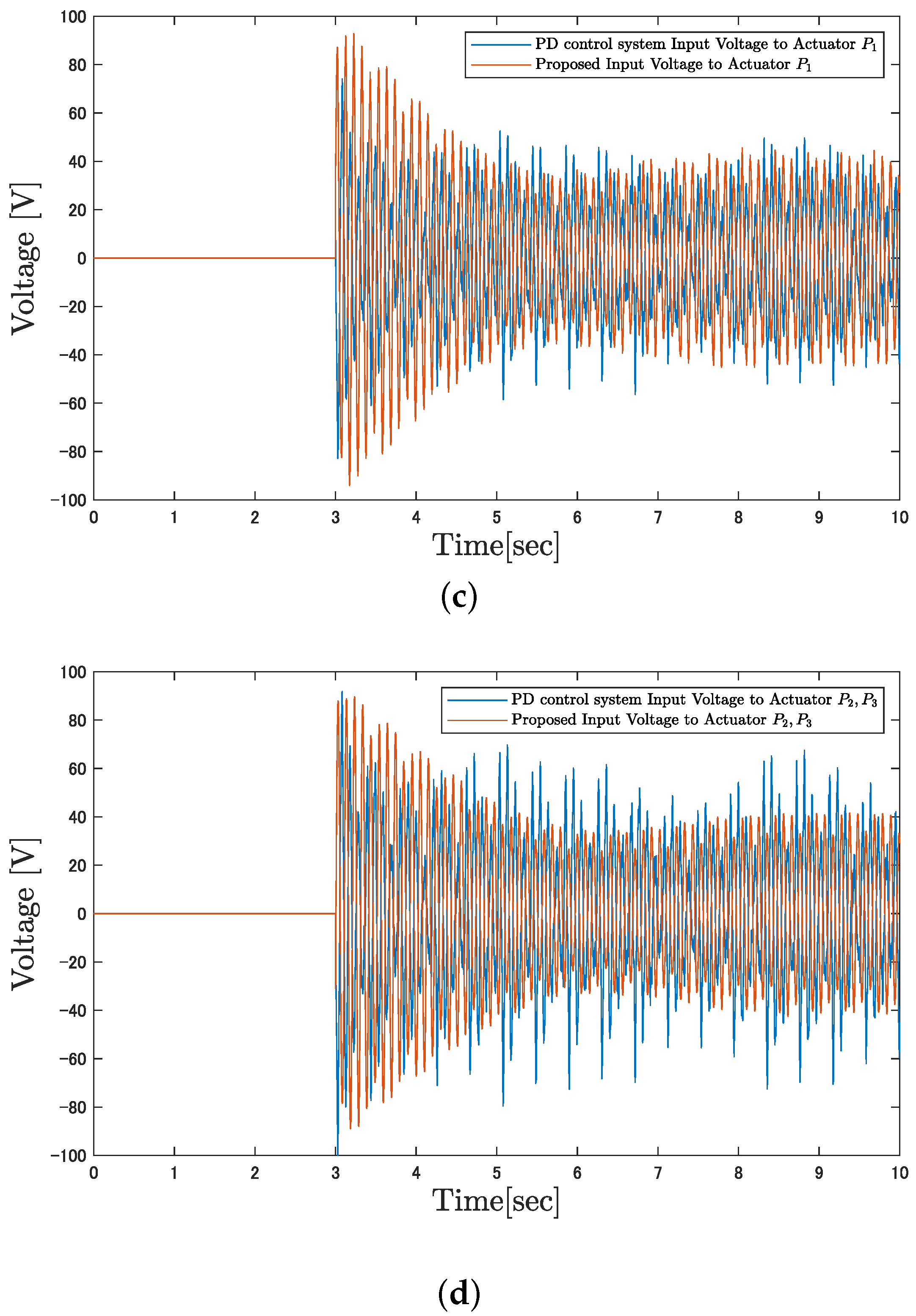
4. Simulation and Experiment
4.1. Simulation Results
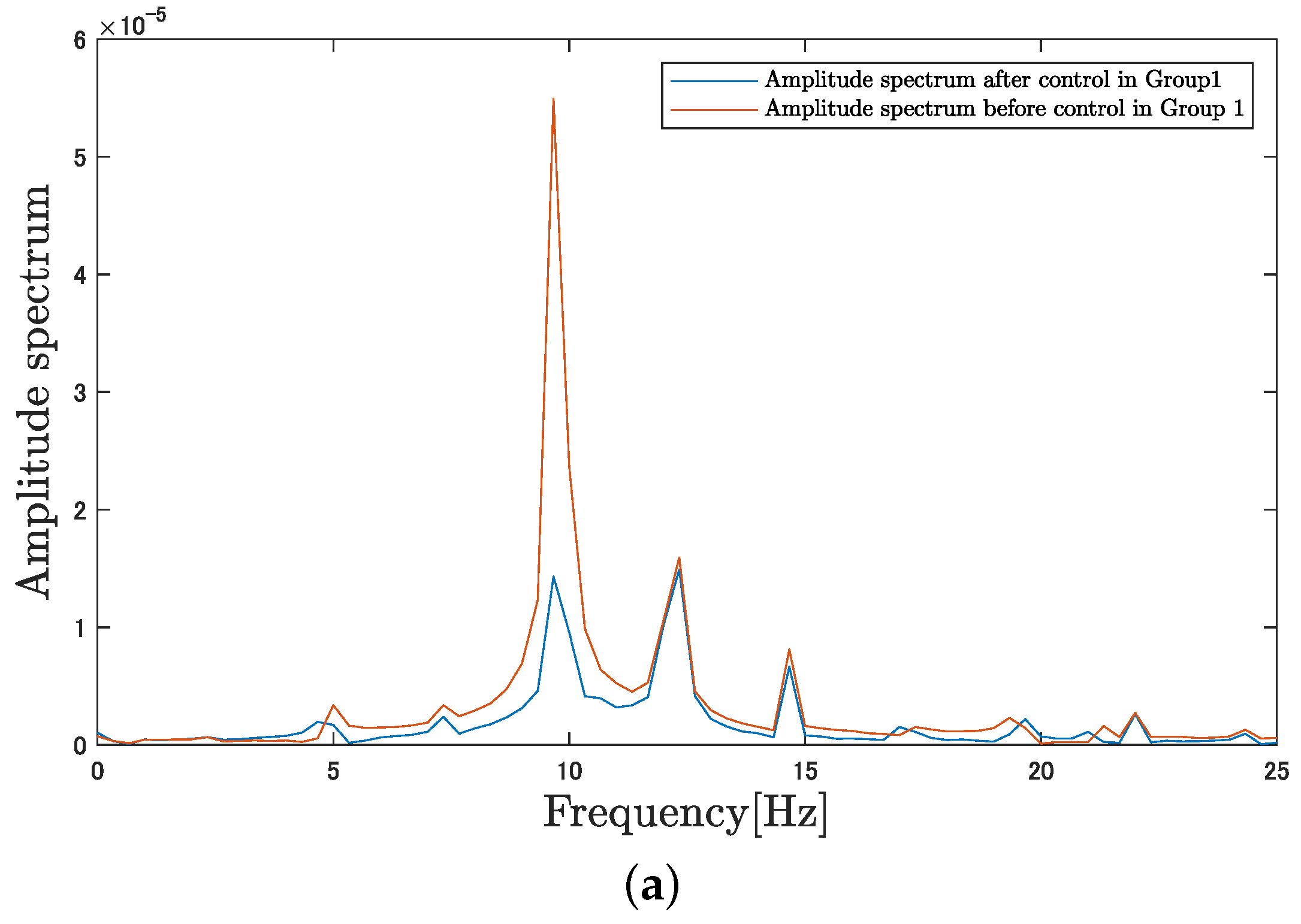
4.2. Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MIMO | Multi-input multi-output |
| M-SVR | Multi-output support vector regression |
References
- Trolier-McKinstry, S.; Newnham, R.E. Sensors, Actuators, and Smart Materials. MRS Bull. 1993, 18, 27–33. [Google Scholar] [CrossRef]
- Deng, Z.; Dapino, M.J. Review of magnetostrictive materials for structural vibration control. Smart Mater. Struct. 2018, 27, 113001. [Google Scholar] [CrossRef]
- Kumar, D.; Daudpoto, J.; Chowdhry, B.S. Challenges for practical applications of shape memory alloy actuators. Mater. Res. Express 2020, 7, 073001. [Google Scholar] [CrossRef]
- Kuhnen, K. Modelingidentification and compensation of complex hysteretic nonlinearities: A modified Prandtl-Ishlinskii approach. Eur. J. Control 2003, 9, 407–418. [Google Scholar] [CrossRef]
- Su, C.Y.; Wang, Q.; Chen, X.; Rakheja, S. Adaptive variable structure control of a class of nonlinear systems with unknown Prandtl-Ishlinskii hysteresis. IEEE Trans. Autom. Control 2005, 50, 2069–2074. [Google Scholar]
- Janaideh, M.A.; Su, C.Y.; Rakheja, S. Development of the rate-dependent Prandtl-Ishlinskii model for smart actuators. Smart Mater. Struct. 2008, 17, 035026. [Google Scholar] [CrossRef]
- Bailey, T.; Hubbart, J.E. Distributed piezoelectric polymer active vibration control of a cantilever beam. J. Guid. Control Dyn. 1985, 8, 605–611. [Google Scholar] [CrossRef]
- Dimitriadis, E.; Fuller, C.; Rogers, C. Piezoelectric actuators for distributed vibration excitation of thin plates. J. Vib. Acoust. 1991, 113, 100–107. [Google Scholar] [CrossRef]
- Wu, Y.; Yu, X.; Man, Z. Terminal sliding mode control design for uncertain dynamic systems. Syst. Control Lett. 1998, 34, 281–287. [Google Scholar] [CrossRef]
- Yu, X.; Okyay, K. Sliding-Mode Control with Soft Computing: A Survey. IEEE Trans. Ind. Electron. 2009, 56, 3275–3285. [Google Scholar]
- Rigatos, G.; Siano, P.; Melkikh, A.; Zervos, N. A Nonlinear H-Infinity Control Approach to Stabilization of Distributed Synchronous Generators. IEEE Syst. J. 2018, 12, 2654–2663. [Google Scholar] [CrossRef]
- Cheung, Y.L.; Wong, W.O. H-infinity optimization of a variant design of the dynamic vibration absorber—Revisited and new results. J. Sound Vib. 2011, 330, 3901–3912. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Jheng, H.-W. Active Vibration Suppression of a Motor-Driven Piezoelectric Smart Structure Using Adaptive Fuzzy Sliding Mode Control and Repetitive Control. Appl. Sci. 2017, 7, 240. [Google Scholar] [CrossRef]
- Hashemi, A.; Jang, J.; Hosseini-Hashemi, S. Smart Active Vibration Control System of a Rotary Structure Using Piezoelectric Materials. Sensors 2022, 22, 5691. [Google Scholar] [CrossRef] [PubMed]
- Deng, M.; Inoue, A.; Ishikawa, K. Operator-based nonlinear feedback controldesign using robust right coprime factorization. IEEE Trans. Autom. 2006, 51, 645–648. [Google Scholar] [CrossRef]
- Deng, M.; Saijo, N.; Gomi, H.; Inoue, A. A robust real ime method for estimating human multijoint arm viscoelasticity. Int. J. Innov. Comput. Control 2006, 2, 705–721. [Google Scholar]
- Furukawa, I.; Deng, M. Multiple feedback loops based nonlinear vibration control of a flexible arm with shape memory alloy actuator. In Proceedings of the International Conference on Advanced Mechatronic Systems, Toyama, Japan, 17–20 December 2022; pp. 183–188. [Google Scholar]
- Masuda, K.; Jin, G.; Deng, M. Nonlinear vibration control of MIMO flat plate system considering interference model using M-SVR. In Proceedings of the Technical Meeting on Control, IEEE, Tasmania, Australia, 11 September 2023; pp. 29–33. (In Japanese). [Google Scholar]
- Deng, M.; Inoue, A.; Goto, S. Operator based Thermal Control of an Aluminum Plate with a Peltier Device. In Proceedings of the Second International Conference on Innovative Computing, Information and Control (ICICIC 2007), Kumamoto, Japan, 5–7 September 2007; p. 319. [Google Scholar]
- Deng, M.; Inoue, A.; Zhu, Q. An integrated study procedure on real-time estimation of time-varying multi-joint human arm viscoelasticity. Trans. Inst. Meas. Control 2011, 33, 919–941. [Google Scholar] [CrossRef]
- Wang, A.; Deng, M. Operator-based robust nonlinear tracking control for a human multi-joint arm-like manipulator with unknown time-varying delays. Appl. Math. Inf. Sci. 2012, 6, 459–468. [Google Scholar]
- Nakagawa, T.; Katsurayama, Y.; Deng, M.; Wakitani, S. Nonlinear Vibration Control for an Aircraft Vertical Tail by Using Operator-based Estimation. In Proceedings of the 5th International Symposium on Advanced Control of Industrial Processes (ADCONIP 2014), Hiroshima, Japan, 28–30 May 2014; pp. 403–408. [Google Scholar]
- Krejčí, P.; Sprekels, J. Elastic-ideally plastic beams and Prandtl-Ishlinskii hysteresis operators. Math. Methods Appl. Sci. 2007, 30, 2371–2393. [Google Scholar] [CrossRef]
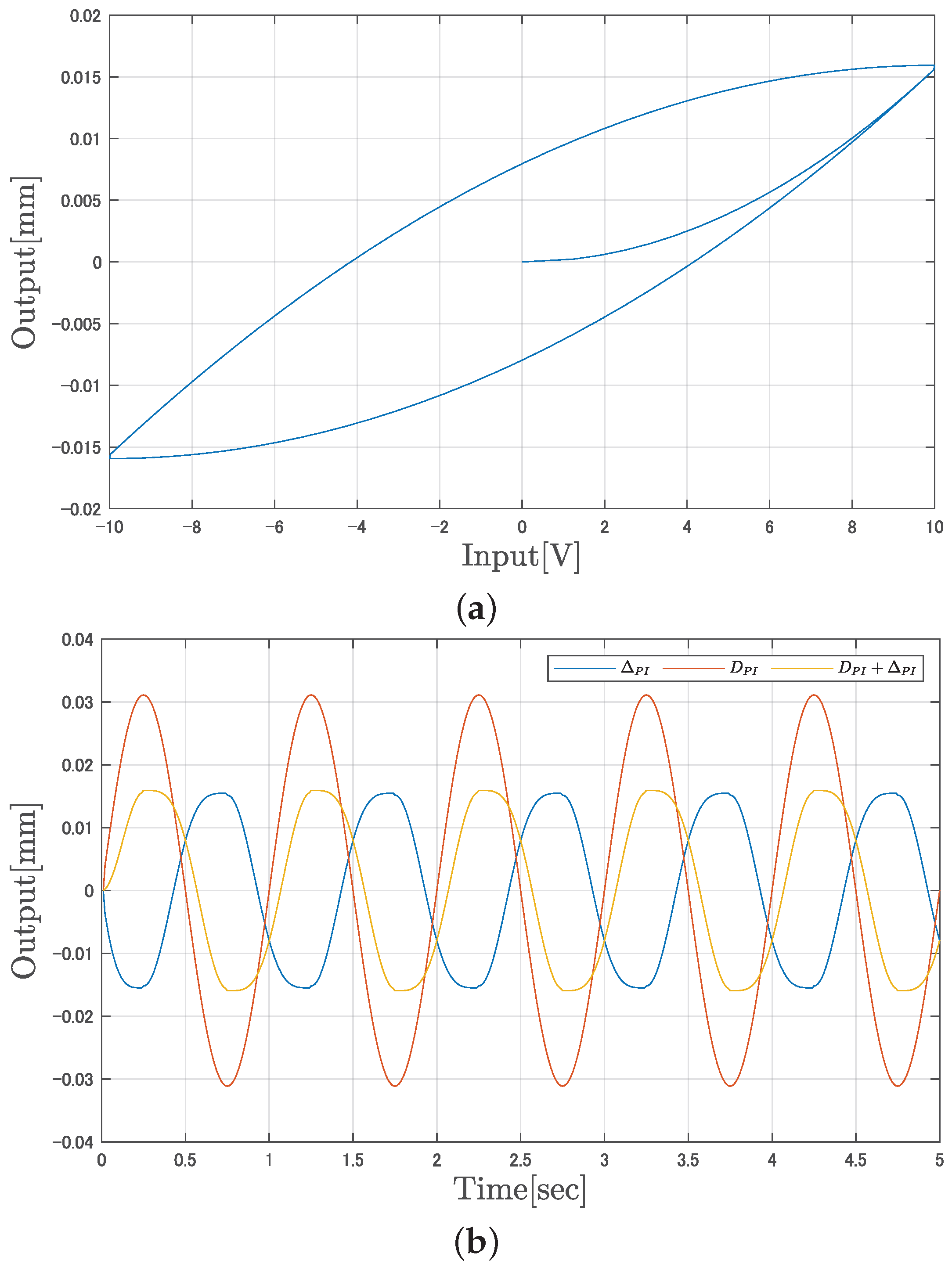



| Parameter | Definition | Value |
|---|---|---|
| a | Length of the plate in the direction | |
| b | Length of the plate in the direction | |
| l | Distance from the servo motor to the plate | |
| Strain | − | |
| u | Deflection in the x direction | |
| v | Deflection in the y direction | |
| Shear strain | − | |
| w | Deflection in the z direction | |
| Stress | ||
| E | Young’s Modulus of a plate | |
| Poisson’s ratio | ||
| Shear stress | ||
| G | Modulus of rigidity | |
| M | Bending moment | |
| Thickness of the plate | ||
| Bending stiffness | ||
| V | Shear force | |
| Density of the plate | ||
| m | Moment | |
| t | Time | |
| Damping coefficient | ||
| R | The threshold of the Play hysteresis operator | 100 |
| Young’s Modulus of actuators |
| Parameter | Definition | Value |
|---|---|---|
| T | Sampling time | |
| Learning rate | ||
| Learning rate | ||
| Parameter for | ||
| Parameter for | ||
| Parameter for | ||
| Parameter for | ||
| Parameter for | ||
| Parameter for | ||
| Designed parameters for | ||
| Designed parameters for |
| Parameter | Definition | Value |
|---|---|---|
| T | Sampling time | |
| Learning rate | ||
| Learning rate | ||
| Parameter for | ||
| Parameter for | ||
| Parameter for | ||
| Parameter for | ||
| Parameter for | ||
| Parameter for | ||
| Designed parameters for | ||
| Designed parameters for | ||
| Designed parameters for PD system at Group 1 | ||
| Designed parameters for PD system at Group 2 | ||
| Designed parameters for PD system at Group 1 | 230 | |
| Designed parameters for PD system at Group 2 | 150 |
| Control Group | |||
|---|---|---|---|
| Group 1 | |||
| Group 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsukioka, M.; Jin, G.; Deng, M. Nonlinear Control System for Flat Plate Structures Considering Interference Based on Operator Theory and Optimization Method. Electronics 2024, 13, 4265. https://doi.org/10.3390/electronics13214265
Tsukioka M, Jin G, Deng M. Nonlinear Control System for Flat Plate Structures Considering Interference Based on Operator Theory and Optimization Method. Electronics. 2024; 13(21):4265. https://doi.org/10.3390/electronics13214265
Chicago/Turabian StyleTsukioka, Masayoshi, Guang Jin, and Mingcong Deng. 2024. "Nonlinear Control System for Flat Plate Structures Considering Interference Based on Operator Theory and Optimization Method" Electronics 13, no. 21: 4265. https://doi.org/10.3390/electronics13214265
APA StyleTsukioka, M., Jin, G., & Deng, M. (2024). Nonlinear Control System for Flat Plate Structures Considering Interference Based on Operator Theory and Optimization Method. Electronics, 13(21), 4265. https://doi.org/10.3390/electronics13214265









