Energy Harvesting Power Converter for Variable Impedance and Voltage Sources
Abstract
1. Introduction
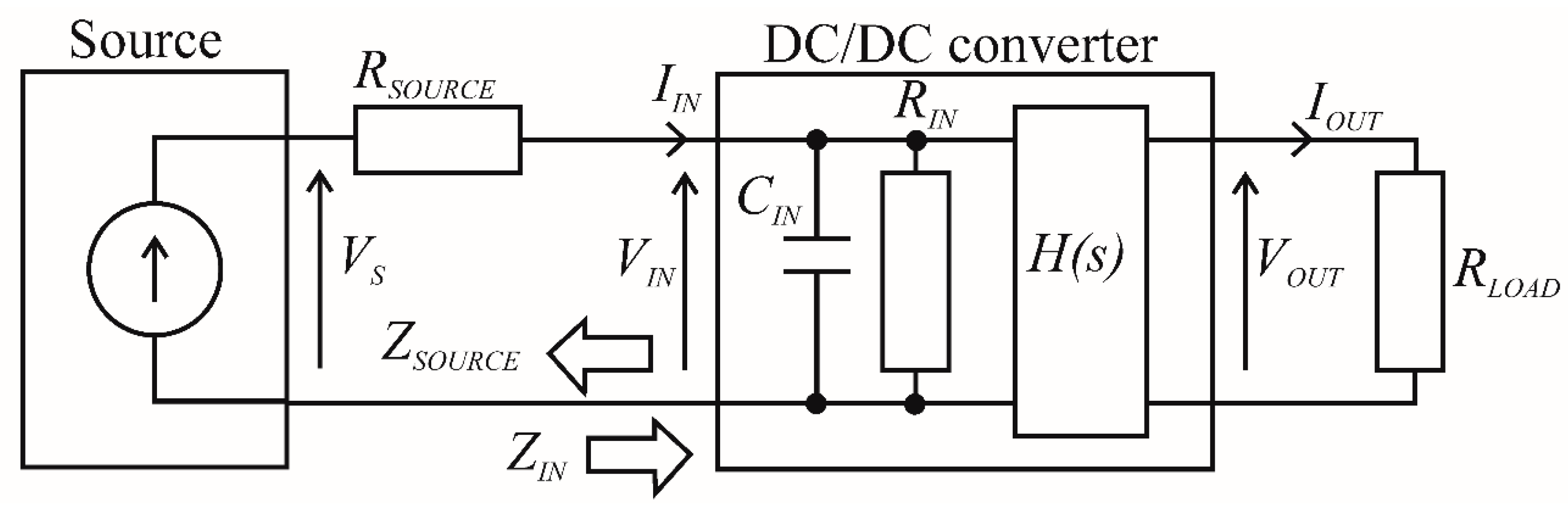
1.1. The Effect of High Source Resistance on DC/DC Converters
1.2. Examples of Converters Operating with High Output Resistance Energy Sources
1.3. The Objectives of the Work
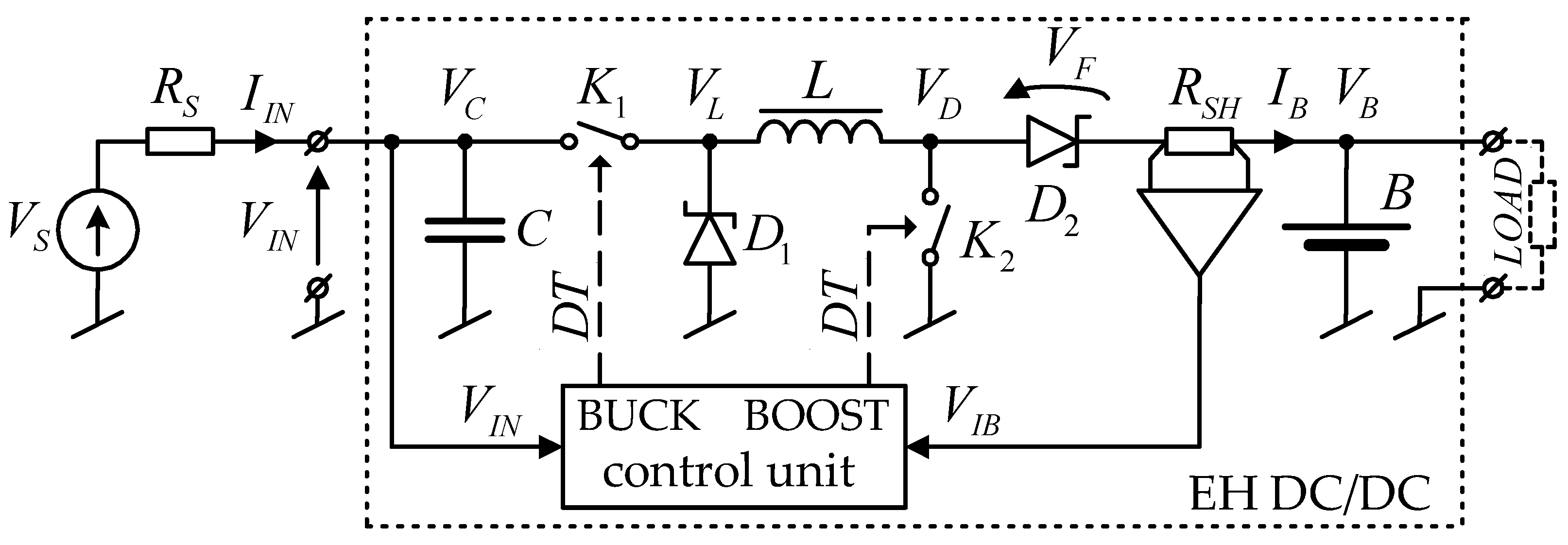
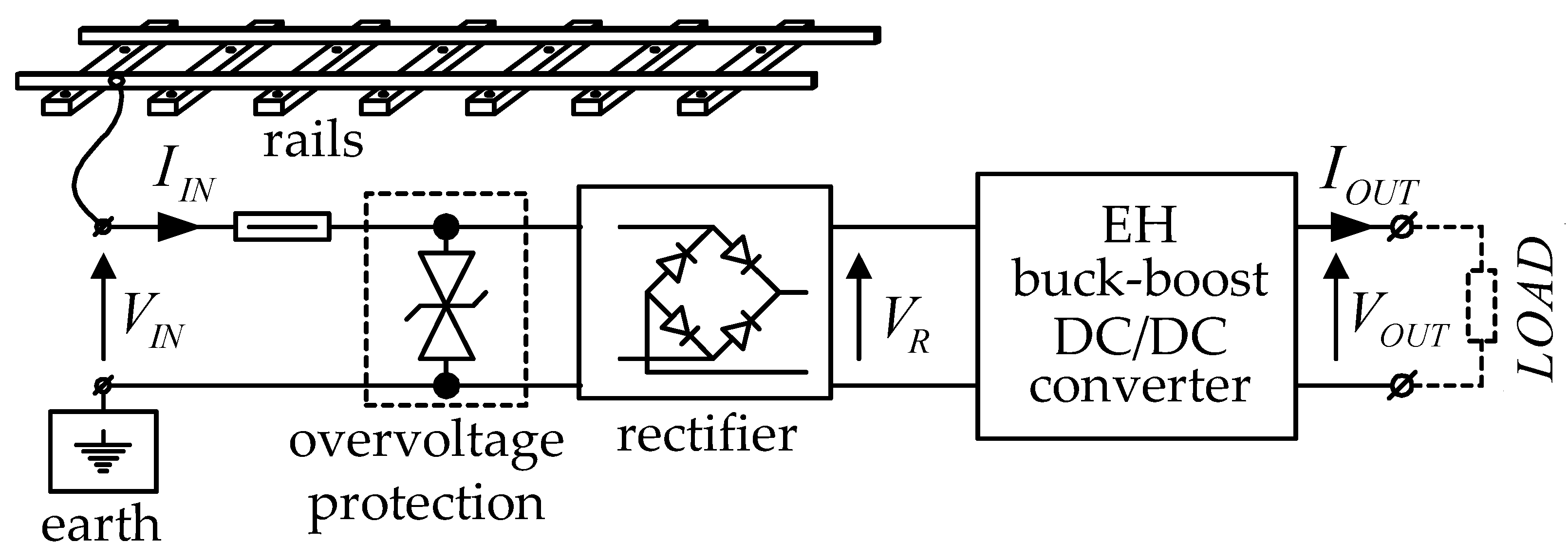
2. Defining the Problem
- Boost mode in which voltage is converted up, switch K1 is turned ON, and K2 is switching;
- Buck mode in which the voltage is converted down, switch K1 is switching, and K2 is turned OFF;
- In a bypass mode when the output voltage is almost half the input voltage, switch K1 is turned ON and K2 is turned OFF.
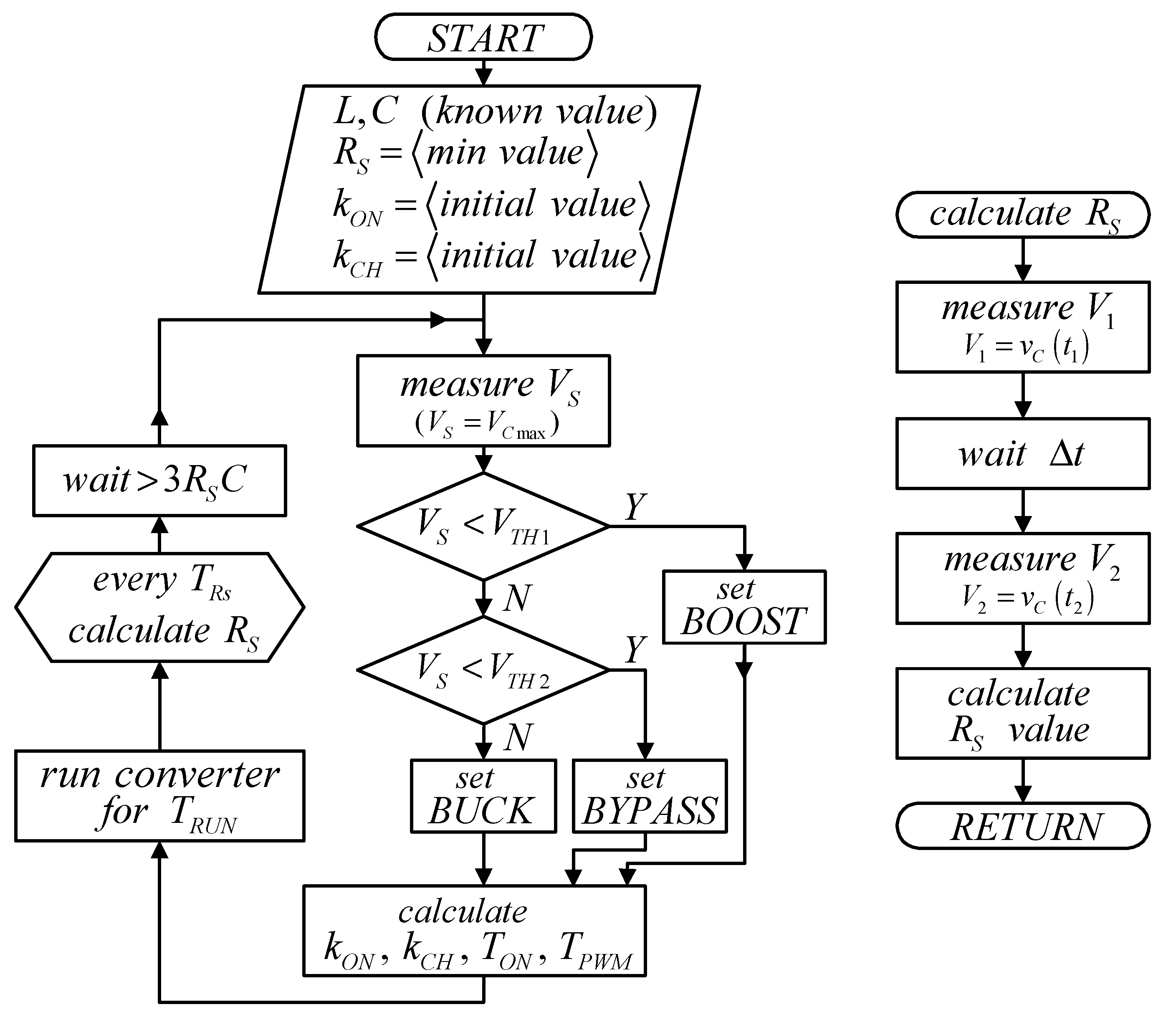
- Estimates the open-circuit voltage and output resistance of the source VS;
- Select the appropriate operating mode of the converter (buck, boost, or bypass);
- Selects the operating frequency of the converter and the duty factor of the control signal of the active switch in a given mode.
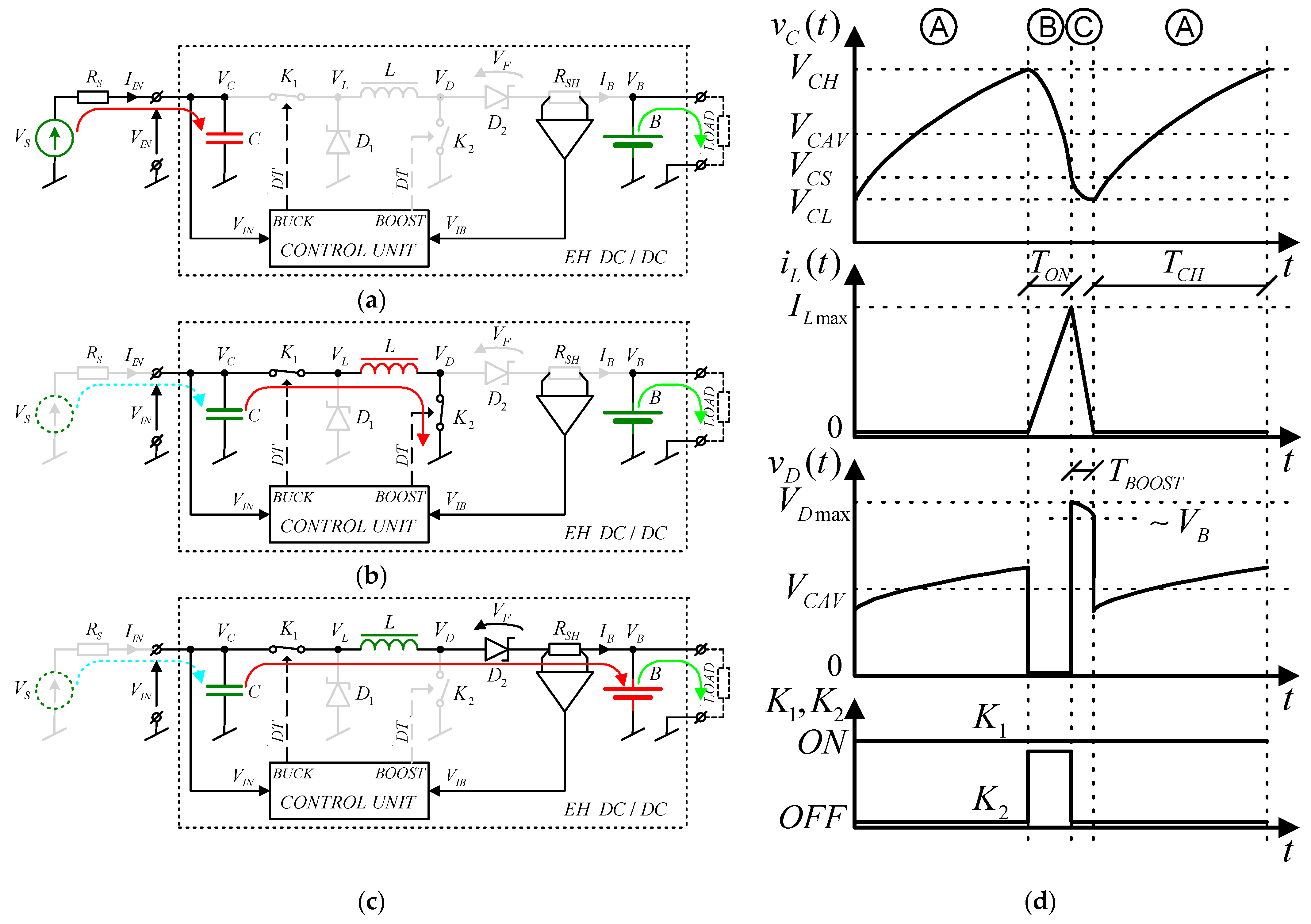
3. Boost Mode Analysis
- Stage A, when switch K2 is turned OFF, the capacitor is charging from the source, and the current of the coil L is zero;
- Stage B, when switch K2 is turned ON and the energy is transferred from capacitor C to inductor L;
- Stage C, when switch K2 is turned OFF, the capacitor is charging from the source, and the energy is transferred from coil L to load and battery B.
3.1. Stage A: Energy Gathering in the Capacitor
3.1.1. Duration of Stage A
3.1.2. Input Voltage
3.2. Stage B: Transferring Energy from Capacitor to Inductor
3.2.1. Input Voltage and Duration of Stage B
3.2.2. Energy Balance
3.3. Stage C: Transferring Energy to the Battery
3.3.1. Input Voltage
3.3.2. Energy Balance
3.3.3. Duration of Stage C
3.4. Determination of the Operating Frequency and the Duty Factor in Boost Mode
4. Buck Mode Analysis
- Stage A, when switch K1 is turned OFF, the capacitor is charging from the source, and at the beginning, the energy is transferred from coil L to load and battery B, and in the second part of this stage the current of coil L is zero;
- Stage B, when switch K1 is turned ON and the energy is transferred from capacitor C to inductor L.
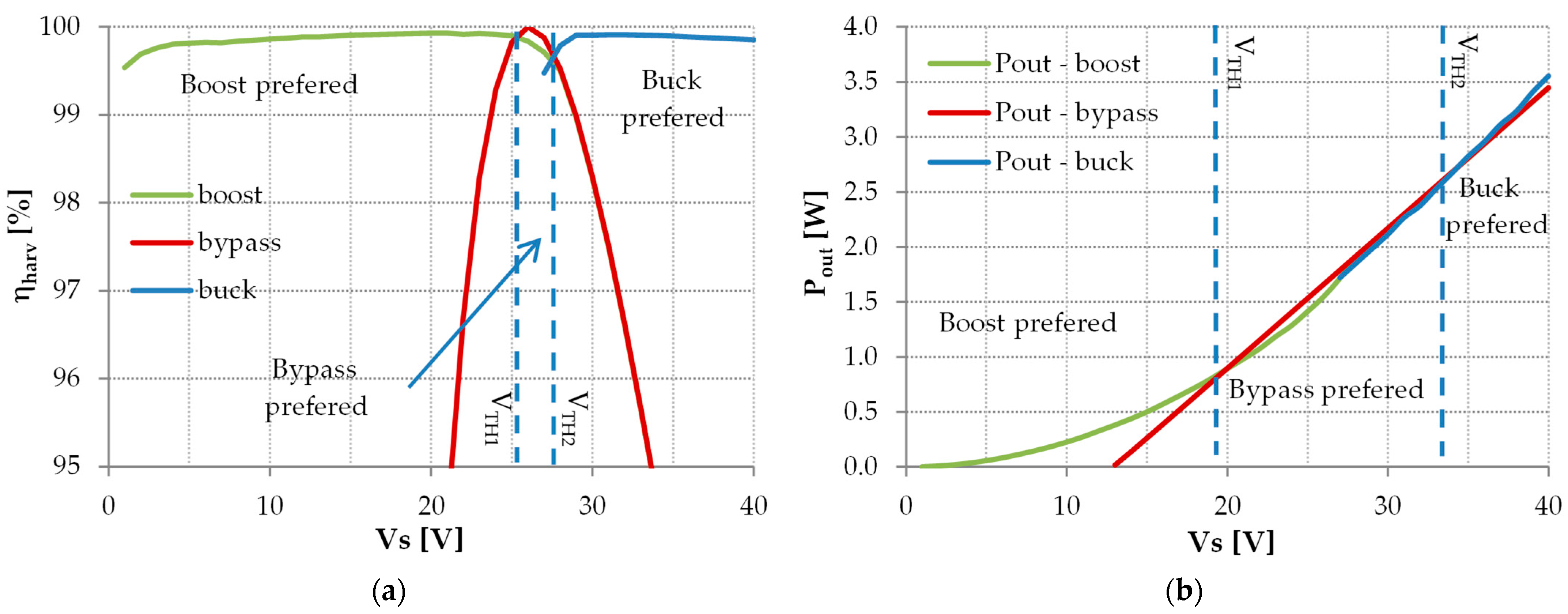
- Buck mode will be used if output voltage VB is significantly lower than input voltage VIN ≈ ½ VS. Noting that switch K2 is always turned OFF in boost mode.
4.1. Stage A: Energy Gathering in the Capacitor
4.2. Stage B: Transferring Energy to Inductor and Battery
4.3. Determination of the Operating Frequency and the Duty Factor in Boost Mode
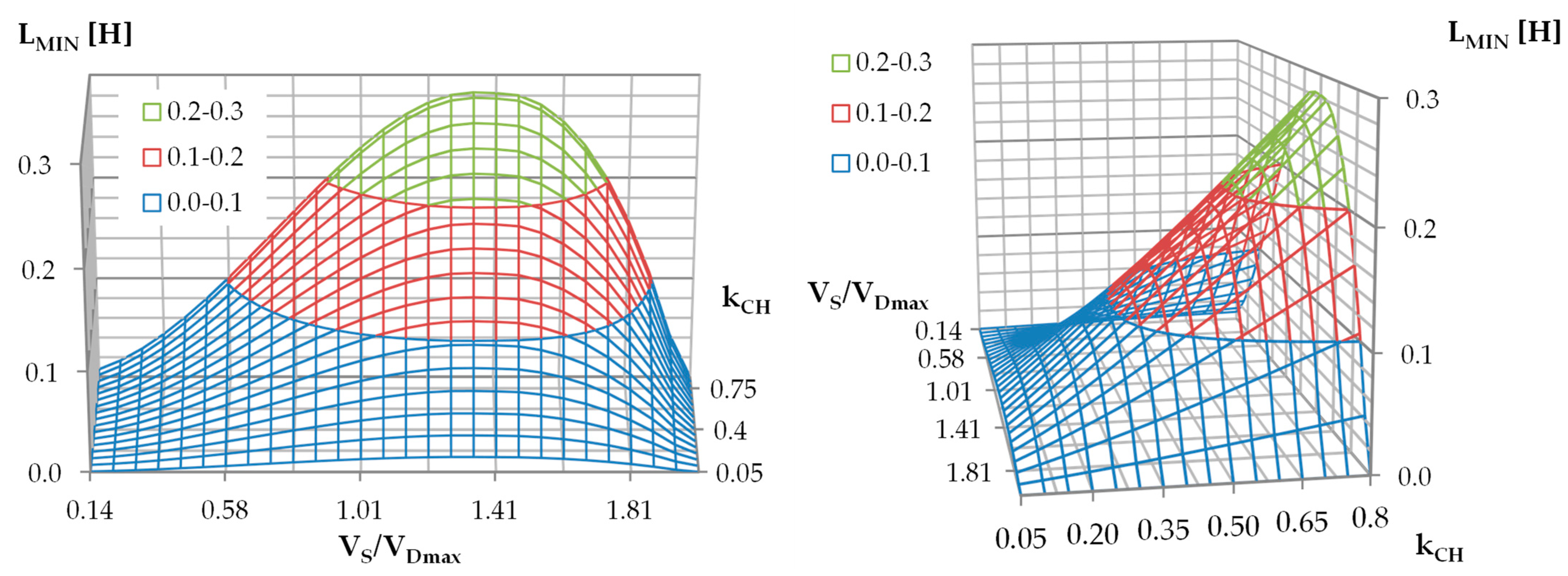
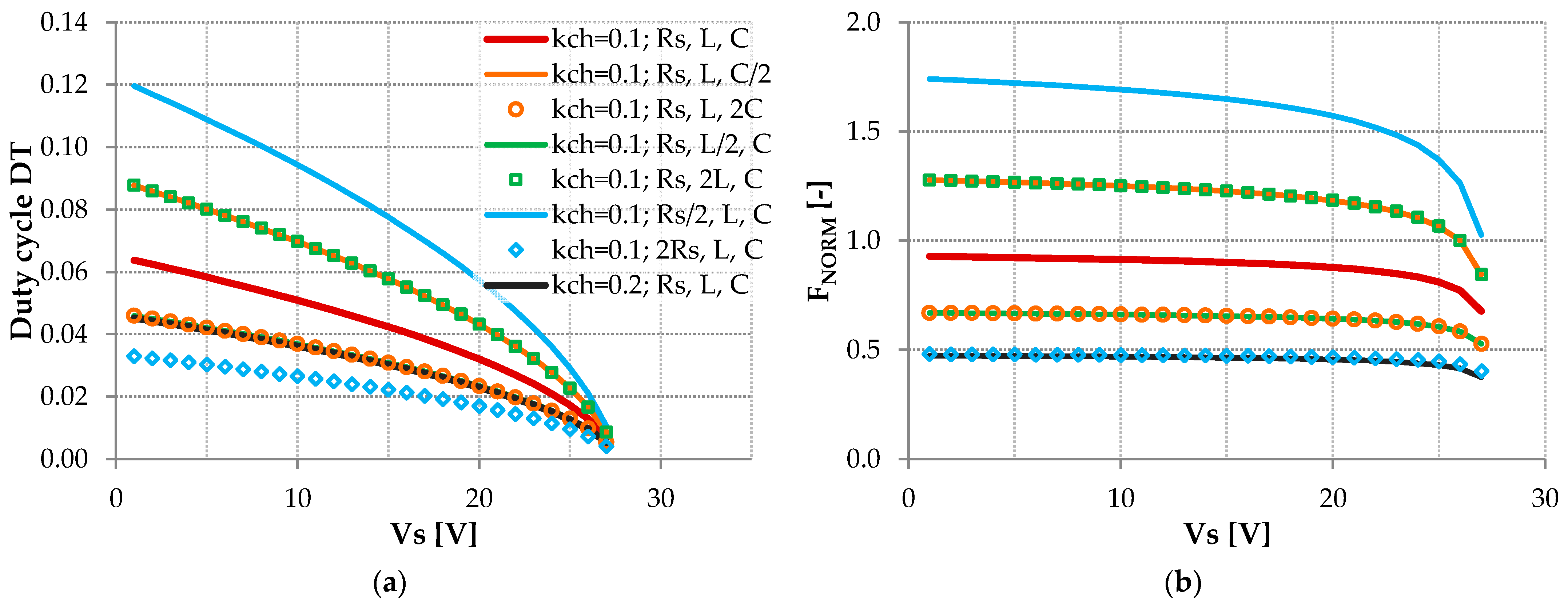
5. Design Recommendations—How to Choose L and C
Example of Choosing the Capacitor C and the Coil L
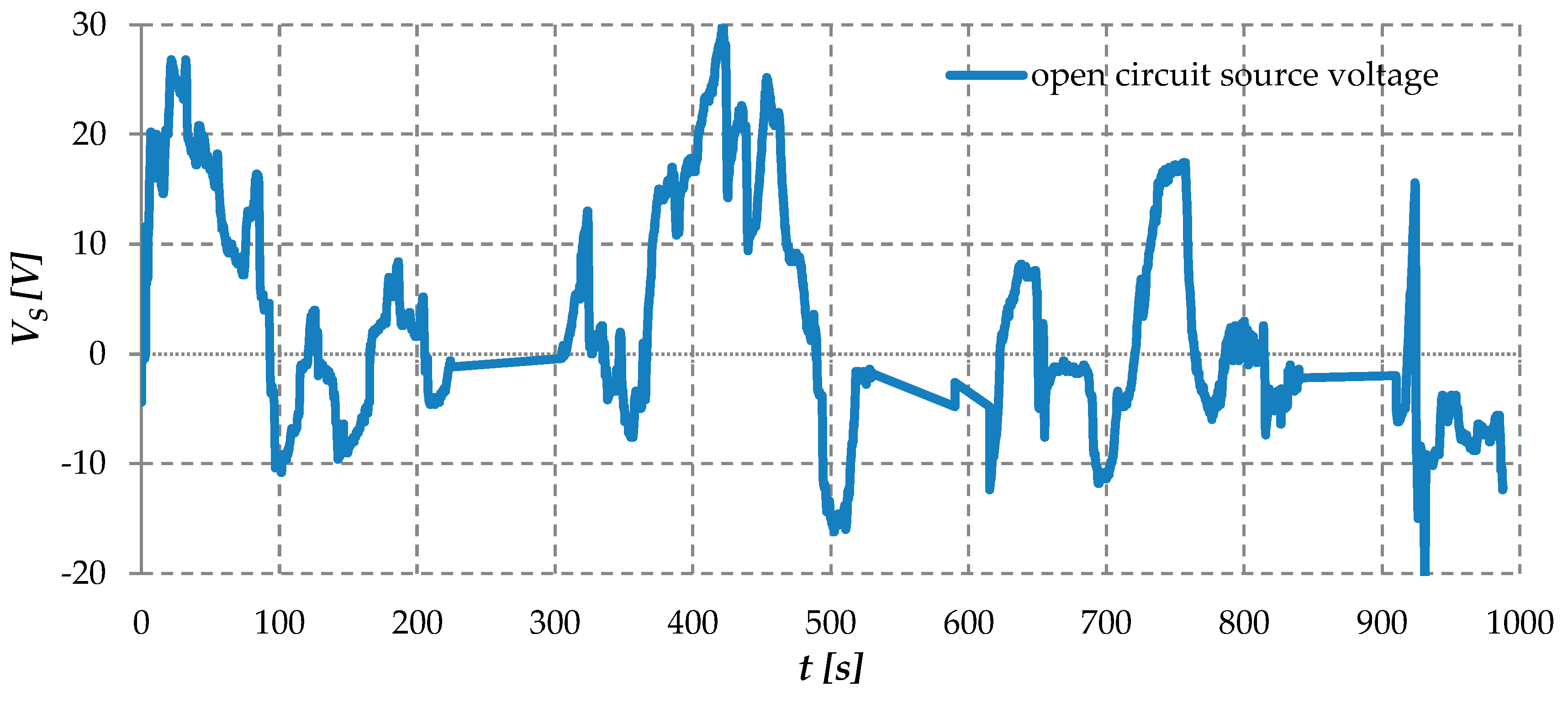
- the open-circuit voltage of the source VS is less than 40 V and changes with slew rate SRS of less than 10 V/s;
- a minimum usable open-circuit voltage VSmin of 2 V;
- source resistance from RS_min = 50 Ω to RS_max = 200 Ω and rate of change much slower than 1 Ω/s.
- The requirements for a converter are as follows:
- an output voltage VB of 12.8 V;
- the voltage drop across the diode VF of 1.0 V;
- a maximum coil current ILmax of 3 A;
- a maximum ratio of amplitude VCpp to open-circuit voltage VS of 10%;
- operating frequency f less than 4 kHz.
6. Control Algorithm
6.1. Measuring the Power Source Parameters
6.2. Choosing the Operating Mode
6.3. Determining Frequency and Duty Factor of the Control Signal
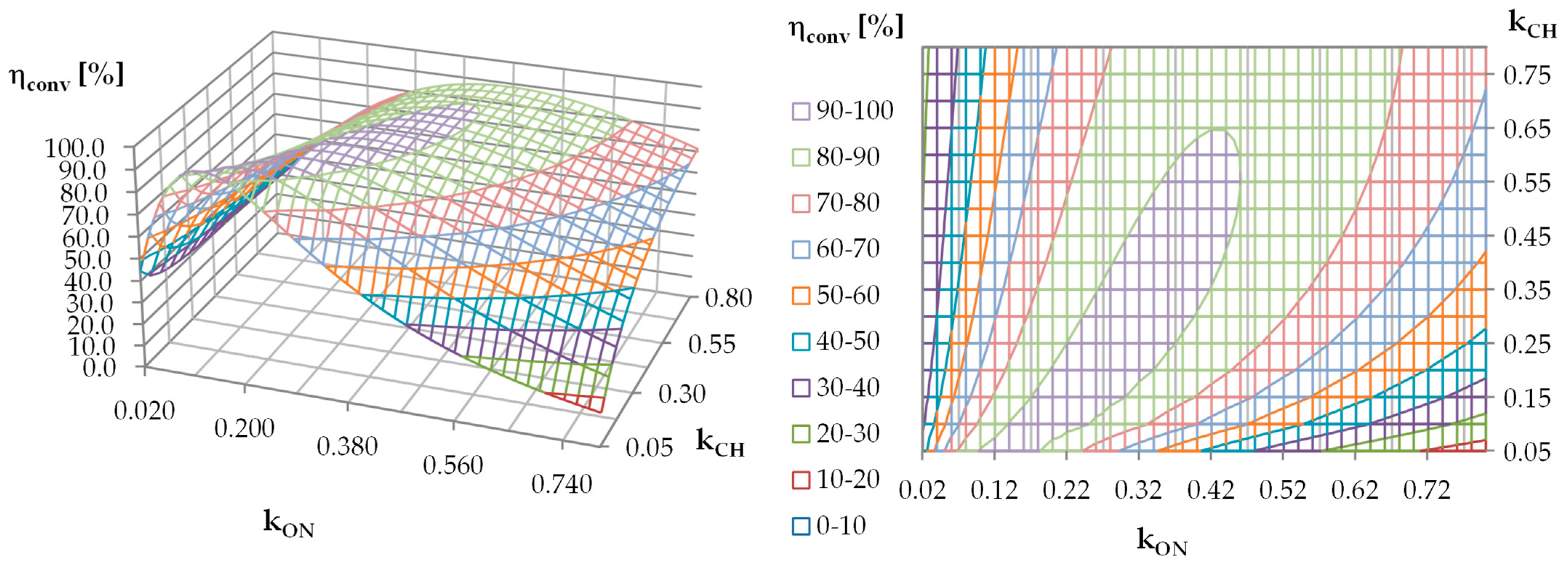
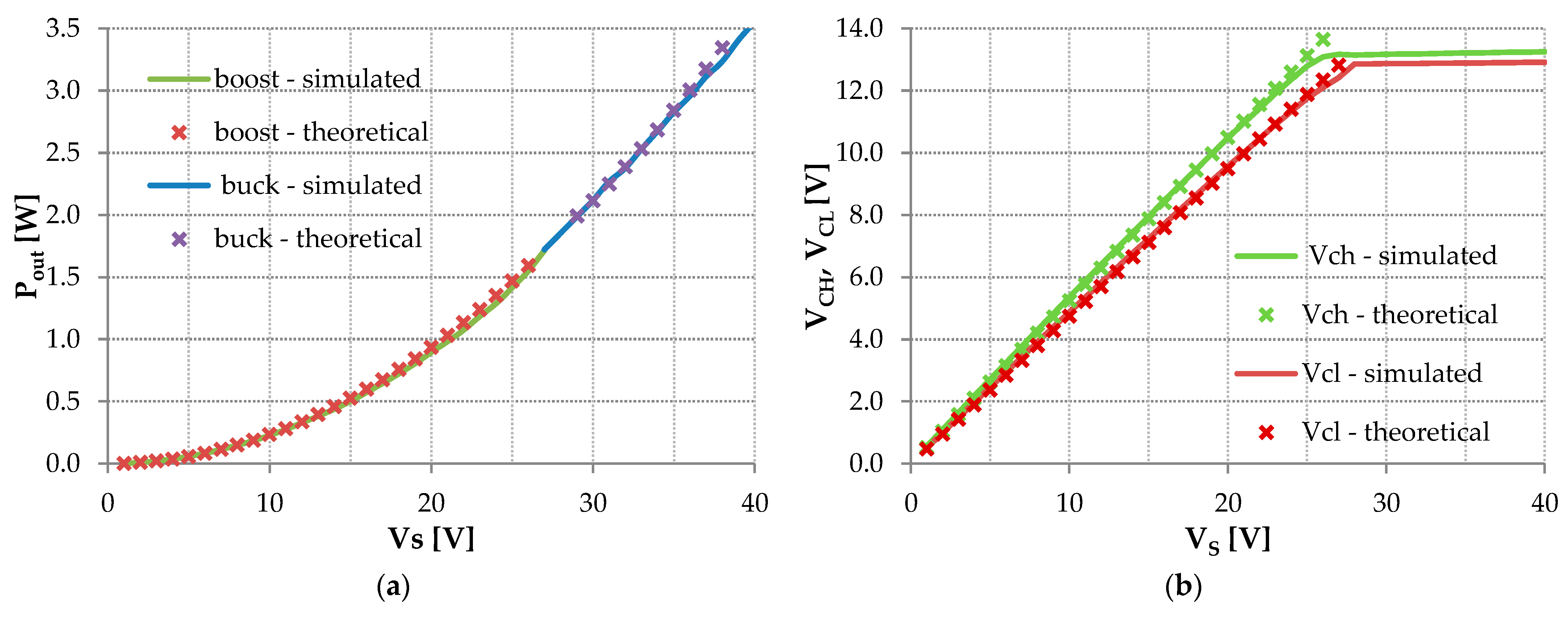
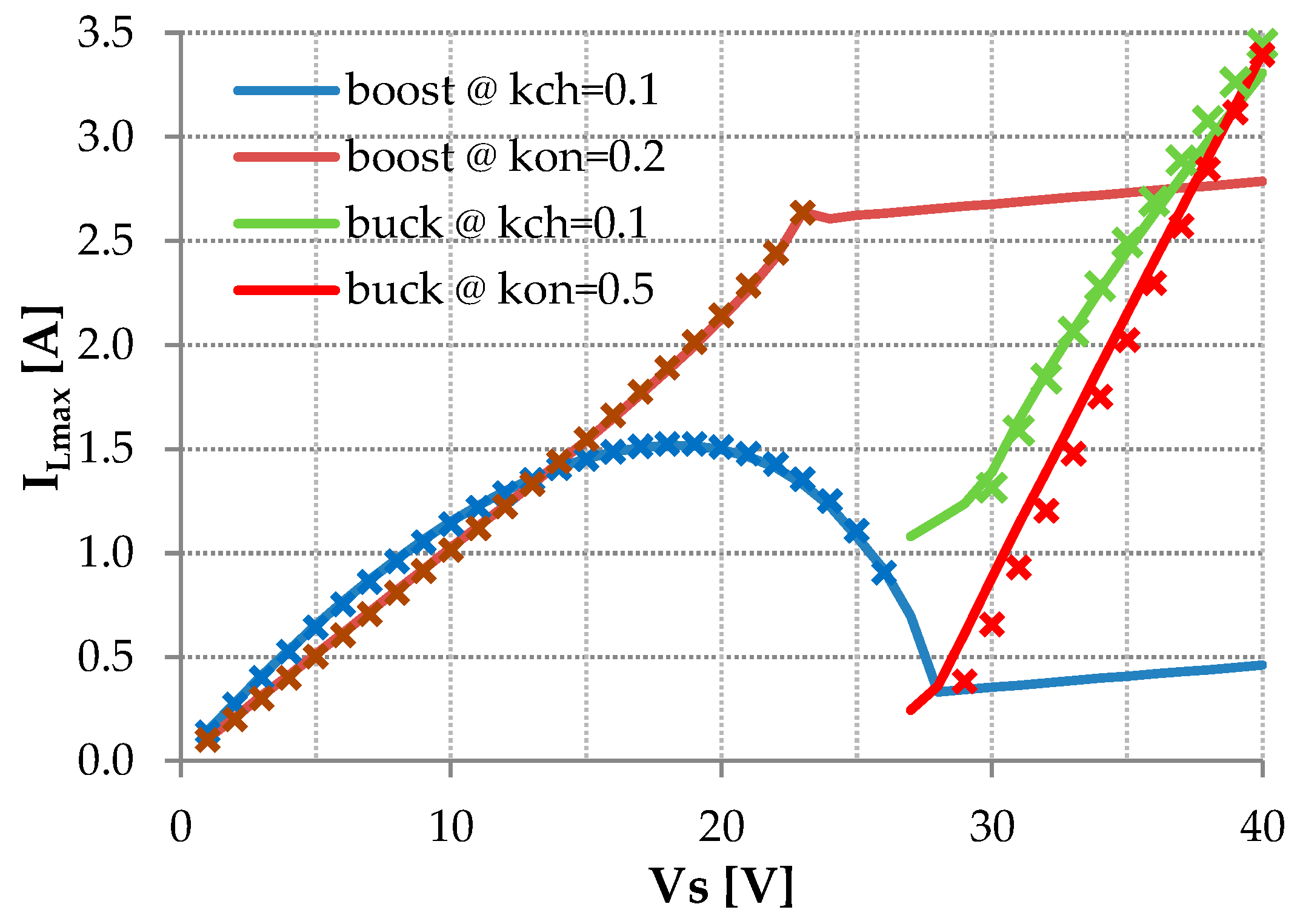
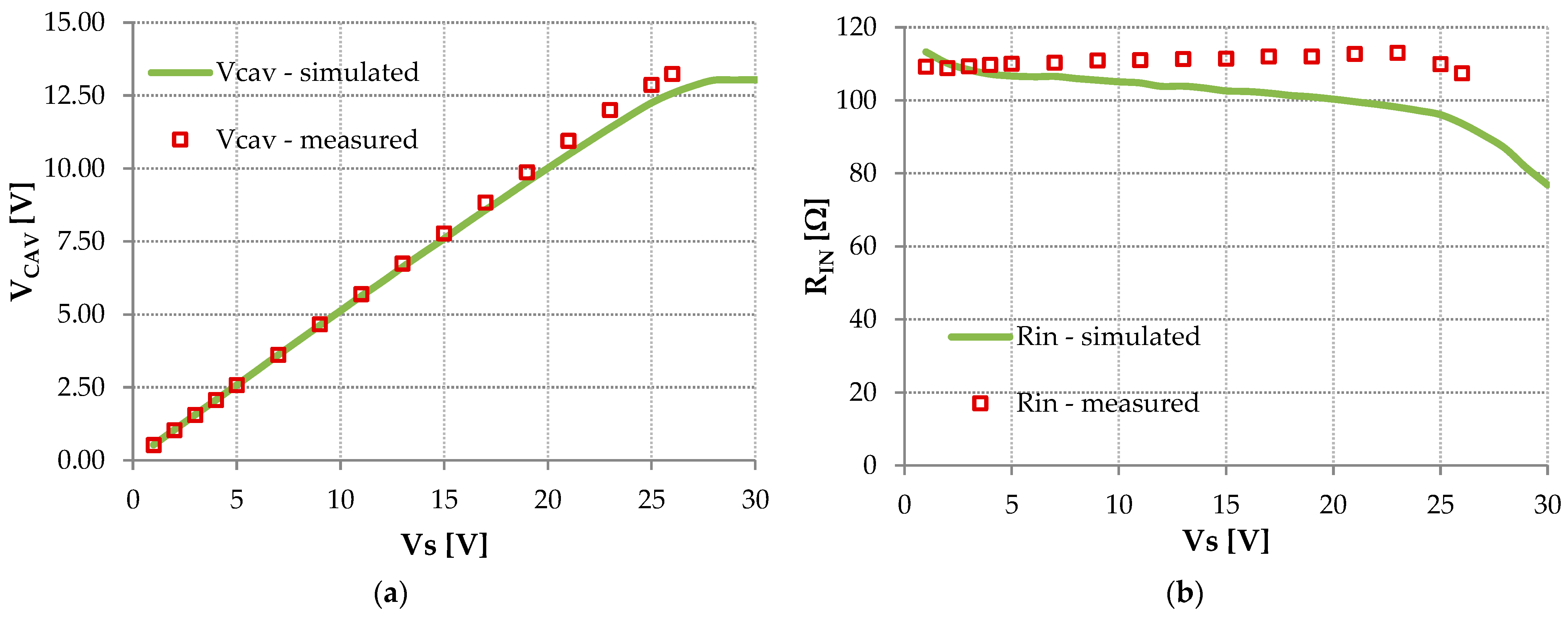
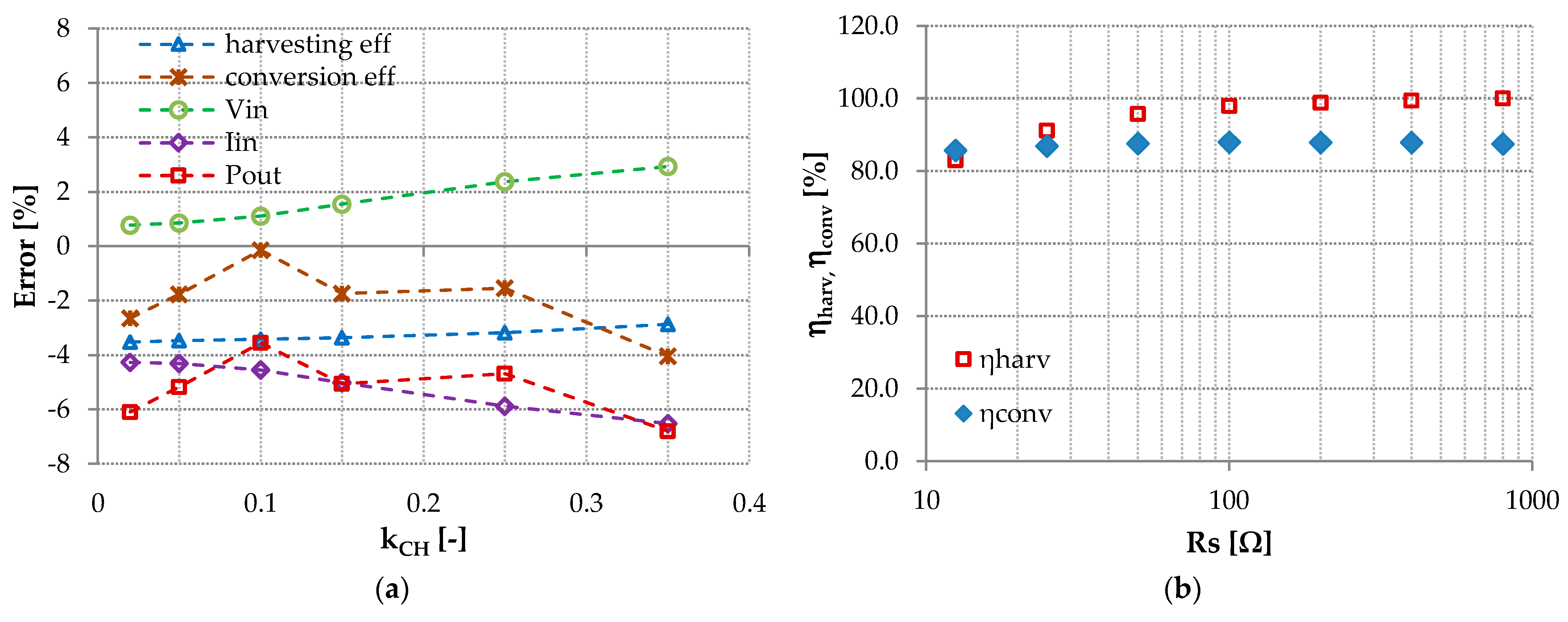
7. Simulations of the Proposed Converter and Verification of the Derived Formulas
8. Hardware Implementation
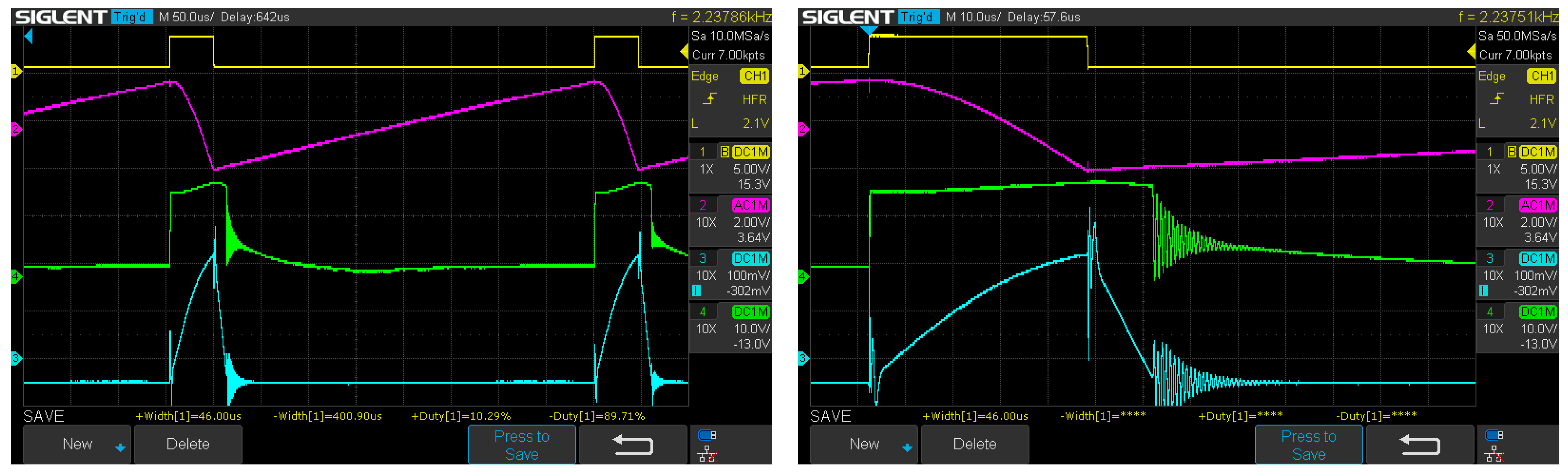
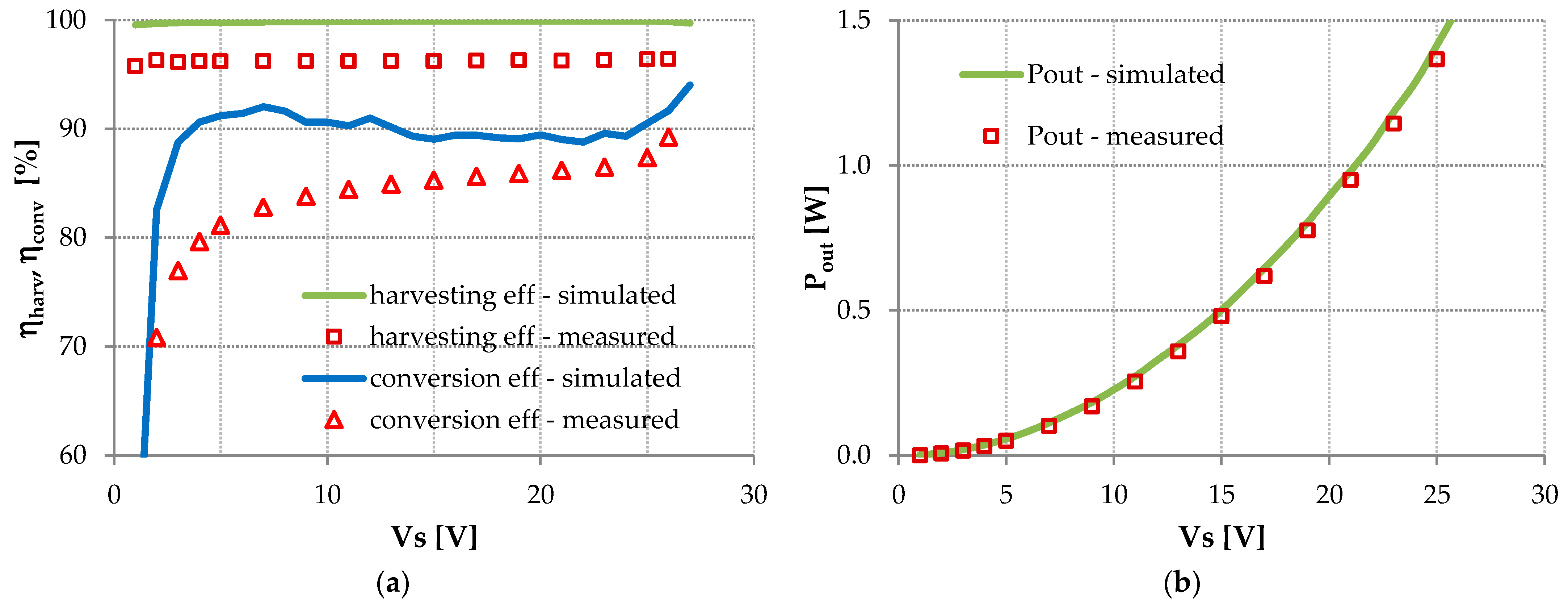
8.1. Static Measurements Without Disturbance
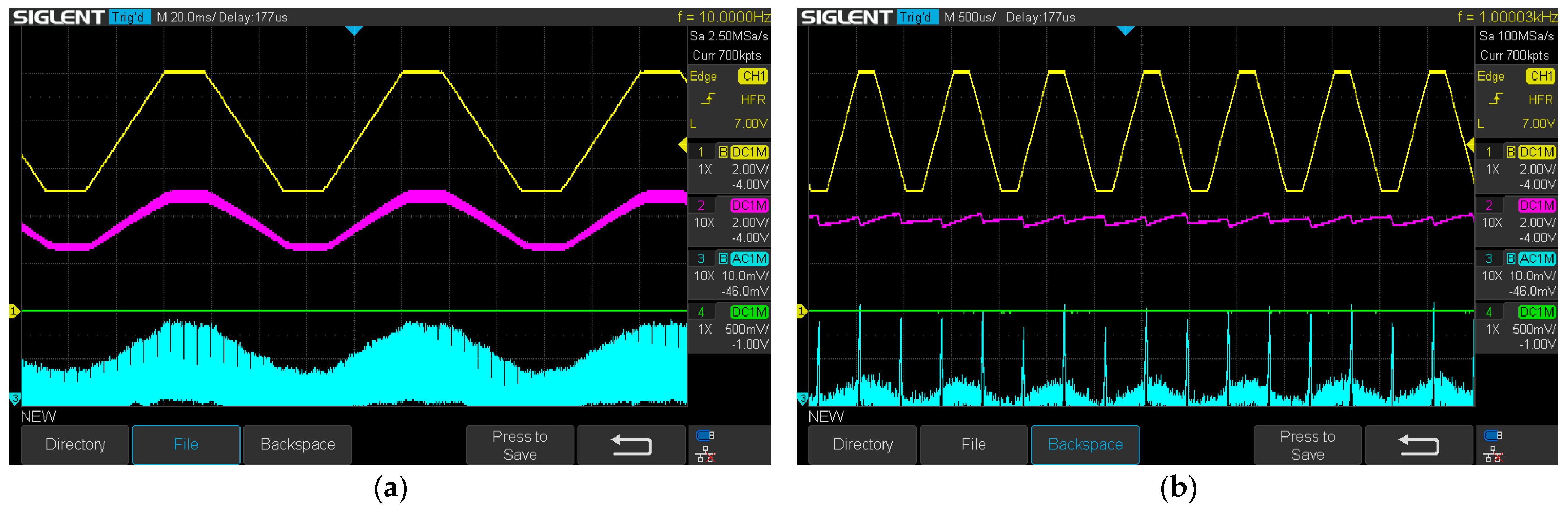
- Charging of the capacitor from the source (stage A), when switch K2 is turned OFF (yellow trace is low) and the current of the coil L is zero (cyan trace is zero);
- energy transfer from capacitor C to inductor L (stage B), when switch K2 is turned ON (yellow trace is high) and the coil’s current increases linearly (ramp up of cyan trace);
- energy transfer from coil L to load and battery B (stage C), when switch K2 is turned OFF (yellow trace is low), the coil’s current decreases linearly (ramp down of cyan trace), and the diode D2 is still biased forward (green trace is high).
- charging of the capacitor from the source (stage A), when switch K1 is turned OFF (yellow trace is low) and the current of the coil L fast and linearly drops to zero at the beginning of the stage and then is zero until the end of the stage (cyan trace);
- energy transfer from capacitor C to inductor L (stage B), when switch K1 is turned ON (yellow trace is high) and the coil’s current increases (cyan trace).
- It should be emphasized that the assumption of an almost linear fall in stage B of the coil current was confirmed during the measurements of the prototype (Figure 20).
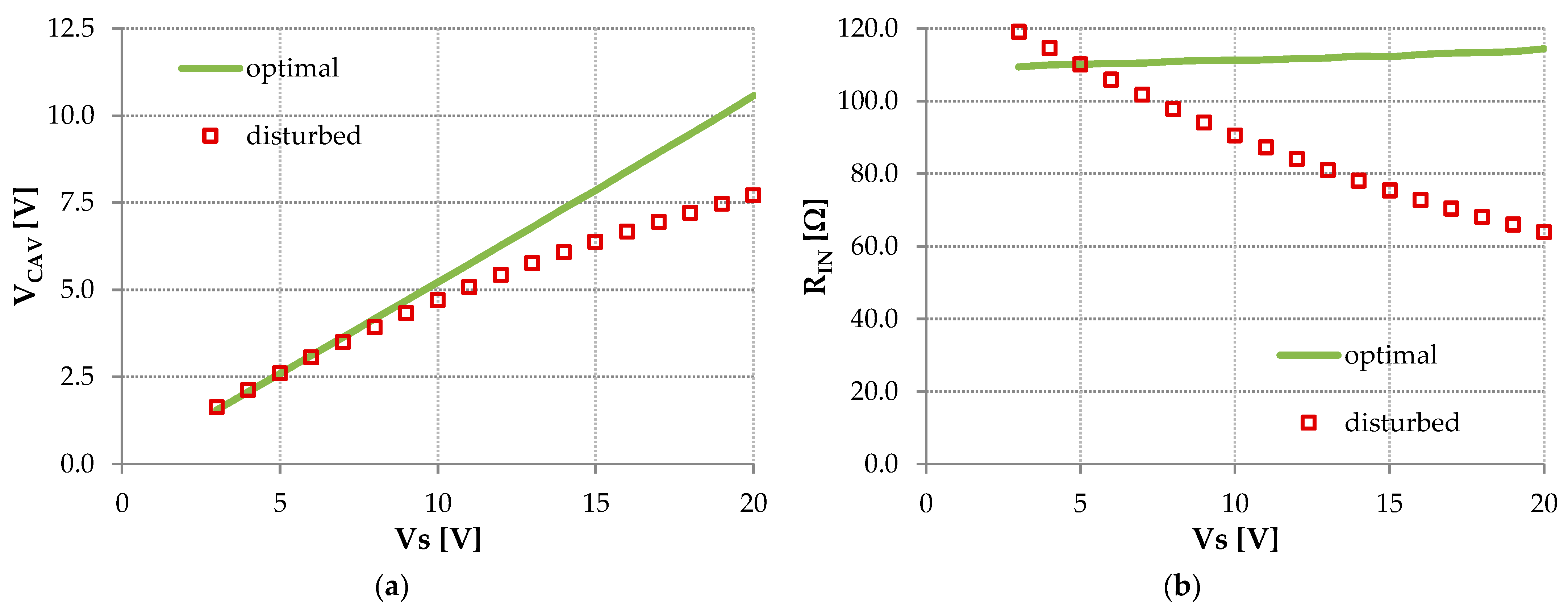
8.2. Static Measurements with Disturbance
8.3. Dynamic Measurements
9. Discussion
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wieczorek, G.; Bernacki, K.; Rymarski, Z.; Oliwa, W. Gathering Energy of the Stray Currents in Electrified Railways Environment for Power Supply. Energies 2021, 14, 6206. [Google Scholar] [CrossRef]
- Xinyu, A.; Baowei, S.; Wenlong, T.; Congcong, T. Design and CFD Simulations of a Vortex-Induced Piezoelectric Energy Converter (VIPEC) for Underwater Environment. Energies 2018, 11, 330. [Google Scholar] [CrossRef]
- Carreon-Bautista, S.; Eladawy, A.; Nader Mohieldin, A.; Sánchez-Sinencio, E. Boost Converter With Dynamic Input Impedance Matching for Energy Harvesting With Multi-Array Thermoelectric Generators. IEEE Trans. Ind. Electron. 2014, 61, 5345–5353. [Google Scholar] [CrossRef]
- Jia, Y.; Yan, J.; Soga, K.; Seshia, A. Parametric resonance for vibration energy harvesting with design techniques to passivelyreduce the initiation threshold amplitude. Smart Mater. Struct. 2014, 23, 065011. [Google Scholar] [CrossRef]
- Gholikhani, M.; Nasouri, R.; Tahami, S.A.; Legette, S.; Dessouky, S.; Montoya, A. Harvesting kinetic energy from roadwaypavement through an electromagnetic speed bump. Appl. Energy 2019, 250, 503–511. [Google Scholar] [CrossRef]
- Kamuda, K.; Klepacki, D.; Sabat, W.; Kuryło, K.; Skoczylas, M.; Jankowski-Mihułowicz, P. Efficiency Measurements of Energy Harvesting from Electromagnetic Environment for Selected General Purpose Telecommunication Systems. Electronics 2024, 13, 3111. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Chandrakasan, A.P. Platform Architecture for Solar, Thermal, and Vibration Energy Combining with MPPT and Single Inductor. IEEE J. Solid-State Circuits 2012, 47, 2199–2215. [Google Scholar] [CrossRef]
- Panizza, M. Input Source Impedance and Its Effects on DC-DC Converter Performance and Characteristics, Europe Applications Engineering, Vicor Corporation. Available online: https://www.vicorpower.com/documents/whitepapers/wp-input-source-impedance-DC-DC-VICOR.pdf (accessed on 30 November 2024).
- Middlebrook, R.D. Input Filter Considerations in Design and Application of Switching Regulators. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Chicago, IL, USA, 11–14 October 1976; pp. 366–382. [Google Scholar]
- Siegers, J.; Domudala, V. How to Design Modular DC/DC Systems, Part 3: Stability Analysis and Decoupling. Available online: https://www.vicorpower.com/resource-library/tutorials/dc-dc-tutorials/dcdc-tutorial-3-stability (accessed on 30 November 2024).
- Input System Instability, SynQor, Application Note PQ-00-05-1 Rev. 2–23 August 2017. Available online: https://www.synqor.com/document-viewer?document=input+system+instability.pdf (accessed on 30 November 2024).
- Application Note 3166 Source Resistance: The Efficiency Killer in DC-DC Converter Circuits, Maxim Integrated. Available online: https://www.analog.com/en/resources/technical-articles/source-resistance-the-efficiency-killer-in-dcdc-converter-circuits.html (accessed on 30 November 2024).
- Di Maria, G. DC/DC Converters: Increasing Efficiency and Avoiding Bistability 23 March 2023. Available online: https://www.powerelectronicsnews.com/dc-dc-converters-increasing-efficiency-and-avoiding-bistability/ (accessed on 30 November 2024).
- Ramadass, Y.K.; Chandrakasan, A.P. A batteryless thermoelectric energy-harvesting interface circuit with 35mV startup voltage. In Proceedings of the 2010 IEEE International Solid-State Circuits Conference—(ISSCC), San Francisco, CA, USA, 7–11 February 2010; pp. 486–487. [Google Scholar] [CrossRef]
- Weng, P.-S.; Tang, H.-Y.; Ku, P.-C.; Lu, L.H. 50 mV-Input Batteryless Boost Converter for Thermal Energy Harvesting. IEEE J. Solid-State Circuits 2013, 48, 1031–1041. [Google Scholar] [CrossRef]
- Kim, J.; Kim, C. A DC–DC Boost Converter With Variation-Tolerant MPPT Technique and Efficient ZCS Circuit for Thermoelectric Energy Harvesting Applications. IEEE Trans. Power Electron. 2013, 28, 3827–3833. [Google Scholar] [CrossRef]
- Carlson, E.J.; Strunz, K.; Otis, B.P. A 20 mV Input Boost Converter With Efficient Digital Control for Thermoelectric Energy Harvesting. IEEE J. Solid-State Circuits 2010, 45, 741–750. [Google Scholar] [CrossRef]
- Umaz, R. Energy Harvesting System with A Single-step Power Conversion Process Achieving Peak Efficiency of 79.1%. In Proceedings of the 2020 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Ankara, Turkey, 26–28 June 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Liu, X.; Sánchez-Sinencio, E. An 86% Efficiency 12 µW Self-Sustaining PV Energy Harvesting System With Hysteresis Regulation and Time-Domain MPPT for IOT Smart Nodes. IEEE J. Solid-State Circuits 2015, 50, 1424–1437. [Google Scholar] [CrossRef]












| Parameters | [3] | [7] | [18] | This Work |
|---|---|---|---|---|
| Energy source | Thermoelectric generator | Thermoelectric Generator, piezo-electric, photovoltaic | Thermoelectric generator | Stray currents |
| Conversion-process | Boost with impedance matching using MPPT | Boost with impedance matching using MPPT | Two charge pumps, IC boost converter, supercapacitor | Boost, flyback, or buck with battery and resistance matching using source and converter modelling |
| Input voltage | 20 mV–150 mV | 50 mV–10 V | >0.3 V | 2 V–60 V |
| Source resistance | 33 Ω–2.7 kΩ | 5 Ω–150 kΩ | 100 Ω | 10 Ω–1 k Ω |
| Output voltage | 1.8 V–2.5 V | 1.8 V–2.5 V | 3.3 V | 12 V |
| Maximum output power | 360 µW @ Vin = 0.14 V | 2.5 mW from photovoltaic | 200 mW @ Vin = 0.8 V | 1.5 W @ Vin = 24 V |
| Efficiency | 61% @ POUT = 360 µW | 83% from photovoltaic | 65% @ POUT = 100 mW | 85% @ Vin = 19 V |
| Comments | a | a | b | c |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wieczorek, G.; Oliwa, W.; Rymarski, Z. Energy Harvesting Power Converter for Variable Impedance and Voltage Sources. Electronics 2025, 14, 52. https://doi.org/10.3390/electronics14010052
Wieczorek G, Oliwa W, Rymarski Z. Energy Harvesting Power Converter for Variable Impedance and Voltage Sources. Electronics. 2025; 14(1):52. https://doi.org/10.3390/electronics14010052
Chicago/Turabian StyleWieczorek, Grzegorz, Wojciech Oliwa, and Zbigniew Rymarski. 2025. "Energy Harvesting Power Converter for Variable Impedance and Voltage Sources" Electronics 14, no. 1: 52. https://doi.org/10.3390/electronics14010052
APA StyleWieczorek, G., Oliwa, W., & Rymarski, Z. (2025). Energy Harvesting Power Converter for Variable Impedance and Voltage Sources. Electronics, 14(1), 52. https://doi.org/10.3390/electronics14010052







