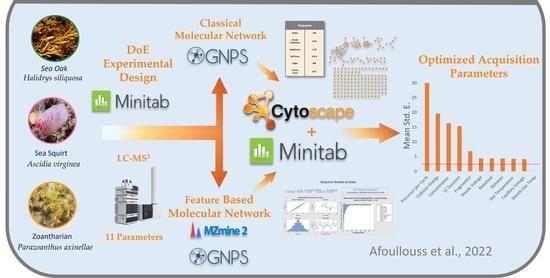
Optimization of LC-MS2 Data Acquisition Parameters for Molecular Networking Applied to Marine Natural Products
Abstract
:1. Introduction
2. Results and Discussion
2.1. Response Models
2.2. Significant Factors and Significant Factor Interactions
2.2.1. Precursor per Cycle
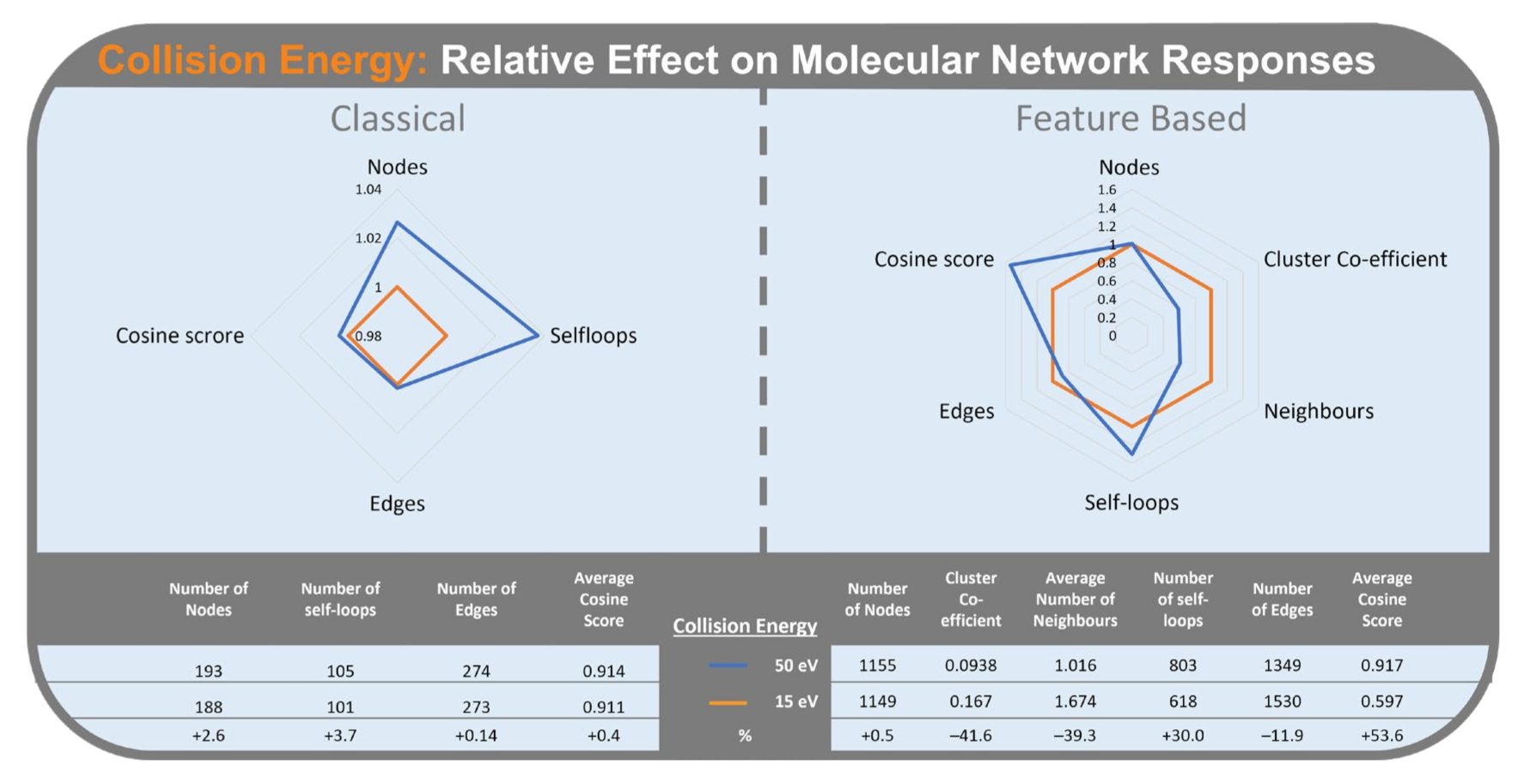
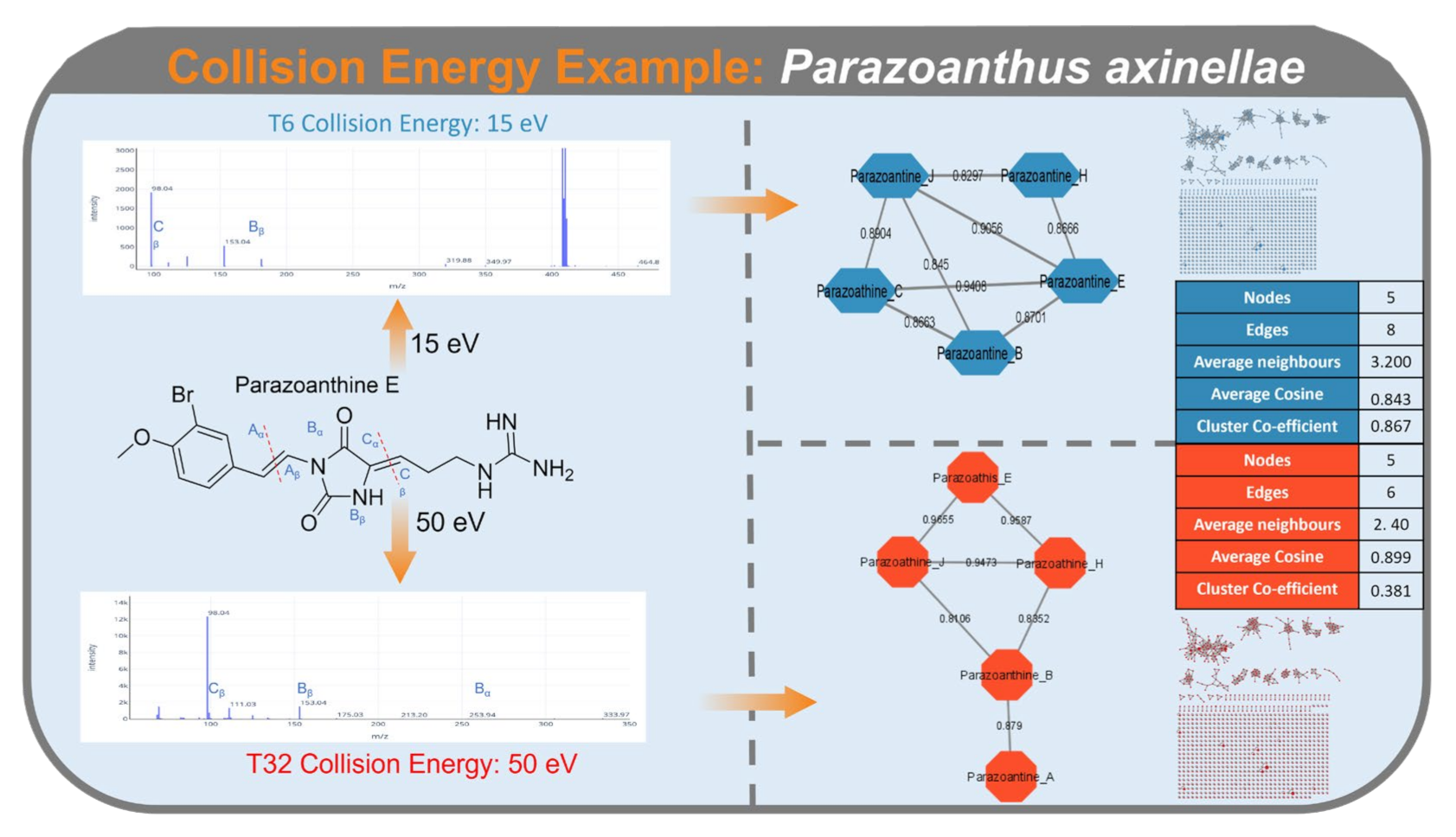
2.2.2. Collision Energy
2.2.3. Concentration
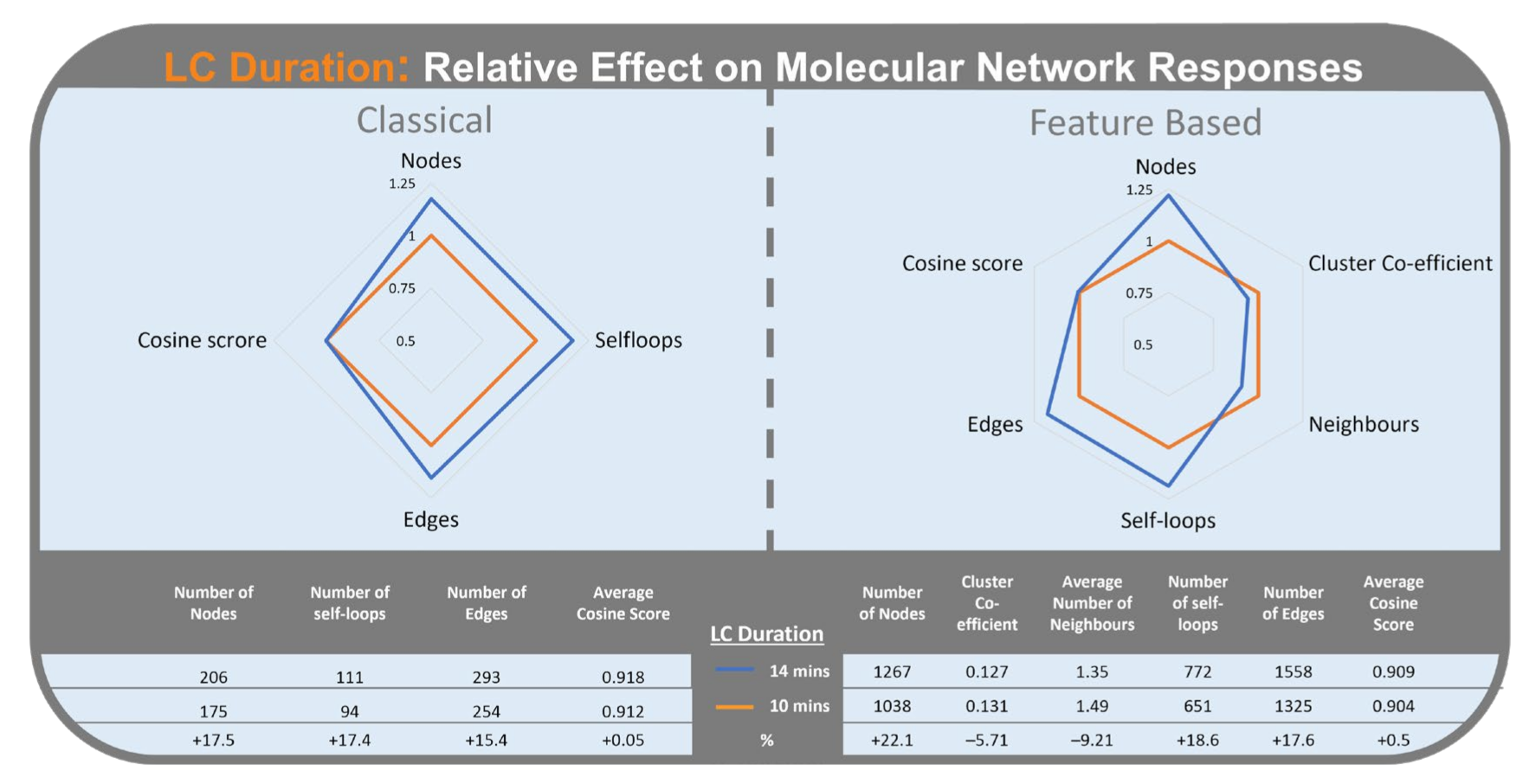
2.2.4. LC Duration
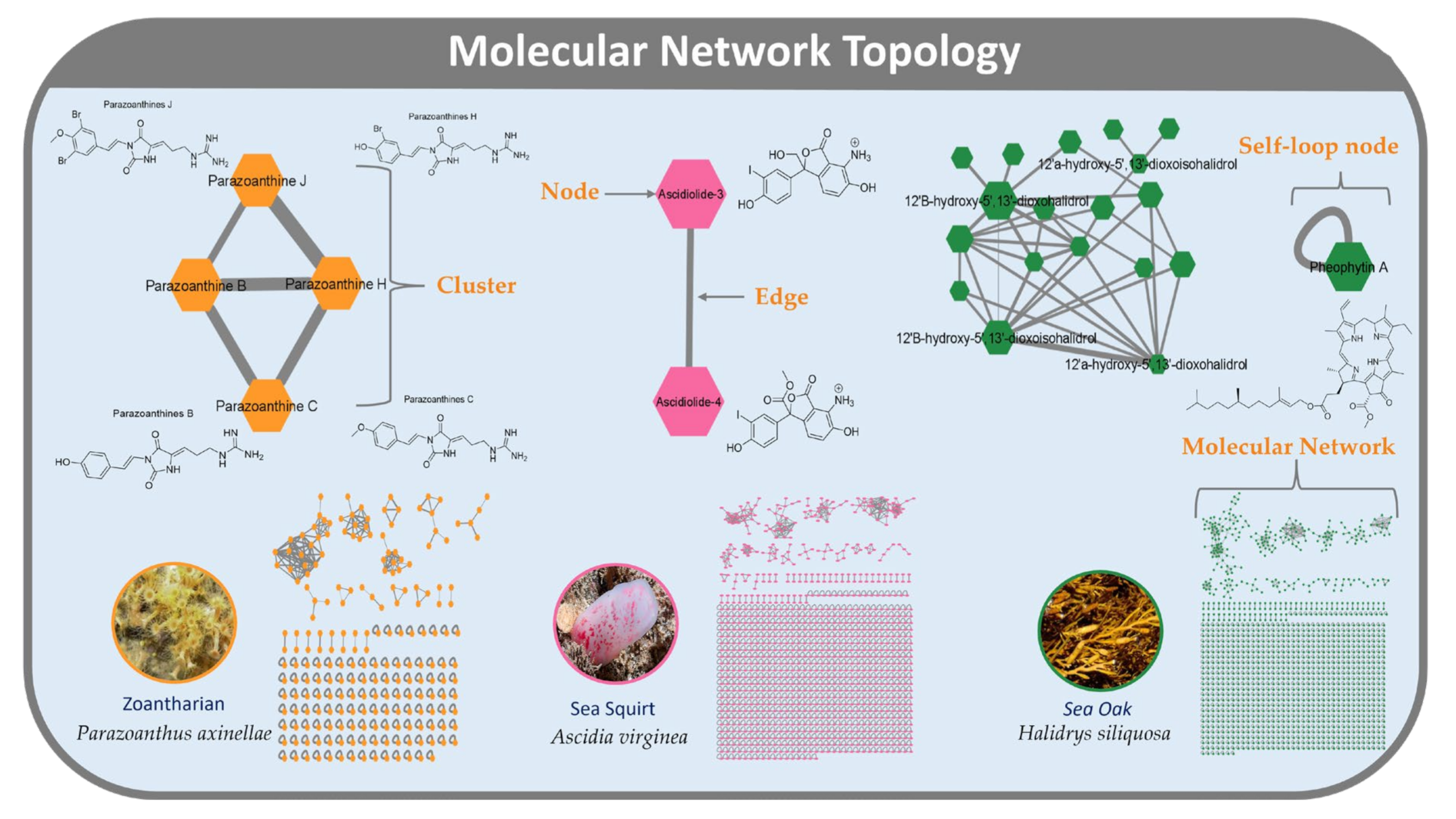
2.2.5. Comparison of CLMN and FBMN
2.2.6. Optimization of Molecular Networking
3. Materials and Methods
3.1. Sample Selection and Preparation
3.2. Experimental Design
3.3. Data Acquisition LC-MS2
3.4. File Conversion
3.5. Classical Based Molecular Networking
3.6. Feature-Based Molecular Networking
3.7. Molecular Network Visualization and Network Analyses
3.8. Design of Experiment Response Analysis
3.9. Visualization of Molecular Networking
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Watrous, J.; Roach, P.; Alexandrov, T.; Heath, B.S.; Yang, J.Y.; Kersten, R.D.; van der Voort, M.; Pogliano, K.; Gross, H.; Raaijmakers, J.M. Mass spectral molecular networking of living microbial colonies. Proc. Natl. Acad. Sci. USA 2012, 109, E1743–E1752. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, J.; Huan, T. Comparison of full-scan, data-dependent, and data-independent acquisition modes in liquid chromatography–mass spectrometry based untargeted metabolomics. Anal. Chem. 2020, 92, 8072–8080. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Carver, J.J.; Phelan, V.V.; Sanchez, L.M.; Garg, N.; Peng, Y.; Nguyen, D.D.; Watrous, J.; Kapono, C.A.; Luzzatto-Knaan, T. Sharing and community curation of mass spectrometry data with Global Natural Products Social Molecular Networking. Nat. Biotechnol. 2016, 34, 828–837. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Allard, P.-M.; Péresse, T.; Bisson, J.; Gindro, K.; Marcourt, L.; Pham, V.C.; Roussi, F.; Litaudon, M.; Wolfender, J.-L. Integration of molecular networking and in-silico MS/MS fragmentation for natural products dereplication. Anal. Chem. 2016, 88, 3317–3323. [Google Scholar] [CrossRef]
- Gao, Y.L.; Wang, Y.J.; Chung, H.H.; Chen, K.C.; Shen, T.L.; Hsu, C.C. Molecular networking as a dereplication strategy for monitoring metabolites of natural product treated cancer cells. Rapid Commun. Mass Spectrom. 2020, 34, e8549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perez De Souza, L.; Alseekh, S.; Brotman, Y.; Fernie, A.R. Network-based strategies in metabolomics data analysis and interpretation: From molecular networking to biological interpretation. Expert Rev. Proteom. 2020, 17, 243–255. [Google Scholar] [CrossRef] [PubMed]
- Shishido, T.K.; Popin, R.V.; Jokela, J.; Wahlsten, M.; Fiore, M.F.; Fewer, D.P.; Herfindal, L.; Sivonen, K. Dereplication of natural products with antimicrobial and anticancer activity from Brazilian cyanobacteria. Toxins 2020, 12, 12. [Google Scholar] [CrossRef] [Green Version]
- Duncan, K.R.; Crüsemann, M.; Lechner, A.; Sarkar, A.; Li, J.; Ziemert, N.; Wang, M.; Bandeira, N.; Moore, B.S.; Dorrestein, P.C. Molecular networking and pattern-based genome mining improves discovery of biosynthetic gene clusters and their products from Salinispora species. Chem. Biol. 2015, 22, 460–471. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paulo, B.S.; Sigrist, R.; Angolini, C.F.; De Oliveira, L.G. New cyclodepsipeptide derivatives revealed by genome mining and molecular networking. ChemistrySelect 2019, 4, 7785–7790. [Google Scholar] [CrossRef]
- Raheem, D.J.; Tawfike, A.F.; Abdelmohsen, U.R.; Edrada-Ebel, R.; Fitzsimmons-Thoss, V. Application of metabolomics and molecular networking in investigating the chemical profile and antitrypanosomal activity of British bluebells (Hyacinthoides non-scripta). Sci. Rep. 2019, 9, 2547. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Silva, E.; da Graça, J.P.; Porto, C.; Martin do Prado, R.; Hoffmann-Campo, C.B.; Meyer, M.C.; de Oliveira Nunes, E.; Pilau, E.J. Unraveling Asian Soybean Rust metabolomics using mass spectrometry and Molecular Networking approach. Sci. Rep. 2020, 10, 138. [Google Scholar] [CrossRef] [PubMed]
- De Vijlder, T.; Valkenborg, D.; Lemière, F.; Romijn, E.P.; Laukens, K.; Cuyckens, F. A tutorial in small molecule identification via electrospray ionization-mass spectrometry: The practical art of structural elucidation. Mass Spectrom. Rev. 2018, 37, 607–629. [Google Scholar] [CrossRef]
- Frank, A.M.; Monroe, M.E.; Shah, A.R.; Carver, J.J.; Bandeira, N.; Moore, R.J.; Anderson, G.A.; Smith, R.D.; Pevzner, P.A. Spectral archives: Extending spectral libraries to analyze both identified and unidentified spectra. Nat. Methods 2011, 8, 587–591. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.Y.; Sanchez, L.M.; Rath, C.M.; Liu, X.; Boudreau, P.D.; Bruns, N.; Glukhov, E.; Wodtke, A.; De Felicio, R.; Fenner, A. Molecular networking as a dereplication strategy. J. Nat. Prod. 2013, 76, 1686–1699. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nothias, L.-F.; Petras, D.; Schmid, R.; Dührkop, K.; Rainer, J.; Sarvepalli, A.; Protsyuk, I.; Ernst, M.; Tsugawa, H.; Fleischauer, M. Feature-based molecular networking in the GNPS analysis environment. Nat. Methods 2020, 17, 905–908. [Google Scholar] [CrossRef]
- Pluskal, T.; Castillo, S.; Villar-Briones, A.; Orešić, M. MZmine: Modular framework for processing, visualizing, and analyzing mass spectrometry-based molecular profile data. BMC Bioinform. 2010, 11, 395. [Google Scholar] [CrossRef] [Green Version]
- Xu, R.; Lee, J.; Chen, L.; Zhu, J. Enhanced detection and annotation of small molecules in metabolomics using molecular-network-oriented parameter optimization. Mol. Omics 2021, 17, 665–676. [Google Scholar] [CrossRef]
- Czitrom, V. One-factor-at-a-time versus designed experiments. Am. Stat. 1999, 53, 126–131. [Google Scholar]
- Hecht, E.S.; Oberg, A.L.; Muddiman, D.C. Optimizing mass spectrometry analyses: A tailored review on the utility of design of experiments. J. Am. Soc. Mass. Spectrom. 2016, 27, 767–785. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Olivon, F.; Roussi, F.; Litaudon, M.; Touboul, D. Optimized experimental workflow for tandem mass spectrometry molecular networking in metabolomics. Anal. Bioanal. Chem. 2017, 409, 5767–5778. [Google Scholar] [CrossRef] [PubMed]
- Balsam, A. Optimization of Molecular Networking for Marine Natural Products Chemistry; NUI Galway: Galway, Ireland, 2020. [Google Scholar]
- Kessner, D.; Chambers, M.; Burke, R.; Agus, D.; Mallick, P. ProteoWizard: Open source software for rapid proteomics tools development. Bioinformatics 2008, 24, 2534–2536. [Google Scholar] [CrossRef] [PubMed]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afoullouss, S.; Balsam, A.; Allcock, A.L.; Thomas, O.P. Optimization of LC-MS2 Data Acquisition Parameters for Molecular Networking Applied to Marine Natural Products. Metabolites 2022, 12, 245. https://doi.org/10.3390/metabo12030245
Afoullouss S, Balsam A, Allcock AL, Thomas OP. Optimization of LC-MS2 Data Acquisition Parameters for Molecular Networking Applied to Marine Natural Products. Metabolites. 2022; 12(3):245. https://doi.org/10.3390/metabo12030245
Chicago/Turabian StyleAfoullouss, Sam, Agata Balsam, A. Louise Allcock, and Olivier P. Thomas. 2022. "Optimization of LC-MS2 Data Acquisition Parameters for Molecular Networking Applied to Marine Natural Products" Metabolites 12, no. 3: 245. https://doi.org/10.3390/metabo12030245