Progress in Solving the Nonperturbative Renormalization Group for Tensorial Group Field Theory
Abstract
:1. Introduction
2. Introduction to the Nonperturbative Renormalization for TGFT

2.1. Wilson–Polchinski Equation

2.1.1. at Order
2.1.2. and at Order
3. Wetterich Flow Equation
Convenient Search of the Ward Identities
- two external edges per external vertices, sharing external faces of length one.
- N external faces of the same color running through the interior of the diagram.


4. Effective Vertex Expansion Method for the Melonic Sector
4.1. Structure Equations and Compactability with Ward Identities






 may be easily computed recursively from the definition of melonic
diagrams or directly using Wick theorem for a one-loop computation with the effective propagator G. The result is:
may be easily computed recursively from the definition of melonic
diagrams or directly using Wick theorem for a one-loop computation with the effective propagator G. The result is:

4.2. Flow Equation from the EVE Method

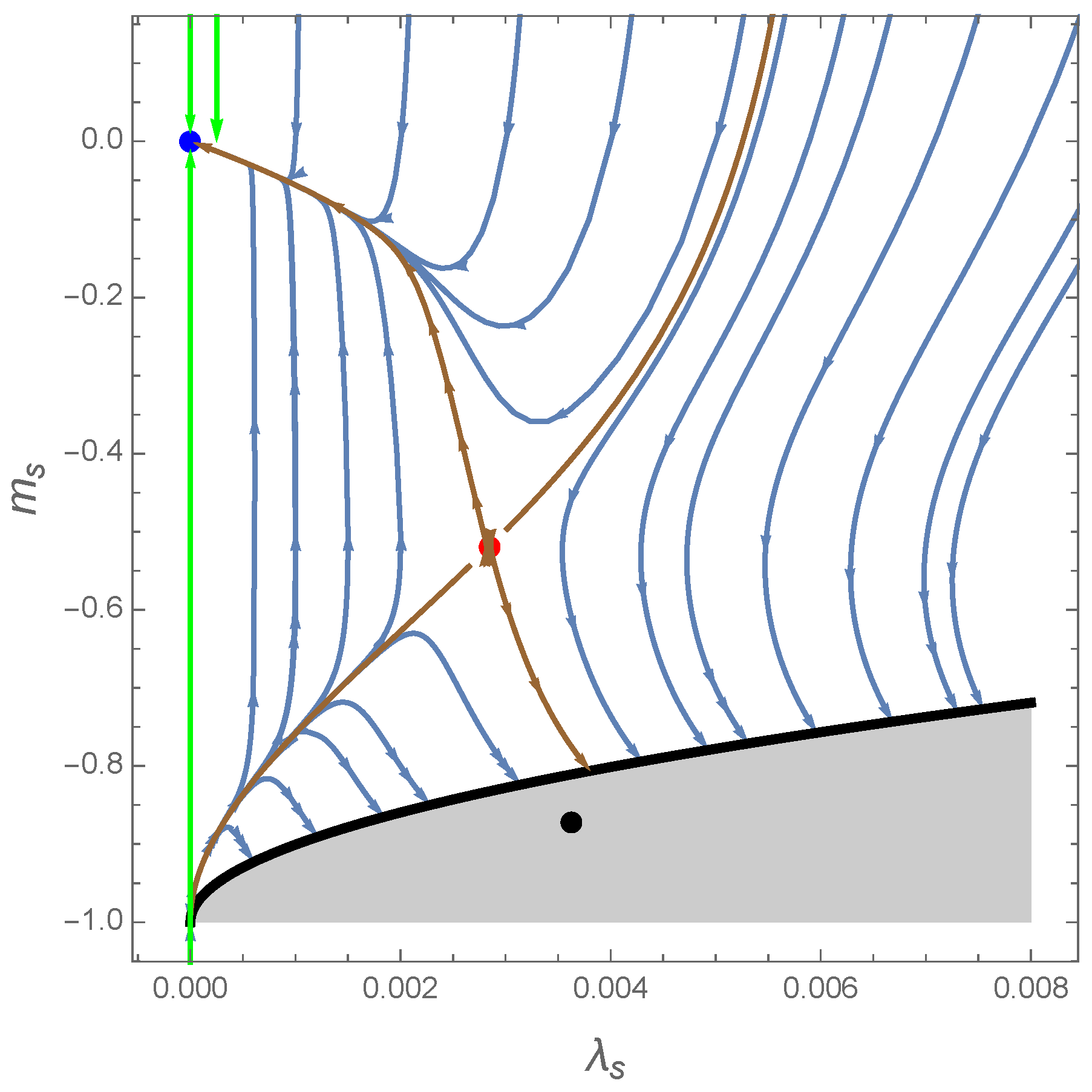
4.3. Exploration of the Physical Phase Space
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rovelli, C. Loop quantum gravity. Living Rev. Relat. 1998, 1, 5. [Google Scholar] [CrossRef] [PubMed]
- Rovelli, C.; Upadhya, P. Loop quantum gravity and quanta of space: A Primer. arXiv, 1998; arXiv:gr-qc/9806079. [Google Scholar]
- Ambjorn, J.; Burda, Z.; Jurkiewicz, J.; Kristjansen, C.F. Quantum gravity represented as dynamical triangulations. Acta Phys. Pol. B 1992, 23, 991–1030. [Google Scholar] [CrossRef]
- Ambjorn, J. Quantum gravity represented as dynamical triangulations. Class. Quantum Gravity 1995, 12, 2079–2134. [Google Scholar] [CrossRef]
- Ambjørn, J.; Görlich, A.; Jurkiewicz, J.; Loll, R. Quantum Gravity via Causal Dynamical Triangulations. In Springer Handbook of Spacetime; Springer: Berlin/Heidelberg, Germany, 2014; pp. 723–741. [Google Scholar]
- Connes, A.; Lott, J. Particle Models and Noncommutative Geometry (Expanded Version). Nucl. Phys. B Proc. Suppl. 1991, 18, 29–47. [Google Scholar] [CrossRef]
- Aastrup, J.; Grimstrup, J.M. Intersecting connes noncommutative geometry with quantum gravity. Int. J. Mod. Phys. A 2007, 22, 1589–1603. [Google Scholar] [CrossRef]
- Oriti, D. A Quantum field theory of simplicial geometry and the emergence of spacetime. J. Phys. Conf. Ser. 2007, 67, 012052. [Google Scholar] [CrossRef]
- De Cesare, M.; Pithis, A.G.A.; Sakellariadou, M. Cosmological implications of interacting Group Field Theory models: Cyclic Universe and accelerated expansion. Phys. Rev. D 2016, 94, 064051. [Google Scholar] [CrossRef]
- Gielen, S.; Sindoni, L. Quantum Cosmology from Group Field Theory Condensates: A Review. arXiv, 2016; arXiv:1602.08104. [Google Scholar] [CrossRef]
- Gielen, S.; Oriti, D. Cosmological perturbations from full quantum gravity. arXiv, 2017; arXiv:1709.01095. [Google Scholar] [CrossRef]
- Oriti, D.; Ryan, J.P.; Thurigen, J. Group field theories for all loop quantum gravity. New J. Phys. 2015, 17, 023042. [Google Scholar] [CrossRef]
- Gurau, R. Colored Group Field Theory. Commun. Math. Phys. 2011, 304, 69–93. [Google Scholar] [CrossRef]
- Rivasseau, V. Constructive Tensor Field Theory. arXiv, 2016; arXiv:1603.07312. [Google Scholar] [CrossRef]
- Rivasseau, V. Random Tensors and Quantum Gravity. arXiv, 2016; arXiv:1603.07278. [Google Scholar] [CrossRef]
- Rivasseau, V. The Tensor Theory Space. Fortschr. Phys. 2014, 62, 835–840. [Google Scholar] [CrossRef]
- Rivasseau, V. The Tensor Track, III. Fortschr. Phys. 2014, 62, 81–107. [Google Scholar] [CrossRef]
- Rivasseau, V. The Tensor Track, IV. arXiv, 2016; arXiv:1604.07860. [Google Scholar]
- Rivasseau, V. The Tensor Track: An Update. arXiv, 2012; arXiv:1209.5284. [Google Scholar]
- Gurau, R. The complete 1/N expansion of colored tensor models in arbitrary dimension. Ann. Henri Poincare 2012, 13, 399–423. [Google Scholar] [CrossRef]
- Gurau, R. The 1/N expansion of colored tensor models. Ann. Henri Poincare 2011, 12, 829. [Google Scholar] [CrossRef]
- Gurau, R. The 1/N Expansion of Tensor Models Beyond Perturbation Theory. Commun. Math. Phys. 2014, 330, 973–1019. [Google Scholar] [CrossRef]
- Carrozza, S.; Oriti, D.; Rivasseau, V. Renormalization of Tensorial Group Field Theories: Abelian U(1) Models in Four Dimensions. Commun. Math. Phys. 2014, 327, 603–641. [Google Scholar] [CrossRef]
- Carrozza, S. Tensorial methods and renormalization in Group Field Theories. arXiv, 2013; arXiv:1310.3736. [Google Scholar]
- Carrozza, S.; Oriti, D.; Rivasseau, V. Renormalization of a SU(2) Tensorial Group Field Theory in Three Dimensions. Commun. Math. Phys. 2014, 330, 581–637. [Google Scholar] [CrossRef]
- Ben Geloun, J. Renormalizable Models in Rank d ≥ 2 Tensorial Group Field Theory. Commun. Math. Phys. 2014, 332, 117–188. [Google Scholar] [CrossRef]
- Lahoche, V.; Oriti, D. Renormalization of a tensorial field theory on the homogeneous space SU(2)/U(1). arXiv, 2015; arXiv:1506.08393. [Google Scholar]
- Lahoche, V.; Oriti, D.; Rivasseau, V. Renormalization of an Abelian Tensor Group Field Theory: Solution at Leading Order. J. High Energy Phys. 2015, 2015, 95. [Google Scholar] [CrossRef]
- Ben Geloun, J.; Livine, E.R. Some classes of renormalizable tensor models. J. Math. Phys. 2013, 54, 082303. [Google Scholar] [CrossRef]
- Ousmane Samary, D.; Vignes-Tourneret, F. Just Renormalizable TGFT’s on U(1)d with Gauge Invariance. Commun. Math. Phys. 2014, 329, 545–578. [Google Scholar] [CrossRef]
- Ben Geloun, J.; Ousmane Samary, D. 3D Tensor Field Theory: Renormalization and One-loop β-functions. Ann. Henri Poincare 2013, 14, 1599–1642. [Google Scholar] [CrossRef]
- Ben Geloun, J.; Rivasseau, V. A Renormalizable 4-Dimensional Tensor Field Theory. Commun. Math. Phys. 2013, 318, 69–109. [Google Scholar] [CrossRef]
- Ben Geloun, J.; Toriumi, R. Renormalizable Enhanced Tensor Field Theory: The quartic melonic case. arXiv, 2017; arXiv:1709.05141. [Google Scholar] [CrossRef]
- Ben Geloun, J.; Bonzom, V. Radiative corrections in the Boulatov-Ooguri tensor model: The 2-point function. Int. J. Theor. Phys. 2011, 50, 2819–2841. [Google Scholar] [CrossRef]
- Ben Geloun, J. Two and four-loop β-functions of rank 4 renormalizable tensor field theories. Class. Quantum Gravity 2012, 29, 235011. [Google Scholar] [CrossRef]
- Ousmane Samary, D. Beta functions of U(1)d gauge invariant just renormalizable tensor models. Phys. Rev. D 2013, 88, 105003. [Google Scholar] [CrossRef]
- Rivasseau, V. Why are tensor field theories asymptotically free? EPL Europhys. Lett. 2015, 111, 60011. [Google Scholar] [CrossRef]
- Carrozza, S. Discrete Renormalization Group for SU(2) Tensorial Group Field Theory. Ann. Inst. Henri Poincaré Comb. Phys. Interact. 2015, 2, 49–112. [Google Scholar] [CrossRef]
- Wilson, K.G. Renormalization Group and Critical Phenomena. I. Phys. Rev. B 1971, 4, 3174–3183. [Google Scholar] [CrossRef]
- Wilson, K.G. Renormalization Group and Critical Phenomena. II. Phys. Rev. B 1971, 4, 3184–3205. [Google Scholar] [CrossRef]
- Polchinski, J. Renormalization and Effective Lagrangians. Nucl. Phys. B 1984, 231, 269–295. [Google Scholar] [CrossRef]
- Wetterich, C. Exact evolution equation for the effective potential. Phys. Lett. B 1993, 301, 90–94. [Google Scholar] [CrossRef]
- Oriti, D. Levels of spacetime emergence in quantum gravity. arXiv, 2018; arXiv:1807.04875. [Google Scholar]
- Oriti, D. Disappearance and emergence of space and time in quantum gravity. Stud. Hist. Philos. Sci. B 2014, 46, 186–199. [Google Scholar] [CrossRef]
- Markopoulou, F. Conserved quantities in background independent theories. J. Phys. Conf. Ser. 2007, 67, 012019. [Google Scholar] [CrossRef]
- Wilkinson, S.A.; Greentree, A.D. Geometrogenesis under Quantum Graphity: Problems with the ripening Universe. Phys. Rev. D 2015, 92, 084007. [Google Scholar] [CrossRef]
- Geloun, J.B.; Martini, R.; Oriti, D. Functional Renormalisation Group analysis of Tensorial Group Field Theories on . arXiv, 2016; arXiv:1601.08211. [Google Scholar]
- Geloun, J.B.; Martini, R.; Oriti, D. Functional Renormalization Group analysis of a Tensorial Group Field Theory on . Europhys. Lett. 2015, 112, 31001. [Google Scholar] [CrossRef]
- Benedetti, D.; Lahoche, V. Functional Renormalization Group Approach for Tensorial Group Field Theory: A Rank-6 Model with Closure Constraint. arXiv, 2015; arXiv:1508.06384. [Google Scholar] [CrossRef]
- Benedetti, D.; Ben Geloun, J.; Oriti, D. Functional Renormalisation Group Approach for Tensorial Group Field Theory: A Rank-3 Model. J. High Energy Phys. 2015, 2015, 84. [Google Scholar] [CrossRef]
- Ben Geloun, J.; Koslowski, T.A.; Oriti, D.; Pereira, A.D. Functional Renormalization Group analysis of rank 3 tensorial group field theory: The full quartic invariant truncation. Phys. Rev. D 2018, 97, 126018. [Google Scholar] [CrossRef]
- Carrozza, S.; Lahoche, V. Asymptotic safety in three-dimensional SU(2) Group Field Theory: Evidence in the local potential approximation. Class. Quantum Gravity 2017, 34, 115004. [Google Scholar] [CrossRef]
- Lahoche, V.; Ousmane Samary, D. Functional renormalization group for the U(1)- tensorial group field theory with closure constraint. Phys. Rev. D 2017, 95, 045013. [Google Scholar] [CrossRef]
- Carrozza, S.; Lahoche, V.; Oriti, D. Renormalizable Group Field Theory beyond melonic diagrams: An example in rank four. Phys. Rev. D 2017, 96, 066007. [Google Scholar] [CrossRef]
- Ben Geloun, J. Ward–Takahashi identities for the colored Boulatov model. J. Phys. A 2011, 44, 415402. [Google Scholar] [CrossRef]
- Lahoche, V.; Ousmane Samary, D. Ward identity violation for melonic T4-truncation. arXiv, 2018; arXiv:1809.06081. [Google Scholar] [CrossRef]
- Lahoche, V.; Ousmane Samary, D. Nonperturbative renormalization group beyond melonic sector: The Effective Vertex Expansion method for group fields theories. arXiv, 2018; arXiv:1809.00247. [Google Scholar] [CrossRef]
- Lahoche, V.; Ousmane Samary, D. Unitary symmetry constraints on tensorial group field theory renormalization group flow. Class. Quantum Gravity 2018, 35, 195006. [Google Scholar] [CrossRef]
- Pérez-Sánchez, C.I. The full Ward–Takahashi Identity for colored tensor models. arXiv, 2016; arXiv:1608.08134. [Google Scholar] [CrossRef]
- Ousmane Samary, D. Closed equations of the two-point functions for tensorial group field theory. Class. Quantum Gravity 2014, 31, 185005. [Google Scholar] [CrossRef]
- Ousmane Samary, D.; Pérez-Sánchez, C.I.; Vignes-Tourneret, F.; Wulkenhaar, R. Correlation functions of a just renormalizable tensorial group field theory: The melonic approximation. Class. Quantum Gravity 2015, 32, 175012. [Google Scholar] [CrossRef]
- Wetterich, C. Average Action and the Renormalization Group Equations. Nucl. Phys. B 1991, 352, 529–584. [Google Scholar] [CrossRef]
- Wetterich, C. Effective average action in statistical physics and quantum field theory. Int. J. Mod. Phys. A 2001, 16, 1951–1982. [Google Scholar] [CrossRef]
- Berges, J.; Tetradis, N.; Wetterich, C. Nonperturbative renormalization flow in quantum field theory and statistical physics. Phys. Rep. 2002, 363, 223–386. [Google Scholar] [CrossRef]
- Delamotte, B. An Introduction to the nonperturbative renormalization group. Lect. Notes Phys. 2012, 852, 49–132. [Google Scholar]
- Nagy, S. Lectures on renormalization and asymptotic safety. Ann. Phys. 2014, 350, 310–346. [Google Scholar] [CrossRef]
- Litim, D.F. Optimization of the exact renormalization group. Phys. Lett. B 2000, 486, 92–99. [Google Scholar] [CrossRef]
- Litim, D.F. Derivative expansion and renormalization group flows. J. High Energy Phys. 2001, 2001, 59. [Google Scholar] [CrossRef]
| 1 | The rank of the tensors is fixed to five, and we denote it by d to clarify the proof(s). |
| 2 | The notations are similar to the ones used for the previous proof. The context however allows excluding any confusion. |






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lahoche, V.; Ousmane Samary, D. Progress in Solving the Nonperturbative Renormalization Group for Tensorial Group Field Theory. Universe 2019, 5, 86. https://doi.org/10.3390/universe5030086
Lahoche V, Ousmane Samary D. Progress in Solving the Nonperturbative Renormalization Group for Tensorial Group Field Theory. Universe. 2019; 5(3):86. https://doi.org/10.3390/universe5030086
Chicago/Turabian StyleLahoche, Vincent, and Dine Ousmane Samary. 2019. "Progress in Solving the Nonperturbative Renormalization Group for Tensorial Group Field Theory" Universe 5, no. 3: 86. https://doi.org/10.3390/universe5030086
APA StyleLahoche, V., & Ousmane Samary, D. (2019). Progress in Solving the Nonperturbative Renormalization Group for Tensorial Group Field Theory. Universe, 5(3), 86. https://doi.org/10.3390/universe5030086




