Magnetized Particle Motion around Black Holes in Conformal Gravity: Can Magnetic Interaction Mimic Spin of Black Holes?
Abstract
:1. Introduction
2. Electromagnetic Fields around Black Holes Immersed in Asymptotically Uniform Magnetic Field
3. Magnetized Particle Motion around Black Holes in Conformal Gravity
4. Magnetized Particles Acceleration around Regular Black Holes Immersed in an External Magnetic Field
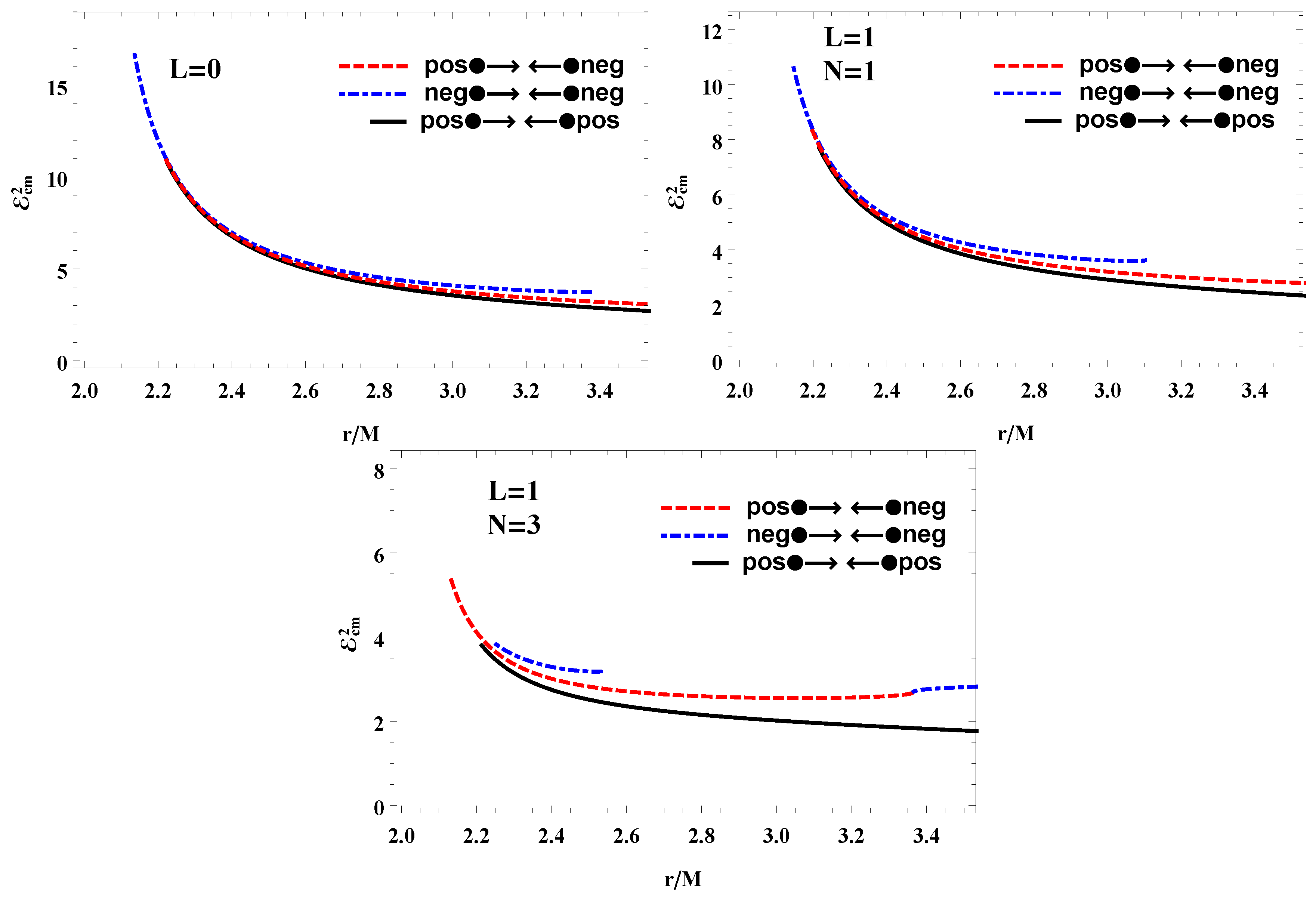
4.1. Collision of two Magnetized Particles
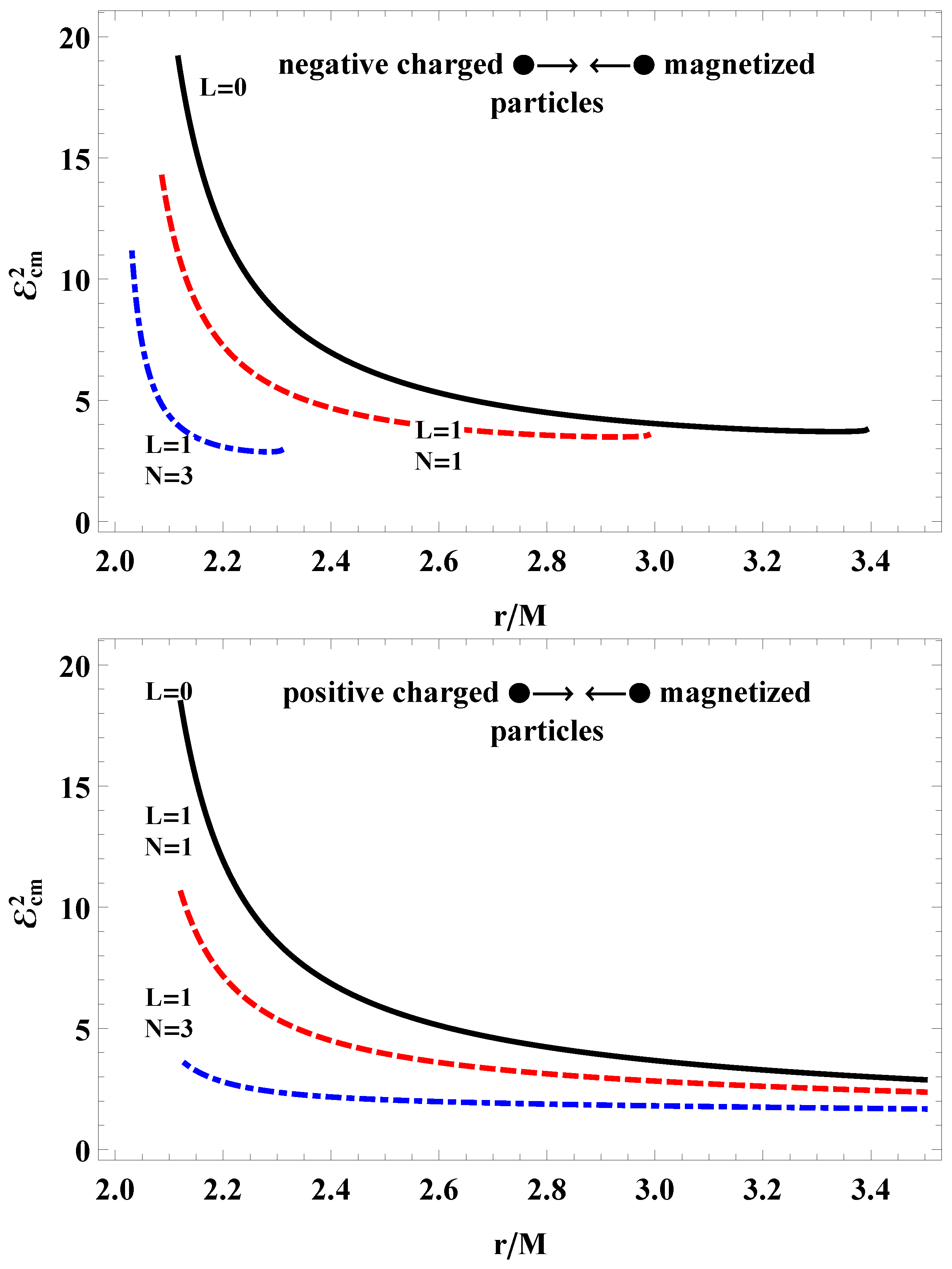
4.2. Collision of Magnetized and Charged Particles
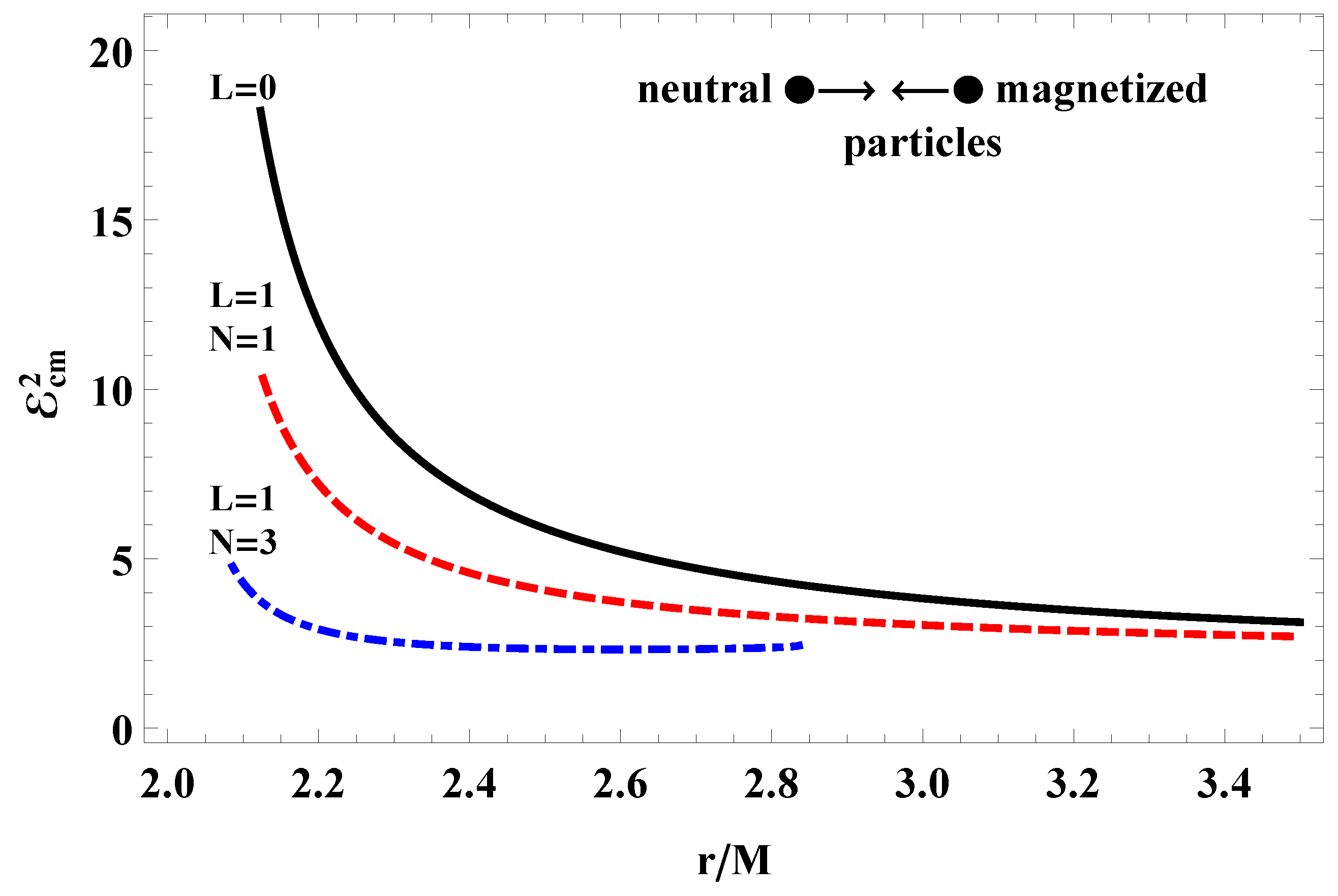
4.3. Collision of Two Magnetized and Neutral Particles
4.4. Collision of Two Charged Particles
5. Astrophysical Applications
6. Conclusions
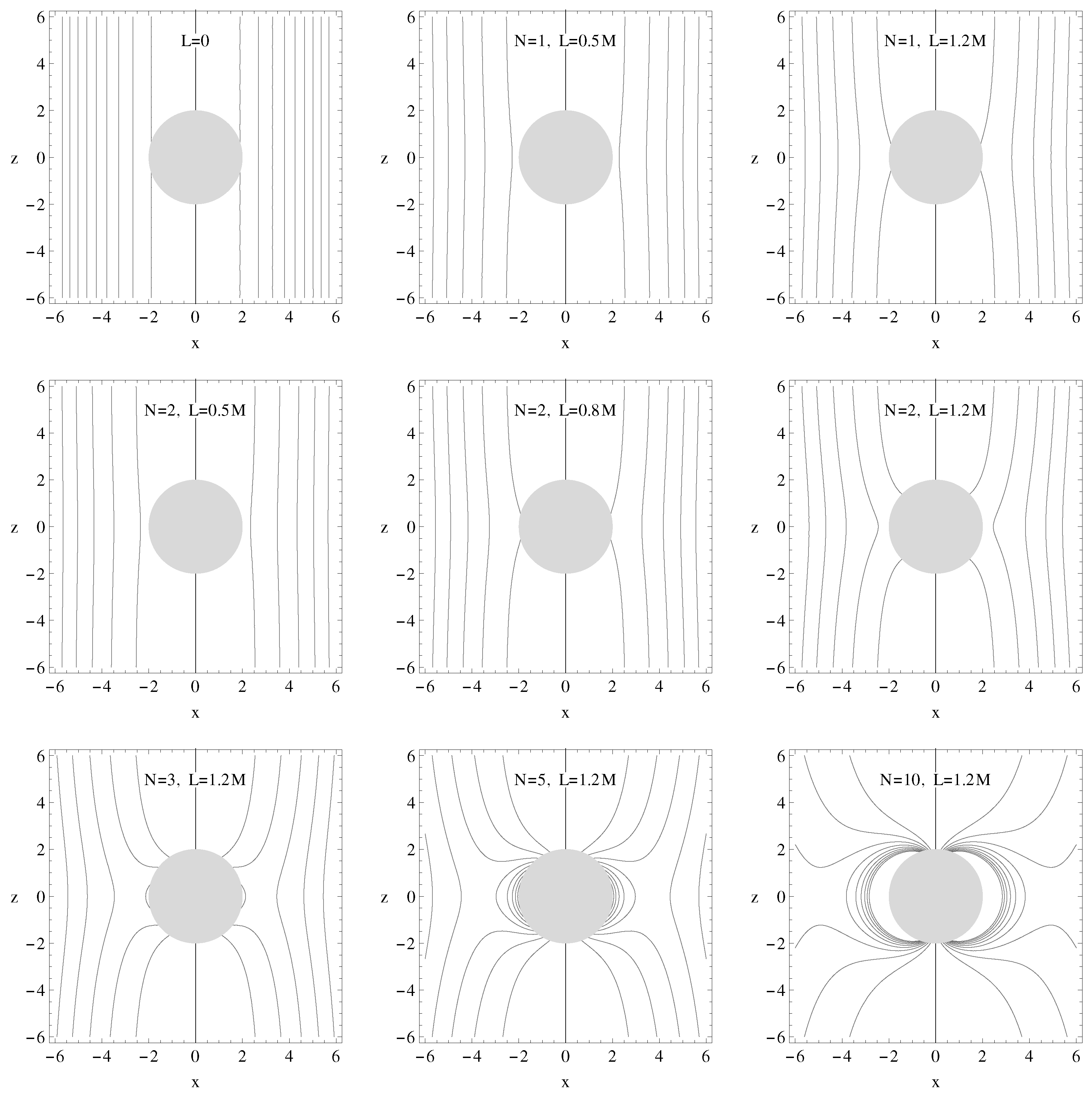
- We have analyzed the behavior of magnetic field near the event horizon of the black hole in conformal gravity. It is shown that with the increase of conformal parameters L and N the value of angular component of magnetic field at the stellar surface decreases. Moreover, the increase of the conformal parameters forces the asymptotically uniform magnetic field lines to be more curved and for the large values of N () the structure of asymptotically uniform magnetic field turns to be a dipolar-like near the event horizon of black holes.
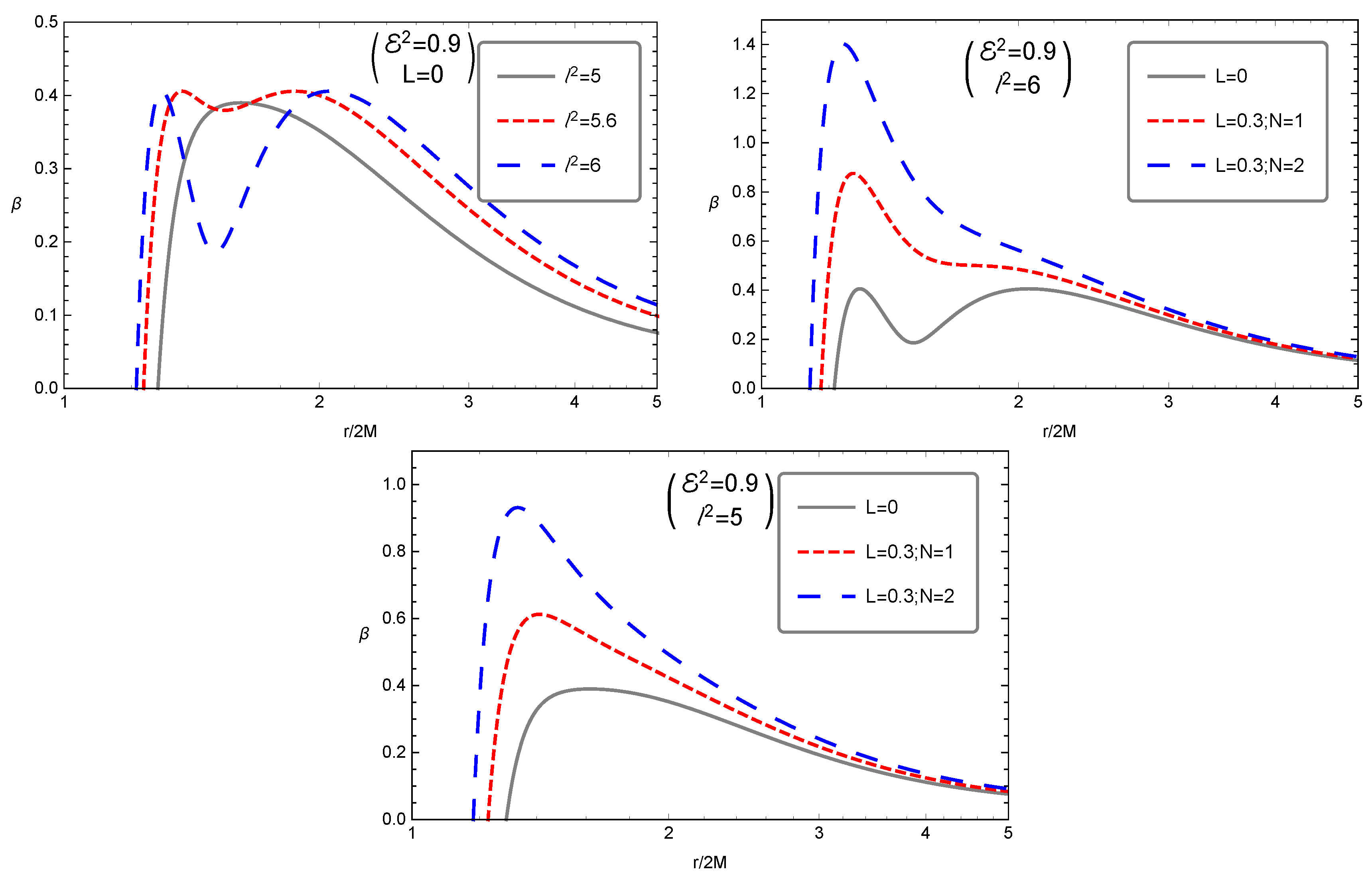
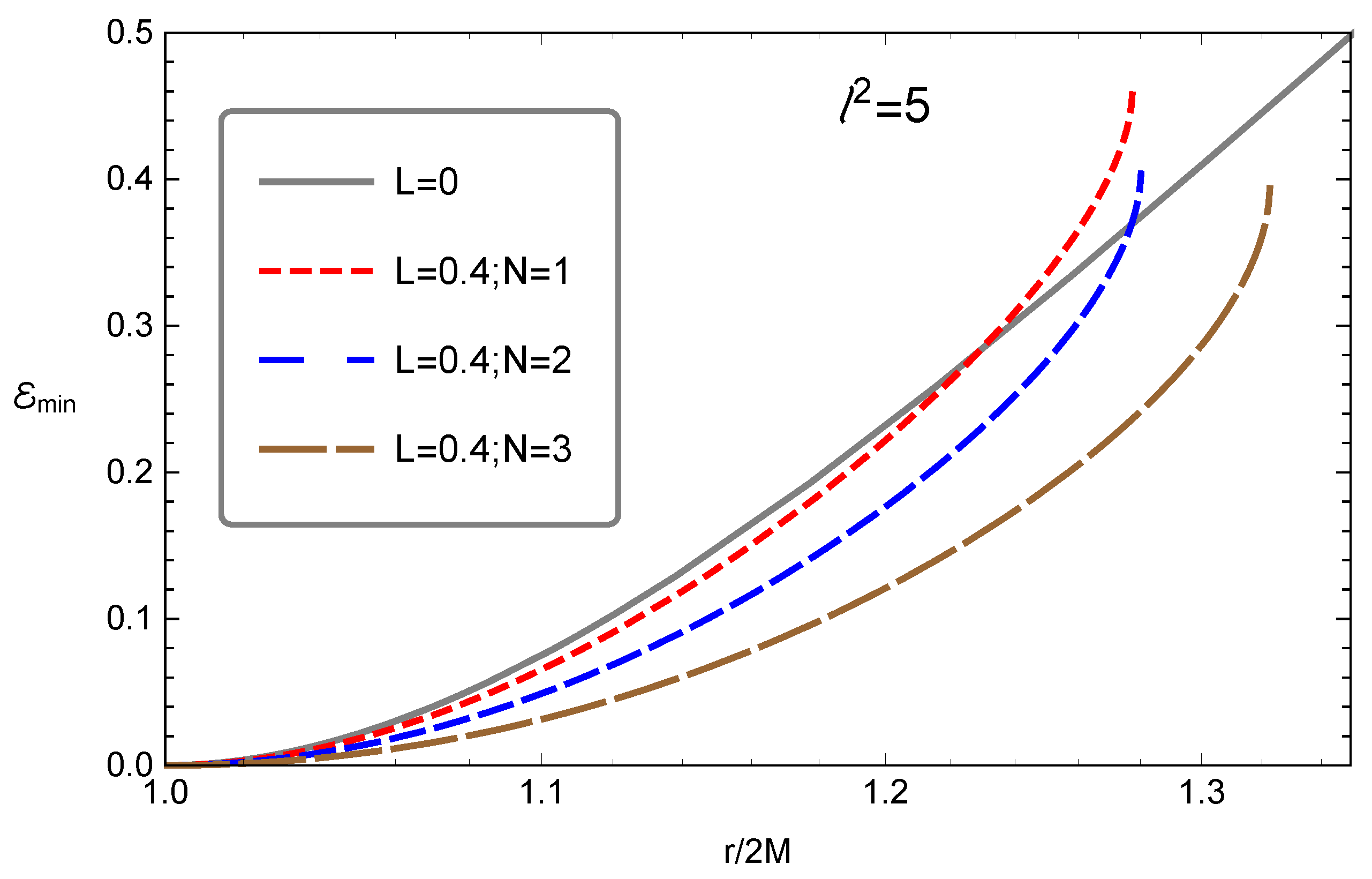
- The maximum value of the effective potential corresponding to circular motion of the magnetized particle increases with the increase of conformal parameters. However, the minimum value of the particle’s specific energy as well as upper and lower limits for minimum values of parameter decrease near .
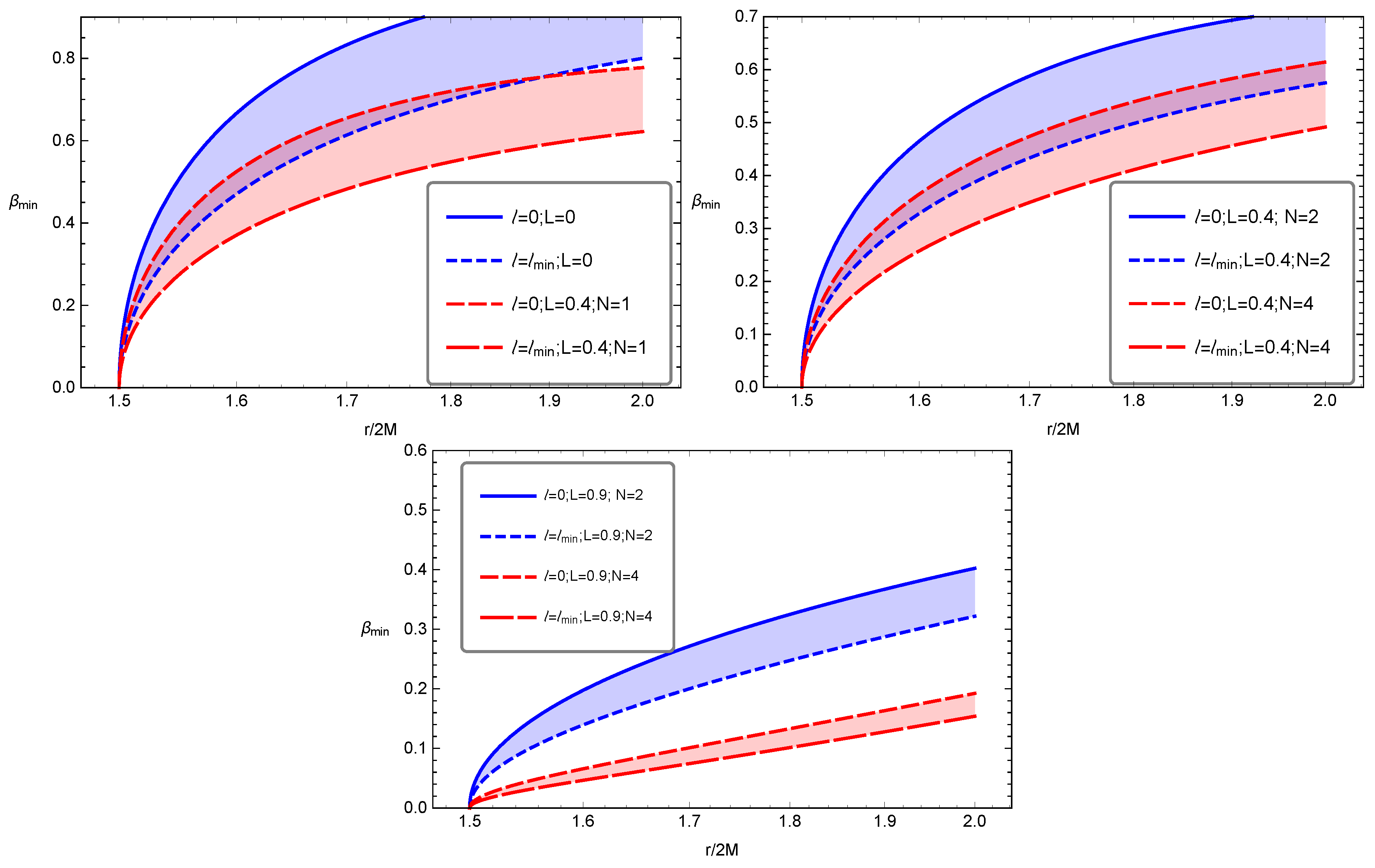
- The colored region in Figure 5 indicating the range between upper and lower limits of the parameter sufficiently shrinks at higher values of conformal parameter L, while the effect of the parameter N to the shrinking is not sufficient.
- Analysis of two colliding particles near the black hole environment shows that in all cases of neutral, charged and magnetized particle collision the center-of-mass energy decreases with the increase of conformal parameters L and N.
- It is shown in Figure 7 that the property/behavior of the center-of-mass energy differs in the case of magnetized particle colliding with positive and negative charged particles in conformal gravity. For instance, in the case of the collision of magnetized and negatively charged particles the innermost collision point comes closer at higher values of the parameters of conformal gravity. However, there is no observed dependence of the collision point on the values of the conformal parameters L and N.
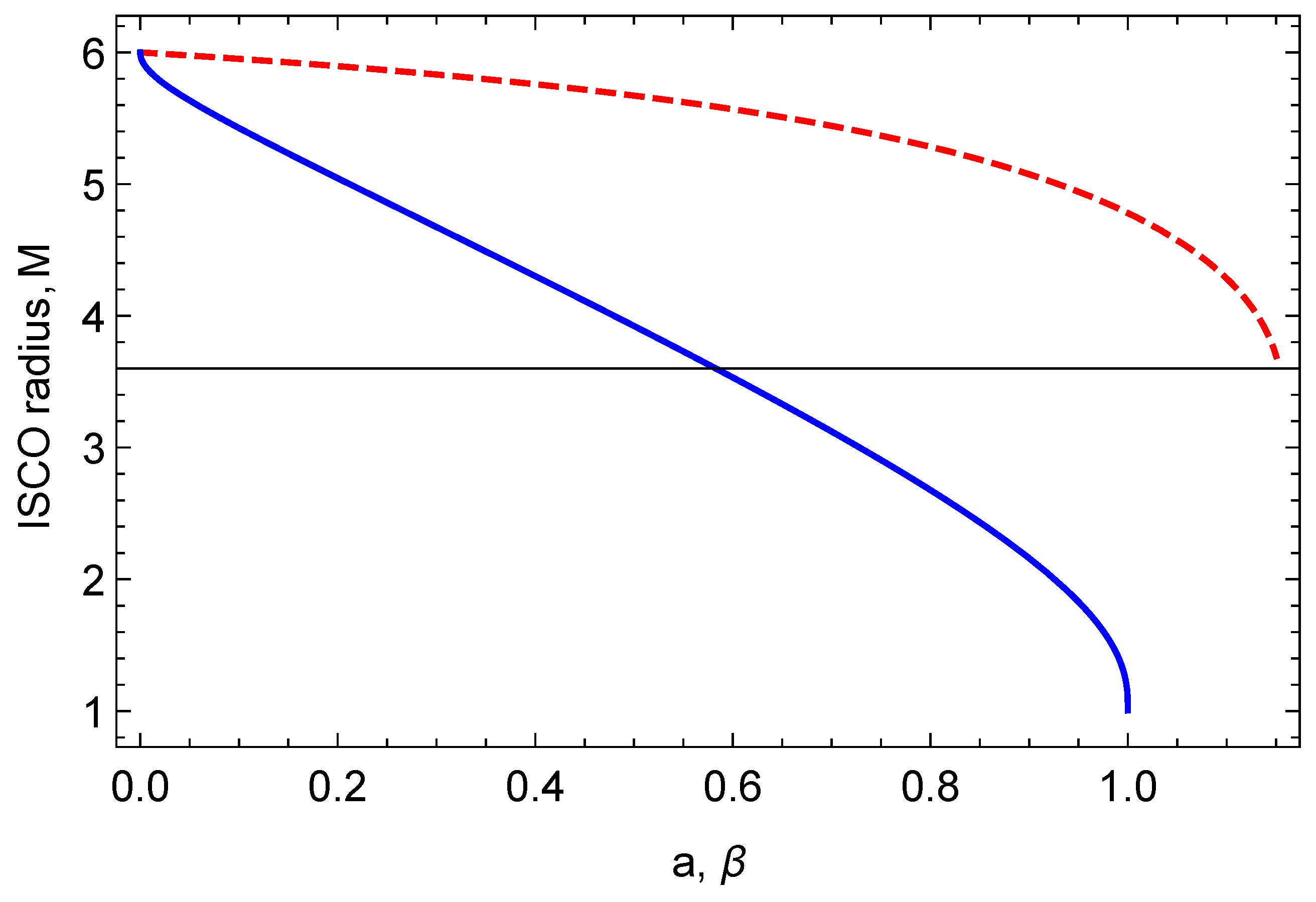
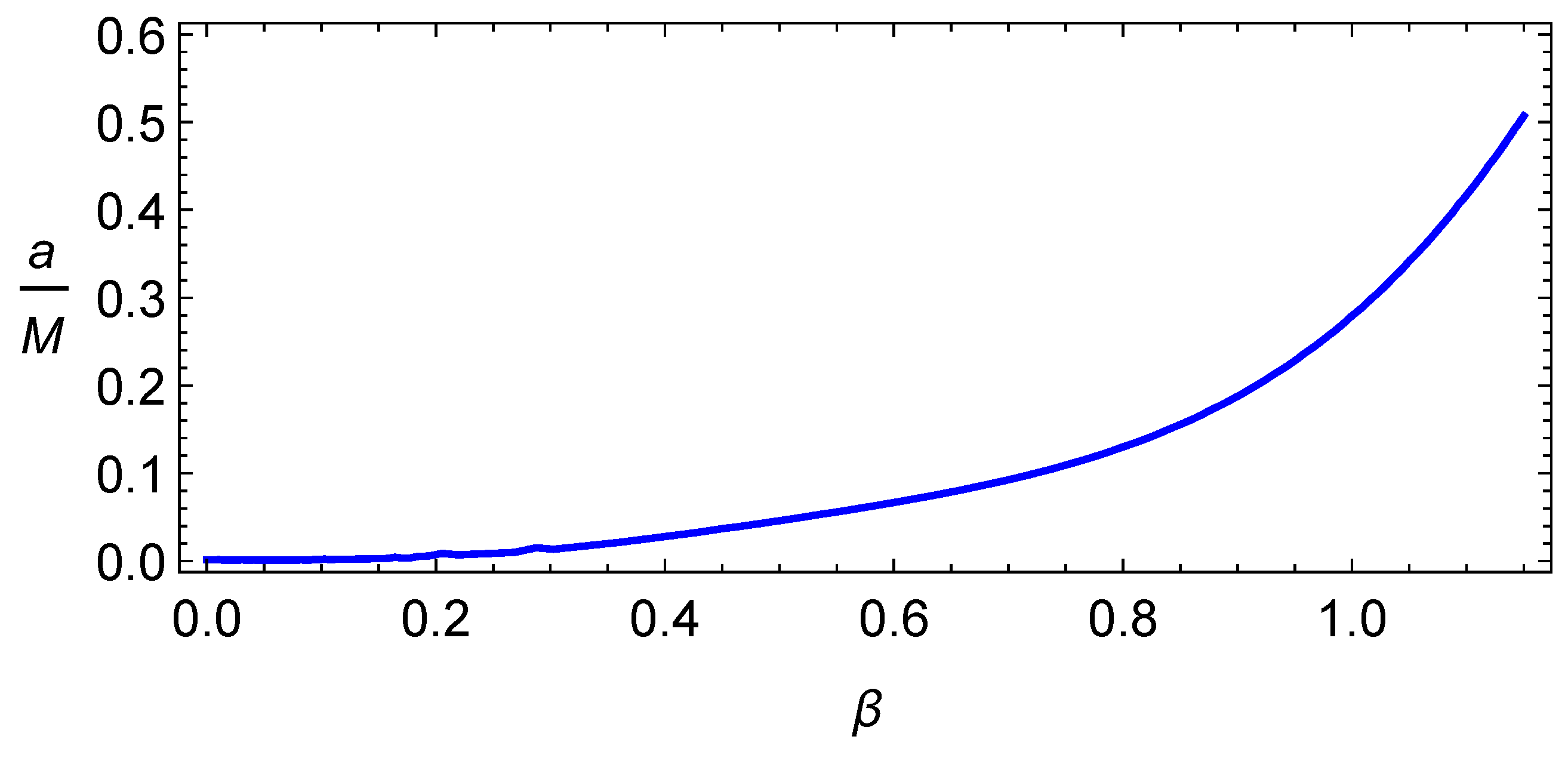
- We have applied the obtained results to the real astrophysical scenario when a pulsar treated as a magnetized particle is orbiting the supermassive black hole (SMBH) Sgr A* in the center of our galaxy in order to obtain the estimation of magnetized compact object’s orbital parameter. The possible detection of pulsar in Sgr A* close environment can provide constraints on black hole parameters. Here we have shown that the interaction of magnetic field Gauss with magnetic moment of magnetized neutron star can in principle mimic spin of Kerr black holes up to .
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bardeen, J. Non-singular general-relativistic gravitational collapse. In Proceedings of the International Conference GR5, USSR, Tbilisi, Georgia, 9–13 September 1968; p. 174. [Google Scholar]
- Hayward, S.A. Formation and Evaporation of Nonsingular Black Holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef] [Green Version]
- Ayón-Beato, E.; García, A. Regular Black Hole in General Relativity Coupled to Nonlinear Electrodynamics. Phys. Rev. Lett. 1998, 80, 5056–5059. [Google Scholar] [CrossRef] [Green Version]
- Ayon-Beato, E. New regular black hole solution from nonlinear electrodynamics. Phys. Lett. B 1999, 464, 25–29. [Google Scholar] [CrossRef] [Green Version]
- Ayon-Beato, E.; Garcia, A. Non-Singular Charged Black Hole Solution for Non-Linear Source. Gen. Relativ. Gravit. 1999, 31, 629–633. [Google Scholar] [CrossRef] [Green Version]
- Fan, Z.Y.; Wang, X. Construction of regular black holes in general relativity. Phys. Rev. D 2016, 94, 124027. [Google Scholar] [CrossRef] [Green Version]
- Toshmatov, B.; Ahmedov, B.; Abdujabbarov, A.; Stuchlík, Z. Rotating regular black hole solution. Phys. Rev. D 2014, 89, 104017. [Google Scholar] [CrossRef] [Green Version]
- Englert, F.; Truffin, C.; Gastmans, R. Conformal invariance in quantum gravity. Nucl. Phys. B 1976, 117, 407–432. [Google Scholar] [CrossRef]
- Narlikar, J.V.; Kembhavi, A.K. Space-time singularities and conformal gravity. Nuovo C. Lett. 1977, 19, 517–520. [Google Scholar] [CrossRef]
- Mannheim, P.D. Making the Case for Conformal Gravity. Found. Phys. 2012, 42, 388–420. [Google Scholar] [CrossRef] [Green Version]
- Bars, I.; Steinhardt, P.; Turok, N. Local conformal symmetry in physics and cosmology. Phys. Rev. D 2014, 89, 043515. [Google Scholar] [CrossRef] [Green Version]
- Bambi, C.; Modesto, L.; Rachwał, L. Spacetime completeness of non-singular black holes in conformal gravity. J. Cosmol. Astropart. Phys. 2017, 2017, 003. [Google Scholar] [CrossRef]
- Bambi, C.; Malafarina, D.; Modesto, L. Black supernovae and black holes in non-local gravity. J. High Energy Phys. 2016, 2016, 147. [Google Scholar] [CrossRef] [Green Version]
- Hořava, P. Quantum gravity at a Lifshitz point. Phys. Rev. D 2009, 79, 084008. [Google Scholar] [CrossRef] [Green Version]
- Hořava, P. Spectral Dimension of the Universe in Quantum Gravity at a Lifshitz Point. Phys. Rev. Lett. 2009, 102, 161301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kehagias, A.; Sfetsos, K. The black hole and FRW geometries of non-relativistic gravity. Phys. Lett. B 2009, 678, 123–126. [Google Scholar] [CrossRef] [Green Version]
- Turimov, B.; Ahmedov, B.; Abdujabbarov, A.; Bambi, C. Electromagnetic fields of slowly rotating magnetized compact stars in conformal gravity. Phys. Rev. D 2018, 97, 124005. [Google Scholar] [CrossRef] [Green Version]
- Zhou, M.; Cao, Z.; Abdikamalov, A.; Ayzenberg, D.; Bambi, C.; Modesto, L.; Nampalliwar, S. Testing conformal gravity with the supermassive black hole in 1H0707-495. Phys. Rev. D 2018, 98, 024007. [Google Scholar] [CrossRef] [Green Version]
- Toshmatov, B.; Bambi, C.; Ahmedov, B.; Abdujabbarov, A.; Stuchlík, Z. Energy conditions of non-singular black hole spacetimes in conformal gravity. Eur. Phys. J. C 2017, 77, 542. [Google Scholar] [CrossRef] [Green Version]
- Toshmatov, B.; Bambi, C.; Ahmedov, B.; Stuchlík, Z.; Schee, J. Scalar perturbations of nonsingular nonrotating black holes in conformal gravity. Phys. Rev. D 2017, 96, 064028. [Google Scholar] [CrossRef] [Green Version]
- Wald, R.M. Black hole in a uniform magnetic field. Phys. Rev. D 1974, 10, 1680–1685. [Google Scholar] [CrossRef]
- Aliev, A.N.; Galtsov, D.V.; Petukhov, V.I. Negative absorption near a magnetized black hole—Black hole masers. Astrophys. Space Sci. 1986, 124, 137–157. [Google Scholar] [CrossRef]
- Aliev, A.N.; Gal’tsov, D.V. REVIEWS OF TOPICAL PROBLEMS: “Magnetized” black holes. Sov. Phys. Uspekhi 1989, 32, 75–92. [Google Scholar] [CrossRef]
- Aliev, A.N.; Özdemir, N. Motion of charged particles around a rotating black hole in a magnetic field. Mon. Not. R. Astron. Soc. 2002, 336, 241–248. [Google Scholar] [CrossRef] [Green Version]
- Frolov, V.P.; Krtouš, P. Charged particle in higher dimensional weakly charged rotating black hole spacetime. Phys. Rev. D 2011, 83, 024016. [Google Scholar] [CrossRef] [Green Version]
- Frolov, V.P. Weakly magnetized black holes as particle accelerators. Phys. Rev. D 2012, 85, 024020. [Google Scholar] [CrossRef] [Green Version]
- Benavides-Gallego, C.A.; Abdujabbarov, A.; Malafarina, D.; Ahmedov, B.; Bambi, C. Charged particle motion and electromagnetic field in γ spacetime. Phys. Rev. D 2019, 99, 044012. [Google Scholar] [CrossRef] [Green Version]
- Shaymatov, S.; Ahmedov, B.; Stuchlík, Z.; Abdujabbarov, A. Effect of an external magnetic field on particle acceleration by a rotating black hole surrounded with quintessential energy. Int. J. Mod. Phys. D 2018, 27, 1850088. [Google Scholar] [CrossRef]
- Oteev, T.; Abdujabbarov, A.; Stuchlík, Z.; Ahmedov, B. Energy extraction and particle acceleration around a rotating black hole in quintessence. Astrophys. Space Sci. 2016, 361, 269. [Google Scholar] [CrossRef]
- Toshmatov, B.; Abdujabbarov, A.; Ahmedov, B.; Stuchlík, Z. Motion and high energy collision of magnetized particles around a Hořava-Lifshitz black hole. Astrophys. Space Sci. 2015, 360, 19. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Schee, J.; Abdujabbarov, A. Ultra-high-energy collisions of particles in the field of near-extreme Kehagias-Sfetsos naked singularities and their appearance to distant observers. Phys. Rev. D 2014, 89, 104048. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Ahmedov, B.; Rahimov, O.; Salikhbaev, U. Magnetized particle motion and acceleration around a Schwarzschild black hole in a magnetic field. Phys. Scr. 2014, 89, 084008. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Ahmedov, B. Test particle motion around a black hole in a braneworld. Phys. Rev. D 2010, 81, 044022. [Google Scholar] [CrossRef] [Green Version]
- Abdujabbarov, A.; Ahmedov, B.; Hakimov, A. Particle motion around black hole in Hořava-Lifshitz gravity. Phys. Rev. D 2011, 83, 044053. [Google Scholar] [CrossRef] [Green Version]
- Abdujabbarov, A.A.; Ahmedov, B.J.; Shaymatov, S.R.; Rakhmatov, A.S. Penrose process in Kerr-Taub-NUT spacetime. Astrophys. Space Sci. 2011, 334, 237–241. [Google Scholar] [CrossRef] [Green Version]
- Abdujabbarov, A.A.; Ahmedov, B.J.; Kagramanova, V.G. Particle motion and electromagnetic fields of rotating compact gravitating objects with gravitomagnetic charge. Gen. Relativ. Gravit. 2008, 40, 2515–2532. [Google Scholar] [CrossRef]
- Karas, V.; Kovar, J.; Kopacek, O.; Kojima, Y.; Slany, P.; Stuchlik, Z. Regular and Chaotic Motion in General Relativity. Case of Magnetized Black Hole and a Massive Magnetic Dipole. In Proceedings of the American Astronomical Society Meeting Abstracts #220, Anchorage, Alaska, 10–14 June 2012; Volume 220. [Google Scholar]
- Stuchlík, Z.; Kološ, M. Acceleration of the charged particles due to chaotic scattering in the combined black hole gravitational field and asymptotically uniform magnetic field. Eur. Phys. J. C 2016, 76, 32. [Google Scholar] [CrossRef] [Green Version]
- Kovář, J.; Kopáček, O.; Karas, V.; Stuchlík, Z. Off-equatorial orbits in strong gravitational fields near compact objects II: Halo motion around magnetic compact stars and magnetized black holes. Class. Quantum Gravity 2010, 27, 135006. [Google Scholar] [CrossRef]
- Kovář, J.; Slaný, P.; Cremaschini, C.; Stuchlík, Z.; Karas, V.; Trova, A. Electrically charged matter in rigid rotation around magnetized black hole. Phys. Rev. D 2014, 90, 044029. [Google Scholar] [CrossRef] [Green Version]
- Kološ, M.; Tursunov, A.; Stuchlík, Z. Possible signature of magnetic fields related to quasi-periodic oscillation observed in microquasars. Eur. Phys. J. C 2017, 77, 860. [Google Scholar] [CrossRef]
- de Felice, F.; Sorge, F. Magnetized orbits around a Schwarzschild black hole. Class. Quantum Gravity 2003, 20, 469–481. [Google Scholar] [CrossRef]
- de Felice, F.; Sorge, F.; Zilio, S. Magnetized orbits around a Kerr black hole. Class. Quantum Gravity 2004, 21, 961–973. [Google Scholar] [CrossRef]
- Rayimbaev, J.R. Magnetized particle motion around non-Schwarzschild black hole immersed in an external uniform magnetic field. Astrophys. Space Sci. 2016, 361, 288. [Google Scholar] [CrossRef]
- Rahimov, O.G.; Abdujabbarov, A.A.; Ahmedov, B.J. Magnetized particle capture cross section for braneworld black hole. Astrophys. Space Sci. 2011, 335, 499–504. [Google Scholar] [CrossRef] [Green Version]
- Rahimov, O.G. Magnetized Particle Motion around Black Hole in Braneworld. Mod. Phys. Lett. A 2011, 26, 399–408. [Google Scholar] [CrossRef]
- Penrose, R. Solutions of the Zero-Rest-Mass Equations. J. Math. Phys. 1969, 10, 38–39. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. Roy. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Dhurandhar, S.V.; Dadhich, N. Energy extraction processes near a Kerr black hole immersed in a magnetic field. Bull. Astron. Soc. India 1983, 11, 85. [Google Scholar]
- Dhurandhar, S.V.; Dadhich, N. Energy-extraction processes from a Kerr black hole immersed in a magnetic field. I. Negative-energy states. Phys. Rev. D 1984, 29, 2712–2720. [Google Scholar] [CrossRef]
- Dhurandhar, S.V.; Dadhich, N. Energy-extraction processes from a Kerr black hole immersed in a magnetic field. II. The formalism. Phys. Rev. D 1984, 30, 1625–1631. [Google Scholar] [CrossRef]
- Wagh, S.M.; Dhurandhar, S.V.; Dadhich, N. Revival of the Penrose process for astrophysical applications. Astrophys. J. 1985, 290, 12–14. [Google Scholar] [CrossRef]
- Bañados, M.; Silk, J.; West, S.M. Kerr Black Holes as Particle Accelerators to Arbitrarily High Energy. Phys. Rev. Lett. 2009, 103, 111102. [Google Scholar] [CrossRef] [Green Version]
- Abdujabbarov, A.A.; Tursunov, A.A.; Ahmedov, B.J.; Kuvatov, A. Acceleration of particles by black hole with gravitomagnetic charge immersed in magnetic field. Astrophys. Space Sci. 2013, 343, 173–179. [Google Scholar] [CrossRef] [Green Version]
- Abdujabbarov, A.A.; Ahmedov, B.J.; Jurayeva, N.B. Charged-particle motion around a rotating non-Kerr black hole immersed in a uniform magnetic field. Phys. Rev. D 2013, 87, 064042. [Google Scholar] [CrossRef]
- Narzilloev, B.; Abdujabbarov, A.; Bambi, C.; Ahmedov, B. Charged particle motion around a quasi-Kerr compact object immersed in an external magnetic field. Phys. Rev. D 2019, 99, 104009. [Google Scholar] [CrossRef] [Green Version]
- Ginzburg, V.L.; Ozernoi, L.M. On gravitational collapse of magnetic stars. Zh. Eksp. Teor. Fiz. 1964, 47, 1030. [Google Scholar]
- Price, R. Nonspherical perturbations of relativistic gravitational collapse. I. Scalar and gravitational perturtbations. Phys. Rev. D 1972, 5, 2419. [Google Scholar] [CrossRef]
- Aliev, A.N.; Gümrükçüoǧlu, A.E. Charged rotating black holes on a 3-brane. Phys. Rev. D 2005, 71, 104027. [Google Scholar] [CrossRef] [Green Version]
- Psaltis, D.; Wex, N.; Kramer, M. A Quantitative Test of the No-hair Theorem with Sgr A* Using Stars, Pulsars, and the Event Horizon Telescope. Astrophys. J. 2016, 818, 121. [Google Scholar] [CrossRef] [Green Version]
- De Laurentis, M.; Younsi, Z.; Porth, O.; Mizuno, Y.; Rezzolla, L. Test-particle dynamics in general spherically symmetric black hole spacetimes. Phys. Rev. D 2018, 97, 104024. [Google Scholar] [CrossRef]
- Frolov, V.P.; Shoom, A.A. Motion of charged particles near a weakly magnetized Schwarzschild black hole. Phys. Rev. D 2010, 82, 084034. [Google Scholar] [CrossRef] [Green Version]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haydarov, K.; Abdujabbarov, A.; Rayimbaev, J.; Ahmedov, B. Magnetized Particle Motion around Black Holes in Conformal Gravity: Can Magnetic Interaction Mimic Spin of Black Holes? Universe 2020, 6, 44. https://doi.org/10.3390/universe6030044
Haydarov K, Abdujabbarov A, Rayimbaev J, Ahmedov B. Magnetized Particle Motion around Black Holes in Conformal Gravity: Can Magnetic Interaction Mimic Spin of Black Holes? Universe. 2020; 6(3):44. https://doi.org/10.3390/universe6030044
Chicago/Turabian StyleHaydarov, Kamoliddin, Ahmadjon Abdujabbarov, Javlon Rayimbaev, and Bobomurat Ahmedov. 2020. "Magnetized Particle Motion around Black Holes in Conformal Gravity: Can Magnetic Interaction Mimic Spin of Black Holes?" Universe 6, no. 3: 44. https://doi.org/10.3390/universe6030044
APA StyleHaydarov, K., Abdujabbarov, A., Rayimbaev, J., & Ahmedov, B. (2020). Magnetized Particle Motion around Black Holes in Conformal Gravity: Can Magnetic Interaction Mimic Spin of Black Holes? Universe, 6(3), 44. https://doi.org/10.3390/universe6030044






