Localization of Dirac Fermions in Finite-Temperature Gauge Theory

Abstract

It is by now well established that Dirac fermions coupled to non-Abelian gauge theories can undergo an Anderson-type localization transition. This transition affects eigenmodes in the lowest part of the Dirac spectrum, the ones most relevant to the low-energy physics of these models. Here we review several aspects of this phenomenon, mostly using the tools of lattice gauge theory. In particular, we discuss how the transition is related to the finite-temperature transitions leading to the deconfinement of fermions, as well as to the restoration of chiral symmetry that is spontaneously broken at low temperature. Other topics we touch upon are the universality of the transition, and its connection to topological excitations (instantons) of the gauge field and the associated fermionic zero modes. While the main focus is on Quantum Chromodynamics, we also discuss how the localization transition appears in other related models with different fermionic contents (including the quenched approximation), gauge groups, and in different space-time dimensions. Finally, we offer some speculations about the physical relevance of the localization transition in these models.

1. Introduction

Quantum Chromodynamics (QCD) is currently our best microscopic description of strong interactions. As is well known, QCD is a gauge theory with gauge group SU(3), coupling six “flavors” of quarks, which are spin-$\frac{1}{2}$ Dirac fermions transforming in the fundamental representation of the group, to the eight spin-1 gauge bosons (known as gluons) associated with the local SU(3) symmetry. Despite their apparently simple form, the interactions of quarks and gluons, as dictated by the gauge principle and encoded in the Dirac operator, give rise to a wide variety of phenomena. Most notably, the low-energy properties of strongly interacting matter are largely determined by the phenomena of confinement and chiral symmetry breaking (see, e.g., Refs. [1,2,3,4]). At zero temperature, quarks and gluons are in fact confined within hadrons by a linearly rising potential, up to distances where a quark-antiquark pair can be created out of the vacuum. Furthermore, there is an approximate chiral symmetry associated with the lightest quarks, which in the limit of exactly massless quarks is broken spontaneously. This determines most of the properties of light hadrons, once the effects of the explicit breaking by the light quark masses is taken into account.

Confinement and chiral symmetry breaking persist also at nonzero but low temperature and densities. It is well established that, at vanishing chemical potential, QCD undergoes a finite-temperature transition to a deconfined, chirally restored phase (quark-gluon plasma), around $T_c\approx 155\mathrm{MeV}$ [5,6]. This transition is a rapid but analytic crossover [7], with both confining and chiral properties of the theory changing dramatically in a relatively narrow interval of temperatures.

In particular, the confining properties are determined by the fate of an approximate ${\mathbb{Z}}_3$ center symmetry, i.e., a symmetry under gauge transformations which are periodic in time up to an element of the group center. At low temperature, center symmetry is only explicitly and mildly broken by the presence of quarks; at higher temperatures, instead, center symmetry is strongly broken spontaneously by the ordering of the Polyakov loop, i.e., the holonomy of the gauge field along a straight path winding around the temporal direction. In the “quenched” limit of infinitely heavy quarks, QCD reduces to SU(3) pure gauge theory, where center symmetry is an exact symmetry of the action, realized at low temperature à la Wigner-Weyl in the Hilbert space of the system, while spontaneously broken at high temperatures. Around the same temperature at which the Polyakov loop starts becoming ordered in QCD, corresponding roughly to the spontaneous breaking of center symmetry, also the chiral properties of the system change radically. The approximate order parameter of chiral symmetry, i.e., the chiral condensate $\langle \overline{\psi }\psi \rangle$, decreases rapidly around $T_c$, corresponding to the disappearance of the effects of spontaneous breaking in the chiral limit. The net effect is an effective restoration of chiral symmetry, up to the explicit breaking due to the quark masses.

While the existence and the nature of the finite-temperature transition are by now well established, the mechanisms of confinement and chiral symmetry breaking, and similarly of deconfinement and chiral symmetry restoration, are not fully understood yet; nor is the apparently close relation between these two phenomena that are in principle completely unrelated. An important role in the breaking and restoration of chiral symmetry is played by the topological properties of the gauge field configurations.

It might be possible to understand the formation of a chiral condensate in the low temperature phase of QCD in terms of instantons and the associated zero modes [8,9,10,11,12,13,14,15]. It is well known that there is an exact zero mode of the Dirac operator associated with an isolated instanton or anti-instanton, and with their finite-temperature versions known as calorons [16,17,18,19,20,21,22,23]. Typical gauge field configurations can be interpreted as a more or less dense medium of instantons and anti-instantons. For a sufficiently high density of topological objects, the associated zero modes will strongly mix and form a finite band of near-zero Dirac modes, which in turn gives rise to a finite condensate via the Banks-Casher relation [24]. At higher temperatures the density of topological objects decreases, and so do the density of near-zero Dirac modes and the chiral condensate, until the symmetry is effectively restored. This is the “disordered medium scenario” for chiral symmetry breaking. The mechanism of confinement is understood less clearly, and various proposals have been put forth: we invite the interested reader to consult Refs. [1,2].

Relatively recently, a third phenomenon has been found to take place in correspondence with deconfinement and chiral symmetry restoration in QCD, namely the localization of the low-lying eigenmodes of the Dirac operator [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]. Localization is a widely studied subject in condensed matter physics, since Anderson’s work on the absence of diffusion in random lattice system [41]. In his seminal paper, Anderson showed how the presence of disorder causes the spatial localization of energy eigenmodes. For electrons in a disordered medium, such as a conductor with impurities, localized modes appear at the band edge, beyond a “mobility edge” separating extended and localized modes. As the amount of impurities/disorder increases, the mobility edge moves towards the band center, eventually leading to all modes becoming localized, and to the conducting sample turning into an insulator. It is outside the scope of this paper (and frankly quite a Herculean task) to provide an exhaustive account of the developments in the theory of Anderson localization, and we refer the interested reader to the reviews [42,43,44,45,46].

It has been shown that a similar localization phenomenon takes place for the low-lying modes of the Dirac operator in QCD above the pseudocritical temperature [27,28,30,33,34,39,40]: up to a critical point in the spectrum, i.e., the analogue of the “mobility edge”, low modes are spatially localized on the scale of the inverse temperature [33,39]. The mobility edge depends on the temperature T, and its extrapolation towards the confined phase vanishes at a temperature compatible with $T_c$ [33,40]. At the mobility edge, a second-order phase transition takes place in the spectrum, which has been shown to be a genuine Anderson transition [34,35,36,37].

A disorder-driven transition, such as the Anderson transition in the Dirac spectrum, obviously needs a source of disorder. This was first identified in the local fluctuations of the topological charge density, treated as a dilute ensemble of pseudoparticles (calorons) [25,26,27,28]. As already mentioned above, these topological objects individually support localized zero modes of the Dirac operator; since they overlap, the corresponding modes mix and shift away from zero, but for a dilute ensemble this effect is small and modes remain localized and near zero. While evidence was produced supporting the connection between localization and topological objects, it turned out that not all localized modes could be explained this way [31], and at least another source of disorder was needed. This was identified in the fluctuations of the Polyakov loop [31], a hypothesis supported by numerical results [31,39,40] and by the critical properties found at the mobility edge [34,35,36,37]. This led to the so-called “sea/islands picture” of localization, proposed in Ref. [31] and further elaborated in Refs. [47,48,49]: Dirac eigenmodes tend to localize on “islands” of Polyakov loop fluctuations away from its ordered value, which form an extended “sea” in the deconfined phase. The sea/islands picture requires only the existence of a phase with ordered Polyakov loop in order for localization to appear, and so leads one to expect the localization of the low Dirac modes in a generic gauge theory with a deconfinement transition. This has been verified in a variety of models [32,49,50,51,52,53,54,55,56], including ones without topology, thus providing further support to the sea/islands picture. This also clearly suggests a strong connection between localization of the low Dirac modes and deconfinement.

The relation between localization and chiral symmetry restoration has received less attention, mostly because of the intrinsic difficulty of studying gauge theories with massless fermions, where chiral symmetry is exact. It is, however, clearly established that localization of the low modes is accompanied by evident changes in the spectral density at the low end of the spectrum. In Refs. [51,54,57,58] it was observed that in the quenched theory a peak of near-zero modes of topological origin forms, followed by a spectral range with low mode density. A similar peak of localized modes was observed in Ref. [38] in the presence of dynamical fermions. (The presence of this peak was discussed before in Ref. [59], and has been studied recently in Refs. [60,61], although the localization properties of the eigenmodes are not studied there.) It is shown in Ref. [58] that the near-zero peak can be explained in terms of a dilute instanton/anti-instanton gas and the associated zero modes. Recently, it has been proposed that the presence of a finite density of near-zero localized modes in the chiral limit can lead to the disappearance of the finite-temperature massless excitations predicted by the finite-temperature version of Goldstone’s theorem [62].

While the presence of localization at high temperature, and its connection with the finite-temperature transition in QCD and in other gauge theories are by now fairly well established, the physical meaning of localization of Dirac modes, and a detailed understanding of the aforementioned connection with deconfinement and chiral symmetry restoration, have proved to be quite elusive. The hope is that a better understanding of localization can shed light on the mechanisms of confinement and chiral symmetry breaking, and on the finite-temperature deconfining and chirally restoring transition.

In this review we will discuss developments in the study of the localization of Dirac modes in finite-temperature gauge theories. While the main focus is on QCD, we will discuss also other models, showing in particular that the connection between localization and deconfinement is a general phenomenon. As this review is aimed both at the particle physics and condensed matter communities (and expected to disappoint them both), we provide brief introductions to the subjects of finite-temperature QCD and Anderson localization in an attempt to bridge the gaps. Older results were already reviewed in Refs. [36,63].

Localization in gauge theories also occurs in a few other contexts, albeit those correspond to physical situations very different from the one discussed in the present review. For this reason here we do not discuss them in detail, and only mention them for completeness. A non-exhaustive list of references includes the following papers. For results concerning the relation between the localization properties of the low Dirac modes and the topological structure of the vacuum in gauge theories, we refer to Refs. [64,65,66,67,68] and references therein. The role played by localization in the Aoki phase of quenched QCD with Wilson fermions, especially concerning the fate of Goldstone modes, is studied in Refs. [69,70]. Localization properties of the eigenmodes of the covariant Laplacian in Yang-Mills theories are studied in Refs. [71,72].

The plan of this paper is as follows. In Section 2 we review finite-temperature QCD and related issues. In Section 3 we review the topic of localization and Anderson transitions in some generality. In Section 4 we discuss localization in QCD at finite temperature. The disordered medium scenario and the sea/islands picture, providing mechanisms for localization, are discussed in Section 5. Localization in gauge theories other than QCD is discussed in Section 6. Finally, in Section 7 we draw our conclusions and show some prospects for the future.

2. QCD at Finite Temperature

In strongly interacting systems such as QCD localization takes place as the systems cross from the hadronic to the high-temperature quark-gluon plasma state. To put localization in QCD in the proper context, in the present section we summarize some basic facts about this finite temperature transition. For an introduction to gauge theories at finite temperature we refer the reader to the literature (see, e.g., Refs. [73,74]).

In an extended sense, QCD is a gauge theory with $N_f$ flavors of quarks transforming in the fundamental representation of the gauge group SU($N_c$) and interacting via the corresponding gauge field, the excitations of which are the gluons. In a stricter sense, in QCD $N_f$ is fixed to six, the number of known quark flavors, and $N_c=3$. At finite temperature, the theory is formally defined by the Euclidean partition function

$$Z_{\mathrm{QCD}}=\int \left[dA\right]e^{-S_{\mathrm{YM}}\left[A\right]}\prod _{f}det\left(\cancel{D}\left[A\right]+m_f\right),$$

(1)

where the product runs over the quark flavors with masses $m_f$, A is the gauge field, $S_{\mathrm{YM}}$ is the Euclidean Yang-Mills action and

$$\cancel{D}\left[A\right]=\sum _{\mu =1}^4{\gamma }_{\mu }({\partial }_{\mu }+ig{A}_{\mu })$$

(2)

is the Euclidean Dirac operator, with ${\gamma }_{\mu }$ the Euclidean, Hermitean gamma matrices and g the coupling constant. The temporal direction is compactified to a circle of size equal to the inverse temperature, and periodic boundary conditions in the temporal direction are imposed on the gauge fields. In this form of the partition function the quark fields, appearing in the action quadratically, have been explicitly integrated out, resulting in the quark determinant. The Dirac operator is an anti-Hermitean operator with purely imaginary spectrum, which is furthermore symmetric about zero thanks to the property $\{{\gamma }_5,\cancel{D}\}=0$.

It is instructive to consider the theory as a function of its parameters, that in reality are fixed by the observed properties of hadrons. The only such parameters of QCD are the quark masses.1 In particular, the low-energy properties of light hadrons are completely determined by the masses of the lightest quarks, the u and d quark, and to some extent the heavier s quark. The other three known quark flavors are so heavy that they have little influence on the low energy physics.

Quark masses are also important parameters from a theoretical point of view, because they crucially influence some symmetries of the system. Even though in nature these are only approximate symmetries, considering them helps to better understand the finite temperature transition of QCD. In an imaginary world with two massless quark flavors, i.e., when $m_u=m_d=0$, QCD would have an exact $\mathrm{SU}{\left(2\right)}_V\times \mathrm{SU}{\left(2\right)}_A\times \mathrm{U}{\left(1\right)}_A$ chiral symmetry. Here $\mathrm{SU}{\left(2\right)}_V$ is a rotation in the two-dimensional $(u,d)$ flavor-space that acts identically on all the Dirac components. In contrast, the flavor non-singlet axial symmetry $\mathrm{SU}{\left(2\right)}_A$ not only mixes the two flavors, but also transforms the left and right Dirac components with opposite phases. Finally, the $\mathrm{U}{\left(1\right)}_A$ flavor-singlet axial symmetry acts trivially in flavor space and rotates the left and right Dirac components with opposite phases. Even though these are all symmetries of the classical Lagrangian, after quantization the $\mathrm{U}{\left(1\right)}_A$ part of the symmetry is anomalously broken. Furthermore, at zero temperature the $\mathrm{SU}{\left(2\right)}_A$ axial symmetry is spontaneously broken. The emerging three Goldstone bosons are the analogues of the pions, and the order parameter of the symmetry breaking is the light quark condensate $\langle \overline{\psi }\psi \rangle$. Finally, the vector part of the symmetry $\mathrm{SU}{\left(2\right)}_V$ remains intact even for finite, but equal quark masses.

In reality, the nonzero and non-equal masses of the u and d quarks explicitly break these symmetries; however, the spontaneous and anomalous breaking inherited from the massless theory both turn out to be much stronger than this explicit breaking. In fact, in an imaginary world with zero u and d quark masses, the low-energy properties of the light hadrons would be much the same as they are in the real world. The only important exceptions would be the pions, which in that case would be exact Goldstone bosons with zero mass.

If one imagines changing the quark masses, the other interesting limit is the one in which quarks are much heavier than in reality. In particular, in the limit of infinitely heavy quarks the quark determinant in the path integral completely decouples and the back-reaction of the quarks on the gauge field disappears. This is the so-called quenched theory. In this limit QCD has a different exact symmetry, the symmetry group being the center of the gauge group, in the case at hand ${\mathbb{Z}}_3$. The symmetry transformation in question is a gauge transformation that is singular along a spacelike hypersurface, and its singularity is characterized by an element of the center ${\mathbb{Z}}_3$. Recalling that the system is finite in the temporal direction with periodic boundary conditions for the gauge field, this symmetry transformation is a gauge transformation that is not periodic in the temporal direction (hence singular), and it multiplies by the same ${\mathbb{Z}}_3$ center element all the holonomies (gauge parallel transporters) going around the system in the temporal direction. The holonomies wrapping around the system in the temporal direction along a straight path are also called Polyakov loops.

Gauge invariant local gluonic quantities are defined in terms of holonomies around small loops, and those never wrap around the system. These types of loops cross the hypersurface where the gauge transformation is singular the same number of times in both directions. As a result, the ${\mathbb{Z}}_3$ factors along such a loop always cancel, and gauge invariant local quantities are invariant with respect to the ${\mathbb{Z}}_3$ center transformations. In contrast, fermionic quantities are affected, since such a singular gauge transformation essentially introduces an extra ${\mathbb{Z}}_3$ twist for the temporal boundary condition of the fermions through the covariant derivative in the Dirac operator. The boundary condition affects the spectrum of the Dirac operator and also its determinant that appears in the path integral. At low temperatures where the correlation length is much smaller than the temporal extent of the system, and Polyakov loops fluctuate locally with little correlation, the temporal boundary condition has only a small impact on the Dirac determinant. Consequently, the quarks only mildly break the ${\mathbb{Z}}_3$ symmetry. However, at high temperature, where the correlation length becomes comparable to or larger than the temporal size of the system, and the Polyakov loops tend to align with each other, this picture changes drastically.

To understand exactly how that happens, let us first recall that in finite temperature quantum field theory the temporal boundary condition for fermions is antiperiodic. For free massless fermions this implies a gap in the spectrum of the Dirac operator equal to the first Matsubara frequency. If by a singular gauge transformation (as defined above) we introduce an additional ${\mathbb{Z}}_3$ twist in the boundary condition then the gap will decrease, because the twist $\pi$ corresponding to the antiperiodic boundary condition will decrease to $\pi \pm 2\pi /3=\pm \pi /3\left(\mathrm{mod}2\pi \right)$. In the interacting theory there is no gap in the spectrum, but through this mechanism the low end of the spectrum is much denser when the spatially averaged Polyakov loop is in the complex center sectors (i.e., close to one of the complex center elements) than when it is in the real one (i.e., close to the identity), where the effective twist comes only from the antiperiodic boundary condition. As a result, the fermion determinant, that disfavors larger low-mode density, strongly favors the real Polyakov loop sector, and for finite quark mass this is the only sector that contributes to the path integral. This is how fermions explicitly break the ${\mathbb{Z}}_3$ center symmetry and select the real Polyakov loop sector out of the three sectors that would be equivalent in their absence. This mechanism is at work also at low temperature, but much less effective there since the average Polyakov loop fluctuates around zero.2

Now going back to the quenched theory, at zero and low temperature, the exact ${\mathbb{Z}}_3$ symmetry of its Lagrangian remains intact, while above a critical temperature this symmetry is spontaneously broken and its order parameter, the trace of the Polyakov loop, develops a nonzero expectation value. In fact, in the quenched theory, the logarithm of the expectation value of the Polyakov loop is proportional to the gauge field energy it costs to insert an infinitely heavy static quark in the system. In this way, the vanishing of the Polyakov loop in the low-temperature phase shows that no free quarks can exist there, so quarks are confined into hadrons. In contrast, the nonzero expectation value of the Polyakov loop in the high temperature phase implies that quarks are not confined there.

The nature of the finite-temperature transition in extended QCD is governed by the chiral and the ${\mathbb{Z}}_3$ symmetries, which—as we have already seen—depend on the quark masses. In the quenched limit (infinite quark mass) lattice simulations have shown the transition to be weakly first order [78,79], and this behavior persists for large enough, but finite quark masses. If the quarks become lighter, the transition weakens and for intermediate quark masses there is a wide region where it is only a crossover. In particular, the light-quark masses in nature fall in this range [7]. For even smaller quark masses, the transition is again expected to become a true phase transition, but its order depends on the number of light quark flavors. For two light flavors (and physical strange quark mass) it is expected to be second order, whereas for three light flavors a first order phase transition is anticipated. However, the presence of these phase transitions, previously predicted based on an epsilon expansion [80] (see also [81] for the role played by the $\mathrm{U}{\left(1\right)}_A$ anomaly), have not yet been confirmed by lattice simulations, because simulations close to the chiral limit are technically challenging.

Most of the results discussed in this review are based on numerical calculations on the lattice. Lattice field theory is a nonperturbative approach to the quantization of quantum field theories, based on the discretization of the relevant path integrals that define the theory in the path-integral approach. We provide here only a very brief introduction to this subject, referring the interested reader to the extensive literature (e.g., the books [73,74,82,83,84]). In the lattice approach to gauge theories devised by Wilson [85], the SU(3) gauge fields of QCD are replaced by unitary SU(3) matrices (link variables) associated with the links of a finite hypercubic lattice. In continuum language, these correspond to the parallel transporters of the gauge fields along the paths connecting neighbouring lattice points. After a suitable discretization of the gauge action, the relevant path integrals are obtained by integrating over the gauge fields, which in practice means integrating the link variables over the group manifold with the invariant (Haar) group measure. The desired, continuum field theory is obtained (if this is possible) by properly tuning the parameters in the action, so that the correlation length of the system in lattice units diverges, and the system “forgets” about the underlying lattice. For pure gauge theories, the only available parameter is the lattice inverse gauge coupling (usually denoted by $\beta$), which ceases to be a freely adjustable parameter and turns instead into a measure of the lattice spacing.3

The approach outlined above is easily generalized to other gauge theories based on different gauge groups, by simply replacing the SU(3) link variables and the corresponding Haar measure with elements of the relevant gauge group and the corresponding Haar measure. The inclusion of fermions instead is not straightforward, especially for what concerns the implementation of chiral symmetry. Nonetheless, there are several viable discretization of the Dirac operator, which are expected to all lead to the same results in the continuum limit. Since they appear below in Section 4, we mention Wilson fermions, staggered fermions (possibly rooted), domain wall fermions, overlap fermions, and twisted mass fermions (see Refs. [83,84] and references therein for details). We finally mention that several improvement schemes exist that bring the system closer to the continuum limit, i.e., that reduce the effects due to the finiteness of the lattice spacing. Such schemes exist both for the gauge action and for the fermionic determinant (see Refs. [83,84] and references therein for details).

Finite-Temperature Transition, Dirac Spectrum, and Localization—An Overview

We have seen that in the two extreme cases, the quenched limit and the chiral limit, two different symmetries, the ${\mathbb{Z}}_3$ center symmetry and the $\mathrm{SU}{\left(2\right)}_A$ axial symmetry govern the transition. The respective order parameters, the Polyakov loop and the quark condensate, signal spontaneous breaking of the symmetry in the high temperature phase for the ${\mathbb{Z}}_3$ symmetry and in the low temperature phase for the $\mathrm{SU}{\left(2\right)}_A$ axial symmetry. In nature, both symmetries are only approximate, the transition is a crossover and the order parameters have only inflection points in the crossover region. It also follows that in real QCD there is no sharply defined transition temperature. In contrast, regardless of the quark mass, the localization transition, i.e., the appearance of the first localized modes at the low edge of the Dirac spectrum, occurs at a sharply defined critical temperature. Moreover—as anticipated in the Introduction, and as we will see below in Section 4 and Section 6—the localization transition occurs in the temperature range of the deconfining and chiral crossover in the case of real QCD, and exactly at the deconfining temperature in the quenched limit. This suggests that there might be a connection between the thermodynamic (chiral and deconfining) transitions on the one hand, and the localization transition on the other hand.

Besides the coincidence of their respective critical or pseudocritical temperatures, these phenomena are also connected through the degrees of freedom playing the most important role in their respective dynamics. When the system crosses into the high temperature phase, the spectral density of the Dirac operator around zero drops considerably, exactly vanishing in the chiral limit. This is how the chiral symmetry, spontaneously broken at low temperature, is restored above the transition. Indeed, through the Banks-Casher relation [24], the order parameter of chiral symmetry breaking, the quark condensate, is proportional in the chiral limit to the spectral density at zero, and generally strongly sensitive to the low end of the spectrum. Lower spectral density also means that eigenmodes close to each other in the spectrum are less likely to be mixed by fluctuations of the gauge field, which might lead to localization at the low end of the Dirac spectrum.

The spectral density, however, is not the only important parameter that influences localization. In the quark mass regions numerically explored so far, where the transition is either a crossover (near and below the physical values of the light quark masses) or a true phase transition governed by (approximate) center symmetry (heavy quark limit), the spectral density does not immediately drop to zero at the (pseudo)critical temperature. In particular, in the quenched limit just above the transition a narrow but tall spike at zero appears in the spectral density (see Figure 1). This is due to near-zero modes associated with a dilute gas of calorons and anticalorons, local fluctuations of the topological charge [58]. Even though the spectrum is dense in the spike, eigenmodes there are localized [86]. A similar peak of near-zero modes is also found for physical, near-physical, and below-physical light-quark masses [38,59,60,61]. For near-physical masses these modes are found to be localized [38], and most likely this persists as the mass is decreased.

Recently, the spike in the spectral density received another interpretation. It was argued that it signals the appearance of a new, previously undiscovered “phase” of QCD, intermediate between the low-temperature confined and the high-temperature deconfined phase [87]. In a more recent paper the same authors studied a newly defined infrared dimension $d_{\mathrm{IR}}$ of the eigenmodes in the low end of the spectrum of the chirally symmetric overlap Dirac operator. They concluded that the exact zero modes have $d_{\mathrm{IR}}=3$, and in the spectral peak $d_{\mathrm{IR}}$ changes rapidly but smoothly from 2 to 1 as one moves up in the spectrum [88]. This behavior persists up to the bulk of the spectrum, where the spectral density, together with the infrared dimension $d_{\mathrm{IR}}$ of the modes starts to increase again. This nontrivial change in the infrared dimension all happens in the region where based on the spectral statistics and the scaling of the participation ratio with the volume, the eigenmodes are thought to be localized. It would be interesting to further investigate how $d_{\mathrm{IR}}$ relates to the usual fractal dimension $D_2$ (see Equation (6)), and what kind of spatial structure in the eigenmodes gives rise to this nontrivial behavior. This could also depend on the chiral and locality properties of the particular discretization of the Dirac operator.

Topological fluctuations and the localization of the eigenmodes are both intimately related to fluctuations of the Polyakov loop, the order parameter of the quenched transition. The spatial localization of low Dirac eigenmodes is found to strongly correlate with local fluctuations of the Polyakov loop away from its symmetry-breaking equilibrium value [31,39,40]. This gives rise to the sea/islands picture of localization that we will discuss in Section 5.2 of the present paper in more details. Localization on calorons and localization on Polyakov loop fluctuations are, however, not mutually exclusive, as calorons always contain large fluctuations of the Polyakov loop. In fact, within a caloron, the Polyakov loop wraps around the gauge group in a topologically nontrivial way. The connection between calorons and Polyakov loop fluctuations is also shown by the strong correlation between the Polyakov loop and the topological susceptibility that can be observed close to the transition in the high temperature phase (see Figure 2).

The finite temperature transition of QCD is a result of the interplay of all those mechanisms that we just discussed, involving the Polyakov loop, the topological fluctuations and the spectral density of the Dirac operator around zero. Since localization is intimately related to all these aspects, it might hold the key to a better intuitive understanding of the dynamics of the transition.

3. Localization and Anderson Transitions

In a classic paper [41], Anderson showed that a sufficiently large amount of disorder in a lattice system prevents quantum-mechanical diffusion. Working in the one-particle tight-binding approximation, and mimicking the effect of disorder by supplementing the tight-binding Hamiltonian with a random potential on the lattice sites, Anderson showed that all the eigenfunctions of the system are localized for sufficiently strong disorder (i.e., for a sufficiently broad distribution for the random potential).

A practical example of this situation is a “dirty” crystal where some of the lattice atoms are replaced by impurities. Anderson’s results imply that all the electron eigenstates become localized for a sufficiently large concentration of impurities. This prevents electron diffusion and the associated transport phenomena; in particular, the d.c. conductivity at zero temperature vanishes [89,90]. Localization then provides a possible mechanism for a disorder-induced metal-insulator transition (MIT).

Anderson’s original arguments were later scrutinized and clarified by several authors [91,92,93,94,95,96,97]. Since then, the topic of disorder-induced localization, or Anderson localization, has been extensively studied in the condensed matter community, and it is impossible for us to provide here a comprehensive survey, or even do justice to the related literature. In this section we limit ourselves to a short review of the main aspects of Anderson localization, especially those relevant to gauge theories, discussed in the next Section. We invite the interested reader to consult the reviews [42,43,44,45,46].

3.1. The Anderson Model

In its simplest form, the (orthogonal) Anderson model Hamiltonian reads

$$H_{\overrightarrow{x},\overrightarrow{y}}^{\mathrm{AM}}={\epsilon }_{\overrightarrow{x}}{\delta }_{\overrightarrow{x},\overrightarrow{y}}+\sum _{\mu =1}^3({\delta }_{\overrightarrow{x}+\widehat{\mu },\overrightarrow{y}}+{\delta }_{\overrightarrow{x}-\widehat{\mu },\overrightarrow{y}}),$$

(3)

where $\overrightarrow{x},\overrightarrow{y}$ label the sites of a simple cubic lattice with lattice vectors $\widehat{\mu }$, $\mu =1,2,3$, and ${\epsilon }_{\overrightarrow{x}}$ is a random on-site potential, with uniform probability distribution in the interval $[-\frac{W}{2},\frac{W}{2}]$. The lattice spacing and the hopping energy are set to 1 for simplicity. The width W of the distribution is a measure of the amount of disorder in the system, with $W=0$ corresponding to a perfectly pure crystal. In this case, for a lattice of side L with periodic boundary conditions the eigenstates of $H^{\mathrm{AM}}$ are plane waves with wave vectors $\overrightarrow{p}=\frac{2\pi \overrightarrow{k}}{L}$, with $k_{\mu }=0,1,\dots ,L-1$. However, as soon as even a small amount of disorder is put into the system, i.e., $W\ne 0$, the eigenmodes $\psi \left(\overrightarrow{x}\right)$ at the band edge become exponentially localized, i.e., $|\psi \left(\overrightarrow{x}\right){|}^2\sim e^{-|\overrightarrow{x}-{\overrightarrow{x}}_0|/\xi }$ for E beyond critical energies $\pm E_c\left(W\right)$ called “mobility edges” [90] (see Figure 3). As the amount of disorder W in the system increases, the mobility edge moves towards the band center. Eventually, for W larger than a critical disorder, $W_c$, all the modes become localized. If Equation (3) describes the conduction band of an electron in some “dirty” crystalline system, for large enough W the Fermi energy will lie in the localized part of the band; d.c. transport then takes place through hopping of electrons from one localized state to another, which has an exponentially small probability of happening, and in the limit of infinite size leads to the absence of charge transport. As the amount of impurities increases past the critical value, the system then undergoes a metal-to-insulator transition.

3.2. Anderson Transitions

When the energy of the modes crosses the mobility edge $E_c\left(W\right)$ at fixed W, or equivalently when the disorder in the system crosses the energy-dependent critical disorder $W_c\left(E\right)$ at fixed mode energy E, the nature of the eigenmodes of $H^{\mathrm{AM}}$ changes from delocalized to localized. As argued in Ref. [98], in three dimensions the associated transition is a second-order phase transition (Anderson transition), with divergent correlation length $\xi \left(E\right)\sim |E-E_c{|}^{-\nu }$ or $\xi \left(W\right)\sim |W-W_c{|}^{-\nu }$, where the same exponent $\nu$ is expected.

This prediction is based on the so-called scaling theory of localization (see Ref. [43] for an introduction): first proposed in Ref. [98] based on previous ideas exposed in Refs. [42,99,100,101], it was later put on a firmer basis through a field-theoretical description of disordered systems and Anderson transitions [102,103,104] (see Ref. [45] for a full list of references). The basic idea is that the change in the conductance $G\left(L\right)$ of the system4 as its size L is increased is controlled only by the localized or delocalized nature of the energy eigenmodes, which in turn is measured by the conductance itself, as a proxy for the disorder in the system. This implies a scaling behavior of the conductance, $\frac{dlnG\left(L\right)}{dlnL}=\beta \left(G\right(L\left)\right)$. Using the asymptotics of the $\beta$ function obtained from localized or delocalized modes is then enough to show that in three dimensions there is an unstable fixed point (in the renormalization-group sense), and so a mobility edge in the energy spectrum and a phase transition at some critical amount of disorder (see Figure 4). In one dimension no Anderson transition is expected as all modes are localized in the presence of disorder [105,106], while the situation in two dimensions is more complicated (see below).

The Anderson model that we just described, Equation (3), is but the simplest disordered Hamiltonian in three dimensions, and can be generalized in various ways. One can consider different probability distributions for the on-site disorder (e.g., the Lloyd model [107]), add off-diagonal disorder by making also the hopping terms random [108,109,110], increase the range of interaction by adding more hopping terms (e.g., Ref. [111]), and so on. However, according to the general theory of the renormalization group (see, e.g., Ref. [112]), critical properties at a second-order phase transition are shared by systems in the same universality class, determined only by general properties such as the dimensionality and the symmetries of the system.5

From a technical point of view, the Anderson model is a model of (sparse) random matrices. The properties of these models are the subject of Random Matrix Theory (RMT) [113,114,115]. For random systems, the relevant symmetry classification has been provided by Dyson [116], later extended by Verbaarschot [117], and completed by Altland and Zirnbauer [118,119,120,121] (see also Refs. [45,122]). The main symmetry classes, relevant to the models discussed in this review, are determined by the existence (or not) of an antiunitary symmetry operator T (“time reversal”) commuting with the Hamiltonian, $[T,H]=0$, and further specified by whether $T^2=1$ or $T^2=-1$. If T exists and $T^2=1$, the system is in the orthogonal class (O): this is the case for the model in Equation (3). If T does not exist, the system is in the unitary class (U). Perhaps the simplest example of a system in this class is the so-called unitary Anderson model (UAM),

$$H_{\overrightarrow{x},\overrightarrow{y}}^{\mathrm{UAM}}={\epsilon }_{\overrightarrow{x}}{\delta }_{\overrightarrow{x},\overrightarrow{y}}+\sum _{\mu =1}^3({\delta }_{\overrightarrow{x}+\widehat{\mu },\overrightarrow{y}}+{\delta }_{\overrightarrow{x}-\widehat{\mu },\overrightarrow{y}})e^{i{\varphi }_{\overrightarrow{x},\overrightarrow{y}}},{\varphi }_{\overrightarrow{y},\overrightarrow{x}}=-{\varphi }_{\overrightarrow{x},\overrightarrow{y}},$$

(4)

which includes also off-diagonal disorder in the form of random phases ${\varphi }_{\overrightarrow{x},\overrightarrow{y}}$ in the hopping terms, mimicking the presence of a random magnetic field. Finally, if T exists and $T^2=-1$, the system is in the symplectic class (S). This classification is complete as far as the statistical properties in the bulk of the spectrum are concerned.

A refined classification is needed if one wants to discuss statistical spectral properties near the origin. In this case, one has to consider whether also a “particle-hole” symmetry exists, realized in terms of an antiunitary operator C obeying $\{C,H\}=0$, and if so whether $C^2=\pm 1$. This gives rise to nine different combinations. The eight combinations obtained when at least T or C exists correspond to eight different symmetry classes. If both T and C exist, it automatically follows that a unitary operator $\mathsf{\Gamma }=TC$ exists, anticommuting with the Hamiltonian, $\{\mathsf{\Gamma },H\}=0$, and satisfying ${\mathsf{\Gamma }}^2=1$. However, a $\mathsf{\Gamma }$ satisfying this property can exist also if T and C are both absent. In this case there are two further symmetry classes, corresponding to whether such a $\mathsf{\Gamma }$ exists or not, for a total of ten. The classification is summarized in

Table 1. Symmetry classes of random matrix ensembles. Entries corresponding to time-reversal (T) and particle-hole (C) symmetry indicate whether the symmetry is absent (0) or, if present, what is its square (±); entries corresponding to chiral symmetry ($\mathsf{\Gamma }$) indicate whether it is absent or present (0 or 1).

T	C	$\mathbf{\Gamma }$	Class
			Wigner-Dyson classes
0	0	0	A	(unitary)
+	0	0	AI	(orthogonal)
−	0	0	AII	(symplectic)
			chiral classes
0	0	1	AIII	(chiral unitary)
+	+	1	BDI	(chiral orthogonal)
−	−	1	CII	(chiral symplectic)
			Bogoliubov-de Gennes classes
0	−	0	C
+	−	1	CI
0	+	0	D
−	+	1	DIII

. In particular, if $\mathsf{\Gamma }$ exists and commutes with T (if this also exists), the system belongs to one of the chiral classes (chO, chU, and chS). Examples of systems of this type are provided by certain lattice models with random hopping terms, and no on-site potential, on bipartite lattices.

3.3. Detecting Localization: Eigenmode Observables

A convenient way to study the localization properties of the eigenmodes of a random lattice Hamiltonian and how they change along the spectrum is by means of the inverse participation ratios (IPRs),6

$${\mathrm{IPR}}_q\equiv \sum _x{\left|\psi \left(x\right)\right|}^{2q},$$

(5)

where it is assumed that eigenmodes obey the usual normalization condition, i.e., ${\sum }_x{\left|\psi \left(x\right)\right|}^2=1$, and x now labels the sites of the relevant lattice, assumed finite and of volume $V=L^d$, with L the linear size and d the dimensionality. Unless specified otherwise, in the following both the term and the notation IPR, without subscript, will be used to refer specifically to the case $q=2$. For modes extended throughout the whole system, one has qualitatively $|{\psi }_{\mathrm{ext}}{\left(x\right)|}^2\sim 1/V$, and so ${\mathrm{IPR}}_q\sim V^{1-q}$: after averaging over the possible realizations of disorder, which will be denoted with $\langle \dots \rangle$, and taking the large-volume limit, one has then $\langle {\mathrm{IPR}}_q\rangle \to 0$ as $V\to \infty$ (for $q>1$). For modes localized in a region of volume $V_0$ one has $|{\psi }_{\mathrm{loc}}{\left(x\right)|}^2\sim 1/V_0$ inside the localization region and negligible outside, and so ${\mathrm{IPR}}_q\sim V_0^{1-q}$: one has then $\langle {\mathrm{IPR}}_q\rangle \to \mathrm{const}.$ as $V\to \infty$. At the mobility edge, instead, the scaling of ${\mathrm{IPR}}_q$ with the volume depends on q in a highly nontrivial way. One has in general

$${\mathrm{IPR}}_q\sim L^{-(q-1)D_q},$$

(6)

where $D_q=d$ for extended modes and $D_q=0$ for localized modes, while at criticality $D_q$ is not a constant. This reflects the multifractal nature of eigenmodes at $E_c$ [124,125], and leads to define a set of multifractal exponents characterizing the critical behavior at the Anderson transition (see Ref. [45]).

Closely related to the IPR is the participation ratio,

$$\mathrm{PR}\equiv \frac{1}{V}{\mathrm{IPR}}^{-1}\left(=\frac{1}{V}{\mathrm{IPR}}_2^{-1}\right),$$

(7)

which measures the fraction of the system effectively occupied by the mode. For localized modes one has in the infinite volume limit $\langle \mathrm{PR}\rangle \to 0$, while for delocalized modes extended throughout the system one finds $\langle \mathrm{PR}\rangle \to$ a nonzero constant. Another equivalent way to measure the localization properties is to use the mode “size”, i.e., $V·\mathrm{PR}={\mathrm{IPR}}^{-1}$, which as $V\to \infty$ (after averaging over the disorder) remains constant for localized modes and diverges for delocalized modes. For systems with nontrivial spin and/or internal degrees of freedom, the eigenvectors ${\psi }_{\alpha ,c}\left(x\right)$ possess extra spin ($\alpha$) and/or internal indices (c). In these cases it is convenient to employ a definition of the IPR which is invariant under spacetime and internal (unitary) rotations, i.e.,

$$\mathrm{IPR}=\sum _x{\left(\sum _{\alpha ,c}{\left|{\psi }_{\alpha ,c}\left(x\right)\right|}^2\right)}^2=\sum _x{\left(\psi {\left(x\right)}^{†}\psi \left(x\right)\right)}^2,$$

(8)

where the normalization condition ${\sum }_x\psi {\left(x\right)}^{†}\psi \left(x\right)=1$ is understood. For example, for eigenmodes of the continuum, Wilson, or overlap Dirac operators, $\alpha =1,\dots ,4$ is the Dirac index, and $c=1,\dots ,N_c$ is the gauge group (“color”) index; for eigenmodes of the staggered operator $\alpha$ is absent but c is present.

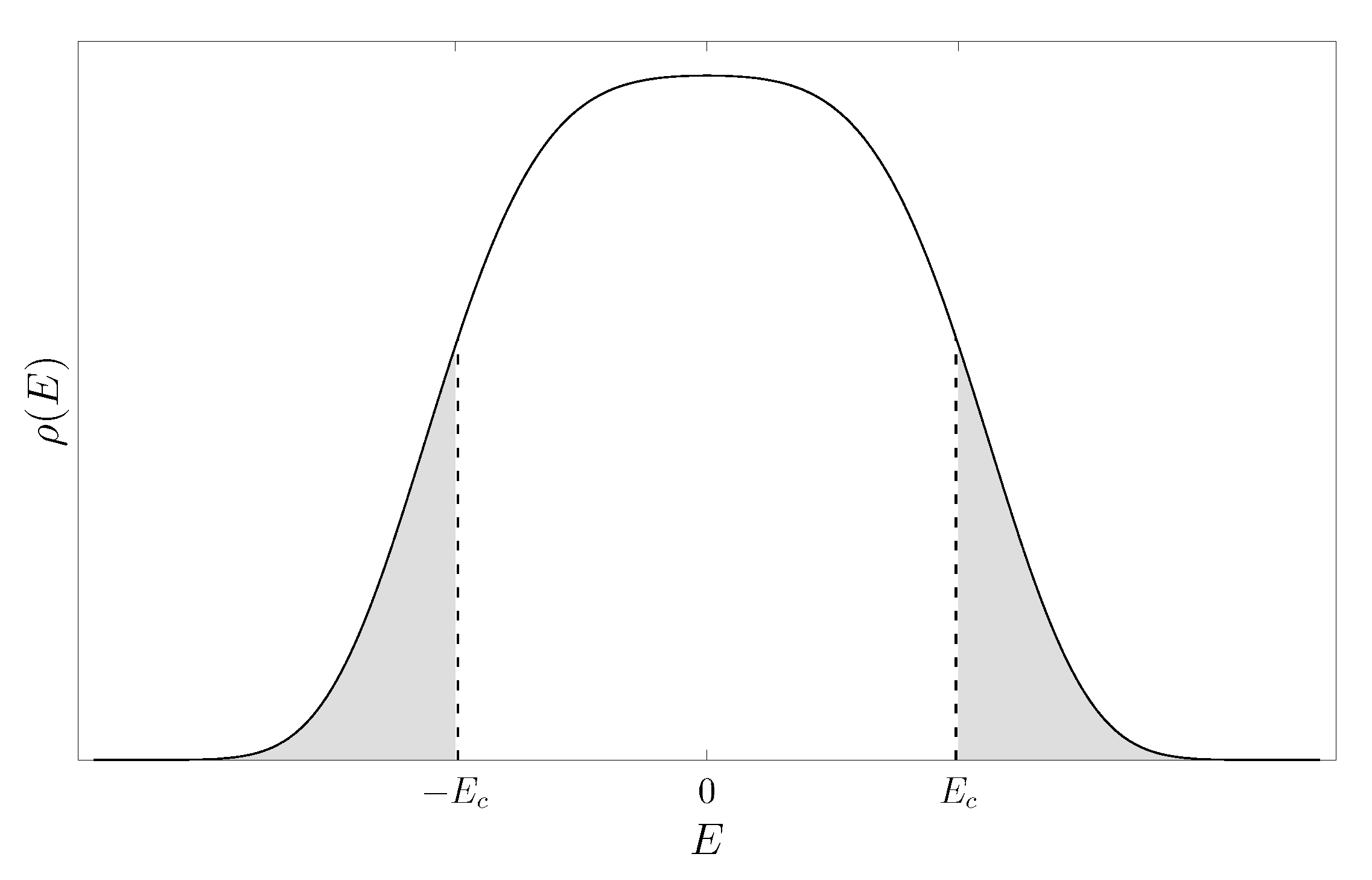
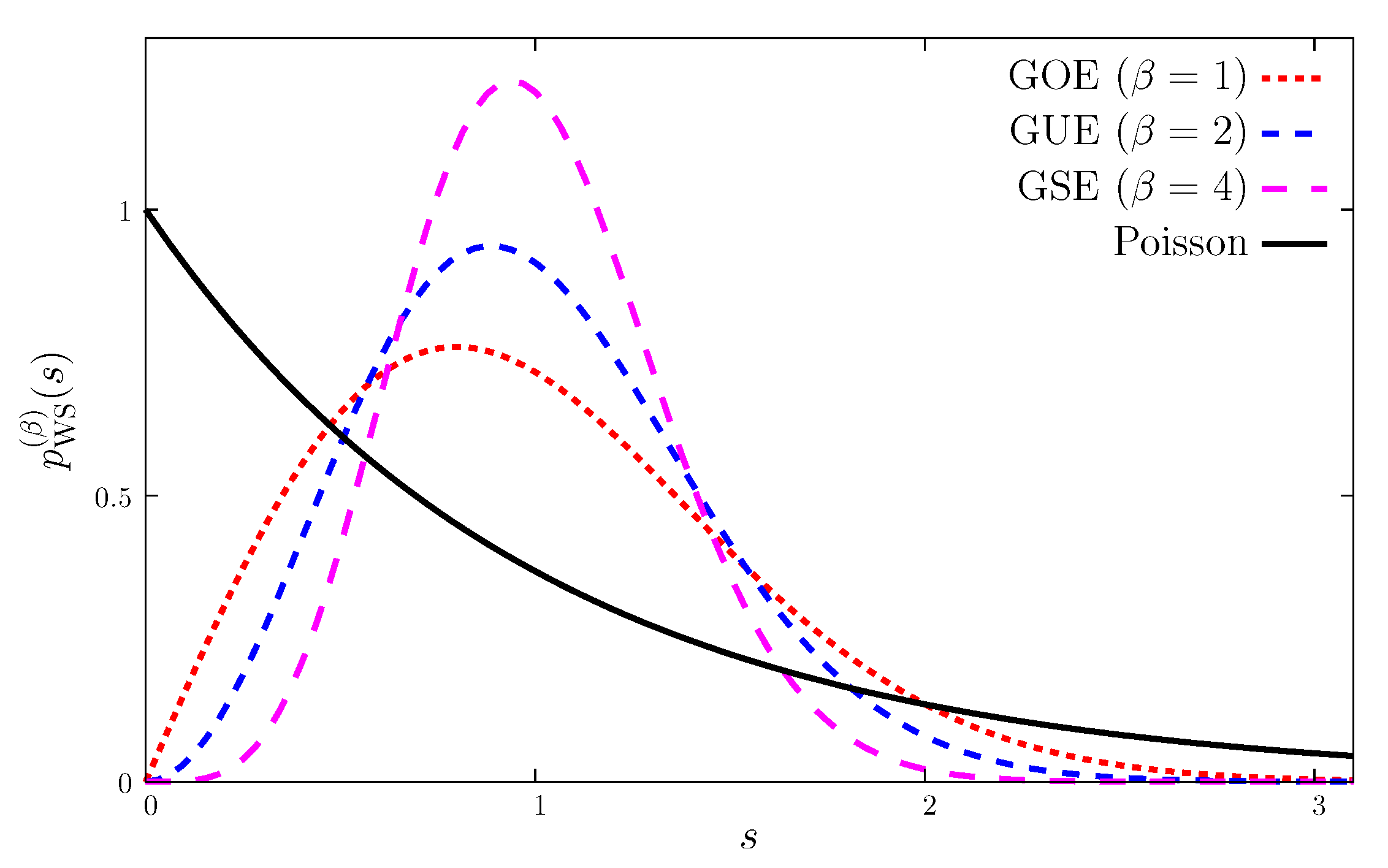
3.4. Detecting Localization: Eigenvalue Observables

Another useful tool to detect localization are the statistical properties of the eigenvalues ${\lambda }_i$ of a random lattice Hamiltonian, which are closely related to the localization properties of its eigenvectors [126]. Localized modes are in fact expected to be sensitive only to local fluctuations in the disorder, and so the corresponding eigenvalues are expected to fluctuate independently. More precisely, after removal of non-universal, model-dependent features by means of the so-called unfolding procedure [113] (see below), the unfolded eigenvalues corresponding to localized modes should obey Poisson statistics. Delocalized modes, on the other hand, are expected to be mixed easily by fluctuations in the disorder, and so the corresponding unfolded spectrum should behave like that of a dense random matrix, and display the statistics of the Gaussian ensemble of Random Matrix Theory [113,114,115] in the appropriate symmetry class.

Unfolding is a monotonic mapping of the eigenvalues ${\lambda }_i$ that makes the spectral density equal to 1 throughout the spectrum. The spectral density is defined as

$$\rho \left(\lambda \right)\equiv \langle \sum _i\delta (\lambda -{\lambda }_i)\rangle .$$

(9)

The unfolded eigenvalues $x_i$ are given by

$${\lambda }_i\to x_i={\int }^{{\lambda }_i}d\lambda \rho \left(\lambda \right),$$

(10)

and it is easy to see that they have unit density, $\overline{\rho }\left(x\right)=\frac{d\lambda }{dx}\rho \left(\lambda \right)=1$. For random matrix models with dense matrices, the bulk statistical properties of the unfolded spectrum are expected to be universal (i.e., to not depend on the details of the model) and uniform throughout the spectrum. This has been proved rigorously for a large class of matrix ensembles (see Refs. [127,128] and references therein). One can then determine these properties in the exactly solvable Gaussian ensembles in the various symmetry classes (orthogonal, unitary, symplectic) [113]. In particular, the probability distribution of the unfolded spacings $s_i=x_{i+1}-x_i$, or unfolded level spacing distribution (ULSD), $p_{\mathrm{ULSD}}\left(s\right)$, can be obtained exactly, although not in closed form. A good approximation for the ULSD is provided by the so-called Wigner surmise in the appropriate symmetry class [114] (see Figure 5),

$$p_{\mathrm{WS}}^{\left(\beta \right)}\left(s\right)=a_{\beta }{s}^{\beta }{e}^{-b_{\beta }{s}^2},$$

(11)

where $\beta$ is the Dyson index of the Gaussian ensemble, and one has for the various symmetry classes7

$$\begin{array}{cccccccccccccc}\hfill \mathrm{orthogonal}:& \hfill & & \hfill & \hfill \beta & =1,\hfill & \hfill & & \hfill a_1& =\frac{\pi }{2},\hfill & & & b_1& =\frac{\pi }{4},\\ \hfill \mathrm{unitary}:& \hfill & & \hfill & \hfill \beta & =2,\hfill & \hfill & & \hfill a_2& =\frac{32}{{\pi }^2},\hfill & & & b_2& =\frac{4}{\pi },\\ \hfill \mathrm{symplectic}:& \hfill & & \hfill & \hfill \beta & =4,\hfill & \hfill & & \hfill a_4& =\frac{262144}{729{\pi }^3},\hfill & & & b_4& =\frac{64}{9\pi }.\end{array}$$

(12)

For chiral classes, the same ULSD is found as for the corresponding non-chiral classes.

For independent eigenvalues, obeying Poisson statistics, the ULSD is the exponential distribution,

$$p_{\mathrm{Poisson}}\left(s\right)=e^{-s}.$$

(13)

Both for localized and delocalized modes, exact analytical results are then available for the statistical properties of the unfolded spectrum, and the transition from one type of modes to the other can be easily monitored across the spectrum. This allows in particular to identify the mobility edge, where a different, critical statistics is expected instead of Poisson or RMT statistics [129,130]. Various families of random matrix models have been developed to describe the critical statistics [131,132,133,134,135,136,137,138].

We mention in passing an alternative approach to the study of universal statistical properties of the spectrum, based on the use of the ratio of consecutive level spacings [139]. Since this ratio is independent of the local spectral density, this approach has the advantage of not requiring any unfolding, and has been shown to provide more precise results than those obtained from the unfolded spectrum in a variety of many-body systems (see Ref. [140] and references therein).

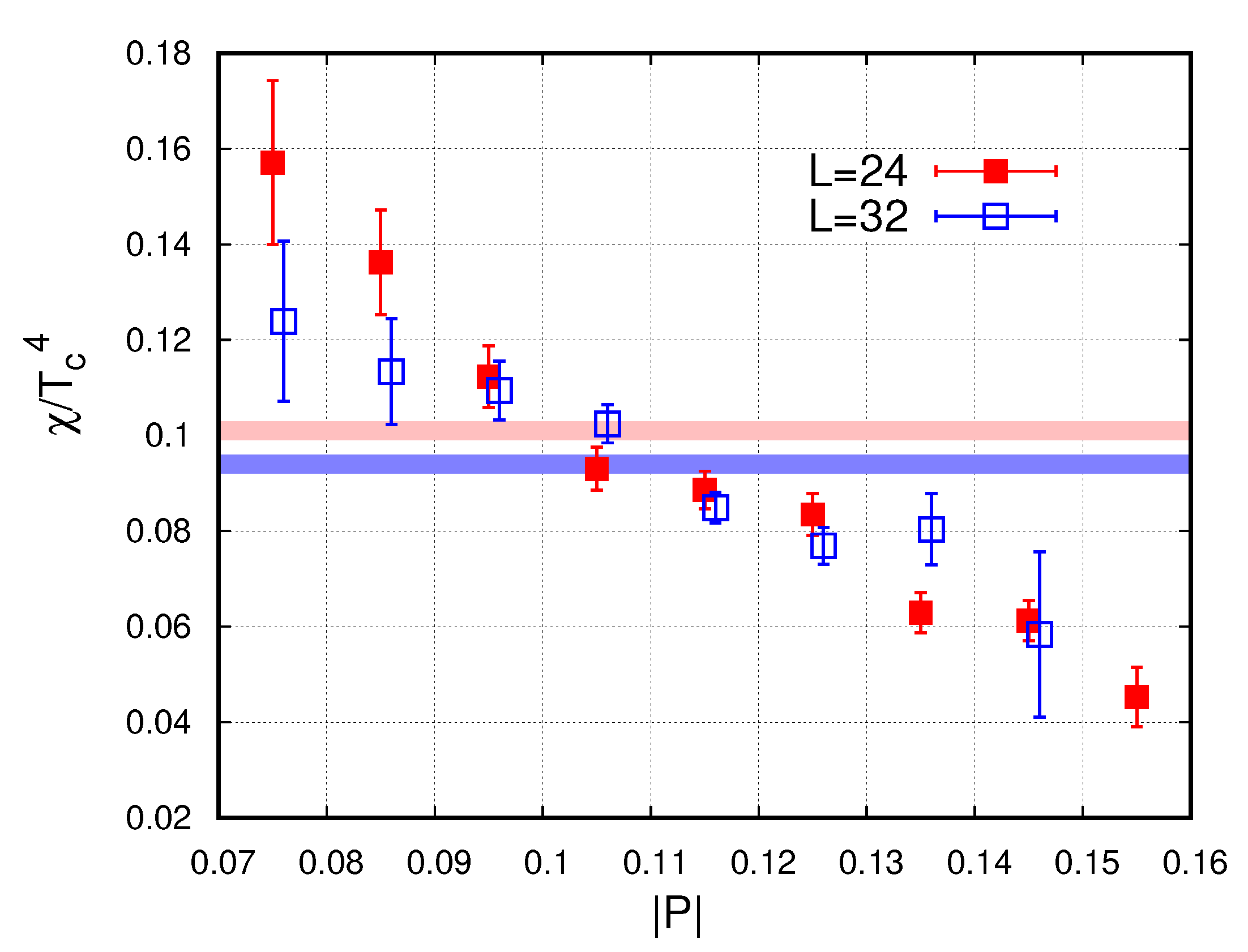
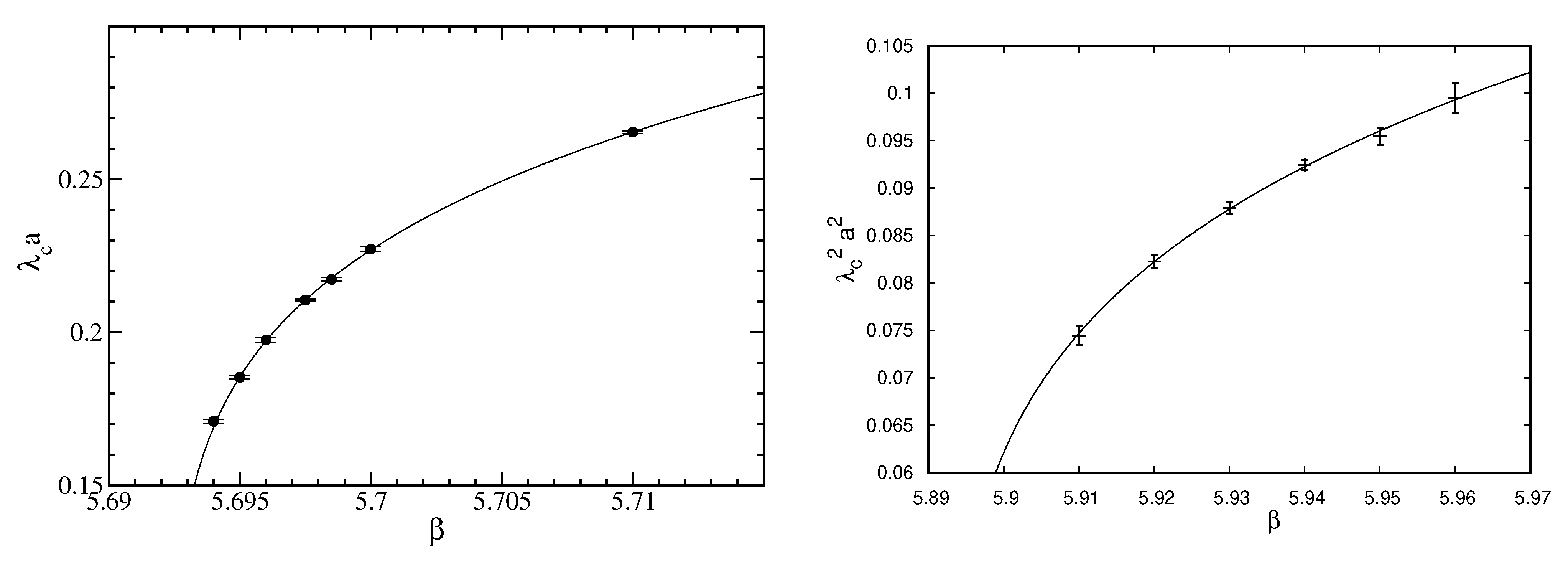
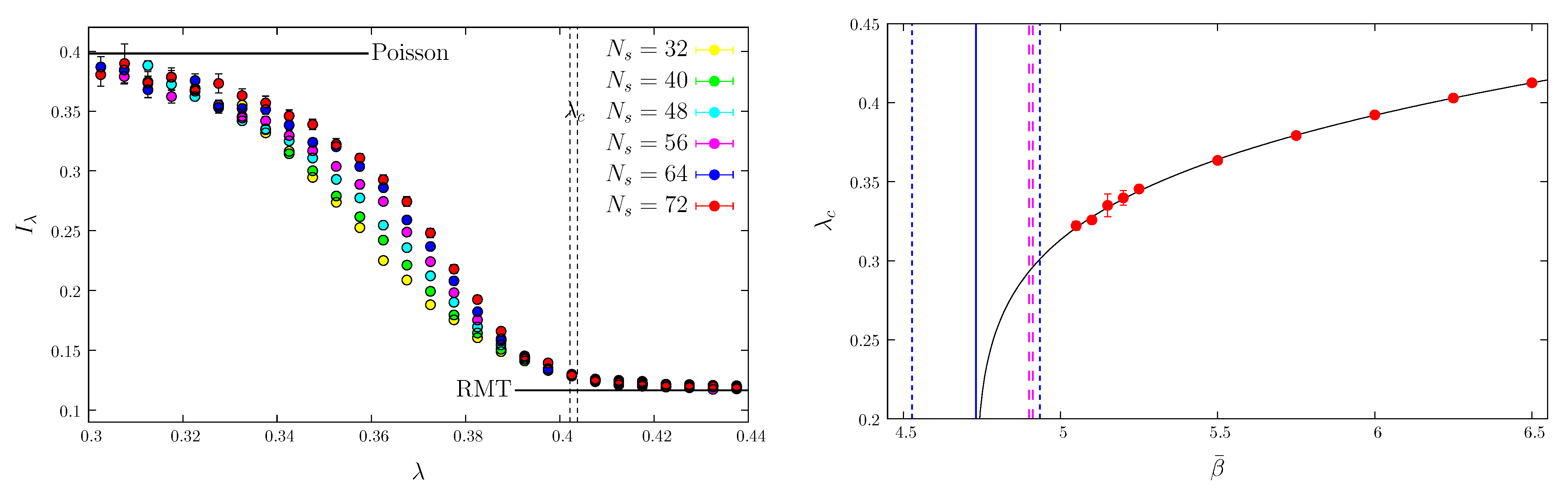
3.5. Finite-Size Scaling at the Anderson Transition

The mobility edge and the correlation-length critical exponent $\nu$ can be obtained by means of a finite-size scaling study [130] of the average ${\mathcal{O}}_L\left(\lambda \right)$ of suitable observables built out of the unfolded spectrum, and computed locally in the spectrum, for lattices of linear size L. Local statistics are defined formally as

$${\mathcal{O}}_L\left(\lambda \right)\equiv \frac{1}{\rho \left(\lambda \right)}\langle \sum _i\delta (\lambda -{\lambda }_i)\mathcal{O}\left({\lambda }_i\right)\rangle \equiv {\langle \mathcal{O}\rangle }_{\lambda },$$

(14)

where $\mathcal{O}\left({\lambda }_i\right)$ is some function of the eigenvalues (e.g., the level spacing $\Delta {\lambda }_i={\lambda }_{i+1}-{\lambda }_i$, or the unfolded level spacing $s_i=x_{i+1}\left({\lambda }_{i+1}\right)-x_i\left({\lambda }_i\right)$ and its powers), and the average is over the ensemble. The last equality sets an alternative notation for local averages.

In practice, for a finite sample of disorder realizations obtained numerically, local statistics are computed by dividing the spectrum in small bins and averaging over modes within those, as well as over the sample. Unfolding is done by first fitting some smooth ${\rho }_{\mathrm{average}}\left(\lambda \right)$ to the numerical data and then applying Equation (10). Alternatively, one can sort the eigenvalues of the sample by magnitude and replace them by their rank divided by the number of disorder realizations. If one is interested only in unfolded level spacings, one can divide $\Delta {\lambda }_i$ by the average level spacing ${\langle \Delta \lambda \rangle }_{\lambda }$ in the relevant spectral region, $s_i=\frac{{\Delta \lambda }_i}{{\langle \Delta \lambda \rangle }_{\lambda }}$ (notice that in the infinite-volume, infinite-statistics limit one has ${\langle \Delta \lambda \rangle }_{\lambda }=1/\rho \left(\lambda \right)$).

For a finite-size scaling study, convenient observables are obtained from the unfolded level spacing distribution, $p_{\mathrm{ULSD}}\left(s\right)$, defined above. Commonly used are the second moment, $\langle s^2\rangle ={\int }_0^{\infty }ds{p}_{\mathrm{ULSD}}\left(s\right)s^2$, and the integrated probability distribution $I_{s_0}={\int }_0^{s_0}ds{p}_{\mathrm{ULSD}}\left(s\right)$. As the system size grows, ${\mathcal{O}}_L\left(\lambda \right)$ tends to its value for Poisson statistics in spectral regions where modes are localized, and to its value for (the appropriate) RMT statistics in spectral regions where modes are delocalized. Near the mobility edge ${\lambda }_c$, renormalization-group arguments and the one-parameter scaling hypothesis [98] imply that ${\mathcal{O}}_L\left(\lambda \right)$ depends on $\lambda$ and L only through the combination $\xi \left(\lambda \right)/L$, where $\xi$ is the correlation length,8 that diverges at ${\lambda }_c$ like $\xi \left(\lambda \right)\sim |\lambda -{\lambda }_c{|}^{-\nu }$. Since ${\mathcal{O}}_L\left(\lambda \right)$ is analytic in $\lambda$ for finite L, it must then take the form ${\mathcal{O}}_L\left(\lambda \right)=f\left((\lambda -{\lambda }_c)L^{1/\nu }\right)$. Corrections to one-parameter scaling due to irrelevant operators can also be included, and the corresponding critical exponents be measured [141] (see Ref. [142] for an introduction). The goodness of one-parameter scaling can be visualized by means of the so-called “shape analysis” [143], obtained by plotting one spectral observable against another. If the scaling hypothesis is correct, only $\xi /L$ should determine the statistical properties of the spectrum, and so points corresponding to different $\lambda$ and system sizes should all lie on a single curve, corresponding to a path in the space of probability distributions connecting RMT and Poisson going through the critical statistics.9 Thanks to the persistence of a remnant of multifractality near the mobility edge [144], one can apply similar finite-size scaling techniques also to the study of eigenmodes near criticality, in order to obtain the multifractal exponents [145], as well as the correlation-length exponent $\nu$ [146].

3.6. Anderson Transitions in Specific Models: Analytic Predictions and Numerical Results

Critical properties at the Anderson transition have been extensively studied by means of numerical simulations in the case of the conventional symmetry classes (O, U, and S), see Refs. [45,142,147,148] and references therein. According to the scaling theory of localization [98], a second-order Anderson transition is expected in all the conventional classes in three dimensions. The existence of these Anderson transitions has been confirmed numerically, and measurements of the correlation length critical exponent $\nu$ have shown that the three classes belong to different universality classes [141,148,149,150,151,152] (see

Table 2. Correlation-length critical exponent for Anderson transitions in the conventional symmetry classes.

Symmetry Class	Method	$\mathit{\nu }$	Reference
orthogonal	localization length of quasi-1d bar	${1.57}_{-0.02}^{+0.02}$	[141]
	multifractal finite-size scaling	${1.590}_{-0.011}^{+0.012}$	[151]
	multifractal finite-size scaling	${1.595}_{-0.013}^{+0.014}$	[148]
unitary	localization length of quasi-1d bar	${1.43}_{-0.04}^{+0.04}$	[149]
	multifractal finite-size scaling	${1.437}_{-0.011}^{+0.011}$	[148]
	multifractal finite-size scaling	${1.446}_{-0.006}^{+0.006}$	[152]
symplectic	localization length of quasi-1d bar	${1.375}_{-0.016}^{+0.016}$	[150]
	multifractal finite-size scaling	${1.383}_{-0.024}^{+0.029}$	[148]

). The expected nontrivial multifractal structure has also been found [145,146,148,151,152]. Universality has been explicitly demonstrated for the orthogonal class using different disorder distributions [141], and for the unitary class using different Hamiltonians [148,152].

In two dimensions, the predictions of the scaling theory of localization depend strongly on the details of the model. Absence of an Anderson transition is predicted in the orthogonal Anderson model, where all modes are expected to be localized for nonzero disorder, while an Anderson transition is predicted in the symplectic case (Ando model) [153,154]. The inclusion of topological effects in the field-theoretical description of disordered systems led one to expect an Anderson transition also in the theory of the integer Quantum Hall Effect [155], which belongs to the unitary class (see Ref. [156] for a review). While numerical evidence qualitatively supported this idea [157], significant quantitative discrepancies between different microscopic models were observed (see Ref. [158] for a summary), in contrast with the expected universality of the transition. A better understanding of the field theory describing the critical point was obtained only recently, in terms of a conformal field theory deformed only by marginal perturbations, that emerge from the spontaneous breaking of the replica (super)symmetry of the relevant nonlinear sigma model [159]. This proposal is quantitatively supported by numerical results, and can explain the apparent numerical discrepancies [158]. A transition between localized and delocalized modes was observed in the two-dimensional unitary Anderson model [160]. This transition is a disorder-induced transition of topological (Berezinskiĭ-Kosterlitz-Thouless [161,162,163]) type, with exponentially divergent correlation length, $log\xi \sim |\lambda -{\lambda }_c{|}^{-1/2}$, in contrast to the usual second-order transition. For the unitary Anderson model there are conflicting theoretical predictions: while perturbative contributions lead to all states being localized (see, e.g., Refs. [45,154]), the inclusion of nonperturbative terms can possibly lead to the presence of an Anderson transition (see references cited in Ref. [160]). A similar transition of topological type was also observed in a model for disordered graphene with strong long-range impurities [164], belonging to the orthogonal class in two dimensions.

For our purposes, it is important to discuss the effect of off-diagonal disorder on localization. In the orthogonal class, theoretical arguments [109,110] suggest that off-diagonal disorder alone cannot localize modes at the band center; only increasing the on-site disorder leads eventually to localization of all the modes. This is confirmed by numerical results in three dimensions for the orthogonal Anderson model with random hopping [165,166,167,168]. The mobility edges $\pm E_c$ separating extended and localized modes move towards the band center as the on-site disorder W is increased, and all modes are localized for $W>W_c$. In the absence of diagonal disorder ($W=0$) for bipartite lattices, this model belongs to the chiral orthogonal class. The critical exponent $\nu$ characterizing the Anderson transition at $E_c\ne 0$ when $W=0$ is found to be in agreement with that of the (non-chiral) orthogonal class, as well as with the one characterizing the transition at $E=0$ as the critical on-site disorder $W_c$ is reached [166,167].

The origin $E=0$ is singled out when the system has chiral symmetry (which is always the case when the lattice is bipartite and only off-diagonal disorder is present). In two dimensions, theoretical arguments predict critical behavior of modes at $E=0$ (i.e., modes are extended but not fully delocalized) [111,169,170,171,172,173,174,175], while all other modes are localized. Numerical results indicate that modes are indeed critical at $E=0$ [174,176,177,178,179,180,181], but an Anderson transition to localized modes can also appear [174,182]. It has been argued that such an Anderson transition can be present due to non-perturbative, topological effects [183]. In three-dimensional models with chiral symmetry, Anderson transitions at the origin ($E_c=0$) are expected to show critical properties differing from those of the correponding conventional class (and from those at $E_c\ne 0$). Ref. [184] studied the Anderson transition at $E\sim 0$ in a chiral unitary model with purely off-diagonal disorder, finding multifractal exponents differing from those of the corresponding non-chiral class. In Refs. [185,186] the Anderson transition at the origin was studied in two-band models with on-site disorder in the chiral orthogonal and chiral unitary classes (as well as in other non-conventional symmetry classes), finding correlation length critical exponents differing from those of the corresponding non-chiral classes (and not entirely universal).

The critical properties of Anderson transitions at $E_c\ne 0$ in systems with chiral symmetry are instead not expected to differ from those in the corresponding conventional classes. Ref. [187] provides evidence of localization near the band center in a chiral unitary model mimicking fermions in a background of correlated spins with antiferromagnetic coupling in three dimensions, with the same critical properties as the non-chiral class; in two dimensions states near the band center seem instead to remain extended. Anticipating the results discussed in the following Sections, Refs. [27,34,35,37,51,53] provide examples of models in the chiral unitary class, both in three and two dimensions, displaying Anderson transitions at finite energy, and showing the same critical properties at the mobility edge as the corresponding non-chiral classes.

4. Localization and Deconfinement in QCD at Finite Temperature

The study of localization in QCD was initially motivated by the idea that the spontaneous breaking of chiral symmetry could have a similar origin as conductivity in a disordered medium [8,9,10,11,12,13,14,15]. The basic idea of the disordered medium scenario is that the near-zero modes responsible for the breaking of chiral symmetry originate from the mixing of the zero modes associated with overlapping instantons (or, more precisely, calorons at finite temperature). At finite temperature these zero modes are exponentially localized on the scale of the inverse temperature. If instantons/calorons overlap sufficiently, mixing of the corresponding zero modes will transform the zero eigenvalues into a near-zero band of levels, and lead to delocalized eigenmodes [10].10 This is analogous, for example, to the Anderson-Mott insulator-metal transition11 driven by the impurity concentration in doped semiconductors (see, e.g., Ref. [189]). Starting from the chirally symmetric phase and decreasing T, the overlap of calorons increases and eventually leads to a finite density of near-zero, delocalized modes. This leads to expect a localization-delocalization transition in the near-zero region.

As we will see below, this scenario is most likely only a part of the story, and overlooks the important role played by deconfinement in localizing the low Dirac modes. Instead of sticking to the disordered medium scenario, we prefer to adopt a more general point of view, looking at the Dirac operator as a random matrix, ignoring initially any relation with topological objects and deconfinement. After a few introductory remarks on this approach, we review the available results regarding localization and Anderson transitions in various lattice approximations for QCD, following a chronological order. Some of the results discussed here deal with the pure gauge theory, sometimes for $N_c=2$, and are included in this section mostly for historical reasons. A summary of the results for QCD proper and organized by topic is provided at the end of the section.

4.1. The Dirac Operator as a Random Matrix

The Dirac operator in the background of fluctuating gauge fields can be intepreted as a sparse random matrix, and the properties of its eigenvalues and eigenvectors can be studied with the machinery discussed in the previous Section. For the continuum anti-Hermitian Dirac operator, $-i\cancel{D}$ can be formally treated as the Hamiltonian of a disordered system, with disorder provided by the gauge fields. If an Anderson transition is present in its spectrum, its critical properties are expected to be determined by the symmetry class of the Dirac operator and by the dimensionality of the space-time over which it is defined.

Concerning the symmetry class, the four-dimensional Dirac operator for fundamental fermions in SU($N_c$) theories belongs to the chiral unitary class for $N_c>2$, and to the chiral orthogonal class for $N_c=2$.12 The spectral correlations of Dirac eigenvalues in QCD ($N_c=3$) are then expected to display GUE-type bulk statistics,13 as long as the corresponding eigenvectors are delocalized.14 If localized modes are present, they are expected to obey Poisson statistics, regardless of the symmetry class.

The discretization of the Dirac operator on a lattice is known to be tricky due to the doubling problem (see Refs. [73,74,82,83,84]), and in some cases its chiral properties are changed (see Ref. [188] and Ref. [115], Section 5.2.1). For staggered fermions [196,197,198] a remnant of the continuum chiral symmetry preserves the chiral nature of the symmetry class, and the staggered Dirac operator belongs to the chiral unitary class, as the continuum operator, for $N_c\ge 3$. For $N_c=2$ the symmetry class is instead changed to the chiral symplectic one.15 Overlap fermions [199,200,201,202] possess an exact lattice chiral symmetry, and belong to the same symmetry class as their continuum counterpart. More precisely, since the overlap operator is not anti-Hermitean, this is true for its anti-Hermitean part. It is then understood, unless specified otherwise, that the imaginary part of the overlap eigenvalues is considered in the following. For the low modes this is an adequate approximation, that becomes exact in the continuum limit. Moreover, since the unfolded spectrum is unaffected by any monotonic mapping, the statistical properties of the low modes are unchanged if one uses other types of projection on the imaginary axis (i.e., eigenvalue magnitude, stereographic projection).16

Concerning the dimensionality of the problem, in finite-temperature field theory the temporal size of the system is fixed (in physical units) in the thermodynamic limit, and only the size of the d spatial directions is sent to infinity in the thermodynamic limit. For $d+1$ spacetime dimensions, the dimensionality of the disordered system described by the Dirac operator in a gauge-field background is then equal to d, while the temporal direction can be technically seen as an internal degree of freedom.

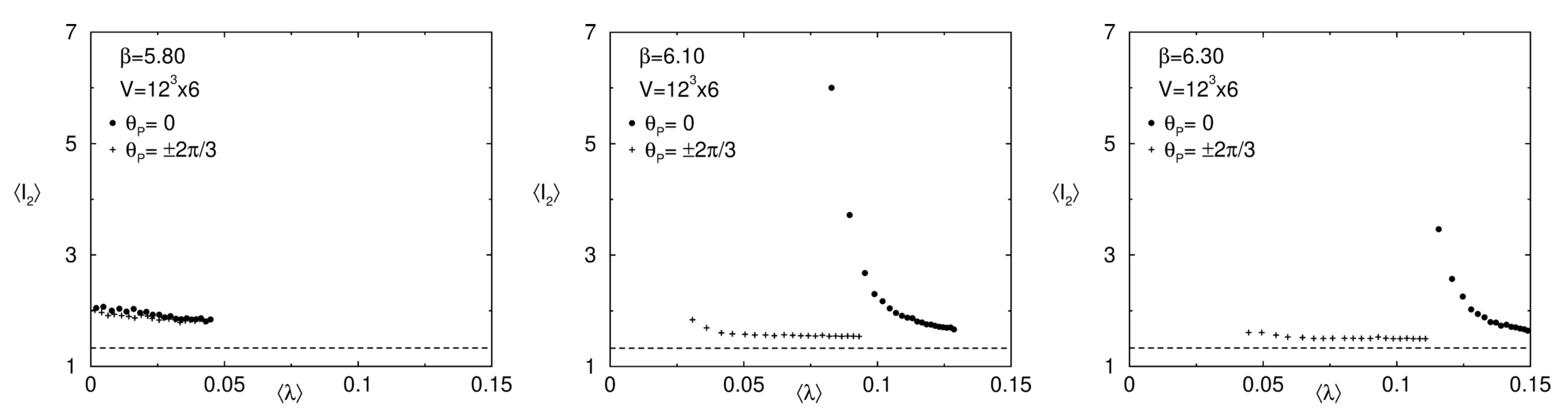
4.2. Numerical Results on the Lattice

The disordered medium scenario was investigated in Ref. [25] by means of numerical simulations of quenched QCD on the lattice on both sides of the finite-temperature transition. They used a single spatial volume, employed the staggered discretization of the Dirac operator, and studied the rotation- and gauge-invariant version of the IPR of an eigenmode $\psi$, Equation (8). They observed that in the physical ${\mathbb{Z}}_3$ sector (real Polyakov loop sector) the IPR of the lowest modes was considerably larger above the transition than below the transition (see Figure 6). Moreover, above $T_c$ it was larger in the real sector than in the complex Polyakov loop sectors, where it does not change much across the transition. Sensitivity to the Polyakov loop sector is equivalent to sensitivity to the temporal boundary conditions, and shows that the low modes cannot be localized in the temporal direction on a scale much shorter than the temporal size.17 This suggests the presence of a localization transition in the physical sector, with spatially localized low modes at high temperature. Evidence for some of the localized modes being related to calorons was also provided. More evidence for localization of the low modes in the real sector appeared in Ref. [26], where more volumes and a chirally improved discretization of the Dirac operator were used. The volume scaling of the IPR of the low modes in the real sector was found to be in qualitative agreement with that expected for localized modes.

The disordered medium scenario was investigated further by García-García and Osborn in Refs. [27,28]. In Ref. [27] they considered an Instanton Liquid Model (ILM) for the QCD vacuum (see Ref. [204]), and studied the behavior of the instantonic zero modes. Changing the temperature, and so the spatial extension of the zero modes, they observed the appearance of a mobility edge near the origin, both in the quenched approximation and in the presence of fermions. In the quenched case, the multifractal properties of the near-zero modes at the transition were found to be consistent with those of the 3d unitary Anderson transition (see Refs. [45,148,152]). With two massless flavors, the mobility edge appears at the same temperature where the chiral condensate shows a drop (see Figure 7, left). Although the thermodynamic limit was not studied, this was taken as an indication that localization of the low modes coincides with the chiral transition.

A test of the disordered medium scenario in a more realistic context was presented in Ref. [28]. There the localization properties of the near-zero modes were studied on the lattice in quenched QCD, i.e., pure gauge SU(3) theory, and “unquenched” QCD, i.e., with 2+1 flavors of dynamical quarks of relatively large masses, leading to heavier-than-physical pions [205,206]. The one-loop Symanzik improved gauge action was used, and the Asqtad-improved [207,208,209,210] staggered discretization was employed for the lattice Dirac operator. In both cases, they found indications of critical (i.e., volume-independent) spectral statistics (from the second moment of the ULSD) at a temperature $T_c^{\mathrm{loc}}$, where also $\mathrm{IPR}·V$ starts increasing with the volume (for the unquenched case see Figure 7, right). In the quenched case, indications of a vanishing spectral density and of an increase of the Polyakov loop are found at a similar temperature $T_c^{\mathrm{dec}/\chi }$, identified with the deconfinement temperature (in the physical ${\mathbb{Z}}_3$ sector). In the unquenched case, $T_c^{\mathrm{loc}}$ is close to the crossover temperature $T_c^{\chi }$ obtained from the chiral susceptibility. Although the use of small lattices does not allow a full quantitative assessment, these indications suggest that an Anderson transition takes place near the origin of the spectrum as the system crosses over from the low-temperature to the high-temperature phase, with the low-lying Dirac modes turning from delocalized to localized, and the formation of a mobility edge that separates them from delocalized modes in the bulk of the spectrum.

Studies of localization in QCD-like settings includes also the case of two flavors of dynamical staggered fermions [29], and that of quenched two-color QCD (i.e., pure gauge SU(2) theory) analyzing overlap [30,31] and staggered [32] spectra. In the two-flavor three-color case Ref. [29] found that $\mathrm{IPR}·V$ of the low modes was volume-independent below the transition temperature $T_c^{2f}$, but above that it scaled with the volume in a manner compatible with localization (see Figure 8, left). Ref. [30] shows evidence of absence of correlations in the low-lying overlap spectrum, which is typical of localized modes, at $T=2.6T_c^{\mathrm{SU}\left(2\right)}$, where $T_c^{\mathrm{SU}\left(2\right)}$ is the deconfinement temperature of the pure gauge SU(2) theory. Ref. [32] shows clear evidence of localization of the low-lying staggered modes, and of the presence of a mobility edge separating them from delocalized bulk modes, again at $T=2.6T_c^{\mathrm{SU}\left(2\right)}$. This is obtained by studying how (i) the scaling with the lattice spatial volume of the spatial “size” ${({\mathrm{IPR}}^{-1}/N_t)}^{\frac{1}{3}}$ of the eigenmodes, and (ii) the ULSD of the corresponding eigenvalues change along the spectrum. The spatial extension of the low modes is volume-independent, while higher up in the spectrum it is seen to increase with the lattice size (see Figure 8, right). Looking at the ULSD in different spectral regions, it is observed that it matches the exponential distribution of Poisson statistics for the lowest modes, changing towards the symplectic Wigner surmise18 as one moves towards the bulk. Finally, in Ref. [31] the transition in the overlap spectrum from localized to delocalized modes is studied via the ULSD at $T=2.6T_c^{\mathrm{SU}\left(2\right)}$. A clear change from the exponential to the orthogonal Wigner surmise is observed.19 Moreover, assuming that there are no strong interactions among instantons and anti-instantons, it is argued that the instanton density is too low to match the density of localized modes at this temperature. Indications of correlations between localized modes and local fluctuations of the Polyakov loop away from its ordered value (i.e., 1, in the physical sector) are also reported (see Section 5.2 for a detailed discussion).

A comprehensive study of localization in the high-temperature phase of real-world QCD appeared in Ref. [33], using a tree-level Symanzik improved gauge action and a two-level stout smeared [211] staggered fermion action for 2+1 quark flavors with physical mass [212]. Several volumes, aspect ratios and lattice spacings were used, covering the temperature range $1.7T_c<T<5T_c$ (here $T_c=155\mathrm{MeV}$ [5]) with lattices of linear size $2\mathrm{fm}\le L\le 6\mathrm{fm}$. Localized modes were observed at the low end of the spectrum (see Figure 9, left). A temperature-dependent mobility edge ${\lambda }_c\left(T\right)$ separating low-lying, localized modes from delocalized bulk modes was found in the whole temperature range, studying how the spectral statistics change along the spectrum from Poisson to unitary RMT type. More precisely, ${\lambda }_c$ was estimated as the inflection point of the variance of the ULSD, ${\langle s^2\rangle }_{\lambda }-{\langle s\rangle }_{\lambda }^2={\langle s^2\rangle }_{\lambda }-1$, computed locally in the spectrum. As T increases, ${\lambda }_c\left(T\right)$ increases as well. Extrapolation to the continuum is studied at $T=400\mathrm{MeV}$. The mobility edge is expected to renormalize like a quark mass, and the ratio ${\lambda }_c/m_{\mathrm{ud}}$ is indeed shown to be independent of the lattice spacing within numerical uncertainties. The localization length $l\equiv a\langle {\mathrm{IPR}}^{-4}\rangle$ of the low modes is also shown to extrapolate to a finite continuum limit, and $lT$ is found to be between 0.7 and 0.9 for all the lattice ensembles. A second-order polynomial fit to the RG-invariant quantity ${\lambda }_c\left(T\right)/m_{\mathrm{ud}}$ shows that it extrapolates to zero at $T_c^{\mathrm{loc}}=170\mathrm{MeV}$ (see Figure 9, right), which is within the temperature range where the system undergoes a crossover from the low-temperature phase to the high-temperature phase [5,6]. This is consistent with localization of the low modes appearing as the system changes from confined and chirally broken to deconfined and chirally restored. The density of localized modes (number of modes per unit spatial volume) is seen to increase with T (see Figure 13 below).

The critical behavior of the eigenmodes at the mobility edge was studied in Refs. [34,35,37]. All these references use the same setup as Ref. [33] with $N_t=4$ and $a=0.125\mathrm{fm}$, corresponding to $T=2.6T_c$. In Ref. [34] it was established, by means of a finite size scaling analysis of the integrated ULSD $I_{s_0}$, that the transition from localized to delocalized modes at the mobility edge is indeed an Anderson transition (see Figure 10, left). The critical exponent was found to be $\nu =1.43\left(6\right)$, in agreement with the one obtained for the 3d unitary Anderson model [149] (see Table 2). In Ref. [35] the critical eigenvalue statistics at the mobility edge was studied in terms of the one-parameter family of deformed random matrix ensembles of Refs. [136,137]. The critical statistics was shown to be indeed volume-independent, and well described by a deformed random matrix ensemble, with deformation parameter consistent with the one found for the 3d unitary Anderson model [148,149,152]. Finally, in Ref. [37] the critical exponent $\nu$ and the multifractal exponents where studied using the finite size scaling techniques for the eigenmode density developed in Refs. [145,146]. All exponents were found to be in agreement with those of the 3d unitary Anderson model [148,152] (see Figure 10, right).

While mostly focussed on the properties of the spectrum, Ref. [38] briefly discussed the localization properties of the low Dirac modes in QCD near the crossover temperature. The spectrum of the overlap operator was studied in the background of gauge configurations generated with tree-level improved Symanzik gauge action and 2+1 flavors of highly improved staggered quarks (HISQ) [213] with near-physical quark masses ($m_l/m_s=1/20$, $m_{\pi }=160\mathrm{MeV}$). Evidence was found of a small peak of localized near-zero modes at $T=1.2T_c$ and $T=1.5T_c$ (here $T_c=154\mathrm{MeV}$). Localization was inferred from the smallness of the PR; the volume scaling was not discussed. It was suggested that near-zero modes in the peak correspond to an approximate superposition of the exact zero modes associated with instanton–anti-instanton pairs. Comparison of the PR of zero and near-zero modes shows however that only a fraction of near-zero modes is compatible with this interpretation. The large fluctuations of the PR of the near-zero modes suggests instead a large variability of the number of topological lumps participating in the superposition.

Localization in two-flavor QCD was studied in Ref. [39] using tree-level improved Symanzik gauge action and dynamical Möbius domain-wall fermions [214,215,216] with stout smearing, and looking at the spectrum of the Hermitian operator ${\gamma }_{5}D$, with D the four-dimensional effective Dirac operator of the five-dimensional domain-wall fermion. This operator is in the chiral unitary class. The temperature range was $0.9T_c\le T\le 1.9T_c$ with $T_c\simeq 175\mathrm{MeV}$ the deconfinement temperature estimated from the average Polyakov loop. A range of bare quark masses, two spatial volumes and two temporal extensions (in lattice units) were used. Above $T_c$, the scaling of the PR of the eigenmodes shows that the lowest modes are localized, while moving up in the spectrum modes become delocalized (see Figure 11, left). The size $v\equiv V·\mathrm{PR}$ of the low modes increases along the spectrum and decreases with T (see Figure 11, right). The localization length $l\equiv v^{\frac{1}{4}}$ of the lowest (nonzero) mode was shown to be of the order of the inverse temperature, $lT\sim 1.3$. The ULSD computed locally in the spectrum was seen to change from Poisson-type to RMT-type in the unitary class as one moves from the lowest modes towards the bulk. By contrast, below $T_c$ RMT statistics was observed everywhere in the spectrum. Changing boundary conditions to periodic in time, low modes were found to be delocalized with RMT statistics also above $T_c$. A clear correlation between the spatial density ${\psi }^{†}\psi \left(x\right)$ of the low modes and the local fluctuations of the Polyakov loop $P\left(\overrightarrow{x}\right)$ away from its ordered value was observed, favoring sites with $\mathrm{Re}\mathrm{tr}P\left(\overrightarrow{x}\right)$ close to $-1$, and becoming stronger as T increases (see Figure 12 below). Correlation with action ($s\left(x\right)$) and topological charge ($q\left(x\right)$) densities was also observed, with localized modes favoring sites with large s and q, in particular “(anti)self-dual” sites where $\left|q\right|/s\sim 1$. The overlap of the left- and right-chirality components of the modes was seen to be the smallest for the lowest modes, and to increase as one moves towards the bulk; it was also seen to increase with temperature, and showed little dependence on the bare quark mass.

In Ref. [40] (see also Ref. [217]), localization was studied in 2+1+1 flavor QCD with physical strange and charm masses but heavy pions ($m_{\pi }\simeq 370\mathrm{MeV}$), looking at the (stereographically projected) spectrum of the overlap operator in the background of configurations generated with Iwasaki gauge action and dynamical twisted-mass Wilson fermions [218,219,220]. Above $T_c\simeq 188\mathrm{MeV}$, a very small PR is found for the lowest modes, which increases to around 0.8 in the bulk. The position of the mobility edge was estimated as the inflection point of the PR in the spectrum. As a function of T, ${\lambda }_c\left(T\right)$ appears to be linear, and its extrapolation vanishes at a temperature compatible with $T_c$. A strong anticorrelation of the localized modes with $\mathrm{Re}\mathrm{tr}P\left(\overrightarrow{x}\right)$ was observed.

4.3. Summary

Let us summarize the results discussed in this section, restricting to QCD “proper”, i.e., gauge group SU(3) and dynamical quarks. QCD-like models and other gauge theories are discussed in detail below in Section 6.

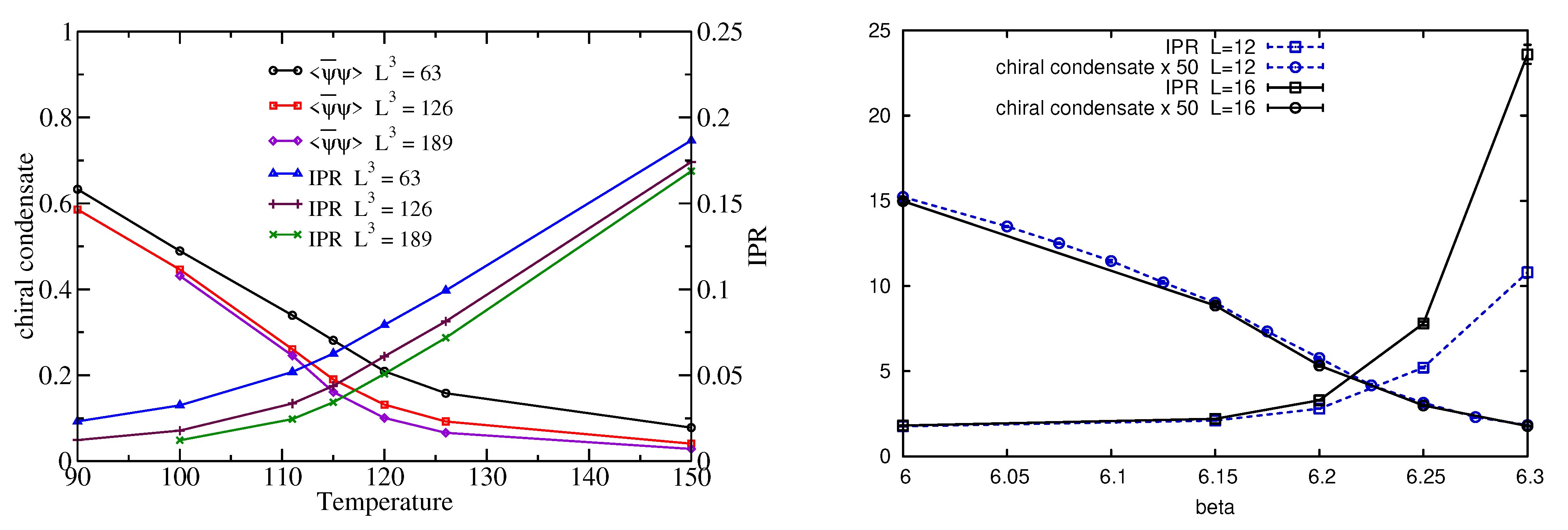
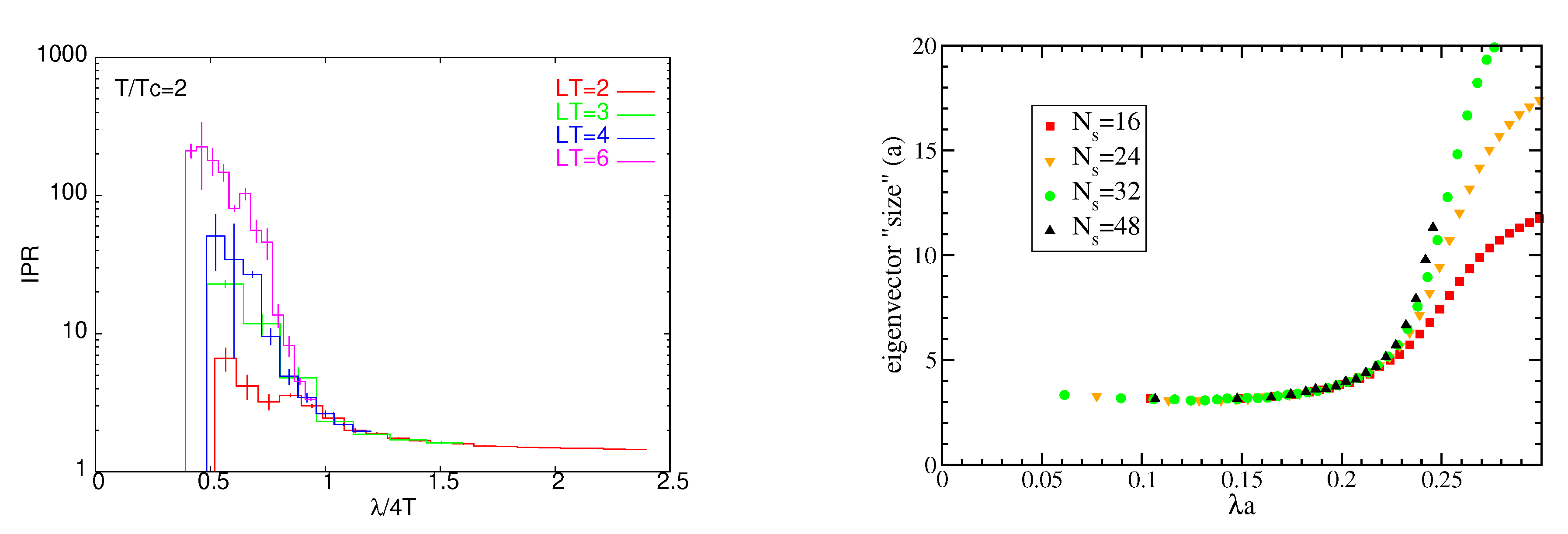
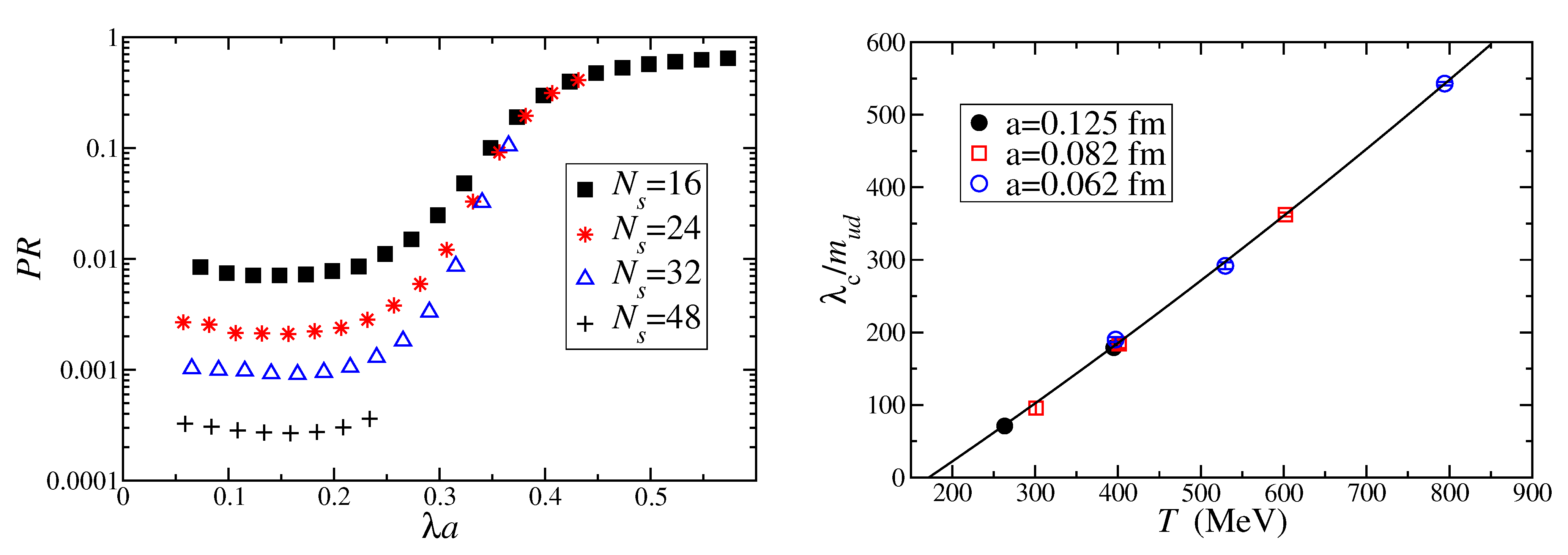
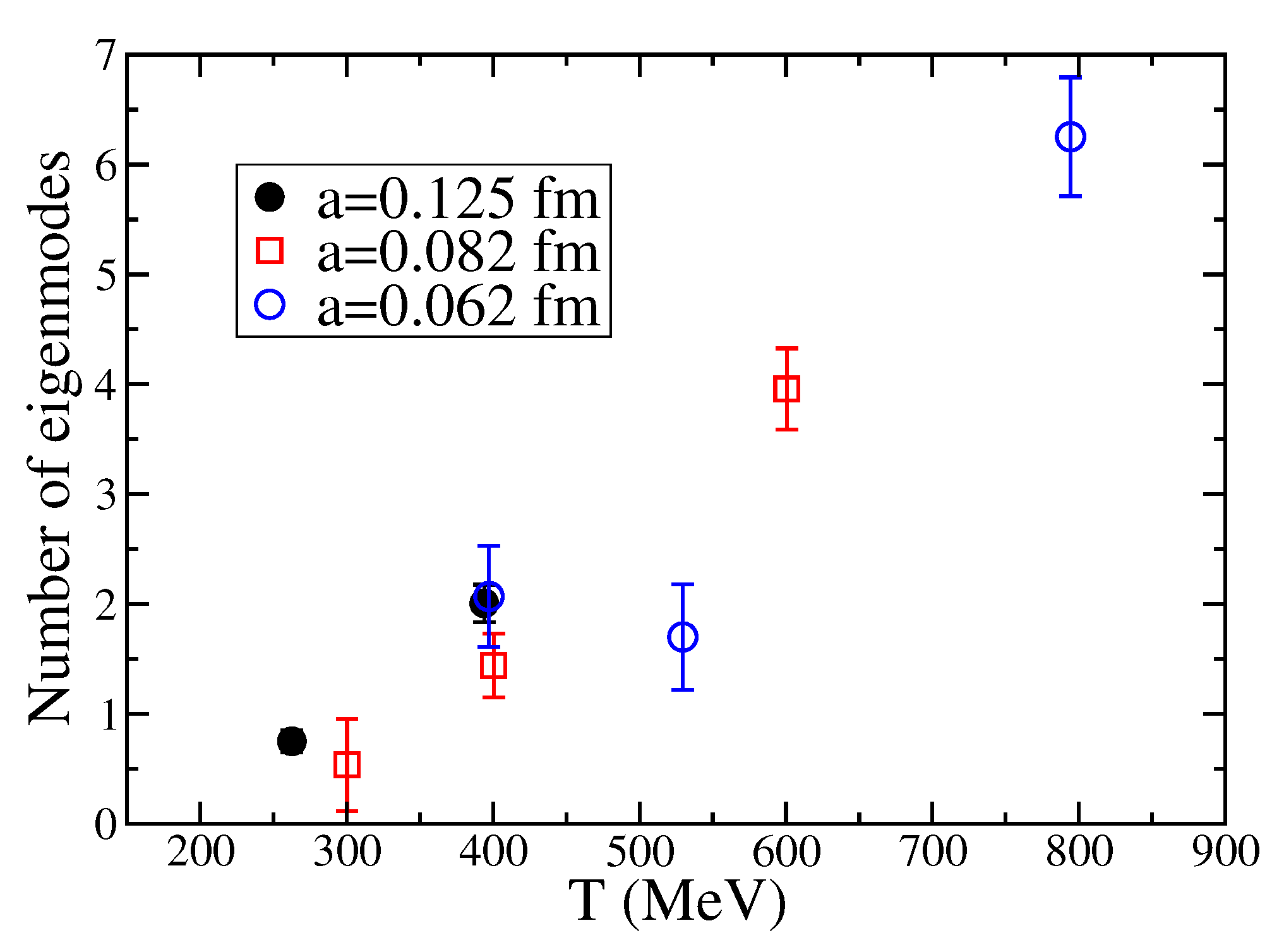
• Low Dirac modes are localized in lattice QCD in the high-temperature phase. More precisely, a large amount of evidence indicates that the low Dirac modes are localized in lattice QCD, for temperatures above the finite-temperature transition, for more or less physical quark content and masses, and different fermion discretizations [28,33,38,39,40]. The available evidence suggests that localization is not a lattice artifact and survives the continuum limit: both the localization length and the renormalized mobility edge seem in fact to possess a continuum limit. Evidence is, however, limited to a single study, and at a single temperature [33].
• Localization appears approximately at the transition. As the transition is only a crossover, this statement can only be of qualitative nature. In all the cases discussed above [28,33,39,40], localization appears somewhere in the range of temperatures where the crossover takes place.
• The localization length is of the order of the inverse temperature [33,39].
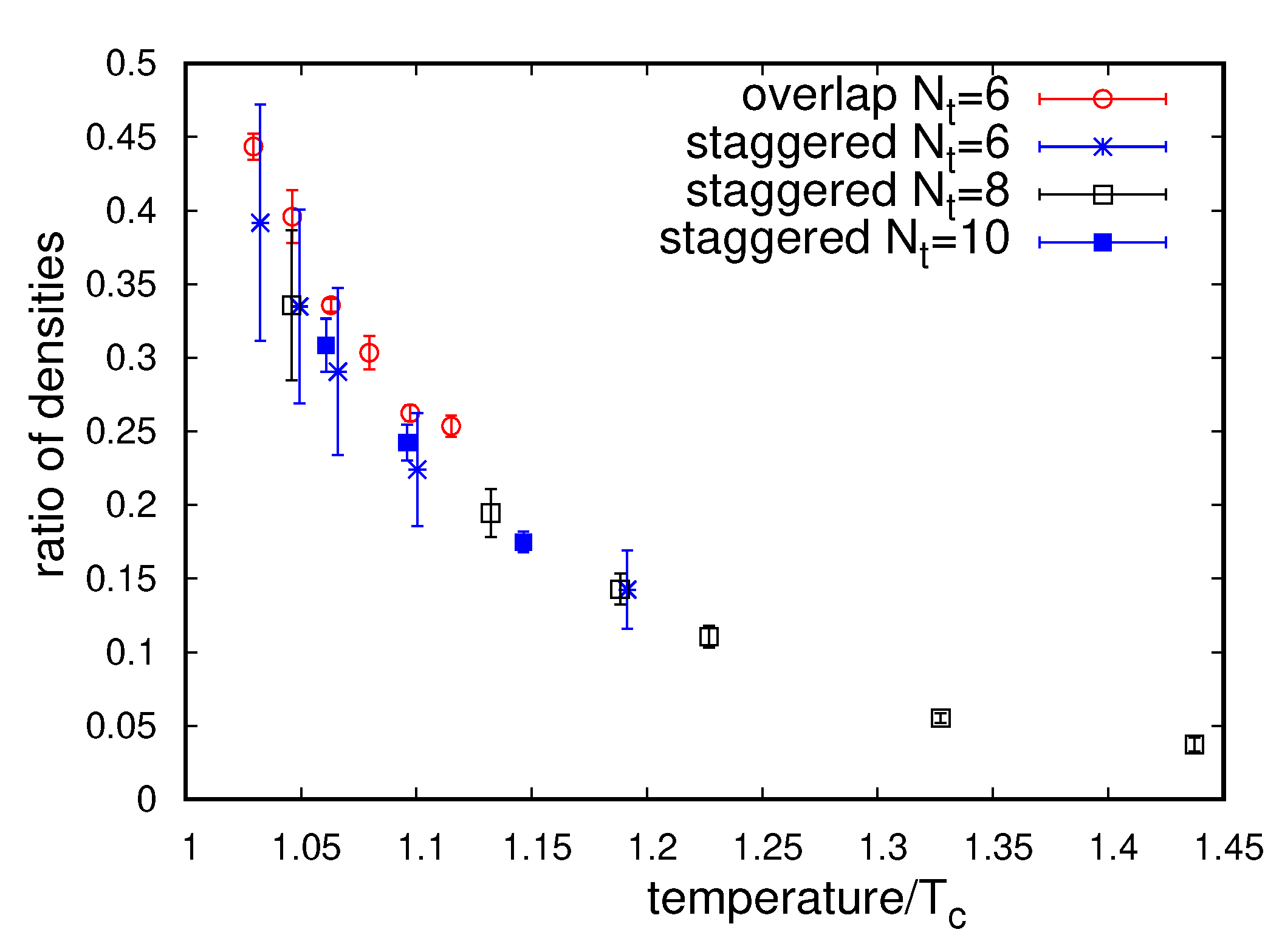
• An Anderson transition takes place in the Dirac spectrum in the high-temperature phase. More precisely, a mobility edge separating localized and delocalized modes in the spectrum is observed on the lattice [33,34,35,37,39,40]. For staggered fermions it has been shown that a genuine Anderson transition takes place at the mobility edge [34,35,37].
• Localized modes correlate with local fluctuations in the confining and topological properties of the configurations. More precisely, the spatial position of localized modes shows correlations with the local fluctuations of the Polyakov loop away from order [39,40], as well as with positive fluctuations of the action density and of the magnitude of the topological charge density, especially at (anti)self-dual points [39].

We now list a few remarks.

• As disordered systems, almost all the models discussed in this section are in the 3d chiral unitary class.20 The appearance of localized modes at the band center contrasts with the delocalized nature of the band center in the 3d chiral orthogonal Anderson model [166,167]. On the other hand, it agrees with what was found in the 3d chiral unitary Anderson model [184], and in the Anderson model with correlated disorder of Ref. [187] in the same class.
• The results of Refs. [34,35,37] indicate that a genuine second-order Anderson transition is present in the staggered Dirac spectrum in high-temperature QCD, in the universality class of the 3d unitary Anderson model. Since QCD is in the 3d chiral unitary class, this suggests that the Anderson transition at nonzero eigenvalue for the 3d chiral and non-chiral unitary classes belong to the same universality class. This is not surprising, as chiral symmetry is not expected to play an important role in the bulk of the spectrum, but only near the origin, around which the spectrum is symmetric precisely due to chiral symmetry. Further support to the lack of any differences in the transition of the chiral and non-chiral model is given by the findings of Ref. [27] concerning the multifractal exponents in the ILM model for QCD, and by the critical statistics found in the Anderson model with correlated disorder of Ref. [187]. A different critical behavior is found instead when the Anderson transition is at the origin in 3d chiral models [184,185,186].
• In the ILM model of Ref. [27], both in the quenched and unquenched cases, a second mobility edge was observed higher up in the spectrum, moving towards the high end as the temperature is decreased. While this part of the spectrum is not representative of real QCD, as the model neglects nonzero modes at the outset, it is nonetheless possible that a similar localization mechanism at the high end of the spectrum applies in QCD as well.21
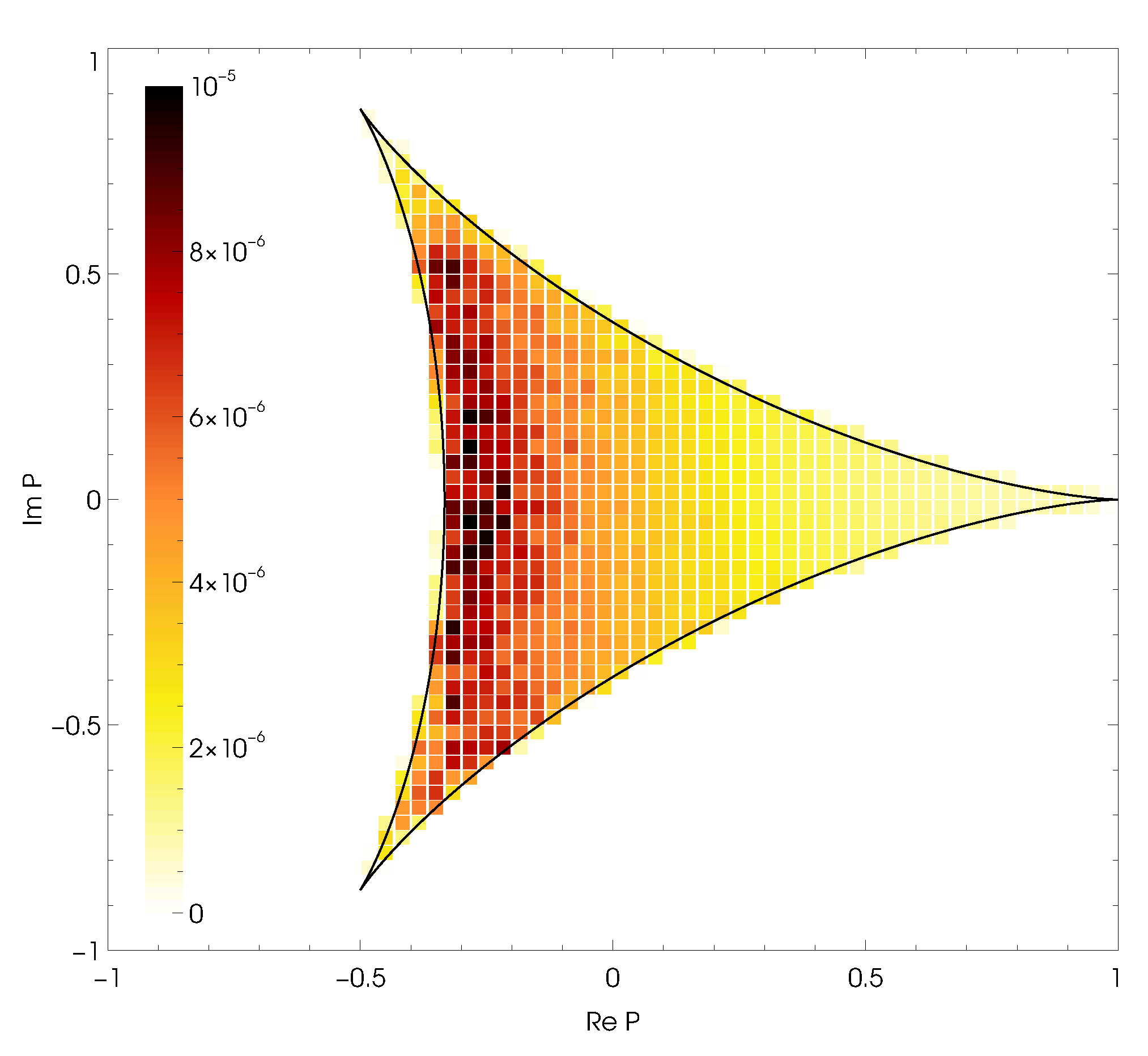
• It is now clear that the Dirac spectral density does not vanish in the deconfined phase of pure gauge SU(3) theory, if one uses sufficiently fine lattices, or lattice discretizations of the Dirac operator with good chiral properties; instead, a peak is formed near the origin (see Refs. [51,57,59]). A sort of “chiral transition” still takes place at deconfinement, where the peak structure appears.
• The disordered medium scenario requires that the densities of instantons and of localized modes match in the high-temperature phase. As observed in Ref. [31] and, in the pure gauge case, in Ref. [86] (see Section 6), the instanton density, obtained assuming an ideal (non-interacting) instanton gas approximation, is lower than the density of localized modes (number of modes per unit spatial volume). Moreover, the latter is seen to increase with T [33], while the instanton density decreases. This indicates that topology can only partially explain the localization of the low Dirac modes.
• An alternative interpretation of localization in terms of topological objects was proposed in Ref. [39]. The authors suggest that localized modes favor regions where L-type (Kaluza-Klein) monopole-antimonopole pairs are located. These are one of the types of monopole constituents inside calorons [20]. This interpretation is supported by the correlation with Polyakov-loop fluctuations, action and topological density, and chirality. A direct identification of monopoles or a quantitative estimate of their density is, however, unavailable.

5. Mechanisms for Localization

In this section, we discuss in some detail the two mechanisms, or more precisely the two sources of disorder, proposed so far to explain localization of the low Dirac modes in QCD: the disordered medium scenario, based on topology fluctuations; and the sea/islands picture, based on fluctuations of the Polyakov loop. We have already briefly discussed the disordered medium scenario in the previous section; here we discuss it again, both to keep this section self-contained, and to give more details.

5.1. The Disordered Medium Scenario

As is well known, the continuum Dirac operator in the background of a gauge configuration of topological charge Q has $n_{\pm }$ exact zero modes of definite chirality $\pm 1$, with $Q=n_{+}-n_{-}$ (index theorem). In particular, for instantons (resp. anti-instantons) of topological charge 1 (resp. $-1$) one finds an exact zero mode of positive (resp. negative) chirality. The same holds for the finite-temperature generalization of instantons known as calorons [16,17,18,19,20,21,22,23].22 The zero modes supported by instantons (i.e., at $T=0$) are algebraically localized, decaying like $1/R^3$ with the distance R from the instanton center. The zero modes supported by calorons are instead fully delocalized in the temporal direction, and exponentially localized in the spatial directions, decaying like $e^{-rT}$, with r the spatial distance from the caloron center and T the temperature of the system. For a dilute ensemble of these objects, their associated zero modes are not exact Dirac eigenmodes any longer, due to the fact that instantons/calorons overlap. The low-lying Dirac eigenmodes are instead linear combinations of these “unperturbed” zero modes,23 obtained by diagonalizing the “perturbed” Dirac operator, which in the zero-mode basis reads (see, e.g., Ref. [204])

$$i\cancel{D}=\left(\begin{array}{cc}\mathbf{0}& T_{IA}\\ T_{AI}& \mathbf{0}\end{array}\right),$$

(15)

with $T_{IA}$ and $T_{AI}=T_{IA}^{†}$ the matrices of the overlap integrals of $i\cancel{D}$ between the unperturbed zero modes associated with an instanton–anti-instanton pair.24 For a dilute ensemble the total topological charge Q is expected to be simply equal to the sum of the individual charges. Out of all the unperturbed zero modes, Q are preserved by topology despite mixing,25 while the remaining ones are not protected by topology and spread around $\lambda =0$ forming a band. The extent of this spreading and the resulting density of near-zero Dirac modes for typical gauge configurations are dynamical issues, determined by the typical density and size of topological objects. In the quenched case, a finite spectral density of near-zero modes is expected to survive as long as a non-negligible density of topological objects supports them. In the presence of dynamical fermions, the fermionic determinant tends to suppress configurations with a higher density of near-zero modes, and so suppresses topological excitations, with respect to the quenched case, but a finite spectral density is still possible. In any case, the details of the dynamics, including especially the temperature and the fermion masses, determine whether a nonzero density of near-zero modes is formed, i.e., loosely speaking, whether chiral symmetry is spontaneously broken.

For sufficiently low temperature, and not too many quark flavors, the density of topological objects and the effect of mixing become strong enough to overcome the repulsive effect of the fermionic determinant, and chiral symmetry breaks spontaneously through the formation of a nonzero density of near-zero modes. This is the disordered medium scenario for chiral symmetry breaking [8,9,10,11,12,13,14,15]. The mixing of the unperturbed modes is also expected to spread them out in space, over topological objects that overlap non-negligibly with their original location. If the typical spatial distance $n^{-\frac{1}{3}}$ between topological objects is large compared to the typical spatial range $1/T$ of the corresponding unperturbed zero modes, one expects the resulting perturbed near-zero modes to remain localized on a few objects only. Here $n=\frac{{\mathcal{N}}_{\mathrm{top}}}{V}$ is the spatial density of ${\mathcal{N}}_{\mathrm{top}}$ calorons and anti-calorons in a finite spatial volume V. At high temperatures both density and range are small, and near-zero modes are expected to be localized. As the temperature decreases, both density and range increase, with more and more topological objects overlapping, and near-zero modes are expected to eventually delocalize over the whole system [10]. It is reasonable to expect that delocalization will take place around the same temperature as chiral symmetry breaking (in the loose sense explained above). It should be clear, however, that finite spectral density and delocalization of modes near the origin are not automatically linked.26

According to the scenario above, near-zero localized modes should be associated with local lumps of topological charge. It is worth noting that (anti)calorons in SU($N_c$) gauge theory are made up of $N_c$ (anti)monopole constituents [20], and that when these are well separated the associated zero mode is localized on a single constituent; which one depends on the holonomy (Polyakov loop) of the gauge field at asymptotic distance from the core [222,223]. For typical high-temperature ordered configurations with Polyakov loop in the trivial sector, the relevant constituent is the type-L monopole, which also has the largest action and topological charge densities, as well as the smallest size (see Ref. [221]). This further characterizes the favorable locations for modes according to the disordered medium scenario.

Refs. [25,26,38,39,86] provide evidence that some of the modes are indeed localized on topological objects. In particular, Ref. [39] shows that the locations favored by some of the localized low modes have all the features of L-type monopoles and antimonopoles: large action and topological charge densities, near (anti)self-duality, and near degeneracy of two eigenvalues of the untraced Polyakov loop (see Figure 12).27 In Refs. [58,86] it is shown that for pure gauge SU(3) theory the distribution of the number of near-zero modes in the peak of the spectral density near zero (see Figure 1) is consistent with the distribution of a dilute gas of topological objects. This suggests that the peak of near-zero modes indeed originates from the zero modes associated with topological objects. This provides further evidence supporting the disordered medium scenario as a viable mechanism for localization, and its close relation with spontaneous chiral symmetry breaking.

If localization were entirely due to mixing topological would-be zero modes, then the density of localized modes would be equal to that of the topological objects (calorons).28 Since above the transition the density of calorons decreases sharply with increasing temperature, we would expect the same behavior of the density of localized modes. However, as shown in Ref. [33], the density of localized modes actually increases with temperature (see Figure 13). In the pure gauge case, no more than half of the localized modes seem to be of topological origin for temperatures as low as $1.03T_c$ [86] and as the temperature increases, this fraction rapidly decreases. In Figure 14 we show the temperature dependence of the fraction of localized modes that can be associated with near-zero modes of topological origin [51,86]. We show results obtained with the overlap Dirac operator, and with the staggered Dirac operator for three different values of the lattice spacing. All the results are consistent and show that with increasing temperature a rapidly decreasing fraction of the localized modes are of topological origin. We can conclude that while topology-related localized modes may suffice to explain the near-zero peak, they cannot explain all the remaining localized modes found in a typical high-temperature gauge configuration, which therefore require a different supplementary mechanism.

5.2. The Sea/Islands Picture

An alternative mechanism has been proposed in Ref. [31], and further elaborated in Refs. [47,48,49]. The basic observation is that the eigenvalues of the untraced Polyakov loop at a spatial site $\overrightarrow{x}$ effectively change the temporal boundary condition felt locally by the quark eigenfunctions $\psi (t,\overrightarrow{x})$. Indeed, working for simplicity in the continuum, if one fixes the gauge to the temporal gauge $A_4(t,\overrightarrow{x})=\mathbf{0}$, the eigenvalue problem reduces to

$$\cancel{D}\psi =({\partial }_4{\gamma }_4+{\cancel{D}}_{\left(3\right)})\psi =i\lambda \psi ,{\cancel{D}}_{\left(3\right)}=\sum _{j=1}^3{\gamma }_j({\partial }_j+ig{A}_j),$$

(16)

while the effect of a nontrivial (untraced) Polyakov loop $P\left(\overrightarrow{x}\right)$ is to change the temporal boundary condition from antiperiodic to

$$\psi (1/T,\overrightarrow{x})=-P\left(\overrightarrow{x}\right)\psi (0,\overrightarrow{x}).$$

(17)

Equations (16) and (17) define the eigenvalue problem in temporal gauge. Clearly, the effective local boundary condition Equation (17) affects the contribution of site $\overrightarrow{x}$ to the Dirac eigenvalue, $i\lambda =(\psi ,\cancel{D}\psi )$.

To gain some insight on the effects of the Polyakov loop, it is useful to study a family of configurations for which the eigenvalue problem can be solved exactly, namely those with $A_{\mu }(t,\overrightarrow{x})=\mathbf{0}$ everywhere, and with a constant but nontrivial Polyakov loop. This can always be diagonalized by means of a global gauge transformation, so without loss of generality we can take $P\left(\overrightarrow{x}\right)=\mathrm{diag}(e^{i{\varphi }_1},e^{i{\varphi }_2},e^{i{\varphi }_3})$, with $e^{i({\varphi }_1+{\varphi }_2+{\varphi }_3)}=1$. On these configurations the eigenfunctions of $-{\cancel{D}}^2$ are plane waves,

$${\psi }_c^{(a,k,\overrightarrow{p})}(t,\overrightarrow{x})={\delta }_{ca}{e}^{i({\omega }_{ak}t+\overrightarrow{p}·\overrightarrow{x})},$$

(18)

where c is the color index,29 with temporal frequency (effective Matsubara frequency) given by

$${\omega }_{ak}=T[(2k+1)\pi +{\varphi }_a],k\in \mathbb{Z},$$

(19)

and corresponding eigenvalues

$${\lambda }_{ak}{\left(\overrightarrow{p}\right)}^2={\omega }_{ak}^2+{\overrightarrow{p}}^2.$$

(20)

Restricting without loss of generality to ${\varphi }_{1,2}\in (-\pi ,\pi ]$, ${\varphi }_1+{\varphi }_2+{\varphi }_3=0$, the lowest positive Dirac eigenvalue is seen to be

$${\lambda }_{\min }=T(\pi -\underset{a}{max}|{\varphi }_a\left|\right),$$

(21)

i.e., it decreseas monotonically and symmetrically as one moves away from ${\varphi }_a=0\forall a$, and vanishes when at least one of the Polyakov loop eigenvalues equals $-1$.

While the configuration discussed above is obviously unrealistic, the result Equation (21) allows understanding qualitatively which sites will be favored by a low Dirac eigenmode when the Polyakov loop configuration is mostly ordered near $P\left(\overrightarrow{x}\right)\approx \mathbf{1}$, with “islands” of fluctuations in the “sea” of ordered Polyakov loops, as it happens at high temperature. One can in fact interpret Equation (21), now with $\overrightarrow{x}$-dependent phases ${\varphi }_a={\varphi }_a\left(\overrightarrow{x}\right)$, as a sort of three-dimensional local potential for the quarks, to which one should add the appropriate “hopping terms” originating from the spatial dependence of the Polyakov loops, as well as from the spatial components of the gauge potential. From this point of view, fluctuations of the Polyakov loop away from order provide regions of lower potential that can “trap” the quarks.

More precisely, at high temperatures ${\varphi }_a\left(\overrightarrow{x}\right)\approx 0$ in an extended region, and neglecting in a first approximation the effect of the islands and of hopping, one finds fully delocalized modes. In the same approximation one finds a spectral gap, with the corresponding (positive) eigenvalues starting at $T\pi$, i.e., the usual lowest (fermionic) Matsubara frequency. The presence of islands and the effect of the interactions are expected to reduce this gap, but the lowest eigenvalue that can be reached by a delocalized mode is expected to remain separated from the origin. On the other hand, localizing on an island of fluctuations can be “energetically” more favorable, and bring the corresponding eigenvalues inside the gap, as long as the gain in potential energy achieved by avoiding the sea of ordered Polyakov loops is sufficiently larger than the price paid for localization in terms of spatial momenta. This leads to expect the following scenario, at least when the islands are sufficiently distant from each other: a region of low spectral density, or pseudogap, opens between the origin and some point ${\lambda }_c$ in the spectrum, or mobility edge, above which modes are extended throughout the whole space; modes in the pseudogap can exist only if they are localized on energetically convenient islands of fluctuations.

The scenario described above, which has been dubbed the sea/islands picture of localization, shows a clear similarity with the Anderson-type models of condensed matter physics, and the terminology has been chosen precisely to reflect this similarity. From the point of view of random Hamiltonians, the local fluctuations of the Polyakov loop provide a three-dimensional source of on-site disorder. This would naturally explain the fact that the critical behavior found at the mobility edge in QCD is the same as that of the three-dimensional unitary Anderson model.30 There are, however, important differences with the simple unitary Anderson model of Equation (4). In that case, localization starts from the band edges and moves towards the band center as the amount of disorder, as measured by the width of its probability distribution, is increased. In QCD, while localization may as well be present at the band edges (cf. the results of Ref. [27] in the ILM model and Ref. [56] in ${\mathbb{Z}}_2$ gauge theory), it is its appearance directly at the band center that characterizes the deconfined phase. Moreover, the actual source of disorder are the eigenvalues of the Polyakov loops, which are complex numbers lying on the unit circle, and so the magnitude of the disorder is actually bounded.

Another important difference, which is relevant also to the problem of spontaneous chiral symmetry breaking, is the different structure of the “free” Hamiltonian associated with the two cases in the absence of fluctuations. For the Anderson model this is simply $H_{\mathrm{free}}^{\left(\mathrm{AM}\right)}={\sum }_{j=1}^3{T}_j+T_j^{†}$ with $T_j$ the translation operator in direction j, while for the Dirac operator one has (for a naive lattice discretization) ${\cancel{D}}_{\mathrm{free}}={\sum }_{\mu =1}^4{\gamma }_{\mu }(T_{\mu }-T_{\mu }^{†})$. Here periodic boundary conditions are understood in the spatial directions; the effective boundary conditions Equation (17) are assumed for the temporal direction. While the spectrum of $H_{\mathrm{free}}^{\left(\mathrm{AM}\right)}$, $E\left(\overrightarrow{p}\right)={\sum }_{j}cos{p}_j$, with $p_j=\frac{2\pi k_j}{L}$, is dense near the origin, the presence of the gamma matrices in ${\cancel{D}}_{\mathrm{free}}$ leads to ${\lambda }_{ak}\left(\overrightarrow{p}\right)=\sqrt{{\omega }_{ak}^2+{\overrightarrow{p}}^2}$. Even in the case ${\omega }_{ak}=0$, in which there is no sharp spectral gap, the spectral density near the origin is low and vanishes at $\lambda =0$.

An important aspect of this scenario is that deconfinement is naturally associated with the two effects that lead to localization of the low modes in high-temperature QCD. The first such effect is of course the formation of a sea of ordered Polyakov loops close to the identity, which can cause the opening of a spectral pseudogap and so make modes that localize on the islands of fluctuations stable against delocalization, as explained above. However, the appearance of the pseudogap requires also a second effect due to the ordering of Polyakov loops at deconfinement, namely the increased correlation between gauge fields on different time slices. The discussion of this effect requires a more detailed description of the Dirac operator in the language of Anderson models, in what can be called the “Dirac-Anderson approach”. Here we sketch the discussion in the continuum in the temporal gauge; a more detailed and mathematically more precise analysis is presented in Ref. [48] for staggered fermions on the lattice.

Due to its compactness, the temporal direction can be treated as an internal degree of freedom, in particular by expanding the quark eigenfunctions on a complete basis of plane waves $e^{i{\omega }_{ak}t}$ obeying the appropriate effective boundary conditions, Equation (17). Here ${\omega }_{ak}$ are the effective Matsubara frequencies of Equation (19), now $\overrightarrow{x}$-dependent, which provide a random on-site potential of the form ${\omega }_{ak}\left(\overrightarrow{x}\right){\gamma }_4$. For every color a with associated Polyakov-loop phase ${\varphi }_a\left(\overrightarrow{x}\right)$, in correspondence to each wave number k there is a different branch of the on-site potential, and so a different associated three-dimensional Anderson-type model, built by adding the on-site disorder to the spatial part of the Dirac operator (projected on the $a,k$ subspace). We will refer to each of these models as a Dirac-Anderson model. The full Dirac operator is obtained by putting the various Dirac-Anderson models together, and by including their coupling induced by the hopping terms (i.e., the spatial part of the operator). The strength of the coupling among the Dirac-Anderson models turns out to be inversely related to the correlation of the gauge fields on different time slices. At low temperatures this correlation is small, the Dirac-Anderson models are strongly coupled, and the internal degree of freedom is effectively one more direction in which the modes can extend, thus facilitating their delocalization. This is in agreement with the effectively four-dimensional nature of QCD in the low temperature phase. As a matter of fact, the pseudogap does not open at low temperatures, where the spectral density is finite near zero, and this can only happen if the various Dirac-Anderson models do mix with each other (see the discussion about the free Dirac operator). In the absence of a pseudogap, localization of a mode is generally unstable against mixing with modes of similar energies. At high temperature, instead, the Polyakov loops become ordered inducing stronger correlations among different time slices, and the Dirac-Anderson models decouple making the problem effectively three-dimensional. In particular, the pseudogap is now expected to appear: it would be present for exactly decoupled Dirac-Anderson models (see again the discussion about the free Dirac operator), and their limited mixing is not sufficient to close it. Localized modes near the band center can then be supported by Polyakov loop fluctuations, as discussed above. As shown in Ref. [48] in a toy model where ordering of the Polyakov loop and correlation of the time slices can be varied independently, both effects are required for localization to appear at the band center.

An important aspect of the sea/islands picture is that it is not incompatible with the growing density of localized modes observed in QCD. Differently from the case of topological charge, Polyakov-loop fluctuations are not quantized. As T grows in the deconfined phase, the volume $V_{\mathrm{fluct}}$ occupied by Polyakov-loop fluctuations is expected to decrease, $V_{\mathrm{fluct}}\sim T^{-c_1}$, as the Polyakov loop becomes more and more ordered. On the other hand, the typical size $V_0$ of the islands of fluctuations is also expected to decrease, $V_0\sim T^{-c_2}$. The number of localized modes is expected to be directly related to the number of islands, $V_{\mathrm{fluct}}/V_0\sim T^{c_2-c_1}$, and whether this number increases or decreases with temperature depends on the details of the dynamics. For example, while increasing in QCD [33] up to $T\sim 5T_c$, it is seen to decrease in 2+1-dimensional SU(3) gauge theory above $T\sim 1.1÷1.2T_c$ [53].

Perhaps the most appealing feature of the sea/islands picture is its simplicity: all that it needs to work is the ordering of the Polyakov loop. This leads immediately to expect that localized modes will appear at the low end of the spectrum whenever an ordering transition takes place, independently of details such as the gauge group and its representation, fermionic content, nontrivial topological features, dimensionality,31 and so on. This is discussed in the next section.

6. Localization in Other Gauge Theories

In this section, we discuss localization of the low Dirac modes in gauge theories other than QCD. Some of the references have been already discussed in Section 4 in connection with QCD, where they where treated as approximations. Here they are briefly discussed again, focussing more on the differences than on the similarities with QCD.

The main motivation in studying more general gauge theories is to investigate further the extent of the connection between localization on one side, and deconfinement and chiral restoration on the other. In particular, studying localization in models with genuine deconfining and/or chirally restoring phase transitions allows one to investigate this connection in a more clear-cut setting than in QCD, where it is somewhat blurred by the crossover nature of the transition. Studying more general gauge theories also allows one to test the sea/islands picture discussed in the previous section, and its generic prediction of localization of low modes in the high-temperature, “ordered” phase.

Genuine deconfining phase transitions are found in pure gauge SU($N_c$) theory. In 3+1 dimensions the transition is second order for $N_c=2$ and first order for $N_c\ge 3$, while in 2+1 dimensions it is second order for $N_c=2,3$ and first order for $N_c\ge 4$ (see, e.g., Refs. [78,79,224,225]). As already mentioned in Section 4, localized low Dirac modes have been found in pure gauge SU(2) theory in 3+1 dimensions, both with the overlap [30,31] and with the staggered [31,32] Dirac operator (see Figure 8, right), above the deconfinement temperature $T_c$. (Further details can be found in Section 4 and will not be repeated here.) No sign of localized modes was found instead below $T_c$. From the random-matrix point of view, the SU(2) case differs from SU($N_c\ge 3$) as the symmetry class is the symplectic instead of the unitary one. This is reflected in the different behavior of the unfolded spectrum in the bulk, which agrees with the symplectic Wigner surmise, Equations (11) and (12). A detailed study of the Anderson transition was not pursued.

Results for pure gauge SU(3) have been presented in Refs. [51,54,86] for the 3+1-dimensional case, and in Ref. [53] for the 2+1-dimensional case. Localized low Dirac modes are found in both cases in the deconfined phase. In 3+1 dimensions the temperature dependence of the mobility edge ${\lambda }_c$ was studied using the Wilson gauge action both with staggered [51] and overlap [54] fermions (using in this case the magnitude of the eigenvalues), smearing the gauge fields with two steps of stout smearing [211] in the staggered case, and two steps of hex smearing [226] in the overlap case. The integrated ULSD computed locally in the spectrum, $I_{s_0}\left(\lambda \right)$, was used to determine ${\lambda }_c$ as the point where $I_{s_0}$ takes its critical value $I_{s_0}^{\left(c\right)}$ [34], i.e., $I_{s_0}\left({\lambda }_c\right)=I_{s_0}^{\left(c\right)}$. Here use was made of the universality of the critical properties of the Anderson transition, which should be shared by QCD and pure gauge SU(3) theory, as they are both in the 3d unitary class. This was confirmed by the volume-independence of the resulting ${\lambda }_c$. For both discretizations, ${\lambda }_c$ is seen to extrapolate to zero at a temperature which agrees with the deconfinement temperature (see Refs. [78,79] and references therein) within numerical errors (see Figure 15).

The 2+1-dimensional case was studied in Ref. [53] using the Wilson gauge action and the staggered discretization (without smearing). Universality arguments lead to expect that the Anderson transition is of BKT type with exponentially divergent correlation length, as found in Ref. [160] for the 2d unitary Anderson model. The results of Ref. [53] support this scenario. In particular, spectral statistics are critical, i.e., volume independent for all $\lambda$ above ${\lambda }_c$, as expected for a BKT-type Anderson transition [227], see Figure 16, left. The mobility edge was determined by means of a finite size scaling study, and found to extrapolate to zero at a temperature compatible with the deconfinement temperature [225] (although with much larger numerical uncertainty), see Figure 16, right. In the confined phase no localization was found, but low modes were seen to display a nontrivial fractal dimension $D_2<2$ (see Equation (6)).

Localization of Dirac modes was studied in ${\mathbb{Z}}_2$ pure gauge theory in 2+1 dimensions in Ref. [56], probed with unimproved staggered fermions. This model has the simplest gauge group, and the lowest dimensionality in which a deconfining transition is found. Studying the fractal dimension $D_2$, it was shown that low modes are localized ($D_2=0$) in the high-temperature, deconfined phase of the theory in the positive center sector (i.e., positive spatially averaged Polyakov loop), while they are delocalized (with $D_2<2$) in the low-temperature, confined phase, and in the high temperature phase in the negative center sector (i.e., negative spatially averaged Polyakov loop). Localized modes are also found at the high end of the spectrum, independently of the phase and of the center sector. Significant correlation between localized modes and both Polyakov loops and clusters of negative plaquettes was observed.

While a genuine phase transition is expected for SU(3) gauge group in the presence of $N_f=3$, light enough dynamical fermions [80], so far a critical point has been observed only on coarse lattices, and disappears in the continuum limit [228,229,230]. Although only a toy model for QCD, the SU(3) theory with $N_f=3$ flavors of unimproved staggered fermions on $N_t=4$ lattices is nonetheless a well-defined statistical model with a genuine first order transition, affecting both its chiral and confining properties, despite the absence of exact chiral and center symmetries. More precisely, as the coupling $\beta$ crosses the critical value ${\beta }_c$, the chiral condensate jumps downwards to a much smaller but still finite value; and the average Polyakov loop jumps upwards from its small but nonzero value to a considerably larger value. Evidence of localization of the low staggered Dirac modes was reported in Ref. [50] for bare fermion mass $m=0.01$, below the critical value $m_c=0.0259$ [230], where genuine first-order phase transitions are present. A mobility edge was shown to be present for $\beta >{\beta }_c$: it increases with $\beta$, and extrapolates to zero close to ${\beta }_c$. The lowest mode was also seen to turn from delocalized to localized at a coupling ${\beta }_{\mathrm{loc}}$ compatible with ${\beta }_c$, i.e., in correspondence with the finite-temperature transition (see Figure 17, left).

The relation between localization and deconfinement was tested at a different deconfinement phase transition in trace-deformed [231,232] pure gauge SU(3) theory at finite temperature in Ref. [55]. In this model a deformation term $\Delta S=h{\sum }_{\overrightarrow{x}}{\left|\mathrm{tr}P\left(\overrightarrow{x}\right)\right|}^2$ is added to the action, which (for $h>0$) tends to locally suppress a nonzero trace for the Polyakov loop $P\left(\overrightarrow{x}\right)$. For temperatures above the deconfinement temperature, $\Delta S$ pushes the theory towards a “reconfined” phase where $\mathrm{tr}P\left(\overrightarrow{x}\right)\sim 0$. This happens when the deformation parameter h crosses a (temperature dependent) critical value $h_c$. Ref. [55] studied the spectrum of the two-stout smeared staggered spectrum at $\beta =6.0$ on $N_t=6$ lattices for various volumes and deformation parameters. Results showed that localized modes are present for $h<h_c$, but disappear as the system crosses over into the reconfined phase. The mobility edge was determined by comparing the fractal dimension of the modes with its value at criticality [148]. While monotonically decreasing with h, it is not clear whether it vanishes continuously at $h_c$ or jumps to zero discontinuously (see Figure 17, right).

Finally, the connection between localization and ordering of the background configuration was studied in spin models in Refs. [47,48,49,52]. Ref. [47] used a simple 3d Hamiltonian in the orthogonal class with on-site disorder provided by the spins of a continuous-spin Ising-type model. In the ordered phase of the spin model, localization was observed for the low modes, with a mobility edge separating them from higher modes, and critical behavior compatible with that of the 3d orthogonal Anderson model. Refs. [48,49] dealt with the Dirac-Anderson form of the staggered operator (see Section 5.2), so in the 3d chiral unitary class, in the case $N_t=2$ in the background of Polyakov loops constructed from a spin model. Localized low modes are observed in the ordered phase of the model [48], appearing at the critical temperature [49]. Ref. [52] reports on the $C{P}^3$ model in 1+1 and 2+1 dimensions. While in 1+1 dimensions localized modes are found in both phases of the model, as expected in one spatial dimension, in the 2+1 case localized modes are found only in the ordered phase. This model belongs to the 2d chiral unitary class.

7. Conclusions and Outlook

The presence of localized modes in the spectrum of the Dirac operator in the high-temperature phase of gauge theories is by now well established. Numerical studies on the lattice have shown that above the transition temperature the low-lying Dirac modes are spatially localized on the scale of the inverse temperature, in QCD and QCD-like theories, as well as in several pure gauge theories and related models in 3+1 and 2+1 dimensions [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,47,48,49,50,51,52,53,54,55,56,86].

The physical significance of localization has so far remained quite elusive. First of all we should emphasize an important difference between localization in electron systems and localization in QCD. In the former case the mobility edge in the spectrum can be “accessed” by tuning a suitable control parameter, such as an electric field or the density of electrons. As the Fermi energy crosses the mobility edge, the system undergoes a genuine phase transition, with the zero-temperature conductivity changing non-analytically. In contrast, the mobility edge in the QCD Dirac spectrum cannot be directly connected to a thermodynamic transition. This is because in that case, in general, there is no control parameter that can be adjusted to make the system sensitive to just the eigenmodes at the mobility edge in the spectrum. The only exception is when the mobility edge is at zero, which happens only at the critical temperature of localization. If at the same time the quark masses are set to zero, the system becomes most sensitive to the lowest Dirac eigenmodes, the ones closest to zero. Thus, only in this double limit when the temperature tends to the critical temperature of localization and the quark mass to zero can one possibly directly connect the localization transition to a genuine thermodynamic phase transition. Unfortunately, this limit is out of the reach of present day lattice simulations and we have no numerical evidence of what happens there.

On the other hand, some progress has been made to understand the physical significance of localization in QCD. A clear connection with deconfinement has emerged: in all the models investigated so far, localization of the low modes shows up when the system transitions from the confined, low-temperature phase to the deconfined, high-temperature phase [28,33,49,50,51,53,54,55,56]. Convincing evidence has been presented for the crucial role played by the ordering of the Polyakov loop and by its fluctuations in the formation of a mobility edge in the Dirac spectrum, separating low-lying, localized modes from the delocalized bulk modes [31,39,40,48,56]. As the Polyakov loop is the (approximate, in the case of QCD) order parameter for confinement, the observed connection between localization and deconfinement has a dynamical explanation, further backed by a viable mechanism (the sea/islands picture [31,47,48,49], see Section 5.2) relating the two phenomena. This raises the hope that further studies can lead to a better understanding of confinement, and possibly to the uncovering of the mechanism behind this remarkable property of gauge theories. In this context, it would be interesting to further elucidate the relation between localization and center symmetry, since so far only models with nontrivial gauge group center have been investigated.

Localization could also help in explaining the close relation observed between deconfinement and restoration of chiral symmetry. These two phenomena in fact take place at the same temperature, or in a relatively narrow interval of temperatures, where also localized low Dirac modes appear. Localization could then provide the key to understanding this relation between in principle unrelated phenomena. Unfortunately, while the connection between deconfinement and localization can be easily studied in a clear-cut situation by investigating pure gauge theories with a genuine deconfining phase transition, studying the connection between chiral symmetry restoration and localization by means of numerical lattice simulations faces the considerable difficulties involved in taking the chiral limit. Studies of this type would be of great interest, especially in the light of the possible role played by localized modes in suppressing the finite-temperature Goldstone excitations, suggested in Ref. [62]. A particularly interesting case would be that of adjoint massless fermions, for which both chiral and center symmetries are exact, and an intermediate, deconfined but chirally broken phase was observed on the lattice for two flavors in Ref. [233]. This suggests that a nonzero density of near-zero, localized modes is present in this phase, and that no Goldstone excitation is present.

Nonetheless, even in theories such as QCD where chiral symmetry is only approximate, the study of the relation between localized modes and topological fluctuations of the gauge fields sheds indirectly some light on the interplay of chiral symmetry and localization. Indeed, a peak of near-zero [59,60,61] localized [38] modes of topological origin appears around the QCD pseudocritical temperature. These modes originate most likely from the mixing of the localized zero modes associated with isolated instantons and anti-instantons, which in the high-temperature phase form a dilute gas of topological excitations (the disordered medium scenario [8,9,10,11,12,13,14,15], see Section 5.1). In contrast, in the low temperature phase these excitations form a dense medium, and the mixing of the associated zero modes leads to a band of near-zero delocalized modes giving rise to a nonzero spectral density near the origin, and so a large increase of the chiral condensate.

An interesting observation is that in the quenched limit of QCD this peak of near-zero modes can be accurately described in terms of a non-interacting gas of topological objects [58,86]. The absence (or near absence) of interactions could be related to why the associated zero modes do not mix efficiently, thus remaining localized and failing to spread in a near-zero band of eigenvalues. On the other hand, as this occurs only in the high-temperature phase, it is natural to expect that deconfinement is responsible for the radical change in the behavior of topological excitations. This aspect surely deserves more attention.

In this review, we summarized what is known (to us, at least) about localization of Dirac modes in the deconfined phase of gauge theories, and highlighted the connections between localized modes, ordering of the Polyakov loop, density of low modes, and topological objects. We hope that this will motivate further investigations of the interplay of confinement, chiral symmetry, topology, and localization in finite-temperature gauge theories.