The Warps and Wefts of a Polyploidy Complex: Integrative Species Delimitation of the Diploid Leucanthemum (Compositae, Anthemideae) Representatives
Abstract
:1. Introduction
2. Results
2.1. RADseq Assembly
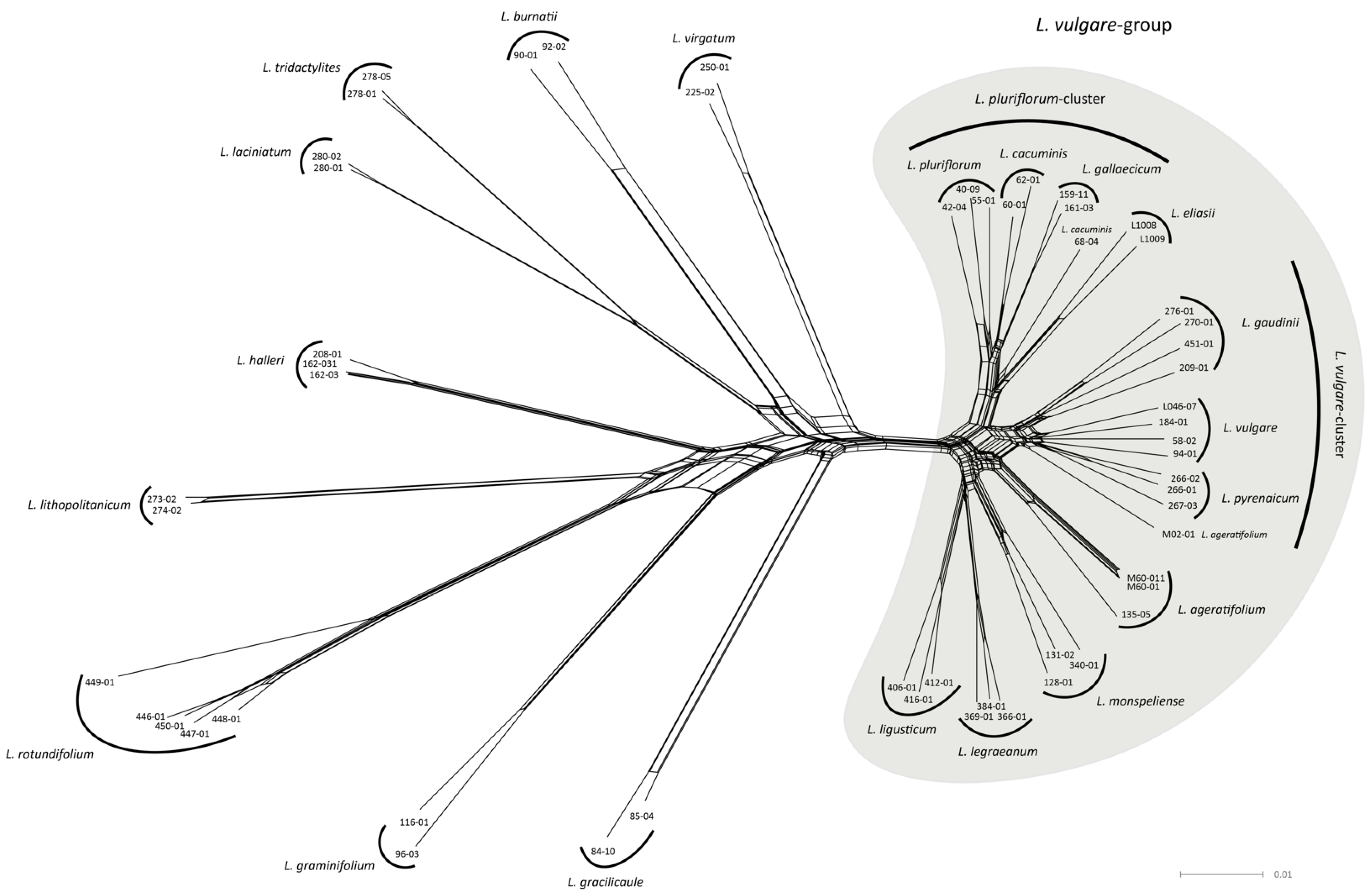
2.2. Network Analysis
2.3. Hybrid Detection
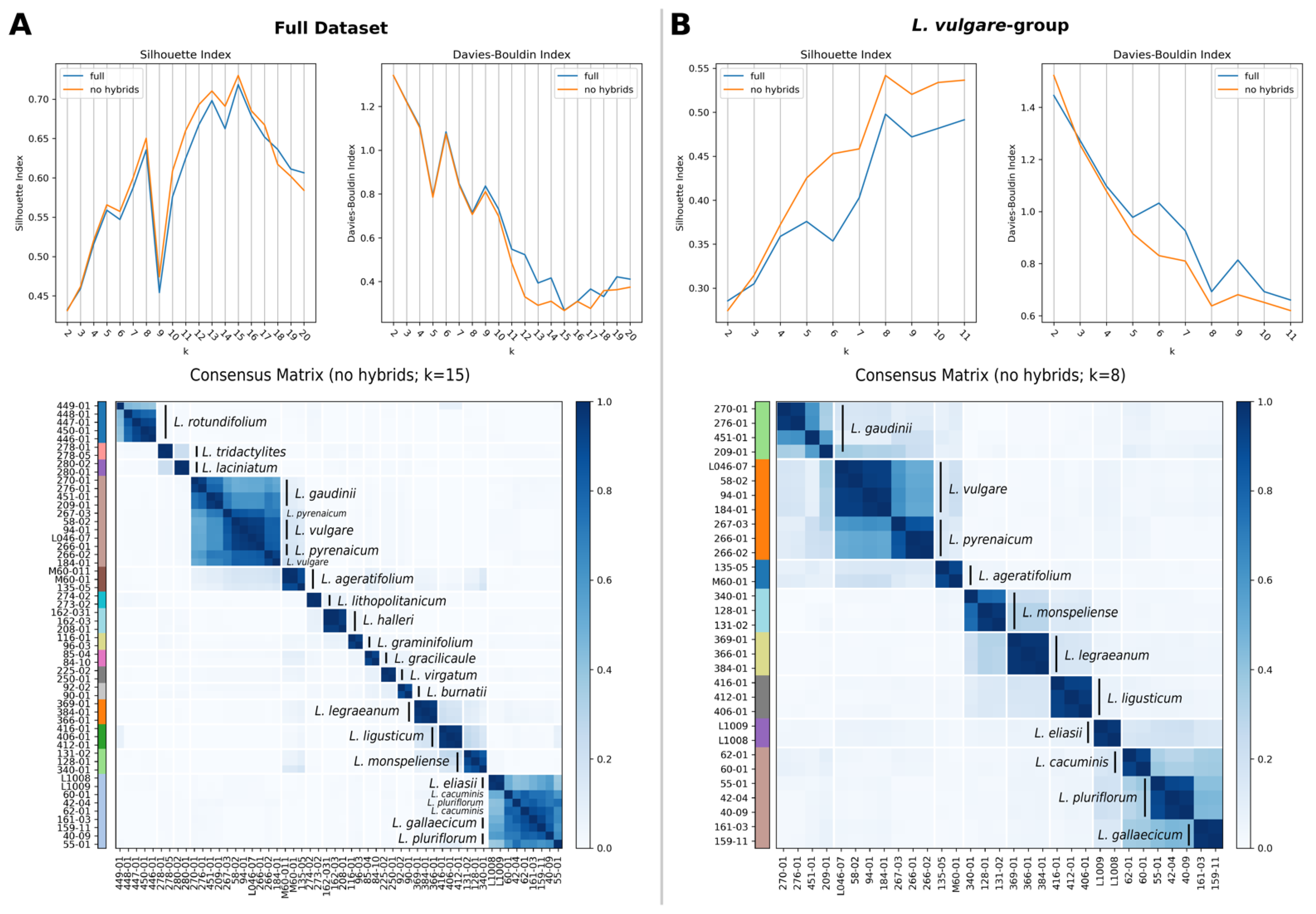
2.4. Species Discovery: Consensus Clustering
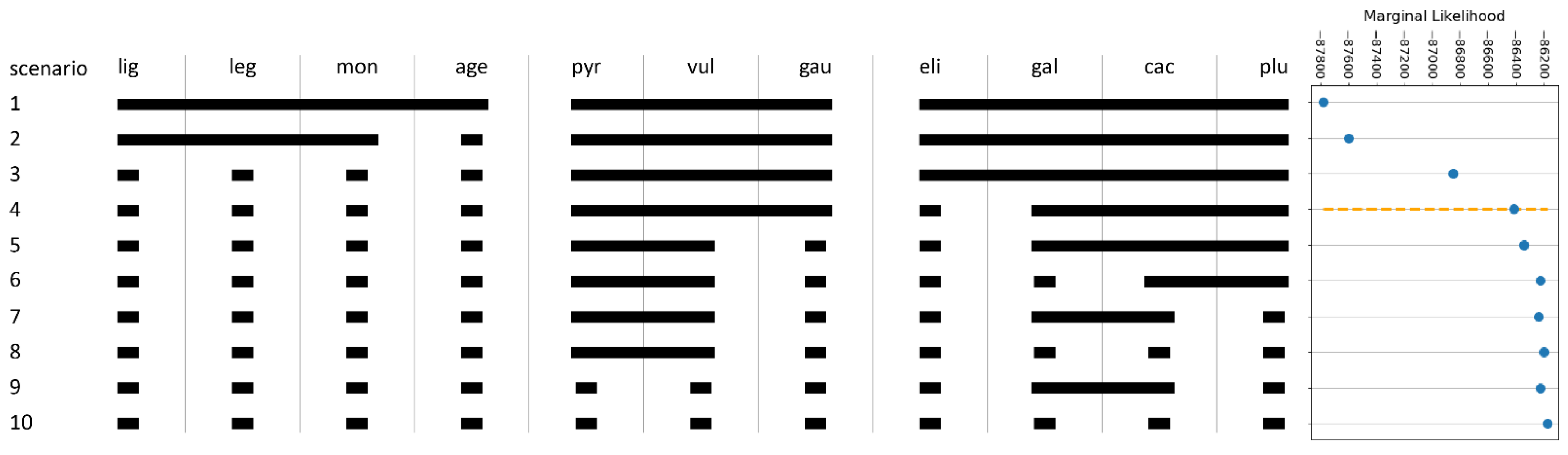
2.5. Species Validation: Coalescent-Based Species Delimitation
2.6. Ecological Analysis
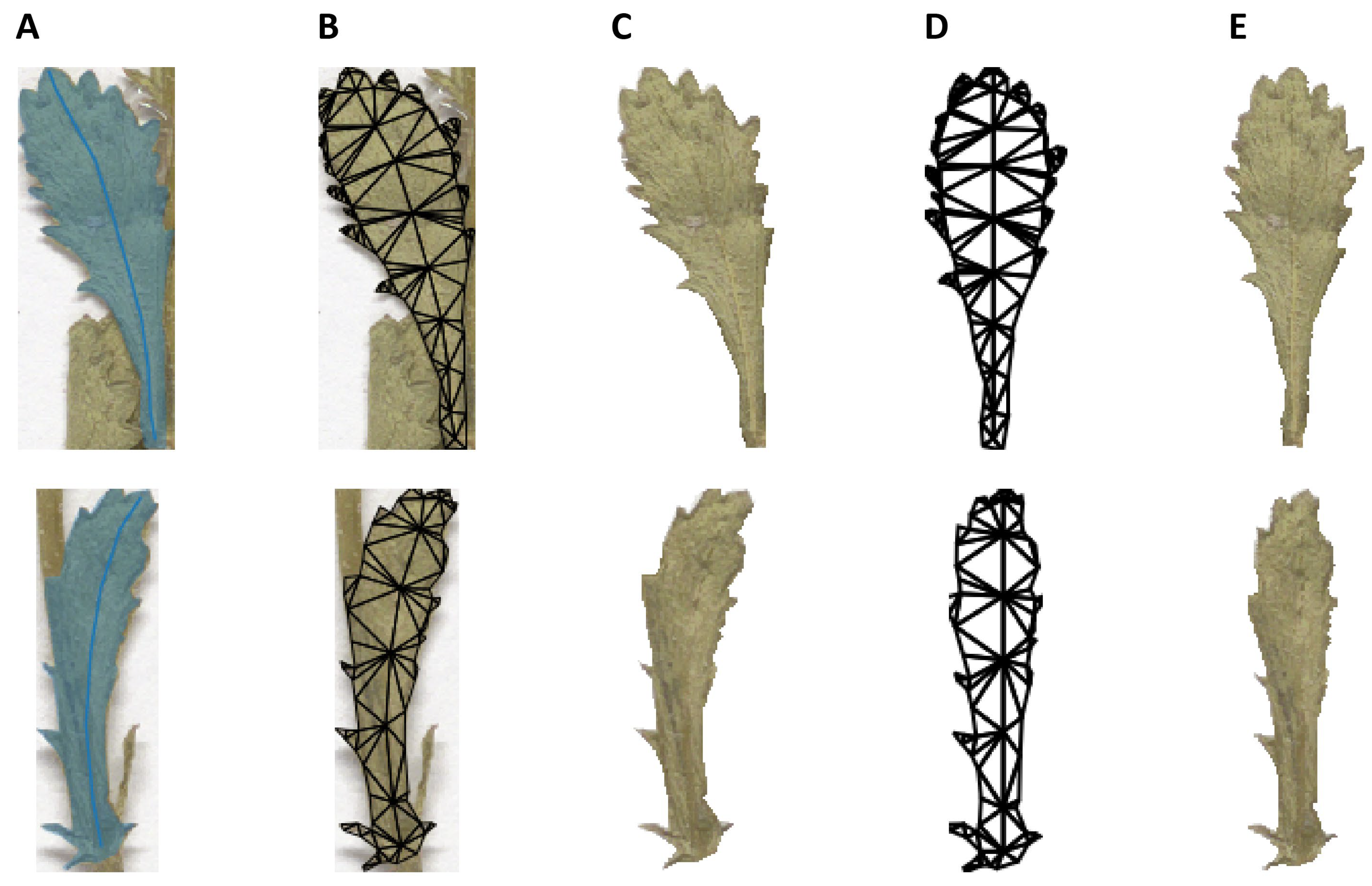
2.7. Morphological Analysis
2.8. Geography
3. Discussion
- (1)
- The Leucanthemum vulgare-group: While L. vulgare is a taxon widespread in Europe, L. gaudinii and L. pyrenaicum are restricted to the Alps and the Pyrenees, respectively. In genealogical respects, L. gaudinii is on the verge of evolving as an independent lineage, with MSC-based SD, in contrast to CKM clustering, showing no significant differentiation, while the other two taxa belong to the same metapopulation system. While both L. gaudinii and L. pyrenaicum are not significantly allopatric to L. vulgare, the former is morphologically different and the latter ecologically. In the case of L. gaudinii, its ecological and geographical overlap with L. vulgare combined with its genealogical (and morphological) distinctness argues for acknowledgment as an independently evolving lineage (i.e., species), while L. pyrenaicum represents only an ecologically deviating facies of L. vulgare—an ecotype that could be at best acknowledged taxonomically as a subspecies of the widespread taxon. Consequently, we propose the following taxonomic treatment for this group:
- (a)
- Leucanthemum gaudinii Dalla Torre in Sonklar & al., Anleit. Wiss. Beob. Alpenreisen 2: 244. 1882 ≡Chrysanthemum gaudinii (Dalla Torre) Dalla Torre & Sarnth., Fl. Tirol 6(3): 543. 1912 ≡Chrysanthemum leucanthemum var. gaudinii (Dalla Torre) Fiori, Nuov. Fl. Italia 2(4): 624. 1927 ≡Chrysanthemum leucanthemum [“f”] gaudinii (Dalla Torre) Fiori in Fiori & Paoletti, Fl. Italia 3(1): 239. 1903—Neotypus [Gutermann, Phyton (Austria) 17: 37. 1975]: Kärnten: Nockgebiet, am Weg zur Falkerthütte—Bocksattel—S des Mallnock, 1850 m; mit Calluna; flachgründiger Boden über Silikat; leg. A. Polatschek P64/312; 2n = 18 (W! [W1965-0020139]).
- (b)
- Leucanthemum vulgare Lam. [subsp. vulgare], Fl. Franç. 2: 137. 1779 ≡Chrysanthemum leucanthemum L., Sp. pl. 888. 1753 ≡Tanacetum leucanthemum (L.) Sch.Bip., Tanaceteen: 35. 1844 ≡Matricaria leucanthemum (L.) Desr. in Lam., Encycl. 3(2): 731. 1792—Lectotypus [Böcher & Larsen, Watsonia 4: 15. 1957]: (BM-Hortus Cliffortianus).
- (c)
- Leucanthemum vulgare subsp. barrelieri (Dufour ex DC.) O.Bolós & Vigo, Pl. Països Catalans 3: 816. 1996 “1995” ≡Pyrethrum halleri var. barrelieri Dufour ex DC., Prodr. 6: 55. 1838 (basionym) ≡Leucanthemum gaudinii subsp. barrelieri (Dufour ex DC.) Vogt in Ruizia 10: 89. 1991 ≡Leucanthemum ceratophylloides var. barrelieri (Dufour ex DC.) Nyman, Consp. Fl. Eur.: 371. 1879 ≡Pontia barrelieri (Dufour ex DC.) Bubani, Fl. Pyr. 2: 219. 1899 ≡Pyrethrum barrelieri Dufour ex DC., Prodr. 6: 55. 1838, pro. syn., nom. inval. ≡Leucanthemum vulgare var. pyrenaicum Rouy, Fl. France 8: 272 and 274. 1903, nom. illegit. ≡Leucanthemum pyrenaicum Rouy, Fl. France 8: 274. 1903, pro syn., nom inval. [non Leucanthemum barrelieri Timb.-Lagr., Bull. Soc. Bot. France 13: 153. 1866 and in Rodet, Bot. Agric. Médic., ed. 2: 447. 1872] ≡Leucanthemum pyrenaicum Vogt et al. in Mol. Phylogenet. Evol. 92: 325. 2015.—Holotype: Pyren., près du Sommet de Monné, 1824 (G-DC! [G00450856]).
- (2)
- The Leucanthemum pluriflorum-group: All three morpho-species of this group are allopatrically distributed: while L. pluriflorum is restricted to the coastline of Galicia in NW Spain (see [17,18,50]), L. gallaecicum is endemic to serpentine outcrops in central Galicia [51], and L. cacuminis (the former L. gaudinii subsp. cantabricum; [20]) is found in the mountainous regions of Northern Spain from the western Pyrenees in the east to the Picos de Europa in the west. Since no significant genealogical independence among the three taxa was found, acknowledgment on the species level is questionable, despite the significant non-overlapping in ecological respects of all three taxa and the morphological distinction of L. gallaecicum from the other two taxa. Therefore, our interpretation of the L. pluriflorum-group as a lineage of allopatrically and ecologically differentiating population groups may be best represented taxonomically by ranking the three taxa as subspecies of a single species:
- (a)
- Leucanthemum pluriflorum Pau [subsp. pluriflorum] in Bol. Soc. Aragonesa Ci. Nat. 1: 31. 1902—Holotype: San Ciprián, Galicia, P. Merino S.J. (MA! [MA128479]).
- (b)
- Leucanthemum pluriflorumsubsp. cantabricum (Font Quer & Guinea) T.Ott, Vogt & Oberpr., comb. nov. ≡Leucanthemum vulgare var. cantabricum Font Quer & Guinea in Guinea, Anales Jard. Bot. Madrid 7: 347–348. 1947 (basionym) ≡Chrysanthemum leucanthemum subsp. cantabricum (Font Quer &Guinea) Guinea, Catálogo florístico de Viscaya: 646. 1980 ≡Leucanthemum gaudinii subsp. cantabricum (Font Quer & Guinea) Vogt in Ruizia 10: 98. 1991 ≡Chrysanthemum leucanthemum var. cacuminis Font Quer & Guinea in Guinea, Bot. Santander: 327. 1953, nom. inval. ≡Leucanthemum cacuminis Vogt et al. in Mol. Phylogenet. Evol. 92: 325. 2015.—Holotype: Picos de Europa: in saxosis l. Vega de Liordes, ad 1890 m alt., 13.8.1944, E. Guinea (BC!).
- (c)
- Leucanthemum pluriflorum subsp. gallaecicum (Rodr.Oubiña & S.Ortiz) T.Ott, Vogt & Oberpr., comb. et stat. nov. ≡Leucanthemum gallaecicum Rodr.Oubiña & S.Ortiz in Anales Jard. Bot. Madrid 47: 498. 1990 (basionym).—Holotype: La Coruña: Toques, Paradela, 20-IX-1987, J. Rodríguez Oubiña & S. Ortiz (SANT; isotype: MA! [MA478919]).
4. Materials and Methods
4.1. RADseq Assembly
4.2. Network Analysis
4.3. Hybrid Detection
4.4. Consensus Clustering
4.5. Coalescent-Based Species Delimitation
4.6. Ecological Niche Modeling
4.7. Morphological Analyses
4.8. Geography
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zachos, F.E. Species Concepts in Biology; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Stankowski, S.; Ravinet, M. Defining the speciation continuum. Evolution 2021, 75, 1256–1273. [Google Scholar] [CrossRef] [PubMed]
- De Queiroz, K. Species concepts and species delimitation. Syst. Biol. 2007, 56, 879–886. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dayrat, B. Towards integrative taxonomy. Biol. J. Linn. Soc. 2005, 85, 407–417. [Google Scholar] [CrossRef]
- Will, K.W.; Mishler, B.D.; Wheeler, Q.D. The perils of DNA barcoding and the need for integrative taxonomy. Syst. Biol. 2005, 54, 844–851. [Google Scholar] [CrossRef] [PubMed]
- Hebert, P.D.N.; Gregory, T.R. The promise of DNA barcoding for taxonomy. Syst. Biol. 2005, 54, 852–859. [Google Scholar] [CrossRef] [PubMed]
- Schlick-Steiner, B.C.; Steiner, F.M.; Seifert, B.; Stauffer, C.; Christian, E.; Crozier, R.H. Integrative taxonomy: A multisource approach to exploring biodiversity. Annu. Rev. Entomol. 2010, 55, 421–438. [Google Scholar] [CrossRef] [PubMed]
- Padial, J.M.; Miralles, A.; De la Riva, I.; Vences, M. The integrative future of taxonomy. Front. Zool. 2010, 7, 16. [Google Scholar] [CrossRef]
- Doyen, J.T.; Slobodchikoff, C.N. An operational approach to species classification. Syst. Biol. 1974, 23, 239–247. [Google Scholar] [CrossRef]
- Guillot, G.; Renaud, S.; Ledevin, R.; Michaux, J.; Claude, J. A unifying model for the analysis of phenotypic, genetic, and geographic data. Syst. Biol. 2012, 61, 897–911. [Google Scholar] [CrossRef] [Green Version]
- Zapata, F.; Jiménez, I. Species delimitation: Inferring gaps in morphology across geography. Syst. Biol. 2012, 61, 179. [Google Scholar] [CrossRef] [Green Version]
- Vásquez-Cruz, M.; Vovides, A.P.; Sosa, V. Disentangling species limits in the Vauquelinia corymbosa complex (Pyreae, Rosaceae). Syst. Bot. 2017, 42, 835–847. [Google Scholar] [CrossRef]
- Solís-Lemus, C.; Knowles, L.L.; Ané, C. Bayesian species delimitation combining multiple genes and traits in a unified framework. Evolution 2015, 69, 492–507. [Google Scholar] [CrossRef] [Green Version]
- Hausdorf, B.; Hennig, C. Species delimitation and geography. Mol. Ecol. Resour. 2020, 20, 950–960. [Google Scholar] [CrossRef]
- The Euro+Med Plantbase Project. Available online: http://ww2.bgbm.org/EuroPlusMed/query.asp (accessed on 24 March 2022).
- Meusel, H.; Jäger, E.J. Vergleichende Chorologie der Zentraleuropäischen Flora, 3rd ed.; Gustav Fischer Verlag: Jena/Stuttgart, Germany; New York, NY, USA, 1992. [Google Scholar]
- Vogt, R. Die Gattung Leucanthemum Mill. (Compositae-Anthemideae) auf der Iberischen Halbinsel. Ruizia 1991, 10, 1–261. [Google Scholar]
- Vogt, R. Leucanthemum Mill. In Flora Iberica; Benedí, C., Buira, A., Rico, E., Crespo, M.B., Quintanar, A., Aedo, C., Eds.; Real Jardín Botánico, CSIC: Madrid, Spain, 2019; Volume 16, pp. 1848–1880. [Google Scholar]
- Oberprieler, C.; Greiner, R.; Konowalik, K.; Vogt, R. The reticulate evolutionary history of the polyploid NW Iberian Leucanthemum pluriflorum clan (Compositae, Anthemideae) as inferred from nrDNA ETS sequence diversity and eco-climatological niche-modelling. Mol. Phylogenetics Evol. 2014, 70, 478–491. [Google Scholar] [CrossRef]
- Konowalik, K.; Wagner, F.; Tomasello, S.; Vogt, R.; Oberprieler, C. Detecting reticulate relationships among diploid Leucanthemum Mill. (Compositae, Anthemideae) taxa using multilocus species tree reconstruction methods and AFLP fingerprinting. Mol. Phylogenet. Evol. 2015, 92, 308–328. [Google Scholar] [CrossRef]
- Wagner, F.; Härtl, S.; Vogt, R.; Oberprieler, C. ‘Fix Me Another Marguerite!’: Species delimitation in a group of intensively hybridizing lineages of ox-eye daisies (Leucanthemum Mill., Compositae-Anthemideae). Mol. Ecol. 2017, 26, 4260–4283. [Google Scholar] [CrossRef]
- Wagner, F.; Ott, T.; Zimmer, C.; Reichhart, V.; Vogt, R.; Oberprieler, C. ‘At the Crossroads towards Polyploidy’: Genomic divergence and extent of homoploid hybridization are drivers for the formation of the ox-eye daisy polyploid complex (Leucanthemum, Compositae-Anthemideae). New Phytol. 2019, 223, 2039–2053. [Google Scholar] [CrossRef]
- Wagner, F.; Ott, T.; Schall, M.; Lautenschlager, U.; Vogt, R.; Oberprieler, C. Taming the Red Bastards: Hybridisation and species delimitation in the Rhodanthemum arundanum-group (Compositae, Anthemideae). Mol. Phylogenet. Evol. 2020, 144, 106702. [Google Scholar] [CrossRef]
- Mason, N.A.; Fletcher, N.K.; Gill, B.A.; Funk, W.C.; Zamudio, K.R. Coalescent-based species delimitation is sensitive to geographic sampling and isolation by distance. Syst. Biodivers. 2020, 18, 269–280. [Google Scholar] [CrossRef]
- Satopaa, V.; Albrecht, J.; Irwin, D.; Raghavan, B. Finding a ‘Kneedle’ in a Haystack: Detecting knee points in system behavior. In Proceedings of the 2011 31st International Conference on Distributed Computing Systems Workshops, Minneapolis, MN, USA, 20–24 June 2011; pp. 166–171. [Google Scholar]
- Stuessy, T.F. Ultrastructural data for the practicing plant systematist. Am. Zool. 1979, 19, 621–636. [Google Scholar] [CrossRef]
- Stuessy, T.F.; Crawford, D.J.; Soltis, D.E.; Soltis, P.S. Plant Systematics: The Origin, Interpretation, and Ordering of Plant Biodiversity; Koeltz Scientific Books: Oberreifenberg, Germany, 2014. [Google Scholar]
- Reydon, T.A.C.; Kunz, W. Species as natural entities, instrumental units and ranked taxa: New perspectives on the grouping and ranking problems. Biol. J. Linn. Soc. 2019, 126, 623–636. [Google Scholar] [CrossRef]
- Ence, D.D.; Carstens, B.C. SpedeSTEM: A rapid and accurate method for species delimitation. Mol. Ecol. Resour. 2011, 11, 473–480. [Google Scholar] [CrossRef]
- Carstens, B.C.; Satler, J.D. The carnivorous plant described as Sarracenia alata contains two cryptic species. Biol. J. Linn. Soc. 2013, 109, 737–746. [Google Scholar] [CrossRef] [Green Version]
- Hedin, M.; Carlson, D.; Coyle, F. Sky island diversification meets the multispecies coalescent—Divergence in the spruce-fir moss spider (Microhexura montivaga, Araneae, Mygalomorphae) on the highest peaks of southern Appalachia. Mol. Ecol. 2015, 24, 3467–3484. [Google Scholar] [CrossRef]
- Heywood, V.H. 81. Leucanthemum Miller. In Flora Europaea; Tutin, T.G., Heywood, V.H., Burges, N.A., Moore, D.M., Valentine, D.H., Walters, S.M., Webb, D.A., Eds.; Cambridge University Press: Cambridge/London, UK; New York, NY, USA; Melbourne, Australia, 1976; Volume 4, pp. 174–177. [Google Scholar]
- Sukumaran, J.; Knowles, L.L. Multispecies coalescent delimits structure, not species. Proc. Natl. Acad. Sci. USA 2017, 114, 1607–1612. [Google Scholar] [CrossRef] [Green Version]
- Bryant, D.; Bouckaert, R.; Felsenstein, J.; Rosenberg, N.A.; RoyChoudhury, A. Inferring species trees directly from biallelic genetic markers: Bypassing gene trees in a full coalescent analysis. Mol. Biol. Evol. 2012, 29, 1917–1932. [Google Scholar] [CrossRef] [Green Version]
- Leaché, A.D.; Fujita, M.K.; Minin, V.N.; Bouckaert, R.R. Species delimitation using genome-wide SNP data. Syst. Biol. 2014, 63, 534–542. [Google Scholar] [CrossRef] [Green Version]
- Monti, S.; Tamayo, P.; Mesirov, J.; Golub, T. Consensus Clustering: A resampling-based method for class discovery and visualization of gene expression microarray Data. Mach. Learn. 2003, 52, 91–118. [Google Scholar] [CrossRef]
- Kincaid, D.T.; Schneider, R.B. Quantification of leaf shape with a microcomputer and Fourier transform. Can. J. Bot. 1983, 61, 2333–2342. [Google Scholar] [CrossRef]
- Kuhl, F.P.; Giardina, C.R. Elliptic Fourier features of a closed contour. Comput. Graph. Image Process. 1982, 18, 236–258. [Google Scholar] [CrossRef]
- Unger, J.; Merhof, D.; Renner, S.S. Computer vision applied to herbarium specimens of German trees: Testing the future utility of the millions of herbarium specimen images for automated identification. BMC Evol. Biol. 2016, 16, 248. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raxworthy, C.J.; Ingram, C.M.; Rabibisoa, N.; Pearson, R.G. Applications of ecological niche modeling for species delimitation: A review and empirical evaluation using day geckos (Phelsuma) from Madagascar. Syst. Biol. 2007, 56, 907–923. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cardillo, M.; Warren, D.L. Analysing patterns of spatial and niche overlap among species at multiple resolutions. Glob. Ecol. Biogeogr. 2016, 25, 951–963. [Google Scholar] [CrossRef]
- Zheng, H.; Fan, L.; Milne, R.I.; Zhang, L.; Wang, Y.; Mao, K. Species delimitation and lineage separation history of a species complex of aspens in China. Front. Plant Sci. 2017, 8, 375. [Google Scholar] [CrossRef]
- Lin, H.-Y.; Gu, K.-J.; Li, W.-H.; Zhao, Y.-P. Integrating coalescent-based species delimitation with ecological niche modeling delimited two species within the Stewartia sinensis complex (Theaceae). J. Syst. Evol. 2021. early view. [Google Scholar] [CrossRef]
- Von Wettstein, R. Grundzüge der Geographisch-Morphologischen Methode der Pflanzensystematik; Gustav Fischer Verlag: Jena, Germany, 1898. [Google Scholar]
- Meyer, L.; Diniz-Filho, J.A.F.; Lohmann, L.G. A Comparison of hull methods for estimating species ranges and richness maps. Plant Ecol. Divers. 2017, 10, 389–401. [Google Scholar] [CrossRef]
- Burgman, M.A.; Fox, J.C. Bias in species range estimates from minimum convex polygons: Implications for conservation and options for improved planning. Anim. Conserv. 2003, 6, 19–28. [Google Scholar] [CrossRef] [Green Version]
- Capinha, C.; Pateiro-López, B. Predicting species distributions in new areas or time periods with alpha-shapes. Ecol. Inform. 2014, 24, 231–237. [Google Scholar] [CrossRef]
- Wiley, E.O. The evolutionary species concept reconsidered. Syst. Biol. 1978, 27, 17–26. [Google Scholar] [CrossRef] [Green Version]
- Valen, L.V. Ecological species, multispecies, and oaks. Taxon 1976, 25, 233–239. [Google Scholar] [CrossRef] [Green Version]
- Greiner, R.; Vogt, R.; Oberprieler, C. Evolution of the polyploid north-west Iberian Leucanthemum pluriflorum clan (Compositae, Anthemideae) based on plastid DNA sequence variation and AFLP fingerprinting. Ann. Bot. 2013, 111, 1109–1123. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez Oubiña, J.; Ortiz, S. Leucanthemum gallaecicum, sp. nov. (Asteraceae). An. Jardín Botánico Madr. 1990, 47, 498–500. [Google Scholar]
- Poland, J.A.; Brown, P.J.; Sorrells, M.E.; Jannink, J.-L. Development of high-density genetic maps for barley and wheat using a novel two-enzyme genotyping-by-sequencing approach. PLoS ONE 2012, 7, e32253. [Google Scholar] [CrossRef] [Green Version]
- Doyle, J.J.; Dickson, E.E. Preservation of plant samples for DNA restriction endonuclease analysis. Taxon 1987, 36, 715–722. [Google Scholar] [CrossRef]
- Eaton, D.A.R.; Overcast, I. Ipyrad: Interactive assembly and analysis of RADseq datasets. Bioinformatics 2020, 36, 2592–2594. [Google Scholar] [CrossRef]
- Mastretta-Yanes, A.; Arrigo, N.; Alvarez, N.; Jorgensen, T.H.; Piñero, D.; Emerson, B.C. Restriction site-associated DNA sequencing, genotyping error estimation and de novo assembly optimization for population genetic inference. Mol. Ecol. Resour. 2015, 15, 28–41. [Google Scholar] [CrossRef]
- Huson, D.H.; Bryant, D. Application of phylogenetic networks in evolutionary studies. Mol. Biol. Evol. 2006, 23, 254–267. [Google Scholar] [CrossRef]
- Paradis, E.; Schliep, K. Ape 5.0: An environment for modern phylogenetics and evolutionary analyses in R. Bioinformatics 2019, 35, 526–528. [Google Scholar] [CrossRef]
- nei_vcf. Available online: https://github.com/TankredO/nei_vcf (accessed on 18 June 2022).
- Joly, S.; Bruneau, A. Incorporating allelic variation for reconstructing the evolutionary history of organisms from multiple genes: An example from Rosa in North America. Syst. Biol. 2006, 55, 623–636. [Google Scholar] [CrossRef] [Green Version]
- pofad. Available online: https://github.com/simjoly/pofad (accessed on 18 June 2022).
- Green, R.E.; Krause, J.; Briggs, A.W.; Maricic, T.; Stenzel, U.; Kircher, M.; Patterson, N.; Li, H.; Zhai, W.; Fritz, M.H.-Y.; et al. A draft sequence of the Neandertal genome. Science 2010, 328, 710–722. [Google Scholar] [CrossRef] [Green Version]
- Durand, E.Y.; Patterson, N.; Reich, D.; Slatkin, M. Testing for ancient admixture between closely related populations. Mol. Biol. Evol. 2011, 28, 2239–2252. [Google Scholar] [CrossRef] [Green Version]
- pyckmeans. Available online: https://github.com/TankredO/pyckmeans (accessed on 18 June 2022).
- Bouckaert, R.; Heled, J.; Kühnert, D.; Vaughan, T.; Wu, C.-H.; Xie, D.; Suchard, M.A.; Rambaut, A.; Drummond, A.J. BEAST 2: A software platform for Bayesian evolutionary analysis. PLoS Comput. Biol. 2014, 10, e1003537. [Google Scholar] [CrossRef] [Green Version]
- Leaché, A.D.; Bouckaert, R.R. Species trees and species delimitation with SNAPP: A tutorial and worked example. In Proceedings of the Workshop on Population and Speciation Genomics, Českỳ Krumlov, Czech Republic, 21 January–3 February 2018. [Google Scholar]
- Index Herbariorum. Available online: http://sweetgum.nybg.org/science/ih/ (accessed on 18 June 2022).
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Hengl, T.; de Jesus, J.M.; Heuvelink, G.B.M.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- raster. Available online: https://CRAN.R-project.org/package=raster (accessed on 18 June 2022).
- Warren, D.L.; Matzke, N.J.; Cardillo, M.; Baumgartner, J.B.; Beaumont, L.J.; Turelli, M.; Glor, R.E.; Huron, N.A.; Simões, M.; Iglesias, T.L.; et al. ENMTools 1.0: An R package for comparative ecological biogeography. Ecography 2021, 44, 504–511. [Google Scholar] [CrossRef]
- MaxEnt. Available online: https://biodiversityinformatics.amnh.org/open_source/maxent/ (accessed on 18 June 2022).
- CVAT. Available online: https://github.com/openvinotoolkit/cvat (accessed on 18 June 2022).
- Igarashi, T.; Moscovich, T.; Hughes, J.F. As-rigid-as-possible shape manipulation. ACM Trans. Graph. 2005, 24, 1134–1141. [Google Scholar] [CrossRef]
- van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. Scikit-Image: Image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef] [PubMed]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Shewchuk, J.R. Triangle: Engineering a 2D quality mesh generator and Delaunay triangulator. In Lecture Notes in Computer Science, Proceedings of the Applied Computational Geometry Towards Geometric Engineering, Philadelphia, PA, USA, 27–28 May 1996; Lin, M.C., Manocha, D., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 203–222. [Google Scholar]
- triangle. Available online: https://github.com/drufat/triangle (accessed on 18 June 2022).
- Libigl. Available online: https://libigl.github.io/ (accessed on 18 June 2022).
- Chew, P.L. Constrained Delaunay triangulations. Algorithmica 1989, 4, 97–108. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- pyefd. Available online: https://github.com/hbldh/pyefd (accessed on 18 June 2022).
| Taxon A | Taxon B | p (D) | p (EFA) | p (LDI) | p(geo) |
|---|---|---|---|---|---|
| L. gaudinii | L. vulgare | 0.03 | 0.00 | 0.02 | 1.00 |
| L. gaudinii | L. pyrenaicum | 0.06 | 0.00 | 0.00 | 0.00 |
| L. vulgare | L. pyrenaicum | 0.03 | 1.00 | 0.34 | 1.00 |
| L. pluriflorum | L. gallaecicum | 0.03 | 0.00 | 0.67 | 0.00 |
| L. pluriflorum | L. cacuminis | 0.03 | 0.28 | 1.00 | 0.00 |
| L. gallaecicum | L. cacuminis | 0.03 | 0.00 | 0.42 | 0.00 |
| Sample | Taxon | Voucher Specimens | Locality | Coordinates (Latitude, Longitude) | Collection Number |
|---|---|---|---|---|---|
| 135-05 | L. ageratifolium Pau | B100386712 | F, Occitania, Pyrénées-Orientales, 410 m | 42.5038, 2.9603 | Konowalik KK42 and Ogrodowczyk |
| M60-01 | L. ageratifolium Pau | B100345012, B100345013 | ES, Castile-La Mancha, Cuenca, 1157 m | 40.1019, −1.521 | Cordel 60 |
| M02-01 | L. ageratifolium Pau | B100297950 | ES, Aragón, Huesca, 755 m | 42.525, −0.669 | Cordel 2 |
| 90-01 | L. burnatii Briq. and Cavill. | B100464678 | F, Provence-Alpes-Côte d’Azur, Alpes-Maritimes, 1235 m | 43.7607, 6.9165 | Vogt 16615 et al. |
| 92-02 | L. burnatii Briq. and Cavill. | B100464676, B100464675 | F, Provence-Alpes-Côte d’Azur, Bouches-du-Rhône, 650 m | 43.545, 5.6626 | Vogt 16618 et al. |
| 60-01 | L. cacuminis Vogt et al. | B100413746 | ES, Galicia, Os Ancares, 1530 m | 42.8315, −6.8569 | Hößl 60 |
| 62-01 | L. cacuminis Vogt et al. | B100413744 | ES, Galicia, Lugo, 750 m | 42.9249, −6.8657 | Hößl 62 |
| 68-04 | L. cacuminis Vogt et al. | B100413738 | ES, Cantabria, Cantabria, 1770 m | 43.1538, −4.8053 | Hößl 68 and Himmelreich |
| L1008 | L. eliasii (Sennen and Pau) Sennen and Pau | B100484003 | ES, Castile and León, Burgos, 880 m | 42.503, −3.706 | Lopéz 2537 et al. |
| L1009 | L. eliasii (Sennen and Pau) Sennen and Pau | B100484004 | ES, Castile and León, Burgos, 920 m | 42.507, −3.705 | Galán Cela 576 and Martín |
| 159-11 | L. gallaecicum Rodr. Oubiña and S. Ortiz | B100386789, B100420775, B100464989 | ES, Galicia, Pontevedra, 375 m | 42.8498, −7.9878 | Konowalik KK67 and Ogrodowczyk |
| 161-03 | L. gallaecicum Rodr. Oubiña and S.Ortiz | No voucher | ES, Galicia, Corunna, 380 m | 42.8533, −7.9994 | Konowalik s.n. et al. |
| 58-02 | L. gallaecicum Rodr. Oubiña and S. Ortiz | B100413748 | ES, Galicia, Lugo, 490 m | 42.8205, −7.9504 | Hößl 58 |
| 209-01 | L. gaudinii Dalla Torre | B100386664 | CH, Bern, Interlaken-Oberhasli, 2260 m | 46.5781, 7.97 | Tomasello TS88 |
| 270-01 | L. gaudinii Dalla Torre | B100413007 | AT, Carinthia, Spittal an der Drau, 2200 m | 47.0025, 13.5275 | Oberprieler 10859 |
| 276-01 | L. gaudinii Dalla Torre | B100413015 | AT, Carinthia, Feldkirchen, 2270 m | 46.8603, 13.8172 | Oberprieler 10866 |
| 451-01 | L. gaudinii Dalla Torre | No voucher | PL, Lesser Poland, Giewont, 1860 m | 49.2505, 19.9343 | Konowalik 20160909-01 |
| 84-10 | L. gracilicaule (Dufour) Pau | B100386704 | ES, Valencian Community, Alicante, 300 m | 38.8379, −0.1853 | Konowalik KK20 and Ogrodowczyk |
| 85-04 | L. gracilicaule (Dufour) Pau | B100386702 | ES, Valencian Community, Valencia, 340 m | 39.3135, −0.681 | Konowalik KK25 and Ogrodowczyk |
| 116-01 | L. graminifolium (L.) Lam. | B100464684, B100464683 | F, Occitania, Hérault, 800 m | 43.7761, 3.2386 | Vogt 16693 et al. |
| 96-03 | L. graminifolium (L.) Lam. | B100464663 | F, Occitania, Aude, 600 m | 43.1494, 2.6294 | Vogt 16656 et al. |
| 162-03 | L. halleri (Vitman) Ducommun | B100386798 | D, Bavaria, Landkreis Garmisch-Partenkirchen, 2340 m | 47.4134, 11.1277 | Konowalik KK67 and Tomasello |
| 208-01 | L. halleri (Vitman) Ducommun | B100386672 | CH, Valais, Sion, 2320 m | 46.3308, 7.2911 | Tomasello TS65 |
| 280-01 | L. laciniatum Huter et al. | B100464203 | I, Calabria, Cosenza, 1580 m | 39.902, 16.1144 | Tomasello 420 |
| 280-02 | L. laciniatum Huter et al. | B100464203 | I, Calabria, Cosenza, 1580 m | 39.902, 16.1144 | Tomasello 420 |
| 366-01 | L. legraeanum (Rouy) B.Bock and J.-M.Tison | B100486634, B100486635, B100486636, B100486637, B100486638 | F, Provence-Alpes-Cote d’Azur, Var, 410 m | 43.1986, 6.3151 | Vogt 17189 |
| 369-01 | L. legraeanum (Rouy) B.Bock and J.-M.Tison | B100486648, B100486649 | F, Provence-Alpes-Cote d’Azur, Var, 210 m | 43.2444, 6.3377 | Vogt 17192 |
| 384-01 | L. legraeanum (Rouy) B.Bock and J.-M.Tison | B100627809, B100627810 | F, Provence-Alpes-Cote d’Azur, Var, 410 m | 43.1988, 6.3151 | Vogt 17434 et al. |
| 406-01 | L. ligusticum Marchetti et al. | B100627838, B100627839 | I, Liguria, La Spezia, 210 m | 44.247, 9.7728 | Vogt 17460 et al. |
| 412-01 | L. ligusticum Marchetti et al. | B100627849, B100627850, B100627851 | I, Liguria, Genova, 700 m | 44.3603, 9.5105 | Vogt 17468 et al. |
| 416-01 | L. ligusticum Marchetti et al. | B100627855, B100627856 | I, Liguria, Genova, 250 m | 44.3458, 9.4588 | Vogt 17471 et al. |
| 273-02 | L. lithopolitanicum | B100413012 | SL, Central Slovenia, 2100 m | 46.3633, 14.5715 | Oberprieler 10862 |
| 274-02 | L. lithopolitanicum | B100413013 | SL, Savinja, 2000 m | 46.375, 14.5663 | Oberprieler 10864 |
| 128-01 | L. monspeliense (E. Mayer) Polatschek | B100464618 | F, Occitania, Gard, 750 m | 44.0888, 3.5786 | Vogt 16712 et al. |
| 131-02 | L. monspeliense (E. Mayer) Polatschek | B100464615 | F, Occitania, Gard, 380 m | 44.1412, 3.7316 | Vogt 16716 et al. |
| 340-01 | L. monspeliense (E. Mayer) Polatschek | B100486666, B100486667 | F, Occitania, Aveyron, 180 m | 44.5822, 2.184 | Vogt 17156 et al. |
| 40-09 | L. pluriflorum Pau | B100413758 | ES, Galicia, Corunna, 100 m | 42.8838, −9.2726 | Hößl 40 |
| 42-04 | L. pluriflorum Pau | No voucher | ES, Galicia, Corunna, 150 m | 43.3069, −8.6186 | Hößl 42 |
| 55-01 | L. pluriflorum Pau | B100413749 | ES, Galicia, Lugo, 10 m | 43.6309, −7.333 | Hößl 55 |
| 266-01 | L. pyrenaicum Vogt et al. | B100464208 | ES, Aragon, Huesca, 1650 m | 42.7806, −0.2467 | Tomasello TS382 |
| 266-02 | L. pyrenaicum Vogt et al. | B100464208 | ES, Aragon, Huesca, 1650 m | 42.7806, −0.2467 | Tomasello TS382 |
| 267-03 | L. pyrenaicum Vogt et al. | B100464210 | ES, Aragon, Huesca, 2000 m | 42.6327, 0.453 | Tomasello TS392 |
| 446-01 | L. rotundifolium (Willd.) DC. | No voucher | PL, Podkarpackie, Bieszczady, 920 m | 49.11905, 22.57755 | Konowalik 20180622-02-01 |
| 447-01 | L. rotundifolium (Willd.) DC. | No voucher | RO, Bihor, Bihor, 1230 m | 46.51887, 22.66133 | Konowalik 20180713-03-01 |
| 448-01 | L. rotundifolium (Willd.) DC. | No voucher | BH, Central Bosnia Canton, 1860 m | 43.95782, 17.74027 | Konowalik 20180714-03-01 |
| 449-01 | L. rotundifolium (Willd.) DC. | No voucher | RO, Hunedoara, Râu de Mori, 1140 m | 45.31588, 22.77045 | Konowalik 20180807-03-01 |
| 450-01 | L. rotundifolium (Willd.) DC. | No voucher | PL, Lesser Poland Voivodeship, Sucha County, 1100 m | 49.58787, 19.55152 | Konowalik 20170920-01 |
| 278-01 | L. tridactylites (A. Kern. and Huter) Huter et al. | B100464207 | I, Abruzzo, Pescara, 2080 m | 42.1384, 14.1101 | Tomasello 417 |
| 278-05 | L. tridactylites (A. Kern. and Huter) Huter et al. | B100464207 | I, Abruzzo, Pescara, 2080 m | 42.1384, 14.1101 | Tomasello 417 |
| 225-02 | L. virgatum (Desr.) Clos | B100411746 | F, Provence-Alpes-Côte d’Azur, Alpes-Maritimes, 430 m | 43.9538, 7.2961 | Vogt 16892 and Oberprieler |
| 250-01 | L. virgatum (Desr.) Clos | B100350169, B100350172 | I, Liguria, Savona, 220 m | 44.0596, 8.0583 | Vogt 16932 and Oberprieler |
| 184-01 | L. vulgare Lam. | B100346626 | BH, Republic of Srpska, Nevesinje, 930 m | 43.2403, 18.3364 | Vogt 16806 and Prem-Vogt |
| L046-07 | L. vulgare Lam. | B100550249 | D, Bavaria, Deuerling, 450 m | 49.0333, 11.8833 | Eder and Oberprieler s.n. |
| 94-01 | L. vulgare Lam. | B100464674 | F, Occitania, Aude, 160 m | 43.1294, 2.6073 | Vogt 16641 et al. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ott, T.; Schall, M.; Vogt, R.; Oberprieler, C. The Warps and Wefts of a Polyploidy Complex: Integrative Species Delimitation of the Diploid Leucanthemum (Compositae, Anthemideae) Representatives. Plants 2022, 11, 1878. https://doi.org/10.3390/plants11141878
Ott T, Schall M, Vogt R, Oberprieler C. The Warps and Wefts of a Polyploidy Complex: Integrative Species Delimitation of the Diploid Leucanthemum (Compositae, Anthemideae) Representatives. Plants. 2022; 11(14):1878. https://doi.org/10.3390/plants11141878
Chicago/Turabian StyleOtt, Tankred, Maximilian Schall, Robert Vogt, and Christoph Oberprieler. 2022. "The Warps and Wefts of a Polyploidy Complex: Integrative Species Delimitation of the Diploid Leucanthemum (Compositae, Anthemideae) Representatives" Plants 11, no. 14: 1878. https://doi.org/10.3390/plants11141878
APA StyleOtt, T., Schall, M., Vogt, R., & Oberprieler, C. (2022). The Warps and Wefts of a Polyploidy Complex: Integrative Species Delimitation of the Diploid Leucanthemum (Compositae, Anthemideae) Representatives. Plants, 11(14), 1878. https://doi.org/10.3390/plants11141878






