Inequality Measure of Leaf Area Distribution for a Drought-Tolerant Landscape Plant
Abstract
:1. Introduction
2. Materials and Methods
2.1. Leaf Sampling Information
2.2. Data Acquisition
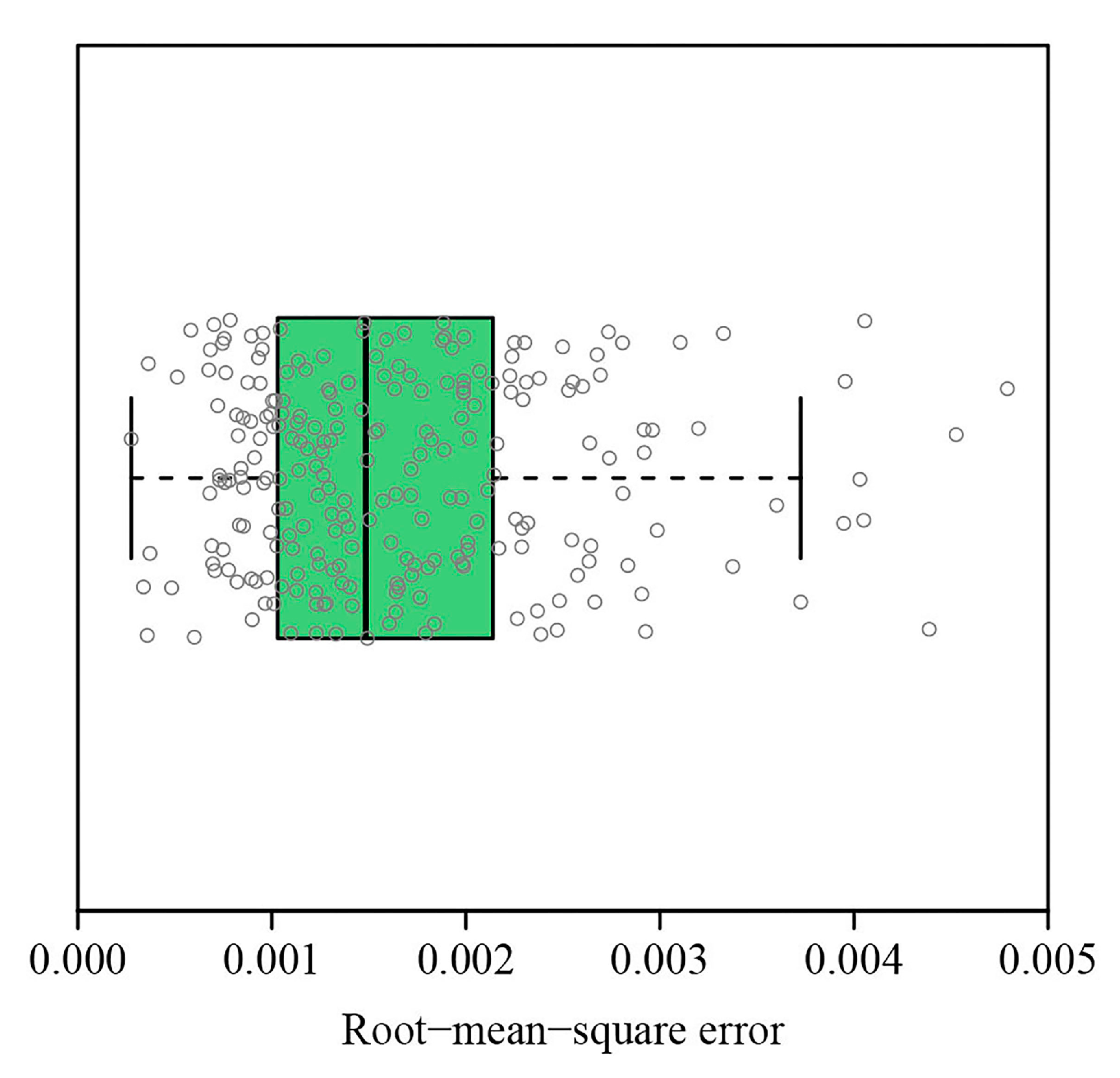
2.3. Fitting the Lorenz Curve
2.4. Four Indices for Quantifying ILAD
3. Results
4. Discussion
4.1. The Links among Four Indices of Measuring ILAD
4.2. Applications of Four Indices to Plant Ecology
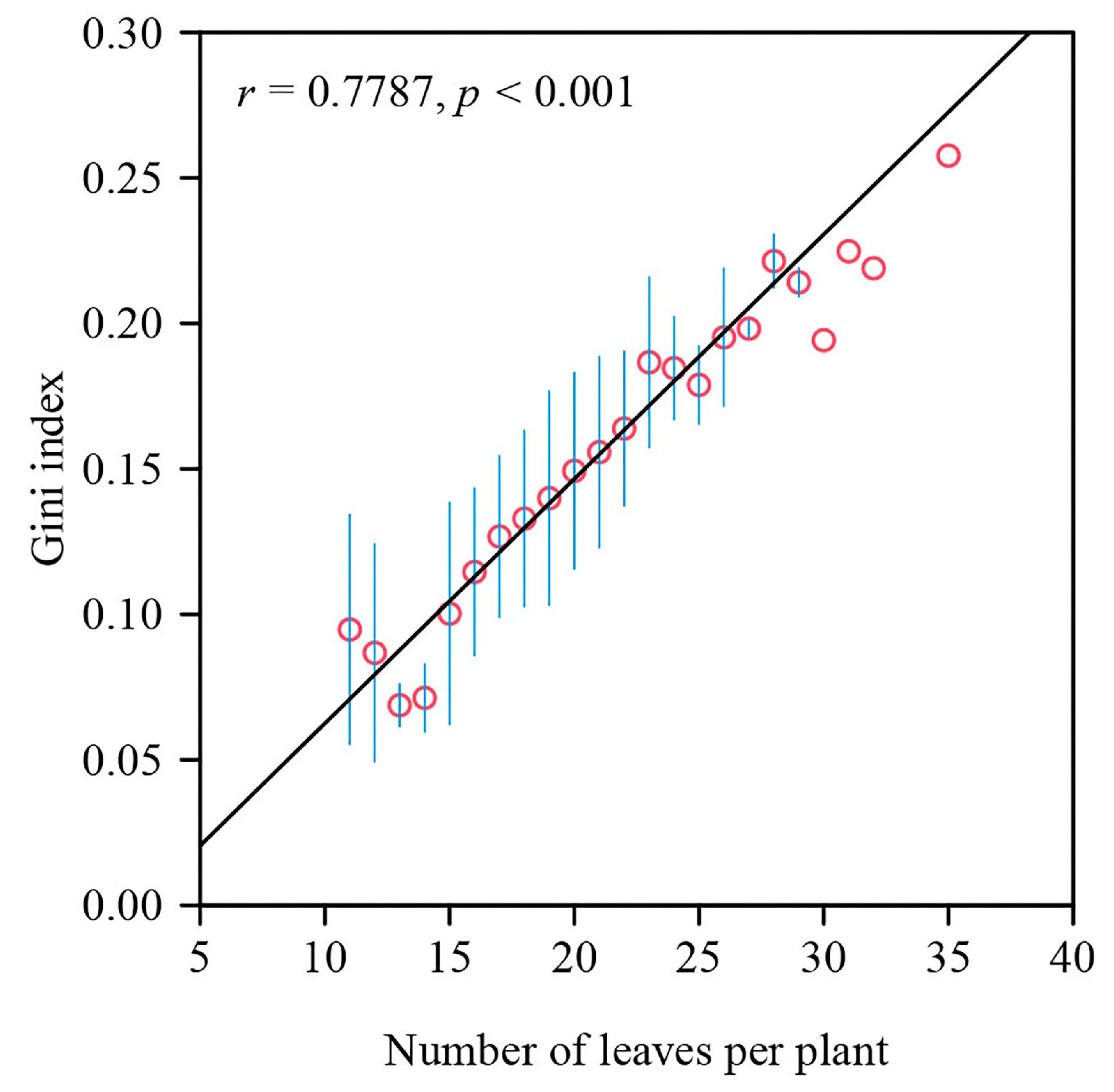
4.3. Correlation between the Gini Index and Number of Leaves per Plant
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Weraduwage, S.M.; Chen, J.; Anozie, F.C.; Morales, A.; Weise, S.E.; Sharkey, T.D. The relationship between leaf area growth and biomass accumulation in Arabidopsis thaliana. Front. Plant Sci. 2015, 9, 6–167. [Google Scholar] [CrossRef]
- Wright, I.J.; Dong, N.; Maire, V.; Prentice, I.C.; Westoby, M.; Díaz, S.; Gallagher, R.V.; Jacobs, B.F.; Kooyman, R.; Law, E.A.; et al. Global climatic drivers of leaf size. Science 2017, 357, 917–921. [Google Scholar] [CrossRef]
- Baird, A.S.; Taylor, S.H.; Pasquet-Kok, J.; Vuong, C.; Zhang, Y.; Watcharamongkol, T.; Scoffoni, C.; Edwards, E.J.; Christin, P.A.; Osborne, C.P.; et al. Developmental and biophysical determinants of grass leaf size worldwide. Nature 2021, 592, 242–247. [Google Scholar] [CrossRef] [PubMed]
- Küppers, M. Ecological significance of above-ground architectural patterns in woody plants: A question of cost-benefit relationships. Trends Ecol. Evol. 1989, 4, 375–379. [Google Scholar] [CrossRef] [PubMed]
- Baldissera, T.C.; Frak, E.; de Faccio Carvalho, P.C.; Louarn, G. Plant development controls leaf area expansion in alfalfa plants competing for light. Ann. Bot. 2014, 113, 145–157. [Google Scholar] [CrossRef]
- Ballaré, C.L.; Scopel, A.L.; Jordan, E.T.; Vierstra, R.D. Signaling among neighboring plants and the development of size inequalities in plant populations. Proc. Natl. Acad. Sci. USA 1994, 91, 10094–10098. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, M.O. Methods of measuring the concentration of wealth. Am. Statist. Assoc. 1905, 9, 209–219. [Google Scholar]
- Kakwani, N.C.; Podder, N. On the estimation of Lorenz curves from grouped observations. Int. Econ. Rev. 1973, 14, 278–292. [Google Scholar] [CrossRef]
- Kakwani, N.C.; Podder, N. Efficient estimation of the Lorenz curve and associated inequality measures from grouped observations. Econometrica 1976, 44, 137–148. [Google Scholar] [CrossRef]
- Aggarwal, V. On optimum aggregation of income distribution data. Indian J. Stat. Ser. B 1984, 46, 343–355. [Google Scholar]
- McDonald, J.B. Some generalized functions for the size distribution of income. Econometrica 1984, 52, 647–663. [Google Scholar] [CrossRef]
- McDonald, J.B.; Xu, Y.J. A generalization of the beta distribution with applications. J. Econom. 1995, 66, 133–152. [Google Scholar] [CrossRef]
- Ortega, P.; Martín, G.; Fernández, A.; Ladoux, M.; García, A. A new functional form for estimating Lorenz curves. Rev. Income Wealth 1991, 37, 447–452. [Google Scholar] [CrossRef]
- Chotikapanich, D. A comparison of alternative functional forms for the Lorenz curve. Econ. Lett. 1993, 41, 21–29. [Google Scholar] [CrossRef]
- Ryu, H.K.; Slottje, D.J. Two flexible functional form approaches for approximating the Lorenz curve. J. Econom. 1996, 72, 251–274. [Google Scholar] [CrossRef]
- Sarabia, J.M.; Castillo, E.; Slottje, D.J. An ordered family of Lorenz curves. J. Econom. 1999, 91, 43–60. [Google Scholar] [CrossRef]
- Chotikapanich, D.; Griffiths, W.E. Estimating Lorenz curves using a Dirichlet distribution. J. Bus. Econ. Stat. 2002, 20, 290–295. [Google Scholar] [CrossRef]
- Wang, Z.X.; Zhang, H.L.; Zheng, H.H. Estimation of Lorenz curves based on dummy variable regression. Econ. Lett. 2019, 177, 69–75. [Google Scholar] [CrossRef]
- Lian, M.; Shi, P.; Zhang, L.; Yao, W.; Gieli, J.; Niklas, K.J. A generalized performance equation and its application in measuring the Gini index of leaf size inequality. Trees Struct. Funct. 2023, 37, 1555–1565. [Google Scholar] [CrossRef]
- Theil, H. Economics and Information Theory; Rand McNally and Company: Chicago, IL, USA, 1967. [Google Scholar]
- Theil, H. Theory and Measurement of Consumer Demand; North-Holland: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Conceição, P.; Galbraith, J.K.; Bradford, P. The Theil Index in sequences of nested and hierarchic grouping structures: Implications for the measurement of inequality through time, with data aggregated at different levels of industrial classification. East. Econ. J. 2001, 27, 491–514. [Google Scholar]
- Bamboo Phylogeny Group. An updated tribal and subtribal classification of the bamboos (Poaceae: Bambusoideae). J. Am. Bamboo Soc. 2012, 24, 1–10. [Google Scholar]
- Wei, N.; Feng, X. Evaluation and application of five dwarf bamboo species for landscape garden in Beijing. World Bamboo Rattan 2015, 13, 32–35. [Google Scholar]
- Ao, G.; Liu, Q.; Wu, W.; Cao, X. A review and prospect of global bamboo forest carbon sink research based on CiteSpace. J. Zhejiang A. F. Univ. 2021, 38, 861–870. [Google Scholar]
- Zhang, L.; Wang, Z.; Cao, X.; Wang, K.; Cao, B.; Zhao, Y. Analysis of drought and cold tolerance of five introduced dwarf bamboo species in Shandong Province. World Bamboo Ratt. 2022, 20 (suppl. S1), 14–19. [Google Scholar]
- Shi, P.; Ratkowsky, D.; Li, Y.; Zhang, L.; Lin, S.; Gielis, J. General leaf-area geometric formula exists for plants—Evidence from the simplified Gielis equation. Forests 2018, 9, 714–768. [Google Scholar] [CrossRef]
- Su, J.; Niklas, K.J.; Huang, W.; Yu, X.; Yang, Y.; Shi, P. Lamina shape does not correlate with lamina surface area: An analysis based on the simplified Gielis equation. Glob. Ecol. Conserv. 2019, 19, e00666. [Google Scholar] [CrossRef]
- Shi, P.; Gielis, J.; Quinn, B.K.; Niklas, K.J.; Ratkowsky, D.A.; Schrader, J.; Ruan, H.; Wang, L.; Niinemets, Ü. ‘biogeom’: An R package for simulating and fitting natural shapes. Ann. N. Y. Acad. Sci. 2022, 1516, 123–134. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 1 June 2022).
- Huey, R.B.; Stevenson, R.D. Integrating thermal physiology and ecology of ectotherms: A discussion of approaches. Amer. Zool. 1979, 19, 357–366. [Google Scholar] [CrossRef]
- Shi, P.; Ge, F.; Sun, Y.; Chen, C. A simple model for describing the effect of temperature on insect developmental rate. J. Asia-Pac. Entomol. 2011, 14, 15–20. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Shorrocks, A.F. Inequality decomposition by factor components. Econometrica 1982, 50, 193–211. [Google Scholar] [CrossRef]
- Rohde, N. Lorenz curves and generalised entropy inequality measures. In Modeling Income Distributions and Lorenz Curves; Chotikapanich, D., Ed.; Springer: New York, NY, USA, 2008; Volume 5, pp. 271–283. [Google Scholar]
- Taylor, K.M.; Aarssen, L.W. Neighbor effects in mast year seedlings of Acer saccharum. Am. J. Bot. 1989, 76, 546–554. [Google Scholar] [CrossRef]
- Metsaranta, J.M.; Lieffers, V.J. Inequality of size and size increment in Pinus banksiana in relation to stand dynamics and annual growth rate. Ann. Bot. 2008, 101, 561–571. [Google Scholar] [CrossRef]
- Chen, B.J.W.; During, H.J.; Vermeulen, P.J.; Anten, N.P.R. The presence of a below-ground neighbour alters within-plant seed size distribution in Phaseolus vulgaris. Ann. Bot. 2014, 114, 937–943. [Google Scholar] [CrossRef]
- Shi, P.; Ge, F.; Wang, J.; Guo, S. Metapopulation model of multispecies competitive coexistence given exotic species invasion. Acta Ecol. Sin. 2009, 29, 1241–1250. [Google Scholar]
- Liu, G.; Hui, C.; Chen, M.; Pile, L.S.; Wang, G.G.; Wang, F.; Shi, P. Variation in individual biomass decreases faster than mean of biomass with density increasing. J. For. Res. 2020, 31, 981–987. [Google Scholar] [CrossRef]
- Falster, D.S.; Westoby, M. Plant height and evolutionary games. Trends Ecol. Evol. 2003, 18, 337–343. [Google Scholar] [CrossRef]
- Sumida, A.; Terazawa, I.; Togashi, A.; Komiyama, A. Spatial arrangement of branches in relation to slope and neighbourhood competition. Ann. Bot. 2002, 89, 301–310. [Google Scholar] [CrossRef]
- Wang, P.; Ratkowsky, D.A.; Xiao, X.; Yu, X.; Su, J.; Zhang, L.; Shi, P. Taylor’s power law for leaf bilateral symmetry. Forests 2018, 9, 500. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Ratkowsky, D.A.; Hui, C.; Gielis, J.; Lian, M.; Yao, W.; Li, Q.; Zhang, L.; Shi, P. Inequality Measure of Leaf Area Distribution for a Drought-Tolerant Landscape Plant. Plants 2023, 12, 3143. https://doi.org/10.3390/plants12173143
Huang L, Ratkowsky DA, Hui C, Gielis J, Lian M, Yao W, Li Q, Zhang L, Shi P. Inequality Measure of Leaf Area Distribution for a Drought-Tolerant Landscape Plant. Plants. 2023; 12(17):3143. https://doi.org/10.3390/plants12173143
Chicago/Turabian StyleHuang, Lichao, David A. Ratkowsky, Cang Hui, Johan Gielis, Meng Lian, Weihao Yao, Qiying Li, Liuyue Zhang, and Peijian Shi. 2023. "Inequality Measure of Leaf Area Distribution for a Drought-Tolerant Landscape Plant" Plants 12, no. 17: 3143. https://doi.org/10.3390/plants12173143
APA StyleHuang, L., Ratkowsky, D. A., Hui, C., Gielis, J., Lian, M., Yao, W., Li, Q., Zhang, L., & Shi, P. (2023). Inequality Measure of Leaf Area Distribution for a Drought-Tolerant Landscape Plant. Plants, 12(17), 3143. https://doi.org/10.3390/plants12173143







