1. Introduction
Wheat is a main staple food crop cultivated all over the world covering more than 220 million hectares and satisfying about 20% of daily diet protein necessities [
1]. Despite increased wheat areas planted, we still need to increase productivity by 60% to feed the projected population of 9.6 billion globally by 2050 under the adverse effects of climate change [
1,
2]. Heat and drought are the major abiotic stresses detrimental to plant development of wheat at various stages of growth, leading to major damage and loss of productivity and quality due to a considerable decline in the activities of antioxidant enzymes and photosynthesis [
3,
4,
5]. Plants adapt various tolerance mechanisms and practices that are complementary to each other at the morpho-physio-biochemical and molecular levels in response to abiotic stresses [
1,
3,
6]. Abiotic stresses also promote the production of reactive oxygen species (ROS) that damage various cellular functions such as chlorophyll degradation and lipid peroxidation [
7]. A common stress response involves enzymes for the scavenging of ROS (which are main factors in assessing stress tolerance level in plants) including superoxide dismutase, peroxidase, catalase, and ascorbate peroxidase [
1,
7,
8,
9]. Thus, improving yield is a major challenge in confronting food insecurity under the adverse effects of climate change, the limited resources available, and the steady increase in the population. Efforts are therefore made to strengthen wheat genotypes through breeding programs targeting agronomic trials to stressed environments and/or simulating them to have more capacity to be adaptable to abiotic stresses and possess high-yielding characteristics [
2,
10,
11,
12].
The agronomic trials’ purpose was to examine the impact of factor level/s on plant characteristics to describe, understand, and analyze natural processes under study [
13,
14,
15]. Toward the end of the trial, the scholars often have more columns (one for each trait), which need analysis to come up with and make inferences on the factor (rows) performance. The analysis of data firstly involves ANOVA (analysis of variance) for each studied attribute aiming at hypothesis testing the effects of the factor/s and secondly identifying which factor is significantly different from which other [
16,
17,
18]. The main objective was to determine the superior factor (this is good for one trait), but it was incredibly difficult to rank the factors according to their performance with multiple traits. Scholars with expertise often take into consideration a combination of plant traits that an “ideal” factor (be it treatments and/or cultivars) should provide. For wheat, for example, plant breeders search for cultivars that have early precocity, a high rate of production, and are adapted to changed environments and stress types [
19,
20]. Breeding improvement strategies for genotypes rely upon an integrative approach across different morpho-physio-biochemical (at the level of leaves and/or the entire plant) traits [
21,
22,
23,
24], aimed at providing regular and timely science-based information to support plant scholars in pinpointing the adaptive behavior of plants, especially with environmental stress. So, the combination of most authoritative traits and high-powered computer modeling of multidimensional data is required to gain a deeper understanding of the complicated mechanisms of the relationships between traits [
21,
25,
26,
27]. For that purpose, it is strongly suggested to use multivariate techniques to take into consideration the type of correlation between traits. Multivariate techniques such as the coefficients of stepwise multiple linear regression (SMLR) analysis, cluster analysis (CA), principal component analysis (PCA), and LDA have been extensively used in plant trials. Despite SMLR and CA’s importance, one weakness is the collinearity often observed across a range of assessed traits leading to unfavorable results or bias if not handled correctly [
15,
28,
29]. PCA and LDA have been thoroughly used for dimensionality minimization and visual convergence of a two-way table combining treatments and traits [
30,
31]. Even though all of the above analyses can provide a holistic view of the relationships between traits, treatments’ classification depending on the trait data continues to be a challenge. Hence, novel multivariate techniques are urgently needed to figure out the best ranking of the treatments depending on the multi-trait stability index (MTSI). Olivoto and Nardino [
20] proposed the MGIDI, which was designed to select superior genotypes depending on multiple traits and has been successfully used by plant breeders [
20,
29,
32,
33,
34]. It can distinguish the strengths and weaknesses of the selected superior genotypes depending on multiple traits [
20,
34]. Therefore, it is a very powerful tool to select the donors’ parents in future hybridization programs to obtain new recombination by integrating all traits into an ideotype. Using the MGIDI in studies evaluating stability can lead to avoiding unnecessary accounts and better strategic decisions, which facilitates making recommendations for excellent cultivars [
15,
20,
29].
Due to variations in the environmental conditions, the genotype performance may vary from strength to weakness and vice versa. This indicates a genotype × environment interplay (GEI) of the crossover type, which means that we need special strategies for improving crops [
12,
29,
35,
36]. The genotypes should have stable yield rates through various seasons and abiotic stresses until they are considered satisfactory by farmers [
12,
37,
38]. The GEI impact is critical for plant breeders because of its negative effects (phenotypic value differs from genotypic value), which adversely impact the selection of adequate genotypes for the environment/s (variety for each region/s) [
12,
39]. Hence, the use of stability and adaptability analyses is great for selecting preferred genotypes (ideotypes) in multi-environment/multiplicative trials with the AMMI model [
12,
40,
41]. This model combines PCA and ANOVA in a single analysis [
12,
21,
34,
42]. The AMMI model has been used extensively in multi-site trial (MST) analysis as it gives a more precise estimate of the GEI with appealing biplot tools [
38]. However, it is inefficient when analyzing the structure of the linear mixed-effect model (LMM). For this reason, Olivoto et al. [
35] suggested a novel model called the WAASB. The WAASB results from the singular value decomposition of the BLUP (best linear unbiased prediction) matrix for GEI effects generated by an LMM to describe ideal genotypes that bring together stability and high performance [
35]. This model joins the distinct attributes of the AMMI and BLUP models into a unique model, which helps plant scholars choose the best genotypes (stable and high performance) in many crops [
14,
34,
43,
44]. The BLUP improves the accuracy of the prediction and gives credible estimates of random effects [
35,
45,
46]; even though these two are statistically different, they possess the ability to differentiate the GEI pattern from the random error. The WAASB biplot quantifies the superior genotypes (stable and highly productive) with a two-dimensional plot, which takes into account all of the interplay principal component axes (IPCAs) of the model for GEI effects [
14,
29,
34], so the WAASB gives more reliable results. There are many multivariate analysis techniques such as SMLR, CA, LDA, factor analysis (FA), MGIDI, AMMI, WAASB, and biplots that are actively involved in the effective and reliable detection of wheat ideotypes under multiple abiotic stresses and complex interplays [
12,
20,
26,
32,
35]. The absolute values of evaluated traits do not express the tolerance performance of the genotype under stress conditions. Thus, the use of tolerance indices can give more precise and reliable estimates of these outcomes [
29]. Compared with our earlier study, herein we aimed to (i) assess six tolerance multi-indices (drought and heat) to 20 wheat genotypes during three cropping seasons and the effects of the GEI; (ii) to check the validity of categories and the prediction of new cases that have not been assigned categories; and (iii) identify ideotype(s) for the best performing genotypes and stability by MGIDI and WAASB techniques via the six tolerance multi-indices.
4. Discussion
The plant’s responses to stress are very complex, which are about acclimation, adaptation, and tolerance. These responses vary with the life stage and plant type, and the plant’s continuity of life under stress conditions is linked to its ability to hold the line against stress [
29,
51,
52]. Previous studies stated that most of the productive and morpho-physiological traits in wheat are influenced by the cultivar used, the growing culture, and the interaction between them, which could be interpreted as the growth and development of wheat being regulated by the complex interaction of a lot of factors, such as temperature, light, day length conditions, and land quality [
12,
21,
53,
54]. The development of cultivars that combine the best qualities of high productivity and stability under varying abiotic stress (drought and heat) levels is one of the top priorities of plant breeders and the greatest goal in modern breeding programs [
6,
29]. The GY is influenced by both genetic and environmental factors. So, the multi-environment trials (METs) model the magnificent efforts in modern breeding programs for the valid and reliable selection of genotypes. The reliability of prediction (the expected value is close to the visible value) is crucial for an appropriate genotype recommendation and delimitation of mega-environments [
12,
15,
35]. According to Gauch and Zobel [
55], to increase the accuracy of prediction in METs, researchers must utilize statistical models that have high prediction abilities [
35]. A special focus on this point was given in our article. Joint ANOVA for the treatments showed highly significant differences for all studied traits, and the interactions were significant for 12 out of 20 traits, suggesting that the genotypes’ tolerance indices differed from one treatment to another (
Table 2). Plant breeders rely primarily on the genetic stability of traits. The major advantage of biplots is that all IPCA axes are used, thus allowing GEI not maintained in IPCA1 to be included in the genotypes’ ranking [
35].
This model also offers the opportunity to appreciate important parameters of quantitative genetics (
h2, As, CVs (g/r),
rge,
R2gei and
h2mg) in greater depth and that these provide material information in a plant breeding program and must be utilized in a MET’s assessment. The phenotypic variation showed values two or three times greater than genetic values for most of the traits, suggesting that the environmental effect played a significant role [
12,
35]. The
h2 values were highly fluctuating (ranging from 20.00% to 89.40%). But
h2mg showed values of >0.7 for all traits, reflecting a significant increase in genetic variation of the genotypes used with an accuracy level of more than 0.82. This high accuracy indicates a high potential for predicting the genetic value [
29,
35,
56]. Correlation estimations are necessary for METs, and the high-value rge refers to a simple interaction (the low value is undesirable for the selection of genotypes) [
29,
35,
51]. The rge showed high values (>0.580) for four out of twenty traits, indicating that the environmental effect played a role in the inheritance of most traits. The genotypic CVs were higher than those obtained from the residual CVs for most traits, which indicates that the CVs (g/r) ratio was greater than 1. These results show small variability within the environment used [
2,
35]. In the present study, we have shown how the advantages of the AMMI model and the performance of multi-indices may be combined to increase the reliability of MET analysis. A study evaluating rice has shown that the estimates using the AMMI model were closer to the “true” value [
57], so predictive precision deserves special attention for model diagnosis in MET analysis [
35,
58].
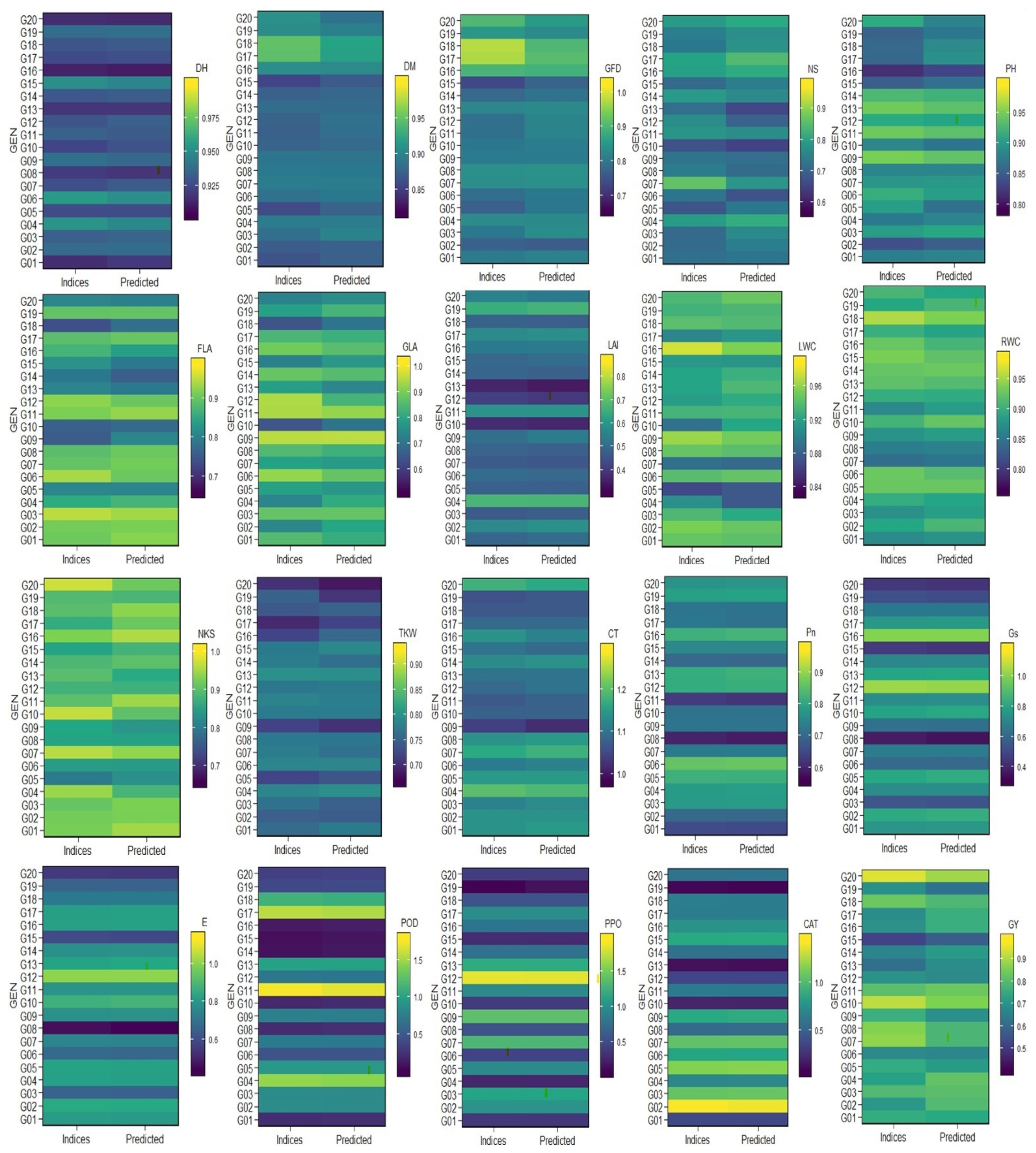
When comparing the AMMI model and the performance of multi-indices, we found that ten traits (DM, GFD, NS, PH, FLA, GLA, LWC, NKS, TKW, and GY) showed clear differences, four traits (DH, LAI, CT, and RWC) showed minor differences, and six traits (Pn, Gs, E, PPO, CAT, and POD) did not show any clear differences (
Figure 1). These results are explained by the heritability (
Table 2). The traits that had high values in heritability showed very low differences in the AMMI model and the performance of multi-indices compared to the traits that had low values in heritability [
14,
51]. Also, the biplots and AMMI model explained the genotypes’ ranking clearly [
35]. SMLR is a meaningful way to comprehend the relationships between influential and affected variables [
2,
37,
52]. We used SMLR to analyze 20 indices studied as influential indices to know which ones are powerful indices of multi-stress tolerance and their contribution to the GY index as an affected index (
Table 3). The SMLR results stated that four indices (Pn, CT, TKW, and DH) were influential to the GY index (R
2 of the SMLR model was 0.868,
p < 0.0001, with a noise value of 0.364), and their contribution ratios were 0.545, 0.190, 0.089, and 0.043, respectively (
Table 3). So, these four multi-indices could be used as influential selection criteria to create the tolerance of wheat genotypes for multiple stresses (drought and heat). It is recognized that the performance of the different genotypes varies from index to index, but at least it depends on one of them [
2,
53]. Also, some traits might show a positive correlation in the same genotype, whereas others may show a negative correlation. As a result, we noticed that the equation of the model (GY,
Table 3), GY = 0.408 − 1.599 × DH + 0.593 × TKW + 0.795 × CT + 0.626 × Pn, showed that the predicted regression GY value, error value, and relative error value differed from 0.617 (G15) to 0.923 (G20), from −0.051 (G05) to 0.053 (G17), and from −0.071 (G05) to 0.068 (G17), respectively, with genotype evaluation accuracy (%) ranging from 92.884 (G05) to 99.900 (G03) with an average value of 96.745 (
Table 3) [
2,
54].
Cluster analysis is proficient when analyzing massive data sets with multiple variables [
55,
56], and at the same time allows for the grouping of the genotypes with identical traits connected to multi-tolerance. The genotypes were grouped into five (HS, S, M, T, and HT) groups for multi-tolerance by a two-way heatmap clustering pattern using standardized MTI values (
Figure 2). The closely associated wheat genotypes were grouped into row clusters, which point to the clustering pattern related to genetic similarity [
56]. Each HT and T cluster consisted of five genotypes, the M cluster consisted of two genotypes, and each S and HS cluster consisted of four genotypes. Traits DH, CT, Pn, TKW, and GY played a crucial role in differentiating tolerant and sensitive groups of wheat genotypes (
Figure 2); it is a great method and more confident than other traditional assessment metrics [
55,
56,
57]. Although, a lot of researchers have used cluster analysis for classification [
12,
21,
58]. But, cross-validation of the grouping method was not used to enhance the reliability of the classification [
2]. The prior and posterior classification of the five (HT, T, M, S, and HT) groups was verified (
Table 4 and
Table 5). In the analysis of all traits studied, compliance was assessed in all genotypes (% correct = 100%), and in the case of the analysis of GY and its related traits (Pn, HD, CT, and TKW), there was compliance in 15 genotypes (% correct = 75%) and misclassification in 5 genotypes (G04, G07, G12, G17, and G20). But cross-validation showed there was compliance in only 5 (G01, G08, G11, G13, and G20) genotypes, and 15 genotypes were misclassified in the case of the analysis of all traits; additionally, there was compliance in 6 (G03, G05, G06, G08, G11, and G13) genotypes and 14 genotypes were misclassified in the case of the analysis of GY and its related traits (
Table 4 and
Table 5). Therefore, discriminant analysis can be a useful statistical tool that is accurate and credible in identifying genetic resources [
2,
22,
59].
The genotypes’ ranking depending on multiple traits in conjunction with the view of strengths and weaknesses is a powerful tool that can be used to direct researchers to better recommendations for selecting correct genotypes. In our experiment, we used PCA and FA to pool impactful studied traits (
Table 6), and the FA managed to reduce the 20 traits to only 8 factors, which explained 85.9%, and 2 factors for GY and its related traits, which explained 60.20%. Using the MGIDI, Olivoto and Nardino [
20] and Olivoto et al. [
15] have shown how to select superior and suitable genotypes in plant experiments that combine all selected traits (MTSI) that satisfy the breeders and achieve their desired goals. In our study, the MGIDI was superior in the process of selecting traits with intended gains. It has a higher degree of computational ability, and it has the ability to treat multicollinearity as well as the main advantage, that the requirements are outlined by the breeder before calculating the index [
20]. The MGIDI revealed that the number of traits with desired gains was 16 out of 20 traits considering all studied traits and 4 out of 5 traits considering GY and its 4 related traits, and rates of increase were 80.53 and 7.18, respectively (
Table 7). Out of 20 genotypes used, 4 wheat genotypes considering all studied traits (G01, G12, G16, and G02) and 4 wheat genotypes considering GY and its related traits (G10, G11, G08, and G20) stand out as desirable genotypes with better mean performance and stability under multi-environment conditions (
Figure 3A,B). Compared to our previous analysis using absolute values [
29], these results are different, which probably can be due to the use of tolerance indices that give more accurate and reliable estimates of genotype performance under stress conditions. Owing to the importance of the MGIDI in evaluating crop cultivars extensively, it is called speed breeding. The overall goal of plant breeders is to identify multivariate techniques to select suitable genotypes that have productive and consistent performance in varied environmental conditions [
15,
20,
29,
34]. So, based on multiple-trait information (MGIDI), the genotypes have been classified as desired and undesired. Assessing the strengths and weaknesses of genotypes serves as a novel technique for better mechanisms of crop management (
Figure 3C,D), and the use MTSI and MGIDI in future studies will lead to avoiding unnecessary calculations and allows for strategic decisions to be made more readily [
29,
60]. The MGIDI ranks the factors into factors that contribute more (plotted at the center and/or close) or contribute less (plotted towards the figure’s edge), which is used to identify distinct genetic traits of the parents for careful selection in future hybridization programs in order to obtain a new recombination known as the ideotype.
Genotypes with high productivity in various environments are the ultimate objective of plant breeders, and they work to develop genotypes to strengthen stability and stabilize yield [
12,
61]. The ANOVA for AMMI revealed that the GEI was highly significant and contributed 26.38% of the total variation and divided the GEI into five IPCAs, of which IPCA1–IPCA3 were highly significant. These results suggest that the cross-reaction gives rise to an overall response and ranking of the genotypes with the yield indices under different biotic stress conditions (
Table 8). In our study, the E1, E3, and E5 indices and the E2, E4, and E6 indices had positive correlations (the angle among them was <90°), indicating that the magnitude of the interaction effects tends to be the same and independent when applying the same abiotic stress (
Figure 4). The obtuse angle of vectors in E1 with E4 and E6 points out the negative association between them. A vertical projection from the genotype to the environmental vector detects the extent of the interaction with the environment [
12,
38,
41]. The plot (
Figure 4) shows that eleven genotypes (G02, G03, G04, G06, G07, G08, G10, G11, G14, G16, and G17) were unstable across the environments. The novel WAASB model explains the GEI, bringing together the AMMI and BLUP models into a unique index to select genotypes based on both index performance and stability [
14,
29,
34,
35]. The WAASB biplot, resulting in four quadrants, was constructed with the storage root number on the
x-axis and WAASB scores on the
y-axis (
Figure 5). The genotypes that have a high WAASB score compared to the WAASB grand mean were regarded as less stable (
Table 9). The WAASB biplot quantifies the stability of genotypes by combining an explanation of the stability and productivity in a two-dimensional plot, taking into account all of the IPCAs of the model for GEI effects not maintained in IPCA1 [
14,
62], so the WAASB gives more reliable results. When we took a closer look at the WAASB results, we found that G01, G03, G06, and G12 are more stable (smaller WAASB values) compared to G02, G07, G08, and G10. The results showed that G07 and G08 had the smallest IPCA1 values (−0.280 and −0.248, respectively), so they were more stable when using only the first IPCA (unlike the WAASB result). This may be because 66.80% of the GEI variance was expounded by IPCA1 while 33.20% of the variance was not being expounded through it. Eventually, further investigation focused on total comprehension of these modern statistical methods would be of benefit and make the method more consistent and useful, to obtain the best (high productivity and stability) genotypes under environmental stresses and to meet increasing demands for crop wheat because of population growth coupled with extreme climatic variations [
12,
29,
34,
63].