Heterogeneity Assessment of Kenaf Breeding Field through Spatial Dependence Analysis on Crop Growth Status Map Derived by Unmanned Aerial Vehicle
Abstract
1. Introduction
2. Results
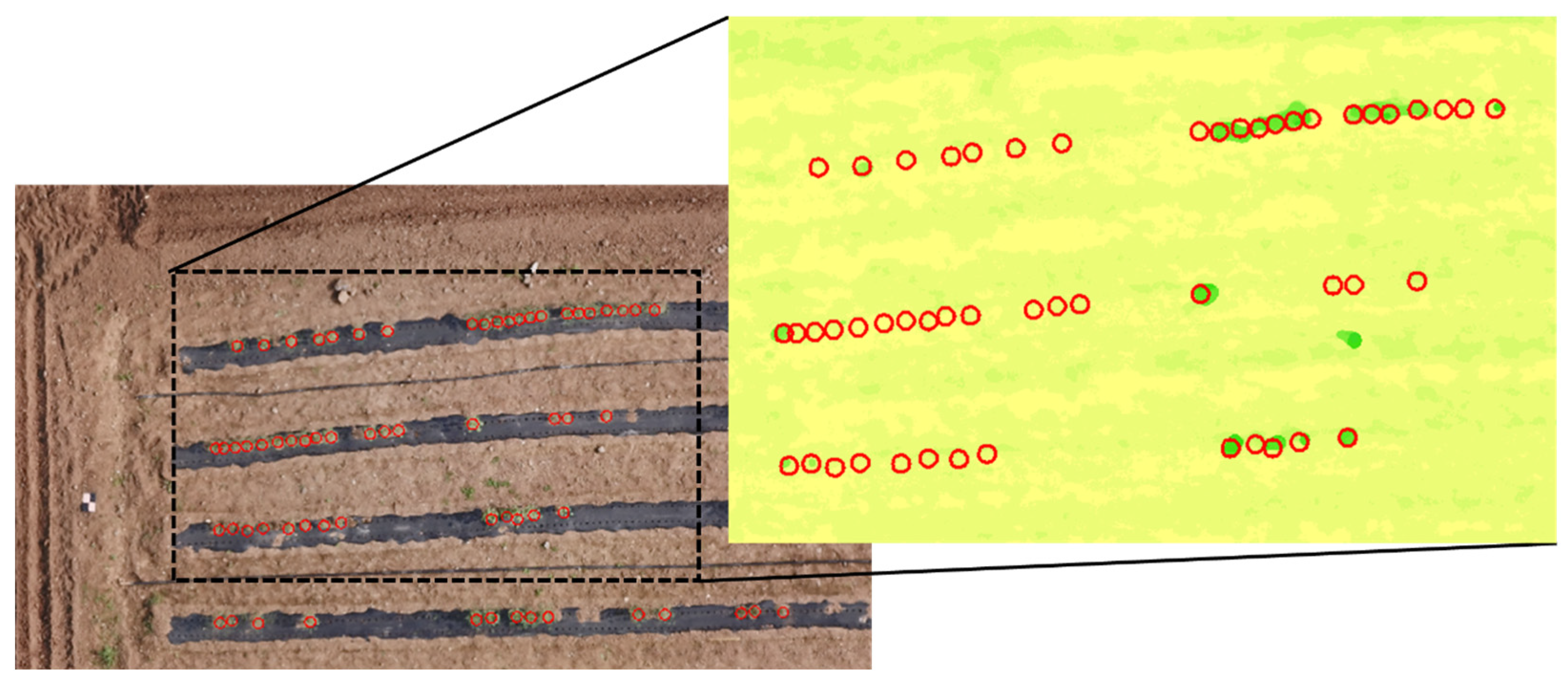
2.1. The Reliability of Crop Height Map
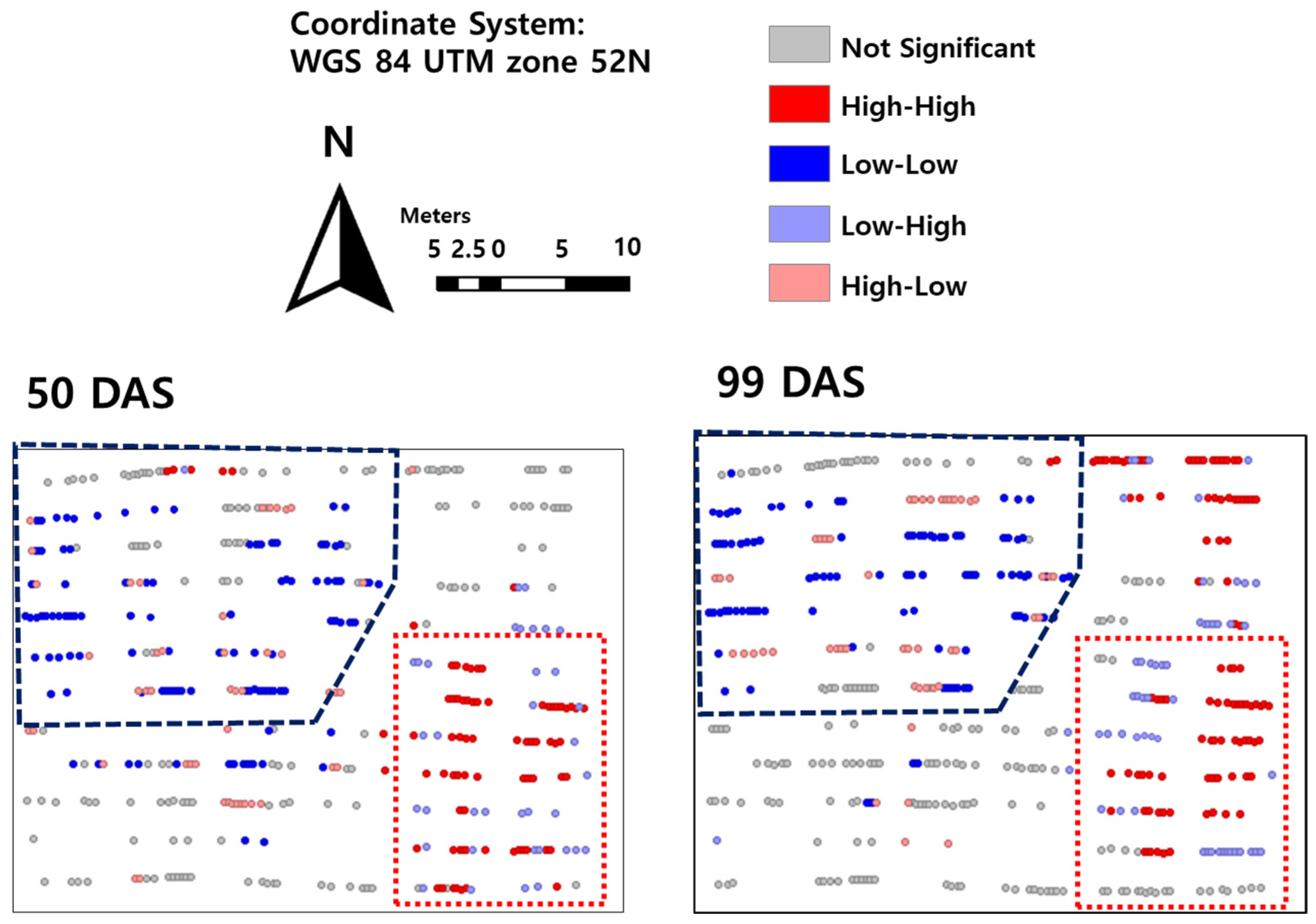
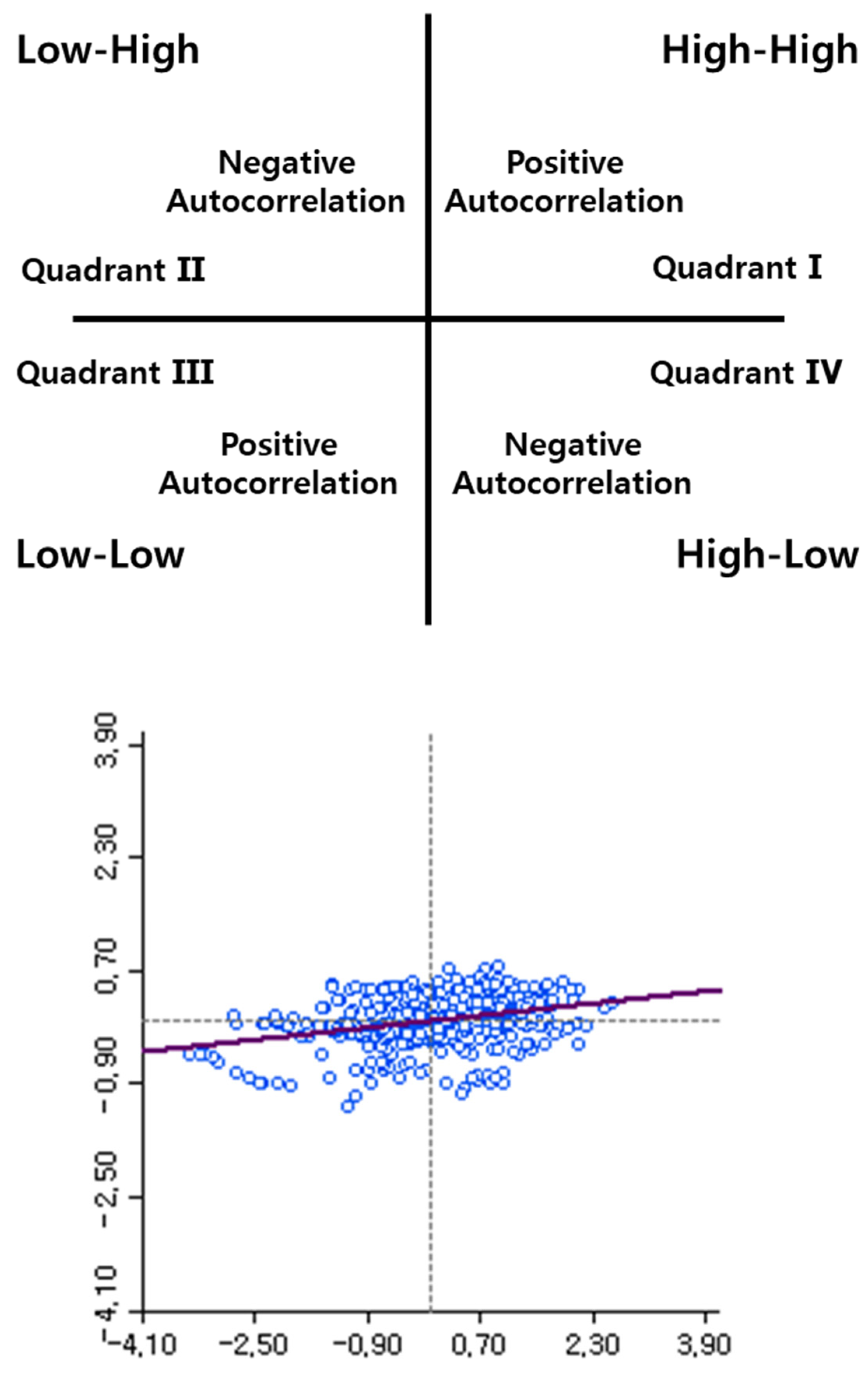
2.2. The Recognition of Cluster Region in Local Indicators of Spatial Autocorrelation (LISA) Map
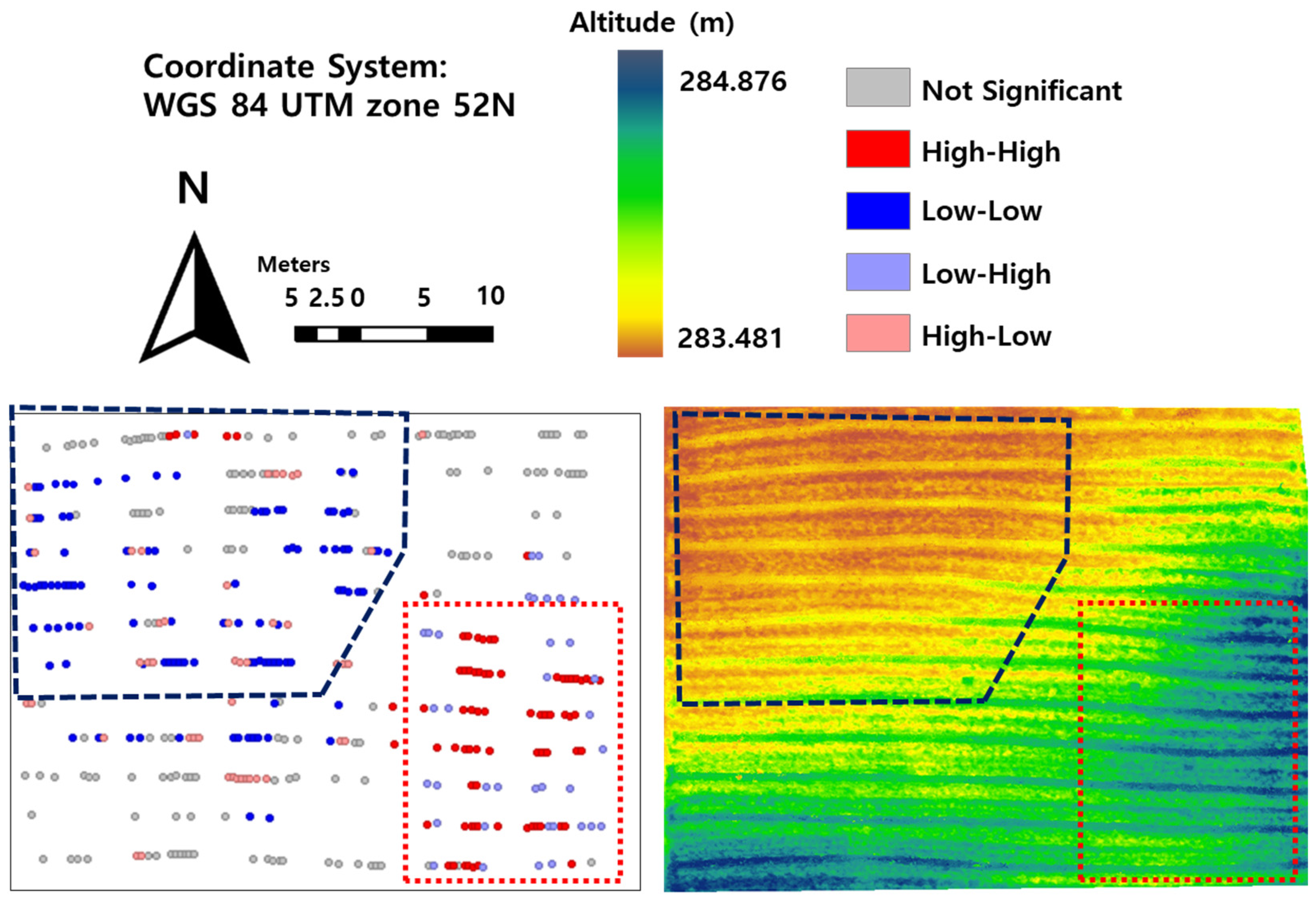
2.3. The Reason of Field Heterogeneity: Slope of High-Clay Field
2.4. Breeding Strategy Considering Heterogeneous of Breeding Field
3. Discussions
4. Materials and Methods
4.1. Study Site and Field Characteristics
4.2. Plant Preparation
4.3. The Generation of Height Map Using UAV-RGB
4.4. The Extraction of Individual Height
4.5. Spatial Dependence Analysis of Breeding Field
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Webber, C.L., III; Bhardwaj, H.L.; Bledsoe, V.K. Kenaf production: Fiber, feed, and seed. Trends New Crops New Uses 2002, 13, 327–339. [Google Scholar]
- Afzal, M.Z.; Ibrahim, A.K.; Xu, Y.; Niyitanga, S.; Li, Y.; Li, D.; Yang, X.; Zhang, L. Kenaf (Hibiscus cannabinus L.) Breeding. J. Nat. Fibers 2020, 19, 1–19. [Google Scholar] [CrossRef]
- Monti, A. Kenaf: A Multi-Purpose Crop for Several Industrial Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Calamari, T.A.; Tao, W.; Goynes, W.R. A preliminary study of kenaf fiber bundles and their composite cells. Tappi J. 1997, 80, 149–154. [Google Scholar]
- Anuar, H.; Zuraida, A. Improvement in mechanical properties of reinforced thermoplastic elastomer composite with kenaf bast fibre. Compos. Part B Eng. 2011, 42, 462–465. [Google Scholar] [CrossRef]
- Kim, J.; Han, G.D.; Muthukathan, G.; Rodrogues, R.; Hyun, D.Y.; Kim, S.-H.; Yu, J.-K.; Park, J.; Yoo, S.-C.; Chung, Y.S. What Traits Should Be Measured for Biomass in Kenaf? Plants 2021, 10, 1394. [Google Scholar] [CrossRef] [PubMed]
- Jang, G.; Kim, J.; Kim, D.; Chung, Y.S.; Kim, H.-J. Field Phenotyping of Plant Height in Kenaf (Hibiscus cannabinus L.) using UAV Imagery. Korean J. Crop Sci. 2022, 67, 274–284. [Google Scholar]
- Bégué, A.; Arvor, D.; Bellon, B.; Betbeder, J.; De Abelleyra, D.; PD Ferraz, R.; Lebourgeois, V.; Lelong, C.; Simões, M.; Verón, S.R. Remote sensing and cropping practices: A review. Remote Sens. 2018, 10, 99. [Google Scholar] [CrossRef]
- Doraiswamy, P.C.; Moulin, S.; Cook, P.W.; Stern, A. Crop yield assessment from remote sensing. Photogramm. Eng. Remote Sens. 2003, 69, 665–674. [Google Scholar] [CrossRef]
- Jang, G.; Kim, J.; Yu, J.-K.; Kim, H.-J.; Kim, Y.; Kim, D.-W.; Kim, K.-H.; Lee, C.W.; Chung, Y.S. Cost-effective unmanned aerial vehicle (UAV) platform for field plant breeding application. Remote Sens. 2020, 12, 998. [Google Scholar] [CrossRef]
- Holman, F.H.; Riche, A.B.; Michalski, A.; Castle, M.; Wooster, M.J.; Hawkesford, M.J. High throughput field phenotyping of wheat plant height and growth rate in field plot trials using UAV based remote sensing. Remote Sens. 2016, 8, 1031. [Google Scholar] [CrossRef]
- Han, G.D.; Jang, G.; Kim, J.; Kim, D.-W.; Rodrogues, R.; Kim, S.-H.; Kim, H.-J.; Chung, Y.S. RGB images-based vegetative index for phenotyping kenaf (Hibiscus cannabinus L.). PLoS ONE 2021, 16, e0256978. [Google Scholar]
- Baye, T.M.; Abebe, T.; Wilke, R.A. Genotype–environment interactions and their translational implications. Pers. Med. 2011, 8, 59–70. [Google Scholar] [CrossRef] [PubMed]
- Ostengo, S.; Cuenya, M.I.; Balzarini, M. Modeling spatial correlation structure in sugarcane (Saccharum spp.) multi-environment trials. J. Crop Improv. 2015, 29, 53–64. [Google Scholar] [CrossRef]
- Taylor, J.; Bates, T. A discussion on the significance associated with Pearson’s correlation in precision agriculture studies. Precis. Agric. 2013, 14, 558–564. [Google Scholar] [CrossRef]
- Stroup, W.W.; Baenziger, P.S.; Mulitze, D.K. Removing spatial variation from wheat yield trials: A comparison of methods. Crop Sci. 1994, 34, 62–66. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, M.X.; Boer, M.P.; van Eeuwijk, F.A.; Eilers, P.H. Correcting for spatial heterogeneity in plant breeding experiments with P-splines. Spat. Stat. 2018, 23, 52–71. [Google Scholar] [CrossRef]
- Duarte, J.B.; Vencovsky, R. Spatial statistical analysis and selection of genotypes in plant breeding. Pesqui. Agropecuária Bras. 2005, 40, 107–114. [Google Scholar] [CrossRef]
- Silva, M.J.d.; Carneiro, A.P.S.; Feres, A.L.G.; Carneiro, J.E.S.; Santos, N.T.; Cecon, P.R. Spatial dependence in experiments of progeny selection for bean (Phaseolus vulgaris L.) yield. Rev. Ceres 2016, 63, 477–485. [Google Scholar] [CrossRef]
- Paget, M.F.; Alspach, P.A.; Anderson, J.A.; Genet, R.A.; Apiolaza, L.A. Trial heterogeneity and variance models in the genetic evaluation of potato tuber yield. Plant Breed. 2015, 134, 203–211. [Google Scholar] [CrossRef]
- Honsdorf, N.; Van Loon, J.; Govaerts, B.; Verhulst, N. Crop Management for Breeding Trials. In Wheat Improvement; Springer: Berlin/Heidelberg, Germany, 2022; pp. 257–274. [Google Scholar]
- Amorim, P.; Figueiredo, M.; Machete, M.; Morato, T.; Martins, A.; Serrão Santos, R. Spatial variability of seabird distribution associated with environmental factors: A case study of marine Important Bird Areas in the Azores. ICES J. Mar. Sci. 2009, 66, 29–40. [Google Scholar] [CrossRef]
- Cursi, D.E.; Gazaffi, R.; Hoffmann, H.P.; Brasco, T.L.; do Amaral, L.R.; Neto, D.D. Novel tools for adjusting spatial variability in the early sugarcane breeding stage. Front. Plant Sci. 2021, 12, 749533. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Miller, H.J. Tobler’s first law and spatial analysis. Ann. Assoc. Am. Geogr. 2004, 94, 284–289. [Google Scholar] [CrossRef]
- Sui, D.Z. Tobler’s first law of geography: A big idea for a small world? Ann. Assoc. Am. Geogr. 2004, 94, 269–277. [Google Scholar] [CrossRef]
- Coelho, I.F.; Peixoto, M.A.; Marcal, T.d.S.; Bernardeli, A.; Alves, R.S.; de Lima, R.O.; Reis, E.F.d.; Bhering, L.L. Accounting for spatial trends in multi-environment diallel analysis in maize breeding. PLoS ONE 2021, 16, e0258473. [Google Scholar]
- Matese, A.; Di Gennaro, S.F.; Santesteban, L.G. Methods to compare the spatial variability of UAV-based spectral and geometric information with ground autocorrelated data. A case of study for precision viticulture. Comput. Electron. Agric. 2019, 162, 931–940. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Hartling, S.; Esposito, F.; Fritschi, F.B. Soybean yield prediction from UAV using multimodal data fusion and deep learning. Remote Sens. Environ. 2020, 237, 111599. [Google Scholar] [CrossRef]
- Bendig, J.; Bolten, A.; Bennertz, S.; Broscheit, J.; Eichfuss, S.; Bareth, G. Estimating biomass of barley using crop surface models (CSMs) derived from UAV-based RGB imaging. Remote Sens. 2014, 6, 10395–10412. [Google Scholar] [CrossRef]
- Kawamura, K.; Asai, H.; Yasuda, T.; Khanthavong, P.; Soisouvanh, P.; Phongchanmixay, S. Field phenotyping of plant height in an upland rice field in Laos using low-cost small unmanned aerial vehicles (UAVs). Plant Prod. Sci. 2020, 23, 452–465. [Google Scholar] [CrossRef]
- Niu, Y.; Zhang, L.; Zhang, H.; Han, W.; Peng, X. Estimating above-ground biomass of maize using features derived from UAV-based RGB imagery. Remote Sens. 2019, 11, 1261. [Google Scholar] [CrossRef]
- Volpato, L.; Pinto, F.; González-Pérez, L.; Thompson, I.G.; Borém, A.; Reynolds, M.; Gérard, B.; Molero, G.; Rodrigues Jr, F.A. High throughput field phenotyping for plant height using UAV-based RGB imagery in wheat breeding lines: Feasibility and validation. Front. Plant Sci. 2021, 12, 185. [Google Scholar] [CrossRef]
- Nyéki, A.; Milics, G.; Kovács, A.; Neményi, M. Effects of soil compaction on cereal yield: A review. Cereal Res. Commun. 2017, 45, 1–22. [Google Scholar] [CrossRef]
- Day, S.D.; Bassuk, N.L. A review of the effects of soil compaction and amelioration treatments on landscape trees. J. Arboric. 1994, 20, 9–17. [Google Scholar] [CrossRef]
- Skiba, U.; Ball, B. The effect of soil texture and soil drainage on emissions of nitric oxide and nitrous oxide. Soil Use Manag. 2002, 18, 56–60. [Google Scholar] [CrossRef]
- Bañuelos, G.S.; Bryla, D.R.; Cook, C.G. Vegetative production of kenaf and canola under irrigation in central California. Ind. Crops Prod. 2002, 15, 237–245. [Google Scholar] [CrossRef]
- Hirschi, M.; Viterbo, P.; Seneviratne, S.I. Basin-scale water-balance estimates of terrestrial water storage variations from ECMWF operational forecast analysis. Geophys. Res. Lett. 2006, 33, L21401. [Google Scholar] [CrossRef]
- Liang, W.-L.; Hung, F.-X.; Chan, M.-C.; Lu, T.-H. Spatial structure of surface soil water content in a natural forested headwater catchment with a subtropical monsoon climate. J. Hydrol. 2014, 516, 210–221. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Viterbo, P.; Lüthi, D.; Schär, C. Inferring changes in terrestrial water storage using ERA-40 reanalysis data: The Mississippi River basin. J. Clim. 2004, 17, 2039–2057. [Google Scholar] [CrossRef]
- Awe, G.; Reichert, J.; Timm, L.; Wendroth, O. Temporal processes of soil water status in a sugarcane field under residue management. Plant Soil 2015, 387, 395–411. [Google Scholar] [CrossRef]
- Abioye, E.A.; Abidin, M.S.Z.; Mahmud, M.S.A.; Buyamin, S.; Ishak, M.H.I.; Abd Rahman, M.K.I.; Otuoze, A.O.; Onotu, P.; Ramli, M.S.A. A review on monitoring and advanced control strategies for precision irrigation. Comput. Electron. Agric. 2020, 173, 105441. [Google Scholar] [CrossRef]
- Adeyemi, O.; Grove, I.; Peets, S.; Norton, T. Advanced monitoring and management systems for improving sustainability in precision irrigation. Sustainability 2017, 9, 353. [Google Scholar] [CrossRef]
- Smith, R.; Baillie, J.; McCarthy, A.; Raine, S.; Baillie, C. Review of Precision Irrigation Technologies and Their Application; University of Southern Queensland: Darling Heights, Australia, 2010. [Google Scholar]
- Kamienski, C.; Soininen, J.-P.; Taumberger, M.; Dantas, R.; Toscano, A.; Cinotti, T.S.; Maia, R.F.; Neto, A.T. Smart water management platform: IoT-based precision irrigation for agriculture. Sensors 2019, 19, 276. [Google Scholar] [CrossRef]
- Smith, R.; Baillie, J. Defining precision irrigation: A new approach to irrigation management. In Proceedings of the Irrigation Australia 2009: Irrigation Australia Irrigation and Drainage Conference: Proceedings, Swan Hill, Australia, 18–21 October 2009. [Google Scholar]
- Anselin, L. Spatial dependence and spatial structural instability in applied regression analysis. J. Reg. Sci. 1990, 30, 185–207. [Google Scholar] [CrossRef]
- Jang, G.; Kim, D.-W.; Kim, H.-J.; Chung, Y.S. Spatial Dependence Analysis as a Tool to Detect the Hidden Heterogeneity in a Kenaf Field. Agronomy 2023, 13, 428. [Google Scholar] [CrossRef]
- Diniz-Filho, J.A.F.; Bini, L.M.; Hawkins, B.A. Spatial autocorrelation and red herrings in geographical ecology. Glob. Ecol. Biogeogr. 2003, 12, 53–64. [Google Scholar] [CrossRef]
- Jang, J.; Yoo, D.-S.; Chun, B.C. Spatial epidemiologic analysis of the liver cancer and gallbladder cancer incidence and its determinants in South Korea. BMC Public Health 2021, 21, 2090. [Google Scholar] [CrossRef] [PubMed]
- Tsai, P.-J.; Lin, M.-L.; Chu, C.-M.; Perng, C.-H. Spatial autocorrelation analysis of health care hotspots in Taiwan in 2006. BMC Public Health 2009, 9, 464. [Google Scholar] [CrossRef] [PubMed]
- Ismail, S. Spatial autocorrelation and real estate studies: A literature review. Malays. J. Real Estate 2006, 1, 1–13. [Google Scholar]
- Griffith, D.A. Visualizing analytical spatial autocorrelation components latent in spatial interaction data: An eigenvector spatial filter approach. Comput. Environ. Urban Syst. 2011, 35, 140–149. [Google Scholar] [CrossRef]
- Griffith, D.A. Modeling spatial autocorrelation in spatial interaction data: Empirical evidence from 2002 Germany journey-to-work flows. J. Geogr. Syst. 2009, 11, 117–140. [Google Scholar] [CrossRef]
- Dalposso, G.H.; Uribe-Opazo, M.A.; Mercante, E.; Lamparelli, R.A. Spatial autocorrelation of NDVI and GVI indices derived from Landsat/TM images for soybean crops in the western of the state of Paraná in 2004/2005 crop season. Eng. Agrícola 2013, 33, 525–537. [Google Scholar] [CrossRef]
- Stojanova, D.; Ceci, M.; Appice, A.; Malerba, D.; Džeroski, S. Dealing with spatial autocorrelation when learning predictive clustering trees. Ecol. Inform. 2013, 13, 22–39. [Google Scholar] [CrossRef]
- Sergeev, A.; Buevich, A.; Baglaeva, E.; Shichkin, A. Combining spatial autocorrelation with machine learning increases prediction accuracy of soil heavy metals. Catena 2019, 174, 425–435. [Google Scholar] [CrossRef]
- Mainali, J.; Chang, H.; Chun, Y. A review of spatial statistical approaches to modeling water quality. Prog. Phys. Geogr. Earth Environ. 2019, 43, 801–826. [Google Scholar] [CrossRef]
- Kim, B.; Rundle, A.G.; Goodwin, A.T.S.; Morrison, C.N.; Branas, C.C.; El-Sadr, W.; Duncan, D.T. COVID-19 testing, case, and death rates and spatial socio-demographics in New York City: An ecological analysis as of June 2020. Health Place 2021, 68, 102539. [Google Scholar] [CrossRef]
- Wang, W.-C.; Chang, Y.-J.; Wang, H.-C. An application of the spatial autocorrelation method on the change of real estate prices in Taitung City. ISPRS Int. J. Geo-Inf. 2019, 8, 249. [Google Scholar] [CrossRef]
- Salazar, J.J.; Garland, L.; Ochoa, J.; Pyrcz, M.J. Fair train-test split in machine learning: Mitigating spatial autocorrelation for improved prediction accuracy. J. Pet. Sci. Eng. 2022, 209, 109885. [Google Scholar] [CrossRef]
- Chen, Y. An analytical process of spatial autocorrelation functions based on Moran’s index. PLoS ONE 2021, 16, e0249589. [Google Scholar] [CrossRef] [PubMed]
- Kunze, G.; Dixon, J.B. Pretreatment for mineralogical analysis. In Methods of Soil Analysis: Part 1 Physical and Mineralogical Methods; Wiley: New York, NY, USA, 1986; Volume 5, pp. 91–100. [Google Scholar]
- Reshetyuk, Y.; Mårtensson, S.G. Generation of highly accurate digital elevation models with unmanned aerial vehicles. Photogramm. Rec. 2016, 31, 143–165. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; Smith, M.W. 3-D uncertainty-based topographic change detection with structure-from-motion photogrammetry: Precision maps for ground control and directly georeferenced surveys. Earth Surf. Process. Landf. 2017, 42, 1769–1788. [Google Scholar] [CrossRef]
- Han, X.; Thomasson, J.A.; Bagnall, G.C.; Pugh, N.A.; Horne, D.W.; Rooney, W.L.; Jung, J.; Chang, A.; Malambo, L.; Popescu, S.C. Measurement and calibration of plant-height from fixed-wing UAV images. Sensors 2018, 18, 4092. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.-W.; Yun, H.S.; Jeong, S.-J.; Kwon, Y.-S.; Kim, S.-G.; Lee, W.S.; Kim, H.-J. Modeling and testing of growth status for Chinese cabbage and white radish with UAV-based RGB imagery. Remote Sens. 2018, 10, 563. [Google Scholar] [CrossRef]
- Jamil, N.; Kootstra, G.; Kooistra, L. Evaluation of Individual Plant Growth Estimation in an Intercropping Field with UAV Imagery. Agriculture 2022, 12, 102. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]

| Plot Number | Germplasm | p-Value at 50 DAS 1 | p-Value at 99 DAS |
|---|---|---|---|
| 1 | EF-1 | * | * |
| 2 | WIR119 | * | 0.175 |
| 3 | ET-2 | * | 0.273 |
| 4 | EF-3 | 0.375 | 0.635 |
| 7 | WIR275 | ** | ** |
| 8 | Cubano | 0.372 | 0.706 |
| 9 | Everglades 71 | ** | * |
| 10 | PI468077 | * | * |
| 13 | PI468075 | ** | ** |
| 14 | Everglades 41 | ** | * |
| 15 | Local | * | 0.103 |
| 16 | PI365441 | * | ** |
| 19 | R | * | 0.157 |
| Plot Number | Germplasm | p-Value at 50 DAS 1 | p-Value at 99 DAS |
|---|---|---|---|
| 1 | EF-1 | * | * |
| 2 | WIR119 | * | 0.175 |
| 3 | ET-2 | * | 0.273 |
| 4 | EF-3 | 0.375 | 0.635 |
| 7 | WIR275 | ** | ** |
| 8 | Cubano | 0.372 | 0.706 |
| 9 | Everglades 71 | ** | * |
| 10 | PI468077 | * | * |
| 13 | PI468075 | ** | ** |
| 14 | Everglades 41 | ** | * |
| 15 | Local | * | 0.103 |
| 16 | PI365441 | * | ** |
| 19 | R | * | 0.157 |
| 20 | WIR214 | 0.157 | * |
| 21 | Kenaf | * | ** |
| 22 | WIR276 | * | * |
| 25 | Kenaf | * | ** |
| 26 | Cubano | 0.372 | 0.706 |
| 27 | WIR333 | 0.105 | * |
| 28 | WIR119 | * | 0.175 |
| 31 | Everglades 41 | ** | * |
| 32 | G-1 | 0.106 | 0.753 |
| 33 | EF-1 | * | * |
| 37 | PI468077 | * | * |
| 38 | WIR274 | * | * |
| 39 | WIR453 | * | 0.204 |
| Parameters | Topsoil (0–20 cm) | Subsoil (20–40 cm) |
|---|---|---|
| Bulk density (g/m−3) | 1.23 ± 0.07 | 1.47 ± 0.17 |
| Soil texture | Silty clay loam | Silty clay loam |
| Clay (%) | 30.6 ± 0.23 | 29.2 ± 1.15 |
| Silt (%) | 56.2 ± 2.15 | 58.9 ± 0.60 |
| Sand (%) | 13.2 ± 1.95 | 11.9 ± 1.60 |
| Date | Flight Altitude (m) | Ground Sampling Distance (cm/pixel) | Wind (m/s) | Image Overlap (%) |
|---|---|---|---|---|
| 26 April 2019 | 30 | 0.65 | 4.4 | >80 |
| 22 June 2019 (50 DAS 1) | 40 | 1.41 | 3.9 | >90 |
| 6 August 2019 (99 DAS) | 40 | 1.34 | 3.2 | >90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, G.; Kim, D.-W.; Park, W.-P.; Kim, H.-J.; Chung, Y.-S. Heterogeneity Assessment of Kenaf Breeding Field through Spatial Dependence Analysis on Crop Growth Status Map Derived by Unmanned Aerial Vehicle. Plants 2023, 12, 1638. https://doi.org/10.3390/plants12081638
Jang G, Kim D-W, Park W-P, Kim H-J, Chung Y-S. Heterogeneity Assessment of Kenaf Breeding Field through Spatial Dependence Analysis on Crop Growth Status Map Derived by Unmanned Aerial Vehicle. Plants. 2023; 12(8):1638. https://doi.org/10.3390/plants12081638
Chicago/Turabian StyleJang, Gyujin, Dong-Wook Kim, Won-Pyo Park, Hak-Jin Kim, and Yong-Suk Chung. 2023. "Heterogeneity Assessment of Kenaf Breeding Field through Spatial Dependence Analysis on Crop Growth Status Map Derived by Unmanned Aerial Vehicle" Plants 12, no. 8: 1638. https://doi.org/10.3390/plants12081638
APA StyleJang, G., Kim, D.-W., Park, W.-P., Kim, H.-J., & Chung, Y.-S. (2023). Heterogeneity Assessment of Kenaf Breeding Field through Spatial Dependence Analysis on Crop Growth Status Map Derived by Unmanned Aerial Vehicle. Plants, 12(8), 1638. https://doi.org/10.3390/plants12081638






