Uncertainty Quantification of Imperfect Diagnostics

Abstract

The operable state of a system is maintained during operation, which requires knowledge of the system’s state. Technical diagnostics, as a process of accurately obtaining information about the system state, becomes a crucial stage in the life cycle of any system. The study deals with the relevant problem of uncertainty quantification of imperfect diagnostics. We considered the most general case when the object of diagnostics, the diagnostic tool, and the human operator can each be in one of the many states. The concept of a diagnostic error is introduced, in which the object of diagnostics is in one of many states but is erroneously identified as being in any other state. We derived the generalized formulas for the probability of a diagnostic error, the probability of correct diagnosis, and the total probability of a diagnostic error. The proposed generalized formulas make it possible to determine the probabilistic indicators of diagnosis uncertainty for any structures of diagnostics systems and any types of failures of the diagnostic tool and human operator. We demonstrated the theoretical material by computing the probabilistic indicators of diagnosis uncertainty for an aircraft VHF communication system and fatigue cracks in the aircraft wings.

1. Introduction

The continuous growth of complexity in modern technical systems and the functions they perform makes ensuring the reliability and effectiveness of their use one of the most urgent scientific and practical tasks. The effectiveness of complex technical systems is heavily reliant on diagnostic quality. Suffice it to point out, for example, that an error in diagnosing the condition of some aviation systems can lead to significant economic losses and tragic consequences [1,2,3,4].

Diagnosing is the process of determining the technical condition of the object being diagnosed. To make a diagnosis for a specific system condition, diagnostics involves testing and other procedures. The system health check is a special case of diagnostics when the number of possible technical states of the object is equal to two. The main objective of technical diagnostics is to determine the system’s current state using measuring data. Diagnosing technical systems at the phase of the operation can significantly improve the quantitative characteristics of reliability, reduce losses due to failures and downtime, and reduce the labor intensity of maintenance.

The most significant characteristic of the quality of the diagnosis is trustworthiness, which is quantitatively characterized by various indicators. The higher the level of trustworthiness, the lower the level of uncertainty in diagnostic results. Obviously, a diagnosis trustworthiness level of 100% corresponds to perfect diagnostics. If the level is less than 100%, such diagnostics are imperfect. When checking the operability of the object of diagnostics (OD), i.e., when the diagnostic tool (DT) distinguishes only two states of OD, we usually use such trustworthiness indicators as true positive, false positive, true negative, and false negative. However, the number of OD states in most problems can be much greater than two. The most basic example of an OD with many states is one whose condition is defined by N diagnostic parameters (DP), and the DT determines the location of the failure with a depth of up to DP. The number of alternative states is m = 2^N in this case. Another example is complex electronic systems, which are distinguished by the presence of numerous types of redundancies in their variable structure and complicated connections among their components. The number of possible states of these kinds of systems is also much greater than two. Diagnostics of such systems can be carried out in various ways, varying in the trustworthiness of the results. We should also note that, in the general case, the diagnostic trustworthiness is affected by the reliability of the human operator (HO) and DT.

The system of technical diagnostics (SoTD) is a combination of DT, OD, and HO. Automated test equipment for diagnostics of avionics systems is a typical example of SoTD. Any DT and HO operate with measurement errors and failures. Therefore, the information obtained because of the diagnosis contains uncertainty. The diagnosis’s trustworthiness depends on the accuracy of measurements and the reliability of DT and HO. Therefore, it is crucial to identify the trustworthiness indicators for systems with a wide range of possible states while considering the accuracy and reliability of the DT as well as the HO.

The following conclusions can be drawn from the literature review in Section 2:

(1).

The SoTD includes OD, DT, and HO. However, the known indicators of diagnostic trustworthiness consider at best only the characteristics of OD and DT. Until now, there have been no published studies that would simultaneously consider the main characteristics of all SoTD components.

(2).

In principle, the assessment of trustworthiness can be carried out using the same statistical methods as in binary classification problems. However, statistical methods necessitate the collection of large amounts of data for evaluating trustworthiness indicators. Furthermore, this will have to be carried out whenever testing algorithms are changed or improved. Analytical models are significantly simpler and less expensive to use.

(3).

The use of the well-known F1 score measure is also impractical to employ for assessing diagnostic trustworthiness for the following reasons. Firstly, it prioritizes precision and recall equally, but in practice, different sorts of classification errors result in various losses, and secondly, the F1 score is calculated using merely a statistical method.

In this study, we consider the problem of determining diagnostic trustworthiness indicators for the general case when the OD, HO, and DT can be in one of the m, k, or n technical states, respectively. We derive formulas for such indicators as the probability of a diagnostic error of type (i, j) in determining the technical state of the OD, the probability of a correct diagnosis, and the total probability of a diagnostic error. Computing the probabilistic indicators of diagnosis trustworthiness for an aircraft VHF communication system and fatigue cracks in the aircraft wings illustrates the theoretical material.

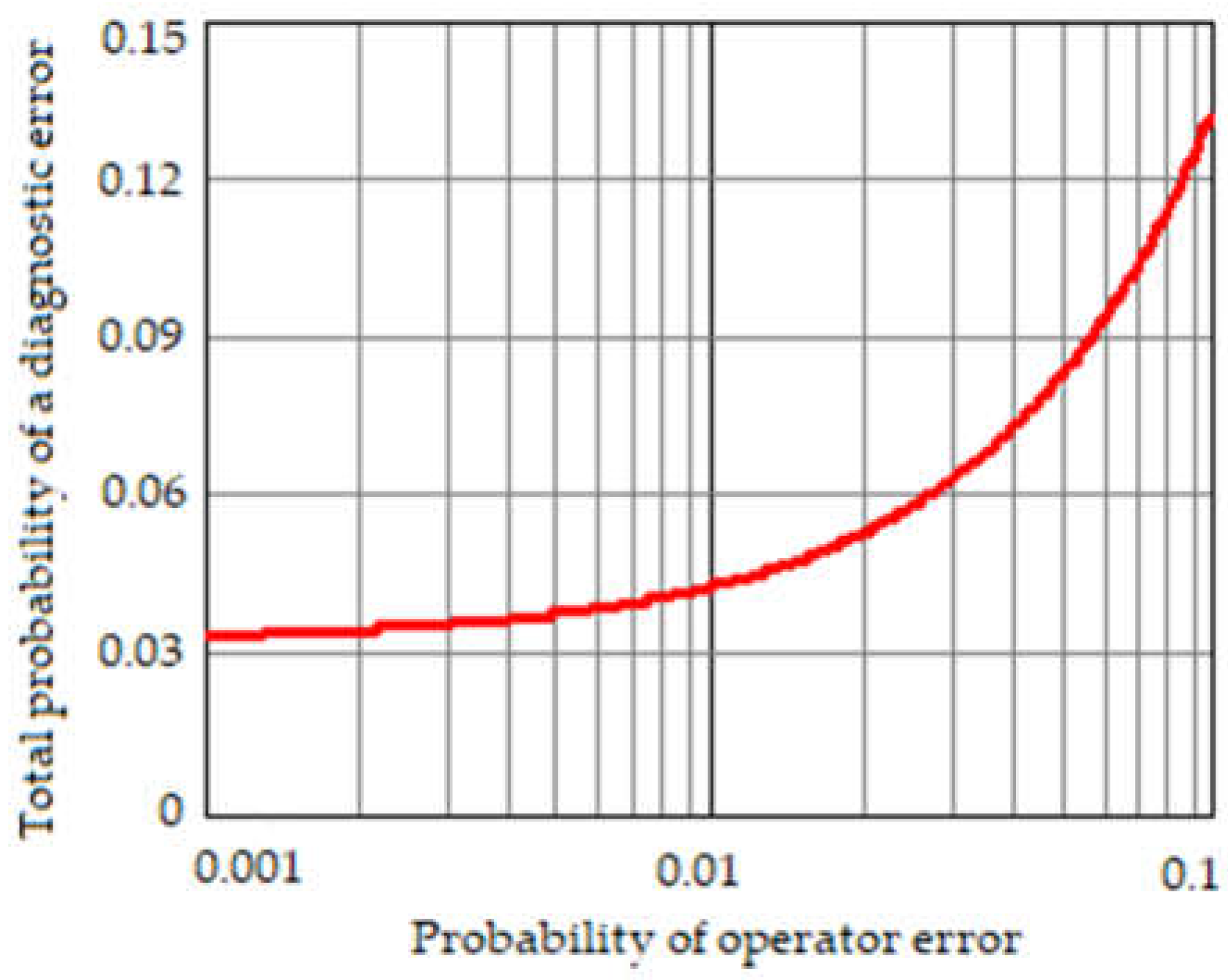
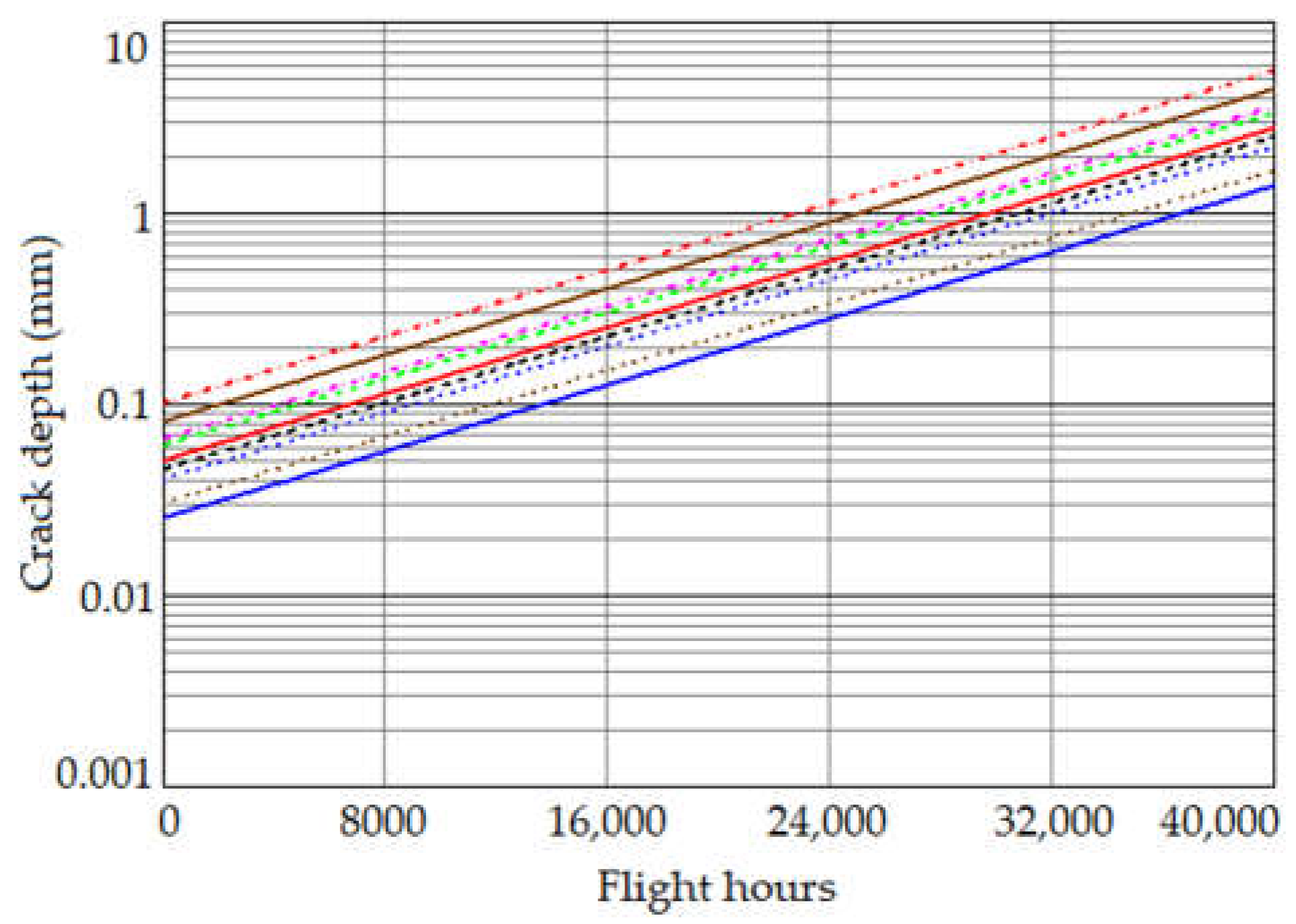
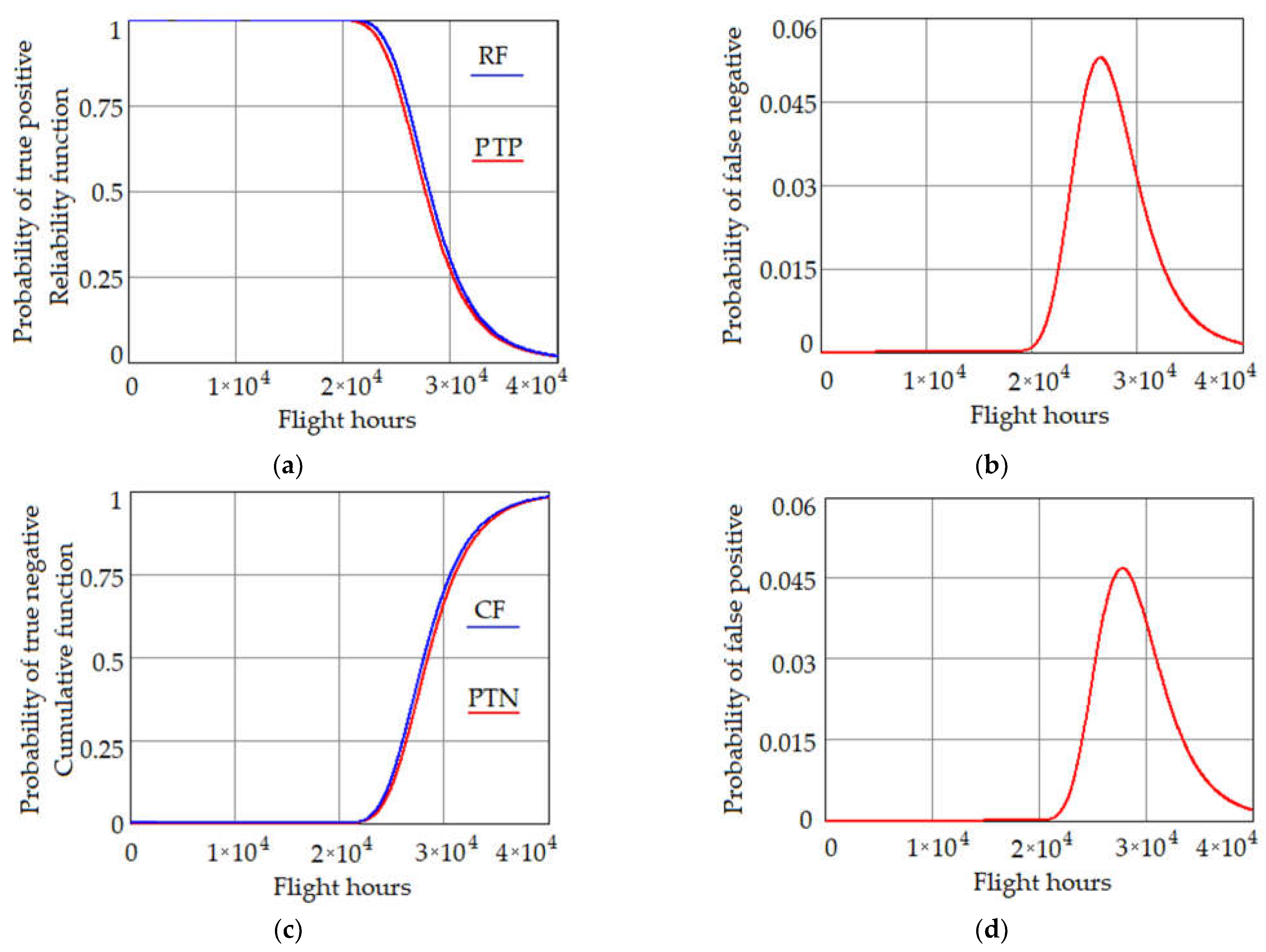
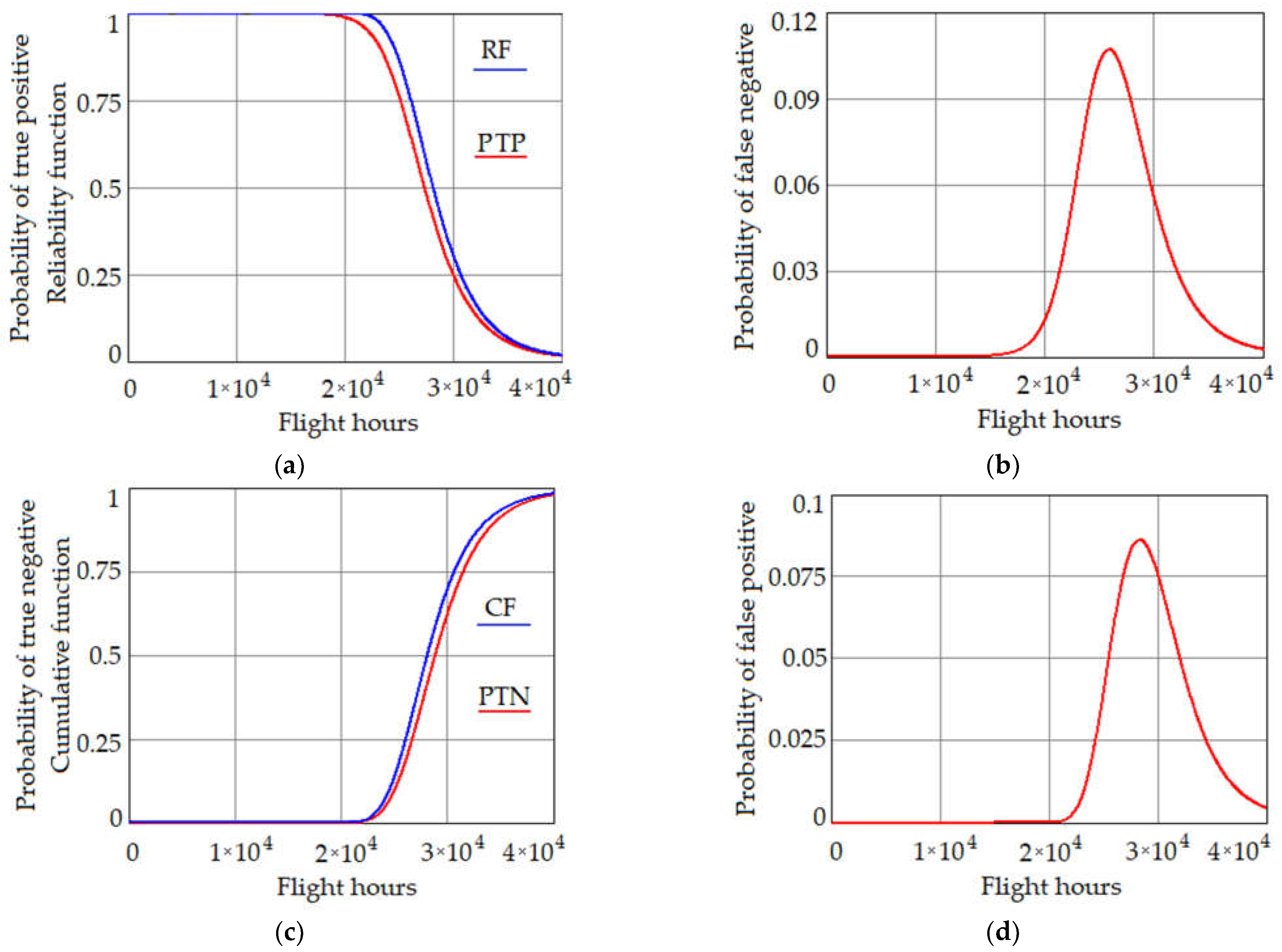
The remainder of the article is organized as follows: Section 2 provides a literature review of the existing analytical and statistical models and algorithms for assessing diagnostic and classification trustworthiness. Section 3 considers mathematical models for quantifying diagnostic uncertainty. Section 4 presents the results and discussion. In Section 5, the conclusions are formulated. Abbreviations and references are given at the article’s end.

2. Literature Review

The first studies on assessing diagnostic trustworthiness were related to the problem of trustworthy checking of DPs. In diagnosing the technical condition of a complex system during the checking of each DP, the following independent and mutually exclusive events are possible: (1) the DP is in the tolerance and evaluated as being in the tolerance; (2) the DP is in the tolerance and evaluated as being outside the tolerance; (3) the DP is outside the tolerance and evaluated as being outside the tolerance; (4) the DP is outside the tolerance and evaluated as being in the tolerance. The listed events are called true positive, false negative, true negative, and false positive, respectively.

Borodachev [5] was the first to publish formulas for calculating the probabilities of a false positive and a false negative when checking a DP. These formulas consider the tolerances for the DP, the probability density function (PDF) of the DP, and the PDF of the measurement error. Mikhailov [6] investigated the problem of determining the optimal operational tolerances based on various criteria in order to improve the trustworthiness of DP checking. The Neumann–Pearson criterion, for example, reduces the probability of a false positive while limiting the probability of a false negative, or reduces the probability of a false negative while limiting the probability of a false positive. Belokon et al. [7] studied the influence of the correlation between DPs on the characteristics of the instrumental trustworthiness of checking the set of DPs. The authors showed that when the correlation coefficient between the DPs is less than 0.5, with sufficient accuracy for practical calculations, we can consider these parameters mutually independent when assessing the trustworthiness of checking. Evlanov [8] proposed equations for estimating the trustworthiness indicators of system diagnosis, which are described by a set of independent DPs. Assuming that the HO and DT are failure-free, he derived formulas for the probabilities of a false positive, a false negative, and a correct diagnosis. Ponomarev et al. [9] and Kudritsky et al. [10] derived equations for the same probabilities assuming that the HO is ideal and the DT can be in one of the three states: operable, inoperable while fixing the operable state of OD, and inoperable while fixing the inoperable state of OD. Goremykin and Ulansky [11] and Ignatov et al. [12] introduced into consideration such a generalized indicator of diagnostic trustworthiness as the probability of a diagnostic error of type (i, j), which is the probability of the joint occurrence of two events: the OD is in the technical state i, and because of the diagnosis, it is judged to be in the technical state j. The authors derived generalized formulas for the probability of a diagnostic error of type (i, j) and the probability of a correct diagnosis for the case when OD and DT can be in one of an arbitrary number of states, provided that the HO is failure-free. The authors also showed that all previously published diagnostic trustworthiness indicators are special cases of generalized formulas. Ulansky et al. [13] proposed a method for evaluating the trustworthiness of health monitoring avionics systems with automated test equipment. The authors derived and estimated trustworthiness indicators such as the probability of false positive, false negative, true positive, and true negative, assuming that the HO and DT are failure-free.

The above references correspond to analytical methods for assessing the diagnosis’s trustworthiness. However, there are several statistical approaches in the literature for estimating the probabilities of a false positive and a false negative that can also be used. Let us consider the most known methods. Ho et al. [14] considered a false positive and false negative assessment procedure that collects appropriate errors from real-world traffic and statistically estimates these cases. Breitgand et al. [15] developed a specific algorithm for assessing the rate of false positives and false negatives. Foss and Zaiane [16] proposed an algorithm for calculating true positive and false positive rates based on a statistical error rate algorithm. Mane et al. [17] developed a capture-recapture-based method to assess false negatives by using two or more independent classifiers. Scott [18] considered performance measures to estimate and compare classifiers, minimizing the probability of a false positive and restricting the probability of a false negative. Ebrahimi [19] considered the issue of deciding thresholds for controlling both false positives and false negatives by employing a particular hazard function. Pounds and Morris [20] proposed to estimate the occurrence of false positives and false negatives in a microarray analysis by the distribution of p-values, which is accurately approximated by the developed model. We should also note the metric F1 score, which is widely used in binary classification and statistical analysis [21,22,23,24,25,26].

3. Quantifying Diagnostic Uncertainty

The purpose of the SoTD is to recognize the technical state of the OD. As already mentioned in the introduction, the most significant characteristic of the quality of a diagnosis is the diagnosis’s trustworthiness.

Let us determine the indicators of diagnostic trustworthiness for the most general case when OD, HO, and DT can each be in one of many states. Let the sets of states of OD, DT, and HO be finite and include, respectively, m, n, and k states. Then the set of all possible outcomes of diagnosing is the space of elementary events Ω. Since a diagnostic error is possible in determining the OD state, the power of the set Ω is equal to m²nk.

Let us introduce the following notation:

$S_i$ is the event that the system is in the state i ($i=\overline{1,m}$),

$R_j$ is the event that the system is recognized in the state j ($j=\overline{1,m}$),

$D_l$ is the event that the DT is in the state l ($l=\overline{1,n}$),

$H_z$ is the event that the HO is in the state z ($z=\overline{1,k}$).

We designate the event $S_i\cap R_j\cap H_z\cap D_l$ $(i\ne j)$ as an elementary diagnostic error, which belongs to the set Ω. It is obvious that

$${\displaystyle \underset{i=1}{\overset{m}{\cup }}{\displaystyle \underset{j=1}{\overset{m}{\cup }}{\displaystyle \underset{z=1}{\overset{k}{\cup }}{\displaystyle \underset{l=1}{\overset{n}{\cup }}\left(S_i{\displaystyle \cap R_j}{\displaystyle \cap H_z}{\displaystyle \cap D_l}\right)}}}}=\Omega$$

(1)

Let Φ be the algebra of events observed during diagnosing, which is the system of all subsets of the set Ω, and {Ω, Φ, P} is the m²nk—dimensional discrete probability space. Then a diagnostic error of type (i, j) is the following event.

$$S_i{\displaystyle \cap R_j}={\displaystyle \underset{z=1}{\overset{k}{\cup }}{\displaystyle \underset{l=1}{\overset{n}{\cup }}\left(S_i{\displaystyle \cap R_j}{\displaystyle \cap H_z}{\displaystyle \cap D_l}\right)}}\in \Phi$$

(2)

Using the general multiplication rule formula, we can present the probability of an elementary diagnostic error as follows.

$$P(S_i{\displaystyle \cap R_j}{\displaystyle \cap H_z}{\displaystyle \cap D_l})=P\left(S_i\right)P\left(H_z\right)P\left(D_l\right)P\left(R_j\left|S_i{\displaystyle \cap H_z}{\displaystyle \cap D_l}\right.\right)$$

(3)

where ${P(S}_i)$, ${P(H}_z)$, and ${P(D}_l)$ are the a priori probabilities of the events $S_i$, $H_z$, and $D_l$, and $P\left(R_j\left|S_i{\displaystyle \cap H_z}{\displaystyle \cap D_l}\right.\right)$ is the conditional probability that the SoTD recognizes the OD as being in technical state j, provided that the OD, HO, and DT are in states i, z, and l, respectively.

Using the general multiplication rule formula, we can write

$$P\left(S_i{\displaystyle \cap R_j}\right)=P\left(S_i\right)P\left(R_j\left|S_i\right.\right)$$

(4)

where ${P(S}_i\bigcap R_j)$ is the probability of the diagnostic error of type (i, j) and $P\left(R_j|S_i\right)$ is the conditional probability of judging the system in state j provided that the system is in state i.

By the total probability rule, we can present the probability $P\left(R_j|S_i\right)$ as follows.

$$P\left(R_j\left|S_i\right.\right)={\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}P\left(R_j\left|S_i{\displaystyle \cap H_z{\displaystyle \cap D_l}}\right.\right)$$

(5)

Substituting (5) to (4) we obtain

$$P\left(S_i{\displaystyle \cap R_j}\right)=P\left(S_i\right){\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}P\left(R_j\left|S_i{\displaystyle \cap H_z{\displaystyle \cap D_l}}\right.\right)$$

(6)

The following event corresponds to the correct determination of the OD technical state.

$${\displaystyle \underset{i=1}{\overset{m}{\cup }}\left(S_i{\displaystyle \cap R_i}\right)}\in \Phi$$

(7)

The probability of the event (7) is the probability of a correct diagnosis (P_CD).

Applying the addition theorem of probability to (8), we obtain

$$P_{CD}={\displaystyle \sum _{i=1}^{m}P\left(S_i{\displaystyle \cap R_i}\right)=1-{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1(j\ne i)}^{m}P\left(S_i{\displaystyle \cap R_j}\right)}}}$$

(8)

The posterior probability of a diagnostic error of type (i, j) we determine by the Bayes formula.

$$P\left(S_i\left|R_j\right.\right)=\frac{P\left(S_i{\displaystyle \cap R_j}\right)}{{\displaystyle \sum _{i=1}^{m}P\left(S_i{\displaystyle \cap R_j}\right)}}$$

(9)

We find the total probability of a diagnostic error as follows.

$$P_{error}=1-P_{CD}={\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1(j\ne i)}^{m}P\left(S_i{\displaystyle \cap R_j}\right)}}$$

(10)

If we characterize the state of the system by a set of N independent DPs and the DT distinguishes m = 2^N states of the system, the probability ${P(S}_i\bigcap S_j)$ is given by

$$P\left(S_i{\displaystyle \cap R_j}\right)={\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}{\displaystyle \prod _{\nu =1}^N{G}_{i,j,\nu ,z,l}}$$

(11)

where

$G_{i,j,\nu ,z,l}=P_{\nu }-F{N}_{\nu ,z,l}$, if in the system states i and j, the ν DP is within the tolerance range, provided that the HO and DT are in the states z and l, respectively,

$G_{i,j,\nu ,z,l}=F{N}_{\nu ,z,l}$, if in the system state i, the ν DP is within the tolerance range and in the system state j, the ν DP is out of the tolerance range, provided that the HO and DT are in the states z and l, respectively,

$G_{i,j,\nu ,z,l}=F{P}_{\nu ,z,l}$, if in the system state i, the ν DP is out of the tolerance range and in the system state j, the ν DP is within the tolerance range, provided that the HO and DT are in the states z and l, respectively,

$G_{i,j,\nu ,z,l}=1-P_{\nu }-F{P}_{\nu ,z,l}$, if in the system states i and j, the ν DP is out of the tolerance range, provided that the HO and DT are in the states z and l, respectively,

$P_{\nu }$ is the prior probability that the ν DP is within the tolerance range,

$F{N}_{\nu ,z,l}$ is the probability of a false negative when checking the ν DP, provided that the HO and DT are in the states z and l, respectively,

$F{P}_{\nu ,z,l}$ is the probability of a false positive when checking the ν DP, provided that the HO and DT are in the states z and l, respectively.

When testing the system’s operability, diagnostic errors of types (1, 2) and (2, 1) are possible. The values of the indices i and j correspond to the following states of the system under test: i = 1 (j = 1)—operable, i = 2 (j = 2)—inoperable.

The probability of a diagnostic error of type (1, 2) is the probability ${\left(P\right(S}_1\bigcap R_2\left)\right)$ of the joint occurrence of two events: the system is in an operable state, and based on the diagnosis, it is considered inoperable.

The probability of a diagnostic error of type (2, 1) is the probability ${\left(P\right(S}_2\bigcap R_1)$ of the joint occurrence of two events: the system is in an inoperable state, and as a result of the diagnosis, it is considered operable.

Using (6), we derive the probabilities ${P(S}_1\bigcap R_2)$ and ${P(S}_2\bigcap R_1)$.

$$P\left(S_1{\displaystyle \cap R_2}\right)=P\left(S_1\right){\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}P\left(R_2\left|S_1{\displaystyle \cap H_z{\displaystyle \cap D_l}}\right.\right)$$

(12)

$$P\left(S_2{\displaystyle \cap R_1}\right)=P\left(S_2\right){\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}P\left(R_1\left|S_2{\displaystyle \cap H_z{\displaystyle \cap D_l}}\right.\right)$$

(13)

where ${P(S}_1)$ is the prior probability that the system is operable, ${P(S}_2)$ is the prior probability that the system is inoperable, $P\left(R_2|S_1\bigcap {H_z\cap D}_l\right)$ is the conditional probability that, as a result of the diagnosis, the system is judged to be inoperable under the conditions that it is operable and the HO and DT are in states z and l, respectively, $P\left(R_1|S_2\bigcap {H_z\cap D}_l\right)$ is the conditional probability that, as a result of the diagnosis, the system is judged to be operable under the conditions that it is inoperable and the HO and DT are in states z and l, respectively.

For i = j = 1, we get the event $S_1\bigcap R_1$ corresponding to the correct diagnosis of the system’s operable state. Analogically, when i = j = 2, the event $S_2\bigcap R_2$ corresponds to the correct diagnosis of the system’s inoperable state.

Applying (6), we obtain the probabilities of events $S_1\bigcap R_1$ and $S_2\bigcap R_2$.

$$P\left(S_1{\displaystyle \cap R_1}\right)=P\left(S_1\right){\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}P\left(R_1\left|S_1{\displaystyle \cap H_z{\displaystyle \cap D_l}}\right.\right)$$

(14)

$$P\left(S_2{\displaystyle \cap R_2}\right)=P\left(S_2\right){\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}P\left(R_2\left|S_2{\displaystyle \cap H_z{\displaystyle \cap D_l}}\right.\right)$$

(15)

where $P\left(R_1|S_1\bigcap H_z\cap D_l\right)$ is the conditional probability that, as a result of the diagnosis, the system is judged as operable under the conditions that it is operable and the HO and DT are in states z and l, respectively, $P\left(R_2|S_2\bigcap {H_z\cap D}_l\right)$ is the conditional probability that, as a result of the diagnosis, the system is judged to be inoperable under the conditions that it is inoperable and the HO and DT are in states z and l, respectively.

If we can characterize the system state by the totality of N independent DPs, the probabilities of diagnostic errors (1, 2) and (2, 1) are calculated as follows.

$$P\left(S_1{\displaystyle \cap R_2}\right)={\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}\left[P\left(S_1\right)-T{P}_{z,l}\right]$$

(16)

$$P\left(S_2{\displaystyle \cap R_1}\right)={\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}\left(P_{P,z,l}-T{P}_{z,l}\right)$$

(17)

where ${TP}_{z,l}$ is the probability of a true-positive when checking the system state, provided that the HO and DT are in states z and l, respectively, and $P_{P,z,l}$ is the probability of recognizing the OD operable when checking its state, provided that the HO and DT are in states z and l, respectively.

Evident formulas determine the probabilities of $P\left(S_1\right)$, ${TP}_{z,l}$, and $P_{P,z,l}$.

$$P\left(S_1\right)={\displaystyle \prod _{\nu =1}^N{P}_{\nu }}$$

(18)

$$T{P}_{z,l}={\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,z,l}\right)}$$

(19)

$$P_{P,z,l}={\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,z,l}+F{P}_{\nu ,z,l}\right)}$$

(20)

Substituting (18)–(20) into (16) and (17), we have

$$P\left(S_1{\displaystyle \cap R_2}\right)={\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}\left[{\displaystyle \prod _{\nu =1}^N{P}_{\nu }-}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,z,l}\right)}\right]$$

(21)

$$P\left(S_2{\displaystyle \cap R_1}\right)={\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}\left[{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,z,l}+F{P}_{\nu ,z,l}\right)-}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,z,l}\right)}\right]$$

(22)

The probabilities of correct diagnoses ${P(S}_1\bigcap R_1$) and $P\left(S_2\bigcap R_2\right)$ we present as follows.

$$P\left(S_1{\displaystyle \cap R_1}\right)={\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}T{P}_{z,l}$$

(23)

$$P\left(S_2{\displaystyle \cap R_2}\right)={\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}\left[P(S_2)-F{P}_{z,l}\right]$$

(24)

The probabilities $P\left(S_2\right)$ and ${FP}_{z,l}$ can be expressed as

$$P\left(S_2\right)=1-P\left(S_1\right)=1-{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}$$

(25)

$$F{P}_{z,l}=P_{P,z,l}-T{P}_{z,l}={\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,z,l}+F{P}_{\nu ,z,l}\right)}-{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,z,l}\right)}$$

(26)

By substituting (19), (25), and (26) into (23) and (24), we get

$$P\left(S_1{\displaystyle \cap R_1}\right)={\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,z,l}\right)}$$

(27)

$$P\left(S_2{\displaystyle \cap R_2}\right)={\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}\left[1-{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}-{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,z,l}+F{P}_{\nu ,z,l}\right)}+{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,z,l}\right)}\right]$$

(28)

The following formula determines the probability of an OD correct diagnosis with a defect search depth up to a DP.

$$P_{CD}={\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right){\displaystyle \prod _{\nu =1}^N\left(1-F{N}_{\nu ,z,l}-F{P}_{\nu ,z,l}\right)}}$$

(29)

The total probability of a diagnostic error is given by

$$P_{error}=1-{\displaystyle \sum _{z=1}^{k}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{n}P\left(D_l\right){\displaystyle \prod _{\nu =1}^N\left(1-F{P}_{\nu ,z,l}-F{N}_{\nu ,z,l}\right)}}$$

(30)

Let us consider the case when checking the system’s operability, the DT can be in one of the following three states [9,10,11]:

l = 1—operability with a correct indication of its state,

l = 2—inoperability of the type “the DT fixes the result “the OD is operable” regardless of the actual condition of the OD” when indicating the operability of the DT,

l = 3—inoperability of the type “the DT fixes the result “the OD is inoperable” regardless of the actual condition of the OD” when indicating the operability of the DT.

The second and third states of the DT can occur due to unrevealed failures. In such failed states, the DT indicates the operable or inoperable state of the system under test independently of its actual condition.

Let the set of HO states also consist of three states: z = 1 is the operability, z = 2 is the inoperability of the type “HO recognizes the OD as operable regardless of the indication of the DT,” and z = 3 is the inoperability of the kind “HO recognizes the OD as inoperable regardless of the indication of the DT.”

In this case, using (12) and (13), we determine the probabilities of diagnostic errors of types (1, 2) and (2, 1) as follows.

$$\begin{array}{c}P\left(S_1{\displaystyle \cap R_2}\right)=P\left(S_1\right){\displaystyle \sum _{z=1}^{3}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{3}P\left(D_l\right)}P\left(R_2\left|S_1{\displaystyle \cap H_z{\displaystyle \cap D_l}}\right.\right)=\\ P\left(S_1\right)\left[P\left(H_1\right)P\left(D_1\right)P\left(R_2\left|S_1{\displaystyle \cap H_1{\displaystyle \cap D_1}}\right.\right)+P\left(H_1\right)P\left(D_3\right)+P\left(H_3\right)\right]\end{array}$$

(31)

$$\begin{array}{c}P\left(S_2{\displaystyle \cap R_1}\right)=P\left(S_2\right){\displaystyle \sum _{z=1}^{3}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{3}P\left(D_l\right)}P\left(R_1\left|S_2{\displaystyle \cap H_z{\displaystyle \cap D_l}}\right.\right)=\\ P\left(S_2\right)\left[P\left(H_1\right)P\left(D_1\right)P\left(R_1\left|S_2{\displaystyle \cap H_1{\displaystyle \cap D_1}}\right.\right)+P\left(H_1\right)P\left(D_2\right)+P\left(H_2\right)\right]\end{array}$$

(32)

Similarly, we derive the probabilities of correct diagnoses based on (14) and (15).

$$\begin{array}{c}P\left(S_1{\displaystyle \cap R_1}\right)=P\left(S_1\right){\displaystyle \sum _{z=1}^{3}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{3}P\left(D_l\right)}P\left(R_1\left|S_1{\displaystyle \cap H_z{\displaystyle \cap D_l}}\right.\right)=\\ P\left(S_1\right)\left[P\left(H_1\right)P\left(D_1\right)P\left(R_1\left|S_1{\displaystyle \cap D_1}\right.\right)+P\left(H_1\right)P\left(D_2\right)+P\left(H_2\right)\right]\end{array}$$

(33)

$$\begin{array}{c}P\left(S_2{\displaystyle \cap R_2}\right)=P\left(S_2\right){\displaystyle \sum _{z=1}^{3}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{3}P\left(D_l\right)}P\left(R_2\left|S_2{\displaystyle \cap H_z{\displaystyle \cap D_l}}\right.\right)=\\ P\left(S_2\right)\left[P\left(H_1\right)P\left(D_1\right)P\left(R_2\left|S_2{\displaystyle \cap D_1}\right.\right)+P\left(H_1\right)P\left(D_3\right)+P\left(H_3\right)\right]\end{array}$$

(34)

If we characterize the system state by a set of N independent DPs and the HO and DT can each be in one of the three states listed, then we can calculate the probabilities of diagnostic errors of types (1, 2) and (2, 1) using (21) and (22).

$$P\left(S_1{\displaystyle \cap R_2}\right)={\displaystyle \sum _{z=1}^{3}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{3}P\left(D_l\right)}\left[{\displaystyle \prod _{\nu =1}^N{P}_{\nu }-}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,z,l}\right)}\right]$$

(35)

$$P\left(S_2{\displaystyle \cap R_1}\right)={\displaystyle \sum _{z=1}^{3}P\left(H_z\right)}{\displaystyle \sum _{l=1}^{3}P\left(D_l\right)}\left[{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{P}_{\nu ,z,l}+F{N}_{\nu ,z,l}\right)-}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{P}_{\nu ,z,l}\right)}\right]$$

(36)

Let us assume that the HO is in the operable state (z = 1). Then, if the DT is in the first state (l = 1), the probabilities $F{P}_{\nu ,1,1}$ and $F{N}_{\nu ,1,1}$ depend on the accuracy and methodology of DP measurement. If the DT is in the second state (l = 2), it is impossible to recognize the OD as inoperable. Similarly, when the DT is in the third state (l = 3), it is impossible to recognize the OD as operable. If the HO is in the second state (z = 2), the SoTD recognizes the OD as operable, regardless of its actual state and the state of the DT. Finally, if the HO is in the third state (z = 3), the SoTD recognizes the OD as inoperable, regardless of the OD and DT states. Therefore, the following relations are proper:

$$\begin{array}{l}{H}_1:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{H}_2:\\ D_1\Rightarrow 0<F{N}_{\nu ,1,1} 1,<0<F{P}_{\nu ,1,1}<1 (\nu =\overline{1,N)}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} D_1\Rightarrow F{N}_{\nu ,2,1}=0, F{P}_{\nu ,2,1}=1-P_{\nu }\\ D_2\Rightarrow F{N}_{\nu ,1,2}=0, F{P}_{\nu ,1,2}=1-P_{\nu }\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} D_2\Rightarrow F{N}_{\nu ,2,2}=0, F{P}_{\nu ,2,2}=1-P_{\nu }\\ D_3\Rightarrow F{N}_{\nu ,1,3}=P_{\nu }, F{P}_{\nu ,1,3}=0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} D_3\Rightarrow F{N}_{\nu ,2,2}=0, F{P}_{\nu ,2,2}=1-P_{\nu }\\ H_3:\\ D_1\Rightarrow F{N}_{\nu ,3,1}=P_{\nu }, F{P}_{\nu ,3,1}=0\\ D_2\Rightarrow F{N}_{\nu ,3,2}=P_{\nu }, F{P}_{\nu ,3,2}=0\\ D_3\Rightarrow F{N}_{\nu ,3,3}=P_{\nu }, F{P}_{\nu ,3,3}=0\end{array}$$

(37)

By substitution (37) into (35) and (36), we obtain

$$P\left(S_1{\displaystyle \cap R_2}\right)=P\left(H_1\right)P\left(D_1\right)\left[{\displaystyle \prod _{\nu =1}^N{P}_{\nu }-}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}\right)}\right]+\left[P\left(H_1\right)P\left(D_3\right)+P\left(H_3\right)\right]{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}$$

(38)

$$\begin{array}{c}P\left(S_2{\displaystyle \cap R_1}\right)=P\left(H_1\right)P\left(D_1\right)\left[{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}+F{P}_{\nu ,1,1}\right)-}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}\right)}\right]+\\ \left[P\left(H_1\right)P\left(D_2\right)+P\left(H_2\right)\right]\left(1-{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}\right)\end{array}$$

(39)

For a general class of DT designed to test system operability, i.e., when considering m = 2 states of OD, we calculate the probability of a correct diagnosis and the total probability of a diagnostic error by the following formulas.

$$P_{CD}=1-P\left(S_1{\displaystyle \cap R_2}\right)-P\left(S_2{\displaystyle \cap R_1}\right)$$

(40)

$$P_{error}=P\left(S_1{\displaystyle \cap R_2}\right)+P\left(S_2{\displaystyle \cap R_1}\right)$$

(41)

Substituting (37) into (27) and (28), we determine the probabilities of correct decisions.

$$P\left(S_1{\displaystyle \cap R_1}\right)=P\left(H_1\right)P\left(D_1\right){\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}\right)+}\left[P\left(H_1\right)P\left(D_2\right)+P\left(H_2\right)\right]{\displaystyle \prod _{\nu =1}^N{P}_{\nu }},$$

(42)

$$\begin{array}{c}P\left(S_2{\displaystyle \cap R_2}\right)=P\left(H_1\right)P\left(D_1\right)\left[1-{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}-{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}+F{P}_{\nu ,1,1}\right)}+{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}\right)}\right]+\\ \left[P\left(H_1\right)P\left(D_3\right)+P\left(H_3\right)\right]\left(1-{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}\right)\end{array}$$

(43)

By substituting (37) into (29) and (30), we determine the probability of a correct diagnosis and the total probability of a diagnostic error when searching for a defect with a depth up to a DP.

$$\begin{array}{c}{P}_{CD}=P\left(H_1\right)P\left(D_1\right){\displaystyle \prod _{\nu =1}^N\left(1-F{N}_{\nu ,1,1}-F{P}_{\nu ,1,1}\right)}+\left[P\left(H_1\right)P\left(D_2\right)+P\left(H_2\right)\right]{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}+\\ \left[P\left(H_1\right)P\left(D_3\right)+P\left(H_3\right)\right]{\displaystyle \prod _{\nu =1}^N\left(1-P_{\nu }\right)}\end{array}$$

(44)

$$\begin{array}{c}{P}_{error}=1-P\left(H_1\right)P\left(D_1\right){\displaystyle \prod _{\nu =1}^N\left(1-F{N}_{\nu ,1,1}-F{P}_{\nu ,1,1}\right)}-\left[P\left(H_1\right)P\left(D_2\right)+P\left(H_2\right)\right]{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}-\\ \left[P\left(H_1\right)P\left(D_3\right)+P\left(H_3\right)\right]{\displaystyle \prod _{\nu =1}^N\left(1-P_{\nu }\right)}\end{array}$$

(45)

Let us consider several special cases of using Formulas (21)–(24) and (27)–(30). In the case of a fully automatic SoTD, we can neglect the impact of the HO on the diagnostic result. So, we can assume that ${P(H}_1)=1$ and ${P(H}_2)={P(H}_3)=0$. In this case, Formulas (21), (22), and (27)–(30) take the following form.

$$P\left(S_1{\displaystyle \cap R_2}\right)={\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}\left[{\displaystyle \prod _{\nu =1}^N{P}_{\nu }-}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,l}\right)}\right]$$

(46)

$$P\left(S_2{\displaystyle \cap R_1}\right)={\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}\left[{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,l}+F{P}_{\nu ,1,l}\right)-}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,l}\right)}\right]$$

(47)

$$P\left(S_1{\displaystyle \cap R_1}\right)={\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,l}\right)}$$

(48)

$$P\left(S_2{\displaystyle \cap R_2}\right)={\displaystyle \sum _{l=1}^{n}P\left(D_l\right)}\left[1-{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}-{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,l}+F{P}_{\nu ,1,l}\right)}+{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,l}\right)}\right]$$

(49)

$$P_{CD}={\displaystyle \sum _{l=1}^{n}P\left(D_l\right){\displaystyle \prod _{\nu =1}^N\left(1-F{N}_{\nu ,1,l}-F{P}_{\nu ,1,l}\right)}}$$

(50)

$$P_{error}=1-{\displaystyle \sum _{l=1}^{n}P\left(D_l\right){\displaystyle \prod _{\nu =1}^N\left(1-F{N}_{\nu ,1,l}-F{P}_{\nu ,1,l}\right)}}$$

(51)

If the DT in the automatic SoTD can be in one of the three states described above, we simplify Equations (46)–(51) as follows.

$$P\left(S_1{\displaystyle \cap R_2}\right)=P\left(D_1\right)\left[{\displaystyle \prod _{\nu =1}^N{P}_{\nu }-}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}\right)}\right]+P\left(D_3\right){\displaystyle \prod _{\nu =1}^N{P}_{\nu }}$$

(52)

$$P\left(S_2{\displaystyle \cap R_1}\right)=P\left(D_1\right)\left[{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}+F{P}_{\nu ,1,1}\right)-}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}\right)}\right]+P\left(D_2\right)\left(1-{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}\right)$$

(53)

$$P\left(S_1{\displaystyle \cap R_1}\right)=P\left(D_1\right){\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}\right)}+P\left(D_2\right){\displaystyle \prod _{\nu =1}^N{P}_{\nu }}$$

(54)

$$P\left(S_2{\displaystyle \cap R_2}\right)=P\left(D_1\right)\left[1-{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}-{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}+F{P}_{\nu ,1,1}\right)+}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}\right)}\right]+P\left(D_3\right)\left(1-{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}\right)$$

(55)

$$P_{CD}=P\left(D_1\right){\displaystyle \prod _{\nu =1}^N\left(1-F{N}_{\nu ,1,1}-F{P}_{\nu ,1,1}\right)}+P\left(D_2\right){\displaystyle \prod _{\nu =1}^N{P}_{\nu }}+P\left(D_3\right){\displaystyle \prod _{\nu =1}^N\left(1-P_{\nu }\right)}$$

(56)

$$P_{error}=1-P\left(D_1\right){\displaystyle \prod _{\nu =1}^N\left(1-F{N}_{\nu ,1,1}-F{P}_{\nu ,1,1}\right)-}P\left(D_2\right){\displaystyle \prod _{\nu =1}^N{P}_{\nu }}-P\left(D_3\right){\displaystyle \prod _{\nu =1}^N\left(1-P_{\nu }\right)}$$

(57)

When we can ignore the probabilities of DT unrevealed failures for automatic SoTD, i.e., ${P(D}_1)=1$ and ${P(D}_2)={P(D}_3)=0$, Equations (52)–(57) take the following form.

$$P\left(S_1{\displaystyle \cap R_2}\right)={\displaystyle \prod _{\nu =1}^N{P}_{\nu }-}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}\right)}$$

(58)

$$P\left(S_2{\displaystyle \cap R_1}\right)={\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}+F{P}_{\nu ,1,1}\right)-}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}\right)}$$

(59)

$$P\left(S_1{\displaystyle \cap R_1}\right)={\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}\right)}$$

(60)

$$P\left(S_2{\displaystyle \cap R_2}\right)=1-{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}-{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}+F{P}_{\nu ,1,1}\right)+}{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}\right)}$$

(61)

$$P_{CD}={\displaystyle \prod _{\nu =1}^N\left(1-F{N}_{\nu ,1,1}-F{P}_{\nu ,1,1}\right)}$$

(62)

$$P_{error}=1-{\displaystyle \prod _{\nu =1}^N\left(1-F{N}_{\nu ,1,1}-F{P}_{\nu ,1,1}\right)}$$

(63)

By the way, the events corresponding to the probabilities (52), (53), (58), and (59) are often called false negatives and false positives when checking the system’s operability [9,10].

For a general class of DTs designed to test system operability, i.e., when considering m = 2 states of OD, we calculate the probability of a correct diagnosis and the total probability of a diagnostic error by the following formulas.

$$P_{CD}=1-P\left(S_1{\displaystyle \cap R_2}\right)-P\left(S_2{\displaystyle \cap R_1}\right)$$

(64)

$$P_{error}=P\left(S_1{\displaystyle \cap R_2}\right)+P\left(S_2{\displaystyle \cap R_1}\right)$$

(65)

We should note that Formulas (46), (47), and (50) were first published in [11,12], and Formulas (52), (53), (56), (58), (59), and (62) in [9,10]. Thus, Formulas (21)–(24), and (27)–(30) are the most general since they consider the characteristics of all SoTD components, i.e., OD, DT, and HO. From these formulas, it is easy to derive all known trustworthiness indicators related to some special cases of constructing SoTD, for example, automatic SoTD.

If the DP is an analog value or signal, then we can calculate the probabilities P_ν, ${FN}_{\nu ,\mathrm{1,1}}$, and ${FP}_{\nu ,\mathrm{1,1}}$ by using the Borodachev formulas [5].

$$P_{\nu }={\displaystyle \underset{a_{\nu }}{\overset{b_{\nu }}{\int }}f\left(x_{\nu }\right)}d{x}_{\nu }$$

(66)

$$F{N}_{\nu ,1,1}={\displaystyle \underset{a_{\nu }}{\overset{b_{\nu }}{\int }}f\left(x_{\nu }\right)}\left[{\displaystyle \underset{-\infty }{\overset{a_{\nu }-x_{\nu }}{\int }}\phi \left(y_{\nu }\right)}d{y}_{\nu }+{\displaystyle \underset{b_{\nu }-x_{\nu }}{\overset{\infty }{\int }}\phi \left(y_{\nu }\right)d{y}_{\nu }}\right]d{x}_{\nu }$$

(67)

$$F{P}_{\nu ,1,1}={\displaystyle \underset{-\infty }{\overset{a_{\nu }}{\int }}f\left(x_{\nu }\right)}{\displaystyle \underset{a_{\nu }-x_{\nu }}{\overset{b_{\nu }-x_{\nu }}{\int }}\phi \left(y_{\nu }\right)}d{y}_{\nu }d{x}_{\nu }+{\displaystyle \underset{b_{\nu }}{\overset{\infty }{\int }}f\left(x_{\nu }\right)}{\displaystyle \underset{a_{\nu }-x_{\nu }}{\overset{b_{\nu }-x_{\nu }}{\int }}\phi \left(y_{\nu }\right)}d{y}_{\nu }d{x}_{\nu }$$

(68)

where f(x_ν) is the probability density function (PDF) of the ν DP, φ(y_ν) is the PDF of the measurement error for the ν DP, and a_ν and b_ν are the lower and upper tolerance limits of the ν DP, respectively.

4. Results and Discussion

4.1. Case Study 1

Let us consider an example of calculating the probabilistic indicators of correct and incorrect system diagnosis in which the OD is an aircraft VHF communication system. The defect searching depth to a DP is used by the DT to identify the state of the OD.

We determine the possible states of the OD by a combination of three DPs, the characteristics of which are in

Table 1. Input data.

Object of Diagnostics	Diagnostic Parameter		Nominal Value	Lower and Upper Tolerance Limits	Standard Deviation
	No.	Name	Nν	aν and bν	Diagnostic Parameter, σν	Measurement Error, σt,ν
VHF communication system	1	Transmitter power, W	20	16	1.79	0.55
	2	Receiver sensitivity, μV	2.5	3	0.23	0.05
	3	Modulation index, %	92.5	85–100	3.48	0.35

. Transmitter power, receiver sensitivity, and modulation index characterize the states of the transmitter, receiver, and modulator, respectively. In the following, we will assume that these DPs are statistically independent.

An analysis of statistical data collected at an aircraft repair enterprise [27] showed that all DPs have a normal distribution with mathematical expectations that coincide with the nominal values and standard deviations σ_ν, where ν is the DP number.

We characterize the DT as being in the state l = 1 by the measurement errors of DPs, which have a normal distribution with zero mathematical expectations and standard deviations σ_t,ν, the values of which are in Table 1.

Statistical processing of data on errors of STD operators at an aircraft repair enterprise showed that, when diagnosing, HO can be in one of three states z = 1, z = 2, and z = 3. The probabilities of the HO states calculated by formulas in [28] are P(H₁) = 0.98, P(H₂) = 0.011, and P(H₃) = 0.009. It is important to highlight that the estimated probabilities match the median probability values of errors made by equipment operators [28,29].

Analysis of failures occurring in the test equipment used for testing VHF communication systems in an aircraft repair enterprise showed that when operating, the DT can be in one of the three states: l = 1, l = 2, or l = 3. The probabilities of the DT states P(D₁) = 0.97, P(D₂) = 0.01, and P(D₃) = 0.02 were calculated by applying the FMECA method [30] to find the failure rates corresponding to the DT states and constructing the Markov chain.

Table 2. A priori probabilities of the system’s states.

Name of Communication System’s State	Technical Condition of the Communication System	A Priori Probability of the System State P(Si)
S1	111	0.942
S2	110	$3.01\times {10}^{-2}$
S3	101	$1.43\times {10}^{-2}$
S4	011	$1.25\times {10}^{-2}$
S5	100	$4.60\times {10}^{-4}$
S6	010	$3.97\times {10}^{-4}$
S7	001	$1.89\times {10}^{-4}$
S8	000	$6.05\times {10}^{-6}$

and

Table 3. Probabilities of correct and incorrect decisions.

Number of the DP No.	A Priori Probability That the ν DP Is within the Tolerance Range ${\mathit{P}}_{\mathit{\nu }}$	A Priori Probability That the OD Is Operable P	Probability of a False Negative for the ν DP ${\mathit{F}\mathit{N}}_{\mathit{\nu },\mathrm{1,1}}$	Probability of a False Positive for the ν DP ${\mathit{F}\mathit{P}}_{\mathit{\nu },\mathrm{1,1}}$
1	0.987	0.942	0.006335	0.002719
2	0.985		0.004430	0.002463
3	0.969		0.003605	0.002749

show the a priori probabilities of the system’s possible states and the probabilities of false negatives and false positives when checking the DPs.

Let us calculate the probabilities $P\left(S_1{\displaystyle \cap R_2}\right)$ and $P\left(S_2{\displaystyle \cap R_1}\right)$ according to Formulas (38) and (39).

$$\begin{array}{c}P\left(S_1{\displaystyle \cap R_2}\right)=P\left(H_1\right)P\left(D_1\right)\left[{\displaystyle \prod _{\nu =1}^3{P}_{\nu }-}{\displaystyle \prod _{\nu =1}^3\left(P_{\nu }-F{N}_{\nu ,1,1}\right)}\right]+\\ \left[P\left(H_1\right)P\left(D_3\right)+P\left(H_3\right)\right]{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}=4.0\times {10}^{-2}\end{array}$$

$$\begin{array}{c}P\left(S_2{\displaystyle \cap R_1}\right)=P\left(H_1\right)P\left(D_1\right)\left[{\displaystyle \prod _{\nu =1}^3\left(P_{\nu }-F{N}_{\nu ,1,1}+F{P}_{\nu ,1,1}\right)-}{\displaystyle \prod _{\nu =1}^3\left(P_{\nu }-F{N}_{\nu ,1,1}\right)}\right]+\\ \left[P\left(H_1\right)P\left(D_2\right)+P\left(H_2\right)\right]\left(1-{\displaystyle \prod _{\nu =1}^3{P}_{\nu }}\right)=8.4\times {10}^{-3}\end{array}$$

During operability testing, we use Formulas (40) and (41) to calculate the probability of a correct diagnosis and the total probability of a diagnostic error.

$$P_{CD}=1-P\left(S_1{\displaystyle \cap R_2}\right)-P\left(S_2{\displaystyle \cap R_1}\right)=1-4.0\times {10}^{-2}-8.4\times {10}^{-3}=0.9516$$

$$P_{error}=P\left(S_1{\displaystyle \cap R_2}\right)+P\left(S_2{\displaystyle \cap R_1}\right)=4.0\times {10}^{-2}+8.4\times {10}^{-3}=4.84\times {10}^{-2}$$

To compare, we use Formula (44) to calculate the probability of an OD correct diagnosis with a defect search depth up to a DP and Formula (45) to calculate the corresponding total probability of a diagnostic error.

$$\begin{array}{c}{P}_{CD}=P\left(H_1\right)P\left(D_1\right){\displaystyle \prod _{\nu =1}^N\left(1-F{N}_{\nu ,1,1}-F{P}_{\nu ,1,1}\right)}+\left[P\left(H_1\right)P\left(D_2\right)+P\left(H_2\right)\right]{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}+\\ \left[P\left(H_1\right)P\left(D_3\right)+P\left(H_3\right)\right]{\displaystyle \prod _{\nu =1}^N\left(1-P_{\nu }\right)}=0.949\end{array}$$

$$P_{error}=1-P_{CD}=1-0.949=5.1\times {10}^{-2}$$

Comparing the values of the total probability of a diagnostic error calculated by Formulas (41) and (45), we note that the value of this probability calculated by (45) is 5% higher than that calculated by (41). This is because in (45), we consider m = 2³ = 8 states of OD, but in (41), only m = 2 states. Therefore, the probabilities of diagnostic errors corresponding to different inoperable states are not present in (41). Accordingly, the value of the probability of a correct diagnosis is higher when calculated by (40) than by (44).

Using (42) and (43), we calculate the probabilities of the correct decisions when checking the OD operability.

$$P\left(S_1{\displaystyle \cap R_1}\right)=P\left(H_1\right)P\left(D_1\right){\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}\right)+}\left[P\left(H_1\right)P\left(D_2\right)+P\left(H_2\right)\right]{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}=0.902$$

$$\begin{array}{c}P\left(S_2{\displaystyle \cap R_2}\right)=P\left(H_1\right)P\left(D_1\right)\left[1-{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}-{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{N}_{\nu ,1,1}+F{P}_{\nu ,1,1}\right)}+{\displaystyle \prod _{\nu =1}^N\left(P_{\nu }-F{P}_{\nu ,1,1}\right)}\right]+\\ \left[P\left(H_1\right)P\left(D_3\right)+P\left(H_3\right)\right]\left(1-{\displaystyle \prod _{\nu =1}^N{P}_{\nu }}\right)=4.96\times {10}^{-2}\end{array}$$

When checking the operability of the OD, we come to the following matrix of diagnostic error probabilities.

$$‖P\left(S_i{\displaystyle \cap R_j}\right)‖=‖\begin{array}{l}P\left(S_1{\displaystyle \cap R_1}\right)\hspace{1em}P\left(S_1{\displaystyle \cap R_2}\right)\\ P\left(S_2{\displaystyle \cap R_1}\right)\hspace{1em}P\left(S_2{\displaystyle \cap R_2}\right)\end{array}‖=‖\begin{array}{l}0.902\hspace{1em}\hspace{1em}\hspace{1em} 4.0\times {10}^{-2}\\ 8.4\times {10}^{-3}\hspace{1em}4.96\times {10}^{-2}\end{array}‖$$

The probability matrix of diagnostic errors with a defect search depth up to DP, i.e., when distinguishing m = 8 states of OD, includes 8² = 64 elements. For illustration, let us determine the matrix’s first column of the diagnostic error probabilities (1, j), where $j=\overline{1,8}$. Using (11), we derive equations for the probabilities of diagnostic errors ${P(S}_1\bigcap R_j)$, $j=\overline{1,8}$ as follows.

$$\begin{array}{ll}(111)\to (111)\Rightarrow & P\left(S_1{\displaystyle \cap R_1}\right)=P\left(H_1\right)P\left(D_1\right){\displaystyle \prod _{\nu =1}^3\left(P_{\nu }-F{P}_{\nu ,1,1}\right)+}\\ & \left[P\left(H_1\right)P\left(D_2\right)+P\left(H_2\right)\right]{\displaystyle \prod _{\nu =1}^3{P}_{\nu }}=0.902\end{array}$$

$$(111)\to (110)\Rightarrow P\left(S_1{\displaystyle \cap R_2}\right)=P\left(H_1\right)P\left(D_1\right){\displaystyle \prod _{\nu =1}^2\left(P_{\nu }-F{P}_{\nu ,1,1}\right)}F{P}_{3,1,1}=3.3\times {10}^{-3}$$

$$(111)\to (101)\Rightarrow P\left(S_1{\displaystyle \cap R_3}\right)=P\left(H_1\right)P\left(D_1\right)\left(P_1-F{P}_{1,1,1}\right)F{P}_{2,1,1}\left(P_3-F{P}_{3,1,1}\right)=3.99\times {10}^{-3}$$

$$(111)\to (011)\Rightarrow P\left(S_1{\displaystyle \cap R_4}\right)=P\left(H_1\right)P\left(D_1\right)F{P}_{1,1,1}{\displaystyle \prod _{\nu =2}^3\left(P_{\nu }-F{P}_{\nu ,1,1}\right)}=5.7\times {10}^{-3}$$

$$(111)\to (100)\Rightarrow P\left(S_1{\displaystyle \cap R_5}\right)=P\left(H_1\right)P\left(D_1\right)\left(P_1-F{P}_{1,1,1}\right){\displaystyle \prod _{\nu =2}^{3}F{P}_{\nu ,1,1}}=1.49\times {10}^{-5}$$

$$(111)\to (010)\Rightarrow P\left(S_1{\displaystyle \cap R_6}\right)=P\left(H_1\right)P\left(D_1\right)F{P}_{1,1,1}\left(P_2-F{P}_{2,1,1}\right)F{P}_{3,1,1}=2.13\times {10}^{-5}$$

$$(111)\to (001)\Rightarrow P\left(S_1{\displaystyle \cap R_7}\right)=P\left(H_1\right)P\left(D_1\right){\displaystyle \prod _{\nu =1}^{2}F{P}_{\nu ,1,1}}\left(P_3-F{P}_{3,1,1}\right)=2.58\times {10}^{-5}$$

$$\begin{array}{ll}(111)\to (000)\Rightarrow & P\left(S_1{\displaystyle \cap R_8}\right)=P\left(H_1\right)P\left(D_1\right){\displaystyle \prod _{\nu =1}^{3}F{P}_{\nu ,1,1}}+\\ & \left[P\left(H_1\right)P\left(D_3\right)+P\left(H_3\right)\right]{\displaystyle \prod _{\nu =1}^3{P}_{\nu }}=2.7\times {10}^{-2}\end{array}$$

Similarly, one can determine the probabilities of diagnostic errors ${P(S}_i\bigcap R_j)$, $i=\overline{2,8}$, $j=\overline{1,8}$.

It is interesting to compare the results of the calculations of the trustworthiness indicators when considering the reliability characteristics of DT and HO and without considering them, i.e., according to Formulas (58)–(63).

$$P\left(S_1{\displaystyle \cap R_2}\right)={\displaystyle \prod _{\nu =1}^3{P}_{\nu }-}{\displaystyle \prod _{\nu =1}^3\left(P_{\nu }-F{P}_{\nu ,1,1}\right)}=1.37\times {10}^{-2}$$

$$P\left(S_2{\displaystyle \cap R_1}\right)={\displaystyle \prod _{\nu =1}^3\left(P_{\nu }-F{P}_{\nu ,1,1}+F{N}_{\nu ,1,1}\right)-}{\displaystyle \prod _{\nu =1}^3\left(P_{\nu }-F{P}_{\nu ,1,1}\right)}=7.57\times {10}^{-3}$$

$$P\left(S_1{\displaystyle \cap R_1}\right)={\displaystyle \prod _{\nu =1}^3\left(P_{\nu }-F{P}_{\nu ,1,1}\right)=}0.9283$$

$$P\left(S_2{\displaystyle \cap R_2}\right)=1-{\displaystyle \prod _{\nu =1}^3{P}_{\nu }}-{\displaystyle \prod _{\nu =1}^3\left(P_{\nu }-F{P}_{\nu ,1,1}+F{N}_{\nu ,1,1}\right)+}{\displaystyle \prod _{\nu =1}^3\left(P_{\nu }-F{P}_{\nu ,1,1}\right)}=5.04\times {10}^{-2}$$

$$P_{CD}={\displaystyle \prod _{\nu =1}^3\left(1-F{P}_{\nu ,1,1}-F{N}_{\nu ,1,1}\right)}=0.9779$$

$$P_{error}=1-{\displaystyle \prod _{\nu =1}^3\left(1-F{P}_{\nu ,1,1}-F{N}_{\nu ,1,1}\right)=2.21\times {10}^{-2}}$$

Table 4. A comparison of the calculated trustworthiness indicators of diagnosis with and without considering the characteristics of the reliability of the human operator and diagnostic tool.

The Values of Reliability Characteristics of HO and DT	The Probabilities of Correct and Incorrect Decisions
	${\mathit{P}(\mathit{S}}_1\cap {\mathit{R}}_2)$	${\mathit{P}(\mathit{S}}_2\cap {\mathit{R}}_1)$	${\mathit{P}(\mathit{S}}_1\cap {\mathit{R}}_1)$	${\mathit{P}(\mathit{S}}_2\cap {\mathit{R}}_2)$	${\mathit{P}}_{\mathit{C}\mathit{D}}$	${\mathit{P}}_{\mathit{e}\mathit{r}\mathit{r}\mathit{o}\mathit{r}}$
P(H1) = 0.98, P(H2) = 0.011, P(H3) = 0.009, P(D1) = 0.97, P(D2) = 0.01, P(D3) = 0.02	$4.0\times {10}^{-2}$	$8.4\times {10}^{-3}$	0.902	$4.96\times {10}^{-2}$	0.949	$5.1\times {10}^{-2}$
P(H1) = 1, P(H2) = P(H3) = 0, P(D1) = 1, P(D2) = P(D3) = 0,	$1.37\times {10}^{-2}$	$7.57\times {10}^{-3}$	0.928	$5.04\times {10}^{-2}$	0.9779	$2.21\times {10}^{-2}$

shows the results of the calculations of the trustworthiness indicators with and without considering the reliability characteristics of HO and DT.

As can be seen in Table 4, considering the real characteristics of the reliability of HO and DT affects the trustworthiness indicators in different ways. The unreliability of HO and DT has the greatest influence on the probabilities ${P(S}_1\cap R_2)$ and $P_{error}$. Indeed, the probability ${P(S}_1\cap R_2)$ increases by 2.9 times, while the probability $P_{error}$ increases by 2.3 times. The probabilities ${P(S}_2\cap R_1)$ and ${P(S}_2\cap R_2)$ are practically independent of the difference in the values of the HO and DT reliability characteristics. The probability $P_{CD}$ is noticeably reduced when considering the reliability of the HO and DT. The probability ${P(S}_1\cap R_1)$ behaves similarly.

Due to operator errors during system diagnosis, the probabilities P(H₂) and P(H₃) are nonzero. We calculated the probabilities of correct and incorrect decisions at P(H₁) = 0.98, P(H₂) = 0.011, and P(H₃) = 0.009. The values of the probabilities P(H₁), P(H₂), and P(H₃) depend on the qualifications of the operators. It is known [28] that the human operator error probability of misreading or failing to note information when observing the system state by display lies in the interval 0.001–0.1. Therefore, it is of interest to investigate the dependence of the trustworthiness indicators on the possible interval of operator error probability. Assume that P(H₂) = P(H₃) = P_oe, where P_oe is the operator error probability. Then, P(H₁) = 1 – 2 P_oe.

Figure 1 demonstrates the dependence of the total probability of a diagnostic error on the operator error probability (see Equation (45)).

As can be seen in Figure 1, the total probability of a diagnostic error increases from 0.035 to 0.134 when the operator error probability changes from 0.001 to 0.1. This result confirms the fact that the trustworthiness of diagnostics significantly depends on the operator’s reliability characteristics.

4.2. Case Study 2

One of the main problems in the aviation sector is aircraft safety. Fatigue cracks in airplane structures are among the root causes of the problem. Localized material separations called cracks occur in the airframe structure during the aircraft’s lifetime. The cracks may develop when airplanes are subjected to various forms of fatigue loading during cyclic loading. The most fundamental kinds of cyclic loadings on an aircraft are takeoffs and landings. The term “crack testing” describes several techniques for identifying and evaluating cracks in aircraft components.

Let us illustrate the calculation of trustworthiness indicators with a case study on ultrasonic testing for fatigue cracks in the airframe components of a fighter [31]. For many materials used in various aircraft types, cracks grow almost exponentially [31,32,33,34], hence measured data, when given on a log crack depth against linear life plot, are well represented by a straight line. A growing crack’s depth dependency on time is a monotonic function. Consequently, the monotonic stochastic process of crack depth growth can be approximated by the following random exponential function:

$$X\left(t\right)=\Lambda e^{\alpha t}$$

(69)

where Λ is the random coefficient of crack depth defined in the interval from 0 to ∞ with known PDF ψ(λ), α is the timing coefficient of crack depth growth (α > 0), and t is the time in terms of flight cycles/hours.

Figure 2 shows a simulated example of crack depth growth curves.

Let us derive formulas to calculate the probabilities of correct and incorrect decisions when testing a single crack. Using the change of variables method [35], we derive the PDF f(x_k) = f[x(t_k)] of random variable X(t_k) as follows:

$$f\left(x_k\right)=e^{-\alpha t_k}\psi \left(x_k{e}^{-\alpha t_k}\right)$$

(70)

where t_k is the time of inspection testing.

Following long mathematical manipulations, we obtain the following analytical formulas for determining the reliability function and probabilities of false negative and false positive when testing a crack depth at time t_k by substituting (70) in (66)–(68):

$$P_{\nu }\left(x_k\right)={\displaystyle \underset{0}{\overset{b_{\nu }{e}^{-\alpha t_k}}{\int }}\psi \left(\lambda \right)}d\lambda$$

(71)

$$F{N}_{\nu ,1,1}\left(x_k\right)={\displaystyle \underset{0}{\overset{b_{\nu }{e}^{-\alpha t_k}}{\int }}\psi \left(\lambda \right)}{\displaystyle \underset{b_{\nu }-\lambda e^{\alpha t_k}}{\overset{\infty }{\int }}\phi \left(y\right)dy}d\lambda$$

(72)

$$F{P}_{\nu ,1,1}\left(x_k\right)={\displaystyle \underset{b_{\nu }{e}^{-\alpha t_k}}{\overset{\infty }{\int }}\psi \left(\lambda \right)}{\displaystyle \underset{-\infty }{\overset{b_{\nu }-\lambda e^{\alpha t_k}}{\int }}\phi \left(y\right)dy}d\lambda$$

(73)

where b_ν is the tolerance limit for the crack depth and φ(y) is the PDF of the measurement error.

Using (71)–(73), we determine the probabilities of true positive and true negative at inspection time t_k as follows:

$$T{P}_{\nu ,1,1}\left(x_k\right)=P_{\nu }\left(x_k\right)-F{N}_{\nu ,1,1}\left(x_k\right)$$

(74)

$$T{N}_{\nu ,1,1}\left(x_k\right)=1-P_{\nu }\left(x_k\right)-F{P}_{\nu ,1,1}\left(x_k\right)=F_{\nu }\left(x_k\right)-F{P}_{\nu ,1,1}\left(x_k\right)$$

(75)

where F_ν(x_k) is the cumulative distribution function of the time to failure (cumulative function) at time t_k.

The study [31] reported that cracks had spread over the wingspan, covering a considerable portion of the span. This indicates that, despite variances in geometrical detail and span-wise position, the crack growth rate was almost similar. For other aircraft, a similar pattern has been noticed [32]. This fact confirms that the coefficient α in (69) can be considered constant. From the data in [31] concerning the lower wing skin of a fighter, it follows that α ≈ 0.0001, m_λ ≈ 0.06 mm, and σ_λ ≈ 0.02 mm, where m_λ and σ_λ are the mathematical expectation and standard deviation of random variable Λ. Onwards, we assume that random variable Λ (0 < Λ < ∞) has a truncated normal distribution.

An increasing trend in the crack growth rate of many typical fatigue cracks in primary aircraft structures is usually observed at the end of life, even if the exponential relationship appears to be a good approximation across most of the life [31]. This fact allows for selecting the tolerance limit for the crack depth (b_ν) as that at which the crack growth rate accelerates. Based on data in [31], we selected b_ν = 1 mm.

As shown in [36], the ultrasonic array post-processing technique can measure the depth of cracks with an accuracy of ±0.1 mm. Therefore, we selected the standard deviation of measurement error σ_e = 0.1 mm. Further, we assume that the measurement error has a normal distribution with zero mathematical expectation.

We should note that alternative ultrasonic diagnostic techniques provide an accuracy of measurement of the crack’s depth that differs from what is reported in [36]. For instance, the study [37] stated that the relative error of crack depth detection using the double-probe ultrasonic detection method is less than 25%. As a result, we consider the case where σ_e = 0.2 mm as well.

Figure 3a–d show the dependences of the probabilities of the true positive and reliability function (a), false negative (b), true negative and cumulative function (c), and false positive (d) versus the time of testing expressed in the number of flight hours when σ_e = 0.1 mm.

The behavior of the curves in Figure 3a–d requires some explanation.

The dependence of the true positive probability is shown in Figure 3a. The probability that the sum of the crack depth and its measurement error is less than the limit b_ν is high when the crack depth is tiny and beyond the tolerance limit. Because of this, the true positive probability is high for small crack depths. However, as the crack depth approaches b_ν, the probability that the measured value of the crack depth is less than the tolerance limit decreases. As a result, the probability of a true positive likewise drops, reaching 1.54% at 40,000 flight hours. The blue color curve in Figure 3a shows the dependence of the reliability function on flying hours. As follows from (71) and (74), the reliability function is greater than the probability of a true positive by the value of FN_ν,1,1.

The dependence of the probability of a false negative in Figure 3b is explained by the behavior of the sum of the crack depth and its measurement error. When the crack depth is small and far from the tolerance limit (b_ν), the probability that the sum of the crack size and measurement error exceeds the tolerance limit is low. That is why, for small crack depths, the probability of a false negative is negligible. However, as the mathematical expectation of the crack depth approaches b_ν, the probability that the sum of the crack depth and measurement error exceeds the tolerance limit increases. Therefore, the probability of a false negative also increases, reaching a maximum of 5.3% at 26,700 flight hours. When the mathematical expectation of the crack depth exceeds the tolerance limit, the probability of false negatives decreases because the unit is most likely in a failed state.

Figure 3c demonstrates that the true negative probability is varied in the opposite way as the true positive probability in Figure 3a. When the crack depth is small and far from the tolerance limit, the probability that the sum of the crack depth and its measurement error exceeds b_ν is low. That is why, for small crack depths, the true negative probability is also low. However, when the crack depth deepens, there is a greater chance that the measured value of the crack depth will exceed the tolerance limit. As a result, at t_k = 40,000 flight hours, the true negative probability rises to 98.2%. The blue color curve in Figure 3c depicts the cumulative function’s dependence on flight hours. As follows from (75), the cumulative function is greater than the probability of a true negative by the value of FP_ν,1,1.

The behavior of the measured crack depth value with respect to the tolerance limit also explains the dependence of the false positive probability in Figure 3d. When the crack depth is small and far from the tolerance limit, the cumulative function is also small, according to Figure 3c. That is why, the probability that the crack depth exceeds b_ν, and that the measured value of the crack depth is less than b_ν, is shallow. Therefore, for a small crack depth, the probability of a false positive is negligible. Beginning from t_k = 22,500 flight hours the cumulative function increases remarkably, which means that an increasing number of realizations of the stochastic process X(t) exceed the tolerance limit. However, for some of these realizations, the measured value of the crack depth is less than b_ν due to measurement errors, which leads to false positives. The probability of a false positive reaches the maximum of 4.7 % at t_k = 27,800 flight hours where the increase in the cumulative function is maximum. When the mathematical expectation of the crack depth moves upside from the tolerance limit, the probability of false positives decreases because it is unlikely that the measured value of the crack depth will be less than the tolerance limit.

Figure 4a–d depict the relationships between the probabilities of the true positive and reliability function (a), false negative (b), true negative and cumulative function (c), and false positive (d), respectively, and the time of testing expressed in the number of flight hours when σ_e = 0.2 mm.

As it follows from Figure 4b, the probability of a false negative has a maximum of 11% occurring at 26,250 flight hours, which is more than two times greater than that at σ_e = 0.1 mm. Therefore, by (74), the probability of a true positive has noticeably decreased, which can be seen in Figure 4a.

According to Figure 4d, a false positive has a maximum probability of 8.6% at 28,500 flight hours, which is nearly twice as high as that for σ_e = 0.1 mm. As a result, by (75), the probability of a true negative has considerably reduced, as seen in Figure 4c.

Figure 5a–d show the dependence of the total probability of a diagnostic error versus the time of the crack depth testing expressed in the number of flight hours when (a) P_oe = 0 and σ_e = 0.1 mm (curve 1) and P_oe = 0.001 and σ_e = 0.1 mm (curve 2), (b) P_oe = 0 and σ_e = 0.1 mm (curve 1) and P_oe = 0.1 and σ_e = 0.1 mm (curve 2), (c) P_oe = 0 and σ_e = 0.2 mm (curve 1) and P_oe = 0.001 and σ_e = 0.2 mm (curve 2), and (d) P_oe = 0 and σ_e = 0.2 mm (curve 1) and P_oe = 0.1 and σ_e = 0.2 mm (curve 2). Thus, the probability of operator error and the root-mean-square value of the crack depth measurement error cover the entire range of values. It is assumed that P(D₁) = 1 and P(D₂) = P(D₃) = 0.

Figure 5a,b show that the probability of a diagnostic error is completely determined by the probability of an operator error in the time interval (0, 20,000) flight hours. The maximum value of the probability of a diagnostic error (P_error = 0.1 at t_k = 27,000 flight hours) is completely determined by the accuracy of ultrasonic diagnostics, as shown in Figure 5a, with a low probability of operator error (P_oe = 0.001). As shown in Figure 5b, the maximum value of the probability of a diagnostic error (P_error = 0.2 at t_k = 27,000 flight hours) is 50% dependent on the operator’s reliability and 50% dependent on the accuracy of ultrasonic diagnostics, with a high probability of operator error (P_oe = 0.1).

Figure 5c shows that when the root mean square error of crack depth measurement is doubled, the interval where the probability of a diagnostic error is completely determined by the probability of an operator error narrows by 30% (0, 13,000 flight hours). Moreover, the maximum value of the probability of a diagnostic error is almost doubled (P_error = 0.18 at t_k = 27,000 flight hours).

In the worst-case scenario, where P_oe = 0.1 and σ_e = 0.2 mm, the probability of a diagnostic error in the time interval (0, 20,000) flight hours is completely determined by the probability of an operator error, as shown in Figure 5d (curve 2). When t_k = 23,000 and t_k = 33,300 flight hours, both operator reliability and measurement accuracy have the same impact on the P_error. Measurement accuracy impacts the total probability of a diagnostic error more than operator reliability between t_k = 23,000 and t_k = 33,300 flight hours. At t_k = 27,000 flight hours, the probability of a diagnostic error of 0.28 is at its highest value. Moreover, out of a total probability of 0.28, operator reliability accounts for 0.1, and 0.18 accounts for measurement accuracy.

Formulas (71)–(75) make it possible to calculate the probabilities of incorrect and correct decisions when diagnosing a single crack. For multiple cracks, Formulas (38)–(65) should be used depending on available data.

5. Conclusions

This article has proposed a generalized mathematical model for assessing diagnostic trustworthiness indicators, assuming that the object of diagnostics, the diagnostic tool, and the human operator can be in a variety of states depending on their reliability and the nature of failures. We have derived the generalized formulas for the probability of a diagnostic error of type (i, j), the probability of a correct diagnosis, and the total probability of a diagnostic error. Because we considered the most general case in which each component of the system of technical diagnostics can be in a variety of states, the proposed generalized formulas allow determining diagnostic trustworthiness indicators for any structure of diagnostic tool and any type of diagnostic tool and human operator failures. As special cases, all existing formulas for determining diagnostic trustworthiness indicators derive from the proposed equations. We have considered in detail the situation where the system’s technical state is characterized by a set of independent diagnostic parameters and derived corresponding equations for the diagnosis trustworthiness indicators for two cases. The first case is the general, where the object of diagnostics, the diagnostic tool, and the human operator can each be in one of a variety of states. The second case considers the situation where the diagnostic tool and human operator can each be in one of the three states. One state corresponds to operability, and two others match inoperability arising from unrevealed failures of the diagnostic tool and human operator. We have demonstrated the theoretical material by calculating the probabilistic indicators of diagnosis trustworthiness for the cases of diagnosing an aircraft VHF communication system and ultrasonic testing of a single fatigue crack depth in a fighter wing. By our calculations, we have shown that considering the real characteristics of the reliability of the human operator affects the trustworthiness indicators. Indeed, when diagnosing the VHF communication system, the probability of a diagnostic error of type (1, 2) increases by 2.9-fold, and the total probability of a diagnostic error rises by 2.3-fold compared to the case where the human operator and diagnostic tool are failure-free. In general, the total probability of a diagnostic error increases from 0.035 to 0.134 when the operator error probability changes from 0.001 to 0.1. We have derived the analytical formulas for calculating the probabilities of correct and incorrect decisions when testing a crack depth in a fighter wing. We demonstrated that the probabilities of false negative and false positive increase from 0 to a maximum of 5.3% and 4.7%, respectively, at 26,700 and 27,800 flight hours, and then decrease. We also demonstrated that over a long period of time, the operator reliability totally determines the total probability of a diagnostic error when testing the crack depth.

Our further work will be devoted to determining the trustworthiness indicators of diagnostic systems with structural redundancy. In such systems, several measurement channels check the same diagnostic parameter. Measuring channels have finite accuracy and non-ideal reliability. Examples of such systems are aircraft control systems, control systems for critical facilities (for example, nuclear power plants), and others.