A Review of Multi-Satellite Imaging Mission Planning Based on Surrogate Model Expensive Multi-Objective Evolutionary Algorithms: The Latest Developments and Future Trends
Abstract
:1. Introduction
- MSIMP is classified in detail from the dimensions of time, space, and task planning and management; in addition, the specific applications of MSIMP in the four phases of pre-processing, task planning, execution, and feedback replanning, considering the related disciplines and various application areas, are introduced in detail. A specific example of forest fire monitoring is used for concrete description. Then, research on MSIMP based on SM-EMOEAs is analyzed in terms of both MSIMP modeling and optimization algorithms.
- The mathematical model of MSIMP is introduced from four aspects: the target mission set, satellite resource set, time window set, and evaluation set. In addition, the currently most commonly used traditional optimization algorithms are classified into two categories—deterministic algorithms and heuristic algorithms—to provide a detailed overview of the traditional optimization algorithms based on MSIMP. We also discuss the strengths and weaknesses of traditional optimization algorithms in solving the MSIMP problem.
- A detailed overview of the classical expensive multi-objective evolutionary algorithms (EMOEAs) and a discussion of the process of EMOEA-based MSIMP are provided. We summarize the main ideas, advantages, and disadvantages of the most commonly used surrogate models from three categories: statistical models, function approximation models, and machine learning models. Then, the surrogate model is selected according to the actual situation in the MSIMP problem, and the EMOEA framework based on the surrogate model is further explored.
- The improved SM-EMOEAs for MSIMP are discussed in terms of surrogate model improvement, adaptive strategy improvement, and the diversity maintenance and quality assessment of the solutions. The improvements provided by four types of surrogate models—namely, the global surrogate model, local surrogate model, bi-layer surrogate model, and aggregation model—are summarized. Then, the improved adaptive strategies, such as the adaptive sampling strategy, multi-group co-evolutionary strategy, and domain knowledge strategy, are further summarized. Finally, the solution diversity maintenance methods and solution quality assessment are discussed.
2. Related Work
2.1. Basic Classification of MSIMP
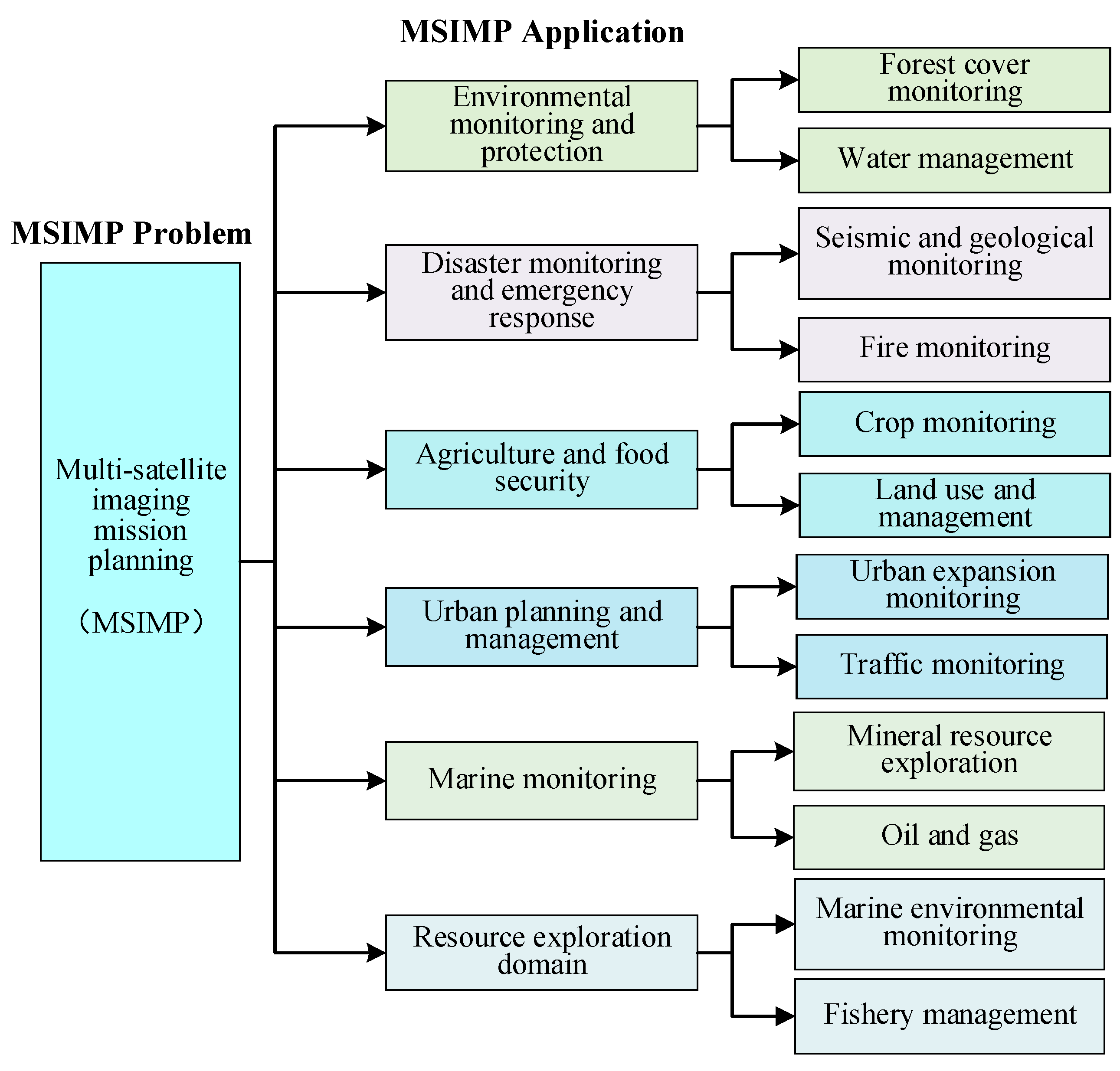
2.2. MSIMP Applications in Different Areas
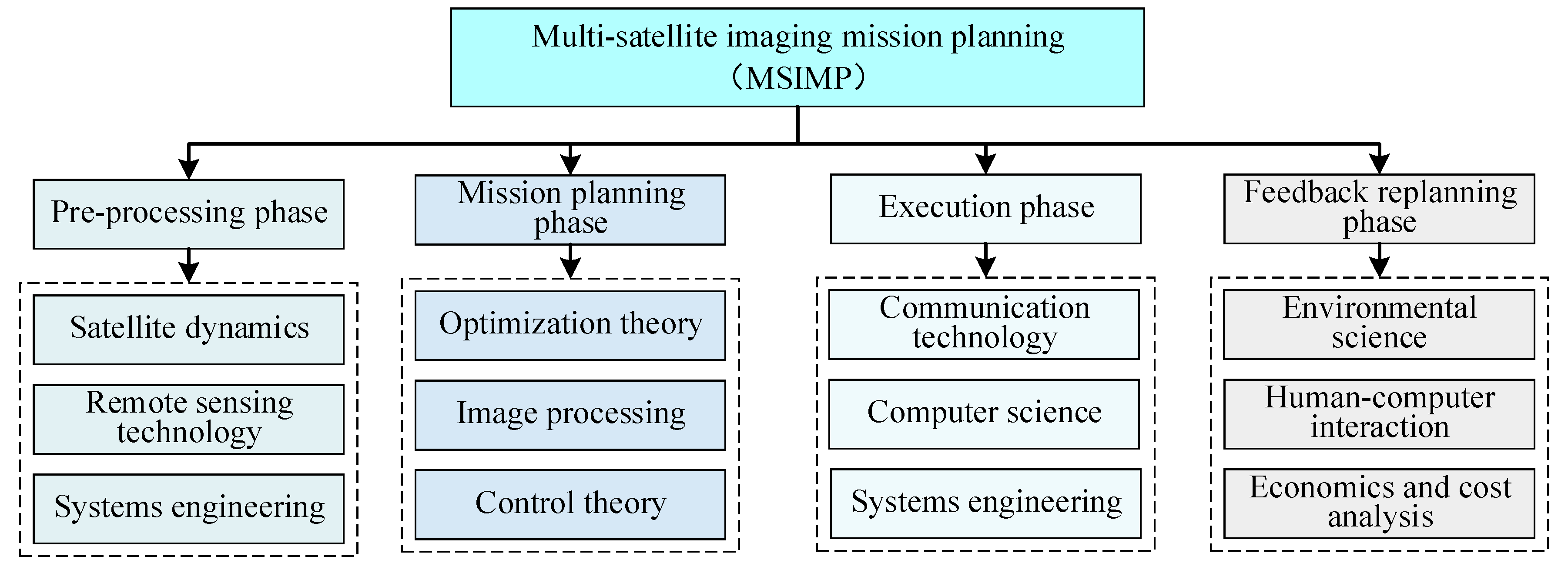
- The pre-processing phase involves satellite dynamics, remote sensing technology, and systems engineering, which are the key areas of knowledge required to provide basic support for the calculation of the initial satellite orbit parameters, the performance of satellite imaging to meet the mission resolution requirements, and the development of the MSIMP system architecture. Knowledge of satellite dynamics ensures the position and attitude control of the satellites during mission execution by accurately calculating their orbital parameters. Remote sensing technology is not only used to ensure that the imaging equipment meets the resolution requirements of a specific mission but also includes the enhancement of geo-positioning accuracy, data acquisition speed, and environmental adaptability to ensure reliable performance under different observation conditions. System engineering comprehensively considers the architectural design and realization of the whole MSIMP process, ensuring the coordinated and efficient operation of the subsystems [21].
- The mission planning phase involves optimization theory, image processing, and control theory. Optimization theory determines the satellite’s imaging mission sequence, which refers to the prioritized order of observation tasks, and the time window, defined as the period during which the satellite can perform a specific imaging task. Various optimization algorithms are used to maximize mission efficiency and resource utilization by optimally scheduling both factors. Image-processing techniques are employed to analyze and process surface observation images captured by satellites during mission execution. These techniques assist in determining the optimal imaging paths and target areas by identifying key regions, analyzing geographic features, and evaluating environmental factors. The goal is to detect spatial distributions, boundaries, and changes in target characteristics, enabling the optimization of satellite flight paths to maximize coverage of the mission area [22].
- The execution phase involves communication technology, computer science, and systems engineering. Communication technology is used to ensure coordinated communication between multiple satellites for the efficient transmission and sharing of data and instructions. Computer science enables the real-time processing, analysis, and storage of imaging data to ensure data availability. Systems engineering is responsible for coordinating the stable operation of the subsystems within the MSIMP system, ensuring the seamless and efficient operation of the different stages of the mission execution process [23].
- The feedback replanning phase involves environmental science, human–computer interaction, and economics and cost analysis. Environmental science techniques are employed to monitor real-time environmental conditions, such as weather changes and light intensity, providing crucial data to the MSIMP. Based on these real-time data, MSIMP dynamically adjusts the satellite observation plan or flight path to mitigate the impact of environmental factors, ensuring that the mission is completed on time and achieves the desired outcomes. Using environmental data, multiple satellites can also adjust parameters such as imaging angle and resolution, optimizing both image quality and overall mission effectiveness. The human–computer interaction system helps the satellite controllers to intuitively and easily make adjustments to the target mission and improve decision making efficiency and accuracy. In addition, economics and cost analysis optimize satellite resource allocation through weighing the costs and benefits of mission replanning to ensure the maximum mission benefits and resource utilization under the premise of controllable costs [24].
2.3. Limitations of MSIMP
2.3.1. Complexity of Mathematical Models
2.3.2. Limitations of Optimization Algorithms
3. Description of MSIMP
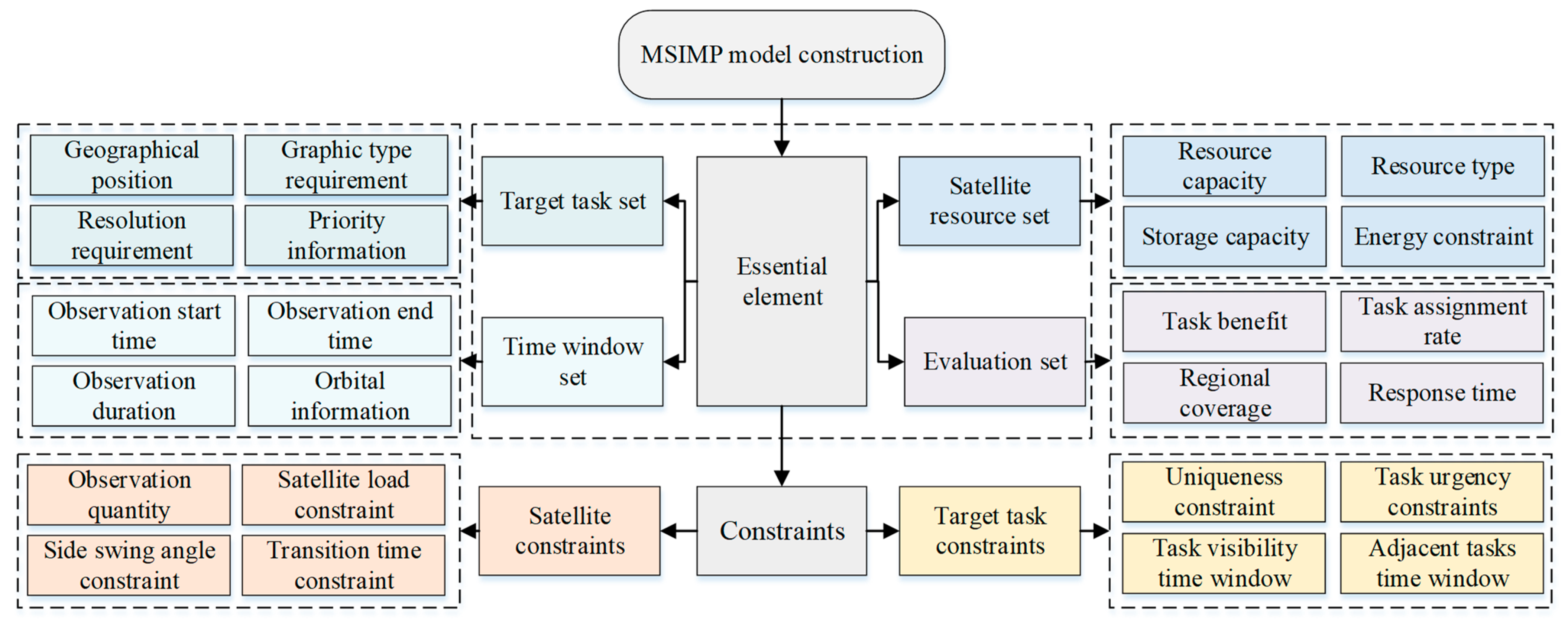
3.1. MSIMP Mathematical Modeling
3.2. MSIMP Based on Traditional Optimization Algorithms
4. MSIMP Based on EMOEAs
4.1. Traditional EMOEAs
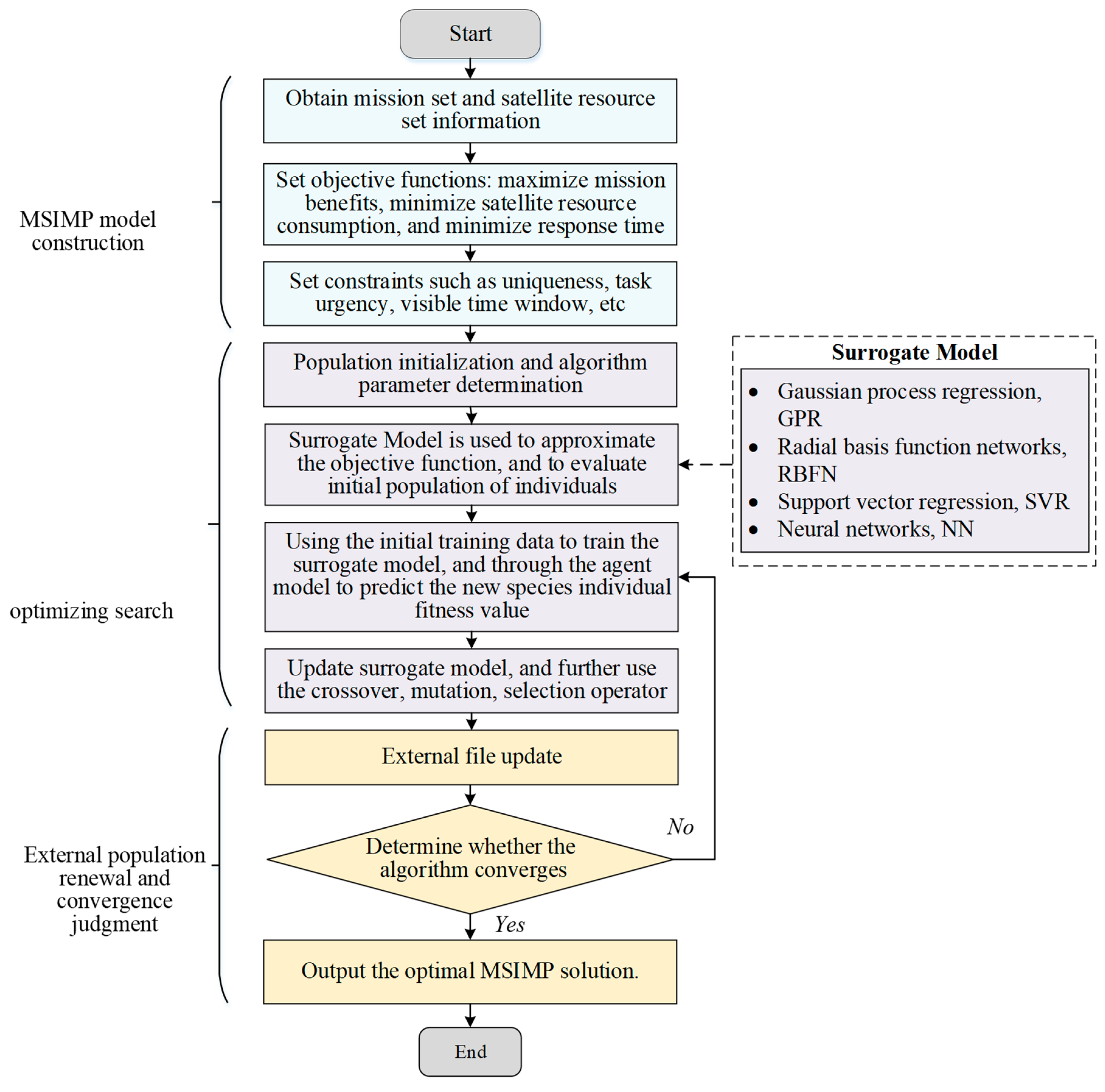
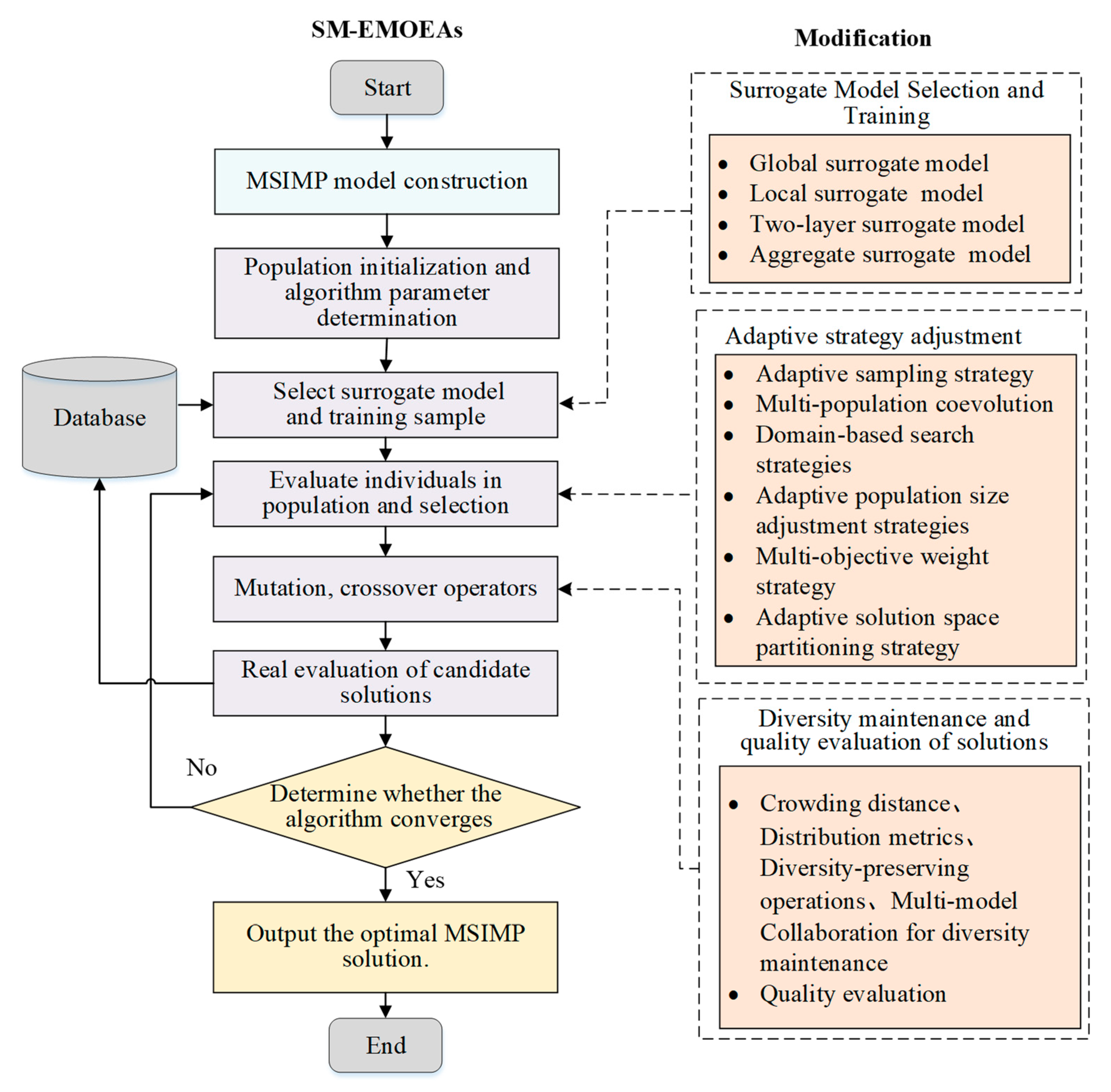
4.2. Flowchart of MSIMP Based on EMOEAs
- In the modeling of the MSIMP problem, information about the mission set and satellite resource set is obtained according to the application scenario. The objective functions, including the maximum mission benefit, minimum satellite resource consumption, and minimum response time, are constructed following the user’s requirements. Moreover, the constraints, such as the mission uniqueness constraint, mission urgency constraint, and visible time window constraint, are set.
- In the optimization search, a set of individuals is randomly generated to form the initial population, and the algorithm’s parameters are configured. The fitness of each individual in the initial population is evaluated based on the objective function. High-quality individuals are selected through processes like crossover, mutation, and selection, which are then used to produce the next generation of the population.
- In the external update and convergence evaluation steps, non-dominated solutions from the new population are stored in an external population, which is updated to preserve population diversity. Once the maximum number of iterations is reached, the final set of non-dominated solutions is produced as the optimal MSIMP scheme for the selected satellite control task [83].
4.3. Surrogate Models
4.4. Surrogate Model for EMOEAs
- They reduce the computational cost and improve the optimization efficiency: The surrogate model replaces the real objective function for evaluation and predicts the objective value of the candidate solution, allowing the evolutionary algorithm to efficiently generate and assess new individuals in each generation. This enables the algorithm to carry out more evaluations and optimizations, substantially reducing the large computational overhead within the limited time and resource constraints, thus accelerating the speed of convergence. The model maintains high computational efficiency when dealing with high-dimensional and complex problems, overcoming the computational bottlenecks of traditional optimization methods when dealing with high-dimensional optimal MSIMP problems.
- They enhance the diversity and quality of the solutions: Through efficient predictions and uncertainty steering provided by surrogate models, the algorithm can effectively balance exploration and exploitation during the evaluation process based on prediction uncertainty. The algorithm tends to prioritize exploring candidate solution areas with higher uncertainty, preventing premature convergence to local optima. For areas with lower uncertainty, the focus shifts to exploitation, further refining the existing solutions. The uncertainty steering encourages the generation of more diverse candidate solutions, thereby promoting population diversity. Additionally, multi-satellite imaging mission planning often involves multiple conflicting objectives, such as imaging coverage, image quality, and task completion time. By incorporating surrogate models with uncertainty guidance, the algorithm achieves balanced optimization across multiple objective functions, thereby improving solution quality.
- They enhance the adaptability of the algorithm: Through continuously updating the surrogate model to cope with dynamic changes in the environment, such as changes in the target area, changes in the mission requirements, and so on, the algorithm can maintain efficient optimization capabilities in the face of dynamic problems. In MSIMP, this adaptability enables the system to cope with changes and uncertainties in the task requirements and ensures the smooth execution of the task.
5. Improved SM-EMOEAs for MSIMP
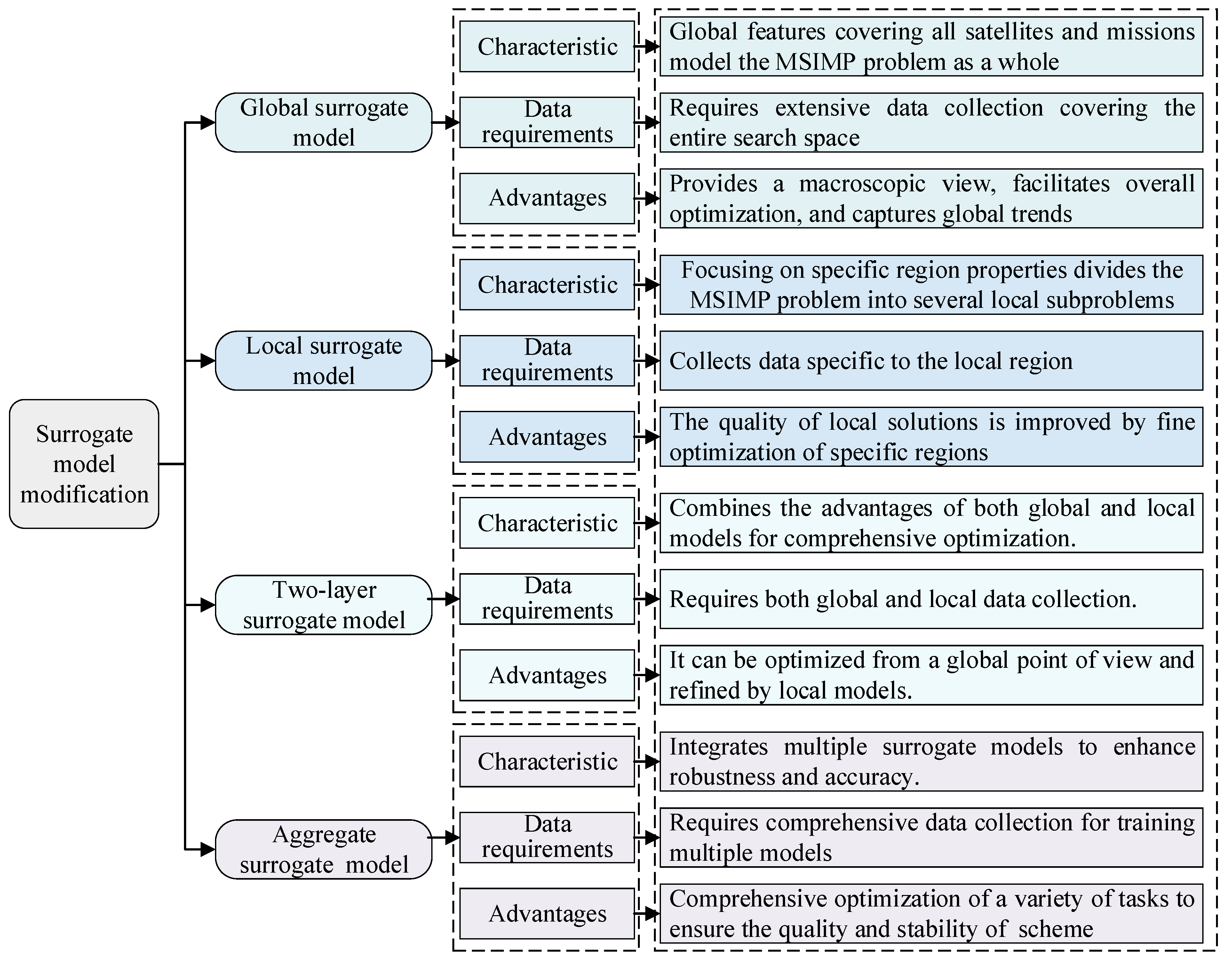
5.1. Surrogate Model Improvement
- The global surrogate model aims to cover the global characteristics of all satellites and missions by modeling the whole MSIMP problem, mainly by using Gaussian process regression, radial basis functions, support vector regression, and so on. Through collecting global data to train the model, the global surrogate model can capture global trends for optimization to find an excellent solution for overall mission planning. It is suitable for mission planning scenarios that require global coverage, such as the monitoring of the global forest cover, through SM-EMOEAs based on global surrogate models. The global multi-satellite coverage area target task is optimized to search and capture the global trends of the forest cover so as to find an excellent overall mission planning solution [110,111,112].
- The local surrogate model focuses on the optimization properties of a specific region, divides the optimal MSIMP problem into several sub-problems, and performs the fine optimization of a specific region by collecting data from this region for training so as to improve the quality of the local solution. Common local surrogate models include local weighted regression, local Gaussian processes, and local radial basis function networks. They are applicable to high-frequency imaging missions in a specific area that requires delicate tuning. For example, after a natural disaster, SM-EMOEAs using local surrogate models are applied to divide the MSIMP into multiple sub-problems for focused local-scale observation. Frequent high-resolution imaging of the affected city is conducted to enhance observation efficiency, monitor the disaster’s impact, and track recovery progress [113,114].
- The two-layer surrogate model first uses the global surrogate model for the initial optimization of the MSIMP problem. It then selects specific regions for local optimization, stores global and local data for the training of the global and local surrogate models, and uses them for different levels of optimization. The two-layer surrogate model mainly includes a two-layer Gaussian process, a hierarchical radial basis function network, and hierarchical support vector regression. It is suitable for complex tasks that require both global and local optimization. For example, in an agricultural monitoring project, multiple satellites are required to monitor crop growth in different agricultural zones. The global surrogate model is used in the initial stage to globally optimize the imaging tasks for the whole agricultural area, and then the local surrogate model is used to assign high-resolution imaging tasks to specific areas. This achieves fast and accurate agricultural monitoring imaging, task assignment, and execution [115,116].
- An aggregate surrogate model involves the integration of artificial neural networks, deep learning, decision tree regression, and other surrogate models. It aims to collect comprehensive data to support multi-model training based on global, local, and uncertainty searches. It aggregates the prediction results of multiple surrogate models through integration techniques to enhance the accuracy and robustness of the overall prediction, thus improving the quality of the overall planning scheme. It is suitable for complex MSIMP scenarios involving many different types of imaging tasks. In practical applications, such as urban planning tasks, the aggregated model can achieve the monitoring and optimization of various aspects, such as urban expansion, traffic flows, green space coverage, and so on, and provide accurate and reliable overall planning solutions [117,118].
5.2. Adaptive Strategy Improvement
- The adaptive sampling strategy improves the accuracy of surrogate model evaluation by dynamically adjusting the density of sampling. In the early stage of the optimized search, coarse sampling is used to cover the search space quickly. Meanwhile, in the middle and late stages of the optimized search, the sampling density is gradually increased to improve the local accuracy of the surrogate model. The adaptive sampling strategy ensures that the sampling density is adaptively adjusted at different stages of the optimal search, thus balancing the needs of the global search and local fine search. Common approaches include the dynamic sampling adjustment strategy [119] and the probabilistic sampling strategy [120].
- The multi-population co-evolution strategy divides the population into multiple sub-populations that are co-evolving; each sub-population independently evolves to explore different solution spaces and exchanges information at the appropriate time, improving the diversity and adaptability of the algorithms through co-evolution and enhancing the overall planning effect. Common approaches include adaptive variable grouping strategies [121] and hierarchical co-evolutionary strategies [122].
- The domain knowledge strategy adaptively selects the knowledge transfer strategy by calculating the difference between the current domain knowledge and the historical knowledge. When the similarity between the two types of knowledge is high, the direct transfer method is used to directly invoke the historical knowledge. The knowledge is adjusted and corrected when the similarity between the two types of knowledge is low, thus helping the algorithm to identify and exploit the properties of the problem during the optimization process and to quickly locate the area covered by the high-quality solution. Common approaches include domain knowledge adaptive strategies [123] and domain knowledge extraction strategies [124].
- The adaptive population size adjustment strategy dynamically adjusts the population size according to the problem convergence speed and complexity to ensure that the algorithm maintains efficient search capabilities at different optimization stages. If the algorithm converges too quickly, it indicates that the algorithm may be trapped in a local optimum and that it is necessary to adaptively increase the population size to increase the diversity of the search space. If the convergence of the algorithm stagnates, the population size needs to be reduced to improve the optimization efficiency. Common methods include the population size adjustment strategy [125] and external file resource allocation strategy [126].
- The multi-objective weighting strategy adjusts the weights of multiple objective functions according to the real-time feedback information obtained during the optimization process. If the prediction error of the surrogate model of the objective function is large, its weight can be temporarily reduced to avoid misleading the optimization. If the prediction error of the surrogate model of the objective function is small, its weight can be increased to effectively advance the optimization process. Commonly used methods include the inverse distance weighting strategy [127] and weighted prediction variance strategy [128].
- The adaptive solution space division strategy dynamically divides the solution space based on the feedback information from the optimal search process, constantly monitors the quality of the candidate solutions and their distribution in the space, and achieves a trade-off between the exploration of new regions and the refinement of the known regions by conducting local and global searches in different solution space regions. Commonly used methods include the spatial hierarchical decomposition strategy [129] and adaptive interval decomposition strategy [130].
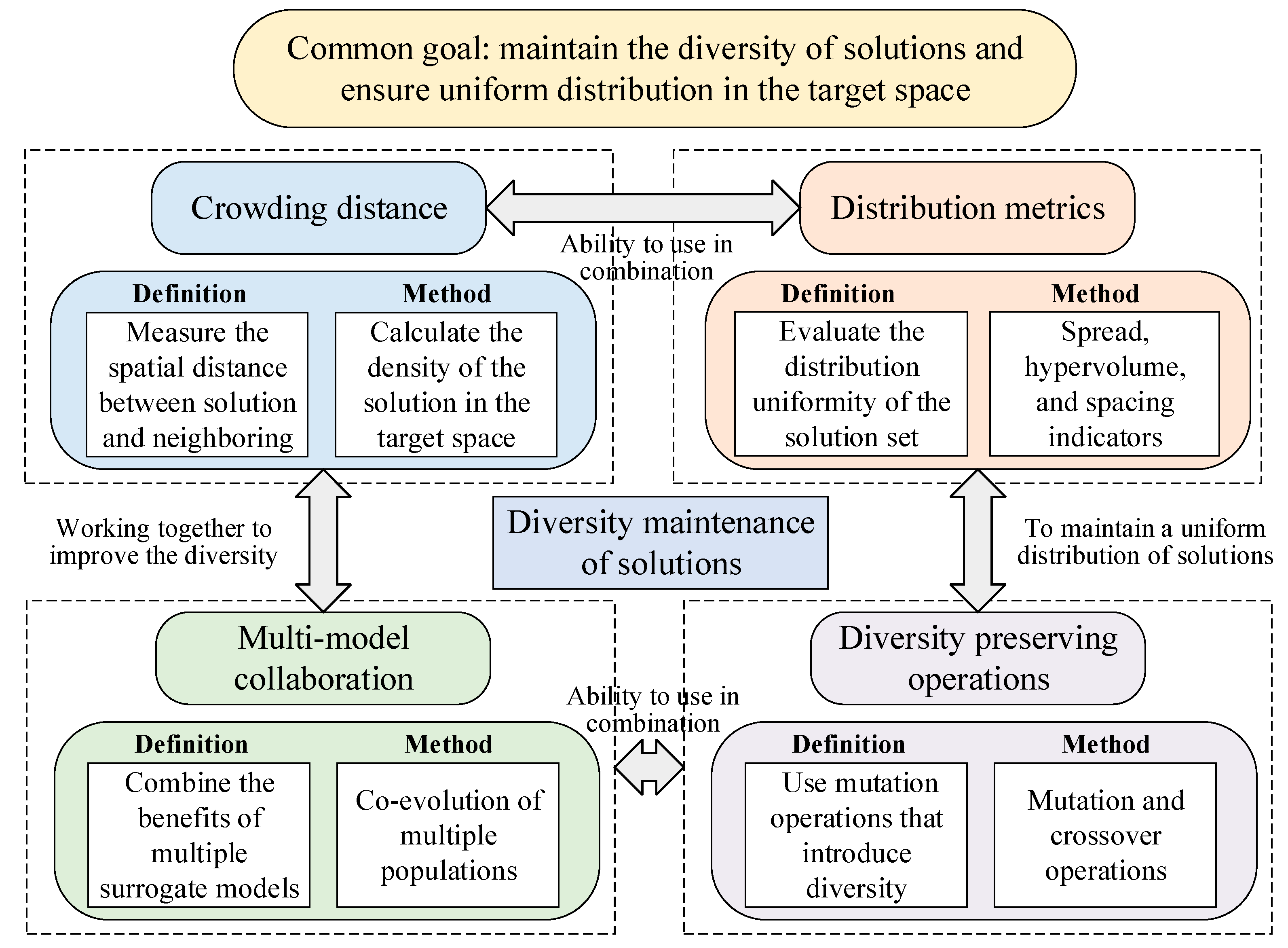
5.3. Diversity Maintenance and Quality Assessment of Solutions
- The crowding distance is used to measure the distance between the current solution and its neighboring solutions in the target space. The candidate solutions are ranked based on their fitness values for the objective functions, followed by calculating the crowding distance for each solution. A larger crowding distance indicates that the solution is located in a sparsely populated region of the objective space, where there are fewer neighboring solutions. Conversely, a smaller crowding distance suggests that the solution is in a densely populated region with more neighboring solutions in the objective space. A larger crowding distance indicates that there are fewer solutions in the current region while a smaller crowding distance indicates that there are more solutions in the current region. Through calculating the crowding distance, the density of each solution in the target space can be effectively evaluated, thus providing a reference for the selection of the next generation of solutions and ensuring the uniform distribution of the solutions in the target space [136,137].
- Distribution metrics are used to assess the uniformity of distribution and the coverage of a solution set in the target space. The specific method is to cluster the solutions using a clustering algorithm, where each cluster centroid represents a subset of the solutions, reflecting the characteristics of each subset in the solution space. The clustering centroids are preferentially selected as part of the next generation of solutions to ensure the uniform distribution of the solutions. Distribution metrics can be used in conjunction with the crowding distance to jointly maintain the solution diversity through different metrics [138,139].
- Diversity-preserving operations aim to introduce and maintain diversity in the population during the optimization search process to prevent the algorithm from falling into a local optimum. The diversity preservation of solutions in the population is achieved by improving the mutation and crossover operations, setting up an external archive to preserve non-dominated solutions, and periodically introducing randomly generated new individuals [140,141].
- Multi-model collaboration combines the advantages of multiple surrogate models through dynamically selecting and updating different surrogate models, guiding the search process to explore the target space more comprehensively by evaluating and exploiting the prediction uncertainty at different stages of the optimization search, and prioritizing the solutions with higher prediction uncertainty for evaluation to maintain the diversity of the solutions [142,143].
6. Discussion
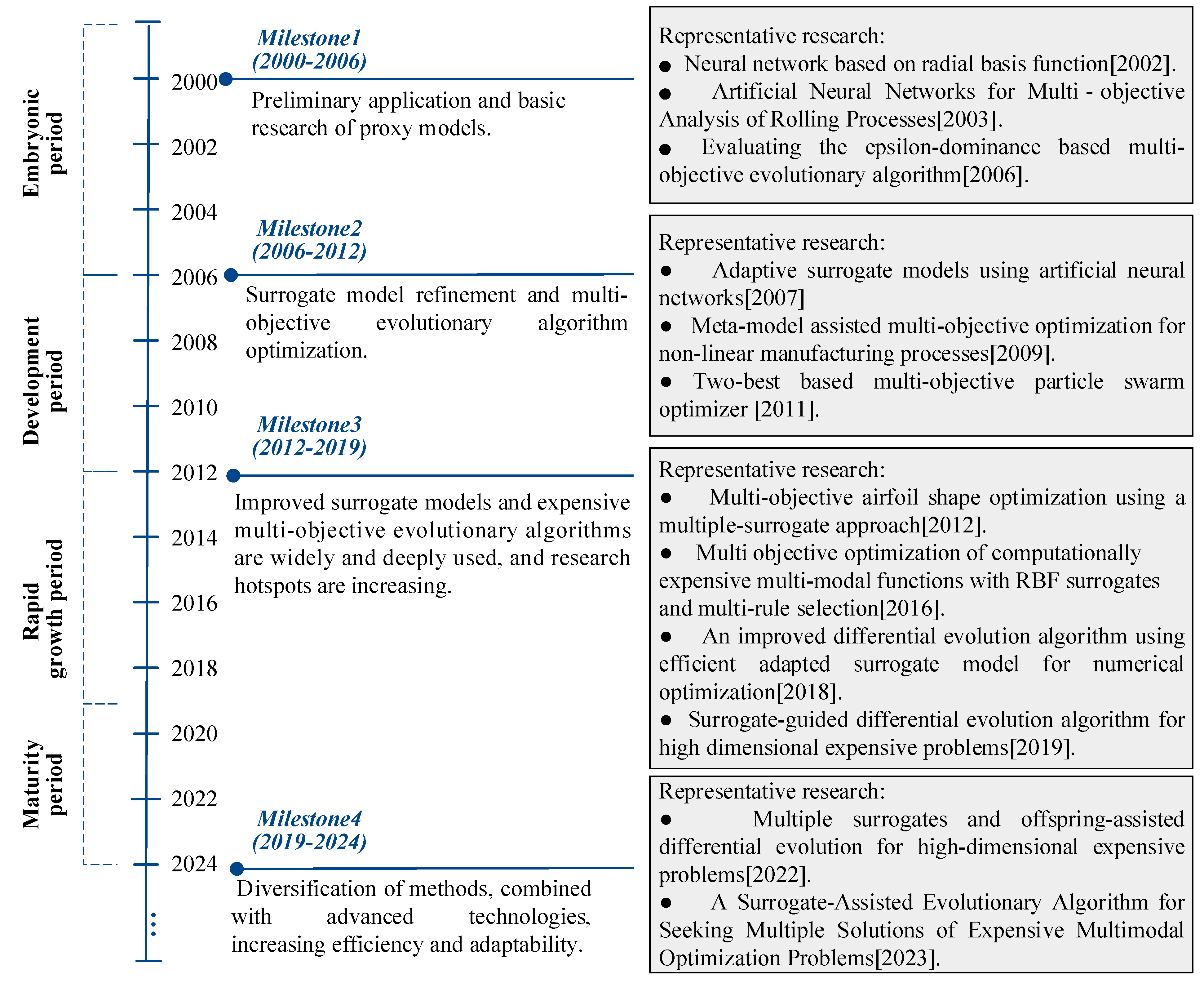
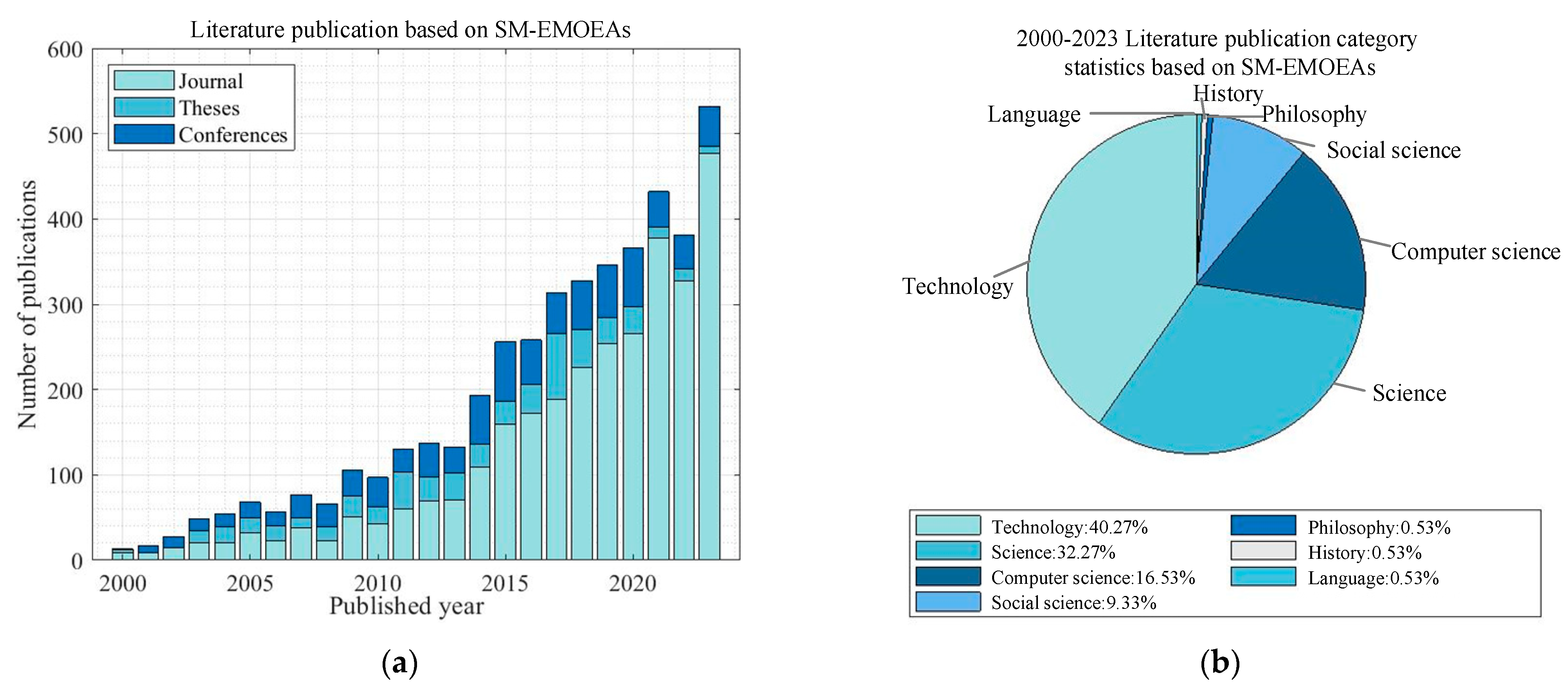
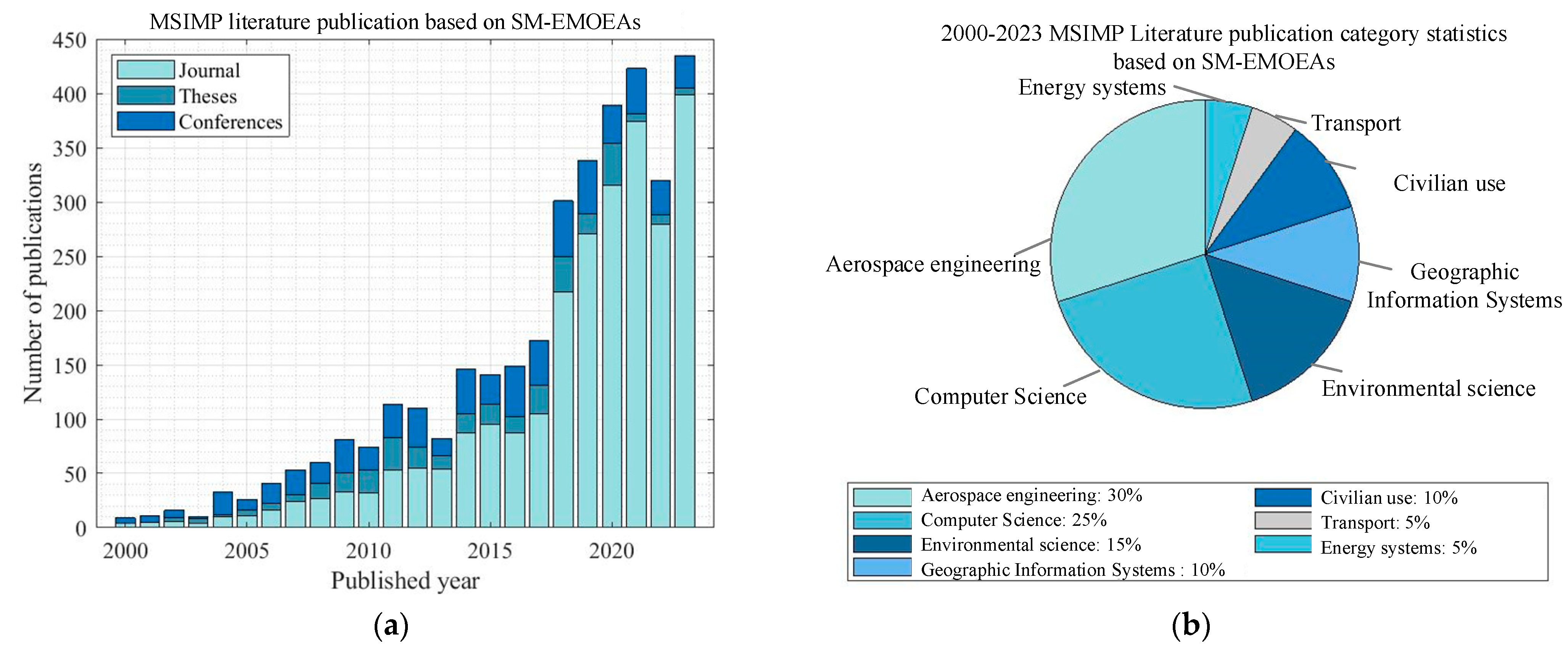
6.1. Publication of Literature on SM-EMOEAs and MSIMP Based on SM-EMOEAs
- Maturity period (2019–2024): combination of advanced technology leads to methodologically diverse SM-EMOEAs, improving their efficiency and adaptability [164].
6.2. Future Research Trends
- Distributed parallel computing combined with MSIMP based on SM-EMOEAs. There has recently been a sharp increase in the demand for observation data for multi-satellite imaging missions, and the training process of surrogate models in SM-EMOEAs involves a large amount of computational data. However, a single node has limited computational capabilities, which makes it difficult to satisfy the huge demand for data processing in a short time. Distributed parallel computing is capable of training surrogate models in a multi-node parallel environment, accelerating agent model training using a distributed deep learning framework and realizing the parallelized evaluation of MSIMP schemes. Thus, it can significantly improve the computational efficiency and processing power of SM-EMOEAs. Therefore, the investigation of efficient and robust distributed parallel computing is of great significance for the future development of MSIMP based on SM-EMOEAs.
- Data-driven and big data analysis combined with MSIMP based on SM-EMOEAs. MSIMP involves mission requirements in a complex environment with multiple objectives, constraints, and dynamic variables, and there is a large number of uncertainties, such as weather variations and satellite orbital drift, in the implementation of the MSIMP scheme. In addition, SM-EMOEAs rely on high-precision surrogate models to evaluate the real objective function, which involves a large amount of observation data. Data-driven and big data analytics enable real-time MSIMP observation and the analysis of historical data, respond to the changing needs of MSIMP in complex environments, and improve the prediction accuracy and generalization of surrogate models. Therefore, the investigation of efficient and intelligent data-driven approaches and big data analysis are crucial for the future development of MSIMP based on SM-EMOEAs.
- Integrating deep and reinforcement learning techniques with MSIMP based on SM-EMOEAs. Optimal MSIMP involves complex decision-making scenarios, such as disaster monitoring and emergency response, crop growth monitoring, urban traffic flows, and so on, and traditional optimization methods have limitations in dealing with high-dimensional complexity. Integrating deep learning with reinforcement learning can improve the optimization accuracy and efficiency through enabling the processing of high-dimensional data through deep neural networks and the capture of complex relationships in mission planning. In addition, an end-to-end learning framework that integrates deep learning with reinforcement learning can extract key features from satellite sensor data to guide MSIMP task allocation. Therefore, the integration of deep learning and reinforcement learning techniques with MSIMP based on SM-EMOEAs can provide powerful technical support and optimization capabilities for MSIMP.
- Augmented reality (AR) and virtual reality (VR)-assisted decision-making combined with MSIMP based on SM-EMOEAs. MSIMP involves high-dimensional data and complex decision-making processes, and traditional decision support systems are limited in terms of interface interaction. AR and VR technologies provide immersive and interactive environments that enable the real-time visualization of the mission progress and satellite status, enabling users to intuitively manipulate and analyze mission planning data in a virtual space. Therefore, investigating the combination of AR- and VR-assisted decision making with MSIMP based on SM-EMOEAs will significantly advance the development of MSIMP visualization.
6.3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MSIMP | Multi-satellite imaging mission planning |
| SM-EMOEAs | Surrogate model expensive multi-objective evolutionary algorithms |
| LP | Linear programming |
| IP | Integer programming |
| MIP | Mixed integer programming |
| DP | Dynamic programming |
| B&B | Branch and bound method |
| CG | Column generation |
| SA | Simulated annealing algorithm |
| GA | Genetic algorithm |
| PSO | Particle swarm optimization |
| ACO | Ant colony algorithm |
| TS | Tabu search |
| DE | Differential evolution algorithm |
| EGO | Efficient global optimization |
| SAEA | Surrogate-assisted evolutionary algorithm |
| KO | Kriging-based optimization |
| ASMO | Adaptive surrogate-model-based optimization |
| ESEA | Ensemble of surrogates-assisted evolutionary algorithm |
| TR-MOEA | Trust-region-based multi-objective evolutionary algorithm |
| EGO | Efficient global optimization |
| ESEA | Ensemble of surrogates-assisted evolutionary algorithm |
| SA-CMA-ES | Surrogate-assisted covariance matrix adaptation evolution strategy |
| GPR | Gaussian process regression |
| RBFNs | Radial basis function networks |
| SVR | Support vector regression |
| NNs | Neural networks |
| RSM | Response surface methodology |
References
- Wang, Z.; Hu, X.; Ma, H.; Xia, W. Learning Multi-Satellite Scheduling Policy with Heterogeneous Graph Neural Network. Adv. Sp. Res. 2024, 73, 2921–2938. [Google Scholar] [CrossRef]
- Zhang, W.; Zheng, G. Scheduling an Agile Multipayload Earth-Observing Satellite. J. Spacecr. Rocket. 2024, 61, 143–156. [Google Scholar] [CrossRef]
- Long, J.; Wu, S.; Han, X.; Wang, Y.; Liu, L. Autonomous Task Planning Method for Multi-Satellite System Based on a Hybrid Genetic Algorithm. Aerospace 2023, 10, 70. [Google Scholar] [CrossRef]
- Liu, R.; Ding, X.; Wu, W.; Guo, W. Distributed Coordination of Space–Ground Multiresources for Remote Sensing Missions. Remote Sens. 2023, 15, 3362. [Google Scholar] [CrossRef]
- He, C.; Dong, Y.; Li, H.; Liew, Y. Reasoning-Based Scheduling Method for Agile Earth Observation Satellite with Multi-Subsystem Coupling. Remote Sens. 2023, 15, 1577. [Google Scholar] [CrossRef]
- Zhibo, E.; Shi, R.; Gan, L.; Baoyin, H.; Li, J. Multi-Satellites Imaging Scheduling Using Individual Reconfiguration Based Integer Coding Genetic Algorithm. Acta Astronaut. 2021, 178, 645–657. [Google Scholar] [CrossRef]
- Han, X.; Yang, M.; Wang, S.; Chao, T. Continuous Monitoring Scheduling for Moving Targets by Earth Observation Satellites. Aerosp. Sci. Technol. 2023, 140, 108422. [Google Scholar] [CrossRef]
- Li, B.; Yang, Y.; Liu, D.; Zhang, Y.; Zhou, A.; Yao, X. Accelerating Surrogate Assisted Evolutionary Algorithms for Expensive Multi-Objective Optimization via Explainable Machine Learning. Swarm Evol. Comput. 2024, 88, 101610. [Google Scholar] [CrossRef]
- Li, B.; Lu, Y.; Qian, H.; Hong, W.; Yang, P.; Zhou, A. Regularity Model Based Offspring Generation in Surrogate-Assisted Evolutionary Algorithms for Expensive Multi-Objective Optimization. Swarm Evol. Comput. 2024, 86, 101506. [Google Scholar] [CrossRef]
- Li, J.; Wang, P.; Dong, H.; Shen, J.; Chen, C. A Classification Surrogate-Assisted Multi-Objective Evolutionary Algorithm for Expensive Optimization. Knowl.-Based Syst. 2022, 242, 108416. [Google Scholar] [CrossRef]
- Tian, Y.; Hu, J.; He, C.; Ma, H.; Zhang, L.; Zhang, X. A Pairwise Comparison Based Surrogate-Assisted Evolutionary Algorithm for Expensive Multi-Objective Optimization. Swarm Evol. Comput. 2023, 80, 101323. [Google Scholar] [CrossRef]
- Cai, X.; Zou, T.; Gao, L. Surrogate-Assisted Operator-Repeated Evolutionary Algorithm for Computationally Expensive Multi-Objective Problems. Appl. Soft Comput. 2023, 147, 110785. [Google Scholar] [CrossRef]
- Wei, L.; Chen, M.; Xing, L.; Wan, Q.; Song, Y.; Chen, Y.; Chen, Y. Knowledge-Transfer Based Genetic Programming Algorithm for Multi-Objective Dynamic Agile Earth Observation Satellite Scheduling Problem. Swarm Evol. Comput. 2024, 85, 101460. [Google Scholar] [CrossRef]
- Gu, Y.; Han, C.; Chen, Y.; Xing, W.W. Mission Replanning for Multiple Agile Earth Observation Satellites Based on Cloud Coverage Forecasting. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 594–608. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, X.; He, R.; Chen, Y. Multi-Satellite Scheduling Framework and Algorithm for Very Large Area Observation. Acta Astronaut. 2020, 167, 93–107. [Google Scholar] [CrossRef]
- Liu, Y.; Wen, Z.; Zhang, S.; Hu, H. Learning-Based Constellation Scheduling for Time-Sensitive Space Multi-Target Collaborative Observation. Adv. Sp. Res. 2024, 73, 4751–4766. [Google Scholar] [CrossRef]
- Qin, J.; Bai, X.; Du, G.; Liu, J.; Peng, N.; Xu, M. Multi-Satellite Scheduling for Moving Targets Using Enhanced Hybrid Genetic Simulated Annealing Algorithm and Observation Strip Selection. IEEE Trans. Aerosp. Electron. Syst. 2024, 73, 1–27. [Google Scholar] [CrossRef]
- Li, G.; Wang, W.; Yue, C.; Zhang, W.; Wang, Y. Two-Stage Adaptive Differential Evolution with Dynamic Dual-Populations for Multimodal Multi-Objective Optimization with Local Pareto Solutions. Inf. Sci. (NY) 2023, 644, 119271. [Google Scholar] [CrossRef]
- Liao, X.; Hu, X.; Liu, Z.; Ma, S.; Xu, L.; Li, X.; Wang, W.; Ghannouchi, F.M. Distributed Intelligence: A Verification for Multi-Agent DRL-Based Multibeam Satellite Resource Allocation. IEEE Commun. Lett. 2020, 24, 2785–2789. [Google Scholar] [CrossRef]
- Xu, S.; Song, B.; Chen, Y.; Chen, J.; Chen, Y.; Wang, F. A Heat Grid-Driven Method for Generation of Satellite Observation Tasks. Adv. Sp. Res. 2024, 24, 2785–2789. [Google Scholar] [CrossRef]
- Wang, T.; Luo, Q.; Zhou, L.; Wu, G. Space Division and Adaptive Selection Strategy Based Differential Evolution Algorithm for Multi-Objective Satellite Range Scheduling Problem. Swarm Evol. Comput. 2023, 83, 101396. [Google Scholar] [CrossRef]
- Cui, K.; Song, J.; Zhang, L.; Tao, Y.; Liu, W.; Shi, D. Event-Triggered Deep Reinforcement Learning for Dynamic Task Scheduling in Multisatellite Resource Allocation. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3766–3777. [Google Scholar] [CrossRef]
- Wei, L.; Chen, Y.; Chen, M.; Chen, Y. Deep Reinforcement Learning and Parameter Transfer Based Approach for the Multi-Objective Agile Earth Observation Satellite Scheduling Problem. Appl. Soft Comput. 2021, 110, 107607. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y.; Wang, R.; Chen, Y. Complex Task Planning Method of Space-Aeronautics Cooperative Observation Based on Multi-Layer Interaction. J. Syst. Eng. Electron. 2023, 34, 1550–1564. [Google Scholar] [CrossRef]
- Song, Y.-J.; Zhang, Z.-S.; Song, B.-Y.; Chen, Y. Improved Genetic Algorithm with Local Search for Satellite Range Scheduling System and Its Application in Environmental Monitoring. Sustain. Comput. Inform. Syst. 2019, 21, 19–27. [Google Scholar] [CrossRef]
- Chen, L.; Tang, F.; Li, X.; Liu, J.; Yang, Y.; Yu, J.; Zhu, Y. Delay-Optimal Cooperation Transmission in Remote Sensing Satellite Networks. IEEE Trans. Mob. Comput. 2022, 22, 5109–5123. [Google Scholar] [CrossRef]
- Tondo, F.A.; Afhamisis, M.; Montejo-Sánchez, S.; López, O.L.A.; Palattella, M.R.; Souza, R.D. Multiple Channel LoRa-to-LEO Scheduling for Direct-to-Satellite IoT. IEEE Access 2024, 12, 30627–30637. [Google Scholar] [CrossRef]
- Lan, Y.-L.; Liu, F.-G.; Huang, Z.; Ng, W.W.Y.; Zhong, J. Two-Echelon Dispatching Problem With Mobile Satellites in City Logistics. IEEE Trans. Intell. Transp. Syst. 2022, 23, 84–96. [Google Scholar] [CrossRef]
- Meng, M.; Hu, B.; Chen, S.; Zhang, J. Cooperative User-Scheduling and Resource Allocation Optimization for Intelligent Reflecting Surface Enhanced LEO Satellite Communication. China Commun. 2024, 21, 227–244. [Google Scholar] [CrossRef]
- Chen, Y.; Shen, X.; Zhang, G.; Lu, Z. Multi-Objective Multi-Satellite Imaging Mission Planning Algorithm for Regional Mapping Based on Deep Reinforcement Learning. Remote Sens. 2023, 15, 3932. [Google Scholar] [CrossRef]
- Feng, X.; Li, Y.; Xu, M. Multi-Satellite Cooperative Scheduling Method for Large-Scale Tasks Based on Hybrid Graph Neural Network and Metaheuristic Algorithm. Adv. Eng. Inform. 2024, 60, 102362. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Bai, X.; Li, S. Real-Time Satellite Constellation Scheduling for Event-Triggered Cooperative Tracking of Space Objects. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 2169–2182. [Google Scholar] [CrossRef]
- Linares, L.; Vazquez, R.; Perea, F.; Galán-Vioque, J. A Mixed Integer Linear Programming Model for Resolution of the Antenna-Satellite Scheduling Problem. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 463–473. [Google Scholar] [CrossRef]
- Kandepi, R.; Saini, H.; George, R.K.; Konduri, S.; Karidhal, R. Agile Earth Observation Satellite Constellations Scheduling for Large Area Target Imaging Using Heuristic Search. Acta Astronaut. 2024, 219, 670–677. [Google Scholar] [CrossRef]
- Yao, F.; Chen, Y.; Wang, L.; Chang, Z.; Huang, P.-Q.; Wang, Y. A Bilevel Evolutionary Algorithm for Large-Scale Multiobjective Task Scheduling in Multiagile Earth Observation Satellite Systems. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 3512–3524. [Google Scholar] [CrossRef]
- He, Y.; Xing, L.; Chen, Y.; Pedrycz, W.; Wang, L.; Wu, G. A Generic Markov Decision Process Model and Reinforcement Learning Method for Scheduling Agile Earth Observation Satellites. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1463–1474. [Google Scholar] [CrossRef]
- Wang, J.; Demeulemeester, E.; Hu, X.; Wu, G. Expectation and SAA Models and Algorithms for Scheduling of Multiple Earth Observation Satellites Under the Impact of Clouds. IEEE Syst. J. 2020, 14, 5451–5462. [Google Scholar] [CrossRef]
- Wu, K.; Zhang, D.; Chen, Z.; Chen, J.; Shao, X. Multi-Type Multi-Objective Imaging Scheduling Method Based on Improved NSGA-III for Satellite Formation System. Adv. Sp. Res. 2019, 63, 2551–2565. [Google Scholar] [CrossRef]
- Du, B.; Li, S. A New Multi-Satellite Autonomous Mission Allocation and Planning Method. Acta Astronaut. 2019, 163, 287–298. [Google Scholar] [CrossRef]
- Fan, H.; Long, J.; Liu, L.; Yang, Z. Dynamic Digital Twin and Online Scheduling for Contact Window Resources in Satellite Network. IEEE Trans. Ind. Inform. 2023, 19, 7217–7227. [Google Scholar] [CrossRef]
- Li, G.; Li, X.; Li, J.; Chen, J.; Shen, X. PTMB: An Online Satellite Task Scheduling Framework Based on Pre-Trained Markov Decision Process for Multi-Task Scenario. Knowl.-Based Syst. 2024, 284, 111339. [Google Scholar] [CrossRef]
- Miao, Y.; Hwang, I.; Liu, M.; Wang, F. Adaptive Fast Nonsingular Terminal Sliding Mode Control for Attitude Tracking of Flexible Spacecraft with Rotating Appendage. Aerosp. Sci. Technol. 2019, 93, 105312. [Google Scholar] [CrossRef]
- Chen, H.; Zhai, B.; Wu, J.; Du, C.; Li, J. A Satellite Observation Data Transmission Scheduling Algorithm Oriented to Data Topics. Int. J. Aerosp. Eng. 2020, 2020, 2180674. [Google Scholar] [CrossRef]
- Qi, J.; Guo, J.; Wang, M.; Wu, C. A Cooperative Autonomous Scheduling Approach for Multiple Earth Observation Satellites With Intensive Missions. IEEE Access 2021, 9, 61646–61661. [Google Scholar] [CrossRef]
- Liang, J.; Zhu, Y.; Luo, Y.; Zhang, J.; Zhu, H. A Precedence-Rule-Based Heuristic for Satellite Onboard Activity Planning. Acta Astronaut. 2021, 178, 757–772. [Google Scholar] [CrossRef]
- Chen, M.; Du, Y.; Tang, K.; Xing, L.; Chen, Y.; Chen, Y. Learning to Construct a Solution for the Agile Satellite Scheduling Problem With Time-Dependent Transition Times. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 5949–5963. [Google Scholar] [CrossRef]
- Wu, J.; Yao, F.; Song, Y.; He, L.; Lu, F.; Du, Y.; Yan, J.; Chen, Y.; Xing, L.; Ou, J. Frequent Pattern-Based Parallel Search Approach for Time-Dependent Agile Earth Observation Satellite Scheduling. Inf. Sci. (NY) 2023, 636, 118924. [Google Scholar] [CrossRef]
- Zhou, C.; Jiang, X.; Yang, H.; Zhong, S.; Ji, Y.; Sun, G.; Li, S. Successive Observation Oriented Scheduling and Task Planning of Heterogeneous Constellation. Adv. Sp. Res. 2024, 74, 2331–2356. [Google Scholar] [CrossRef]
- Wang, X.; Wu, J.; Shi, Z.; Zhao, F.; Jin, Z. Deep Reinforcement Learning-Based Autonomous Mission Planning Method for High and Low Orbit Multiple Agile Earth Observing Satellites. Adv. Sp. Res. 2022, 70, 3478–3493. [Google Scholar] [CrossRef]
- Long, Y.; Shan, C.; Shang, W.; Li, J.; Wang, Y. Deep Reinforcement Learning-Based Approach With Varying-Scale Generalization for the Earth Observation Satellite Scheduling Problem Considering Resource Consumptions and Supplements. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 2572–2585. [Google Scholar] [CrossRef]
- Ren, L.; Ning, X.; Li, J. Hierarchical Reinforcement-Learning for Real-Time Scheduling of Agile Satellites. IEEE Access 2020, 8, 220523–220532. [Google Scholar] [CrossRef]
- Lee, K.; Kim, D.-J.; Chung, D.-W.; Lee, S. Optimal Mission Planning for Multiple Agile Satellites Using Modified Dynamic Programming. J. Aerosp. Inf. Syst. 2024, 21, 279–289. [Google Scholar] [CrossRef]
- He, L.; Liang, B.; Li, J.; Sheng, M. Joint Observation and Transmission Scheduling in Agile Satellite Networks. IEEE Trans. Mob. Comput. 2022, 21, 4381–4396. [Google Scholar] [CrossRef]
- Li, G. Online Scheduling of Distributed Earth Observation Satellite System under Rigid Communication Constraints. Adv. Sp. Res. 2020, 65, 2475–2496. [Google Scholar] [CrossRef]
- Wu, G.; Wang, H.; Pedrycz, W.; Li, H.; Wang, L. Satellite Observation Scheduling with a Novel Adaptive Simulated Annealing Algorithm and a Dynamic Task Clustering Strategy. Comput. Ind. Eng. 2017, 113, 576–588. [Google Scholar] [CrossRef]
- Chu, X.; Chen, Y.; Tan, Y. An Anytime Branch and Bound Algorithm for Agile Earth Observation Satellite Onboard Scheduling. Adv. Sp. Res. 2017, 60, 2077–2090. [Google Scholar] [CrossRef]
- Seman, L.O.; Rigo, C.A.; Camponogara, E.; Bezerra, E.A.; Coelho, L. dos S. Explainable Column-Generation-Based Genetic Algorithm for Knapsack-like Energy Aware Nanosatellite Task Scheduling. Appl. Soft Comput. 2023, 144, 110475. [Google Scholar] [CrossRef]
- Han, C.; Gu, Y.; Wu, G.; Wang, X. Simulated Annealing-Based Heuristic for Multiple Agile Satellites Scheduling Under Cloud Coverage Uncertainty. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 2863–2874. [Google Scholar] [CrossRef]
- Song, Y.; Wei, L.; Yang, Q.; Wu, J.; Xing, L.; Chen, Y. RL-GA: A Reinforcement Learning-Based Genetic Algorithm for Electromagnetic Detection Satellite Scheduling Problem. Swarm Evol. Comput. 2023, 77, 101236. [Google Scholar] [CrossRef]
- Yan, B.; Wang, Y.; Xia, W.; Hu, X.; Ma, H.; Jin, P. An Improved Method for Satellite Emergency Mission Scheduling Scheme Group Decision-Making Incorporating PSO and MULTIMOORA. J. Intell. Fuzzy Syst. 2022, 42, 3837–3853. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, F.; Zhang, N. Ant Colony Algorithm for Satellite Control Resource Scheduling Problem. Appl. Intell. 2018, 48, 3295–3305. [Google Scholar] [CrossRef]
- Peng, B.; Zhang, Y.; Cheng, T.C.E.; Lü, Z.; Punnen, A.P. A Two-Individual Based Path-Relinking Algorithm for the Satellite Broadcast Scheduling Problem. Knowl.-Based Syst. 2020, 196, 105774. [Google Scholar] [CrossRef]
- Luo, Q.; Peng, W.; Wu, G.; Xiao, Y. Orbital Maneuver Optimization of Earth Observation Satellites Using an Adaptive Differential Evolution Algorithm. Remote Sens. 2022, 14, 1966. [Google Scholar] [CrossRef]
- Sun, R.; Duan, Q.; Mao, X. A Multi-Objective Adaptive Surrogate Modelling-Based Optimization Algorithm for Constrained Hybrid Problems. Environ. Model. Softw. 2022, 148, 105272. [Google Scholar] [CrossRef]
- Li, J.; Dong, H.; Wang, P.; Shen, J.; Qin, D. Multi-Objective Constrained Black-Box Optimization Algorithm Based on Feasible Region Localization and Performance-Improvement Exploration. Appl. Soft Comput. 2023, 148, 110874. [Google Scholar] [CrossRef]
- Deb, K.; Mohan, M.; Mishra, S. Evaluating the ε-Domination Based Multi-Objective Evolutionary Algorithm for a Quick Computation of Pareto-Optimal Solutions. Evol. Comput. 2005, 13, 501–525. [Google Scholar] [CrossRef]
- Yu, H.; Yalaoui, F.; Châtelet, Ė.; Chu, C. Optimal Design of a Maintainable Cold-Standby System. Reliab. Eng. Syst. Saf. 2007, 92, 85–91. [Google Scholar] [CrossRef]
- Kleijnen, J.P.C. Kriging Metamodeling in Simulation: A Review. Eur. J. Oper. Res. 2009, 192, 707–716. [Google Scholar] [CrossRef]
- Kuo, Y.-C.; Chou, J.-S. Enhancement of Condominium Management Based on the Effect of Quality Attributes on Satisfaction Improvement. Expert Syst. Appl. 2012, 39, 5418–5425. [Google Scholar] [CrossRef]
- Xu, W.; Liang, W.; Lin, X.; Yu, J.X. Finding Top-k Influential Users in Social Networks under the Structural Diversity Model. Inf. Sci. (NY) 2016, 355–356, 110–126. [Google Scholar] [CrossRef]
- He, W.; Liu, Y. To Regularize or Not: Revisiting SGD with Simple Algorithms and Experimental Studies. Expert Syst. Appl. 2018, 112, 1–14. [Google Scholar] [CrossRef]
- Jiao, R.; Zeng, S.; Li, C.; Jiang, Y.; Jin, Y. A Complete Expected Improvement Criterion for Gaussian Process Assisted Highly Constrained Expensive Optimization. Inf. Sci. (NY) 2019, 471, 80–96. [Google Scholar] [CrossRef]
- Talaei, K.; Rahati, A.; Idoumghar, L. A Novel Harmony Search Algorithm and Its Application to Data Clustering. Appl. Soft Comput. 2020, 92, 106273. [Google Scholar] [CrossRef]
- Li, Z.; Gao, T.; Tian, K.; Wang, B. Elite-Driven Surrogate-Assisted CMA-ES Algorithm by Improved Lower Confidence Bound Method. Eng. Comput. 2023, 39, 2543–2563. [Google Scholar] [CrossRef]
- Yang, Z.; Qiu, H.; Gao, L.; Chen, L.; Liu, J. Surrogate-Assisted MOEA/D for Expensive Constrained Multi-Objective Optimization. Inf. Sci. (NY) 2023, 639, 119016. [Google Scholar] [CrossRef]
- Capitanescu, F.; Ahmadi, A.; Benetto, E.; Marvuglia, A.; Tiruta-Barna, L. Some Efficient Approaches for Multi-Objective Constrained Optimization of Computationally Expensive Black-Box Model Problems. Comput. Chem. Eng. 2015, 82, 228–239. [Google Scholar] [CrossRef]
- Gu, Q.; Wang, Q.; Xiong, N.N.; Jiang, S.; Chen, L. Surrogate-Assisted Evolutionary Algorithm for Expensive Constrained Multi-Objective Discrete Optimization Problems. Complex Intell. Syst. 2022, 8, 2699–2718. [Google Scholar] [CrossRef]
- Shen, J.; Wang, P.; Dong, H.; Wang, W.; Li, J. Surrogate-Assisted Evolutionary Algorithm with Decomposition-Based Local Learning for High-Dimensional Multi-Objective Optimization. Expert Syst. Appl. 2024, 240, 122575. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Y.; He, L.; Xing, L.; Tan, Y. Learning-Driven Many-Objective Evolutionary Algorithms for Satellite-Ground Time Synchronization Task Planning Problem. Swarm Evol. Comput. 2019, 47, 72–79. [Google Scholar] [CrossRef]
- Du, Y.; Xing, L.; Zhang, J.; Chen, Y.; He, Y. MOEA Based Memetic Algorithms for Multi-Objective Satellite Range Scheduling Problem. Swarm Evol. Comput. 2019, 50, 100576. [Google Scholar] [CrossRef]
- Cong, H.; Wang, B.; Wang, Z. A Novel Gaussian Process Surrogate Model with Expected Prediction Error for Optimization under Constraints. Mathematics 2024, 12, 1115. [Google Scholar] [CrossRef]
- Zhang, S.; Pang, Y.; Liu, F.; Wang, M.; Kan, Z.; Song, X. Random Projection Enhancement: A Novel Method for Improving Performance of Surrogate Models. Swarm Evol. Comput. 2024, 89, 101645. [Google Scholar] [CrossRef]
- Funk, S.; Airoud Basmaji, A.; Nackenhorst, U. Globally Supported Surrogate Model Based on Support Vector Regression for Nonlinear Structural Engineering Applications. Arch. Appl. Mech. 2023, 93, 825–839. [Google Scholar] [CrossRef]
- Tsay, C. Sobolev Trained Neural Network Surrogate Models for Optimization. Comput. Chem. Eng. 2021, 153, 107419. [Google Scholar] [CrossRef]
- Zheng, N.; Wang, H.; Liu, J. Formulating Approximation Error as Noise in Surrogate-Assisted Multi-Objective Evolutionary Algorithm. Swarm Evol. Comput. 2024, 90, 101666. [Google Scholar] [CrossRef]
- Zheng, N.; Wang, H. A Noise-Resistant Infill Sampling Criterion in Surrogate-Assisted Multi-Objective Evolutionary Algorithms. Swarm Evol. Comput. 2024, 86, 101492. [Google Scholar] [CrossRef]
- Li, F.; Yang, Y.; Shang, Z.; Li, S.; Ouyang, H. Kriging-Assisted Indicator-Based Evolutionary Algorithm for Expensive Multi-Objective Optimization. Appl. Soft Comput. 2023, 147, 110736. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, H. A Data Augmentation Based Kriging-Assisted Reference Vector Guided Evolutionary Algorithm for Expensive Dynamic Multi-Objective Optimization. Swarm Evol. Comput. 2022, 75, 101173. [Google Scholar] [CrossRef]
- Geng, H.; Song, F.; Shen, J.; Li, J. A Classification and Regression Assisted Optimization Algorithm for High-Dimensional Expensive Many-Objective Problems. Neurocomputing 2024, 586, 127629. [Google Scholar] [CrossRef]
- Chen, J.; Luo, F.; Li, G.; Wang, Z. Batch Bayesian Optimization with Adaptive Batch Acquisition Functions via Multi-Objective Optimization. Swarm Evol. Comput. 2023, 79, 101293. [Google Scholar] [CrossRef]
- Li, A.-D.; He, Z.; Zhang, Y. Robust Multi-Response Optimization Considering Location Effect, Dispersion Effect, and Model Uncertainty Using Hybridization of NSGA-II and Direct Multi-Search. Comput. Ind. Eng. 2022, 169, 108247. [Google Scholar] [CrossRef]
- Wu, M.; Wang, L.; Xu, J.; Hu, P.; Xu, P. Adaptive Surrogate-Assisted Multi-Objective Evolutionary Algorithm Using an Efficient Infill Technique. Swarm Evol. Comput. 2022, 75, 101170. [Google Scholar] [CrossRef]
- Yu, Q.; Lin, Q.; Zhu, Z.; Wong, K.-C.; Coello, C.A.C. A Dynamic Multi-Objective Evolutionary Algorithm Based on Polynomial Regression and Adaptive Clustering. Swarm Evol. Comput. 2022, 71, 101075. [Google Scholar] [CrossRef]
- Iruela, J.R.S.; Ruiz, L.G.B.; Criado-Ramón, D.; Pegalajar, M.C.; Capel, M.I. A GPU-Accelerated Adaptation of the PSO Algorithm for Multi-Objective Optimization Applied to Artificial Neural Networks to Predict Energy Consumption. Appl. Soft Comput. 2024, 160, 111711. [Google Scholar] [CrossRef]
- Shao, S.; Tian, Y.; Zhang, X. Deep Reinforcement Learning Assisted Automated Guiding Vector Selection for Large-Scale Sparse Multi-Objective Optimization. Swarm Evol. Comput. 2024, 88, 101606. [Google Scholar] [CrossRef]
- Gao, K.; Xu, L. Novel Strategies Based on a Gradient Boosting Regression Tree Predictor for Dynamic Multi-Objective Optimization. Expert Syst. Appl. 2024, 237, 121532. [Google Scholar] [CrossRef]
- Chugh, T.; Jin, Y.; Miettinen, K.; Hakanen, J.; Sindhya, K. A Surrogate-Assisted Reference Vector Guided Evolutionary Algorithm for Computationally Expensive Many-Objective Optimization. IEEE Trans. Evol. Comput. 2018, 22, 129–142. [Google Scholar] [CrossRef]
- Wang, X.; Jin, Y.; Schmitt, S.; Olhofer, M.; Allmendinger, R. Transfer Learning Based Surrogate Assisted Evolutionary Bi-Objective Optimization for Objectives with Different Evaluation Times. Knowl.-Based Syst. 2021, 227, 107190. [Google Scholar] [CrossRef]
- Zhang, T.; Li, F.; Zhao, X.; Qi, W.; Liu, T. A Convolutional Neural Network-Based Surrogate Model for Multi-Objective Optimization Evolutionary Algorithm Based on Decomposition. Swarm Evol. Comput. 2022, 72, 101081. [Google Scholar] [CrossRef]
- Hernández-Lobato, J.M.; Gelbart, M.A.; Adams, R.P.; Hoffman, M.W.; Ghahramani, Z. A General Framework for Constrained Bayesian Optimization Using Information-Based Search. Swarm Evol. Comput. 2015, 72, 101081. [Google Scholar] [CrossRef]
- de Winter, R.; Milatz, B.; Blank, J.; van Stein, N.; Bäck, T.; Deb, K. Parallel Multi-Objective Optimization for Expensive and Inexpensive Objectives and Constraints. Swarm Evol. Comput. 2024, 86, 101508. [Google Scholar] [CrossRef]
- Li, F.; Yang, Y.; Liu, Y.; Liu, Y.; Qian, M. Bi-Level Model Management Strategy for Solving Expensive Multi-Objective Optimization Problems. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 86, 1–15. [Google Scholar] [CrossRef]
- Tetik, T.; Sena Daş, G.; Birgoren, B. A Multi-Objective Perspective to Satellite Design and Reliability Optimization. Expert Syst. Appl. 2024, 246, 123178. [Google Scholar] [CrossRef]
- Wu, H.; Chen, Q.; Jin, Y.; Ding, J.; Chai, T. A Surrogate-Assisted Expensive Constrained Multi-Objective Optimization Algorithm Based on Adaptive Switching of Acquisition Functions. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 2050–2064. [Google Scholar] [CrossRef]
- Gu, Q.; Wang, Q.; Li, X.; Li, X. A Surrogate-Assisted Multi-Objective Particle Swarm Optimization of Expensive Constrained Combinatorial Optimization Problems. Knowl.-Based Syst. 2021, 223, 107049. [Google Scholar] [CrossRef]
- Long, W.; Wang, P.; Dong, H.; Li, J.; Fu, C. A Data-Driven Co-Evolutionary Exploration Algorithm for Computationally Expensive Constrained Multi-Objective Problems. Appl. Soft Comput. 2024, 163, 111857. [Google Scholar] [CrossRef]
- Wu, H.; Jin, Y.; Gao, K.; Ding, J.; Cheng, R. Surrogate-Assisted Evolutionary Multi-Objective Optimization of Medium-Scale Problems by Random Grouping and Sparse Gaussian Modeling. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 163, 1–16. [Google Scholar] [CrossRef]
- Younis, A.; Dong, Z. Adaptive Surrogate Assisted Multi-Objective Optimization Approach for Highly Nonlinear and Complex Engineering Design Problems. Appl. Soft Comput. 2024, 150, 111065. [Google Scholar] [CrossRef]
- Liao, P.; Sun, C.; Zhang, G.; Jin, Y. Multi-Surrogate Multi-Tasking Optimization of Expensive Problems. Knowl.-Based Syst. 2020, 205, 106262. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, C.; Liu, F.; Duan, Z.; Zhao, H. A Trust-Region-like Algorithm for Expensive Multi-Objective Optimization. Appl. Soft Comput. 2023, 148, 110892. [Google Scholar] [CrossRef]
- Tang, J.; Wang, H.; Xiong, L. Surrogate-Assisted Multi-Objective Optimization via Knee-Oriented Pareto Front Estimation. Swarm Evol. Comput. 2023, 77, 101252. [Google Scholar] [CrossRef]
- Li, F.; Gao, L.; Shen, W. Surrogate-Assisted Multi-Objective Evolutionary Optimization With Pareto Front Model-Based Local Search Method. IEEE Trans. Cybern. 2024, 54, 173–186. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Zhang, Y.; Gong, D.; Ji, X. A Review of Surrogate-Assisted Evolutionary Algorithms for Expensive Optimization Problems. Expert Syst. Appl. 2023, 217, 119495. [Google Scholar] [CrossRef]
- Shen, J.; Dong, H.; Wang, P.; Li, J.; Wang, W. An Inverse Model-Guided Two-Stage Evolutionary Algorithm for Multi-Objective Optimization. Expert Syst. Appl. 2023, 225, 120198. [Google Scholar] [CrossRef]
- Ma, Y.; Song, C.; Wang, Z.; Jiang, Z.; Sun, B.; Xiao, R. Efficient Design Optimization of Cable-Stayed Bridges: A Two-Layer Framework with Surrogate-Model-Assisted Prediction of Optimum Cable Forces. Appl. Sci. 2024, 14, 2007. [Google Scholar] [CrossRef]
- Wang, X.; Ma, L.; Yang, S.; Huang, M.; Wang, X.; Zhao, J.; Shen, X. An Aggregated Pairwise Comparison-Based Evolutionary Algorithm for Multi-Objective and Many-Objective Optimization. Appl. Soft Comput. 2020, 96, 106641. [Google Scholar] [CrossRef]
- Abel, E.; Mikhailov, L.; Keane, J. Group Aggregation of Pairwise Comparisons Using Multi-Objective Optimization. Inf. Sci. (NY) 2015, 322, 257–275. [Google Scholar] [CrossRef]
- Zheng, N.; Wang, H.; Yuan, B. An Adaptive Model Switch-Based Surrogate-Assisted Evolutionary Algorithm for Noisy Expensive Multi-Objective Optimization. Complex Intell. Syst. 2022, 8, 4339–4356. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, H.; Xu, X.; Xiong, M.; Li, Q. An Efficient Global Optimization Algorithm Combining Revised Expectation Improvement Criteria and Kriging. Eng. Optim. 2024, 56, 608–624. [Google Scholar] [CrossRef]
- Xu, Y.; Renteria, A.; Wang, P. Adaptive Surrogate Models with Partially Observed Information. Reliab. Eng. Syst. Saf. 2022, 225, 108566. [Google Scholar] [CrossRef]
- Wang, R.; Zhou, Y.; Chen, H.; Ma, L.; Zheng, M. A Surrogate-Assisted Many-Objective Evolutionary Algorithm Using Multi- Classification and Coevolution for Expensive Optimization Problems. IEEE Access 2021, 9, 159160–159174. [Google Scholar] [CrossRef]
- Han, X.; Liu, X.; Wang, H.; Liu, G. An Automatic Completion Method for Design Domain Knowledge Graph Using Surrogate Model, for Rapid Performance Evaluation. J. Eng. Des. 2024, 9, 1–23. [Google Scholar] [CrossRef]
- Li, Z.; Tian, K.; Zhang, S.; Wang, B. Efficient Multi-Objective CMA-ES Algorithm Assisted by Knowledge-Extraction-Based Variable-Fidelity Surrogate Model. Chin. J. Aeronaut. 2023, 36, 213–232. [Google Scholar] [CrossRef]
- Yu, L.; Ren, C.; Meng, Z. A Surrogate-Assisted Differential Evolution with Fitness-Independent Parameter Adaptation for High-Dimensional Expensive Optimization. Inf. Sci. (NY) 2024, 662, 120246. [Google Scholar] [CrossRef]
- Cai, X.; Li, Y.; Fan, Z.; Zhang, Q. An External Archive Guided Multiobjective Evolutionary Algorithm Based on Decomposition for Combinatorial Optimization. IEEE Trans. Evol. Comput. 2015, 19, 508–523. [Google Scholar] [CrossRef]
- Li, F.; Shang, Z.; Liu, Y.; Shen, H.; Jin, Y. Inverse Distance Weighting and Radial Basis Function Based Surrogate Model for High-Dimensional Expensive Multi-Objective Optimization. Appl. Soft Comput. 2024, 152, 111194. [Google Scholar] [CrossRef]
- Long, J.; Liao, Y.; Yu, P. Multi-Response Weighted Adaptive Sampling Approach Based on Hybrid Surrogate Model. IEEE Access 2021, 9, 45441–45453. [Google Scholar] [CrossRef]
- Bai, H.; Zheng, J.; Yu, G.; Yang, S.; Zou, J. A Pareto-Based Many-Objective Evolutionary Algorithm Using Space Partitioning Selection and Angle-Based Truncation. Inf. Sci. (NY) 2019, 478, 186–207. [Google Scholar] [CrossRef]
- Chen, G.; Guo, Y.; Jiang, M.; Yang, S.; Zhao, X.; Gong, D. A Subspace-Knowledge Transfer Based Dynamic Constrained Multiobjective Evolutionary Algorithm. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 1500–1512. [Google Scholar] [CrossRef]
- Wu, H.; Chen, Q.; Chen, J.; Jin, Y.; Ding, J.; Zhang, X.; Chai, T. A Multi-Stage Expensive Constrained Multi-Objective Optimization Algorithm Based on Ensemble Infill Criterion. IEEE Trans. Evol. Comput. 2024, 8, 1. [Google Scholar] [CrossRef]
- Zou, M.; Zhu, X.; Tian, Y.; Wang, J.; Chen, H. PRETTY: A Parallel Transgenerational Learning-Assisted Evolutionary Algorithm for Computationally Expensive Multi-Objective Optimization. Inf. Sci. (NY) 2023, 623, 748–766. [Google Scholar] [CrossRef]
- Li, J.; Wang, P.; Dong, H.; Shen, J. A Two-Stage Surrogate-Assisted Evolutionary Algorithm (TS-SAEA) for Expensive Multi/Many-Objective Optimization. Swarm Evol. Comput. 2022, 73, 101107. [Google Scholar] [CrossRef]
- Li, F.; Gao, L.; Garg, A.; Shen, W.; Huang, S. Two Infill Criteria Driven Surrogate-Assisted Multi-Objective Evolutionary Algorithms for Computationally Expensive Problems with Medium Dimensions. Swarm Evol. Comput. 2021, 60, 100774. [Google Scholar] [CrossRef]
- Qin, S.; Sun, C.; Liu, Q.; Jin, Y. A Performance Indicator-Based Infill Criterion for Expensive Multi-/Many-Objective Optimization. IEEE Trans. Evol. Comput. 2023, 27, 1085–1099. [Google Scholar] [CrossRef]
- Cao, J.; Qi, Z.; Chen, Z.; Zhang, J. A Multi-Modal Multi-Objective Evolutionary Algorithm Based on Scaled Niche Distance. Appl. Soft Comput. 2024, 152, 111226. [Google Scholar] [CrossRef]
- Feng, D.; Li, Y.; Liu, J.; Liu, Y. A Particle Swarm Optimization Algorithm Based on Modified Crowding Distance for Multimodal Multi-Objective Problems. Appl. Soft Comput. 2024, 152, 111280. [Google Scholar] [CrossRef]
- Nuh, J.A.; Koh, T.W.; Baharom, S.; Osman, M.H.; Kew, S.N. Performance Evaluation Metrics for Multi-Objective Evolutionary Algorithms in Search-Based Software Engineering: Systematic Literature Review. Appl. Sci. 2021, 11, 3117. [Google Scholar] [CrossRef]
- Qiao, J.; Li, F.; Yang, S.; Yang, C.; Li, W.; Gu, K. An Adaptive Hybrid Evolutionary Immune Multi-Objective Algorithm Based on Uniform Distribution Selection. Inf. Sci. (NY) 2020, 512, 446–470. [Google Scholar] [CrossRef]
- Massaro, A.; Benini, E. A Surrogate-Assisted Evolutionary Algorithm Based on the Genetic Diversity Objective. Appl. Soft Comput. 2015, 36, 87–100. [Google Scholar] [CrossRef]
- Gu, Q.; Wang, X.; Wang, D.; Liu, D. A Kriging-Assisted Multi-Stage Evolutionary Algorithm for Expensive Many-Objective Optimization Problems. Struct. Multidiscip. Optim. 2024, 67, 53. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Y.; Wang, Y.; Pan, Q.; Wang, L. Sustainable Scheduling of Distributed Flow Shop Group: A Collaborative Multi-Objective Evolutionary Algorithm Driven by Indicators. IEEE Trans. Evol. Comput. 2024, 67, 1. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, J.; Liang, J.; Wang, Y.; Ashraf, U.; Yue, C.; Yu, K. A Two-Archive Model Based Evolutionary Algorithm for Multimodal Multi-Objective Optimization Problems. Appl. Soft Comput. 2022, 119, 108606. [Google Scholar] [CrossRef]
- Li, J.; Zhu, J.; Xu, D.; Wang, J.; Li, Z.; Zhang, K. Earth Observation Satellite Scheduling with Interval-Varying Profits. IEEE Trans. Aerosp. Electron. Syst. 2024, 119, 1–16. [Google Scholar] [CrossRef]
- He, L.; Liu, X.-L.; Chen, Y.-W.; Xing, L.-N.; Liu, K. Hierarchical Scheduling for Real-Time Agile Satellite Task Scheduling in a Dynamic Environment. Adv. Sp. Res. 2019, 63, 897–912. [Google Scholar] [CrossRef]
- He, Q.; Sun, J.; Guan, N.; Lv, M.; Sun, Z. Real-Time Scheduling of Conditional DAG Tasks With Intra-Task Priority Assignment. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2023, 42, 3196–3209. [Google Scholar] [CrossRef]
- Song, Y.; Suganthan, P.N.; Pedrycz, W.; Yan, R.; Fan, D.; Zhang, Y. Energy-Efficient Satellite Range Scheduling Using A Reinforcement Learning-Based Memetic Algorithm. IEEE Trans. Aerosp. Electron. Syst. 2024, 59, 1–15. [Google Scholar] [CrossRef]
- Yang, W.; He, L.; Liu, X.; Chen, Y. Onboard Coordination and Scheduling of Multiple Autonomous Satellites in an Uncertain Environment. Adv. Sp. Res. 2021, 68, 4505–4524. [Google Scholar] [CrossRef]
- Jameel, M.; Abouhawwash, M. A New Proximity Metric Based on Optimality Conditions for Single and Multi-Objective Optimization: Method and Validation. Expert Syst. Appl. 2024, 241, 122677. [Google Scholar] [CrossRef]
- Menchaca-Mendez, A.; Coello Coello, C.A. An Alternative Hypervolume-Based Selection Mechanism for Multi-Objective Evolutionary Algorithms. Soft Comput. 2017, 21, 861–884. [Google Scholar] [CrossRef]
- da Costa Oliveira, A.L.; Britto, A.; Gusmão, R. A Framework for Inverse Surrogate Modeling for Fitness Estimation Applied to Multi-Objective Evolutionary Algorithms. Appl. Soft Comput. 2023, 146, 110672. [Google Scholar] [CrossRef]
- Ming, F.; Gong, W.; Jin, Y. Growing Neural Gas Network-Based Surrogate-Assisted Pareto Set Learning for Multimodal Multi-Objective Optimization. Swarm Evol. Comput. 2024, 87, 101541. [Google Scholar] [CrossRef]
- Li, F.; Gao, L.; Shen, W.; Garg, A. Surrogate-Assisted Multi-Objective Evolutionary Optimization with a Multi-Offspring Method and Two Infill Criteria. Swarm Evol. Comput. 2023, 79, 101315. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Li, S.; Zhao, Y. A Performance Indicator-Based Evolutionary Algorithm for Expensive High-Dimensional Multi-/Many-Objective Optimization. Inf. Sci. (NY) 2024, 678, 121045. [Google Scholar] [CrossRef]
- Srinivasa, P.; Nagabhushana, T.N.; Ramakrishna Rao, P.K. Flank Wear Estimation in Face Milling Based on Radial Basis Function Neural Networks. Int. J. Adv. Manuf. Technol. 2002, 20, 241–247. [Google Scholar] [CrossRef]
- Qureshi, I.M.; Naveed, A.; Cheema, T.A.; Jalil, A. Artificial Neural Networks for Microstructure Analysis of Rolling Process. Inf. Technol. J. 2002, 2, 65–68. [Google Scholar] [CrossRef]
- Zhao, S.; Jiao, L. Multi-Objective Evolutionary Design and Knowledge Discovery of Logic Circuits Based on an Adaptive Genetic Algorithm. Genet. Program. Evolvable Mach. 2006, 7, 195–210. [Google Scholar] [CrossRef]
- Deb, K.; Nain, P.K.S. An Evolutionary Multi-Objective Adaptive Meta-Modeling Procedure Using Artificial Neural Networks. In Evolutionary Computation in Dynamic and Uncertain Environments; Palmerini, G., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 13, pp. 297–322. ISBN 978-1-4673-8414-8. [Google Scholar]
- Ejday, M.; Fourment, L. Meta-Model Assisted Multi-Objective Optimization for Non-Steady 3D Metal Forming Processes. Int. J. Mater. Form. 2009, 2, 335–338. [Google Scholar] [CrossRef]
- Zhao, S.-Z.; Suganthan, P.N. Two- Lbests Based Multi-Objective Particle Swarm Optimizer. Eng. Optim. 2011, 43, 1–17. [Google Scholar] [CrossRef]
- Li, K.; Kwong, S.; Cao, J.; Li, M.; Zheng, J.; Shen, R. Achieving Balance between Proximity and Diversity in Multi-Objective Evolutionary Algorithm. Inf. Sci. (NY) 2012, 182, 220–242. [Google Scholar] [CrossRef]
- Akhtar, T.; Shoemaker, C.A. Multi Objective Optimization of Computationally Expensive Multi-Modal Functions with RBF Surrogates and Multi-Rule Selection. J. Glob. Optim. 2016, 64, 17–32. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Mallipeddi, R.; Suganthan, P.N. An Improved Differential Evolution Algorithm Using Efficient Adapted Surrogate Model for Numerical Optimization. Inf. Sci. (NY) 2018, 451–452, 326–347. [Google Scholar] [CrossRef]
- Cai, X.; Gao, L.; Li, X.; Qiu, H. Surrogate-Guided Differential Evolution Algorithm for High Dimensional Expensive Problems. Swarm Evol. Comput. 2019, 48, 288–311. [Google Scholar] [CrossRef]
- Ji, J.-Y.; Tan, Z.; Zeng, S.; See-To, E.W.K.; Wong, M.-L. A Surrogate-Assisted Evolutionary Algorithm for Seeking Multiple Solutions of Expensive Multimodal Optimization Problems. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 377–388. [Google Scholar] [CrossRef]

| Algorithm Type | Algorithm | Computation Costs /Response Time | Application Scenario/Algorithm Feature |
|---|---|---|---|
| Deterministic algorithm | Linear programming (LP) | Low/Fast | It solves optimization problems under linear constraints, such as maximizing imaging coverage and minimizing imaging time. |
| Integer programming (IP) | Moderate/Moderate | It solves task allocation problems that require integer solutions and ensures the rationality of task and resource allocation. | |
| Mixed integer programming (MIP) | High/Slow | It is used to solve complex programming problems with both continuous and discrete variables. | |
| Dynamic programming (DP) | High/Slow | It is used for phased decision problems to ensure that the optimal decision at each stage can find the global optimal solution. | |
| Branch and bound (B&B) | High/Moderate | It is used for integer and combinatorial optimization problems to find the optimal solution by systematically dividing search space. | |
| Column generation (CG) | Moderate/Fast | It is used for large-scale integer programming and mixed integer programming, optimized by decomposing the problem and gradually generating solution columns. | |
| Heuristic algorithm | Simulated annealing algorithm (SA) | Moderate/Moderate | It solves global optimization in search space and achieves optimization from global to local by gradually reducing randomness. |
| Genetic algorithm (GA) | High/Slow | It is used to search for the approximate optimal solution in the large-scale space for global search by simulating natural selection genetic variation. | |
| Particle swarm optimization (PSO) | Moderate/Fast | It is used for optimization in continuous search space to search for optimal solutions through group behavior simulation. | |
| Ant colony algorithm (ACO) | High/Moderate | It is used in discrete optimization problems to find the optimal task assignment method by simulating ant foraging behavior. | |
| Tabu search (TS) | Moderate/Moderate | It is used for global optimization to avoid falling into local optimality by recording and prohibiting certain solutions. | |
| Differential evolution algorithm (DE) | Moderate/Fast | It is used for global optimization, and the optimal solution is found through the difference and recombination between individuals suitable for continuous optimization problems. |
| Algorithm | Proposed/Published | Computation Costs /Response Time | Main Ideas |
|---|---|---|---|
| Evaluating the Epsilon-Domination-Based Multi-Objective Evolutionary Algorithm (EEMOEA) [66] | Kalyanmoy Deb/2005 | Moderate/Moderate | The application of a distribution metric in an expensive multi-objective evolutionary algorithm is emphasized in the ε-MOEA, which is realized by an ε-dominating metric. |
| Surrogate-Assisted Evolutionary Algorithm (SAEA) [67] | Keane/2006 | Low/Fast | The target value of the candidate solution is predicted by the Gaussian process and radial basis function to reduce the expensive calculation cost. |
| Kriging-Based Optimization (KO) [68] | Kleijnen/2009 | Moderate/Slow | The optimization method based on the Kriging model provides the prediction of fitness value and variance and effectively realizes the global optimization. |
| Adaptive Surrogate-Model-Based Optimization (ASMO) [69] | Zhou/2012 | Moderate/Moderate | The sampling method is used to optimize and update the proxy model and gradually approach the global optimal, which has strong adaptability. |
| Ensemble of Surrogates-Assisted Evolutionary Algorithm (ESEA) [70] | Chugh/2016 | Low/Fast | A Gaussian process, neural network, and decision tree are used to complement each other in prediction and evaluation to reduce the calculation cost. |
| Trust Region-Based Multi-Objective Evolutionary Algorithm (TR-MOEA) [71] | Cai, Jianping/2018 | Moderate/Moderate | By combining the trust region and evolutionary algorithm, the optimization search is limited to a potential region by updating and iterating the trust region to improve search efficiency. |
| Efficient Global Optimization (EGO) [72] | Letham, Benjamin/2019 | Low/Fast | A Gaussian process is used as the cost model, and the expected improvement in the acquisition function is used to guide the selection of sampling points, which promotes the fast convergence of the algorithm. |
| Ensemble of Surrogates-Assisted Evolutionary Algorithm (ESAEA) [73] | Zhao, Rui/2020 | Low/Fast | A variety of surrogate models are combined to approximate the expensive objective function, and the surrogate model is used to improve the prediction accuracy and search efficiency. |
| Surrogate-Assisted Covariance Matrix Adaptation Evolution Strategy (SA-CMA-ES) [74] | Ulmer, Hannah/2021 | Moderate/Moderate | The surrogate model is combined with the covariance matrix adaptive evolution strategy to effectively explore and develop the search space. |
| Types | Surrogate Model | Main Ideas | Advantages and Disadvantages |
|---|---|---|---|
| Statistical Model | Kriging | Assuming that the value of the objective function follows the multivariable normal distribution, the candidate solution is predicted by historical data. | Advantages: it can provide the prediction and variance of the objective function value, and is suitable for dealing with highly nonlinear problems. Disadvantages: it has high computational complexity for large-scale data sets. |
| Support Vector Regression | To minimize the error, a hyperplane is found in the higher-dimensional space by classification and analysis. | Advantages: it performs well in high-dimensional space and has good generalization ability. Disadvantages: the selection kernel function and parameter tuning are complex. | |
| Bayesian Optimization | Bayesian statistics and surrogate models are used to approximate the objective function, and the acquisition function is used to select new evaluation points. | Advantages: it effectively handles expensive black-box function optimization problems, balancing exploration and development. Disadvantages: it is very sensitive to the quality and quantity of initial data, and improper selection of initial samples may lead to a poor performance of proxy models. | |
| Function approximation model | Response Surface Methodology | Lower-order polynomial functions, such as linear polynomials, are often used to approximate objective functions and optimize stochastic processes. | Advantages: the calculation is simple and suitable for linear or low-order nonlinear problems. Disadvantages: for complex systems, the model is overly sensitive to training data, which can lead to overfitting and affect generalization ability. |
| Radial Basis Function | The influence of each sample point is expressed as a function of distance, and the objective function is approximated and fitted. | Advantages: it is suitable for processing multidimensional nonlinear problems with high flexibility. Disadvantages: it has low computational efficiency for processing large-scale data sets. | |
| Polynomial Regression | The objective function is fitted using polynomial functions. | Advantages: it is suitable for low-dimensional problems and the calculation is simple. Disadvantages: it is not effective for high-dimensional nonlinear problems. | |
| Machine learning models | ANN | Complex objective functions are fitted through multiple hidden layers and nonlinear activation functions. | Advantages: it can deal with highly complex and nonlinear problems and has strong adaptability. Disadvantages: it requires a large amount of data for training and complex parameter adjustment. |
| Deep Learning | By increasing the depth of the network, it is able to handle more complex pattern recognition and prediction tasks. | Advantages: it adjusts the network architecture and loss function to adapt to different types of optimization problems. Disadvantages: it has high data requirements and a need to label the data before training. | |
| Decision Tree Regression | By constructing a decision tree, the dataset is split into regions and a simple regression is performed within each region. | Advantages: it has a good processing effect on nonlinear and complex data sets and is suitable for processing large-scale data. Disadvantages: Making local decisions at each node cannot capture the global optimization solution. |
| Categories | Main Ideas | Advantages and Disadvantages |
|---|---|---|
| Cooperative Surrogate Models for Multi-Objective Optimization [98] | Multiple surrogate models are combined for collaborative optimization, and the optimization effect is improved by weighted average prediction results. According to the feedback of the optimization process, the model weight and combination strategy are dynamically adjusted to meet the optimization needs of different stages. | Advantages: The synthesis of different surrogate models makes the advantages of each model complementary, reduces the possible bias of a single model, and improves the data generalization ability of the algorithm. Disadvantages: The training and evaluation of multiple surrogate models greatly increases computational complexity and resource consumption. |
| Transfer Learning for Surrogate-Assisted Multi-Objective Optimization [99] | The similarities and differences between the source and target domains are analyzed, effective knowledge migration methods are designed to migrate the surrogate models trained on the source domain to the target domain, and the adaptability of the surrogate models to new tasks is improved. | Advantages: Using historical knowledge to construct more accurate initial prediction models and transferring knowledge from the source domain to the target domain to speed up the convergence of EMOEAs. Disadvantages: The similarity and difference judgments between different tasks are complex and highly dependent on the quality of historical data. |
| Parallel Surrogate Models for Multi-Objective Optimization [100] | Multiple surrogate models are trained in parallel, the fitness value of each objective function is estimated separately, and an incremental sampling strategy is designed to increase the sample points in the optimal search process chapter foot to accelerate the training process of surrogate models using parallel computing resources. | Advantages: Accelerates model training and evaluation through parallel computing, capable of handling large-scale datasets and high-dimensional problems, and greatly reduces surrogate model training time. Disadvantages: The implementation of parallel computing requires high-computational resources and needs to solve the problems of data synchronization and load balancing. |
| Multi-Objective Bayesian Optimization [101] | Different approximate objective functions of the surrogate model are selected for each objective function, acquisition functions suitable for multi-objective optimization are designed to select new evaluation points, and the surrogate model is updated according to the new evaluation points to ensure its applicability and robustness in different scenarios. | Advantages: Effectively balancing exploration and exploitation through Bayesian modeling and acquisition functions enables optimization problems with high dimensionality and complex constraints to be handled with less unnecessary evaluation. Disadvantages: Bayesian model optimization consumes a large amount of computational resources and is ineffective for optimization with insufficient data. |
| Improvement Strategy | Specific Improvement Methods | Year | Main Ideas |
|---|---|---|---|
| Adaptive sampling strategy | Probabilistic sampling strategy | 2023 | The probability improvement criterion is used to adjust the sampling, the probability guidance algorithm is used to sample the candidate solution successfully, and the region with a high fitness value is sampled emphatically. |
| Dynamic sampling adjustment strategy | 2023 | The radial basis function (RBF) network model for denoising is established according to the real-time feedback noise level in the process of evolution, and dynamic adjustment of data sampling density is carried out. | |
| Multi-population co-evolutionary strategy | Adaptive variable grouping strategy | 2022 | The Bayesian Gaussian process latent variable model is combined with adaptive sampling to iteratively select new partially observable training sample points. |
| Hierarchical co-evolution strategy | 2022 | In the stage of model training, a multi-classification model is constructed to divide the whole population into several classes to ensure diversity. In the evolutionary phase, a coevolutionary framework is used to guide evolution according to the new selection criteria. | |
| Domain knowledge strategy | Domain knowledge adaptive strategy | 2024 | The schema layer is built based on domain knowledge, the query sentence is used to extract knowledge, and the knowledge graph is established to extract and reuse domain knowledge adaptively. |
| Domain knowledge extraction strategy | 2023 | A variable fidelity proxy model is established to obtain the low-fidelity undominated solution. A K-means clustering algorithm is used to extract knowledge from the low-fidelity undominated solution to search space. | |
| Adaptive population size adjustment strategies | Population size adjustment strategy | 2024 | The spatial determination mechanism and population size reduction strategy are implemented by improving the dimension between the test vector and the target vector. |
| External file resource allocation strategy | 2022 | An external archive is constructed to periodically add vectors from external archives to the population in the iterative process to achieve adaptive population size adjustment. | |
| Multi-objective weight strategy | Inverse distance weighting strategy | 2024 | Inverse distance weighting and radial basis function strategies are established to provide prediction target values and uncertainty, and an improved lower confidence boundary filling criterion is proposed. |
| Weighted prediction variance strategy | 2023 | The output fitting uncertainty index is calculated based on the weighted prediction variance strategy, and the uncertainty of sample dispersion and surrogate model fitting is taken into account. | |
| Adaptive solution space partitioning strategy | Spatial hierarchical decomposition strategy | 2019 | The object space is divided into multiple subspaces, and the best individual of adjacent estimates in each subspace is selected. |
| Adaptive interval decomposition strategy | 2024 | The objective space is divided into a series of optimization subproblems, and a feasible solution of each subspace is saved to a feasible solution set of a partition. Once a subspace has a feasible solution, the search strategy is changed from a constrained search to unconstrained search. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Hu, M.; Huang, G.; Lin, P.; Wang, Y. A Review of Multi-Satellite Imaging Mission Planning Based on Surrogate Model Expensive Multi-Objective Evolutionary Algorithms: The Latest Developments and Future Trends. Aerospace 2024, 11, 793. https://doi.org/10.3390/aerospace11100793
Yang X, Hu M, Huang G, Lin P, Wang Y. A Review of Multi-Satellite Imaging Mission Planning Based on Surrogate Model Expensive Multi-Objective Evolutionary Algorithms: The Latest Developments and Future Trends. Aerospace. 2024; 11(10):793. https://doi.org/10.3390/aerospace11100793
Chicago/Turabian StyleYang, Xueying, Min Hu, Gang Huang, Peng Lin, and Yijun Wang. 2024. "A Review of Multi-Satellite Imaging Mission Planning Based on Surrogate Model Expensive Multi-Objective Evolutionary Algorithms: The Latest Developments and Future Trends" Aerospace 11, no. 10: 793. https://doi.org/10.3390/aerospace11100793
APA StyleYang, X., Hu, M., Huang, G., Lin, P., & Wang, Y. (2024). A Review of Multi-Satellite Imaging Mission Planning Based on Surrogate Model Expensive Multi-Objective Evolutionary Algorithms: The Latest Developments and Future Trends. Aerospace, 11(10), 793. https://doi.org/10.3390/aerospace11100793






