A Calibrated Individual Semantic Based Failure Mode and Effect Analysis and Its Application in Industrial Internet Platform

Abstract

This article proposes a calibrated individual semantic (CIS)-based failure mode and effect analysis (FMEA) to deal with the risk evaluation of industrial internet platforms (IIP) from four perspectives: network security, data processing capability, equipment performance, and openness. The novelty of the CIS model is based on the deviation between linguistic terms and numerical values to calibrate linguistic scales of decision-makers (DMs). Not only can it handle situations in which different DMs have different understandings of the same term, but it is also suitable for multiple attributes decision-making with uncertainty. In addition, this new FMEA framework considers the consensus-reaching process as a way to eliminate the disagreement among DMs from different departments. Finally, a comparison between the proposed and traditional method is presented to illustrate the advantages of new method.

1. Introduction

1.1. Background

The Industrial Internet has already attracted great interest from both industry and academia due to the explosive growth of novel technologies, such as big data, cloud computing, artificial intelligence, etc. [1]. In response to the “fourth industrial revolution”, General Electric (GE) first proposed the concept of the Industrial Internet in 2012, defining it as “the convergence of the global industrial system with the power of advanced computing, analytics, low-cost sensing and new levels of connectivity permitted by the Internet” [2].

IIP, one of the most important core products of the Industrial Internet, is a service system that is based on the needs of digitalization, networking, and intelligence in manufacturing [3]. Though a large number of benefits have been brought to enterprises by IIPs, such as cost reductions, efficiency increases, improvements in products and services, innovations in business models, etc., there are still several problems in the construction and implementation of IIP, such as digital technology [2], integration of systems [3], cybersecurity [4], openness of platform [5], etc. However, few studies have focused on the overall risk management of the IIP. Therefore, in this paper we will introduce the framework of FMEA to reduce the problems and challenges posed by the implementation of IIP.

FMEA, originating from NASA in the 1960s, is a powerful risk management tool and engineering technique that can effectively manage the quality and reliability of products [6,7]. It has been widely used in identifying and eliminating potential failures, problems, errors from systems, designs, processes, and services [8]. Different from general risk evaluation methods that analyze problems after an adverse event occurs, FMEA is a tool for proactive risk assessment and management, evaluating and eliminating failures before they occur or reach customers [9,10]. Therefore, it has been widely utilized in various practical scenarios, such as cold-chain logistics management [11], healthcare services [12], energy issues [13,14], semiconductor manufacturing [15], etc. Usually, a classic FMEA model includes the following four steps: (1) failure modes (FMs) and their causes and results are identified; (2) the risk priorities of FMs are determined by risk priority numbers (RPNs), which involves three risk factors: the probability of occurrence (O), the severity of effects (S), and the difficulty of detection (D); (3) the risk priority ranking of FMs is obtained, such that the FMs with larger RPN values would cause severer problems, requiring higher priorities; (4) corresponding measures are taken for high-risk issues [10,16,17].

1.2. Related Work

FMEA has made a huge number of contributions in many fields, however, there are still some drawbacks for the traditional FMEA method.

On the one hand, DMs need to use crisp numbers to provide the risk factors number about FMs in the traditional FMEA approach [9]. However, it is difficult for DMs, as human beings and not machines, to describe risk levels of FMs precisely. To deal with uncertainty of evaluation in FMEA, a large number of approaches have been introduced, mainly including fuzzy set theory, evidence-based reasoning theory, developed methods based on 2-tuple linguistic model, etc. [18]. For example, a fuzzy FMEA was proposed that allows the RFs and their relative weights to be evaluated in a linguistic manner [19]; evidence-based reasoning theory was introduced into FMEA techniques to improve the effectiveness and flexibility of subjective information processing in uncertain environments [20,21,22]. However, these approaches to deal with uncertainty are still far-removed from human expression habits, i.e., using linguistic labels or terms [9].

On the other hand, computing with words (CW) was proposed by [23] and the 2-tuple linguistic representation model was initiated by [24]. A large number of extended methods based on the 2-tuple linguistic model have been developed to a notable degree [9,25,26]; probabilistic hesitant fuzzy language was presented to solve the problem of DMs hesitating between multiple options in the evaluation process [27]; linguistic distribution assessments can enable DMs to better reflect their actual experience and avoid information loss and distortion [9,25]; double hierarchy hesitant fuzzy linguistic term sets allow DMs to evaluate problems and solutions using a much more intuitive expression method [13].

However, a problem still needs to be solved by these linguistic extended methods in that the same term has different meanings for different DMs. Thus, an optimization-based PIS model was designed to achieve linguistic calibration for different DMs [28]. Subsequently, more extended methods based on PIS have been reported. A consensus model for large-scale linguistic group decision-making (GDM) based on clustered PIS were created to improve the willingness of DMs who have to revise their preference [29]. To estimate the ignorance elements in incomplete distribution linguistic preference relations (DLPRs) and obtain the personalized numerical meanings of linguistic expressions to DMs, a consistency-driven methodology to manage DLPRs with PIS was proposed [30].

However, a PIS model needs to assume that the preferences of individual DMs are as consistent as possible, which causes it to only accept pairwise comparisons of alternatives under one criterion. It is not friendly to DMs in the multi-attribute decision-making problem, because all the pairwise comparison matrices under different attributes must be provided by DMs. To solve this issue, we found an approach used to obtain personalized membership function. Ishizaka et al. [31] proposed a method of calibrating the membership functions with comparisons given by DMs on alternatives with known measures. The best-matching scale of each DM is selected according to the mental representation of the verbal scale [32]. This article creates a novel individual semantic evaluation approach, called the CIS model, by combining membership function and verbal scale calibration to calibrate the linguistic terms provided by DMs.

1.3. Contribution

The primary work of this article can be summarized as follows. First, a designed linguistic calibration experiment is created to obtain the CISs to deal with the linguistic calibration and unify expression habits of DMs. Second, the possible inconsistencies of the FMEA team are solved by introducing the consensus reach process with minimum adjustment cost. Third, the developed method is applied into the risk management of IIP with 15 proposed FMs. Its main advantages are as follows:

• It proposes an experiment procedure based on the area of figures; essentially, it is a step of calibrating the psychological score of each DM for linguistic terms according to the membership function calibration proposed by Ishizaka et al. [31,32].
• The proposed CIS model is concise when it is applied to multi-attribute decision making. Compared with PIS model, a framework based on an optimization model is not necessary and it has a simpler converting process between linguistic terms and crisp value.
• This article uses the FMEA method to evaluation the risks of IIP. To the best of our knowledge, this is the first time of FMEA in an IIP risk evaluation. All data were obtained from questionnaires provided to staff of the company in this article.

The rest of this paper is organized as follows. In Section 2, a novel framework of FMEA is designed based on a CIS model considering a consensus-reaching process; the CIS model is proposed to convert linguistic terms into crisp values and is described in detail. Section 3 provides a real case of FMEA on IIP and applies it to the proposed model to analyze the FMs. In Section 4, the comparisons between the proposed and related FMEA methods are given to discuss its advantages. Finally, Section 5 concludes this article and points out future directions.

2. Materials and Methods

In this section, we will develop an extended linguistic FMEA method based on CIS considering the consensus-reaching process of multiple DMs, whose framework is shown in Figure 1. In detail, first, each DM needs to evaluate the FMs of IIP according to the given linguistic term set and provide an evaluation matrix. Second, every DM has to participate in a linguistic calibration experiment which is performed through the evaluation of measurable alternatives with the given linguistic term set. Third, a consensus-reaching process is introduced to ensure that all DMs achieve consensus. Finally, the rank of all FMs can be calculated by the collective evaluation matrix.

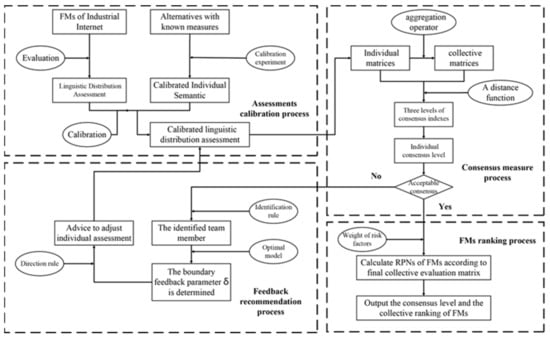
Figure 1. The framework of proposed FMEA method.

The main innovation of the tdeveloped method is to propose a novel linguistic calibration approach, he CIS model. Compared with most existing linguistic methods, it considers the situation that different DMs have different understandings of the same term. It has a unique advantage in that it is based on the theoretical foundation of graphic area calibration experiments, avoiding the primary assumption that individuals’ preferences are as consistent as possible, in contrast to the PIS model. In addition, a process of group risk evaluations is involved in the FMEA method, where there usually exists disagreement among DMs. Thus, this article introduces a consensus-reaching process with a minimum adjustment cost feedback mechanism [33]; the consensus measure, inconsistency identification, and minimum adjustment cost feedback are described in [33], but are not repeated.

When DMs express their evaluation about FMs, linguistic expressions are more in line with human habits than numerical expressions. However, the same words have different meanings for different individuals, which may lead to final error results. While PIS is a useful tool to deal with this problem, it assumes that the preferences of individual DMs are completely consistent, i.e., if alternative A is better than alternative B and if alternative B is better than alternative C, then alternative A cannot be worse than alternative C. In addition, the original preferences must be provided by pairwise comparison matrices in PIS model, which is not friendly to DMs in the multi-attribute decision-making problem, because all the pairwise comparison matrices under different attributes must be provided by DMs. Thus, this article proposes a novel individual semantic evaluation approach to calibrate the linguistic terms provided by DMs.

Inspired by the method of calibrating membership function [31,32], this article designs a CIS model to transform the linguistic terms provided by DMs into crisp numbers and includes two steps: (1) linguistic term collection based on the areas of graphics and (2) the calibration process of linguistic terms, as shown in Figure 2.

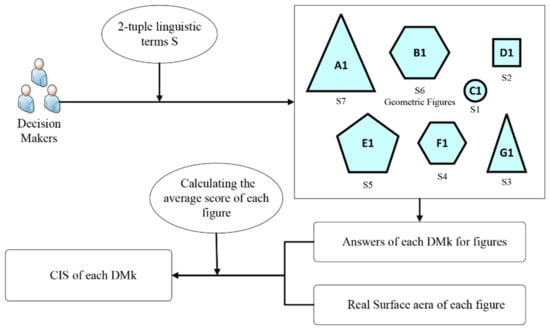
Figure 2. The basic framework of CIS model.

Herrera and Martinez [24] proposed the 2-tuple linguistic model in the framework of computing with words, which is a linguistic representation model widely used in different fields. Definition 1 illustrates:

Definition 1.

(The 2-tuple linguistic model). Let $S=\left\{s_0,s_1,\cdots ,s_g\right\}$ be a linguistic term set, and β ∈ [0,g] be a value representing the result of a symbolic aggregation operation. The 2-tuple linguistic model involves the transformation function between 2-tuples and numerical values as follows.

$$\mathsf{\Delta }:\left[0,g\right]\to \overline{S}$$

(1)

$$\mathsf{\Delta }\left(\beta \right)=\left(s_t,\alpha \right),with \left\{\begin{array}{c}{s}_t,t=round\left(\beta \right)\\ \alpha =\beta -t,\alpha \in \left[-0.5,0.5\right)\end{array}\right.$$

(2)

where function ∆ is a one-to-one mapping whose inverse function ${\mathsf{\Delta }}^{-1}:\overline{S}\to \left[0,g\right]$ is equal to ${\mathsf{\Delta }}^{-1}\left(s_t,\alpha \right)=t+\alpha$.

Based on Definition 1, each DM in FMEA team uses a 2-tuple linguistic model to evaluate the areas of u sets of graphics, there are g figures in each set, and their real areas are $1, 2, \dots , g$, respectively, where the area of xth figure in yth set is $A^k={\left(a_{yx}^k\right)}_{u\times g}$ as provided by $D{M}_k, k=1,2,\dots ,m$, where $a_{yx}^k$ is a 2-tuple linguistic term. Please note that the area of each figure provided to DMs in each set of graphics is random, but in the u sets of graphics, there are g figures with area $t$, which is beyond doubt. This guarantees that DMs will provide the area of the figures based on their judgment, rather than the ordering of graphics, so as to obtain the true psychological measurement error of DMs. The real areas of graphics and the mean value of the linguistic term provided by DMs are matched to calibrate the DMs’ linguistic term in the calibration process of linguistic terms. Thus, the CIS of $D{M}_k$ about each linguistic term $s_t$ can be obtained as follows.

$$CI{S}^k\left(s_t\right)=\frac{1}{u}{\displaystyle \sum }_{y=1}^u{\mathsf{\Delta }}^{-1}\left(a_{yx}^k\right)$$

(3)

Here, $CI{S}^k\left(s_t\right)<CI{S}^k\left(s_{t+1}\right)$. If it happens that $CI{S}^k\left(s_t\right)\ge CI{S}^k\left(s_{t+1}\right)$, there exists wrong information provided by DMs or wrong information about figures, thus, DMs must update their evaluation or the information about figures is revised.

Example 1.

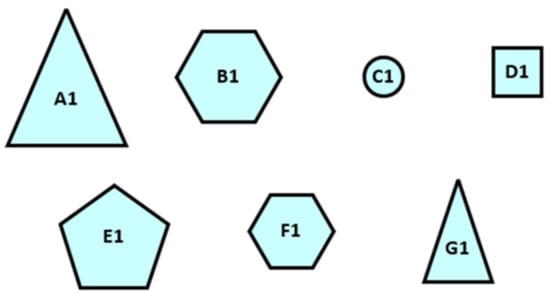
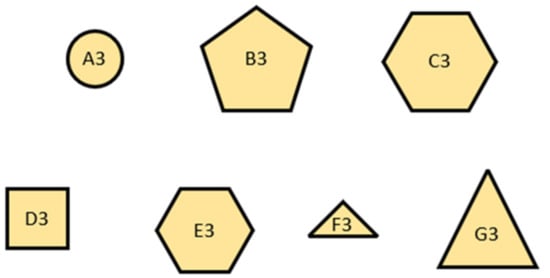
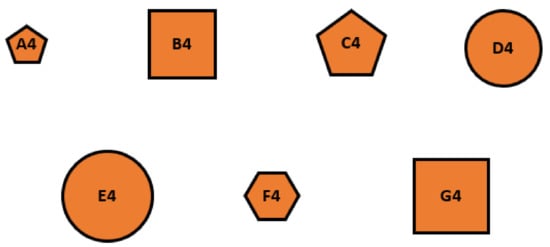
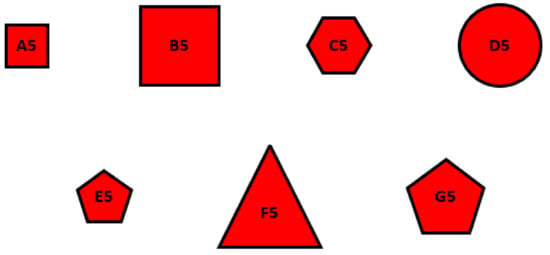
(Process of Calibrated Individual Semantic). A CIS numerical scales $CI{S}^k\left(s_t\right)$ of different individual $D{M}_k$ is required to convert the linguistic terms into crisp values. Suppose five DMs provide the areas of five sets of figures (there are 7 figures in each set) by the linguistic terms set, where the figures are depicted as Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 and the area of figures provided by DMs are shown as Table 1, Table 2, Table 3, Table 4 and Table 5.

Figure 3. The first set of graphics.

Figure 4. The second set of graphics.

Figure 5. The third set of graphics.

Figure 6. The fourth set of graphics.

Figure 7. The fifth set of graphics.

Table 1. Answers for calibration experiment of $D{M}_1$.

	Fig.A	Fig.B	Fig.C	Fig.D	Fig.E	Fig.F	Fig.G
Set 1	$s_5$	$s_6$	$s_1$	$s_2$	$s_6$	$s_4$	$s_3$
Set 2	$s_3$	$s_6$	$s_7$	$s_2$	$s_4$	$s_1$	$s_5$
Set 3	$s_2$	$s_6$	$s_7$	$s_3$	$s_5$	$s_1$	$s_4$
Set 4	$s_1$	$s_4$	$s_3$	$s_5$	$s_7$	$s_2$	$s_5$
Set 5	$s_1$	$s_7$	$s_3$	$s_5$	$s_1$	$s_5$	$s_5$

Table 2. Answers for calibration experiment of $D{M}_2$.

	Fig.A	Fig.B	Fig.C	Fig.D	Fig.E	Fig.F	Fig.G
Set 1	$s_6$	$s_6$	$s_2$	$s_3$	$s_5$	$s_4$	$s_4$
Set 2	$s_3$	$s_5$	$s_6$	$s_4$	$s_4$	$s_2$	$s_4$
Set 3	$s_3$	$s_6$	$s_6$	$s_4$	$s_5$	$s_2$	$s_4$
Set 4	$s_1$	$s_3$	$s_2$	$s_4$	$s_5$	$s_2$	$s_4$
Set 5	$s_2$	$s_5$	$s_4$	$s_5$	$s_3$	$s_5$	$s_4$

Table 3. Answers for calibration experiment of $D{M}_3$.

	Fig.A	Fig.B	Fig.C	Fig.D	Fig.E	Fig.F	Fig.G
Set 1	$s_7$	$s_6$	$s_1$	$s_2$	$s_5$	$s_3$	$s_4$
Set 2	$s_3$	$s_6$	$s_7$	$s_2$	$s_4$	$s_1$	$s_5$
Set 3	$s_2$	$s_6$	$s_7$	$s_3$	$s_5$	$s_1$	$s_4$
Set 4	$s_1$	$s_5$	$s_3$	$s_4$	$s_7$	$s_2$	$s_6$
Set 5	$s_1$	$s_7$	$s_3$	$s_5$	$s_2$	$s_6$	$s_4$

Table 4. Answers for calibration experiment of $D{M}_4$.

	Fig.A	Fig.B	Fig.C	Fig.D	Fig.E	Fig.F	Fig.G
Set 1	$s_5$	$s_6$	$s_1$	$s_2$	$s_7$	$s_4$	$s_3$
Set 2	$s_3$	$s_6$	$s_7$	$s_2$	$s_5$	$s_1$	$s_4$
Set 3	$s_2$	$s_6$	$s_7$	$s_3$	$s_5$	$s_1$	$s_4$
Set 4	$s_1$	$s_5$	$s_3$	$s_4$	$s_6$	$s_2$	$s_7$
Set 5	$s_1$	$s_7$	$s_3$	$s_5$	$s_2$	$s_6$	$s_4$

Table 5. Answers for calibration experiment of $D{M}_5$.

	Fig.A	Fig.B	Fig.C	Fig.D	Fig.E	Fig.F	Fig.G
Set 1	$s_7$	$s_5$	$s_1$	$s_2$	$s_6$	$s_3$	$s_4$
Set 2	$s_3$	$s_5$	$s_7$	$s_3$	$s_4$	$s_1$	$s_4$
Set 3	$s_3$	$s_6$	$s_6$	$s_4$	$s_5$	$s_2$	$s_5$
Set 4	$s_1$	$s_4$	$s_3$	$s_4$	$s_5$	$s_2$	$s_5$
Set 5	$s_3$	$s_5$	$s_4$	$s_5$	$s_3$	$s_6$	$s_4$

After processing, we get matrix $A^k$ as follows.

$$\begin{gathered} A^1={(a_{yx}^1)}_{5\times 7}=\left[\begin{array}{ccccccc}{s}_1& s_2& s_3& s_4& s_6& s_6& s_5\\ s_1& s_2& s_3& s_4& s_6& s_6& s_7\\ s_1& s_2& s_3& s_5& s_5& s_5& s_7\\ s_1& s_2& s_3& s_4& s_4& s_5& s_7\\ s_1& s_1& s_3& s_5& s_5& s_5& s_7\end{array}\right] \\ {A}^2={(a_{yx}^2)}_{5\times 7}=\left[\begin{array}{ccccccc}{s}_2& s_3& s_4& s_4& s_5& s_6& s_6\\ s_2& s_4& s_3& s_4& s_5& s_6& s_6\\ s_2& s_3& s_4& s_4& s_5& s_4& s_6\\ s_1& s_2& s_2& s_4& s_3& s_5& s_5\\ s_2& s_3& s_4& s_4& s_4& s_5& s_5\end{array}\right] \\ {A}^3={(a_{yx}^3)}_{5\times 7}=\left[\begin{array}{ccccccc}{s}_1& s_2& s_4& s_3& s_5& s_6& s_7\\ s_1& s_2& s_3& s_4& s_6& s_6& s_7\\ s_1& s_2& s_3& s_5& s_5& s_6& s_7\\ s_1& s_2& s_3& s_4& s_5& s_5& s_7\\ s_1& s_2& s_3& s_4& s_4& s_6& s_7\end{array}\right] \\ {A}^4={(a_{yx}^4)}_{5\times 7}=\left[\begin{array}{ccccccc}{s}_1& s_2& s_3& s_4& s_7& s_6& s_5\\ s_1& s_2& s_3& s_5& s_6& s_6& s_7\\ s_1& s_2& s_3& s_4& s_5& s_7& s_7\\ s_1& s_2& s_3& s_4& s_5& s_5& s_6\\ s_1& s_2& s_3& s_4& s_4& s_6& s_7\end{array}\right] \\ {A}^5={(a_{yx}^5)}_{u\times o}=\left[\begin{array}{ccccccc}{s}_1& s_2& s_4& s_3& s_6& s_5& s_7\\ s_1& s_3& s_3& s_4& s_5& s_6& s_7\\ s_2& s_3& s_4& s_4& s_5& s_5& s_6\\ s_1& s_2& s_3& s_5& s_4& s_5& s_5\\ s_3& s_3& s_4& s_4& s_4& s_6& s_5\end{array}\right] \end{gathered}$$

Thus, the CIS numerical scale and the semantic curves of CIS are obtained for different $D{M}_k$ based on Equation (3), as shown in Table 6 and Figure 8.

Table 6. The CIS numerical scales for different DM_k.

CISk(St)	t = 1	t = 2	t = 3	t = 4	t = 5	t = 6	t = 7
k = 1	1	1.8	3	4.4	5.2	5.4	6.6
k = 2	1.8	3	3.4	4	4.4	5.2	5.6
k = 3	1	2	3.2	4	5	5.8	7
k = 4	1	2	3	4.2	5.4	6	6.4
k = 5	1.6	2.6	3.6	4	4.8	5.4	6

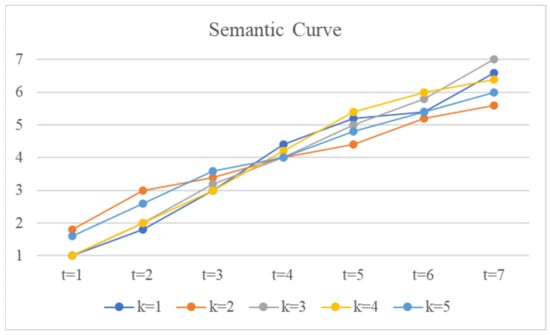
Figure 8. The semantic curves of CIS.

After finishing the calibration process of the 2-tuple linguistic model, all the 2-tuple linguistic terms are transformed into numerical values. Here, we assume that a 2-tuple linguistic individual evaluation matrix about $F{M}_i \left(i=1,2,\dots ,m\right)$ regarding three risk factors $\left(R{F}_j, j=1,2,3\right)$, including occurrence (O), severity (S), and detection (D), is $V^k={\left(v_{ij}^k\right)}_{n\times 3} \left(k=1,2,\dots ,m;i=1,2,\dots ,n;j=1,2,3\right)$, as provided by each $D{M}_k \left(k=1,2,\dots ,m\right)$ in the FMEA team. Next, $V^k={\left(v_{ij}^k\right)}_{n\times 3} \left(k=1,2,\dots ,m;i=1,2,\dots ,n;j=1,2,3\right)$ can be transformed into numerical individual evaluation matrix $E^k={\left(e_{ij}^k\right)}_{n\times 3} \left(k=1,2,\dots ,m;i=1,2,\dots ,n;j=1,2,3\right)$ by the proposed CIS model. Then, the numerical collective evaluation matrix $E^c={\left(e_{ij}^c\right)}_{n\times 3} \left(i=1,2,\dots ,n;j=1,2,3\right)$ can be calculated as follows.

$$e_{ij}^c={\displaystyle \sum }_{k=1}^m{e}_{ij}^k·w_k$$

(4)

3. The Extended FMEA for Industrial Internet Platform

In this section, a case of IIP FMEA is provided, where five experts are invited to be the DMs to provided risk evaluations of fifteen FMs in Section 3 by 2-tuple linguistic terms for analysis of the potential failures of the IIP and improvement of its quality and reliability. Wherever the CIS model is used to revise the linguistic terms of DMs, a CRP with the minimum adjustment cost feedback mechanism is adopted to eliminate the disagreement among DMs, and a ranking process of FMs is achieved according to the final collective evaluation results.

3.1. Case Background

As mentioned in introduction, it is necessary to implement comprehensive risk management for IIP. However, there has been little investigation into the comprehensive risk management of IIP to date. Therefore, this article proposes fifteen FMs for IIP according to the literature from the four perspectives of network security $\left(F{M}_1~F{M}_4\right)$, data processing capability $\left(F{M}_5~F{M}_9\right)$, equipment performance $\left(F{M}_{10}~F{M}_{12}\right)$, and openness $\left(F{M}_{13}~F{M}_{15}\right)$, as shown in Table 7.

Table 7. Failure Modes for Industrial Internet Platform.

No.	Failure Modes	Causes	Effects
FM1	Safeguard for private information is deficient	There are defects in security management of private information, or safeguard can not cover all processes.	The users’ private information is leaked
FM2	Lack of information for security contingency plan	Lack of experience or insufficient plans in handling emergency information security incidents	Inability to deal with information security incidents in time
FM3	Lag in technology for network security	There are only traditional passive protection methods and a lack of relatively active defense measures	The network security of the platform is low and vulnerable to attacks
FM4	Lack of safeguards for data storage	Lack of means to respond to emergencies, such as cloud backup or remote disaster recovery	The core data of the platform are prone to damage in the event of an accident
FM5	Cloud computing capability is less adaptable	Cloud computing capabilities cannot be dynamically adjusted according to demand	Resource shortage at peak times, waste of resources at trough times
FM6	Poor adaptability of storage capacity	The storage capacity of the platform cannot be dynamically adjusted according to demand	Data cannot be entered during peak hours, and space is greatly wasted during low valleys
FM7	Data processing is deficient	Failure to sufficiently understand the type, content, and structure of data required by users	Data redundancy and backlog
FM8	Poor data modeling ability	Insufficient number of various models and algorithms based on big data intelligent analysis	Reduced efficiency and effectiveness in business
FM9	Poor data visualization	Too much emphasis on design and functionality, leading to overly flashy data visualization	Inability to effectively communicate ideas, concepts, and information
FM10	Lag in device authentication technology	Device connection, identification, and permission granting require manual authorization	High human resource consumption and time waste
FM11	Device access is limited	Specific data interface access is required, or the types of accessible resources are limited	Low efficiency of data access
FM12	The edge data response delay is serious	The hardware facilities of users and equipment connected to the platform are poor	The speed of information exchange and feedback is reduced
FM13	Less data-sharing with users	There are many restrictions on the amount of openly shared data, the type of data, and the objects to whom data-sharing services are provided.	The requirements of users cannot be satisfied
FM14	Low platform co-construction capability	The benefit-sharing mechanism is lacking or incomplete, or it cannot reasonably reflect the value created by the platform partners	Conflict between relevant parties is not conducive to the long-term development of the platform
FM15	Poor platform innovation ability	The number and fields of cooperation involved in platform construction and operation are relatively small	Inability to improve functions and services according to the demands of industrial manufacturing in time

3.2. Risk Information Collective and CIS Application

Five DMs are required to provide their risk evaluation matrices $\left\{V^1,V^2,\dots ,V^5\right\}$ of $F{M}_i \left(i=1,2,\dots ,15\right)$ regarding three $R{F}_j$, including Occurrence (O), Severity (S), and Detection (D), using linguistic terms set S = {$s_1$= ‘extremely little’; $s_2$= ‘very little’; $s_3$= ‘little’; $s_4$= ‘moderate’; $s_5$= ‘large’; $s_6$= ‘very large’; $s_7$= ‘extremely large’}, as follows.

$$\begin{gathered} V^1=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& s_7& s_5& s_3\\ F{M}_2& s_6& s_4& s_3\\ F{M}_3& s_5& s_6& s_4\\ F{M}_4& s_6& s_4& s_4\\ F{M}_5& s_5& s_4& s_4\\ F{M}_6& s_4& s_5& s_3\\ F{M}_7& s_5& s_5& s_5\\ F{M}_8& s_6& s_5& s_5\\ F{M}_9& s_7& s_6& s_6\\ F{M}_{10}& s_5& s_4& s_4\\ F{M}_{11}& s_4& s_4& s_4\\ F{M}_{12}& s_4& s_4& s_4\\ F{M}_{13}& s_4& s_4& s_4\\ F{M}_{14}& s_4& s_4& s_4\\ F{M}_{15}& s_4& s_4& s_5\end{array}\right] \\ {V}^2=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& s_5& s_5& s_3\\ F{M}_2& s_4& s_5& s_6\\ F{M}_3& s_6& s_5& s_5\\ F{M}_4& s_4& s_6& s_3\\ F{M}_5& s_4& s_4& s_3\\ F{M}_6& s_3& s_3& s_2\\ F{M}_7& s_5& s_3& s_3\\ F{M}_8& s_6& s_5& s_3\\ F{M}_9& s_7& s_5& s_3\\ F{M}_{10}& s_4& s_4& s_4\\ F{M}_{11}& s_3& s_5& s_1\\ F{M}_{12}& s_5& s_4& s_3\\ F{M}_{13}& s_5& s_4& s_4\\ F{M}_{14}& s_6& s_4& s_4\\ F{M}_{15}& s_6& s_4& s_2\end{array}\right] \\ {V}^3=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& s_4& s_6& s_6\\ F{M}_2& s_5& s_6& s_6\\ F{M}_3& s_6& s_6& s_6\\ F{M}_4& s_3& s_7& s_4\\ F{M}_5& s_4& s_4& s_4\\ F{M}_6& s_3& s_3& s_2\\ F{M}_7& s_4& s_6& s_3\\ F{M}_8& s_6& s_6& s_6\\ F{M}_9& s_3& s_6& s_2\\ F{M}_{10}& s_4& s_5& s_4\\ F{M}_{11}& s_6& s_4& s_2\\ F{M}_{12}& s_5& s_5& s_2\\ F{M}_{13}& s_6& s_6& s_2\\ F{M}_{14}& s_6& s_5& s_5\\ F{M}_{15}& s_6& s_6& s_2\end{array}\right] \\ {V}^4=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& s_3& s_5& s_4\\ F{M}_2& s_3& s_4& s_4\\ F{M}_3& s_3& s_4& s_3\\ F{M}_4& s_3& s_3& s_4\\ F{M}_5& s_3& s_4& s_3\\ F{M}_6& s_3& s_3& s_3\\ F{M}_7& s_3& s_3& s_3\\ F{M}_8& s_4& s_4& s_4\\ F{M}_9& s_3& s_3& s_3\\ F{M}_{10}& s_3& s_4& s_4\\ F{M}_{11}& s_3& s_3& s_3\\ F{M}_{12}& s_4& s_4& s_4\\ F{M}_{13}& s_4& s_3& s_4\\ F{M}_{14}& s_3& s_3& s_4\\ F{M}_{15}& s_4& s_3& s_4\end{array}\right] \\ {V}^5=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& s_4& s_6& s_4\\ F{M}_2& s_4& s_6& s_4\\ F{M}_3& s_4& s_6& s_5\\ F{M}_4& s_5& s_6& s_5\\ F{M}_5& s_5& s_5& s_4\\ F{M}_6& s_5& s_5& s_4\\ F{M}_7& s_5& s_7& s_4\\ F{M}_8& s_5& s_7& s_4\\ F{M}_9& s_5& s_7& s_5\\ F{M}_{10}& s_5& s_4& s_5\\ F{M}_{11}& s_5& s_4& s_4\\ F{M}_{12}& s_6& s_6& s_5\\ F{M}_{13}& s_6& s_5& s_3\\ F{M}_{14}& s_6& s_4& s_3\\ F{M}_{15}& s_5& s_5& s_4\end{array}\right] \end{gathered}$$

According to Table 5, the numerical risk evaluation matrix $E^k$ of $D{M}^k$ is generated as follows.

$$\begin{gathered} E^1=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& 6.6& 5.2& 3\\ F{M}_2& 5.4& 4.4& 3\\ F{M}_3& 5.2& 5.4& 4.4\\ F{M}_4& 5.4& 4.4& 4.4\\ F{M}_5& 5.2& 4.4& 4.4\\ F{M}_6& 4.4& 5.2& 3\\ F{M}_7& 5.2& 5.2& 5.2\\ F{M}_8& 5.4& 5.2& 5.2\\ F{M}_9& 6.6& 5.4& 5.4\\ F{M}_{10}& 5.2& 4.4& 4.4\\ F{M}_{11}& 4.4& 4.4& 4.4\\ F{M}_{12}& 4.4& 4.4& 4.4\\ F{M}_{13}& 4.4& 4.4& 4.4\\ F{M}_{14}& 4.4& 4.4& 4.4\\ F{M}_{15}& 5.2& 4.4& 4.4\end{array}\right] \\ {E}^2=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& 4.8& 4.8& 3.4\\ F{M}_2& 4& 4.8& 5.8\\ F{M}_3& 5.8& 4.8& 4.8\\ F{M}_4& 4& 5.8& 3.4\\ F{M}_5& 4& 4& 3.4\\ F{M}_6& 3.4& 3.4& 3\\ F{M}_7& 4.8& 3.4& 3.4\\ F{M}_8& 5.8& 4.8& 3.4\\ F{M}_9& 6.6& 4.8& 3.4\\ F{M}_{10}& 4& 4& 4\\ F{M}_{11}& 3.4& 3.4& 1.8\\ F{M}_{12}& 4.8& 4& 3.4\\ F{M}_{13}& 4.8& 4& 4\\ F{M}_{14}& 5.8& 4& 4\\ F{M}_{15}& 5.8& 4& 3\end{array}\right] \\ {E}^3=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& 4& 5.8& 5.8\\ F{M}_2& 5& 5.8& 5.8\\ F{M}_3& 5.8& 5.8& 5.8\\ F{M}_4& 3.2& 7& 4\\ F{M}_5& 4& 4& 4\\ F{M}_6& 3.2& 3.2& 2\\ F{M}_7& 4& 5.8& 3.2\\ F{M}_8& 5.8& 5.8& 5.8\\ F{M}_9& 3.2& 5.8& s_2\\ F{M}_{10}& 4& 5& 4\\ F{M}_{11}& 5.8& 4& 2\\ F{M}_{12}& 5& 5& 2\\ F{M}_{13}& 5.8& 5.8& 2\\ F{M}_{14}& 5.8& 5& 5\\ F{M}_{15}& 5.8& 5.8& 2\end{array}\right] \\ {E}^4=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& 3& 5.4& 4.2\\ F{M}_2& 3& 4.2& 4.2\\ F{M}_3& 3& 4.2& 3\\ F{M}_4& 3& 3& 4.2\\ F{M}_5& 3& 4.2& 3\\ F{M}_6& 3& 3& 3\\ F{M}_7& 3& 3& 3\\ F{M}_8& 4.2& 4.2& 4.2\\ F{M}_9& 3& 3& 3\\ F{M}_{10}& 3& 4.2& 4.2\\ F{M}_{11}& 3& 3& 3\\ F{M}_{12}& 4.2& 4.2& 4.2\\ F{M}_{13}& 4.2& 3& 4.2\\ F{M}_{14}& 3& 3& 4.2\\ F{M}_{15}& 4.2& 3& 4.2\end{array}\right] \\ {E}^5=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& 4& 5.4& 4\\ F{M}_2& 4& 5.4& 4\\ F{M}_3& 4& 5.4& 4.8\\ F{M}_4& 4.8& 5.4& 4.8\\ F{M}_5& 4.8& 4.8& 4\\ F{M}_6& 4.8& 4.8& 4\\ F{M}_7& 4.8& 6& 4\\ F{M}_8& 4.8& 6& 4\\ F{M}_9& 4.8& 6& 4.8\\ F{M}_{10}& 4.8& 4& 4.8\\ F{M}_{11}& 4.8& 4& 4\\ F{M}_{12}& 5.4& 5.4& 4.8\\ F{M}_{13}& 5.4& 4.8& 3.6\\ F{M}_{14}& 5.4& 4& 3.6\\ F{M}_{15}& 4.8& 4.8& 4\end{array}\right] \end{gathered}$$

3.3. Consensus Measure and Feedback Recommendation

The weights of the five DMs are assigned as $W={\left(w_1,w_2,w_3,w_4,w_5\right)}^T={\left(0.23,0.23,0.18,0.18,0.18\right)}^T$ based on their positions and work experience. Then, collective numerical risk evaluation matrix $E^c$ can be aggregated by individual numerical risk evaluation matrices $\left\{E^1,E^2,E^3,E^4,E^5\right\}$, according to Equation (4), as follows.

$$E^c=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& 4.602& 5.334& 3.992\\ F{M}_2& 4.276& 4.888& 4.406\\ F{M}_3& 4.742& 5.072& 4.564\\ F{M}_4& 4.096& 4.980& 4.134\\ F{M}_5& 4.286& 4.272& 3.774\\ F{M}_6& 3.774& 4.004& 3.000\\ F{M}_7& 4.470& 4.688& 3.860\\ F{M}_8& 5.056& 5.226& 4.544\\ F{M}_9& 4.786& 4.964& 3.742\\ F{M}_{10}& 4.286& 4.308& 4.272\\ F{M}_{11}& 4.242& 3.774& 3.046\\ F{M}_{12}& 4.744& 4.560& 3.774\\ F{M}_{13}& 4.888& 4.380& 3.696\\ F{M}_{14}& 4.764& 4.092& 4.236\\ F{M}_{15}& 5.102& 4.380& 3.538\end{array}\right]$$

Subsequently, the three levels of consensus indexes (CIs) of DMs are obtained [33,34,35], as follows. The element-level CIs of DMs are:

$$\begin{gathered} {\mathit{CE}}^1=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& 0.667& 0.989& 0.835\\ F{M}_2& 0.846& 0.919& 0.766\\ F{M}_3& 0.890& 0.979& 0.973\\ F{M}_4& 0.816& 0.903& 0.956\\ F{M}_5& 0.814& 0.979& 0.896\\ F{M}_6& 0.896& 0.767& 1.000\\ F{M}_7& 0.845& 0.881& 0.743\\ F{M}_8& 0.976& 0.971& 0.857\\ F{M}_9& 0.698& 0.961& 0.757\\ F{M}_{10}& 0.814& 0.985& 0.979\\ F{M}_{11}& 0.974& 0.896& 0.774\\ F{M}_{12}& 0.943& 0.973& 0.896\\ F{M}_{13}& 0.919& 0.997& 0.883\\ F{M}_{14}& 0.939& 0.949& 0.973\\ F{M}_{15}& 0.950& 0.997& 0.856\end{array}\right] \\ {\mathit{CE}}^2=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& 0.967& 0.911& 0.901\\ F{M}_2& 0.954& 0.985& 0.868\\ F{M}_3& 0.924& 0.955& 0.961\\ F{M}_4& 0.984& 0.963& 0.878\\ F{M}_5& 0.952& 0.955& 0.938\\ F{M}_6& 0.938& 0.899& 1.000\\ F{M}_7& 0.945& 0.785& 0.923\\ F{M}_8& 0.976& 0.929& 0.809\\ F{M}_9& 0.864& 0.973& 0.943\\ F{M}_{10}& 0.952& 0.949& 0.955\\ F{M}_{11}& 0.860& 0.938& 0.792\\ F{M}_{12}& 0.991& 0.907& 0.938\\ F{M}_{13}& 0.985& 0.937& 0.949\\ F{M}_{14}& 0.927& 0.985& 0.961\\ F{M}_{15}& 0.984& 0.9367& 0.910\end{array}\right] \\ {\mathit{CE}}^3=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& 0.900& 0.922& 0.699\\ F{M}_2& 0.879& 0.848& 0.768\\ F{M}_3& 0.824& 0.879& 0.794\\ F{M}_4& 0.851& 0.663& 0.978\\ F{M}_5& 0.952& 0.955& 0.962\\ F{M}_6& 0.904& 0.866& 0.833\\ F{M}_7& 0.922& 0.815& 0.890\\ F{M}_8& 0.876& 0.904& 0.791\\ F{M}_9& 0.736& 0.861& 0.710\\ F{M}_{10}& 0.952& 0.885& 0.955\\ F{M}_{11}& 0.740& 0.962& 0.826\\ F{M}_{12}& 0.957& 0.927& 0.704\\ F{M}_{13}& 0.848& 0.763& 0.717\\ F{M}_{14}& 0.827& 0.849& 0.873\\ F{M}_{15}& 0.884& 0.763& 0.744\end{array}\right] \\ {\mathit{CE}}^4=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& 0.733& 0.989& 0.965\\ F{M}_2& 0.787& 0.885& 0.966\\ F{M}_3& 0.710& 0.855& 0.739\\ F{M}_4& 0.817& 0.670& 0.989\\ F{M}_5& 0.786& 0.988& 0.871\\ F{M}_6& 0.871& 0.833& 1.000\\ F{M}_7& 0.755& 0.719& 0.857\\ F{M}_8& 0.857& 0.829& 0.943\\ F{M}_9& 0.702& 0.673& 0.876\\ F{M}_{10}& 0.786& 0.982& 0.988\\ F{M}_{11}& 0.793& 0.871& 0.992\\ F{M}_{12}& 0.909& 0.940& 0.929\\ F{M}_{13}& 0.706& 0.770& 0.916\\ F{M}_{14}& 0.850& 0.818& 0.994\\ F{M}_{15}& 0.884& 0.770& 0.890\end{array}\right] \\ {\mathit{CE}}^5=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& 0.890& 0.989& 0.999\\ F{M}_2& 0.954& 0.915& 0.932\\ F{M}_3& 0.876& 0.945& 0.961\\ F{M}_4& 0.883& 0.930& 0.889\\ F{M}_5& 0.914& 0.912& 0.962\\ F{M}_6& 0.829& 0.867& 0.833\\ F{M}_7& 0.945& 0.781& 0.978\\ F{M}_8& 0.957& 0.871& 0.909\\ F{M}_9& 0.998& 0.827& 0.824\\ F{M}_{10}& 0.914& 0.949& 0.912\\ F{M}_{11}& 0.907& 0.962& 0.841\\ F{M}_{12}& 0.891& 0.860& 0.829\\ F{M}_{13}& 0.915& 0.930& 0.984\\ F{M}_{14}& 0.894& 0.985& 0.894\\ F{M}_{15}& 0.950& 0.930& 0.923\end{array}\right] \end{gathered}$$

CIs of DMs at FMs levels are:

$${\mathit{CF}}^{\mathit{k}}=\left[\begin{array}{cccccc}FMs& \mathit{K}=1& \mathit{K}=2& \mathit{K}=3& \mathit{K}=4& \mathit{K}=5\\ F{M}_1& 0.830& 0.926& 0.840& 0.896& 0.962\\ F{M}_2& 0.843& 0.936& 0.832& 0.879& 0.934\\ F{M}_3& 0.947& 0.946& 0.832& 0.768& 0.927\\ F{M}_4& 0.892& 0.942& 0.831& 0.825& 0.901\\ F{M}_5& 0.896& 0.948& 0.956& 0.882& 0.930\\ F{M}_6& 0.888& 0.946& 0.868& 0.901& 0.843\\ F{M}_7& 0.823& 0.886& 0.875& 0.777& 0.901\\ F{M}_8& 0.935& 0.905& 0.857& 0.876& 0.913\\ F{M}_9& 0.805& 0.927& 0.869& 0.750& 0.883\\ F{M}_{10}& 0.926& 0.952& 0.931& 0.919& 0.925\\ F{M}_{11}& 0.881& 0.863& 0.843& 0.885& 0.903\\ F{M}_{12}& 0.937& 0.945& 0.863& 0.926& 0.860\\ F{M}_{13}& 0.933& 0.957& 0.776& 0.857& 0.943\\ F{M}_{14}& 0.954& 0.958& 0.850& 0.839& 0.925\\ F{M}_{15}& 0.934& 0.944& 0.797& 0.836& 0.934\end{array}\right]$$

The CIs of DMs are: $\left(C{I}_1, C{I}_2, C{I}_3,C{I}_4,C{I}_5\right)=\left(0.895,0.9319,0.8479,0.8545,0.9122\right)$. Based on the identification rules [33,36,37,38] and given consensus threshold $\gamma =0.85$, $D{M}_3$ is inconsistent and the set of inconsistent elements is such that:

$$\begin{array}{l}APS=\{(3,1,3),(3,2,2),(3,2,3),(3,3,1),(3,4,2),(3,6,3),(3,7,2),(3,8,3),(3,9,1),(3,9,3),\\ (3,11,1),(3,11,3),(3,12,3),(3,13,1),(3,13,2),(3,13,3),(3,14,1),(3,14,2),(3,15,2),(3,15,3)\}\end{array}$$

According to the minimum adjustment cost model [39], the minimum adjustment cost feedback parameter $\delta$ for $D{M}_3$ is solved as ${\delta }_3=0.03$. Then, the adjusted numerical risk evaluation matrix of $D{M}_3$ and updated collective numerical risk evaluation matrix can be obtained as follows:

$$\begin{gathered} {\mathit{RE}}^3=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& 4.000& 5.850& 5.746\\ F{M}_2& 5.000& 5.773& 5.758\\ F{M}_3& 5.768& 5.800& 5.763\\ F{M}_4& 3.200& 6.939& 4.000\\ F{M}_5& 4.000& 4.000& 4.000\\ F{M}_6& 3.200& 3.200& 2.030\\ F{M}_7& 4.000& 5.767& 3.200\\ F{M}_8& 5.800& 5.800& 5.762\\ F{M}_9& 3.248& 5.800& 2.052\\ F{M}_{10}& 4.000& 5.000& 4.000\\ F{M}_{11}& 5.753& 4.000& 2.031\\ F{M}_{12}& 5.000& 5.000& 2.053\\ F{M}_{13}& 5.773& 5.757& 2.051\\ F{M}_{14}& 5.769& 4.973& 5.000\\ F{M}_{15}& 5.800& 5.757& 2.046\end{array}\right] \\ {\mathit{RE}}^{\mathit{c}}=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& 4.602& 5.334& 3.982\\ F{M}_2& 4.276& 4.883& 4.399\\ F{M}_3& 4.736& 5.072& 4.557\\ F{M}_4& 4.096& 4.969& 4.134\\ F{M}_5& 4.286& 4.272& 3.744\\ F{M}_6& 3.774& 4.004& 3.005\\ F{M}_7& 4.470& 4.682& 3.860\\ F{M}_8& 5.056& 5.226& 4.537\\ F{M}_9& 4.795& 4.964& 3.751\\ F{M}_{10}& 4.286& 4.308& 4.272\\ F{M}_{11}& 4.234& 3.774& 3.052\\ F{M}_{12}& 4.744& 4.560& 3.784\\ F{M}_{13}& 4.883& 4.372& 3.705\\ F{M}_{14}& 4.758& 4.087& 4.236\\ F{M}_{15}& 5.102& 4.372& 3.546\end{array}\right] \end{gathered}$$

After the feedback mechanism, the new CIs of DMs are calculated as $C{I}^{\prime }=\left(C{I}_1^{\prime }, C{I}_2^{\prime }, C{I}_3^{\prime },C{I}_4^{\prime },C{I}_5^{\prime }\right)=\left(0.8951,0.9319,0.8505,0.8548,0.9122\right)$. Since the CI of each DM in FMEA team has reached the consensus threshold, the final stage is activated to rank FMs.

3.4. Ranking of Failure Modes

According to the updated collective numerical risk evaluation matrix $R{E}^c$ and the relative weight of risk factors $W=\left(w_O,w_S,w_D\right)=\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)$, the RPN values of FMs are calculated by Equation (5), shown in Table 8, and the FMs are sorted in descending order according to the RPN value, like so: $F{M}_8>F{M}_3>F{M}_1>F{M}_2>F{M}_9>F{M}_4>F{M}_{14}>F{M}_{12}>F{M}_7>F{M}_{15}>F{M}_{13}>F{M}_{10}>F{M}_5>F{M}_{11}>F{M}_6$.

$$RPN=O\cdot w_O\times S\cdot w_S\times D\cdot w_D$$

(5)

Table 8. The CIS numerical scales for different $D{M}_k$.

FMs	FM1	FM2	FM3	FM4	FM5
RPN	32.584	30.613	36.493	28.047	23.034
FMs	FM6	FM7	FM8	FM9	FM10
RPN	15.138	26.928	39.962	29.761	26.293
FMs	FM11	FM12	FM13	FM14	FM15
RPN	16.253	27.283	26.369	27.461	26.370

Notice that this article assumes that the weights of RFs are assigned evenly, and the weights of DMs are given in advance based on position and experience of DMs; however, a full explanation of these techniques is beyond the scope of this paper. In the managerial practice of the proposed methodology, more interesting techniques can be introduced to extend the entire FMEA framework.

4. Comparison and Discussion

In order to demonstrate the advantages of the proposed method of FMEA for IIP, a comparison analysis is performed between the proposed method and the traditional FMEA without CIS in this subsection. The collective numerical risk evaluation matrix without CIS model, ${\mathrm{E}}^{\mathrm{c}\prime }$, is calculated; the CIs of DMs in FMEA team are exhibited in Figure 9. As can be seen in Figure 9, the CIs of DMs have improved by accepting CIS. Meanwhile, according to the threshold, $D{M}_4$ has already achieved consensus after using CIS and no extra feedback recommendation process for $D{M}_4$ is required.

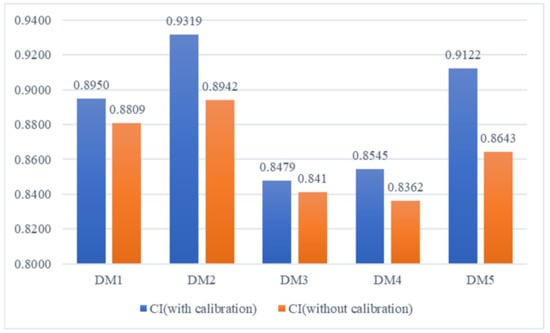
Figure 9. The CI of DMs under different linguistic models.

Subsequently, the CRP with the minimum adjustment cost feedback mechanism is carried out without CIS. Boundary feedback parameters are ${\delta }_3=0.11, {\delta }_4=0.14$, respectively, and the updated collective numerical risk evaluation matrix without CIS model $R{E}^{c\prime }$ is calculated as:

$$R{E}^{c\prime }=\left[\begin{array}{cccc}FMs& O& S& D\\ F{M}_1& 4.799& 5.360& 3.990\\ F{M}_2& 4.486& 4.953& 4.590\\ F{M}_3& 4.895& 5.435& 4.603\\ F{M}_4& 4.338& 5.201& 3.950\\ F{M}_5& 4.266& 4.180& 3.590\\ F{M}_6& 3.590& 3.820& 2.770\\ F{M}_7& 4.506& 4.739& 3.640\\ F{M}_8& 5.486& 5.382& 4.360\\ F{M}_9& 5.301& 5.461& 3.870\\ F{M}_{10}& 4.266& 4.180& 4.180\\ F{M}_{11}& 4.122& 3.590& 2.770\\ F{M}_{12}& 4.770& 4.540& 3.590\\ F{M}_{13}& 4.953& 4.362& 3.460\\ F{M}_{14}& 5.032& 4.006& 4.000\\ F{M}_{15}& 5.246& 4.362& 3.180\end{array}\right]$$

Then, the RPNs of FMs is calculated according to $R{E}^{c\prime }$, shown in Table 9 and the ranking of FMs is $F{M}_8>F{M}_3>F{M}_9>F{M}_2>F{M}_1>F{M}_4>F{M}_{14}>F{M}_{12}>F{M}_7>F{M}_{13}>F{M}_{10}>F{M}_{15}>F{M}_5>F{M}_{11}>F{M}_6$.

Table 9. The CIS numerical scales for different DM_k.

FMs	FM1	FM2	FM3	FM4	FM5
RPN	33.438	33.996	40.818	29.708	21.338
FMs	FM6	FM7	FM8	FM9	FM10
RPN	12.662	25.907	42.913	37.338	24.844
FMs	FM11	FM12	FM13	FM14	FM15
RPN	13.665	25.915	24.921	26.875	24.258

Based on the above comparison analysis, it is obvious that linguistic expressions of DMs are a key issue affecting the final result of group decision-making by affecting the CIs among DMs, in addition to knowledge background, work experience, and so on, which means that an additional adjustment cost will be paid for the individual differences in linguistic terms.

Additionally, the technique of linguistic calibration will affect the final rank of FMs by comparing the final ranking results of FMs, whose differences can be attributed to the implementation of linguistic calibration. There exists a similar result between the proposed and traditional method in the ranking of FMs with the highest and least risk, which demonstrates that the proposed method is effective.

In order to illustrate the distinctions of the proposed mechanism, a theoretical comparison with existing FMEA methods is presented from four perspectives: ‘what expression preference is used?’, ‘what linguistic calibration mechanism is adopted?’, ‘is a consensus process involved?’ and ‘to what practice is it applied?’, as shown in Table 10. In terms of expression preference, different linguistic expressions have their unique advantages. While the more complex the linguistic method is, the less loss of information there will be, the difficulty of application will also increase significantly. Therefore, 2-tuple linguistic methods are more popular with the public than other approaches due to their practicality. As for linguistic calibration, it is very important to address the fact that different DMs have different understandings of the same term. Compared with the PIS model, there exists no assumption that each preference is as consistent as possible in the CIS model, and so it is much easier to tackle the multi-attribute multi-alternative decision-making problem. Compared to [13,39,40], it is crucial to achieve consensus for a group of DMs in order to better implement the result of FMEA, because the DMs of an FMEA team often come from different fields and organizations with various professional skills, education backgrounds, and work experiences. In practice, the FMEA method proposed by Huang et.al. [9] was applied to the risk evaluation of a grinding wheel system, while Duan et.al. [13] proposed a FMEA model with double hierarchy hesitant fuzzy linguistic term sets and k-means clustering for the risk evaluation of floating offshore wind turbines. FMEA based on possibilistic hesitant fuzzy linguistic information with consensus process has been applied in the risk evaluation of proton beam radiotherapy [39], and a large-scale FMEA model with social network analysis and fairness-oriented consensus process has been utilized for photovoltaic systems [41]. In addition, a PIS-based FMEA approach with incomplete preference was adopted to the reliability management of blood transfusion [40].

Table 10. Comparisons with related FMEA methods.

FMEA Methods	Expression Preference	Linguistic Calibration	Consensus	FMEA Application
The proposed method	2-tuple linguistic term	CIS	Consensus	IIP
Huang et.al. [9]	Linguistic distribution assessment	No calibration	Without consensus	Grinding wheel system
Duan et.al. [13]	Double hierarchy linguistic term	No	Duan et.al.	Double hierarchy linguistic term
Zhang et.al. [39]	Possibilistic hesitant fuzzy linguistic term	No calibration	Consensus	Proton beam radiotherapy
Zhang et.al. [40]	Linguistic distribution assessment	PIS	Without consensus	Blood transfusion
Tang et.al. [41]	Crisp numbers	No calibration	Considered	Photovoltaic systems

5. Conclusions and Future Work

This article proposes a novel FMEA framework based on a CIS model considering a consensus-reaching process. Its main contributions are as follows:

An improved FMEA approach must address issues such as effectiveness, difficulty, practicality, etc. The proposed method does so as follows. First, compared with the conventional FMEA method, the proposed method has improved ability to tackle information uncertainties compared to the crisp values of RFs given by the 2-tuple linguistic model. Second, in contrast to the existing linguistic calibration method, not only is the figure-based CIS model more convenient to operate than the PIS model, but it also has a stronger reference foundation, making it more suitable for practical scenarios. Third, the proposed FMEA framework can better solve the disagreement between different DMs via a consensus-reaching process with a minimum adjustment cost feedback mechanism, as DMs in FMEA evaluation teams are usually from different organizations and departments. Fourth, the use of a real case of IIP illustrates the proposed FMEA framework, where the data involved are sourced from the staff of an industrial internet company.

In the future, the frameworks of large-scale group decision-making models will be introduced into FMEA problems to extend application scenarios, because there are usually a large number of FMEA evaluation members from multiple departments who are involved in complex decision-making. However, the relative weights of DMs are not considered in this article, being beyond the scope of the present research focus. Thus, in future work, the weights of DMs will be assigned based on the deviation between individual CIS curves and original curves. Furthermore, as the possible interrelationships between risk factors can affect the outcomes of risk rankings, such interrelationships will also be considered in the adjustment of risk factor weights in future work.