Two-Step Neural-Network-Based Fault Isolation for Stochastic Systems
Abstract
:1. Introduction
2. Static Modeling and Weighted Dynamic Modeling
2.1. Output PDFs’ Static Modeling
2.2. Nonlinear Dynamic Weight Model
3. Fault Detection Filter Design
4. Fault Isolation Filter Design
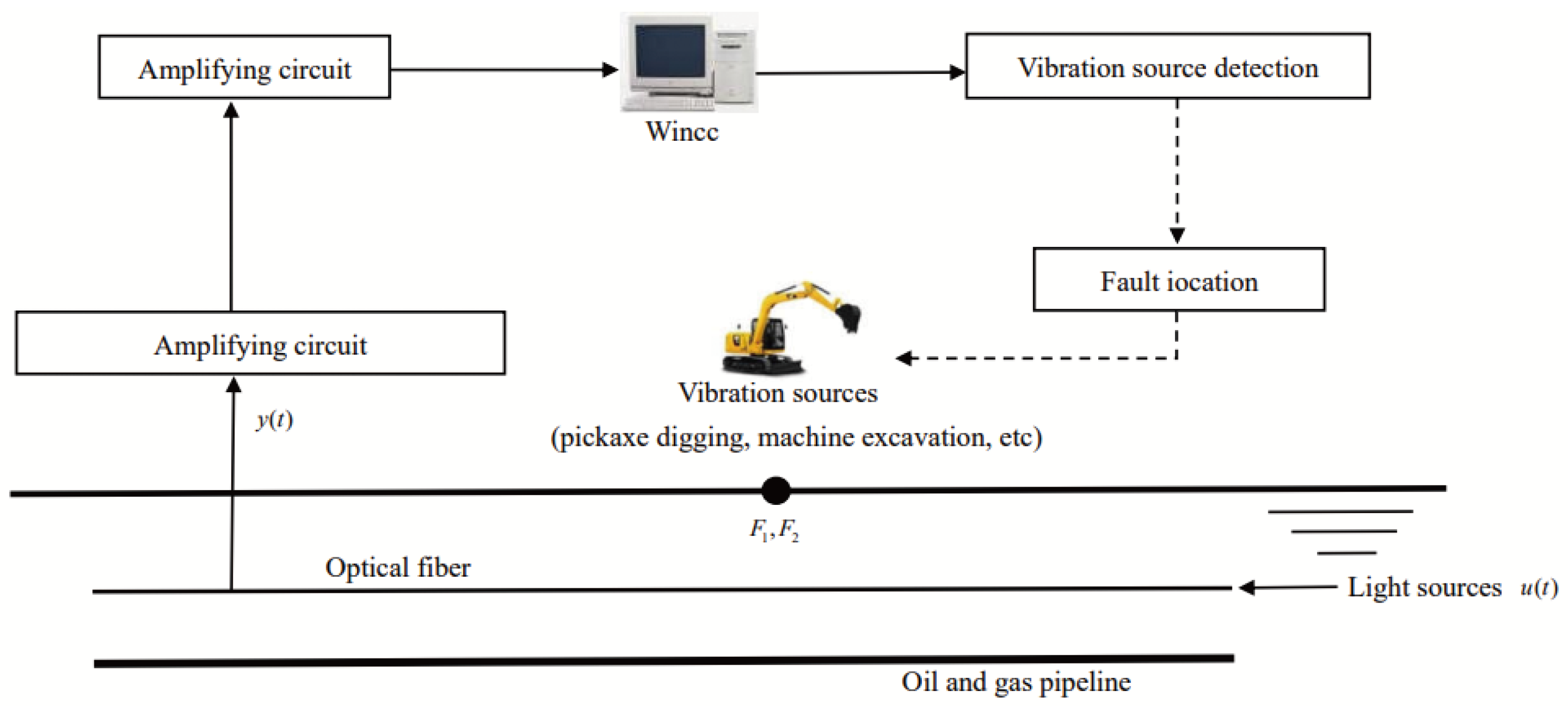
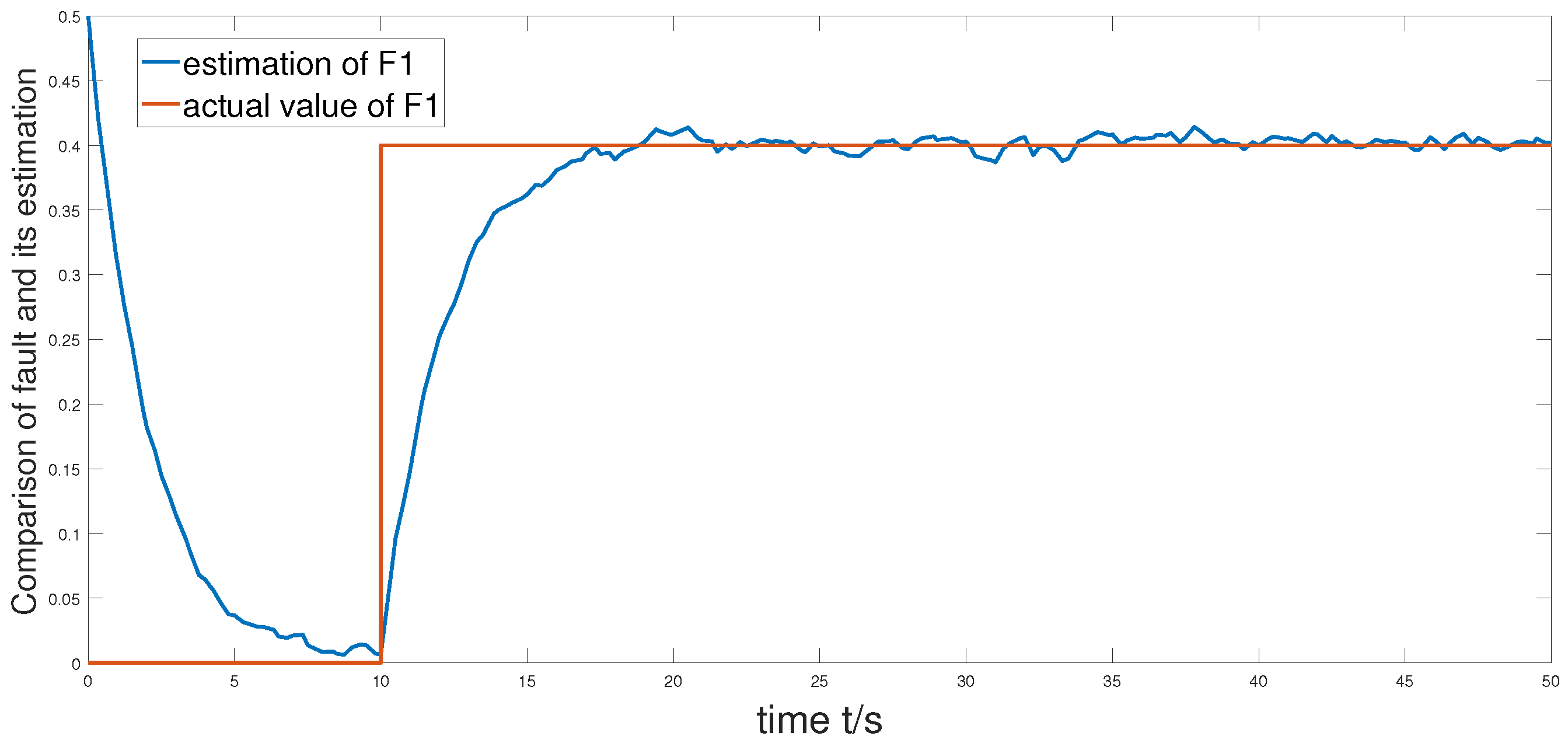
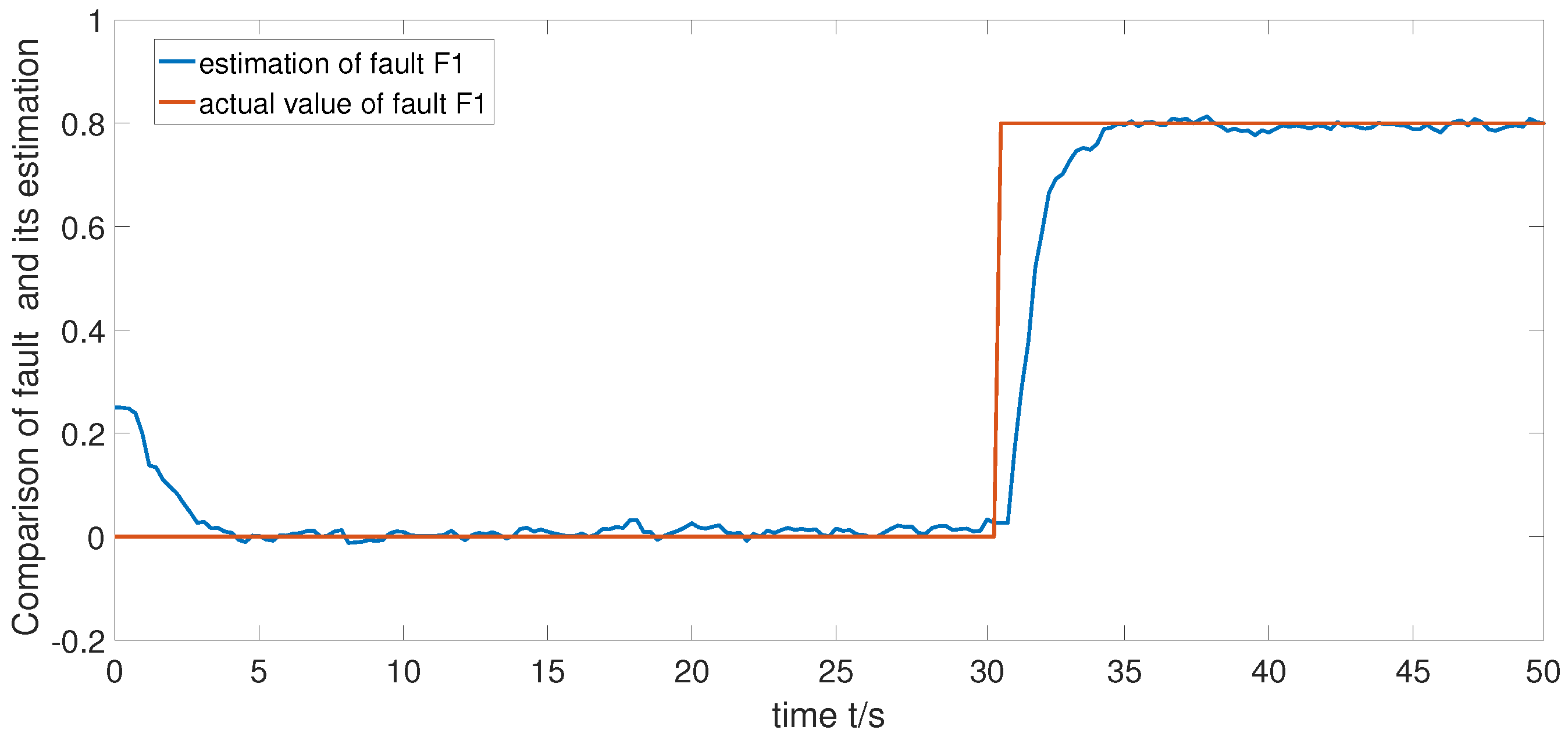
5. Simulation
6. Conclusions
7. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| output PDFs | |
| estimated output PDFs | |
| state vector | |
| estimated value of the state vector | |
| Fault 1 | |
| estimates of fault | |
| Fault 2 | |
| estimates of fault | |
| the corresponding weights of B-spline expansion | |
| model error term | |
| the pre-specified basis functions | |
| system output | |
| state error vector | |
| input of nonlinear stochastic optical fiber vibration detection system | |
| fault detection residual vector | |
| P | positive definite matrix to be solved |
| L | gain of fault diagnosis filter |
| nonlinear function | |
| probability density functions | |
| linear matrix inequalities | |
| fault detection and isolation |
References
- Yu, X.; Jiang, B.; Ke, Z. Observer-Based Fault Detection of Broken Rotor Bars in Traction Motors. In Proceedings of the 2017 29th IEEE Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 309–314. [Google Scholar]
- Venghi, L.E.; Aguilera, F.; de la Barrera, P.M.; De Angelo, C.H. Detection and isolation of current-sensor and open-switch faults in electric traction drives. IEEE Lat. Am. Trans. 2021, 19, 1335–1346. [Google Scholar] [CrossRef]
- Qiang, X.; Xue, R.; Zhu, Y. Multi-sensor Fusion Approach with Fault Detection and Isolation Based on two-state Probability Ratio. In Proceedings of the 2021 Sixth International Conference on Wireless Communications, Signal Processing and Networking, Chennai, India, 25–27 March 2021; pp. 325–329. [Google Scholar]
- Yin, L.; Wang, H.; Guo, L.; Zhang, H. Data-driven Pareto-DE-based intelligent optimal operational control for stochastic processes. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 4443–4452. [Google Scholar] [CrossRef]
- Yan, B.; Tian, Z.; Shi, S. A Novel Distributed Approach to Robust Fault Detection and Identification. Int. J. Electr. Power Energy Syst. 2008, 30, 343–360. [Google Scholar] [CrossRef]
- Wang, H.; Yao, L.N. Sensor Fault Diagnosis and Fault-Tolerant Control for Non-Gaussian Stochastic Distribution Systems. Math. Probl. Eng. 2019, 50, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Yao, L.; Xu, J.; Xu, F. Minimum Entropy Fault-Tolerant Control of the Non-Gaussian Stochastic Distribution System. IET Control Theory Appl. 2016, 10, 1194–1201. [Google Scholar] [CrossRef]
- Guo, L.; Wang, H. Fault Detection and Diagnosis for General Stochastic Systems Using B-Spline Expansions and Nonlinear Filters. IEEE Trans. Circuits Syst. I Regul. Pap. 2005, 52, 1644–1652. [Google Scholar]
- Cao, S.Y.; Guo, L. Fault Diagnosis with Disturbance Rejection Performance Based on Disturbance Observer. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, Shanghai, China, 16–18 December 2009; pp. 6947–6951. [Google Scholar]
- Zhang, J.; Gao, Q.; Yuan, C.; Zeng, W.; Dai, S.L.; Wang, C. Similar Fault Isolation of Discrete-Time Nonlinear Uncertain Systems: An Adaptive Threshold Based Approach. IEEE Access 2020, 8, 80755–80770. [Google Scholar] [CrossRef]
- Wang, H.; Kang, Y.; Yao, L.; Wang, H.; Gao, Z. Fault Diagnosis and Fault Tolerant Control for T–S Fuzzy Stochastic Distribution Systems Subject to Sensor and Actuator Faults. IEEE Trans. Fuzzy Syst. 2021, 29, 3561–3569. [Google Scholar] [CrossRef]
- Zhang, Y.W. Data Based Fault Isolation; Northeast University Press: Shenyang, China, 2016. [Google Scholar]
- Wang, Y.Q.; Hao, Y.E.; Ding, X.S.; Wang, G.Z. Fault Detection of Networked Control Systems Based on Optimal Robust Fault Detection Filter. Acta Autom. Sin. 2008, 34, 1534–1539. [Google Scholar] [CrossRef]
- Yang, L.; Wang, Z.; Xiao, H.; Zhou, D. Least Square Fault Estimation for a Class of Sensor Networks. In Proceedings of the 2013 25th Chinese Control and Decision Conference (CCDC), Guiyang, China, 25–27 May 2013; pp. 4984–4988. [Google Scholar]
- Biswas, S.; Nayak, P.K. A Fault Detection and Classification Scheme for Unified Power Flow Controller Compensated Transmission Lines Connecting Wind Farms. IEEE Syst. J. 2021, 15, 297–306. [Google Scholar] [CrossRef]
- Tran, M.Q.; Elsisi, M.; Liu, M.K. Effective Feature Selection with Fuzzy Entropy and Similarity Classifier for Chatter Vibration Diagnosis. Measurement 2021, 184, 109962. [Google Scholar] [CrossRef]
- Tran, M.Q.; Liu, M.K.; Elsisi, M. Effective Multi-sensor Data Dusion for Chatter Detection in Milling Process. ISA Trans. 2022, 125, 514–527. [Google Scholar] [CrossRef]
- Ren, M.F.; Zhang, J.H.; Wang, H. Control and Filtering for Non-Gaussian Systems; Science Press: Beijing, China, 2016. [Google Scholar]
- Cheng, Y.; Chen, B.; Zhang, W. Adaptive Multipoint Optimal Minimum Entropy Deconvolution Adjusted and Application to Fault Diagnosis of Rolling Element Bearings. IEEE Sens. J. 2019, 19, 12153–12164. [Google Scholar] [CrossRef]
- Guo, L.; Yin, L.; Wang, H.; Chai, T. Entropy Optimization Filtering for Fault Isolation of Nonlinear Non-Gaussian Stochastic Systems. IEEE Trans. Autom. Control 2009, 54, 804–810. [Google Scholar]
- Yin, L.; Lai, L.; Zhu, Z.; Li, T. Maximum Power Point Tracking Control for Non-Gaussian Wind Energy Conversion System by Using Survival Information Potential. Entropy 2022, 24, 818. [Google Scholar] [CrossRef]
- Shu, M.X. Research on False Alarm Control Algorithm for Fiber Vibration Source Detection under Non-Stationary Disturbances. Master’s Thesis, Nanjing University of Information Science & Technology, Nanjing, China, 2019. [Google Scholar]
- Han, D. Alarm Control and Simulation Platform Construction for Disturbed Optical Fiber Vibration Detection. Master’s Thesis, Nanjing University of Information Science & Technology, Nanjing, China, 2020. [Google Scholar]
- Cai, Y. Research Progress on Safety State Monitoring Technology of Oil and Gas Pipeline System. Pet. New Energy 2022, 34, 65–70. [Google Scholar]
- Wang, H. Bounded Dynamic Stochastic Systems, Modelling and Control; Springer Group: Berlin, Germany, 1999. [Google Scholar]
- Guo, L.; Yi, Y.; Yin, L.P.; Wang, H. Modeling, Analysis and Control Theory of Non-Gaussian Stochastic Distribution System; Science Press: Beijing, China, 2019. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, L.; Liu, J.; Qu, H.; Li, T. Two-Step Neural-Network-Based Fault Isolation for Stochastic Systems. Mathematics 2022, 10, 4261. https://doi.org/10.3390/math10224261
Yin L, Liu J, Qu H, Li T. Two-Step Neural-Network-Based Fault Isolation for Stochastic Systems. Mathematics. 2022; 10(22):4261. https://doi.org/10.3390/math10224261
Chicago/Turabian StyleYin, Liping, Jianguo Liu, Hongquan Qu, and Tao Li. 2022. "Two-Step Neural-Network-Based Fault Isolation for Stochastic Systems" Mathematics 10, no. 22: 4261. https://doi.org/10.3390/math10224261




