Adaptive Guided Spatial Compressive Cuckoo Search for Optimization Problems
Abstract
:1. Introduction
- (1)
- Improve Flight. Flight is proposed to enhance the disorder and randomness in the search process to increase the diversity of solutions. It combines considerable step length with a small step length to strengthen global searchability. Researchers modified Flight to achieve a faster convergence. Naik cancelled the step of flight and made the adaptive step according to the fitness function value and its current position in the search space [25]. In reference [26], Ammar Mansoor Kamoona improved CS by replacing the Gaussian random walk with a virus diffusion instead of the Lévy flights for a more stable process of nest updating in traditional optimization problems. Hu Peng et al. [27] used the combination of Gaussian distribution and distribution to control the global search by means of random numbers. S. Walton et al. [28] changed the step size generation method in flight and obtained a better performance. A new nearest neighbor strategy was adopted to replace the function of flight [29]. Moreover, he changed the strategy for crossover in global search. Jiatang Cheng et al. [30] drew lessons from ABC and employed two different one-dimensional update rules to balance the global and local search performance.
- (2)
- Secondly, the parameter and strategy adjustment have always been a significant concern for improving the metaheuristic algorithm. The accuracy and convergence speed of CS are increased through the adaptive adjustment of parameters or the innovation of strategies in the algorithm. For example, Pauline adopted a new adaptive step size adjustment strategy for the Flight weight factor, which can converge to the global optimal solution faster [31]. Tong et al. [32] proposed an improved CS; ImCS drew on the opposite learning strategy and combined it with the dynamic adjustment of the score probability. It was used for the identification of the photovoltaic model. Wang et al. [33] used chaotic mapping to adjust the step size of cuckoo in the original CS method and applied an elite strategy to retain the best population information. Hojjat Rakhshani et al. [34] proposed two population models and a new learning strategy. The strategy provided an online trade-off between the two models, including local and global searches via two snap and drift modes.
- (3)
- Thirdly, the combination of optimization and other algorithms is another improvement focus. For example, M. Shehab et al. [35] innovatively adopted the hill-climbing method into CS. The algorithm used CS to obtain the best solution and passed the solution to the hill-climbing algorithm. This intensification process accelerated the search and overcame the slow convergence of the standard CS algorithm. Jinjin Ding et al. [23] combined PSO with CS. The selection scheme of PSO and the elimination mechanism of CS gave the new algorithm a better performance. DE and CS also could be combined. In ref [36], Z. Zhang et al. made use of the characteristics of the two algorithms dividing the population into two subgroups independently.
- (1)
- An initialization method of a logistic chaotic map is used to replace the random number generation method regardless of the dimension.
- (2)
- A guiding method that includes the information of optimal solutions and worst solutions is used to facilitate the generation of offspring.
- (3)
- An adaptive update step size replaces the random step size to make the search radius more reasonable.
- (4)
- In the iterative process, the SC technique is added to compress the space to help rapid convergence artificially.
2. Cuckoo Search (CS)
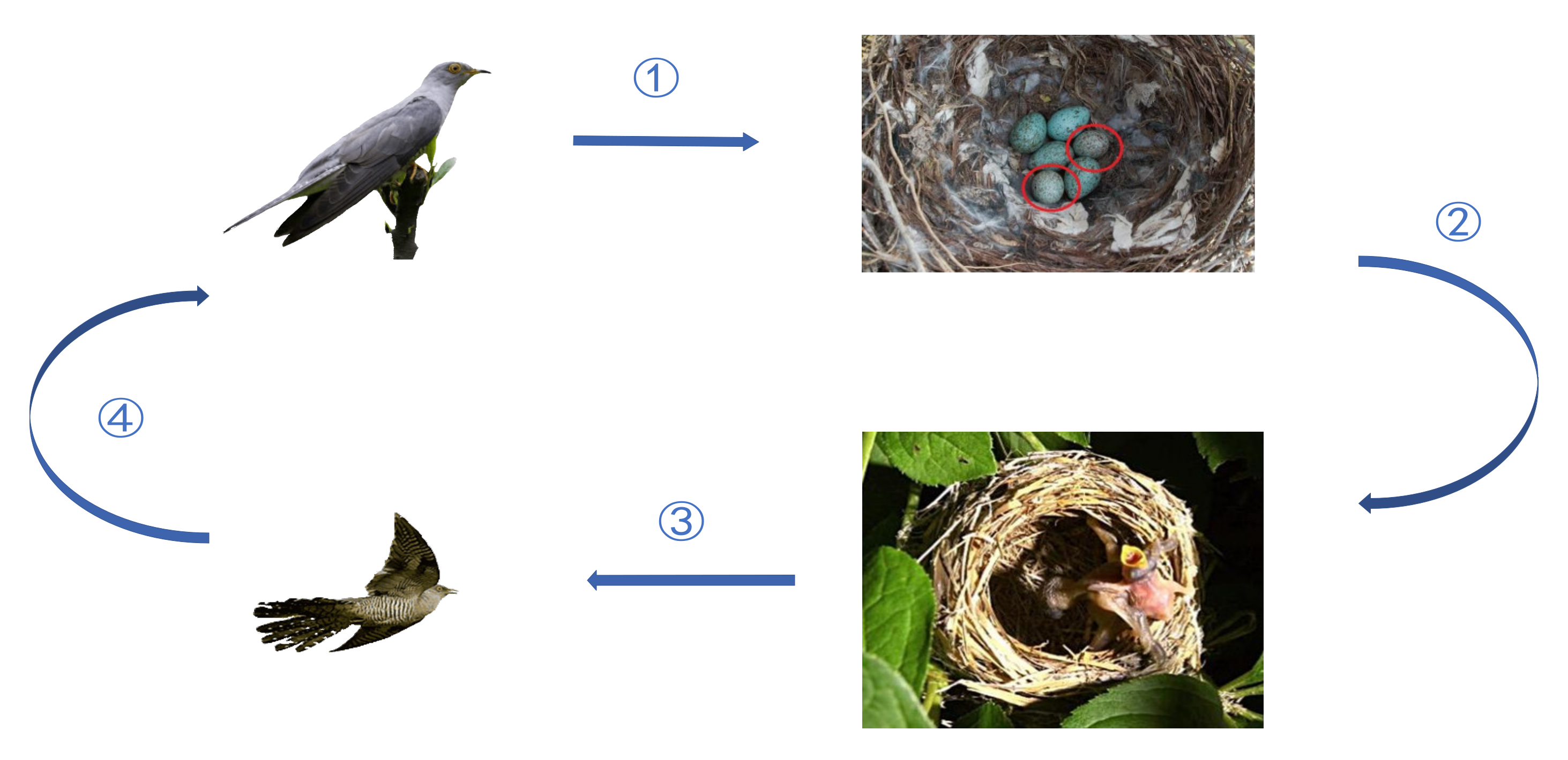
2.1. Cuckoo Breeding Behavior
2.2. Lévy Flights Random Walk (LFRW)
2.3. Local Random Walk
| Algorithm 1 The pseudo-code of CS |
| Input: : the population size : the dimension of the population : the maximum iteration numbers : the current iteration : the possibility of being discovered |
| : a single solution in the population |
| the best solution of all solution vectors in the current iteration |
| 1: For |
| 2: Initialize the 3: End |
| 4: Calculate , find the best nest and record its fitness |
| 5: While do |
| 6: Randomly choose th solution to make a LFRW and calculate fitness |
| 7: If |
| 8: Replace by and update the location of the nest by Equation (2) |
| 9: End If |
| 10: For = 1: |
| 11: If the egg is discovered by the host |
| 12: Random walk on current generation and generate a new solution by Equation (9) |
| 13: If |
| 14: Replace by and update the location of the nest |
| 15: End If |
| 16: End If |
| 17: End for |
| 18: Replace with the best solution obtained so far |
| 19: |
| 20: End while |
| Output: The best solution |
3. Main Ideas of Improved AGSCCS
3.1. Initialization
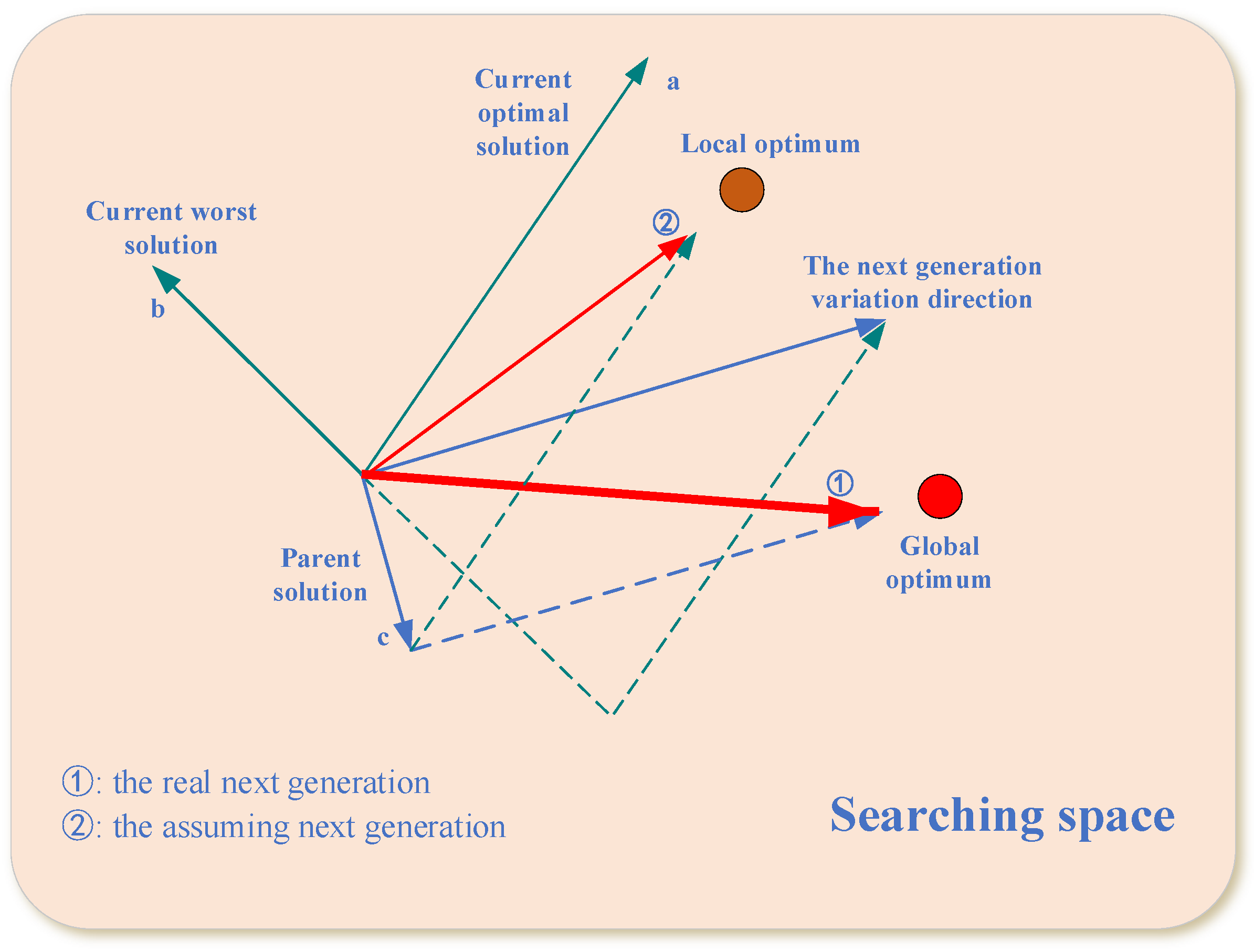
3.2. A Scheme of Updating Personalized Adaptive Guided Local Location Areas
| Algorithm 2 The pseudo-code of |
| Input: : the current iteration |
| : the maximum number of iterations |
| 1: |
| 2: Initialize , |
| 3: |
| 4: Update , |
| 5: Judge whether the current is within the threshold |
| 6: If rand < threshold do |
| 7: |
| 8: Else |
| 9: 10: End if 11: Calculate new step size by Equation (12) |
| Output: The value of |
3.3. Spatial Compressions Technique
| Algorithm 3 The pseudo-code of shrink space technique |
| Input: : the current iteration |
| : the maximum number of iterations |
| : the population size |
| 1: Initialize , |
| 2: If mod (g) = 0 |
| 3: For to do |
| 4: Calculating and for different individuals in the population by Equations (13) and (14) |
| 5: If < do |
| 6: choose as shrinking operator |
| 7: Else |
| 8: choose as shrinking operator 9: End if |
| 10: End for |
| 11: Update the new upper and lower bounds by Equation (15) |
| 12: End if |
| Output: new upper and lower bounds |
| Algorithm 4 The pseudo-code of AGSCCS |
| Input: : the population size |
| : the dimension of decision variables |
| : the maximum iteration number |
| : the possibility of being discovered |
| : a single solution in the population |
| the best solution of the all solutions in the current iteration |
| 1: For |
| 2: Initialize the population by Equation (11) 3: End |
| 4: Calculate , find the best nest and record its fitness |
| 5: While do |
| 6: Make a LFRW for and calculate fitness |
| 7: If |
| 8: Replace with and update the location of the nest |
| 9: End If |
| 10: Sort the population and find the top and bottom |
| 11: If the egg is discovered by the host |
| 12: Calculate the adaptive step size by Algorithm 2 and Equation (12) |
| 13: Random walk on current generation and generate a new solution |
| 14: End If |
| 15: If |
| 16: Replace with and update the location of the nest |
| 17: End If |
| 18: Replace with the best solution obtained so far |
| 19: If |
| 20: Conduct the shrink space technique as shown in Algorithm 3 |
| 21: If the new boundary value is not within limits |
| 22: Conduct boundary condition control |
| 23: End if |
| 24: End if |
| 25: |
| 26: End while |
| Output: The best solution after iteration |
3.4. Computational Complexity
- (1)
- The chaotic mapping of AGSCCS initialization in time.
- (2)
- Adaptive guided local location areas require time.
- (3)
- Adaptive operator F requires time.
- (4)
- The shrinking space technique demands , where T is the threshold controlling spatial compress technique.
4. Experiment and Analysis
4.1. Benchmark Test
- (1)
- Unimodal Functions ()
- (2)
- Simple multimodal Functions ()
- (3)
- Hybrid functions ()
- (4)
- Composition functions ()
4.2. Comparison between AGSCCS and Other Algorithms
- (1)
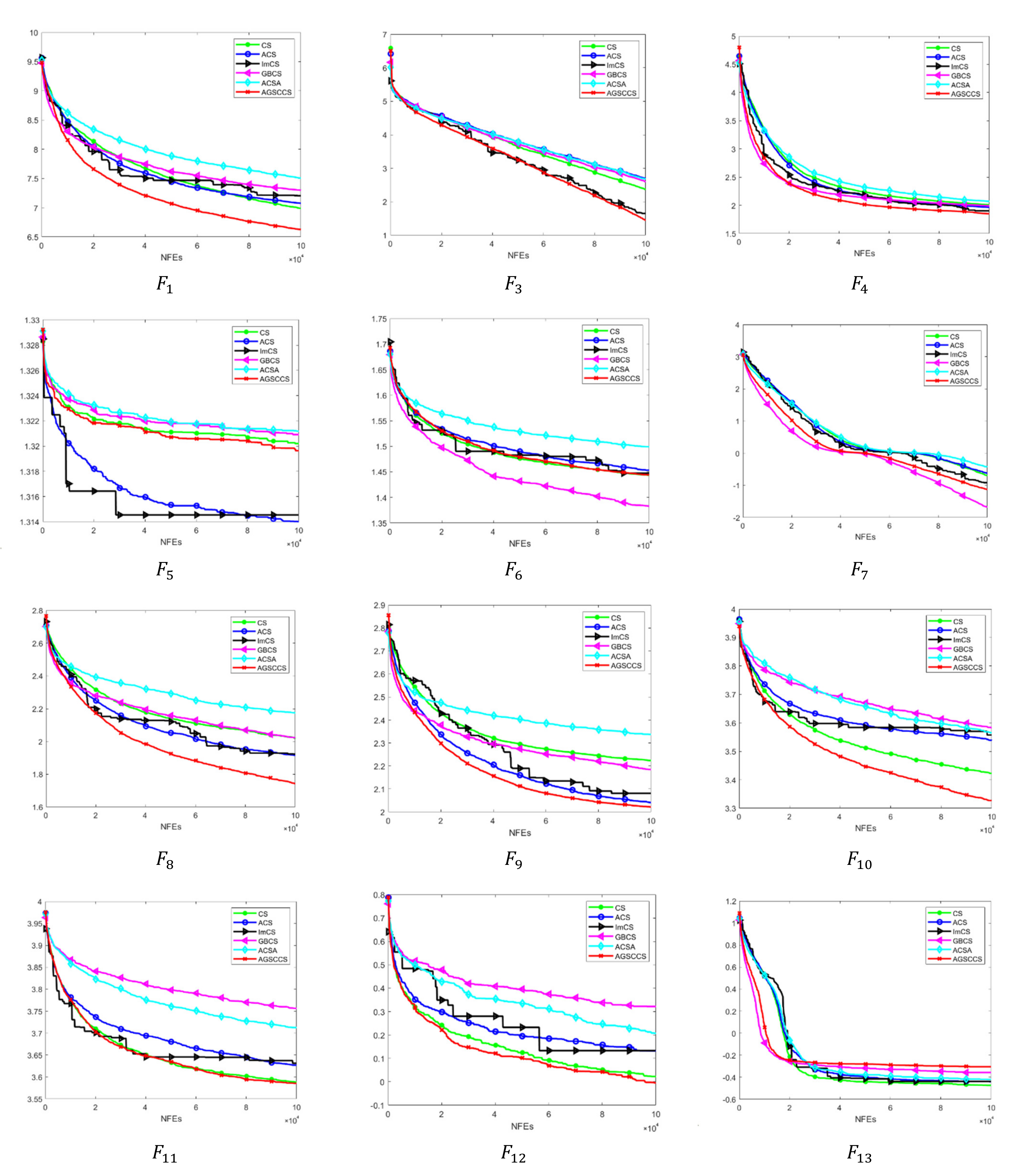
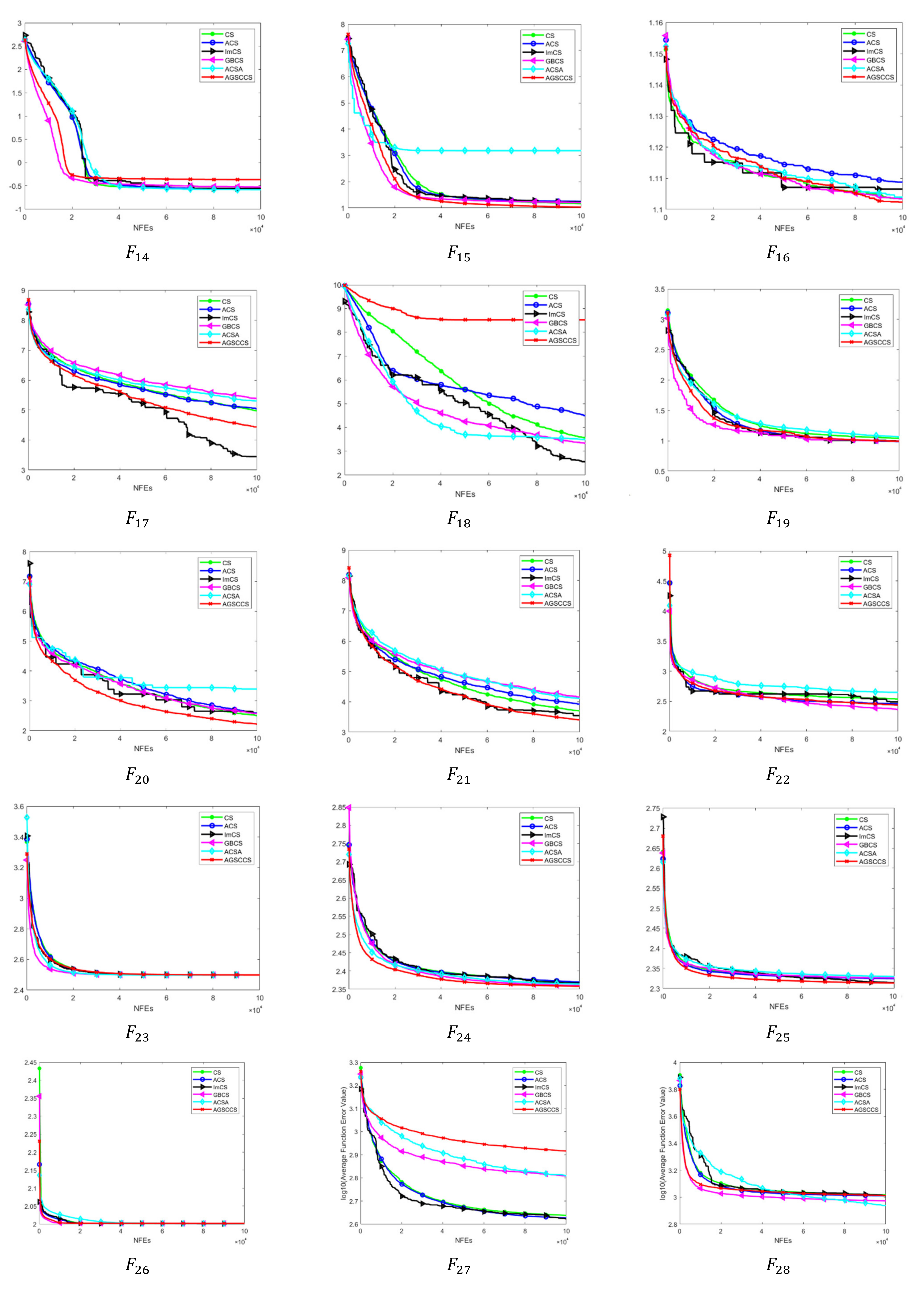
- Unimodal functions (). In Table 1, AGSCCS shows better performances in two functions in a group of three algorithms compared with CS, ACS, ImCS, GBCS, and ACSA when D = 30. Actually, except for function , it may be because the CS algorithm cannot find the best value for the function, whereas AGSCCS always gets the best results in and compared to the other four algorithms. Given that the whole domain of the unimodal function is smooth, it is easy for the algorithm to find the minimum on the unimodal function. In this situation, AGSCCS can also score the best grades that prove the pretty exploitation capacity compared to other algorithms. This may owe to the SC technique. It quickly distinguishes the current environment to the extreme value of the region. Additionally, it benefits the capacity for algorithm convergence.
- (2)
- Simple multimodal functions (). These functions are comparatively difficult for iterations compared to unimodal functions, given that they have more local extremums. In a total of 13 functions, AGSCCS performs better compared to eight functions, while CS, ACS, ImCS, GBCS, and ACSA have outstanding performances in functions 2, 1, 1, 3, 2, respectively; especially shown in Figure 6, given that it is a shifted and rotated expanded function with multiple extreme points. Moreover, it adds some characteristics of the Rosenbrock function into the search space, which strengthens the difficulty for finding the solution. AGSCCS achieves good iterative results on this function, which shows an excellent exploration capacity. This good exploration capacity is from the adaptive guided updating location method. The guided differential step size method can help the algorithm search for the direction of good solutions while avoiding bad solutions.
- (3)
- Hybrid functions (). In these functions, AGSCCS still achieves the best compared to the other four algorithms. It has better performances on , , , and . In the total of six functions, CS, ACS, ImCS, GBCS, and ACSA lead in only functions 0, 1, 1, 2, 0. In , the six algorithms almost converge to smaller values while AGSCCS can converge to a better value, which exhibits the excellent capacity of exploration of AGSCCS. Although GBCS has better results in , AGSCCS is extremely close to its results. These experimental results can prove the leading position of AGSCCS in hybrid functions.
- (4)
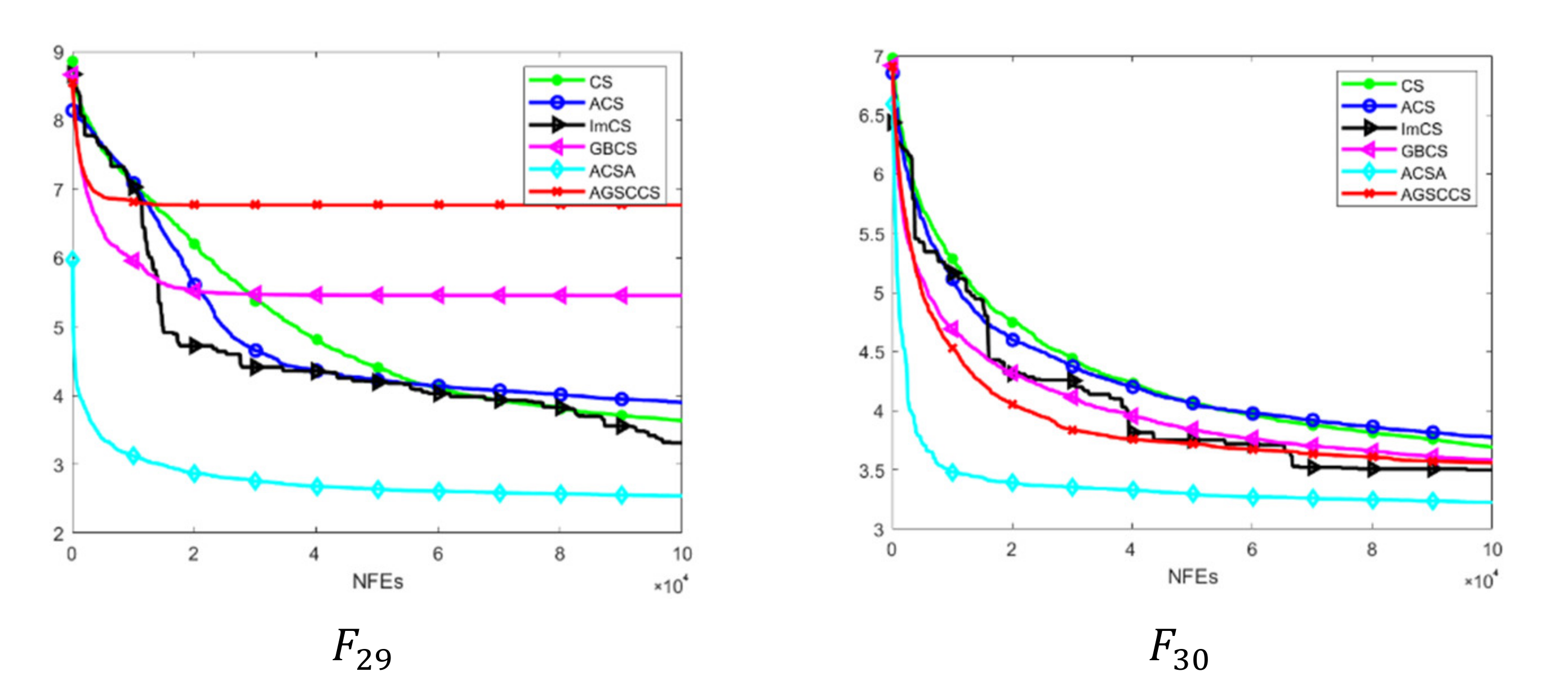
- Composition functions (). In , AGSCCS shows better performances in four functions in total. Intuitively, AGSCCS has the best results in . In these four functions, it always gets full marks. Although ACS performs unsatisfactorily on , it cannot deny its excellent exploration and exploration ability. On the previous unimodal and multimodal functions, the comprehensive performances of ACS have been certified. The poor performances of ACS may be due to the instability of its state under multi-dimensional and multimodal problems. Therefore, AGSCCS does not show any disadvantages compared with the other four algorithms in hybrid composition functions.
 ,
,  , and
, and  , which belong to the multimodal functions. Hence, it is not hard to conclude that GBCS has a worse iteration capacity than AGSCCS. Due to the SC technique, AGSCCS can easily and quickly find the optimal value in the searching space. The adaptive random replacement nest step ensures that the searching direction is not easy to fall into the local optimal. Therefore, in terms of comprehensive strength, the AGSCCS algorithm performs better.
, which belong to the multimodal functions. Hence, it is not hard to conclude that GBCS has a worse iteration capacity than AGSCCS. Due to the SC technique, AGSCCS can easily and quickly find the optimal value in the searching space. The adaptive random replacement nest step ensures that the searching direction is not easy to fall into the local optimal. Therefore, in terms of comprehensive strength, the AGSCCS algorithm performs better.4.3. Discussion
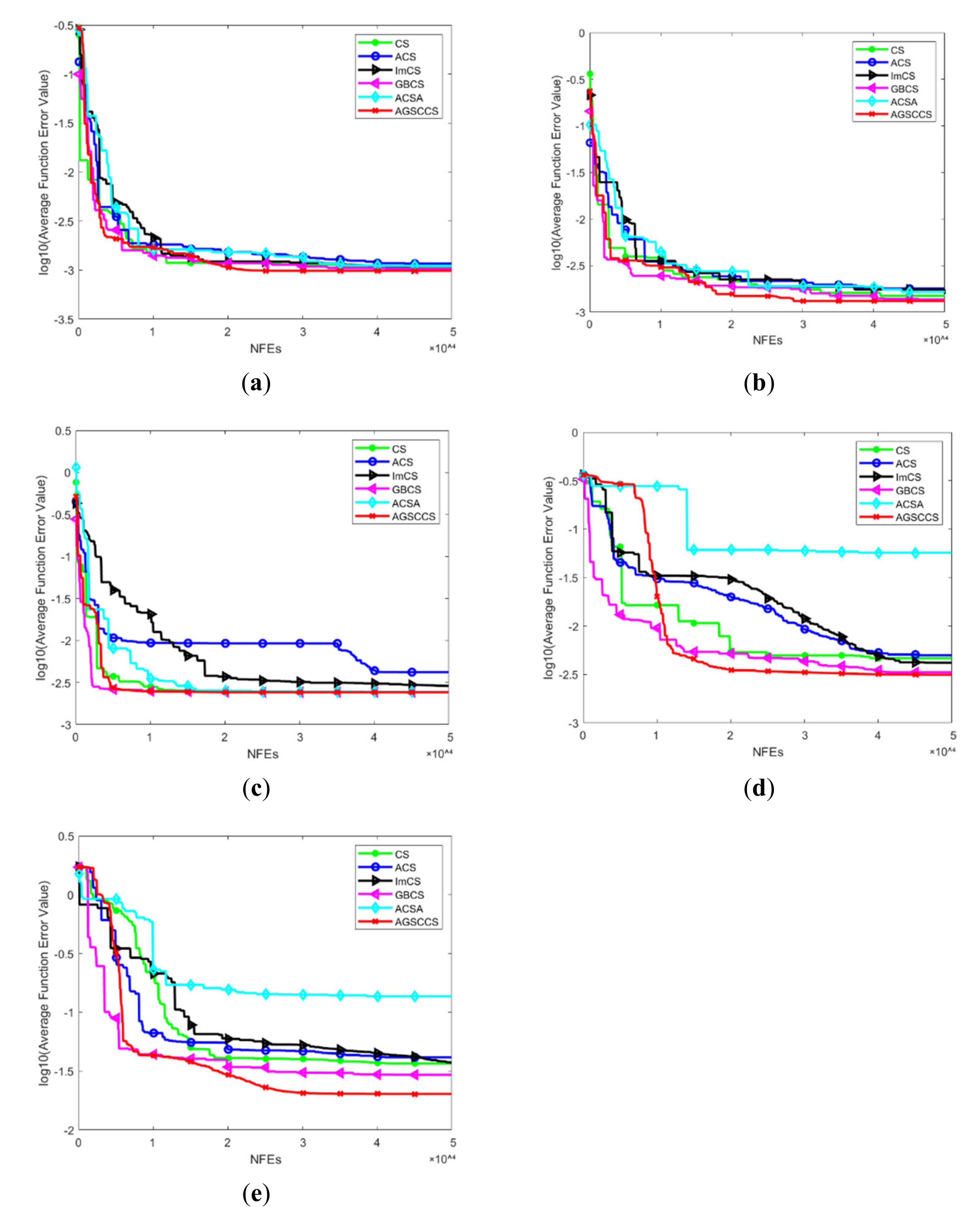
4.4. Statistical Analysis
5. Engineering Applications of AGSCCS
5.1. Problem Formulation
5.1.1. Single Diode Model (SDM)
5.1.2. Double Diode Model
5.1.3. PV Module Model
5.2. Results and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sinha, N.; Chakrabarti, R.; Chattopadhyay, P.K. Evolutionary programming techniques for economic load dispatch. IEEE Trans. Evol. Comput. 2003, 7, 83–94. [Google Scholar] [CrossRef]
- Boushaki, S.I.; Kamel, N.; Bendjeghaba, O. A new quantum chaotic cuckoo search algorithm for data clustering. Expert Syst. Appl. 2018, 96, 358–372. [Google Scholar] [CrossRef]
- Tejani, G.G.; Pholdee, N.; Bureerat, S.; Prayogo, D.; Gandomi, A.H. Structural optimization using multi-objective modified adaptive symbiotic organisms search. Expert Syst. Appl. 2019, 125, 425–441. [Google Scholar] [CrossRef]
- Kamoona, A.M.; Patra, J.C. A novel enhanced cuckoo search algorithm for contrast enhancement of gray scale images. Appl. Soft Comput. 2019, 85, 105749. [Google Scholar] [CrossRef]
- Bérubé, J.-F.; Gendreau, M.; Potvin, J.-Y. An exact-constraint method for biobjective combinatorial optimization problems: Application to the Traveling Salesman Problem with Profits. Eur. J. Oper. Res. 2009, 194, 39–50. [Google Scholar] [CrossRef]
- Dodu, J.C.; Martin, P.; Merlin, A.; Pouget, J. An optimal formulation and solution of short-range operating problems for a power system with flow constraints. Proc. IEEE 1972, 60, 54–63. [Google Scholar] [CrossRef]
- Vorontsov, M.A.; Carhart, G.W.; Ricklin, J.C. Adaptive phase-distortion correction based on parallel gradient-descent optimization. Opt. Lett. 1997, 22, 907–909. [Google Scholar] [CrossRef]
- Parikh, J.; Chattopadhyay, D. A multi-area linear programming approach for analysis of economic operation of the Indian power system. IEEE Trans. Power Syst. 1996, 11, 52–58. [Google Scholar] [CrossRef]
- Kim, J.S.; Ed Gar, T.F. Optimal scheduling of combined heat and power plants using mixed-integer nonlinear programming. Energy 2014, 77, 675–690. [Google Scholar] [CrossRef]
- Fan, J.Y.; Zhang, L. Real-time economic dispatch with line flow and emission constraints using quadratic programming. IEEE Trans. Power Syst. 1998, 13, 320–325. [Google Scholar] [CrossRef]
- Reid, G.F.; Hasdorff, L. Economic Dispatch Using Quadratic Programming. IEEE Trans. Power Appar. Syst. 1973, 6, 2015–2023. [Google Scholar] [CrossRef]
- Oliveira, P.; Mckee, S.; Coles, C. Lagrangian relaxation and its application to the unit-commitment-economic-dispatch problem. Ima J. Manag. Math. 1992, 4, 261–272. [Google Scholar] [CrossRef]
- El-Keib, A.A.; Ma, H. Environmentally constrained economic dispatch using the LaGrangian relaxation method. Power Syst. IEEE Trans. 1994, 9, 1723–1729. [Google Scholar] [CrossRef]
- Aravindhababu, P.; Nayar, K.R. Economic dispatch based on optimal lambda using radial basis function network. Int. J. Electr. Power Energy Syst. 2002, 24, 551–556. [Google Scholar] [CrossRef]
- Obioma, D.D.; Izuchukwu, A.M. Comparative analysis of techniques for economic dispatch of generated power with modified Lambda-iteration method. In Proceedings of the IEEE International Conference on Emerging & Sustainable Technologies for Power & Ict in A Developing Society, Owerri, Nigeria, 14–16 November 2013; pp. 231–237. [Google Scholar]
- Mohammadian, M.; Lorestani, A.; Ardehali, M.M. Optimization of Single and Multi-areas Economic Dispatch Problems Based on Evolutionary Particle Swarm Optimization Algorithm. Energy 2018, 161, 710–724. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Deb, K. A Comparative Analysis of Selection Schemes Used in Genetic Algorithms. Found. Genet. Algorithm. 1991, 1, 69–93. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the Icnn95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Yang, X. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO); Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Sm, A.; Smm, B.; Al, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar]
- Yang, X.S.; Deb, S. Engineering Optimisation by Cuckoo Search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar] [CrossRef]
- Ding, J.; Wang, Q.; Zhang, Q.; Ye, Q.; Ma, Y. A Hybrid Particle Swarm Optimization-Cuckoo Search Algorithm and Its Engineering Applications. Math. Probl. Eng. 2019, 2019, 5213759. [Google Scholar] [CrossRef]
- Mareli, M.; Twala, B. An adaptive Cuckoo search algorithm for optimisation. Appl. Comput. Inform. 2018, 14, 107–115. [Google Scholar] [CrossRef]
- Naik, M.K.; Panda, R. A novel adaptive cuckoo search algorithm for intrinsic discriminant analysis based face recognition. Appl. Soft Comput. 2016, 38, 661–675. [Google Scholar] [CrossRef]
- Selvakumar, A.I.; Thanushkodi, K. Optimization using civilized swarm: Solution to economic dispatch with multiple minima. Electr. Power Syst. Res. 2009, 79, 8–16. [Google Scholar] [CrossRef]
- Hu, P.; Deng, C.; Hui, W.; Wang, W.; Wu, Z. Gaussian bare-bones cuckoo search algorithm. In Proceedings of the the Genetic and Evolutionary Computation Conference Companion, Kyoto, Japan, 15–19 July 2018. [Google Scholar]
- Walton, S.; Hassan, O.; Morgan, K.; Brown, M.R. Modified cuckoo search: A new gradient free optimisation algorithm. Chaos Solitons Fractals 2011, 44, 710–718. [Google Scholar] [CrossRef]
- Wang, L.; Zhong, Y.; Yin, Y. Nearest neighbour cuckoo search algorithm with probabilistic mutation. Appl. Soft Comput. 2016, 49, 498–509. [Google Scholar] [CrossRef]
- Cheng, J.; Wang, L.; Jiang, Q.; Xiong, Y. A novel cuckoo search algorithm with multiple update rules. Appl. Intell. 2018, 48, 4192–4211. [Google Scholar] [CrossRef]
- Ong, P. Adaptive cuckoo search algorithm for unconstrained optimization. Sci. World J. 2014, 2014, 943403. [Google Scholar] [CrossRef] [PubMed]
- Kang, T.; Yao, J.; Jin, M.; Yang, S.; Duong, T. A Novel Improved Cuckoo Search Algorithm for Parameter Estimation of Photovoltaic (PV) Models. Energies 2018, 11, 1060. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.G.; Deb, S.; Gandomi, A.H.; Zhang, Z.; Alavi, A.H. Chaotic cuckoo search. Soft Comput. 2016, 20, 3349–3362. [Google Scholar] [CrossRef]
- Rakhshani, H.; Rahati, A. Snap-drift cuckoo search: A novel cuckoo search optimization algorithm. Appl. Soft Comput. 2017, 52, 771–794. [Google Scholar] [CrossRef]
- Shehab, M.; Khader, A.T.; Al-Betar, M.A.; Abualigah, L.M. Hybridizing cuckoo search algorithm with hill climbing for numerical optimization problems. In Proceedings of the 2017 8th International Conference on Information Technology (ICIT), Amman, Jordan, 17–18 May 2017. [Google Scholar]
- Zhang, Z.; Ding, S.; Jia, W. A hybrid optimization algorithm based on cuckoo search and differential evolution for solving constrained engineering problems. Eng. Appl. Artif. Intell. 2019, 85, 254–268. [Google Scholar] [CrossRef]
- Pareek, N.K.; Patidar, V.; Sud, K.K. Image encryption using chaotic logistic map. Image Vis. Comput. 2006, 24, 926–934. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Mohamed, A.K. Adaptive guided differential evolution algorithm with novel mutation for numerical optimization. Int. J. Mach. Learn. Cybern. 2017, 10, 253–277. [Google Scholar] [CrossRef]
- Aguirre, A.H.; Rionda, S.B.; Coello Coello, C.A.; Lizárraga, G.L.; Montes, E.M. Handling constraints using multiobjective optimization concepts. Int. J. Numer. Methods Eng. 2004, 59, 1989–2017. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Zhou, Y. Accelerating adaptive trade-off model using shrinking space technique for constrained evolutionary optimization. Int. J. Numer. Methods Eng. 2009, 77, 1501–1534. [Google Scholar] [CrossRef]
- Kaveh, A. Cuckoo Search Optimization; Springer: Cham, Switzerland, 2014; pp. 317–347. [Google Scholar] [CrossRef]
- Ley, A. The Habits of the Cuckoo. Nature 1896, 53, 223. [Google Scholar] [CrossRef]
- Humphries, N.E.; Queiroz, N.; Dyer, J.; Pade, N.G.; Musyl, M.K.; Schaefer, K.M.; Fuller, D.W.; Brunnsc Hw Eiler, J.M.; Doyle, T.K.; Houghton, J. Environmental context explains Lévy and Brownian movement patterns of marine predators. Nature 2010, 465, 1066–1069. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Cui, X.; Li, Y. Self-Adaptive adjustment of cuckoo search K-means clustering algorithm. Appl. Res. Comput. 2018, 35, 3593–3597. [Google Scholar]
- Wilk, G.; Wlodarczyk, Z. Interpretation of the Nonextensivity Parameter q in Some Applications of Tsallis Statistics and Lévy Distributions. Phys. Rev. Lett. 1999, 84, 2770–2773. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.T.; Phung, T.A.; Truong, A.V. A novel method based on adaptive cuckoo search for optimal network reconfiguration and distributed generation allocation in distribution network. Int. J. Electr. Power Energy Syst. 2016, 78, 801–815. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. Modified cuckoo search algorithm with self adaptive parameter method. Inf. Sci. 2015, 298, 80–97. [Google Scholar] [CrossRef]
- Naik, M.; Nath, M.R.; Wunnava, A.; Sahany, S.; Panda, R. A new adaptive Cuckoo search algorithm. In Proceedings of the IEEE International Conference on Recent Trends in Information Systems, Kolkata, India, 9–11 July 2015. [Google Scholar]
- Farswan, P.; Bansal, J.C. Fireworks-inspired biogeography-based optimization. Soft Comput. 2018, 23, 7091–7115. [Google Scholar] [CrossRef]
- Birx, D.L.; Pipenberg, S.J. Chaotic oscillators and complex mapping feed forward networks (CMFFNs) for signal detection in noisy environments. In Proceedings of the International Joint Conference on Neural Networks, Baltimore, MD, USA, 7–11 June 2002. [Google Scholar]
- Qi, W. A self-adaptive embedded chaotic particle swarm optimization for parameters selection of Wv-SVM. Expert Syst. Appl. 2011, 38, 184–192. [Google Scholar]
- Wang, L.; Yin, Y.; Zhong, Y. Cuckoo search with varied scaling factor. Front. Comput. Sci. 2015, 9, 623–635. [Google Scholar] [CrossRef]
- Das, S.; Mallipeddi, R.; Maity, D. Adaptive evolutionary programming with p-best mutation strategy. Swarm Evol. Comput. 2013, 9, 58–68. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.S. JADE: Adaptive Differential Evolution With Optional External Archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Armani, R.F.; Wright, J.A.; Savic, D.A.; Walters, G.A. Self-Adaptive Fitness Formulation for Evolutionary Constrained Optimization of Water Systems. J. Comput. Civ. Eng. 2005, 19, 212–216. [Google Scholar] [CrossRef]
- Bo, Y.; Gallagher, M. Experimental results for the special session on real-parameter optimization at CEC 2005: A simple, continuous EDA. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005. [Google Scholar]
- Liang, J.J.; Qu, B.Y.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2014 Special Session and Competition on Single Objective Real-Parameter Numerical Optimization; Technical Report 201311; Computational Intelligence Laboratory, Zhengzhou University: Zhengzhou, China; Nanyang Technological University: Singapore, December 2013. [Google Scholar]
- Yang, X.; Gong, W. Opposition-based JAYA with population reduction for parameter estimation of photovoltaic solar cells and modules. Appl. Soft Comput. 2021, 104, 107218. [Google Scholar] [CrossRef]



| CS | ACS | ImCS | GBCS | ACSA | AGSCCS | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| f1 | 9.76 × 106 | 2.42 × 106 | 1.19 × 107 | 3.35 × 106 | 1.60 × 107 | 2.34 × 105 | 1.99 × 107 | 5.97 × 106 | 3.21 × 107 | 1.05 × 107 | 4.23 × 106 | 1.40 × 106 |
| f2 | 1.00 × 1010 | 0.00 | 1.00 × 1010 | 0.00 | 1.00 × 1010 | 0.00 | 1.00 × 1010 | 0.00 | 1.00 × 1010 | 0.00 | 1.00 × 1010 | 0.00 |
| f3 | 2.31 × 102 | 8.32 × 101 | 4.98 × 102 | 1.34 × 102 | 4.49 × 101 | 1.98 × 101 | 3.99 × 102 | 9.55 × 101 | 4.76 × 102 | 2.10 × 102 | 2.80 × 101 | 7.34 |
| f4 | 1.02 × 102 | 1.87 × 101 | 9.24 × 101 | 2.54 × 101 | 7.94 × 101 | 2.29 × 101 | 9.79 × 101 | 1.80 × 101 | 1.18 × 102 | 2.12 × 101 | 7.08 × 101 | 2.28 × 101 |
| f5 | 2.09 × 101 | 8.99 × 10−2 | 2.06 × 101 | 5.57 × 10−2 | 2.06 × 101 | 4.87 × 10−2 | 2.09 × 101 | 5.06 × 10−2 | 2.09 × 101 | 5.56 × 10−2 | 2.09 × 101 | 7.94 × 10−2 |
| f6 | 2.77 × 101 | 9.62 × 10−1 | 2.84 × 101 | 2.29 | 2.80 × 101 | 2.39 | 2.42 × 101 | 3.36 | 3.16 × 101 | 1.69 | 2.78 × 101 | 1.32 |
| f7 | 2.03 × 10−1 | 5.60 × 10−2 | 2.35 × 10−1 | 7.40 × 10−2 | 1.20 × 10−1 | 5.70 × 10−2 | 2.12 × 10−2 | 1.30 × 10−2 | 3.70 × 10−1 | 9.40 × 10−2 | 7.51 × 10−2 | 5.61 × 10−2 |
| f8 | 1.04 × 102 | 1.44 × 101 | 8.24 × 101 | 1.41 × 101 | 8.39 × 101 | 1.30 × 101 | 1.05 × 102 | 1.54 × 101 | 1.49 × 102 | 1.69 × 101 | 5.53 × 101 | 8.21 |
| f9 | 1.67 × 102 | 2.16 × 101 | 1.10 × 102 | 1.55 × 101 | 1.21 × 102 | 1.42 × 101 | 1.53 × 102 | 1.46 × 101 | 2.18 × 102 | 1.80 × 101 | 1.05 × 102 | 1.48 × 101 |
| f10 | 2.65 × 103 | 1.81 × 102 | 3.45 × 103 | 4.12 × 102 | 3.61 × 103 | 4.40 × 102 | 3.83 × 103 | 5.35 × 102 | 3.68 × 103 | 4.45 × 102 | 2.12 × 103 | 1.96 × 102 |
| f11 | 3.87 × 103 | 1.91 × 102 | 4.23 × 103 | 5.23 × 102 | 4.28 × 103 | 3.90 × 102 | 5.70 × 103 | 4.25 × 102 | 5.16 × 103 | 2.14 × 102 | 3.85 × 103 | 2.67 × 102 |
| f12 | 1.05 | 1.23 × 10−1 | 1.36 | 2.29 × 10−1 | 1.36 | 2.34 × 10−1 | 2.10 | 3.45 × 10−1 | 1.61 | 2.18 × 10−1 | 9.89 × 10−1 | 1.43 × 10−1 |
| f13 | 3.37 × 10−1 | 4.61 × 10−2 | 3.64 × 10−1 | 3.85 × 10−2 | 3.66 × 10−1 | 4.43 × 10−2 | 4.40 × 10−1 | 5.97 × 10−2 | 3.81 × 10−1 | 5.12 × 10−2 | 4.97 × 10−1 | 5.75 × 10−2 |
| f14 | 2.70 × 10−1 | 2.67 × 10−2 | 2.68 × 10−1 | 2.83 × 10−2 | 2.79 × 10−1 | 2.97 × 10−2 | 3.00 × 10−1 | 3.44 × 10−2 | 2.62 × 10−1 | 2.14 × 10−2 | 4.31 × 10−1 | 2.80 × 10−1 |
| f15 | 1.47 × 101 | 1.38 | 1.78 × 101 | 1.81 | 1.66 × 101 | 1.52 | 1.61 × 101 | 1.41 | 1.82 × 101 | 1.36 | 1.07 × 101 | 1.01 |
| f16 | 1.27 × 101 | 1.72 × 10−1 | 1.28 × 101 | 1.89 × 10−1 | 1.28 × 101 | 2.09 × 10−1 | 1.27 × 101 | 1.97 × 10−1 | 1.27 × 101 | 3.91 × 10−1 | 1.27 × 101 | 2.34 × 10−1 |
| f17 | 9.32 × 104 | 3.24 × 104 | 1.11 × 105 | 4.40 × 104 | 2.87 × 104 | 3.86 × 102 | 1.99 × 105 | 6.36 × 104 | 2.44 × 105 | 1.02 × 105 | 2.72 × 104 | 7.89 × 103 |
| f18 | 3.69 × 103 | 4.06 × 103 | 3.12 × 104 | 1.55 × 104 | 3.60 × 102 | 1.42 × 102 | 2.17 × 103 | 1.25 × 103 | 3.11 × 103 | 3.66 × 103 | 3.33 × 108 | 1.83 × 109 |
| f19 | 1.10 × 101 | 6.24 × 10−1 | 9.83 | 6.15 × 10−1 | 9.91 | 5.67 × 10−1 | 9.88 | 8.77 × 10−1 | 1.16 × 101 | 2.13 | 9.83 | 1.58 |
| f20 | 3.21 × 102 | 5.94 × 101 | 3.86 × 102 | 9.66 × 101 | 3.76 × 102 | 1.75 × 101 | 3.69 × 102 | 1.13 × 102 | 7.06 × 102 | 1.72 × 103 | 1.65 × 102 | 3.27 × 101 |
| f21 | 5.08 × 103 | 1.08 × 103 | 8.29 × 103 | 1.67 × 103 | 3.53 × 103 | 1.80 × 102 | 1.41 × 104 | 5.17 × 103 | 1.29 × 104 | 4.31 × 103 | 2.54 × 103 | 4.35 × 102 |
| f22 | 3.45 × 102 | 9.51 × 101 | 2.87 × 102 | 1.12 × 102 | 3.08 × 102 | 7.07 × 101 | 2.31 × 102 | 9.23 × 101 | 4.45 × 102 | 1.79 × 102 | 2.64 × 102 | 1.15 × 102 |
| f23 | 3.15 × 102 | 2.59 × 10−3 | 3.15 × 102 | 1.10 × 10−2 | 3.15 × 102 | 4.61 × 10−3 | 3.15 × 102 | 3.54 × 10−4 | 3.15 × 102 | 4.27 × 10−5 | 3.15 × 102 | 1.49 × 10−1 |
| f24 | 2.34 × 102 | 4.11 | 2.34 × 102 | 3.50 | 2.33 × 102 | 3.34 | 2.29 × 102 | 5.04 | 2.31 × 102 | 2.09 | 2.28 × 102 | 2.09 |
| f25 | 2.12 × 102 | 1.23 | 2.11 × 102 | 2.18 | 2.07 × 102 | 1.26 | 2.12 × 102 | 1.61 | 2.14 × 102 | 1.83 | 2.06 × 102 | 1.23 |
| f26 | 1.00 × 102 | 4.02 × 10−2 | 1.00 × 102 | 4.05 × 10−2 | 1.00 × 102 | 3.44 × 10−2 | 1.00 × 102 | 6.63 × 10−2 | 1.00 × 102 | 7.58 × 10−2 | 1.00 × 102 | 8.99 × 10−2 |
| f27 | 4.34 × 102 | 1.07 × 101 | 4.24 × 102 | 6.68 | 4.19 × 102 | 1.22 × 101 | 6.43 × 102 | 1.93 × 102 | 6.45 × 102 | 2.02 × 102 | 8.25 × 102 | 2.12 × 102 |
| f28 | 1.06 × 103 | 4.33 × 101 | 1.03 × 103 | 4.44 × 101 | 1.03 × 103 | 5.14 × 101 | 9.41 × 102 | 3.91 × 101 | 8.68 × 102 | 2.68 × 102 | 1.03 × 103 | 1.19 × 102 |
| f29 | 4.31 × 103 | 1.99 × 103 | 7.85 × 103 | 3.10 × 103 | 2.05 × 103 | 5.96 × 102 | 2.83 × 105 | 1.53 × 106 | 3.46 × 102 | 9.98 × 101 | 5.85 × 106 | 4.59 × 106 |
| f30 | 4.93 × 103 | 9.64 × 102 | 5.96 × 103 | 2.56 × 103 | 3.16 × 103 | 7.30 × 102 | 3.81 × 103 | 8.84 × 102 | 1.68 × 103 | 2.09 × 102 | 3.62 × 103 | 1.32 × 103 |
| +/−/≈ | 22/3/5 | 22/4/4 | 18/8/4 | 17/8/5 | 19/6/5 | - | ||||||
| AGSCCS-1 | AGSCCS-2 | AGSCCS-3 | AGSCCS | |
|---|---|---|---|---|
| IM 1 (Logistic chaotic mapping) | × | √ | √ | √ |
| IM 2 (Adaptive guided updating local areas) | √ | × | √ | √ |
| IM 3 (SC technique) | √ | √ | × | √ |
| AGSCCS-1 | AGSCCS-2 | AGSCCS-3 | AGSCCS | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| f1 | 5.24 × 106 | 2.01 × 106 | 9.60 × 106 | 2.74 × 106 | 5.38 × 106 | 1.82 × 106 | 4.23 × 106 | 1.40 × 106 |
| f2 | 1.00 × 1010 | 0.00 | 1.00 × 1010 | 0.00 | 1.00 × 1010 | 0.00 | 1.00 × 1010 | 0.00 |
| f3 | 2.90 × 101 | 7.75 | 2.10 × 102 | 5.89 × 101 | 2.96 × 101 | 1.09 × 101 | 2.80 × 101 | 7.34 |
| f4 | 8.02 × 101 | 2.56 × 101 | 9.86 × 101 | 1.35 × 101 | 6.95 × 101 | 3.26 × 101 | 7.08 × 101 | 2.28 × 101 |
| f5 | 2.09 × 101 | 7.14 × 10−2 | 2.09 × 101 | 5.53 × 10−2 | 2.09 × 101 | 6.35 × 10−2 | 2.09 × 101 | 7.94 × 10−2 |
| f6 | 2.69 × 101 | 1.21 | 2.79 × 101 | 1.29 | 2.68 × 101 | 1.18 | 2.78 × 101 | 1.32 |
| f7 | 8.43 × 10−2 | 5.51 × 10−2 | 2.23 × 10−1 | 7.58 × 10−2 | 8.09 × 10−2 | 6.20 × 10−2 | 7.51 × 10−2 | 5.61 × 10−2 |
| f8 | 5.96 × 101 | 8.44 | 1.04 × 102 | 1.43 × 101 | 5.68 × 101 | 8.98 | 5.53 × 101 | 8.21 |
| f9 | 1.05 × 102 | 1.66 × 101 | 1.63 × 102 | 1.82 × 101 | 1.08 × 102 | 1.46 × 101 | 1.05 × 102 | 1.48 × 101 |
| f10 | 2.33 × 103 | 2.56 × 102 | 2.63 × 103 | 1.83 × 102 | 2.25 × 103 | 2.53 × 102 | 2.12 × 103 | 1.96 × 102 |
| f11 | 3.89 × 103 | 2.09 × 102 | 3.91 × 103 | 2.10 × 102 | 3.78 × 103 | 2.09 × 102 | 3.85 × 103 | 2.67 × 102 |
| f12 | 1.10 | 1.61 × 10−1 | 1.04 | 1.73 × 10−1 | 1.10 | 1.36 × 10−1 | 9.89 × 10−1 | 1.43 × 10−1 |
| f13 | 4.61 × 10−1 | 8.30 × 10−2 | 3.36 × 10−1 | 4.15 × 10−2 | 4.66 × 10−1 | 8.13 × 10−2 | 4.97 × 10−1 | 5.75 × 10−2 |
| f14 | 4.33 × 10−1 | 2.71 × 10−1 | 2.61 × 10−1 | 2.46 × 10−2 | 4.01 × 10−1 | 2.37 × 10−1 | 4.31 × 10−1 | 2.80 × 10−1 |
| f15 | 1.08 × 101 | 1.57 | 1.45 × 101 | 1.85 | 1.08 × 101 | 1.08 | 1.07 × 101 | 1.01 |
| f16 | 1.27 × 101 | 2.52 × 10−1 | 1.28 × 101 | 2.22 × 10−1 | 1.28 × 101 | 2.52 × 10−1 | 1.27 × 101 | 2.34 × 10−1 |
| f17 | 3.13 × 104 | 1.30 × 104 | 8.39 × 104 | 3.65 × 104 | 3.29 × 104 | 1.42 × 104 | 2.72 × 104 | 7.89 × 103 |
| f18 | 5.03 × 102 | 1.13 × 102 | 2.86 × 103 | 1.91 × 103 | 4.75 × 102 | 1.05 × 102 | 3.33 × 108 | 1.83 × 109 |
| f19 | 9.86 | 1.45 | 1.09 × 101 | 5.97 × 10−1 | 9.37 | 1.12 | 9.83 | 1.58 |
| f20 | 1.70 × 102 | 3.37 × 101 | 3.15 × 102 | 8.00 × 101 | 1.67 × 102 | 2.56 × 101 | 1.65 × 102 | 3.27 × 101 |
| f21 | 2.65 × 103 | 4.75 × 102 | 4.90 × 103 | 8.26 × 102 | 2.60 × 103 | 3.03 × 102 | 2.54 × 103 | 4.35 × 102 |
| f22 | 3.44 × 102 | 9.97 × 101 | 3.91 × 102 | 8.90 × 101 | 3.09 × 102 | 1.09 × 102 | 2.74 × 102 | 1.15 × 102 |
| f23 | 3.15 × 102 | 7.55 × 10−5 | 3.15 × 102 | 3.32 × 10−3 | 3.15 × 102 | 3.76 × 10−5 | 3.15 × 102 | 1.49 × 10−1 |
| f24 | 2.29 × 102 | 3.86 | 2.35 × 102 | 3.72 | 2.28 × 102 | 2.98 | 2.28 × 102 | 2.09 |
| f25 | 2.06 × 102 | 1.05 | 2.11 × 102 | 1.51 | 2.07 × 102 | 1.16 | 2.06 × 102 | 1.23 |
| f26 | 1.00 × 102 | 9.09 × 10−2 | 1.00 × 102 | 4.51 × 10−2 | 1.09 × 102 | 4.83 × 101 | 1.00 × 102 | 8.99 × 10−2 |
| f27 | 7.94 × 102 | 2.44 × 102 | 4.30 × 102 | 9.86 | 8.42 × 102 | 1.99 × 102 | 8.25 × 102 | 2.12 × 102 |
| f28 | 1.06 × 103 | 2.10 × 102 | 1.05 × 103 | 4.76 × 101 | 1.06 × 103 | 1.49 × 102 | 1.03 × 103 | 1.19 × 102 |
| f29 | 6.41 × 105 | 2.44 × 106 | 4.53 × 103 | 2.07 × 103 | 6.19 × 106 | 2.08 × 106 | 5.85 × 106 | 4.59 × 106 |
| f30 | 3.64 × 103 | 1.69 × 103 | 4.23 × 103 | 8.66 × 102 | 3.80 × 103 | 2.41 × 103 | 3.62 × 103 | 1.32 × 103 |
| +/−/≈ | 19/5/6 | 20/6/4 | 22/7/1 | - | ||||
| Algorithm | Ranking (D = 30) |
|---|---|
| CS | 3.4000 |
| ACS | 3.6833 |
| ImCS | 3.0000 |
| GBCS | 3.8333 |
| ACSA | 4.5667 |
| AGSCCS | 2.5167 |
| CS | ACS | ImCS | GBCS | ACSA | AGSCCS | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| SDM | 1.08 × 10−3 | 6.73 × 10−5 | 1.16 × 10−3 | 9.57 × 10−5 | 1.01 × 10−3 | 4.84 × 10−5 | 1.04 × 10−3 | 4.84 × 10−5 | 1.05 × 10−3 | 5.92 × 10−5 | 9.89 × 10−4 | 1.26 × 10−5 |
| DDM | 1.49 × 10−3 | 2.18 × 10−4 | 1.80 × 10−3 | 3.32 × 10−4 | 1.80 × 10−3 | 3.09 × 10−4 | 1.35 × 10−3 | 2.36 × 10−4 | 1.69 × 10−3 | 2.89 × 10−4 | 1.33 × 10−3 | 3.28 × 10−4 |
| Photowatt-PWP-201 | 2.44 × 10−3 | 7.93 × 10−6 | 3.00 × 10−3 | 1.58 × 10−3 | 2.88 × 10−3 | 1.12 × 10−3 | 2.43 × 10−3 | 1.17 × 10−6 | 2.45 × 10−3 | 3.61 × 10−5 | 2.43 × 10−3 | 5.32 × 10−6 |
| STM6-40/36 | 4.66 × 10−3 | 5.42 × 10−4 | 4.97 × 10−3 | 6.27 × 10−4 | 4.17 × 10−3 | 5.90 × 10−4 | 3.35 × 10−3 | 2.95 × 10−4 | 5.51 × 10−2 | 1.03 × 10−1 | 3.14 × 10−3 | 5.76 × 10−3 |
| STP6-120/36 | 3.68 × 10−2 | 4.91 × 10−3 | 4.17 × 10−2 | 6.37 × 10−3 | 3.74 × 10−2 | 3.40 × 10−3 | 2.95 × 10−2 | 5.19 × 10−3 | 1.38 × 10−1 | 3.23 × 10−1 | 2.02 × 10−2 | 5.85 × 10−3 |
| Algorithm | RMSE | |||||
|---|---|---|---|---|---|---|
| CS | 0.7607 | 3.70 × 10−7 | 0.0358 | 57.3751 | 1.4943 | 1.08 × 10−3 |
| ACS | 0.7606 | 4.36 × 10−7 | 0.0352 | 64.9443 | 1.5110 | 1.16 × 10−3 |
| ImCS | 0.7607 | 3.54 × 10−7 | 0.0360 | 56.7892 | 1.4905 | 1.01 × 10−3 |
| GBCS | 0.7607 | 3.64 × 10−7 | 0.0359 | 58.2349 | 1.4928 | 1.04 × 10−3 |
| ACSA | 0.7607 | 3.57 × 10−7 | 0.0360 | 57.2252 | 1.4910 | 1.05 × 10−3 |
| AGSCCS | 0.7608 | 3.47 × 10−7 | 0.0362 | 54.9470 | 1.4860 | 9.89 × 10−4 |
| Algorithm | RMSE | |||||||
|---|---|---|---|---|---|---|---|---|
| CS | 0.7606 | 4.15 × 10−7 | 0.0350 | 69.7383 | 1.6110 | 2.67 × 10−7 | 1.6206 | 1.49 × 10−3 |
| ACS | 0.7607 | 4.88 × 10−7 | 0.0343 | 79.6598 | 1.7060 | 4.13 × 10−7 | 1.6896 | 1.80 × 10−3 |
| ImCS | 0.7606 | 3.65 × 10−7 | 0.0340 | 83.2859 | 1.5794 | 3.40 × 10−7 | 1.5826 | 1.80 × 10−3 |
| GBCS | 0.7607 | 2.77 × 10−7 | 0.0355 | 66.2202 | 1.7133 | 3.38 × 10−7 | 1.6354 | 1.35 × 10−3 |
| ACSA | 0.7608 | 4.24 × 10−7 | 0.0350 | 65.8916 | 1.6702 | 2.98 × 10−7 | 1.6187 | 1.69 × 10−3 |
| AGSCCS | 0.7594 | 2.69 × 10−7 | 0.0400 | 79.9490 | 1.3166 | 6.61 × 10−8 | 1.6569 | 1.33 × 10−3 |
| Algorithm | RMSE | ||||||
|---|---|---|---|---|---|---|---|
| Photowatt-PWP-201 | CS | 1.0302 | 3.67 × 10−6 | 1.1959 | 1048.6362 | 48.8467 | 2.44 × 10−3 |
| ACS | 1.0316 | 3.09 × 10−6 | 1.2298 | 928.8406 | 47.6362 | 3.00 × 10−3 | |
| ImCS | 1.0466 | 2.68 × 10−6 | 1.2030 | 802.3769 | 46.7762 | 2.88 × 10−3 | |
| GBCS | 1.0304 | 3.55 × 10−6 | 1.1992 | 1007.7580 | 48.7176 | 2.43 × 10−3 | |
| ACSA | 1.0304 | 3.53 × 10−6 | 1.2003 | 1005.9862 | 48.6883 | 2.45 × 10−3 | |
| AGSCCS | 1.0305 | 3.48 × 10−6 | 1.2013 | 982.0053 | 48.6428 | 2.43 × 10−3 | |
| STM6-40/36 | CS | 1.6552 | 6.95 × 10−6 | 0.0002 | 88.9366 | 1.6890 | 4.66 × 10−3 |
| ACS | 1.6556 | 7.41 × 10−6 | 0.0002 | 157.7937 | 1.6976 | 4.97 × 10−3 | |
| ImCS | 1.6603 | 5.57 × 10−6 | 0.0004 | 30.7576 | 1.6591 | 4.17 × 10−3 | |
| GBCS | 1.6603 | 5.43 × 10−6 | 0.0004 | 28.2830 | 1.6562 | 3.35 × 10−3 | |
| ACSA | 1.6468 | 2.27 × 10−5 | 0.0060 | 167.4477 | 1.8746 | 5.51 × 10−2 | |
| AGSCCS | 1.6633 | 4.69 × 10−6 | 0.0034 | 161.7657 | 1.7099 | 3.14 × 10−3 | |
| STP6-120/36 | CS | 7.4960 | 1.57 × 10−5 | 0.0036 | 596.5901 | 1.4274 | 3.68 × 10−2 |
| ACS | 7.5113 | 2.30 × 10−5 | 0.0032 | 558.4491 | 1.4857 | 4.17 × 10−2 | |
| ImCS | 7.5110 | 2.14 × 10−5 | 0.0034 | 1034.5552 | 1.4677 | 3.74 × 10−2 | |
| GBCS | 7.4909 | 1.03 × 10−5 | 0.0038 | 826.8380 | 1.3977 | 2.95 × 10−2 | |
| ACSA | 7.4705 | 4.37 × 10−1 | 0.0028 | 349.0301 | 4.6720 | 1.38 × 10−1 | |
| AGSCCS | 7.4708 | 3.57 × 10−6 | 0.0044 | 418.9095 | 1.2865 | 2.02 × 10−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Yu, X. Adaptive Guided Spatial Compressive Cuckoo Search for Optimization Problems. Mathematics 2022, 10, 495. https://doi.org/10.3390/math10030495
Xu W, Yu X. Adaptive Guided Spatial Compressive Cuckoo Search for Optimization Problems. Mathematics. 2022; 10(3):495. https://doi.org/10.3390/math10030495
Chicago/Turabian StyleXu, Wangying, and Xiaobing Yu. 2022. "Adaptive Guided Spatial Compressive Cuckoo Search for Optimization Problems" Mathematics 10, no. 3: 495. https://doi.org/10.3390/math10030495
APA StyleXu, W., & Yu, X. (2022). Adaptive Guided Spatial Compressive Cuckoo Search for Optimization Problems. Mathematics, 10(3), 495. https://doi.org/10.3390/math10030495






