Analysis of the Influences of Parameters in the Fractional Second-Grade Fluid Dynamics
Abstract
1. Introduction
2. Constructive Equations
3. Solution Procedures
3.1. Fractional Heat Equation
3.2. The Velocity Profile
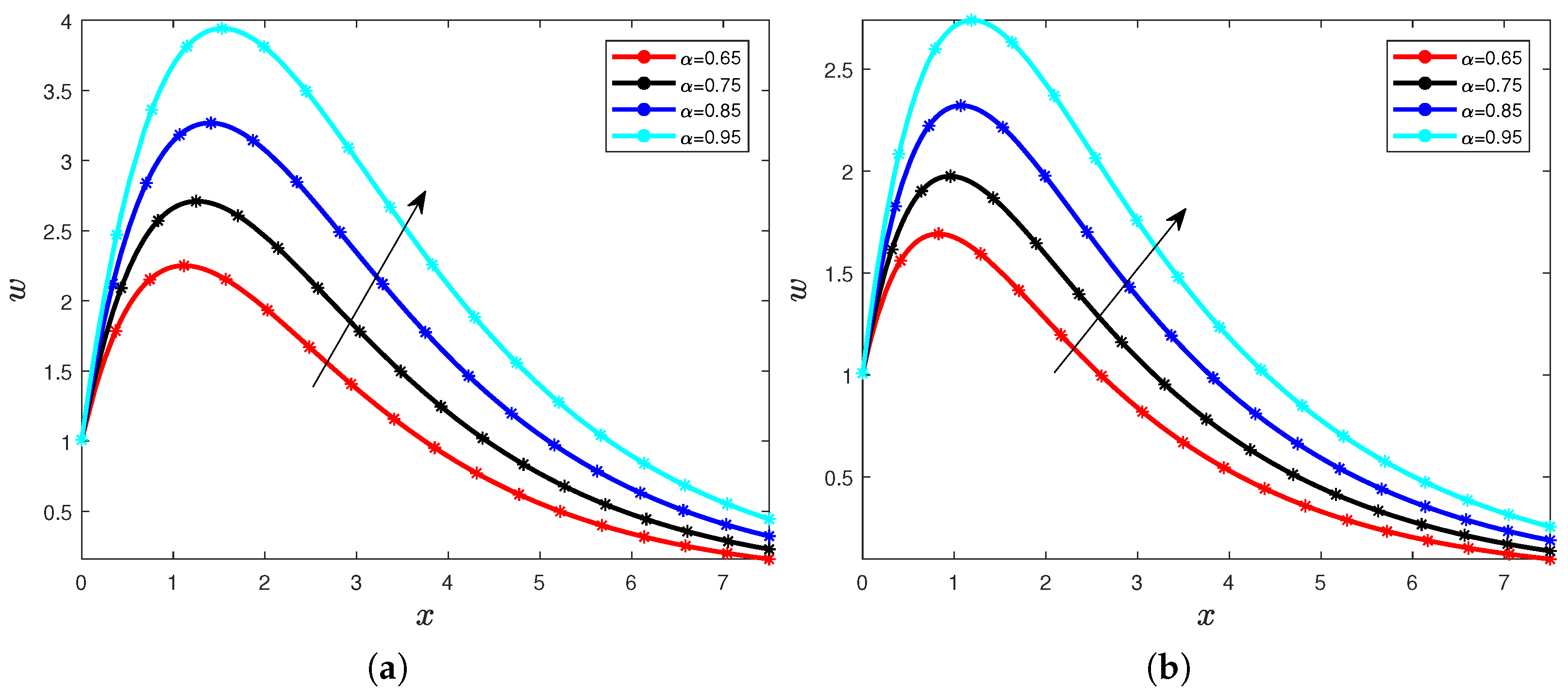
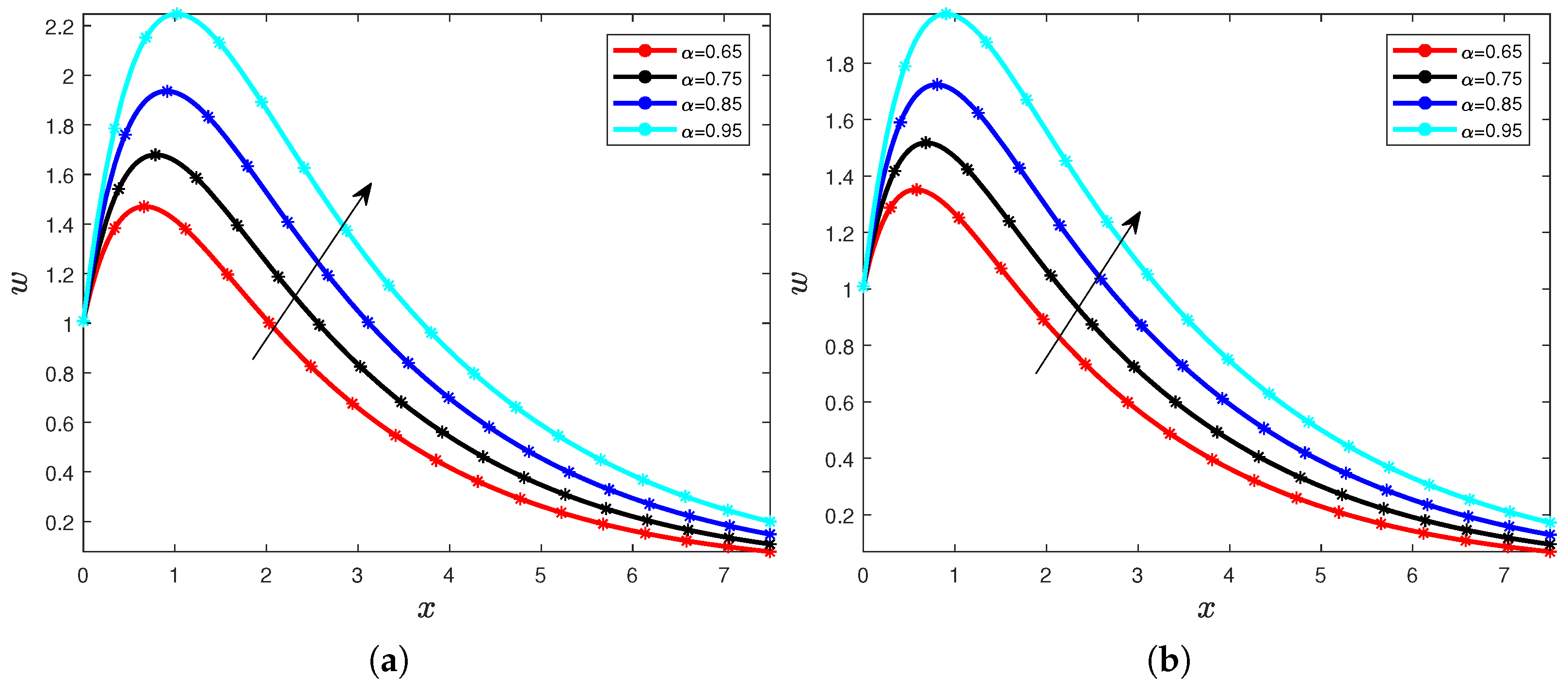
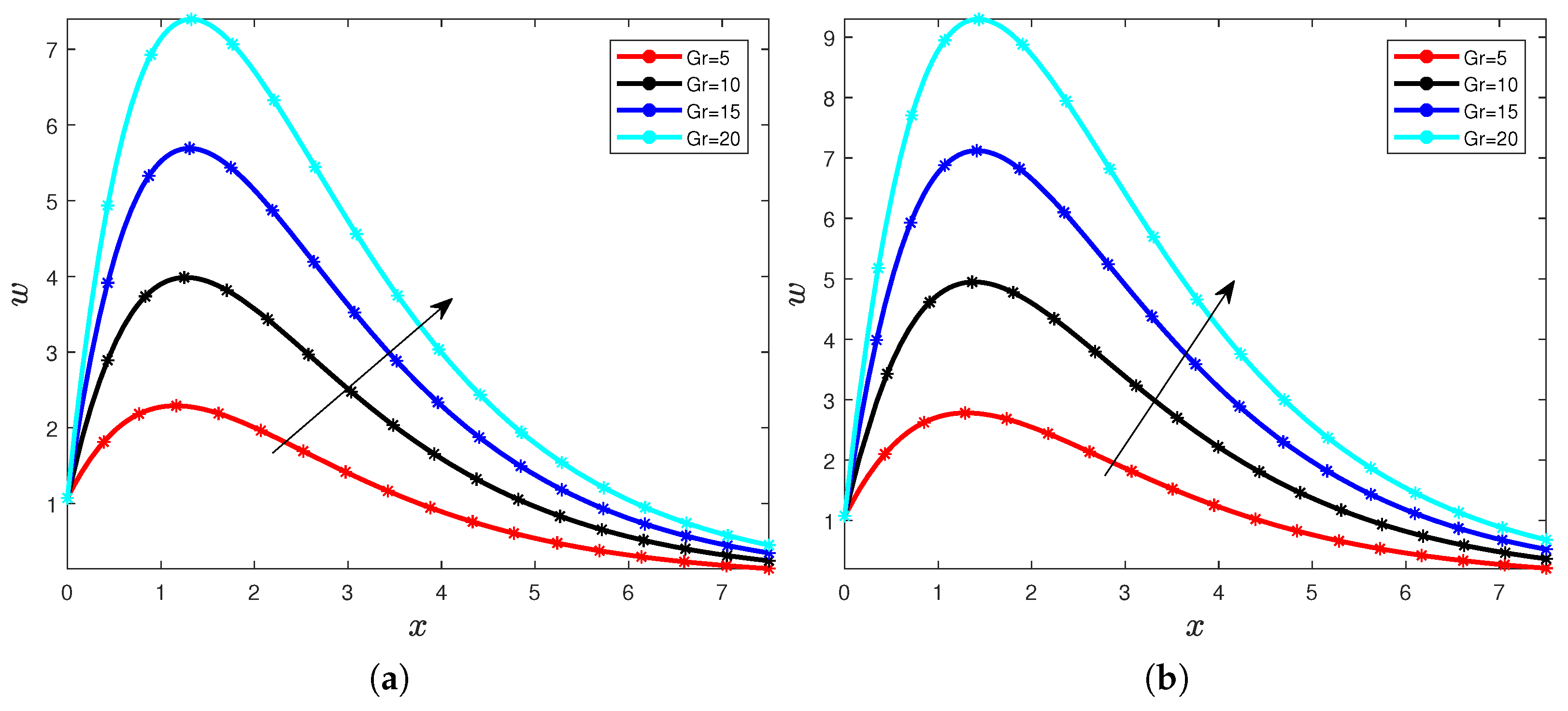
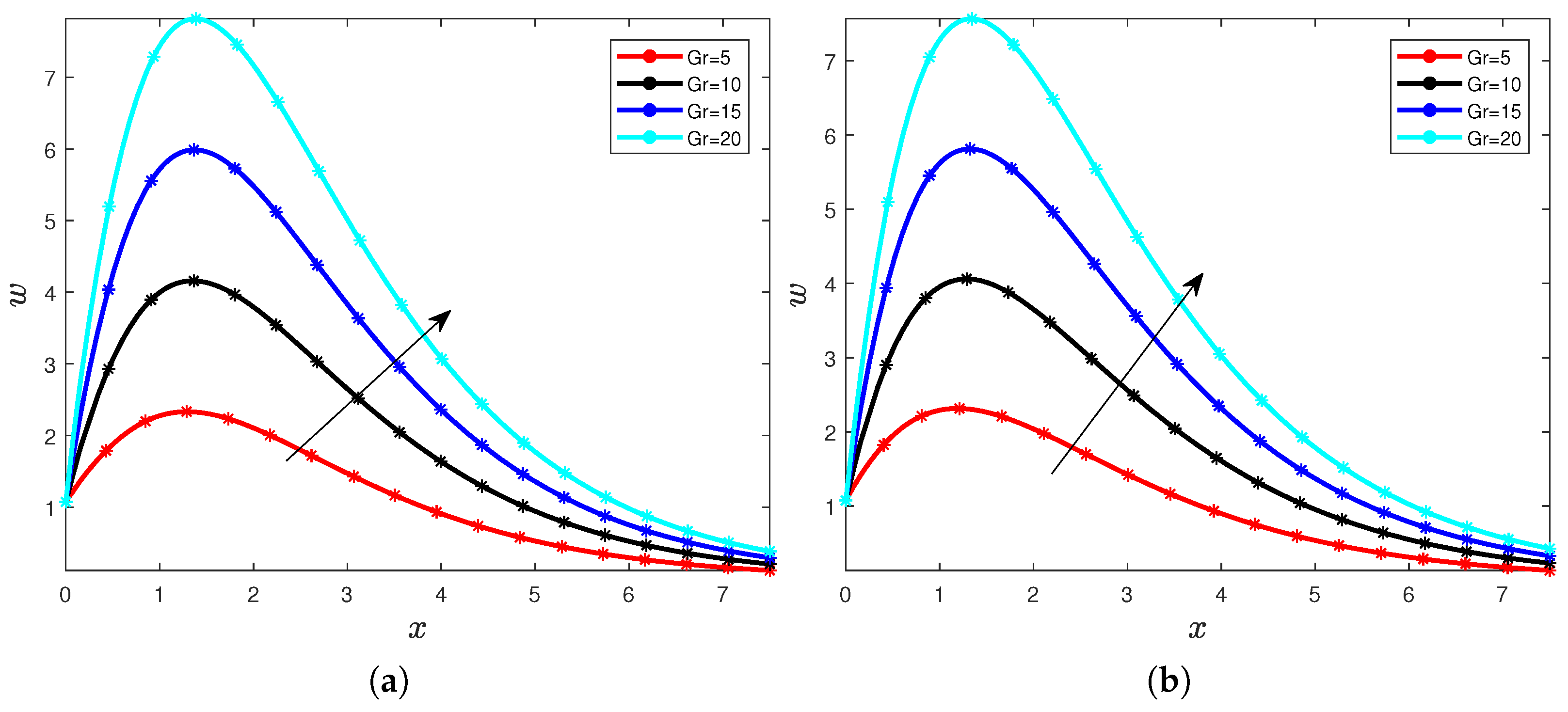
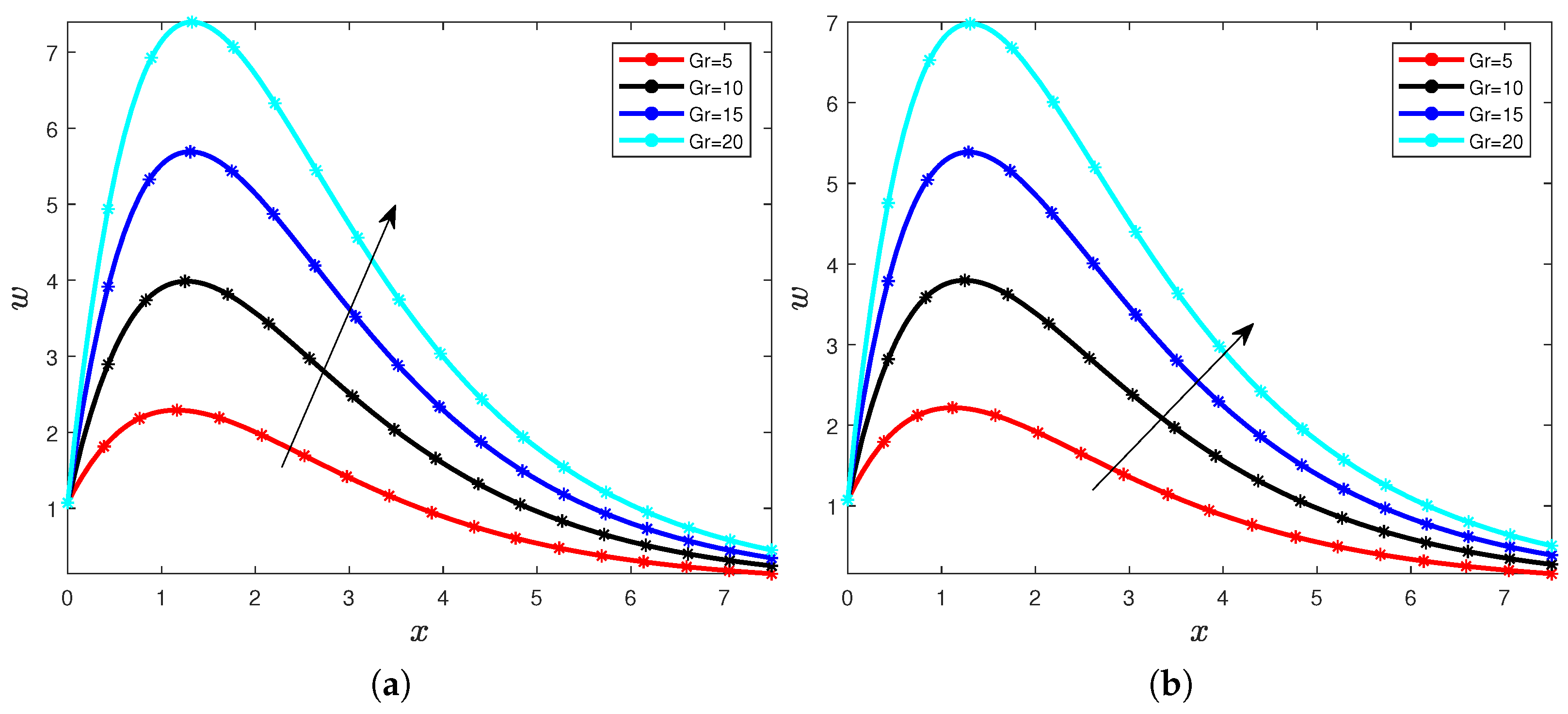
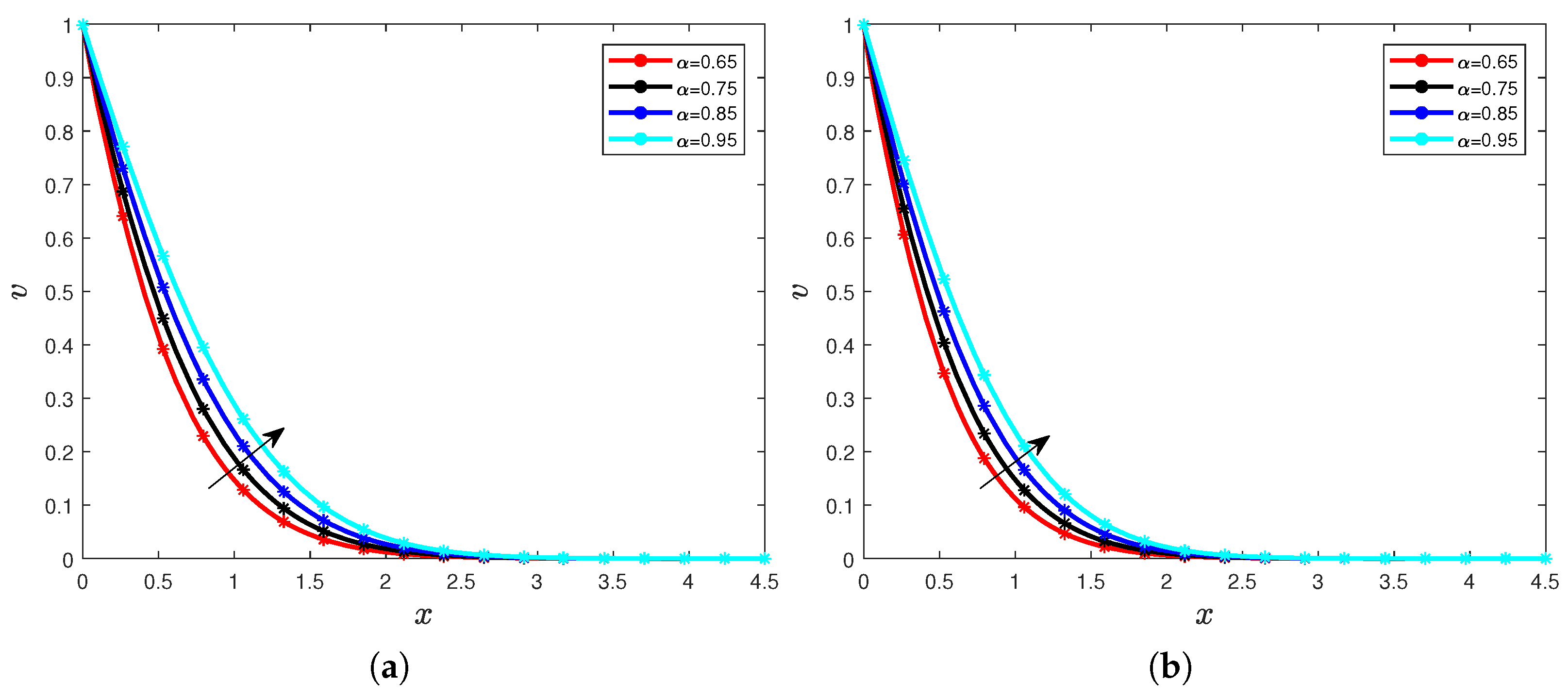
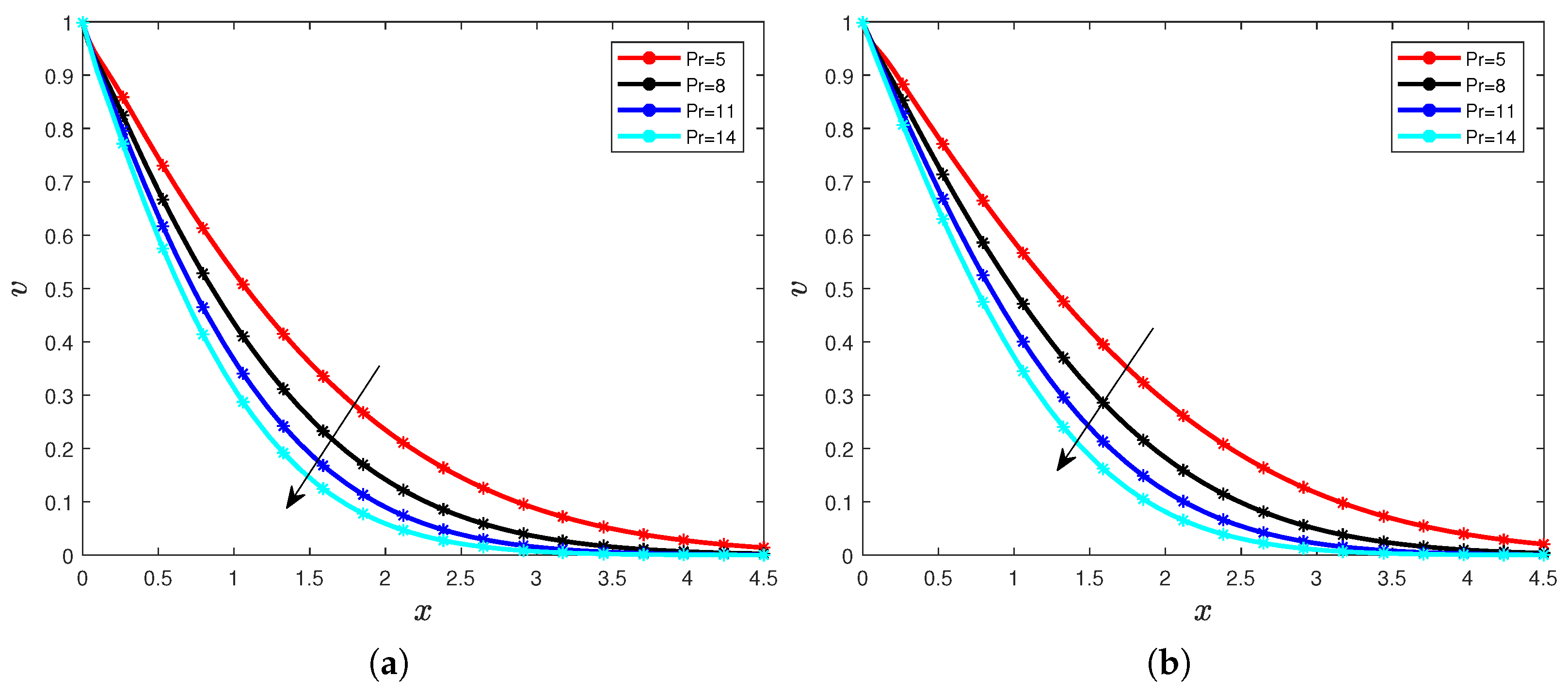
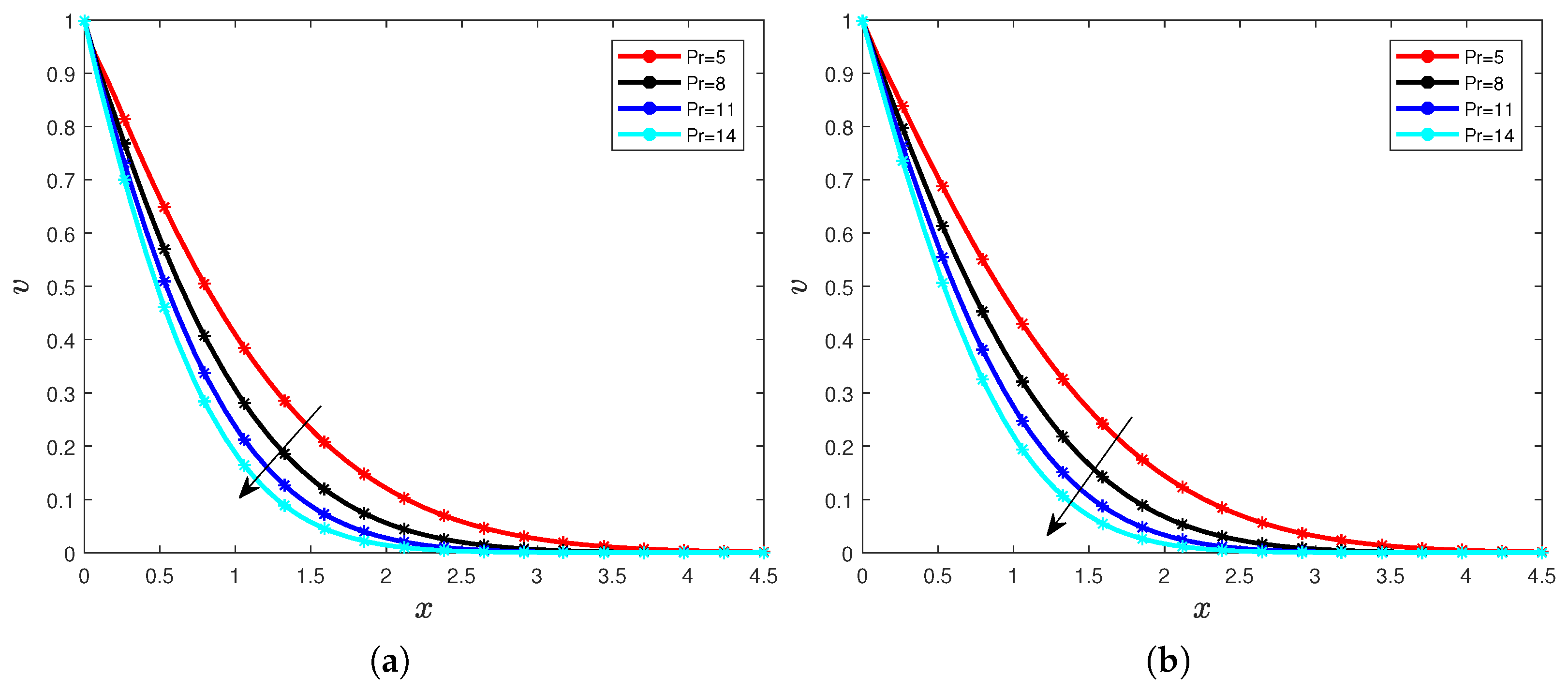
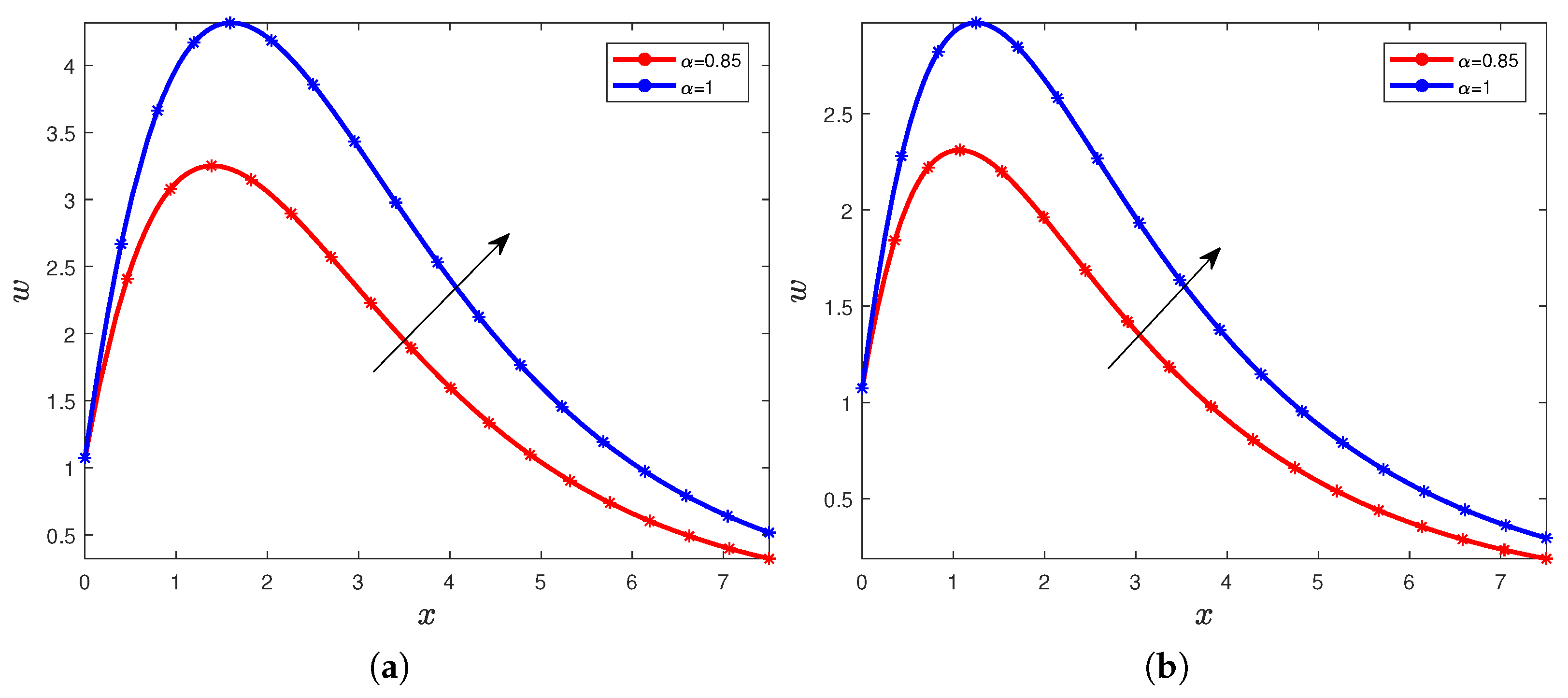
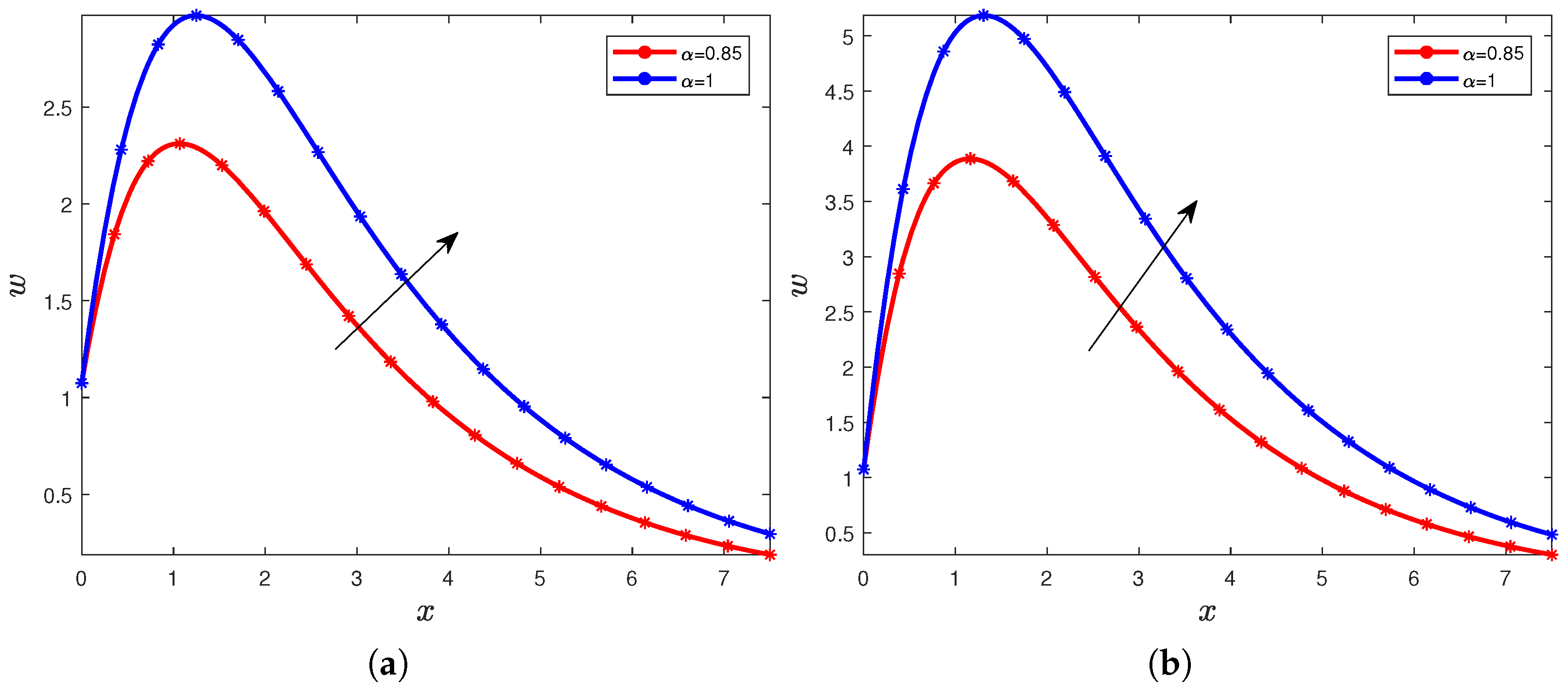
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Fractional Calculus Operators
References
- Lohana, B.; Abro, K.A.; Shaikh, A.W. Thermodynamical analysis of heat transfer of gravity-driven fluid flow via fractional treatment: An analytical study. J. Therm. Anal. 2021, 144, 155–165. [Google Scholar] [CrossRef]
- Pramanik, S. Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation. Ain Shams Eng. J. 2014, 5, 205–212. [Google Scholar] [CrossRef]
- Riaz, M.B.; Imran, M.A.; Shabbir, K. Analytic solutions of Oldroyd-B fluid withfractional derivatives in a circular duct that appliesa constant couple. Alex. Eng. J. 2016, 55, 3267–3275. [Google Scholar] [CrossRef]
- Imran, M.A.; Shah, N.A.; Khan, I.; Aleem, M. Applications of non-integer Caputo time fractional derivatives to natural convection flow subject to arbitrary velocity and Newtonian heating. Neural Comput. Appl. 2018, 30, 1589–1599. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A.; Shaikh, A.A.; Inc, M.; Baleanu, D. Fractional modeling of blood ethanol concentration system with real data application. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013143. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T.; Baleanu, D. On the generalized fractional derivatives and their Caputo modification. J. Nonlinear Sci. Appl. 2017, 10, 2607–2619. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; p. 204. [Google Scholar]
- Podlubny. Fractional Differential Equations, Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1999; p. 198. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 1–15. [Google Scholar]
- Atangana, A.; Mekkaoui, T. Trinition the complex number with two imaginary parts: Fractal, chaos and fractional calculus. Chaos Solitons Fractals 2019, 128, 366–381. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Owolabi, K.; Atangana, A. On the formulation of Adams-Bashforth scheme with Atangana-Baleanu-Caputo fractional derivative to model chaotic problems. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 023111. [Google Scholar] [CrossRef] [PubMed]
- Vieru, D.; Fetecau, C.; Fetecau, C. Time-fractional free convection flow near a vertical plate with Newtonian heating and mass diffusion. Therm. Sci. 2015, 19, 85–98. [Google Scholar] [CrossRef]
- Khan, A.; Abro, K.A.; Tassaddiq, A.; Khan, I. Atangana–Baleanu and Caputo Fabrizio Analysis of Fractional Derivatives for Heat and Mass Transfer of Second Grade Fluids over a Vertical Plate: A Comparative Study. Entropy 2017, 19, 279. [Google Scholar] [CrossRef]
- Khalid, A.; Khan, I.; Khan, A.; Shafie, S. Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium. Eng. Sci. Technol. Int. J. 2015, 18, 309–317. [Google Scholar] [CrossRef]
- Ali, F.; Sheikh, N.A.; Khan, I.; Saqib, M. Magnetic field effect on blood flow of Casson fluid in axisymmetric cylindrical tube: A fractional model. J. Magn. Magn. Mater. 2017, 423, 327–336. [Google Scholar] [CrossRef]
- Imran, M.; Sarwar, S. Effects of slip on free convection flow of Casson fluid over an oscillating vertical plate. Bound. Value Probl. 2016, 2016, 30. [Google Scholar] [CrossRef][Green Version]
- Haq, S.U.; Jan, S.U.; Shah, S.I.A.; Khan, I.; Singh, J. Heat and mass transfer of fractional second grade fluid with slippage and ramped wall temperature using Caputo-Fabrizio fractional derivative approach. AIMS Math. 2020, 5, 3056–3088. [Google Scholar] [CrossRef]
- Saad, K.; Baleanu, D.; Atangana, A. New fractional derivatives applied to the Korteweg–de Vries and Korteweg–de Vries–Burger’s equations. Comput. Appl. Math. 2019, 37, 5203–5216. [Google Scholar] [CrossRef]
- Veeresha, P. A Numerical Approach to the Coupled Atmospheric Ocean Model Using a Fractional Operator. Math. Model. Numer. Simul. Appl. 2021, 1, 1–10. [Google Scholar] [CrossRef]
- Jajarmi, A.; Yusuf, A.; Baleanu, D.; Inc, M. A new fractional HRSV model and its optimal control: A non-singular operator approach. Phys. A Stat. Mech. Appl. 2020, 547, 123860. [Google Scholar] [CrossRef]
- Allegretti, S.; Bulai, I.M.; Marino, R.; Menandro, M.A.; Parisi, K. Vaccination effect conjoint to fraction of avoided contacts for a Sars-Cov-2 mathematical model. Math. Model. Numer. Simul. Appl. 2021, 1, 56–66. [Google Scholar] [CrossRef]
- Naik, P.A.; Yavuz, M.; Qureshi, S.; Zu, J.; Townley, S. Modeling and analysis of COVID-19 epidemics with treatment in fractional derivatives using real data from Pakistan. Eur. Phys. J. Plus 2020, 135, 1–42. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, Z. Dynamic Analysis of a Delayed Fractional-Order SIR Model with Saturated Incidence and Treatment Functio. Int. J. Bifurc. Chaos 2018, 28, 1850180. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A.; Shaikh, A.A.; Inc, M. Transmission dynamics of varicella zoster virus modeled by classical and novel fractional operators using real statistical data. Phys. A Stat. Mech. Appl. 2019, 534, 122149. [Google Scholar] [CrossRef]
- Riaz, M.B.; Abro, K.A.; Abualnaja, K.M.; Akgül, A.; Rehman, A.U.; Abbas, M.; Hamed, Y.S. Exact solutions involving special functions for unsteady convective flow of magnetohydrodynamic second grade fluid with ramped conditions. Adv. Differ. Equ. 2021, 2021, 408. [Google Scholar] [CrossRef]
- Martínez-Farías, F.J.; Alvarado-Sánchez, A.; Rangel-Cortes, E.; Hernández-Hernández, A. Bi-dimensional crime model based on anomalous diffusion with law enforcement effect. Math. Model. Numer. Simul. Appl. 2022, 2, 26–40. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. On the analysis of vibration equation involving a fractional derivative with Mittag-Leffler law. Math. Methods Appl. Sci. 2020, 43, 443–457. [Google Scholar] [CrossRef]
- Gholami, M.; Ghaziani, R.K.; Eskandari, Z. Three-dimensional fractional system with the stability condition and chaos control. Math. Model. Numer. Simul. Appl. 2022, 2, 41–47. [Google Scholar] [CrossRef]
- Joshi, H.; Jha, B.K. Chaos of calcium diffusion in Parkinson s infectious disease model and treatment mechanism via Hilfer fractional derivative. Math. Model. Numer. Simul. Appl. 2021, 1, 84–94. [Google Scholar] [CrossRef]
- Sene, N. Analysis of a Four-Dimensional Hyperchaotic System Described by the Caputo–Liouville Fractional Derivative. Complexity 2020, 2020, 8889831. [Google Scholar] [CrossRef]
- Hammouch, Z.; Yavuz, M.; Özdemir, N. Numerical Solutions and Synchronization of a Variable-Order Fractional Chaotic System. Math. Model. Numer. Simul. Appl. 2021, 1, 11–23. [Google Scholar] [CrossRef]
- Fahd, J.; Abdeljawad, T. Generalized fractional derivatives and Laplace transform. Discrete Contin. Dyn. Syst.-S 2020, 13, 709. [Google Scholar]
- Baleanu, D.; Fernandez, A.; Akgül, A. On a Fractional Operator Combining Proportional and Classical Differintegrals. Mathematics 2020, 8, 360. [Google Scholar] [CrossRef]
- Yokuş, A. Construction of Different Types of Traveling Wave Solutions of the Relativistic Wave Equation Associated with the Schrödinger Equation. Math. Model. Numer. Simul. Appl. 2021, 1, 24–31. [Google Scholar] [CrossRef]
- Saqib, M.; Khan, I.; Shafie, S. Application of Atangana–Baleanu fractional derivative to MHD channel flow of CMC-based-CNT’s nanofluid through a porous medium. Chaos Solitons Fractals 2018, 116, 79–85. [Google Scholar] [CrossRef]
- Ali, F.; Saqib, M.; Khan, I.; Sheikh, N.A. Application of Caputo-Fabrizio derivatives to MHD free convection flow of generalized Walters’-B fluid model. Eur. Phys. J. Plus 2016, 131, 377. [Google Scholar] [CrossRef]
- Sene, N. A Numerical Algorithm Applied to Free Convection Flows of the Casson Fluid along with Heat and Mass Transfer Described by the Caputo Derivative. Adv. Math. Phys. 2021, 2021, 5225019. [Google Scholar] [CrossRef]
- Abro, K.A. A fractional and analytic investigation of thermo-diffusion process on free convection flow: An application to surface modification technology. Eur. Phys. J. Plus 2020, 135, 31. [Google Scholar] [CrossRef]
- Yavuz, M.; Sene, N. Approximate solutions of the model describing fluid flow using generalized ρ-Laplace transform method and heat balance integral method. Axioms 2020, 9, 123. [Google Scholar] [CrossRef]
- Sene, N. Second-grade fluid with Newtonian heating under Caputo fractional derivative: Analytical investigations via Laplace transforms. Math. Model. Numer. Simul. Appl. 2022, 2, 13–25. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Shah, N.A.; Wakif, A.; Mahanthesh, B.; Sivaraj, R.; Koriko, O.K. Ratio of Momentum Diffusivity to Thermal Diffusivity: Introduction, Meta-Analysis, and Scrutinization, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2022. [Google Scholar] [CrossRef]
- Tzou, D.Y. A Unified Field Approach for Heat Conduction From Macro- to Micro-Scales. J. Heat Transf. 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Olivar-Romero, F.; Rosas-Ortiz, O. Transition from the Wave Equation to Either the Heat or the Transport Equations through Fractional Differential Expressions. Symmetry 2018, 10, 524. [Google Scholar] [CrossRef]
- Vieru, D.; Imran, M.A.; Rauf, A.; Asjad, M.I. Slip effect on free convection flow of second grade fluids with ramped wall temperature. Heat Transf. Res. 2015, 46, 713–724. [Google Scholar] [CrossRef]




| Parameters | Descriptions |
|---|---|
| density | |
| dynamic viscosity | |
| first normal stress module | |
| g | acceleration due to gravity |
| volumetric coefficient of thermal expansion | |
| specific heat of the fluid at constant pressure | |
| thermal conductivity | |
| Kinematics viscosity of the fluid |
| Time | Prandtl Number | Nusselt Number |
|---|---|---|
| 0.1 | 10 | 5.43022 |
| 0.1 | 15 | 6.65063 |
| 0.1 | 20 | 7.67948 |
| 0.1 | 25 | 8.58592 |
| 0.4 | 10 | 3.0126 |
| 0.4 | 15 | 3.68967 |
| 0.4 | 20 | 4.26046 |
| 0.4 | 25 | 4.76334 |
| 0.7 | 10 | 2.37493 |
| 0.7 | 15 | 2.90868 |
| 0.7 | 20 | 3.35865 |
| 0.7 | 25 | 3.75509 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yavuz, M.; Sene, N.; Yıldız, M. Analysis of the Influences of Parameters in the Fractional Second-Grade Fluid Dynamics. Mathematics 2022, 10, 1125. https://doi.org/10.3390/math10071125
Yavuz M, Sene N, Yıldız M. Analysis of the Influences of Parameters in the Fractional Second-Grade Fluid Dynamics. Mathematics. 2022; 10(7):1125. https://doi.org/10.3390/math10071125
Chicago/Turabian StyleYavuz, Mehmet, Ndolane Sene, and Mustafa Yıldız. 2022. "Analysis of the Influences of Parameters in the Fractional Second-Grade Fluid Dynamics" Mathematics 10, no. 7: 1125. https://doi.org/10.3390/math10071125
APA StyleYavuz, M., Sene, N., & Yıldız, M. (2022). Analysis of the Influences of Parameters in the Fractional Second-Grade Fluid Dynamics. Mathematics, 10(7), 1125. https://doi.org/10.3390/math10071125








