A Comparative Numerical Study of Heat and Mass Transfer Individualities in Casson Stagnation Point Fluid Flow Past a Flat and Cylindrical Surfaces
Abstract
:1. Introduction
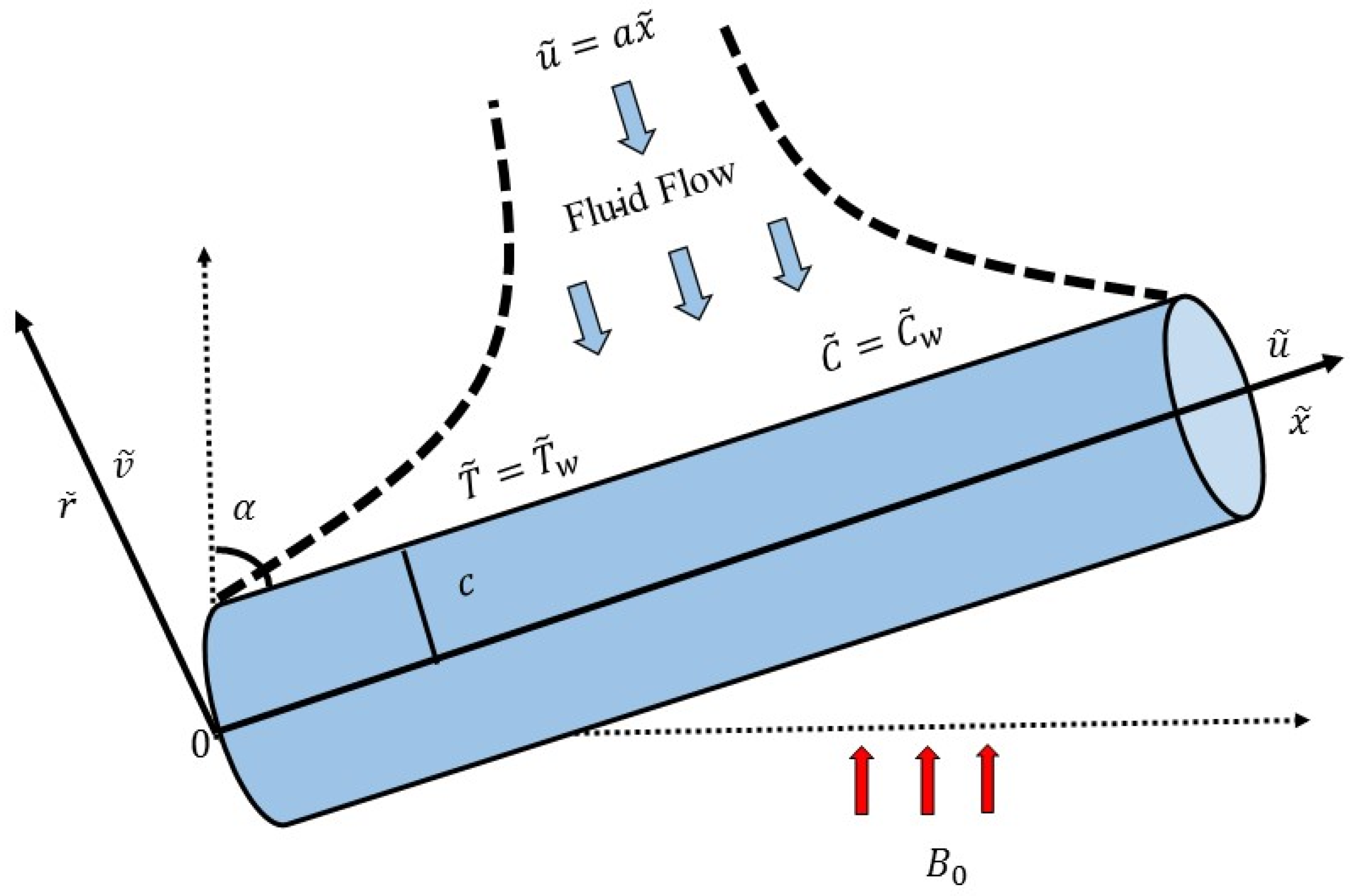
2. Mathematical Formulation
3. Numerical Scheme
4. Problem Analysis
5. Conclusions
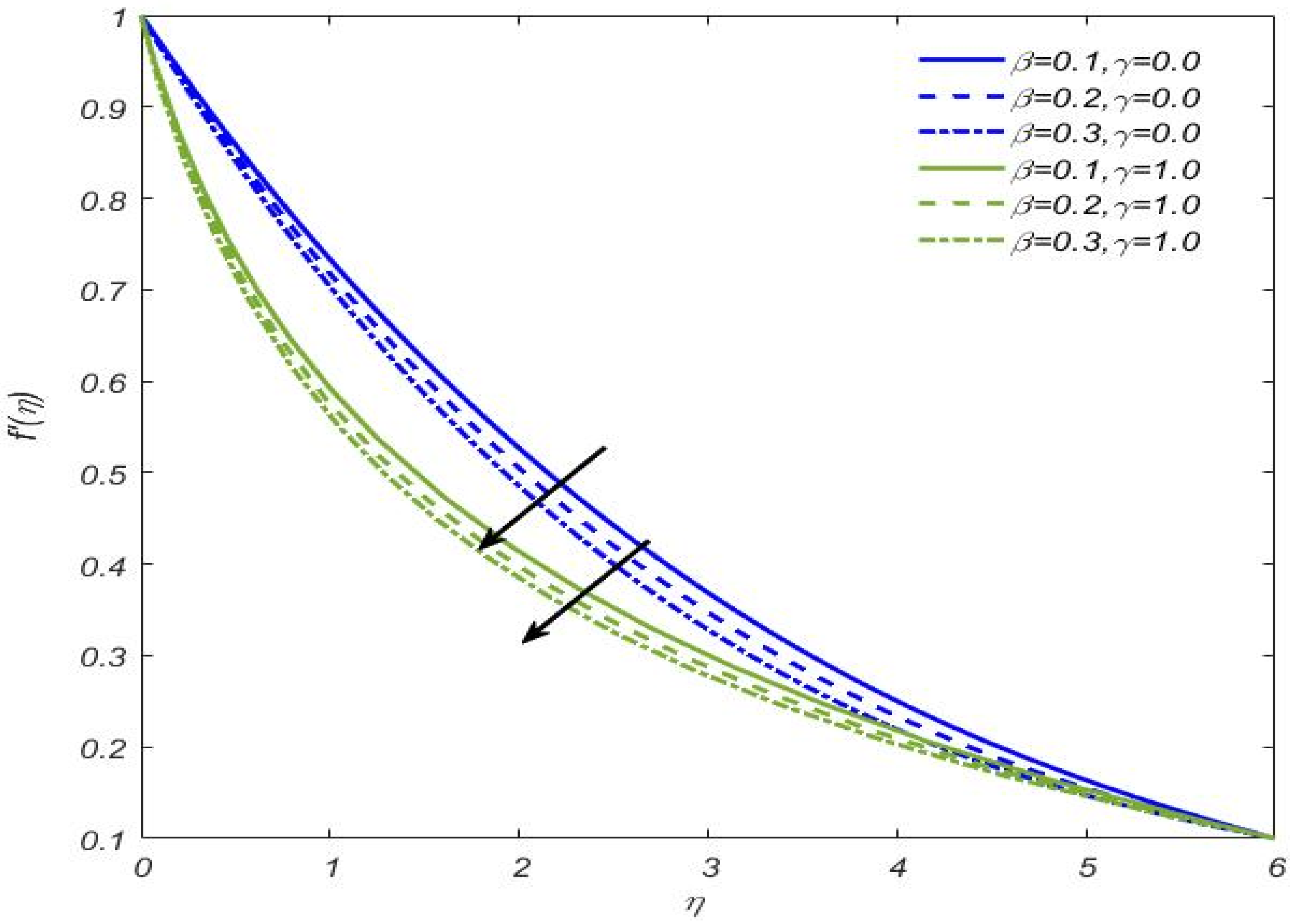
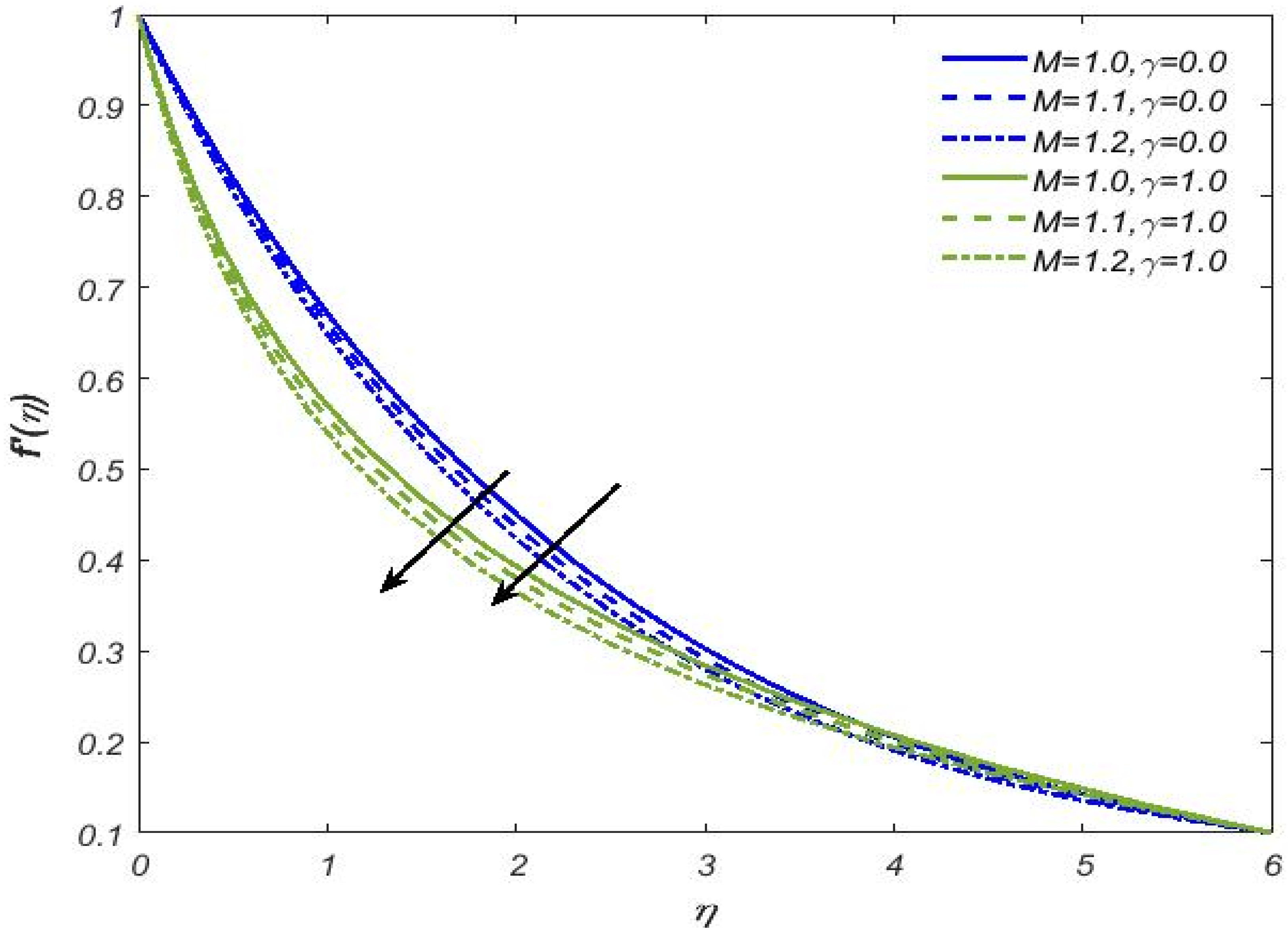
- For both cylindrical and flat surfaces, the Casson fluid velocity shows a declining nature towards magnetic and Casson fluid parameters while the opposite is the case for the velocity’s ratio parameter;
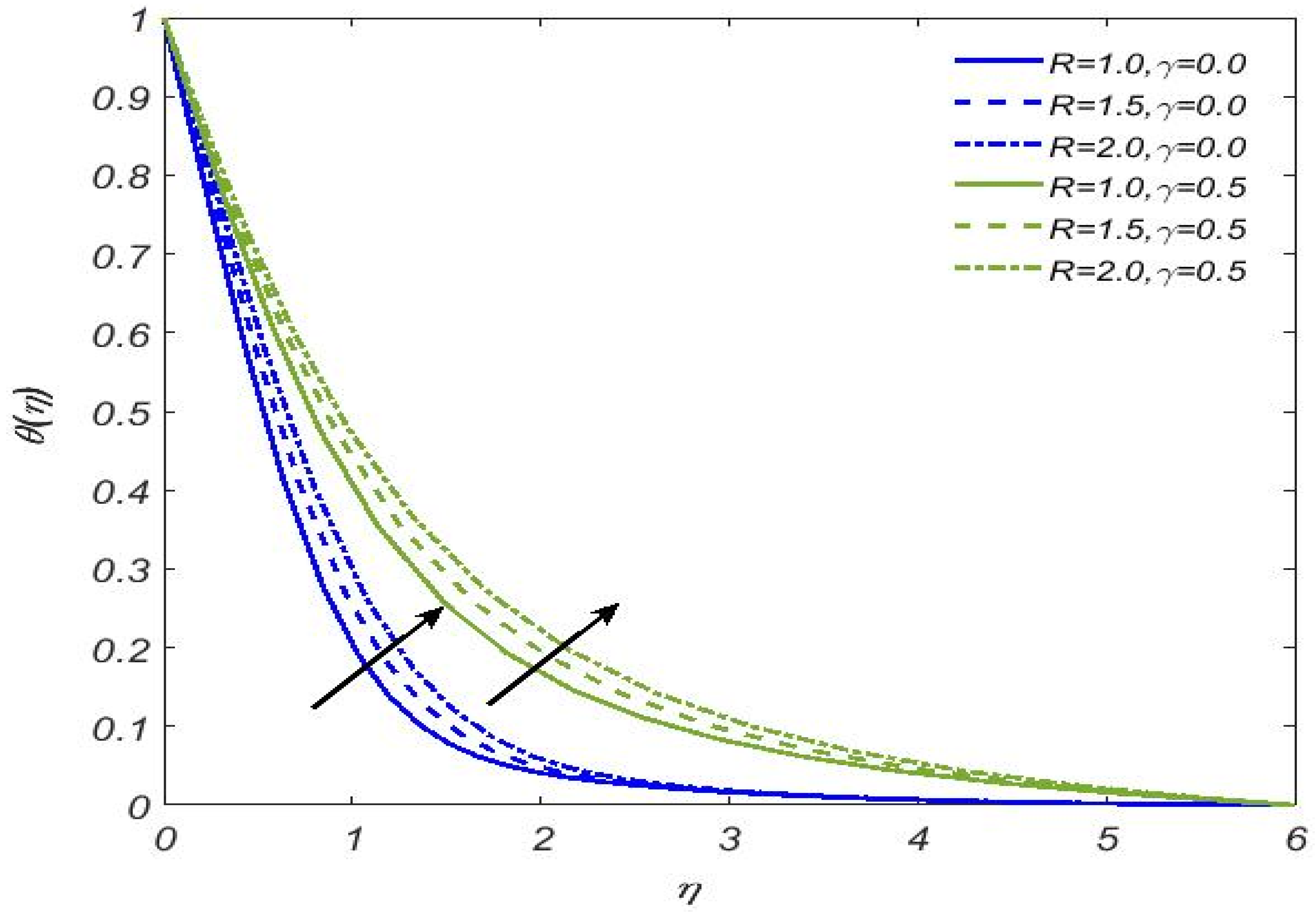
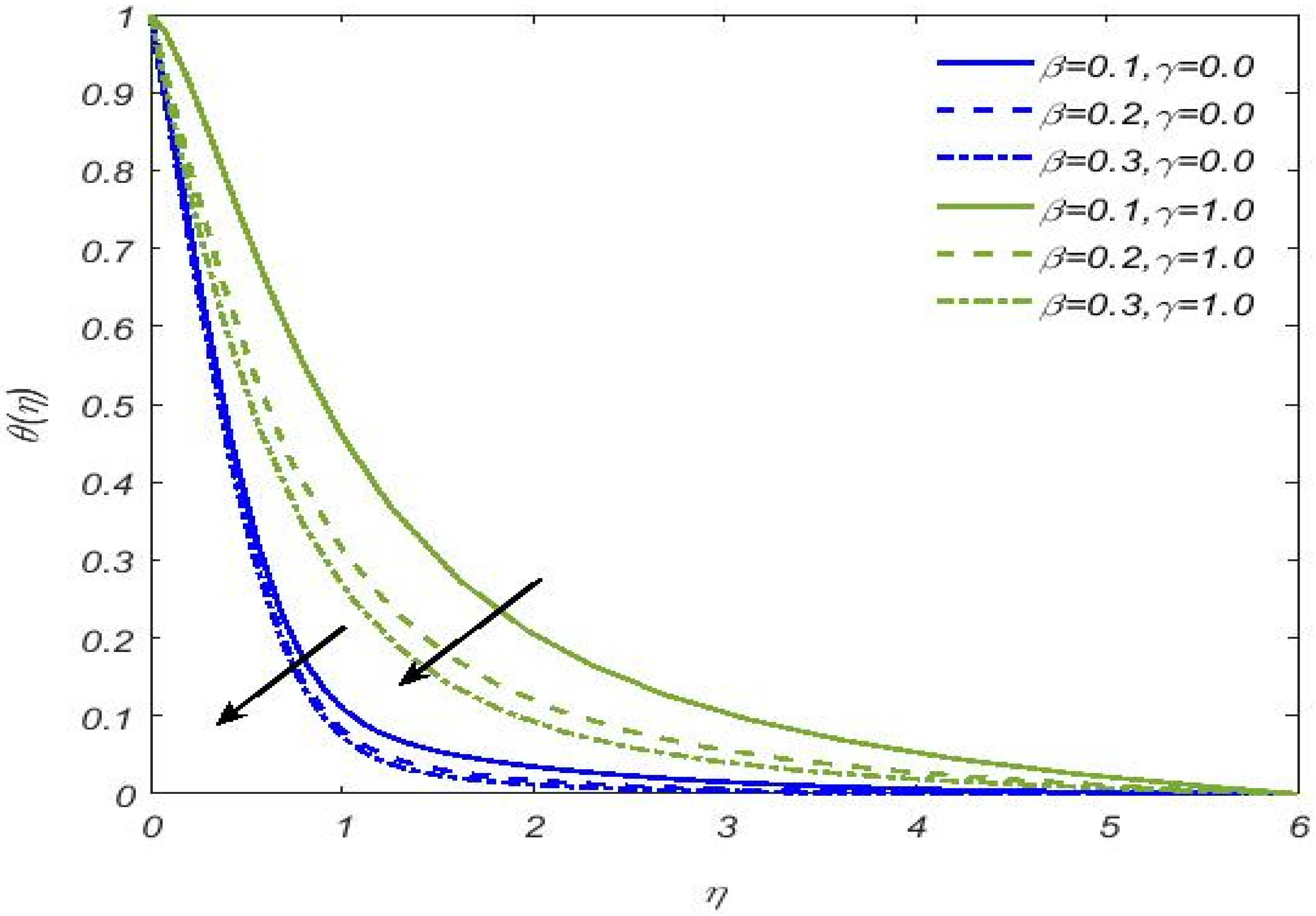
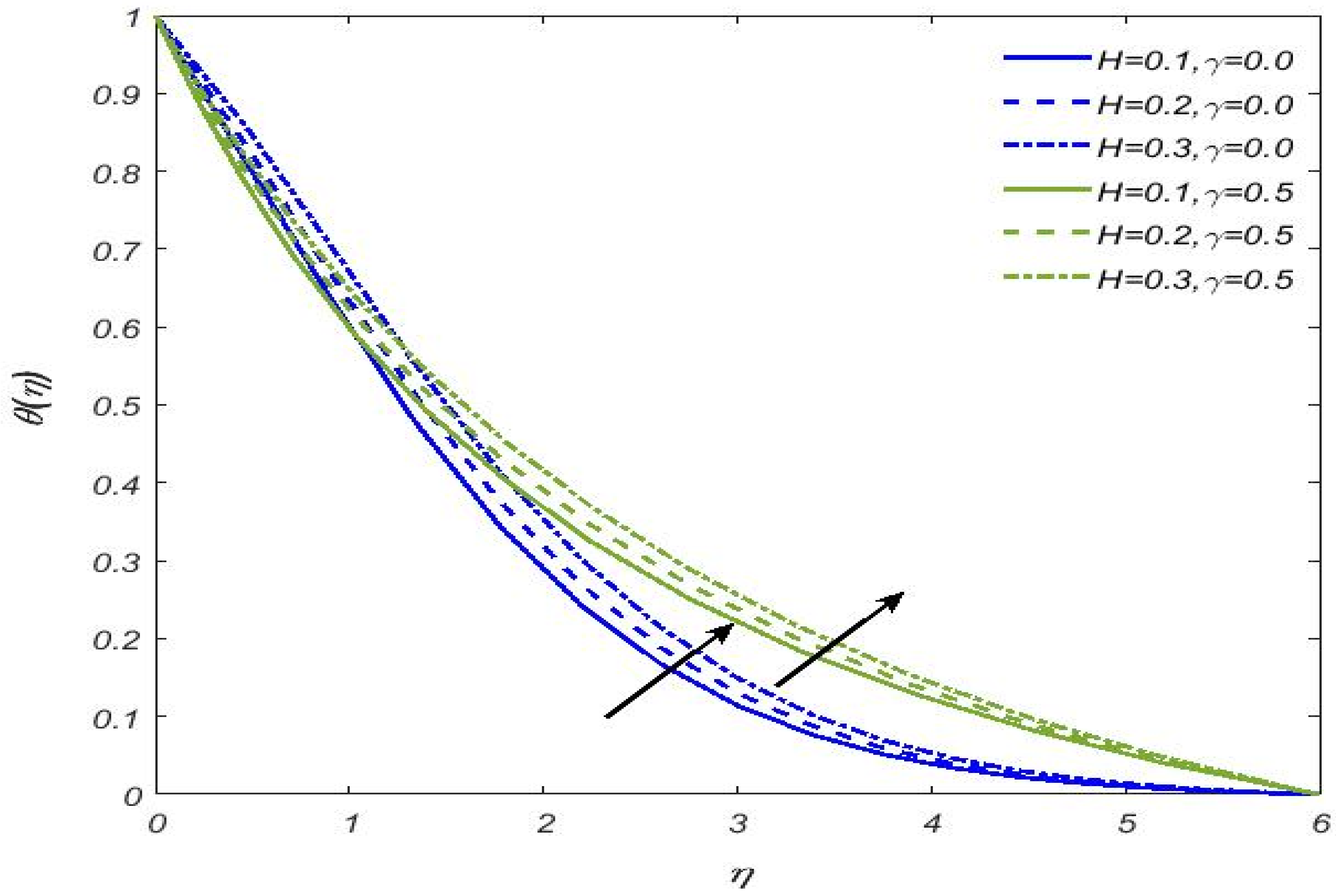
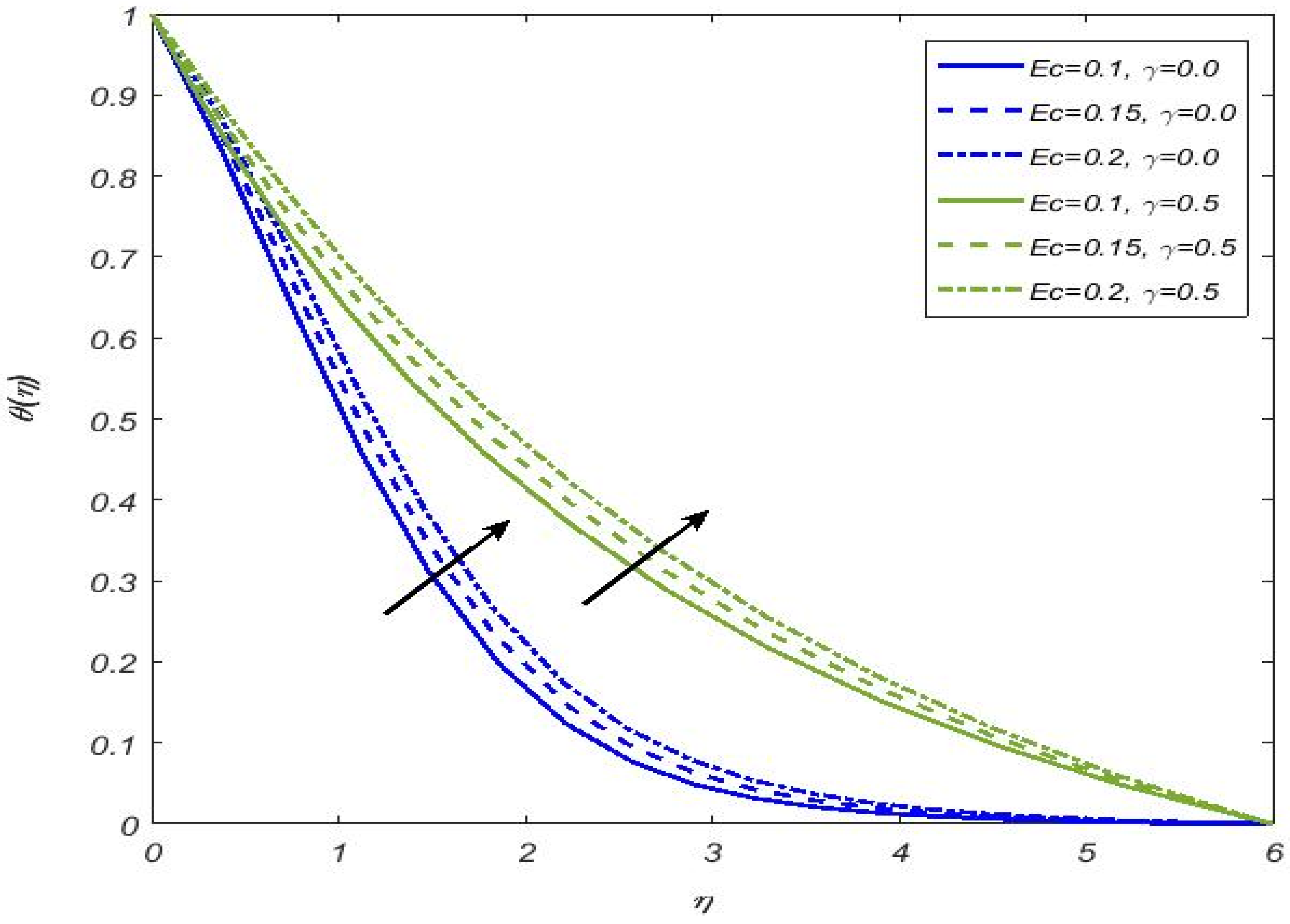
- Casson fluid temperature shows decline values for Casson fluid parameter and Prandtl number, while the opposite is a trend for thermal radiation, heat generation, variable thermal conductivity parameters, and Eckert number. The temperature is noticeably higher in the case of a cylindrical surface;
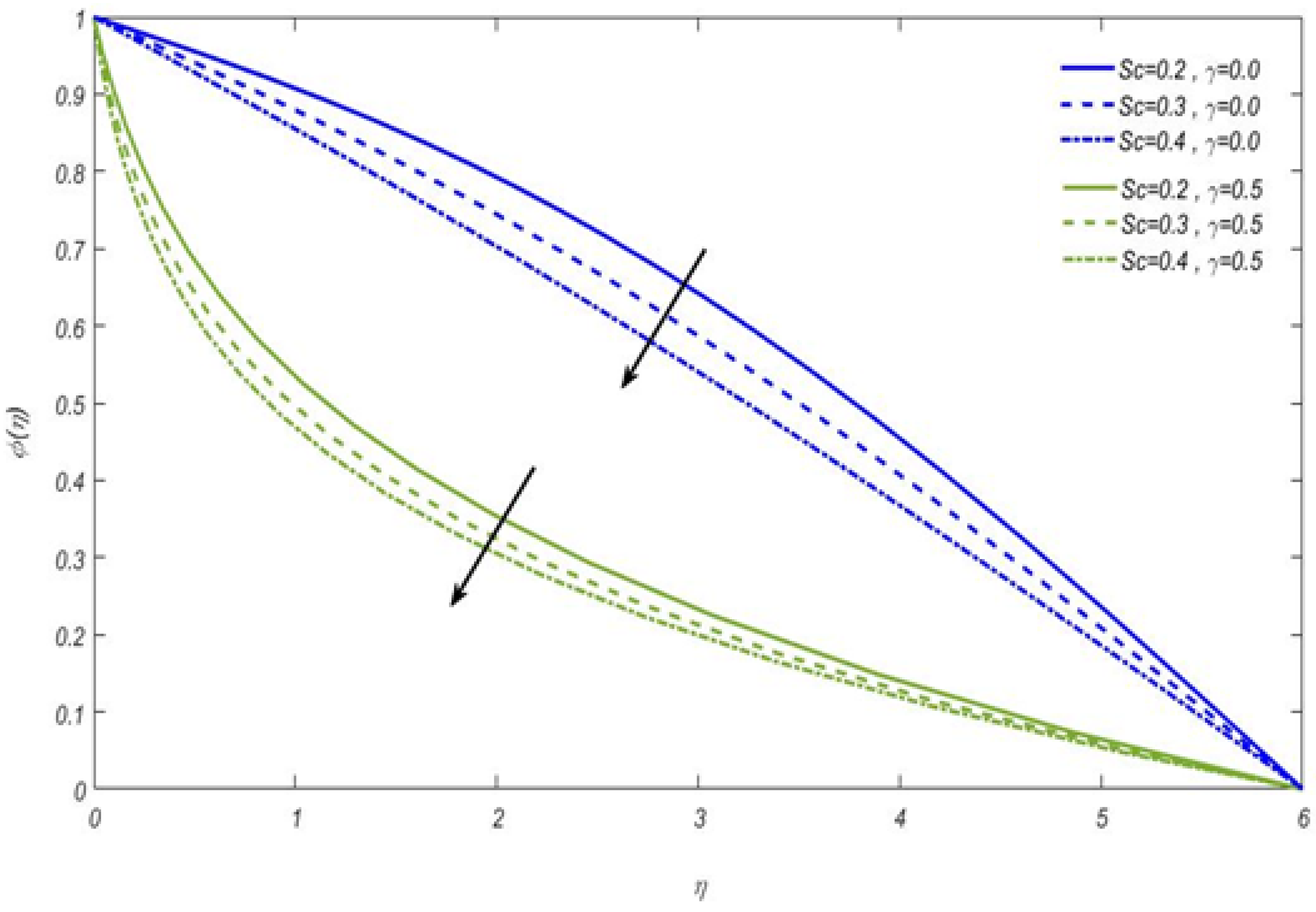
- For both cylindrical and flat surfaces, the positive values of Schmidt number the Casson fluid concentration admit inverse trends;
- The SFC shows the opposite trend for both the thermal Grashof number and concentration Grashof number. The magnitude of SFC is higher for the case cylindrical surface in comparison with a flat surface;
- The Nusselt number admits direct relation for thermal radiation parameter, while the opposite is the case for the Casson parameter. The magnitude of the Nusselt number is higher at the cylindrical surface for positive iteration in Casson fluid parameter.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Cylindrical coordinates | |
| Velocity components | |
| Kinematic viscosity | |
| Casson fluid parameter | |
| Thermal expansion coefficient | |
| Gravitational acceleration | |
| Angle of inclination | |
| Solutal expansion coefficient | |
| Ambient temperature | |
| Temperature of fluid | |
| Magnetic field constant | |
| Concentration of fluid | |
| Ambient concentration | |
| Free stream velocity | |
| Fluid electrical conductivity | |
| Specific heat at constant pressure | |
| Fluid density | |
| Radiative heat flux | |
| Variable thermal conductivity | |
| Dynamic viscosity | |
| Heat generation/absorption coefficient | |
| Characteristic length | |
| Small parameter | |
| Radius of cylinder | |
| Surface concentration | |
| Reference velocity | |
| Surface temperature | |
| Mass diffusivity | |
| Fluid velocity | |
| Fluid concentration | |
| Fluid temperature | |
| Temperature Grashof number | |
| Concentration Grashof number | |
| Pr | Prandtl number |
| A | Velocity’s ratio parameter |
| Radiation parameter | |
| Magnetic field parameter | |
| Curvature parameter | |
| Coefficient of mean absorption | |
| Ec | Eckert number |
| Sc | Schmidt number |
| Stefan–Boltzmann constant | |
| H | Heat generation/absorption parameter |
References
- Batra, R.; Jena, B. Flow of a Casson fluid in a slightly curved tube. Int. J. Eng. Sci. 1991, 29, 1245–1258. [Google Scholar] [CrossRef]
- Das, B.; Batra, R. Secondary flow of a Casson fluid in a slightly curved tube. Int. J. Non-linear Mech. 1993, 28, 567–577. [Google Scholar] [CrossRef]
- Srivastava, V.; Saxena, M. Two-layered model of Casson fluid flow through stenotic blood vessels: Applications to the cardiovascular system. J. Biomech. 1994, 27, 921–928. [Google Scholar] [CrossRef] [PubMed]
- Dash, R.K.; Mehta, K.N.; Jayaraman, G. Casson fluid flow in a pipe filled with a homogeneous porous medi-um. Int. J. Eng. Sci. 1996, 34, 1145–1156. [Google Scholar] [CrossRef]
- Eldabe, N.T.; Saddeck, M.G.; El-Sayed, A.F. Heat transfer of MHD non-Newtonian Casson fluid flow between two rotating cylinders. Mech. Mech. Eng. 2001, 5, 237–251. [Google Scholar]
- Mernone, A.; Mazumdar, J.; Lucas, S. A mathematical study of peristaltic transport of a casson fluid. Math. Comput. Model. 2002, 35, 895–912. [Google Scholar] [CrossRef]
- Das, M.; Mahato, R.; Nandkeolyar, R. Newtonian heating effect on unsteady hydromagnetic Casson fluid flow past a flat plate with heat and mass transfer. Alex. Eng. J. 2015, 54, 871–879. [Google Scholar] [CrossRef] [Green Version]
- Raju, C.; Sandeep, N. Nonlinear radiative magnetohydrodynamic Falkner-Skan flow of Casson fluid over a wedge. Alex. Eng. J. 2016, 55, 2045–2054. [Google Scholar] [CrossRef]
- Ahmed, S.E.; Mansour, M.; Mahdy, A.; Mohamed, S.S. Entropy generation due to double diffusive convective flow of Casson fluids over nonlinearity stretching sheets with slip conditions. Eng. Sci. Technol. Int. J. 2017, 20, 1553–1562. [Google Scholar] [CrossRef]
- Ali, M.; Sandeep, N. Cattaneo-Christov model for radiative heat transfer of magnetohydrodynamic Casson-ferrofluid: A numerical study. Results Phys. 2017, 7, 21–30. [Google Scholar] [CrossRef] [Green Version]
- Zia, Q.Z.; Ullah, I.; Waqas, M.; Alsaedi, A.; Hayat, T. Cross diffusion and exponential space dependent heat source impacts in radiated three-dimensional (3D) flow of Casson fluid by heated surface. Results Phys. 2018, 8, 1275–1282. [Google Scholar] [CrossRef]
- Larisa, M. Axisymmetric squeeze flow of a Casson medium. J. Non-Newton. Fluid Mech. 2019, 267, 35–50. [Google Scholar]
- Alwawi, F.A.; Alkasasbeh, H.T.; Rashad, A.; Idris, R. MHD natural convection of Sodium Alginate Casson nanofluid over a solid sphere. Results Phys. 2019, 16, 102818. [Google Scholar] [CrossRef]
- Divya, B.; Manjunatha, G.; Rajashekhar, C.; Vaidya, H.; Prasad, K. Analysis of temperature dependent properties of a peristaltic MHD flow in a non-uniform channel: A Casson fluid model. Ain Shams Eng. J. 2021, 12, 2181–2191. [Google Scholar] [CrossRef]
- Liu, J.; Abidi, A.; Khan, M.R.; Rasheed, S.; Allehiany, F.M.; Mahmoud, E.E.; Galal, A.M. Thermal analysis of a radiative slip flow of an unsteady casson nanofluid toward a stretching surface subject to the convective condi-tion. J. Mater. Res. Technol. 2021, 15, 468–476. [Google Scholar] [CrossRef]
- Azam, M.; Xu, T.; Nayak, M.K.; Khan, W.A.; Khan, M. Gyrotactic microorganisms and viscous dissipation features on radiative Casson nanoliquid over a moving cylinder with activation energy. Waves Random Complex Media 2022, 1–23. [Google Scholar] [CrossRef]
- Kodi, R.; Mopuri, O. Unsteady MHD oscillatory Casson fluid flow past an inclined vertical porous plate in the presence of chemical reaction with heat absorption and Soret effects. Heat Transf. 2021, 51, 733–752. [Google Scholar] [CrossRef]
- Ramudu, A.C.V.; Kumar, K.A.; Sugunamma, V.; Sandeep, N. Impact of Soret and Dufour on MHD Casson fluid flow past a stretching surface with convective–diffusive conditions. J. Therm. Anal. Calorim. 2021, 147, 2653–2663. [Google Scholar] [CrossRef]
- Azam, M.; Abbas, N.; Kumar, K.G.; Wali, S. Transient bioconvection and activation energy impacts on Casson nanofluid with gyrotactic microorganisms and nonlinear radiation. Waves Random Complex Media 2022, 1–20. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, S.A.; Momani, S. Finite difference analysis for entropy optimized flow of Casson fluid with thermo diffusion and diffusion-thermo effects. Int. J. Hydrog. Energy 2022, 47, 8048–8059. [Google Scholar] [CrossRef]
- Hayat, T.; Asad, S.; Alsaedi, A. Flow of variable thermal conductivity fluid due to inclined stretching cylinder with viscous dissipation and thermal radiation. Appl. Math. Mech. 2014, 35, 717–728. [Google Scholar] [CrossRef]
- Rehman, K.U.; Malik, A.A.; Malik, M.; Sandeep, N.; Saba, N.U. Numerical study of double stratification in Casson fluid flow in the presence of mixed convection and chemical reaction. Results Phys. 2017, 7, 2997–3006. [Google Scholar] [CrossRef]
- Khan, A.U.; Al-Zubaidi, A.; Munir, S.; Saleem, S.; Duraihem, F.Z. Closed form solutions of cross flows of Casson fluid over a stretching surface. Chaos Solitons Fractals 2021, 149, 111067. [Google Scholar] [CrossRef]
- Azam, M. Effects of Cattaneo-Christov heat flux and nonlinear thermal radiation on MHD Maxwell nanofluid with Arrhenius activation energy. Case Stud. Therm. Eng. 2022, 34, 102048. [Google Scholar] [CrossRef]
- Azam, M. Bioconvection and nonlinear thermal extrusion in development ofchemically reactive Sutterby nano-material due to gyrotactic microorganisms. Int. Commun. Heat Mass Transf. 2021, 130, 105820. [Google Scholar] [CrossRef]
- Barnoon, P.; Ashkiyan, M. Magnetic field generation due to the microwaves by an antenna connected to a power supply to destroy damaged tissue in the liver considering heat control. J. Magn. Magn. Mater. 2020, 513, 167245. [Google Scholar] [CrossRef]
- Nazım, K.; Zontul, H.; Sahin, B. Heat transfer and flow characteristics in a sinusoidally curved con-verging-diverging channel. Int. J. Therm. Sci. 2020, 148, 106163. [Google Scholar]
- Barnoon, P. Numerical assessment of heat transfer and mixing quality of a hybrid nanofluid in a microchannel equipped with a dual mixer. Int. J. Thermofluids 2021, 12, 100111. [Google Scholar] [CrossRef]
- Nazım, K. Experimental investigation of flow structure and heat transfer characteristics for confined cylin-ders. Int. Commun. Heat Mass Transf. 2022, 133, 105959. [Google Scholar]
- Monfared, R.H.; Niknejadi, M.; Toghraie, D.; Barnoon, P. Numerical investigation of swirling flow and heat transfer of a nanofluid in a tube with helical ribs using a two-phase model. J. Therm. Anal. Calorim. 2021, 147, 3403–3416. [Google Scholar] [CrossRef]
- Azam, M.; Mabood, F.; Khan, M. Bioconvection and activation energy dynamisms on radiative sutterby melting nanomaterial with gyrotactic microorganism. Case Stud. Therm. Eng. 2021, 30, 101749. [Google Scholar] [CrossRef]



(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 0.1 | −0.2998 | −0.5554 | −3.2978 | −6.1094 |
| 0.2 | −0.2949 | −0.5488 | −3.2439 | −6.0368 |
| 0.3 | −0.2899 | −0.5423 | −3.1889 | −5.9653 |
| 0.4 | −0.2850 | −0.5357 | −3.1350 | −5.8927 |
| 0.5 | −0.2801 | −0.5292 | −3.0811 | −5.8212 |
| 0.6 | −0.2752 | −0.5227 | −3.0272 | −5.7497 |
| 0.7 | −0.2703 | −0.5162 | −2.9733 | −5.6782 |
| 0.8 | −0.2654 | −0.5097 | −2.9194 | −5.6067 |
| 0.9 | −0.2605 | −0.5033 | −2.8655 | −5.5363 |
| 1.0 | −0.2557 | −0.4968 | −2.8127 | −5.4648 |
(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 0.1 | −0.2695 | −0.5429 | −2.9645 | −5.9719 |
| 0.2 | −0.2617 | −0.5335 | −2.8787 | −5.8685 |
| 0.3 | −0.2539 | −0.5252 | −2.7929 | −5.7772 |
| 0.4 | −0.2462 | −0.5170 | −2.7082 | −5.6870 |
| 0.5 | −0.2385 | −0.5087 | −2.6235 | −5.5957 |
| 0.6 | −0.2308 | −0.5004 | −2.5388 | −5.5044 |
| 0.7 | −0.2231 | −0.4922 | −2.4541 | −5.4142 |
| 0.8 | −0.2155 | −0.4840 | −2.3705 | −5.3240 |
| 0.9 | −0.2078 | −0.4758 | −2.2858 | −5.2338 |
| 1.0 | −0.2002 | −0.4676 | −2.2022 | −5.1436 |
(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 0.1 | −0.2724 | −0.5423 | −2.9964 | −5.9653 |
| 0.2 | −0.2625 | −0.5319 | −2.8875 | −5.8509 |
| 0.3 | −0.2552 | −0.5215 | −2.8072 | −5.7365 |
| 0.4 | −0.2514 | −0.5110 | −2.7654 | −5.6210 |
| 0.5 | −0.2475 | −0.5006 | −2.7225 | −5.5066 |
| 0.6 | −0.2434 | −0.4901 | −2.6774 | −5.3911 |
| 0.7 | −0.2391 | −0.4979 | −2.6301 | −5.4769 |
| 0.8 | −0.2301 | −0.4692 | −2.5311 | −5.1612 |
| 0.9 | −0.2199 | −0.4588 | −2.4189 | −5.0468 |
| 1.0 | −0.2080 | −0.4483 | −2.2880 | −4.9313 |
(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 0.1 | −0.2695 | −0.5419 | −2.9645 | −5.9609 |
| 0.2 | −0.2625 | −0.5315 | −2.8875 | −5.8465 |
| 0.3 | −0.2551 | −0.5210 | −2.8061 | −5.731 |
| 0.4 | −0.2473 | −0.5106 | −2.7203 | −5.6166 |
| 0.5 | −0.2390 | −0.5001 | −2.629 | −5.5011 |
| 0.6 | −0.2299 | −0.4897 | −2.5289 | −5.3867 |
| 0.7 | −0.2197 | −0.4792 | −2.4167 | −5.2712 |
| 0.8 | −0.2077 | −0.4688 | −2.2847 | −5.1568 |
| 0.9 | −0.1993 | −0.4583 | −2.1923 | −5.0413 |
| 1.0 | −0.1863 | −0.4478 | −2.0493 | −4.9258 |
(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 0.1 | −0.4278 | −0.5235 | 0.4848 | 0.5933 |
| 0.2 | −0.4058 | −0.5215 | 0.5140 | 0.6605 |
| 0.3 | −0.3868 | −0.5200 | 0.5415 | 0.7280 |
| 0.4 | −0.3703 | −0.5188 | 0.5678 | 0.7954 |
| 0.5 | −0.3557 | −0.5179 | 0.5929 | 0.8631 |
| 0.6 | −0.3428 | −0.5171 | 0.6170 | 0.9308 |
| 0.7 | −0.3314 | −0.5166 | 0.6407 | 0.9988 |
| 0.8 | −0.3212 | −0.5161 | 0.6638 | 1.0667 |
| 0.9 | −0.3121 | −0.5157 | 0.6867 | 1.1345 |
| 1.0 | −0.3038 | −0.5154 | 0.7089 | 1.2026 |
(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 0.1 | −1.4994 | −0.9564 | 1.6993 | 1.0839 |
| 0.2 | −1.4302 | −0.9383 | 1.8116 | 1.1885 |
| 0.3 | −1.3699 | −0.9213 | 1.9179 | 1.2898 |
| 0.4 | −1.3167 | −0.9054 | 2.0189 | 1.3883 |
| 0.5 | −1.2693 | −0.8905 | 2.1155 | 1.4842 |
| 0.6 | −1.2267 | −0.8765 | 2.2081 | 1.5777 |
| 0.7 | −1.1882 | −0.8633 | 2.2972 | 1.669 |
| 0.8 | −1.1530 | −0.8509 | 2.3829 | 1.7585 |
| 0.9 | −1.1208 | −0.8392 | 2.4658 | 1.8462 |
| 1.0 | −1.0912 | −0.8281 | 2.5461 | 1.9322 |
(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 0.1 | −0.4052 | −0.6093 | 0.5673 | 0.8530 |
| 0.2 | −0.3953 | −0.6095 | 0.5534 | 0.8533 |
| 0.3 | −0.3911 | −0.6089 | 0.5475 | 0.8525 |
| 0.4 | −0.3888 | −0.6085 | 0.5443 | 0.8519 |
| 0.5 | −0.3863 | −0.6082 | 0.5408 | 0.8515 |
| 0.6 | −0.3855 | −0.6080 | 0.5397 | 0.8512 |
| 0.7 | −0.3850 | −0.6078 | 0.5390 | 0.8509 |
| 0.8 | −0.3845 | −0.6077 | 0.5383 | 0.8508 |
| 0.9 | −0.3840 | −0.6076 | 0.5376 | 0.8506 |
| 1.0 | −0.3838 | −0.6075 | 0.5373 | 0.8505 |
(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 1.0 | −0.2982 | −0.2125 | 0.4175 | 0.2975 |
| 2.0 | −0.3281 | −0.4017 | 0.4593 | 0.5624 |
| 3.0 | −0.3412 | −0.4635 | 0.4777 | 0.6489 |
| 4.0 | −0.3489 | −0.4940 | 0.4885 | 0.6916 |
| 5.0 | −0.3534 | −0.5120 | 0.4948 | 0.7168 |
| 6.0 | −0.3562 | −0.5238 | 0.4987 | 0.7333 |
| 7.0 | −0.3582 | −0.5283 | 0.5015 | 0.7396 |
| 8.0 | −0.3592 | −0.5384 | 0.5029 | 0.7538 |
| 9.0 | −0.3605 | −0.5432 | 0.5047 | 0.7605 |
| 10 | −0.4250 | −0.5470 | 0.5950 | 0.7658 |
| Sc | ||
|---|---|---|
| 0.1 | −0.4131 | 0.4131 |
| 0.2 | −0.3493 | 0.3493 |
| 0.3 | −0.2724 | 0.2724 |
| 0.4 | −0.1767 | 0.1767 |
| 0.5 | −0.0527 | 0.0527 |
| 0.6 | 0.1167 | −0.1167 |
| 0.7 | 0.2040 | −0.2040 |
| 0.8 | 0.7897 | −0.7897 |
| 1.0 | 1.7318 | −1.7318 |
| Sc | ||
|---|---|---|
| 0.3 | −0.4543 | 0.4543 |
| 0.4 | −0.1782 | 0.1782 |
| 0.45 | −0.0365 | 0.0365 |
| 0.5 | −0.0301 | 0.0301 |
| 0.55 | 0.1494 | −0.1494 |
| 0.6 | 0.2486 | −0.2486 |
| 0.7 | 0.3067 | −0.3067 |
| 0.8 | 0.5355 | −0.5355 |
| 1.0 | 0.6399 | −0.6399 |
| 0.1 | −0.0098 | 0.0098 |
| 0.2 | −0.0190 | 0.0190 |
| 0.3 | −0.0374 | 0.0374 |
| 0.4 | −0.1680 | 0.1680 |
| 0.5 | −0.2724 | 0.2724 |
| 0.6 | −0.3591 | 0.3591 |
| 0.7 | −0.4354 | 0.4354 |
| 0.8 | −0.5049 | 0.5049 |
| 0.9 | −0.5697 | 0.5697 |
| 1.0 | −0.6308 | 0.6308 |
| Ref. [21] | Present Study | ||
|---|---|---|---|
| 1.0 | 0.1 | 1.2347 | 1.2135 |
| 1.5 | 0.1 | 1.1082 | 1.1030 |
| 2.1 | 0.1 | 1.0310 | 1.0150 |
| 2.0 | 0.0 | 0.9966 | 0.9643 |
| 2.0 | 0.1 | 1.0409 | 1.0214 |
| 2.0 | 0.2 | 1.0850 | 1.0413 |
| 2.0 | 0.1 | 1.2165 | 1.2032 |
| 2.0 | 0.1 | 1.0976 | 1.0743 |
| 2.0 | 0.1 | 0.9311 | 0.9101 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, K.U.; Shatanawi, W.; Yaseen, S. A Comparative Numerical Study of Heat and Mass Transfer Individualities in Casson Stagnation Point Fluid Flow Past a Flat and Cylindrical Surfaces. Mathematics 2023, 11, 470. https://doi.org/10.3390/math11020470
Rehman KU, Shatanawi W, Yaseen S. A Comparative Numerical Study of Heat and Mass Transfer Individualities in Casson Stagnation Point Fluid Flow Past a Flat and Cylindrical Surfaces. Mathematics. 2023; 11(2):470. https://doi.org/10.3390/math11020470
Chicago/Turabian StyleRehman, Khalil Ur, Wasfi Shatanawi, and Saba Yaseen. 2023. "A Comparative Numerical Study of Heat and Mass Transfer Individualities in Casson Stagnation Point Fluid Flow Past a Flat and Cylindrical Surfaces" Mathematics 11, no. 2: 470. https://doi.org/10.3390/math11020470
APA StyleRehman, K. U., Shatanawi, W., & Yaseen, S. (2023). A Comparative Numerical Study of Heat and Mass Transfer Individualities in Casson Stagnation Point Fluid Flow Past a Flat and Cylindrical Surfaces. Mathematics, 11(2), 470. https://doi.org/10.3390/math11020470







