Dynamic Binary-Medium Model for Jointed Rock Subjected to Cyclic Loading
Abstract
:1. Introduction
2. Binary-Medium Model
3. Static Binary-Medium Model for Jointed Rock
3.1. Constitutive Relation of Bonded Elements
3.2. Constitutive Relation of Frictional Elements
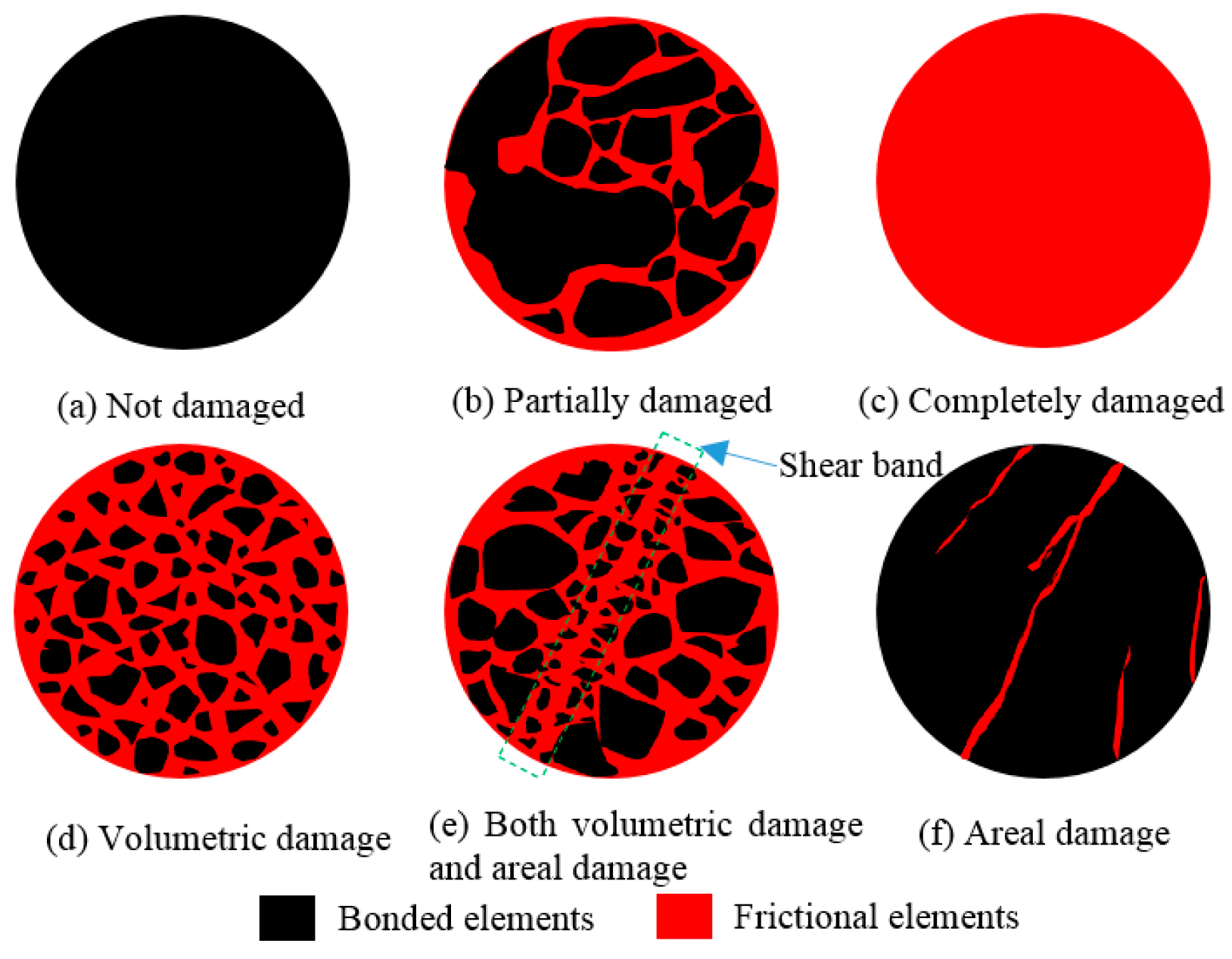
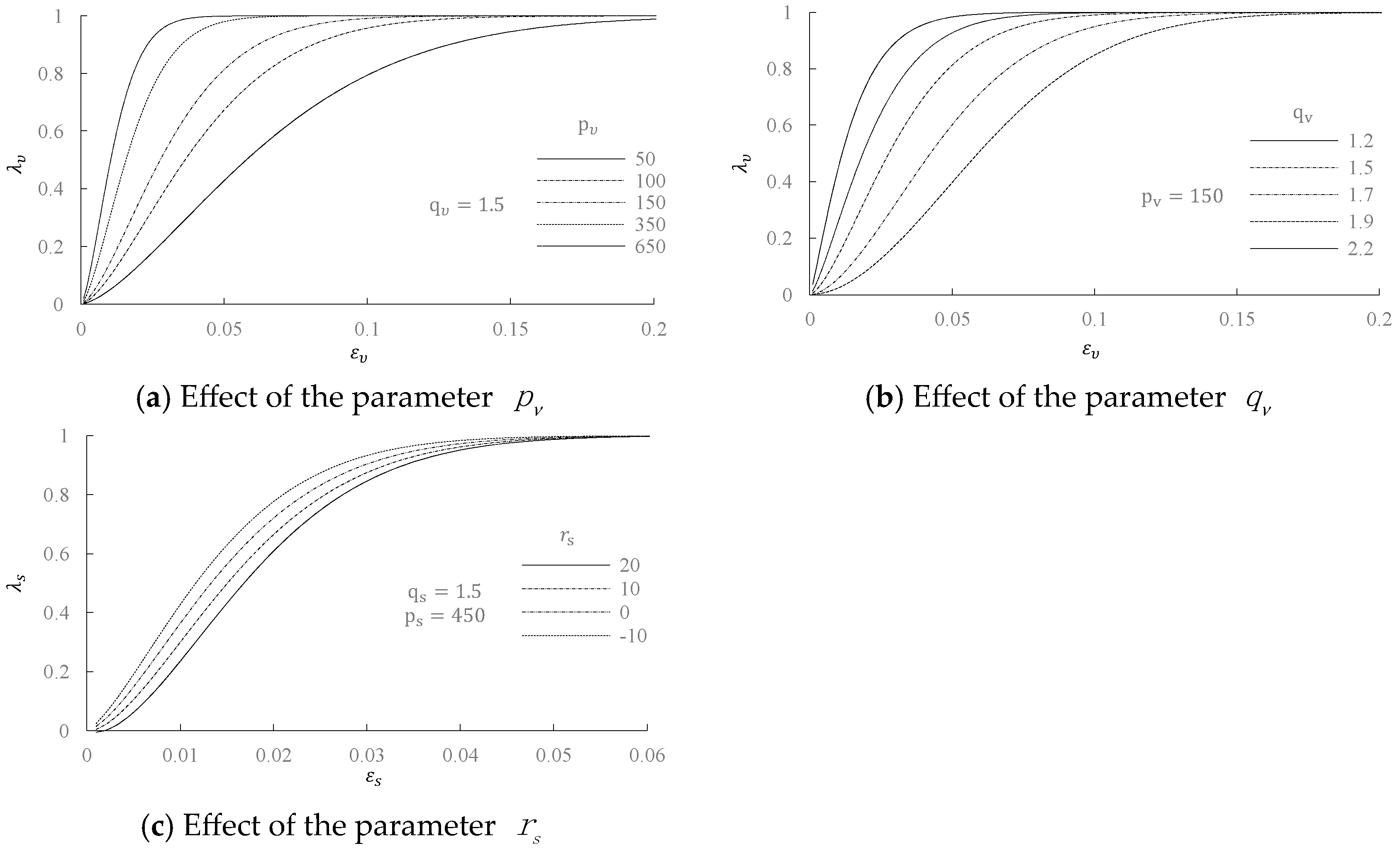
3.3. Evolution Laws of Breakage Ratio
3.4. Evolution Laws of Strain Concentration Coefficients
4. Dynamic Binary-Medium Model for Jointed Rock Subjected to Cyclic Loading
4.1. Stress–Strain Relationship at the Monotone Loading Stage
4.2. Stress–Strain Relationship at the Unloading Stage
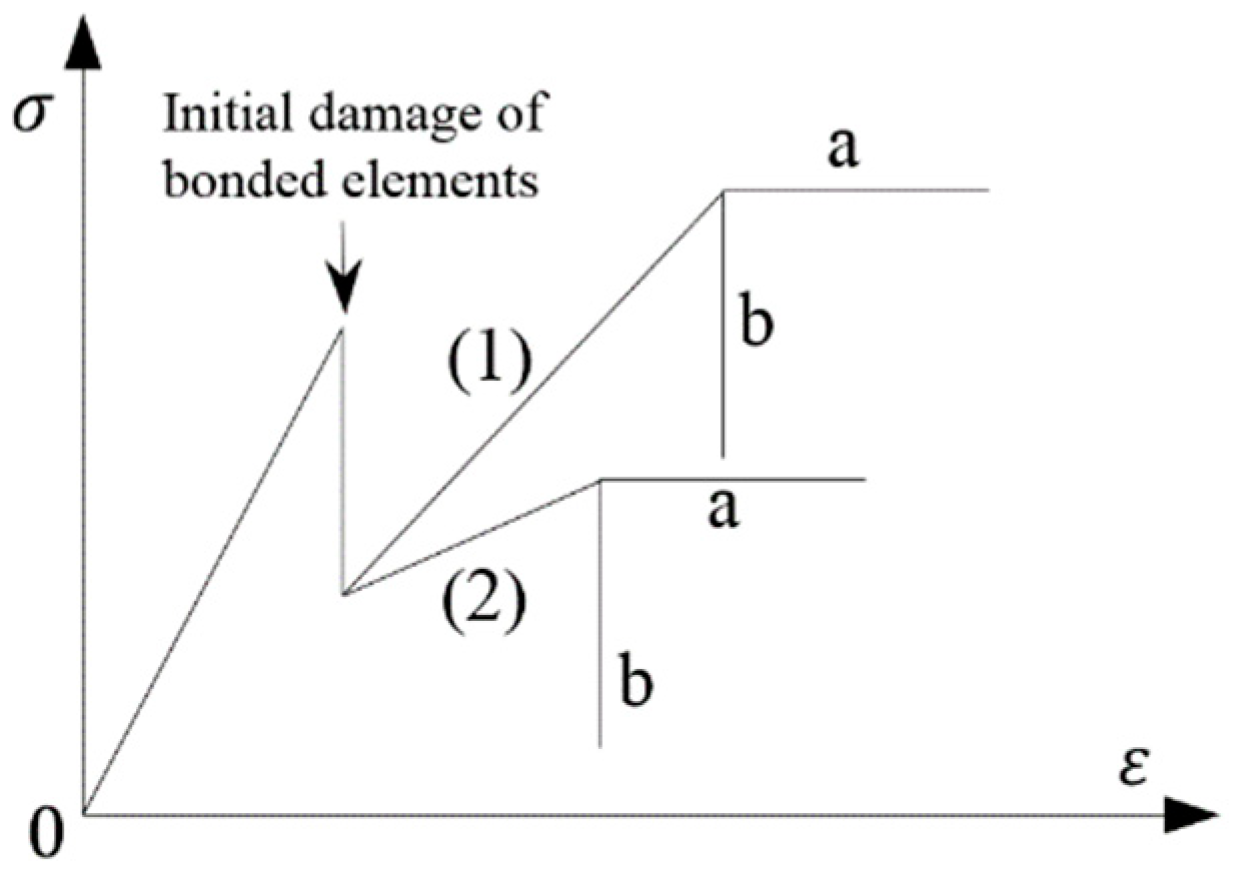
4.3. Stress–Strain Relationship at the Cyclic Loading Stage
5. Experimental Verification of Static and Dynamic Binary-Medium Model
5.1. Experiment Method
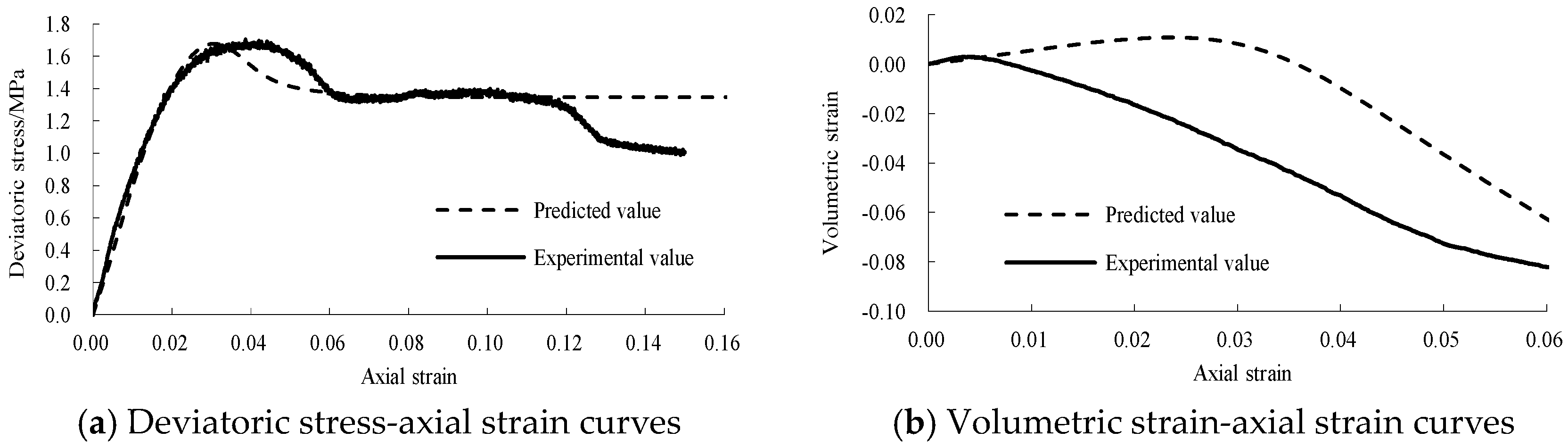
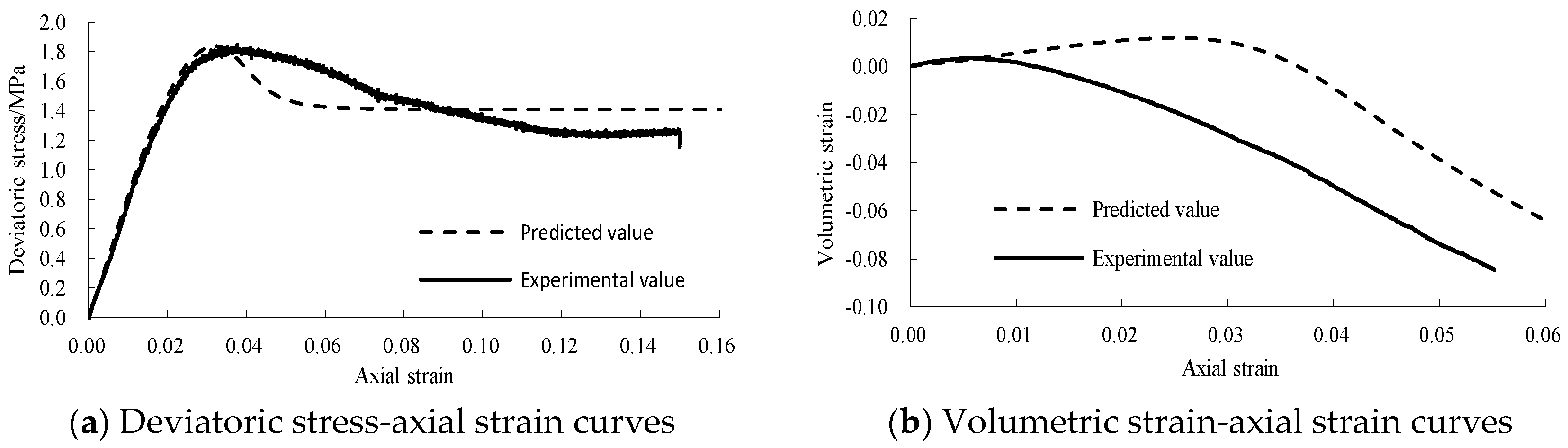
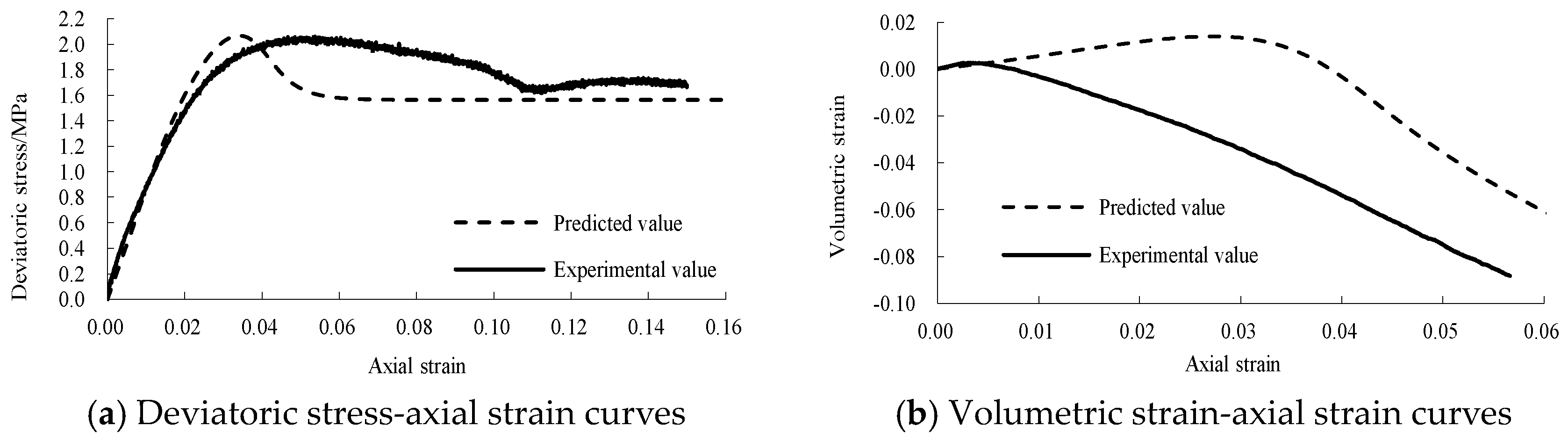
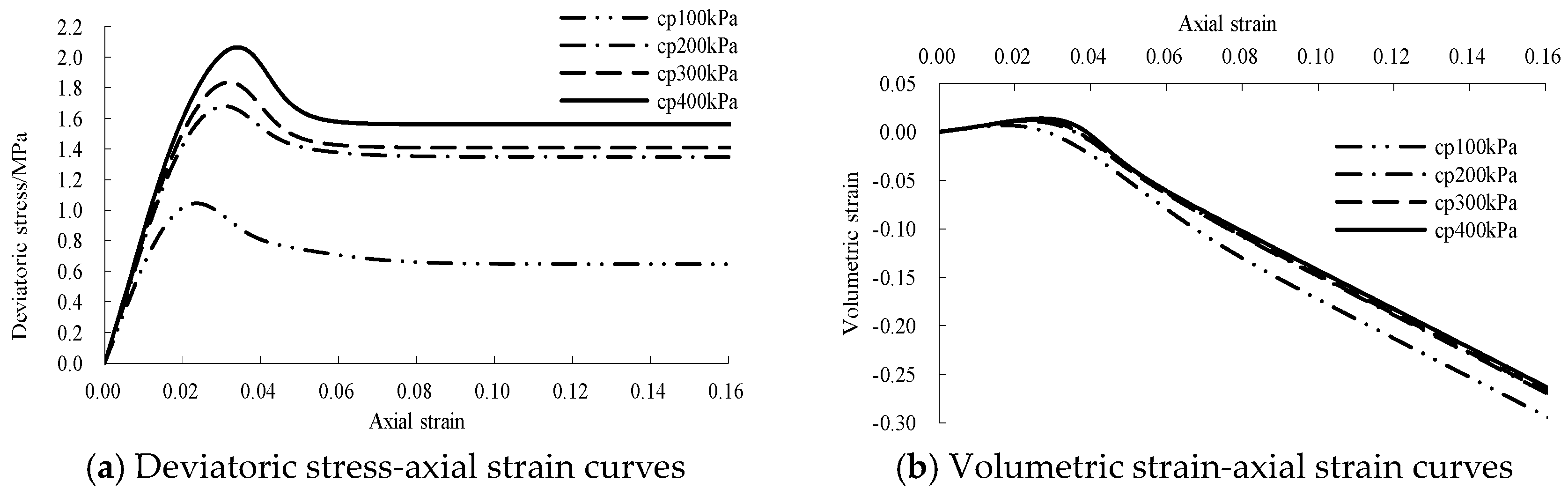
5.2. Verification of Static Triaxial Tests
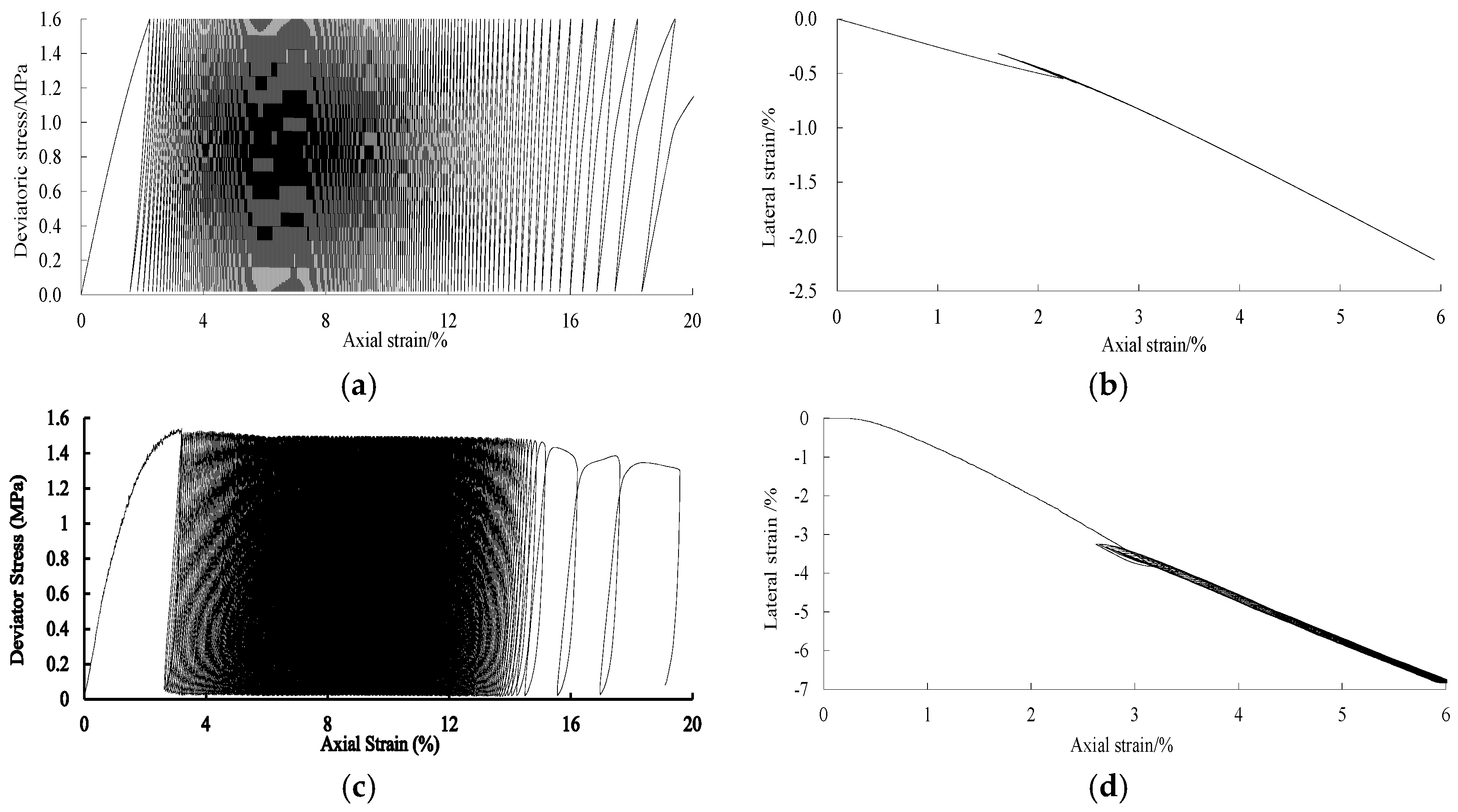
5.3. Verification of Cyclic Triaxial Tests
6. Conclusions
- (1)
- A breakage classification method for geomaterial, which is described by volume breakage ratios and area breakage ratios together, is proposed based on the binary-medium theory and the framework for the breakage mechanics of geological materials.
- (2)
- A static binary-medium model of jointed rock samples is obtained based on the Mohr–Coulomb yield criterion and the improved breakage ratio formula. The model was verified by static triaxial tests of jointed rock samples, and it was found that the proposed static binary-medium model can describe the stress–strain properties of jointed rock samples under different confining pressures. The strain-softening behavior, the volumetric strain characteristics and the influences of confining pressure on the strength and deformation behavior can be reflected well.
- (3)
- Based on the homogenization theory and the binary-medium theory, by introducing the breakage parameters and structural parameters and considering the influences of cyclic loading and unloading, the cyclic dynamic binary-medium model of jointed rock samples is established. It is found from the test verification that the predicted stress–strain curves using the dynamic model match with test results to a certain extent. They can describe the ratchet effect and the cyclic softening behavior well. They can effectively reflect the evolution laws of stress–strain curves varying from sparse to dense to sparse and the typical three-stage evolution laws of residual deformation. They describe the nonlinear stress–strain characteristics of the unloading and loading curves well and can reflect the effects of cyclic loading on the deformation and damage of jointed rock samples. Meanwhile, the lateral deformation characteristics are also described relatively well.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, M.M.; Zhang, Z.Q.; Li, N. Experimental investigation and empirical model to determine the damping and shear stiffness properties of soft rock under multistage cyclic loading. Soil Dyn. Earthq. Eng. 2021, 147, 106818. [Google Scholar] [CrossRef]
- Mamou, A.; Powrie, W.; Clayton, C.; Priest, J.A. Suitability of empirical equations for estimating permanent settlement of railway foundation materials subjected to cyclic loading with principal stress rotation. Can. Geotech. J. 2021, 58, 1603–1610. [Google Scholar] [CrossRef]
- Cai, Y.Q.; Guo, L.; Jardine, R.J.; Yang, Z.X.; Wang, J. Stress-strain response of soft clay to traffic loading. Geotechnique 2017, 67, 446–451. [Google Scholar] [CrossRef]
- Taylor, L.M.; Chen, E.P.; Kuszmaul, J.S. Microcrack-induced damage accumulation in brittle rock under dynamic loading. Comput. Methods Appl. Mech. Eng. 1986, 55, 301–320. [Google Scholar] [CrossRef]
- Chen, E.P. Non-local effects on dynamic damage accumulation in brittle solids. Int. J. Numer. Anal. Methods Géoméch. 1999, 23, 1–21. [Google Scholar] [CrossRef]
- Song, J.; Kim, K. Micromechanical modeling of the dynamic fracture process during rock blasting. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1996, 33, 387–394. [Google Scholar] [CrossRef]
- Shu, Y.; Zhu, Z.M.; Wang, M.; Ying, P.; Wang, F.; Wan, D.; Li, X.; Gao, W. A plastic damage constitutive model for rock-like material focusing on the hydrostatic pressure induced damage and the interaction of tensile and shear damages under impact and blast loads. Comput. Geotech. 2022, 15, 104921. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. A plastic-damage concrete model for earthquake analysis of dams. Earthq. Eng. Struct. Dyn. 1998, 27, 937–956. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Wang, J.G. A method for evaluating dynamic tensile damage of rock. Eng. Fract. Mech. 2008, 75, 2812–2825. [Google Scholar] [CrossRef]
- Liu, M.X.; Liu, M.X. Dynamic mechanical properties of artificial jointed rock samples subjected to cyclic triaxial loading. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 2017, 98, 54–66. [Google Scholar] [CrossRef]
- Jing, L.; Stephansson, O.; Nordlund, E. Study of rock joints under cyclic loading conditions. Rock Mech. Rock Eng. 1993, 26, 215–232. [Google Scholar] [CrossRef]
- Souley, M.; Homand, F.; Amadei, B. An extension to the Saeb and Amadei constitutive model for rock joints to include cyclic loading paths. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 101–109. [Google Scholar] [CrossRef]
- Belem, T.; Souley, M.; Homand, F. Modeling surface roughness degradation of rock joint wall during monotonic and cyclic shearing. Acta Geotech. 2007, 2, 227–248. [Google Scholar] [CrossRef]
- White, A.J. Anisotropic damage of rock joints during cyclic loading: Constitutive framework and numerical integration. Int. J. Numer. Anal. Methods Géoméch. 2014, 38, 1036–1057. [Google Scholar] [CrossRef]
- Cui, Z.; Sheng, Q.; Leng, X.L.; Ma, Y. Analysis of the seismic performance of a rock joint with a modified Continuously Yielding model. Rock Mech. Rock Eng. 2017, 50, 2695–2707. [Google Scholar] [CrossRef]
- Li, Y.C.; Wu, W.; Tang, C.A.; Liu, B. Predicting the shear characteristics of rock joints with asperity degradation and debris backfilling under cyclic loading conditions. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 2019, 120, 108–118. [Google Scholar] [CrossRef]
- Xiao, J.Q.; Ding, D.X.; Xu, G.; Jiang, F.L. Inverted S-shaped model for nonlinear fatigue damage of rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 2009, 46, 643–648. [Google Scholar] [CrossRef]
- Zhou, S.W.; Xia, C.C.; Hu, C.C.; Zhou, Y. Damage modeling of basaltic rock subjected to cyclic temperature and uniaxial stress. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 2015, 77, 163–173. [Google Scholar] [CrossRef]
- Wang, Y.S.; Ma, L.J.; Fan, P.X.; Chen, Y. A fatigue damage model for rock salt considering the effects of loading frequency and amplitude. Int. J. Min. Sci. Technol. 2016, 26, 955–958. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, F. A damage constitutive model for intermittent jointed rocks under cyclic uniaxial compression. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 2018, 103, 289–301. [Google Scholar] [CrossRef]
- Tian, J.Q.; Lai, Y.M.; Liu, E.L.; He, C. A thermodynamics-based micro-macro elastoplastic micropolar continuum model for granular materials. Comput. Geotech. 2023, 162, 105653. [Google Scholar] [CrossRef]
- Ren, C.H.; Yu, J.; Liu, X.Y.; Zhang, Z.Q.; Cai, Y.Y. Cyclic constitutive equations of rock with coupled damage induced by compaction and cracking. Int. J. Min. Sci. Technol. 2022, 32, 1153–1165. [Google Scholar] [CrossRef]
- Mo, H.H. Investigation of cyclic loading tests and constitutive relation of rock. Chin. J. Rock Mech. Eng. 1988, 7, 215. [Google Scholar]
- Feng, X.T.; Pan, X.T.; Zhou, H. Simulation of the rock microfracturing process under uniaxial compression using an elasto-plastic cellular automaton. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 2006, 43, 1091–1108. [Google Scholar] [CrossRef]
- Liu, E.L.; Zhang, J.H.; He, S.M.; Zhang, S.S.; Ge, K. Binary medium model of rock subjected to cyclic loading. J. Chongqing Inst. Technol. 2013, 27, 6–12. [Google Scholar]
- Li, Z.Z.; Nguyen, T.S.; Su, G.; Labrie, D.; Barnichon, J.D. Development of a viscoelastoplastic model for a bedded argillaceous rock from laboratory triaxial tests. Can. Geotech. J. 2017, 54, 359–372. [Google Scholar] [CrossRef]
- Zhou, Y.Q.; Sheng, Y.Q.; Li, N.N.; Fu, X.D.; Zhang, Z.P.; Gao, L.S. A Constitutive model for rock materials subjected to triaxial cyclic compression. Mech. Mater. 2020, 144, 103341. [Google Scholar] [CrossRef]
- Shen, Z.J.; Chen, T.L. Breakage mechanics for geological materials basic concepts, goal, and, task. In Proceedings of the 7th Academic Conference of Chinese Society of Rock Mechanics and Engineering, Beijing, China, 10–12 September 2002; pp. 9–12. [Google Scholar]
- Liu, E.L. Research on Breakage Mechanics of Structural Blocks and Binary Medium Model for Geomaterials. Doctoral Dissertation, Tsinghua University, Beijing, China, 2005. [Google Scholar]
- Liu, E.L.; Shen, E.L.; Chen, T.L. Experimental study on breaking process of prismatic structural bodies. Rock Soil Mech. 2006, 27, 93–98. [Google Scholar]
- Liu, M.X.; Liao, M.K.; Liu, E.L. Experimental research on mechanical properties of jointed rock mass with different angles of inclination. J. Beijing Univ. Technol. 2018, 44, 336–343. [Google Scholar]



| Bonded Elements | Frictional Elements | ||||
|---|---|---|---|---|---|
| Confining Pressure | /MPa | /MPa | |||
| 100 kPa | 70 | 0.25 | 25 | 0.3 | 0.54 |
| 200 kPa | 75 | 0.25 | 25 | 0.3 | 0.54 |
| 300 kPa | 80 | 0.25 | 25 | 0.3 | 0.54 |
| 400 kPa | 85 | 0.25 | 25 | 0.3 | 0.54 |
| Confining Pressure | |||||||
|---|---|---|---|---|---|---|---|
| 100 kPa | 27 | 550 | 1.5 | 250 | 1.5 | 0.001 | 0.05 |
| 200 kPa | 27 | 455 | 1.5 | 300 | 1.5 | 0.001 | 0.05 |
| 300 kPa | 27 | 403 | 1.5 | 350 | 1.5 | 0.001 | 0.05 |
| 400 kPa | 27 | 364 | 1.5 | 400 | 1.5 | 0.001 | 0.05 |
| Parameters | Monotone Loading | Unloading | Loading | |
|---|---|---|---|---|
| Bonded elements | /MPa | 56.67 | 56.67 | 56.67 |
| /MPa | 34 | 34 | 34 | |
| −0.2 | 1.5 | 1.4 | ||
| −0.03 | 0.8 | 0.7 | ||
| Frictional elements | /MPa | 25 | 25 | 25 |
| −0.02 | 0.45 | 0.40 | ||
| 0.3 | 0.3 | 0.3 | ||
| /MPa | 0.3 | 0.3 | 0.3 | |
| 35° | 35° | 35° |
| 60 | 1.5 | 400 | 1.5 | 0.001 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Liu, E.; Liu, X.; Zheng, Q. Dynamic Binary-Medium Model for Jointed Rock Subjected to Cyclic Loading. Mathematics 2024, 12, 1765. https://doi.org/10.3390/math12111765
Liu M, Liu E, Liu X, Zheng Q. Dynamic Binary-Medium Model for Jointed Rock Subjected to Cyclic Loading. Mathematics. 2024; 12(11):1765. https://doi.org/10.3390/math12111765
Chicago/Turabian StyleLiu, Mingxing, Enlong Liu, Xingyan Liu, and Qingsong Zheng. 2024. "Dynamic Binary-Medium Model for Jointed Rock Subjected to Cyclic Loading" Mathematics 12, no. 11: 1765. https://doi.org/10.3390/math12111765
APA StyleLiu, M., Liu, E., Liu, X., & Zheng, Q. (2024). Dynamic Binary-Medium Model for Jointed Rock Subjected to Cyclic Loading. Mathematics, 12(11), 1765. https://doi.org/10.3390/math12111765






