Design and Comparison of Fractional-Order Controllers in Flotation Cell Banks and Flotation Columns Used in Copper Extraction Processes
Abstract
:1. Introduction
- To optimize the process for both a series-connected flotation cell bank and a flotation column, mathematical models have been derived from real operating plants [30,34]. The primary approach of this work is to utilize this relevant information to design fractional controllers based on data from actual industrial processes.
- The design of FOPID and FOMRAC controllers is proposed for both a flotation cell bank and a flotation column. Unlike previous research, which has primarily focused on traditional or model-based controllers, this work explores the application of fractional controllers to these processes. The novelty of this approach lies in its application of fractional-order control techniques to flotation systems, a domain where such methods have not been previously implemented. By leveraging fractional calculus, this research aims to enhance the control performance and robustness of flotation processes, providing a new perspective on optimizing these complex systems.
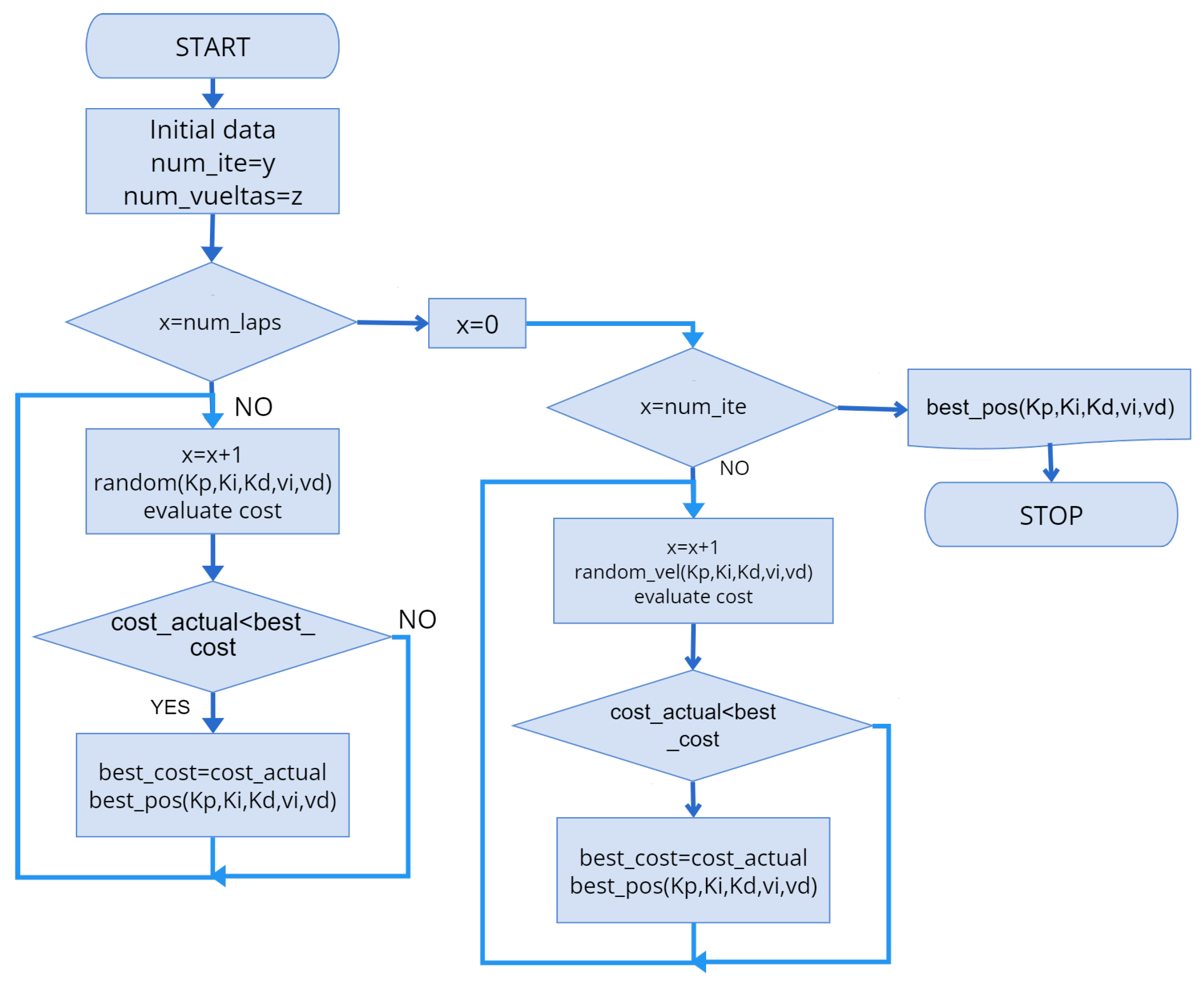
- A comparison of our fractional controllers, a FOPID controller and a FOMRAC, was carried out, determining the gains of both controllers via particle swarm optimization (PSO) and comparing these with that of their integer counterparts.
2. Preliminaries
2.1. Fractional Control Concepts
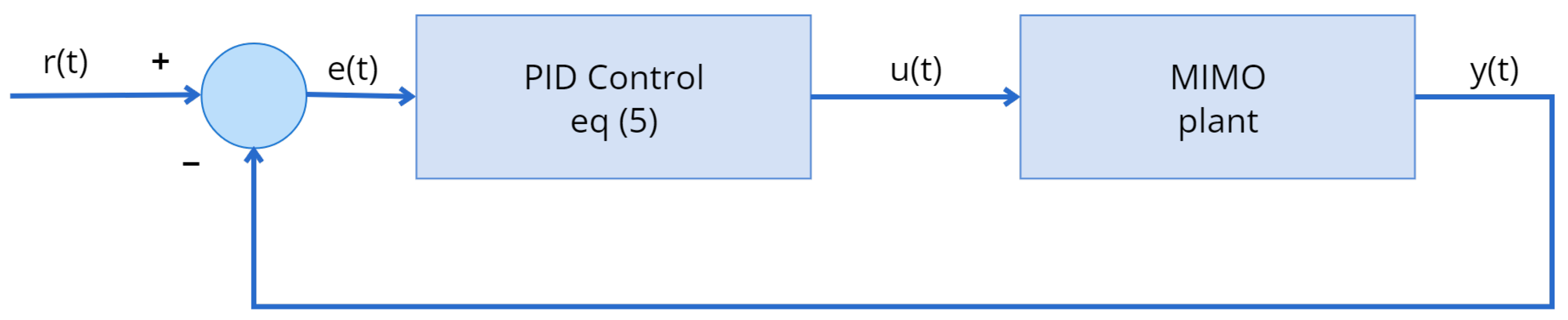
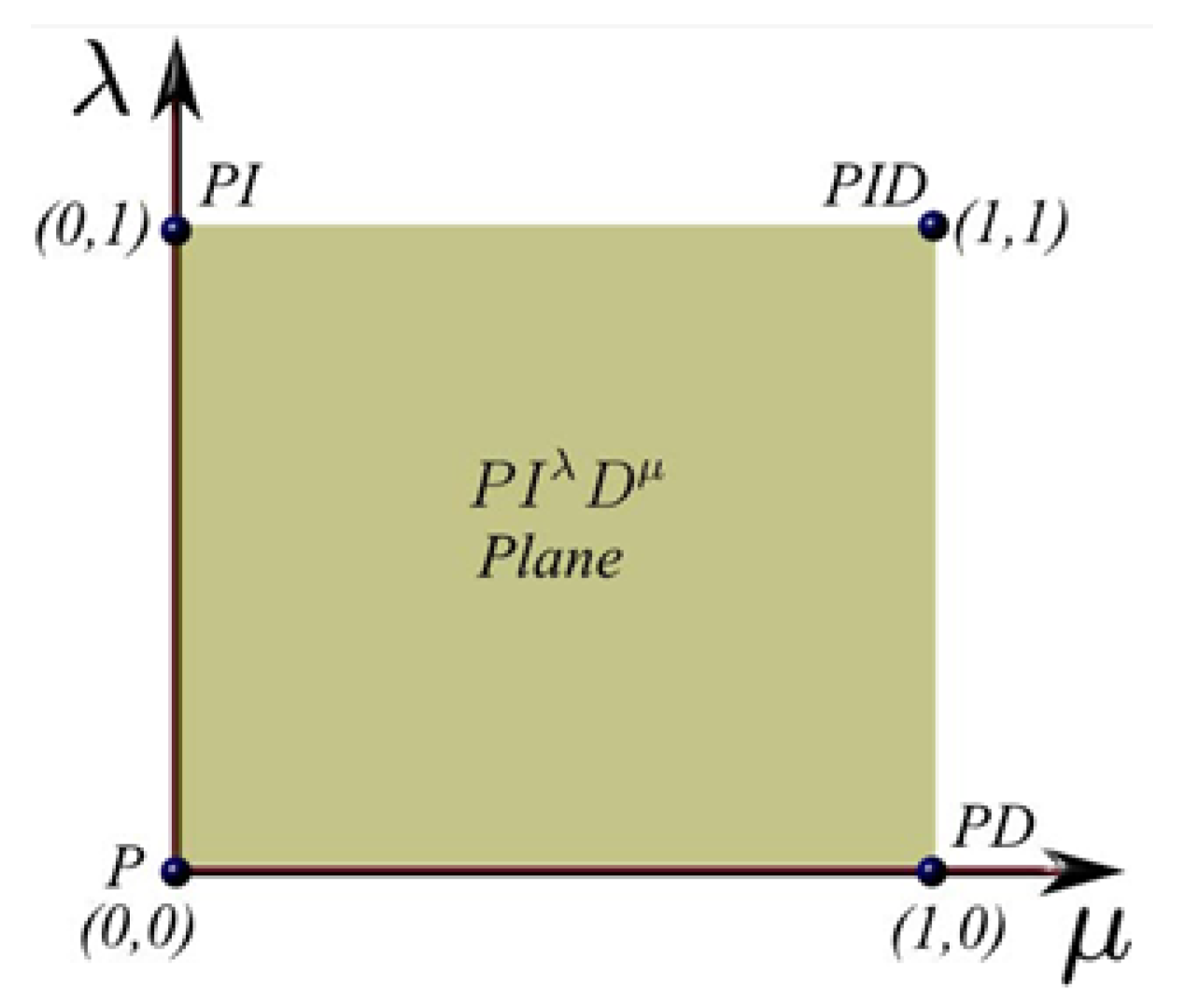
2.2. Fractional-Order PID Control
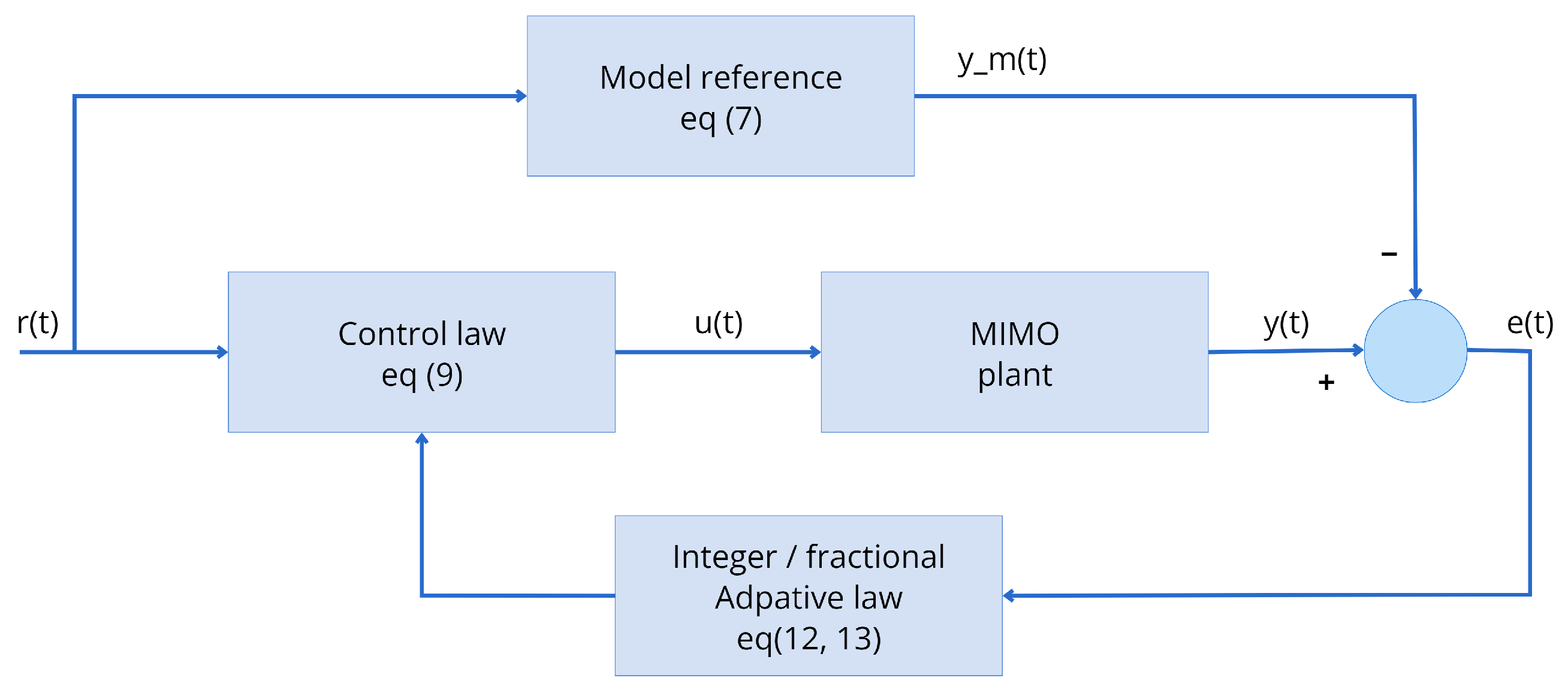
2.3. Fractional-Order Model Reference Adaptive Control
- is any transfer function of a full-rank, stable and minimum phase (i.e., all zeros of are in the left half of the complex plane).
- The upper bound on the observability index v of is known.
- The high-frequency gain matrix of is such that is a symmetric and positive definite matrix for some known matrix S.
- The modified left interactor matrix of is a lower triangle polynomial matrix denoted as .
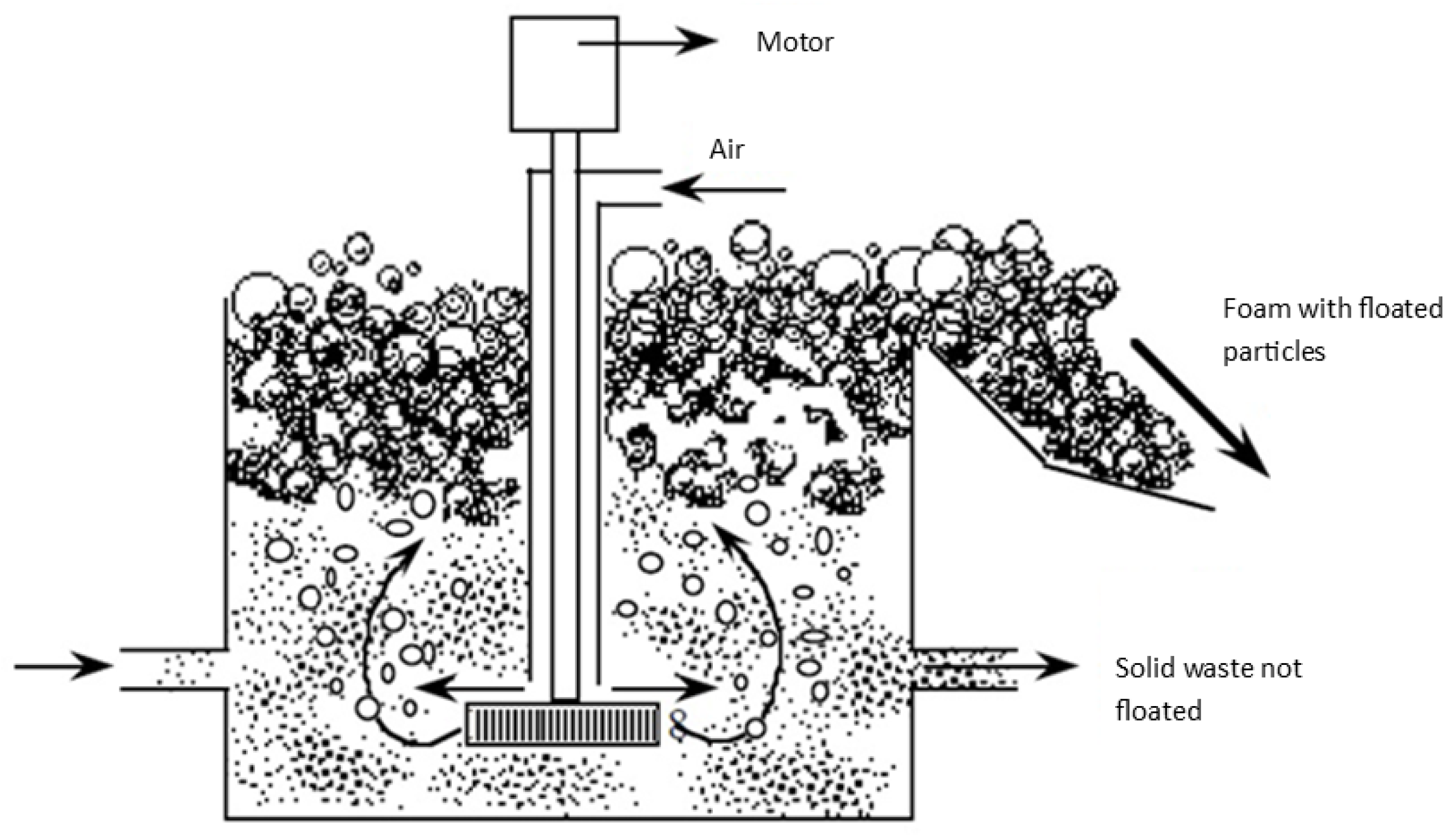
2.4. Flotation Process
3. Model Description
3.1. Flotation Cell Bank Modeling
3.2. Flotation Column Modeling
- When controlling the interface level (H), the main reference is the flow of the queues.
- When controlling the air holdup (), the main reference is the airflow.
- The other inputs can be kept constant.
- This system is still considered MIMO, because the constants and other signals still act, although with a smaller impact than that of the main variable, according to the output.
4. Case Studies and Comparative Analysis
4.1. Controller Tuning
- The initial population cannot be the same as the one chosen as in the literature, since up to three times as many parameters are optimized in our study. As the number of initial individuals is specific to each problem, in this study 150 particles were defined for the search process.
- The variable inertia factor was chosen to be and .
- The acceleration constants were chosen to be and .
- The maximum number of interactions was set as .
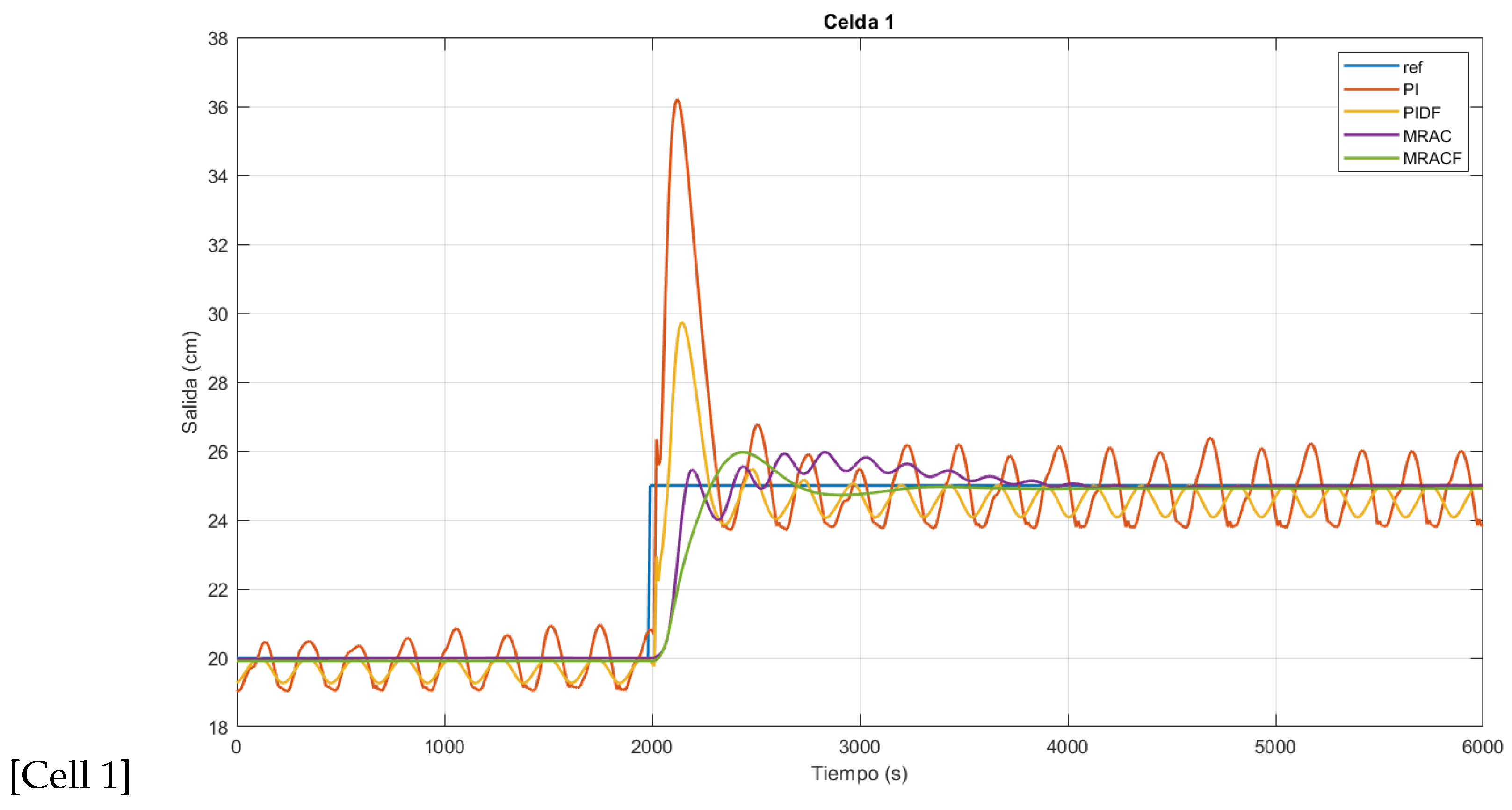
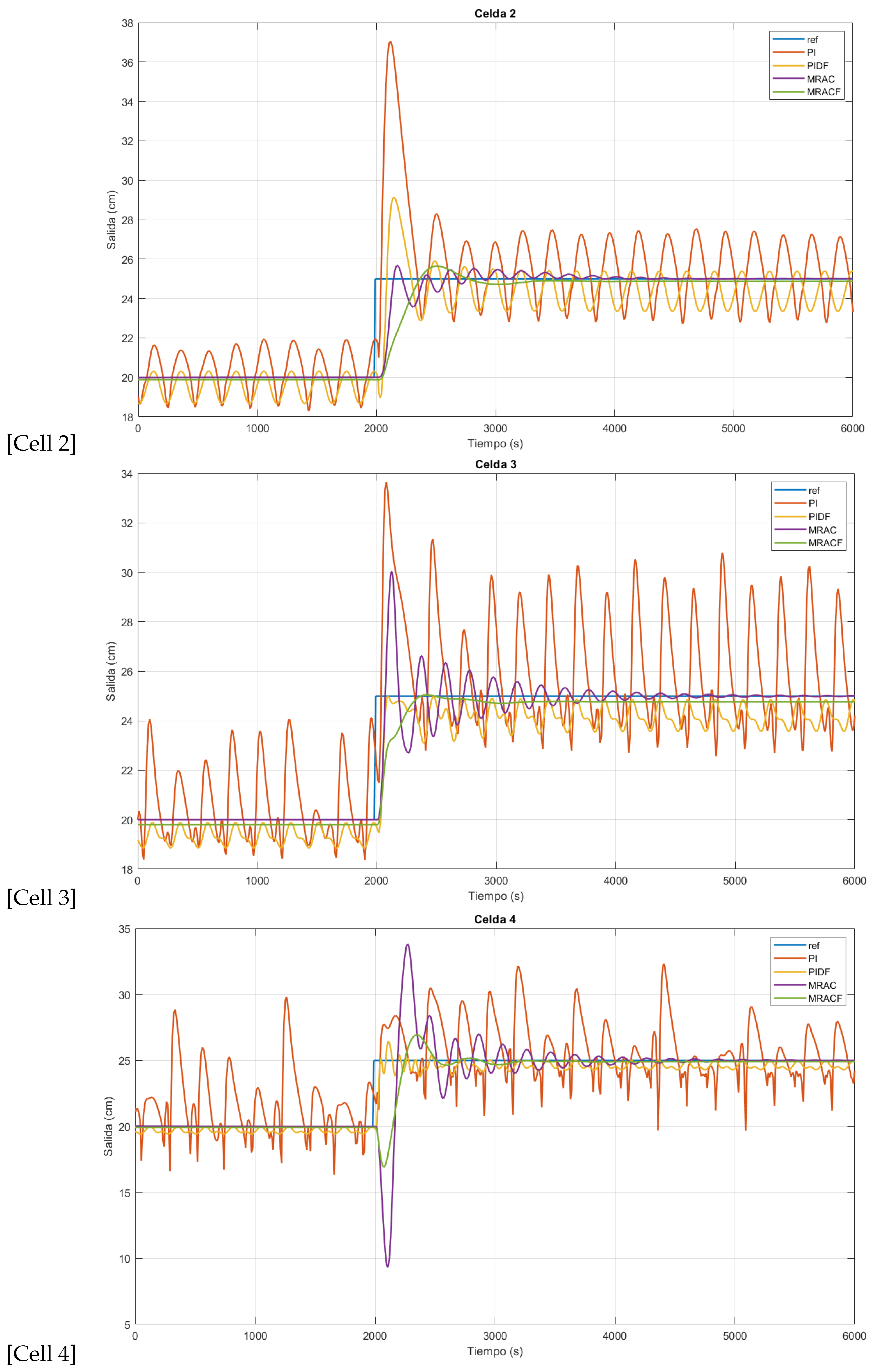
4.2. Flotation Cell Bank Behavior under Reference-Based Variations
4.3. Flotation Column Behavior against Reference-Based Variations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier Science: Amsterdam, The Netherlands, 1974; pp. 1–322. [Google Scholar]
- Li, Z.; Chen, Q.; Wang, Y.; Li, X. Solving Two-Sided Fractional Super-Diffusive Partial Differential Equations with Variable Coefficients in a Class of New Reproducing Kernel Spaces. Fractal Fract. 2022, 6, 492. [Google Scholar] [CrossRef]
- Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Gallegos, J.A.; Travieso-Torres, J.C. Fractional-order model reference adaptive controllers for first-order integer plants. In New Perspectives and Applications of Modern Control Theory: In Honor of Alexander S. Poznyak; Springer: Cham, Switzerland, 2018; pp. 121–151. [Google Scholar]
- Aguila-Camacho, N.; García-Bustos, J.E.; Castillo-López, E.I.; Gallegos, J.A.; Travieso-Torres, J.C. Switched Fractional Order Model Reference Adaptive Control for First Order Plants: A Simulation-Based Study. J. Dyn. Syst. Meas. Control 2022, 144, 044502. [Google Scholar] [CrossRef]
- Fuerstenau, M.C.; Han, K.N. Principles of Mineral Processing; SME: Littleton, CO, USA, 2003. [Google Scholar]
- Vinagre, B.M.; Monje, C.A. Introduccion al control fraccionario. Rev. Iberoam. Autom. Inform. Ind. 2006, 3, 5–23. [Google Scholar]
- Thivierge, A.; Bouchard, J.; Desbiens, A. Economic model predictive control of a high-pressure grinding rolls circuit: Energy considerations. IFAC-PapersOnLine 2022, 55, 55–60. [Google Scholar] [CrossRef]
- Vinagre, B.M.; Monje, C.A. Fractional PID Controllers for Industry Application. A Brief Introduction. J. Vib. Control 2007, 13, 1419–1429. [Google Scholar] [CrossRef]
- Fujii, S.; Mizuno, N. Multivariable Discrete Model Reference Adaptive Control Using an Autoregressive Model with Dead Time of the Plant and Its Application. Trans. Soc. Instrum. Control Eng. 1982, 18, 238–245. [Google Scholar] [CrossRef]
- Elliott, H.; Wolovich, W. A parameter adaptive control structure for linear multivariable systems. IEEE Trans. Autom. Control 1982, 27, 340–352. [Google Scholar] [CrossRef]
- Quintanilla, P.; Navia, D.; Neethling, S.J.; Brito-Parada, P.R. Economic model predictive control for a rougher froth flotation cell using physics-based models. Miner. Eng. 2023, 196, 108050. [Google Scholar] [CrossRef]
- Anzoom, S.J.; Bournival, G.; Ata, S. Coarse particle flotation: A review. Miner. Eng. 2024, 206, 108499. [Google Scholar] [CrossRef]
- Azhin, M.; Popli, K.; Prasad, V. Modelling and boundary optimal control design of hybrid column flotation. Can. J. Chem. Eng. 2021, 99, S369–S388. [Google Scholar] [CrossRef]
- Xu, X.; Tian, Y.; Yuan, Y.; Luan, X.; Liu, F.; Dubljevic, S. Output regulation of linearized column froth flotation process. IEEE Trans. Control Syst. Technol. 2020, 29, 249–262. [Google Scholar] [CrossRef]
- Chen, J.; Chimonyo, W.; Peng, Y. Flotation behaviour in reflux flotation cell–A critical review. Miner. Eng. 2022, 181, 107519. [Google Scholar] [CrossRef]
- Quintanilla, P.; Neethling, S.J.; Navia, D.; Brito-Parada, P.R. A dynamic flotation model for predictive control incorporating froth physics. Part I: Model development. Miner. Eng. 2021, 173, 107192. [Google Scholar] [CrossRef]
- Quintanilla, P.; Neethling, S.J.; Mesa, D.; Navia, D.; Brito-Parada, P.R. A dynamic flotation model for predictive control incorporating froth physics. Part II: Model calibration and validation. Miner. Eng. 2021, 173, 107190. [Google Scholar] [CrossRef]
- Norlund, F. Comparison of Level Control Strategies for a Flotation Series in the Mining Industry. Master’s Thesis, Lund University, Lund, Sweden, 2022. [Google Scholar]
- Yianatos, J.; Vallejos, P.; Grau, R.; Yañez, A. New approach for flotation process modelling and simulation. Miner. Eng. 2020, 156, 106482. [Google Scholar] [CrossRef]
- Yianatos, J.; Vallejos, P. Limiting conditions in large flotation cells: Froth recovery and bubble loading. Miner. Eng. 2022, 185, 107695. [Google Scholar] [CrossRef]
- Jera, T.M.; Bhondayi, C. A review on froth washing in flotation. Minerals 2022, 12, 1462. [Google Scholar] [CrossRef]
- Quintanilla, P.; Navia, D.; Neethling, S.; Brito-Parada, P. Experimental Implementation of an Economic Model Predictive Control for Froth Flotation. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2024; Volume 53, pp. 1759–1764. [Google Scholar]
- Sun, B.; Yang, W.; He, M.; Wang, X. An integrated multi-mode model of froth flotation cell based on fusion of flotation kinetics and froth image features. Miner. Eng. 2021, 172, 107169. [Google Scholar] [CrossRef]
- Nasseri, S.; Khalesi, M.R.; Ramezani, A.; Abdollahi, M.; Mohseni, M. An Adaptive Decoupling Control Design for Flotation Column: A Comparative Study Against Model Predictive Control. IETE J. Res. 2022, 68, 3994–4007. [Google Scholar] [CrossRef]
- Maldonado, M.; Desbiens, A.; Del Villar, R. Potential use of model predictive control for optimizing the column flotation process. Int. J. Miner. Process. 2009, 93, 26–33. [Google Scholar] [CrossRef]
- Tian, Y.; Luan, X.; Liu, F.; Dubljevic, S. Model predictive control of mineral column flotation process. Mathematics 2018, 6, 100. [Google Scholar] [CrossRef]
- Calisaya, D.; Poulin, É.; Desbiens, A.; del Villar, R.; Riquelme, A. Multivariable predictive control of a pilot flotation column. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 4022–4027. [Google Scholar]
- Mohanty, S. Artificial neural network based system identification and model predictive control of a flotation column. J. Process Control 2009, 19, 991–999. [Google Scholar] [CrossRef]
- Riquelme, A.; Desbiens, A.; Del Villar, R.; Maldonado, M. Predictive control of the bubble size distribution in a two-phase pilot flotation column. Miner. Eng. 2016, 89, 71–76. [Google Scholar] [CrossRef]
- Ccarita-Cruz, J.C. Diseño de un Controlador Predictivo Generalizado Multivariable para el Control de una Celda de Flotación tipo Columna Utilizada en el Proceso de Recuperación de Cobre. Master’s Thesis, Pontifica Universidad Católica del Perú, San Miguel, Peru, 2017. [Google Scholar]
- Quintanilla, P.; Neethling, S.J.; Brito-Parada, P.R. Modelling for froth flotation control: A review. Miner. Eng. 2021, 162, 106718. [Google Scholar] [CrossRef]
- Jovanović, I.; Miljanović, I. Contemporary advanced control techniques for flotation plants with mechanical flotation cells–A review. Miner. Eng. 2015, 70, 228–249. [Google Scholar] [CrossRef]
- Putz, E.; Cipriano, A. Hybrid model predictive control for flotation plants. Miner. Eng. 2015, 70, 26–35. [Google Scholar] [CrossRef]
- Troncoso-Garay, C.E. Diseño e implementación de estrategia de control predictivo en proceso de flotación de minerales. Master’s Thesis, Universidad Técnica Federico Santa María, Valparaíso, Chile, 2016. [Google Scholar]
- Duarte-Mermoud, M.A. Advances in Fractional Control. In Proceedings of the CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies, Santiago, Chile, 28–30 October 2015; pp. 413–415. [Google Scholar]
- Jauregui, C.; Duarte-Mermoud, M.; Orostica, R. Conical Tank Level Control with Fractional PID. IEEE Lat. Am. Trans. 2016, 14, 2598–2604. [Google Scholar] [CrossRef]
- Bürger, R.; Diehl, S.; Martí, M.C.; Vásquez, Y. Simulation and control of dissolved air flotation and column froth flotation with simultaneous sedimentation. Water Sci. Technol. 2020, 81, 1723–1732. [Google Scholar] [CrossRef]
- Wepener, D.; le Roux, J.; Craig, I. Disturbance Propagation Through a Grinding-Flotation Circuit. IFAC-PapersOnLine 2021, 54, 19–24. [Google Scholar] [CrossRef]
- Le Roux, J.D.; Craig, I.K. Plant-wide control framework for a grinding mill circuit. Ind. Eng. Chem. Res. 2019, 58, 11585–11600. [Google Scholar] [CrossRef]
- Jämsä-Jounela, S.L.; Dietrich, M.; Halmevaara, K.; Tiili, O. Control of pulp levels in flotation cells. Control Eng. Pract. 2003, 11, 73–81. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; pp. 1–337. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations, Ilustrada ed.; Wiley: Hoboken, NJ, USA, 1993; pp. 1–384. [Google Scholar]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations, 1st ed.; van Mill, J., Ed.; Elsevier: Amsterdam, The Netherlands, 2006; pp. 1–523. [Google Scholar]
- Pan, I.; Das, S. Intelligent Fractional Order Systems and Control; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–298. [Google Scholar]
- Nanendra, K.S.; Annaswamy, A.M. Stable Adaptive Systems, 5th ed.; Dover Publications: Mineola, NY, USA, 2005; pp. 1–512. [Google Scholar]
- El-Khazali, R. Fractional-order PID (fractional) controller design. Comput. Math. Appl. 2013, 66, 639–646. [Google Scholar] [CrossRef]
- Ostalczyk, P. Stability analysis of a discrete-time system with a variable, fractional-order controller. Inst. Autom. 2010, 58, 613–619. [Google Scholar] [CrossRef]
- Vinagre, B.M.; Feliu-Batlleb, V.; Tejadoa, I. Control fraccionario: Fundamentos y guia de uso. Rev. Iberoam. Automát. Informát. Ind. 2016, 13, 265–280. [Google Scholar] [CrossRef]
- Sagayaraj, M.R.; Selvam, A.G.M. Discrete fractional calculus: Definitions and applications. Int. J. Pure Eng. Math. 2014, 2, 93–102. [Google Scholar]
- Dzieliński, A.; Sierociuk, D.; Sarwas, G. Some applications of fractional order calculus. Bull. Pol. Acad. Sci. 2010, 58, 583–592. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Y.; Tao, G. Multivariable MRAC with state feedback for output tracking. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 592–597. [Google Scholar]
- Tao, G. Model reference adaptive control of multivariable plants with delays. Int. J. Control. 1992, 55, 393–414. [Google Scholar] [CrossRef]
- Das, M. Multivariable Adaptive Model Matching Using Less A Priori Information. J. Dyn. Syst. Meas. Control 1986, 108, 151–153. [Google Scholar] [CrossRef]
- Guo, J.; Tao, G.; Liu, Y. A multivariable MRAC scheme with application to a nonlinear aircraft model. Automatica 2011, 47, 804–812. [Google Scholar] [CrossRef]
- Guo, J.; Tao, G. A discrete-time multivariable MRAC scheme applied to a nonlinear aircraft model with structural damage. Automatica 2015, 53, 43–52. [Google Scholar] [CrossRef]
- Hsu, L.; Minhoto-Teixeira, M.C.; Costa, R.R. Lyapunov design of multivariable MRAC via generalized passivation. Asian J. Control 2015, 17, 1484–1497. [Google Scholar] [CrossRef]
- Lazo-Berrezueta, A.A. Implementación de un Controlador Adaptativo por Modelo de Referencia para Sistemas de Segundo Orden. Master’s Thesis, Universidad Politecnica Salesiana Ecuador, Cuenca, Ecuador, 2016. [Google Scholar]
- Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Gallegos, J.A.; Castro-Linares, R. Using general quadratic Lyapunov functions to prove Lyapunov uniform stability for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 650–659. [Google Scholar] [CrossRef]
- Sutulov, A. Flotación de Minerales; Universidad de Concepción, Instituto de Investigaciones Tecnológicas: Concepción, Chile, 1963; pp. 1–331. [Google Scholar]
- Salager, G. Fundamentos de La Flotación de Minerales; Universidad de los Andes: Bogotá, Colombia, 2007; pp. 1–21. [Google Scholar]
- Cruz, E.B. Simulation of Computer Control Strategies for Column Flotation. Master’s Thesis, Virginia Tech, Blacksburg, VA, USA, 1994. [Google Scholar]
- Rasool, H.; Rasool, A.; Ikram, A.A.; Rasool, U.; Jamil, M. Compatibility of objective functions with simplex algorithm for controller tuning of HVDC system. Ing. E Investig. 2019, 39, 34–43. [Google Scholar] [CrossRef]
- Panda, S.; Sahu, B.K.; Mohanty, P.K. Design and performance analysis of PID controller for an automatic voltage regulator system using simplified particle swarm optimization. J. Frankl. Inst. 2012, 349, 2609–2625. [Google Scholar] [CrossRef]
- Ortiz-Quisbert, M.; Duarte-Mermoud, M.; Milla, F.; Castro-Linares, R. Control Adaptativo Fraccionario Optimizado por Algoritmos Genéticos, Aplicado a Reguladores Automáticos de Voltaje. Rev. Iberoam. De Automát. Informát. Ind. RIAI 2016, 13, 403–409. [Google Scholar] [CrossRef]
- Chatterjee, A.; Mukherjee, V.; Ghoshal, S.P. Velocity relaxed and craziness-based swarm optimized intelligent PID and PSS controlled AVR system. Int. J. Electr. Power Energy Syst. 2009, 31, 323–333. [Google Scholar] [CrossRef]
- Ogata, K. Ingenieria de Control Moderna; Pearson: London, UK, 2010; pp. 1–965. [Google Scholar]
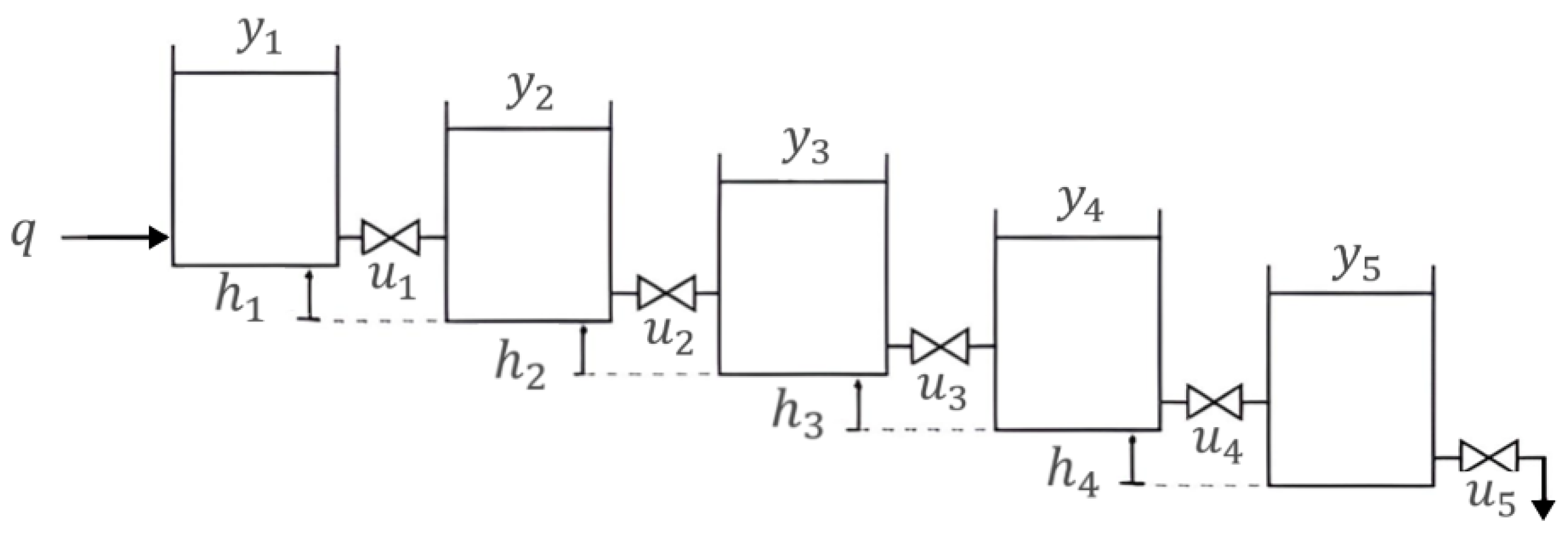

| Variable | Interface Level (H) |
|---|---|
| Washing water () | |
| Tailings () | |
| Pulp feeding () | |
| Air flux () | |
| Air holdup () | |
| Washing water () | |
| Tailings () | |
| Pulp feeding () | |
| Air flux () |
| Controller | Gains | Mp (%) | (s) | (s) | ISE | ITSE | IAE | ITAE | |
|---|---|---|---|---|---|---|---|---|---|
| Cell 1 | IOPI | 44.87 | 2020 | ∞ | 1.83 × 104 | 4.33 × 107 | 5599 | 1.62 × 107 | |
| FOPID | 18.93 | 2080 | ∞ | 4032 | 1.04 × 107 | 3090 | 9.06 × 106 | ||
| IOMRAC | 3.86 | 2170 | 3270 | 2677 | 5.81 × 106 | 1327 | 3.43 × 106 | ||
| FOMRAC | 3.84 | 2290 | 2580 | 2949 | 6.21 × 106 | 1488 | 3.67 × 106 | ||
| Cell 2 | IOPI | 48.17 | 2040 | ∞ | 2.96 × 104 | 7.74 × 107 | 8858 | 2.65 × 107 | |
| FOPID | 16.5 | 2090 | ∞ | 8311 | 2.32 × 107 | 5137 | 1.54 × 107 | ||
| IOMRAC | 2.68 | 2150 | 2840 | 2289 | 4.81 × 106 | 1030 | 2.54 × 106 | ||
| FOMRAC | 2.58 | 2370 | 2600 | 3619 | 7.68 × 106 | 1799 | 4.59 × 106 | ||
| Cell 3 | IOPI | 34.56 | 2040 | ∞ | 3.28 × 104 | 1.04 × 108 | 1.03 × 104 | 3.24 × 107 | |
| FOPID | 0.032 | 2090 | ∞ | 5649 | 1.71 × 107 | 4784 | 1.48 × 107 | ||
| IOMRAC | 20.04 | 2080 | 3290 | 3356 | 7.44 × 106 | 1663 | 4.31 × 106 | ||
| FOMRAC | 0.19 | 2370 | 2270 | 1921 | 4.25 × 106 | 1736 | 4.9 × 106 | ||
| Cell 4 | IOPI | 29.29 | 2050 | ∞ | 4.3 × 104 | 1.03 × 108 | 1.2 × 104 | 3.23 × 107 | |
| FOPID | 5.84 | 2050 | ∞ | 1834 | 5.25 × 106 | 2565 | 7.86 × 106 | ||
| IOMRAC | 35.31 | 2190 | 3590 | 2.91 × 104 | 6.34 × 107 | 4181 | 1.02 × 107 | ||
| FOMRAC | 7.75 | 2250 | 2480 | 8011 | 1.68 × 107 | 2075 | 4.93 × 106 | ||
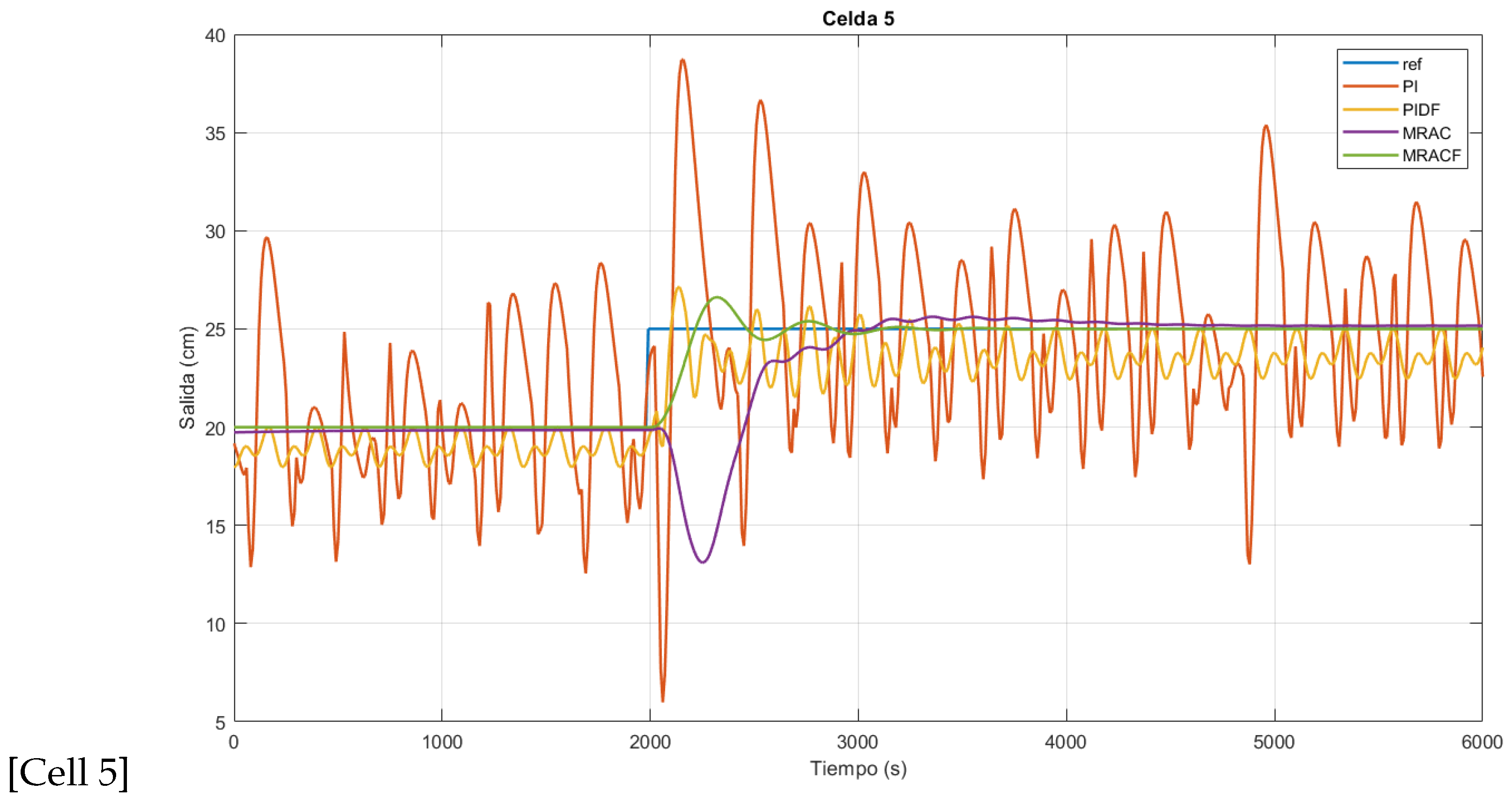
| Cell 5 | IOPI | 54.86 | 2110 | ∞ | 1.42 × 105 | 4 × 108 | 2.35 × 104 | 6.95 × 107 | |
| FOPID | 8.55 | 2100 | ∞ | 1.56 × 104 | 4.85 × 107 | 8191 | 2.54 × 107 | ||
| IOMRAC | 2.49 | 3060 | 3790 | 3.58 × 104 | 8.13 × 107 | 5704 | 1.42 × 107 | ||
| FOMRAC | 6.47 | 2220 | 2590 | 2963 | 6.22 × 106 | 1105 | 2.51 × 106 | ||
| Controller | Gains | (%) | (s) | (s) | ISE | ITSE | IAE | ITAE | |
|---|---|---|---|---|---|---|---|---|---|
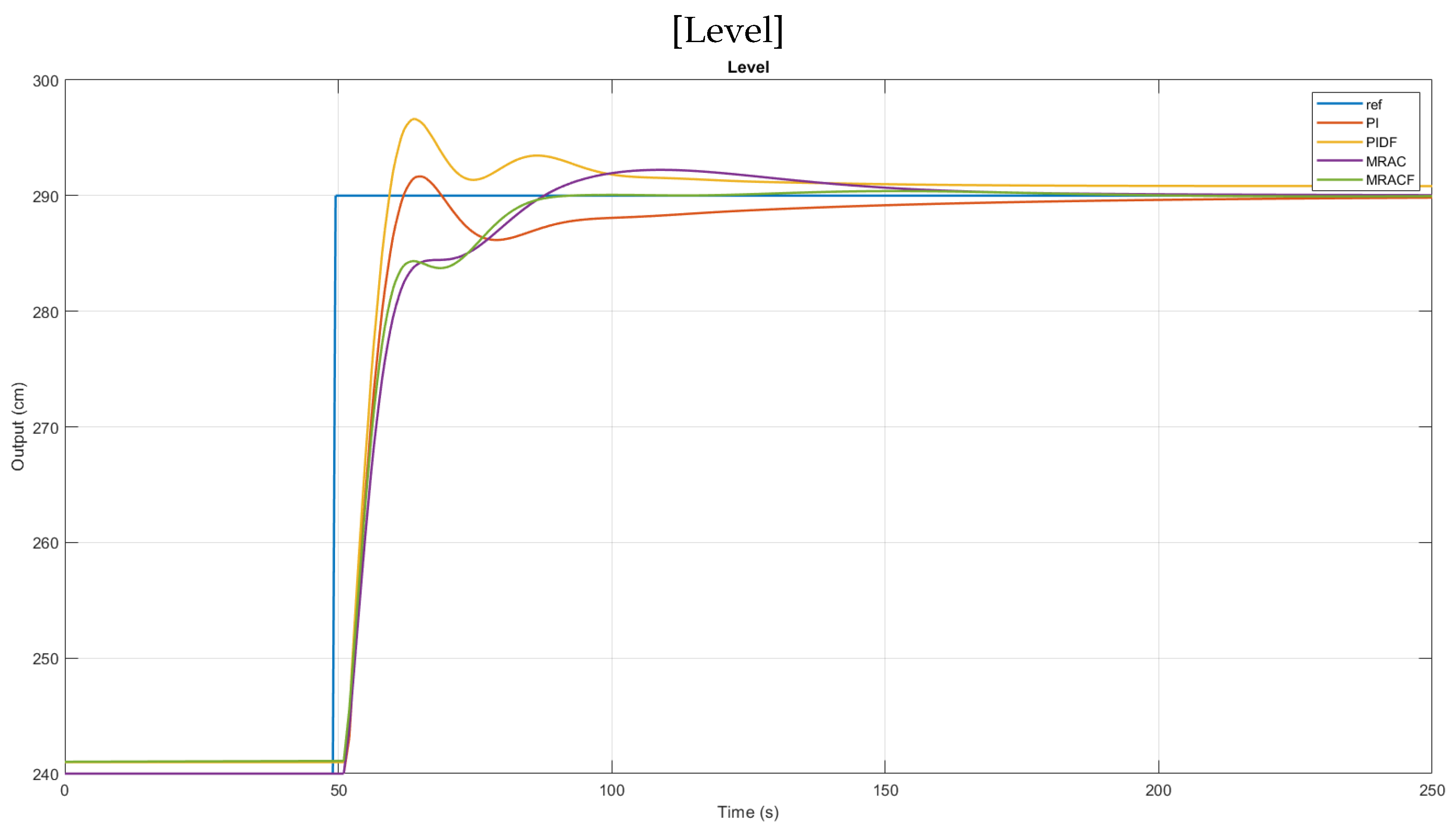
| Level | IOPI | 0.75 | 62 | 139.5 | 1101 | 5.85 × 104 | 144.9 | 9797 | |
| FOPID | 2.29 | 59.5 | 148.5 | 1046 | 5.75 × 104 | 190.8 | 16,530 | ||
| IOMRAC | 0.76 | 88 | 141 | 1328 | 7.25 × 104 | 180.4 | 13,180 | ||
| FOMRAC | 0.13 | 92.5 | 83 | 1169 | 6.24 × 104 | 156.6 | 9302 | ||
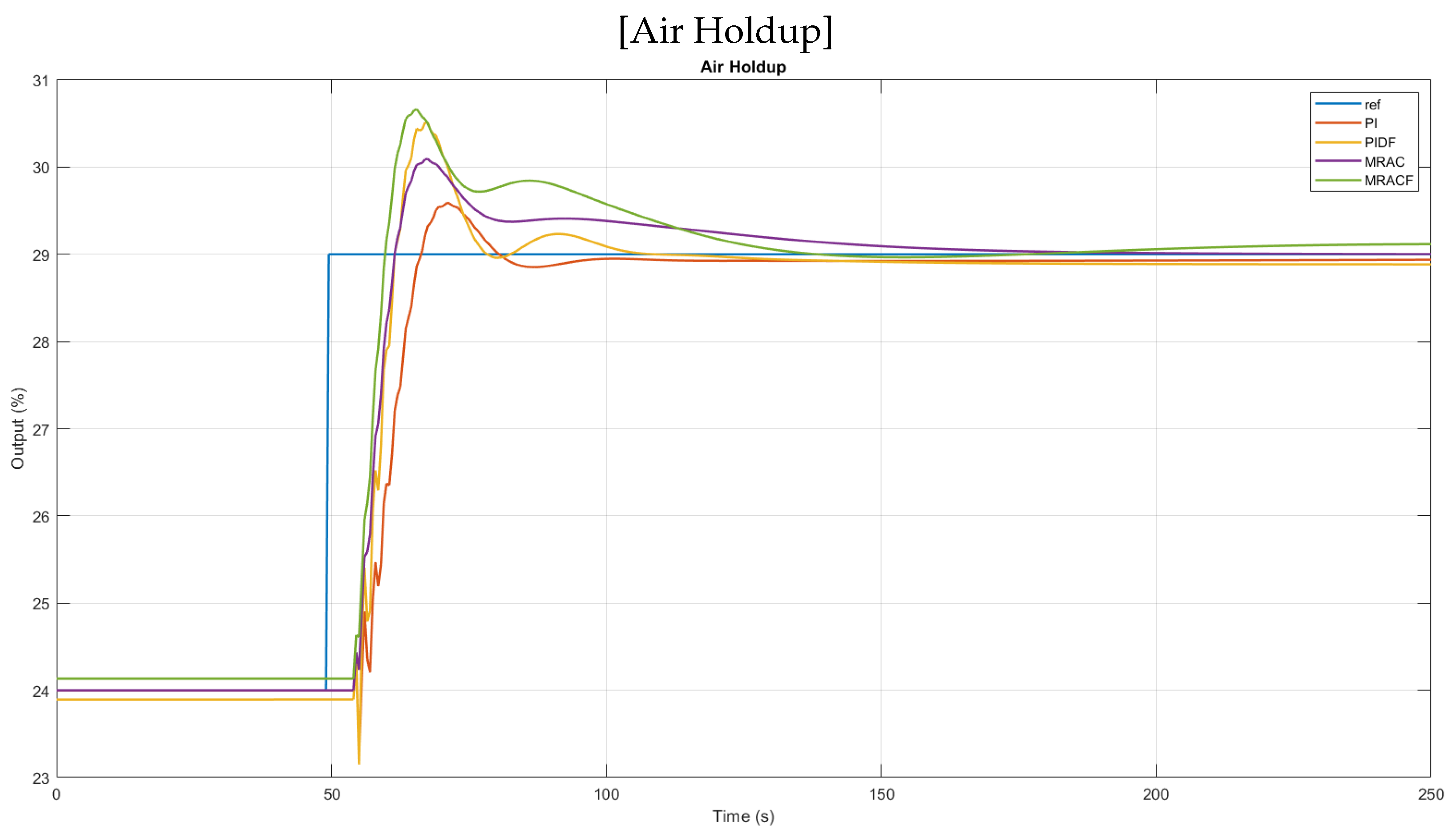
| Air Holdup | IOPI | 2.04 | 67 | 78 | 2721 | 1.53 × 105 | 288 | 2.48 × 104 | |
| FOPID | 5.2 | 54.5 | 99.5 | 2367 | 1.32 × 105 | 261.3 | 2.07 × 104 | ||
| IOMRAC | 3.77 | 61.5 | 148.5 | 2068 | 1.16 × 105 | 248.7 | 1.87 × 104 | ||
| FOMRAC | 5.74 | 60 | 126 | 2113 | 1.24 × 105 | 312.7 | 2.43 × 104 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duarte-Mermoud, M.A.; Ricaldi-Morales, A.; Travieso-Torres, J.C.; Castro-Linares, R. Design and Comparison of Fractional-Order Controllers in Flotation Cell Banks and Flotation Columns Used in Copper Extraction Processes. Mathematics 2024, 12, 2789. https://doi.org/10.3390/math12172789
Duarte-Mermoud MA, Ricaldi-Morales A, Travieso-Torres JC, Castro-Linares R. Design and Comparison of Fractional-Order Controllers in Flotation Cell Banks and Flotation Columns Used in Copper Extraction Processes. Mathematics. 2024; 12(17):2789. https://doi.org/10.3390/math12172789
Chicago/Turabian StyleDuarte-Mermoud, Manuel A., Abdiel Ricaldi-Morales, Juan Carlos Travieso-Torres, and Rafael Castro-Linares. 2024. "Design and Comparison of Fractional-Order Controllers in Flotation Cell Banks and Flotation Columns Used in Copper Extraction Processes" Mathematics 12, no. 17: 2789. https://doi.org/10.3390/math12172789








