Data-Driven Conjugate Heat Transfer Analysis of a Gas Turbine Vane
Abstract
1. Introduction
2. Data-Driven CHT Method
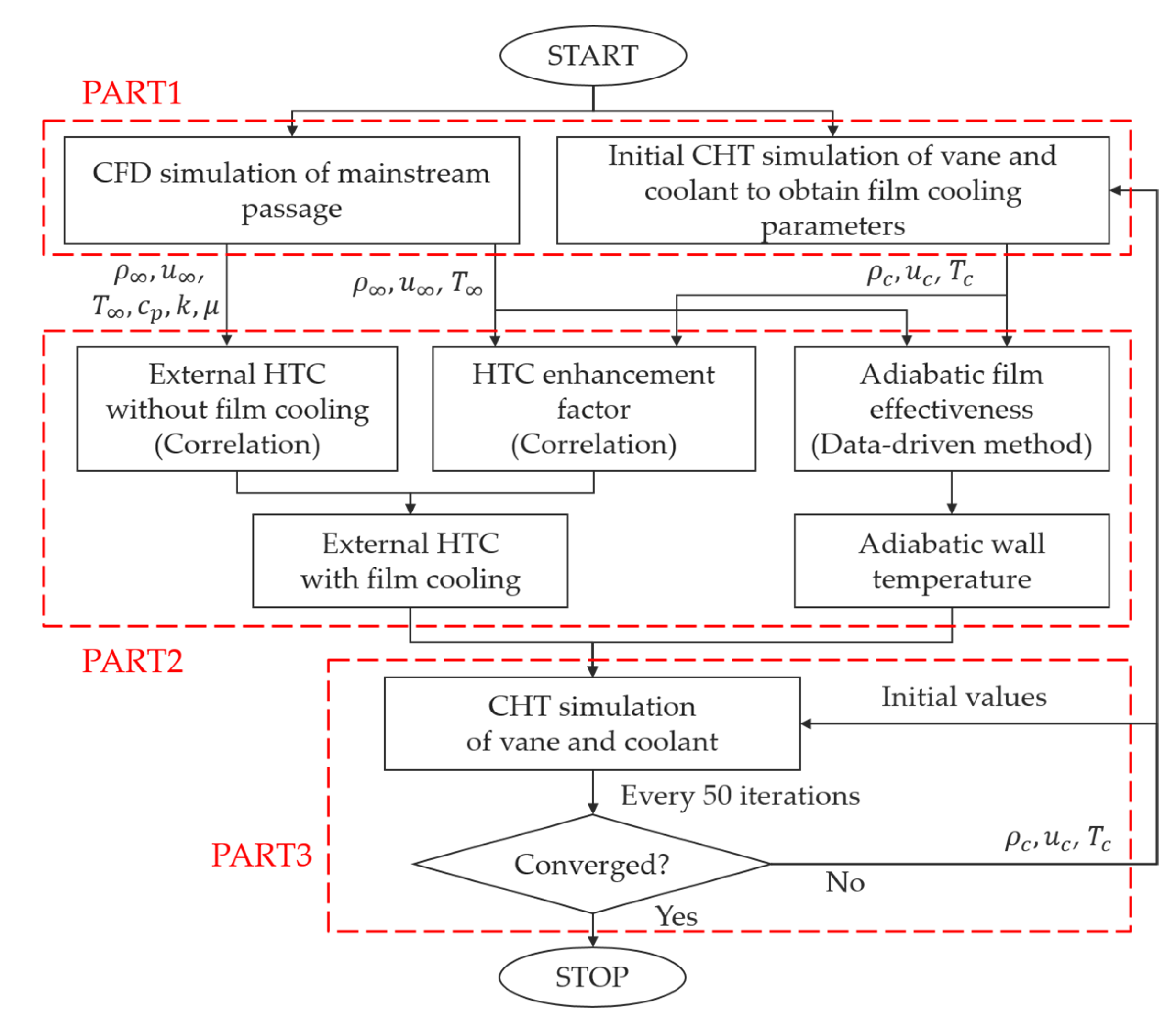
2.1. General Simulation Strategy
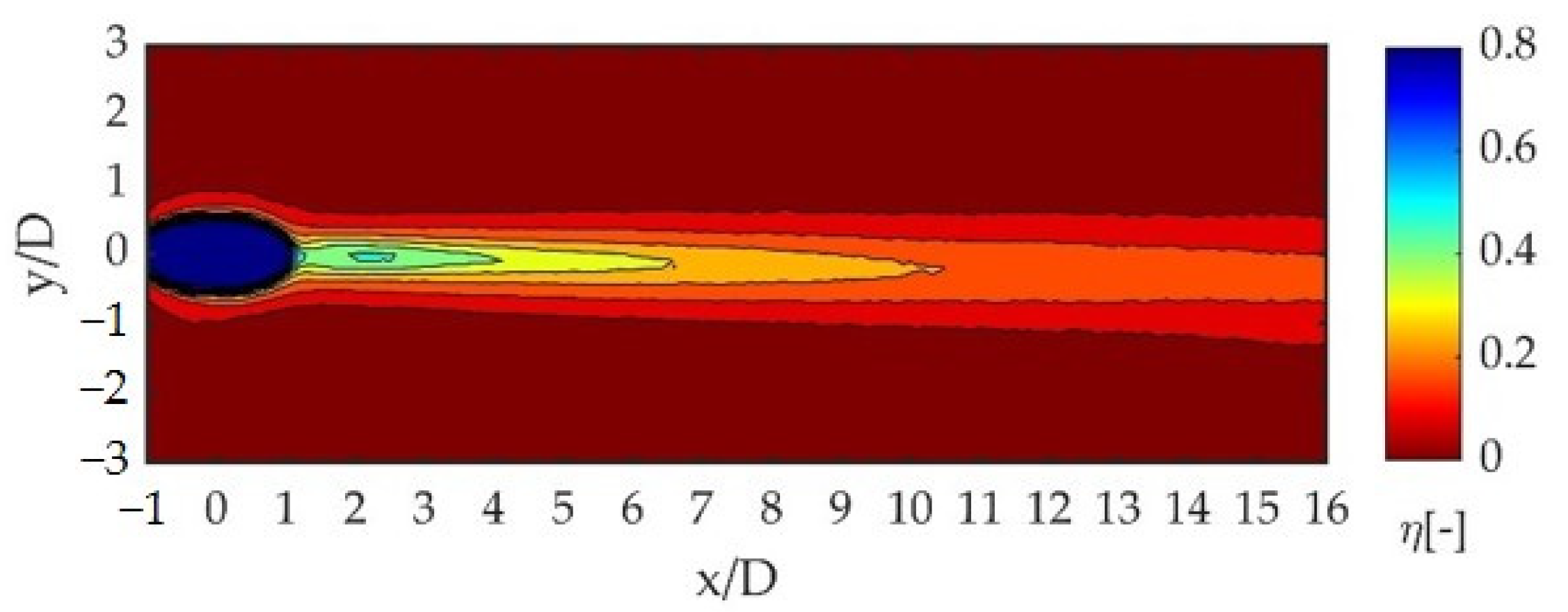
2.2. Experimental Database of Film Cooling Effectiveness
2.3. Integration of Database with CHT Algorithm
3. Calculation Analysis
3.1. Governing Equations and Computational Technique
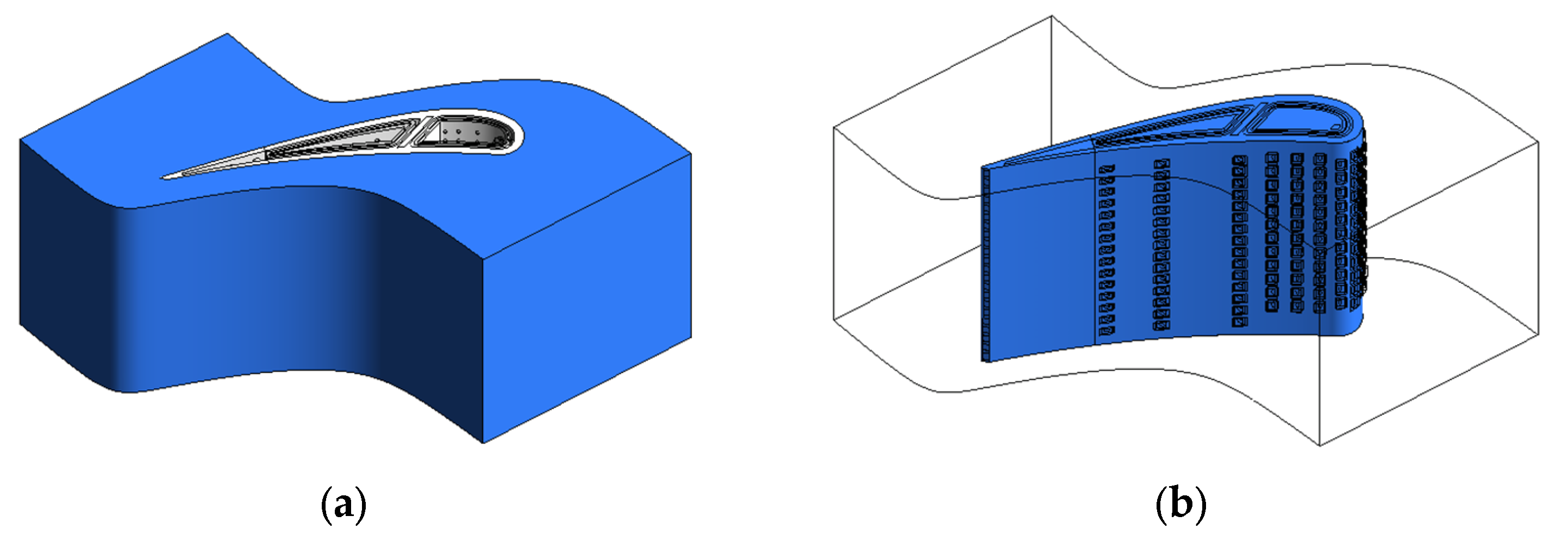
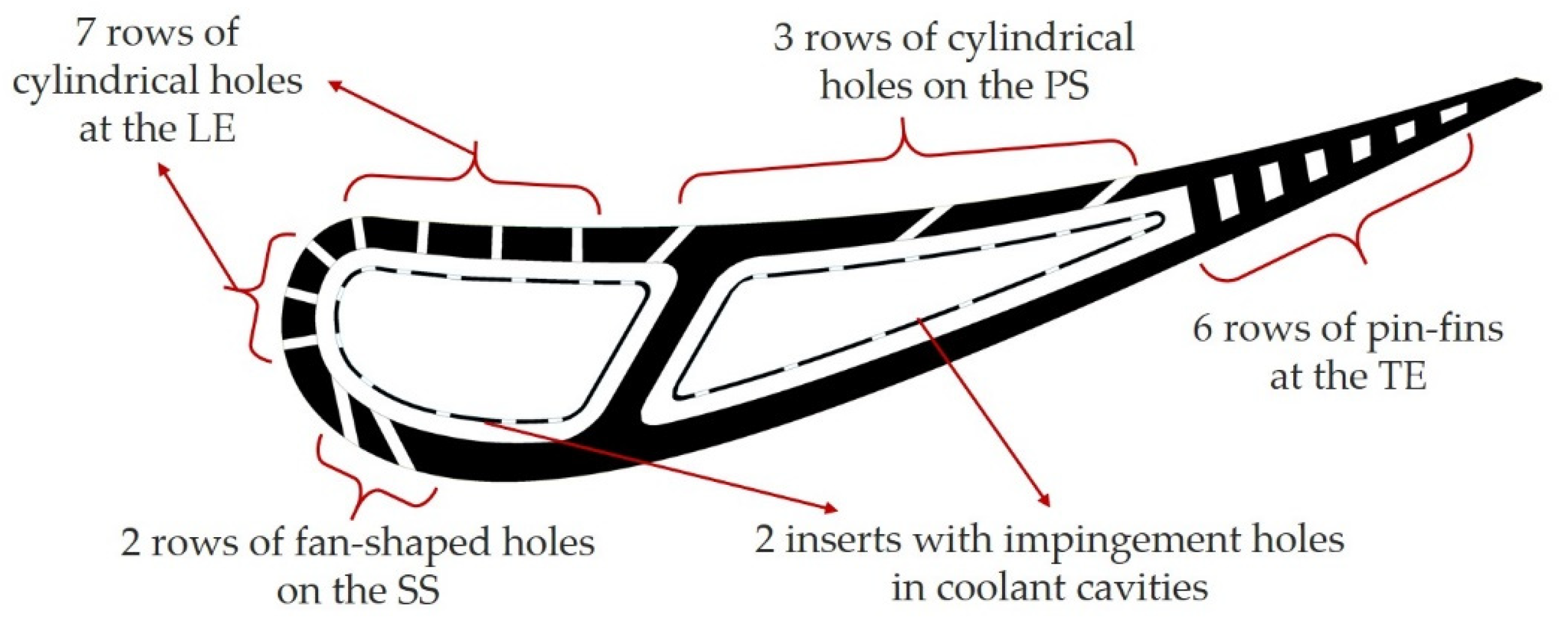
3.2. Vane’s Geometry
3.3. Mesh Applied on Calculation
3.4. Boundary Set-Ups
4. Results
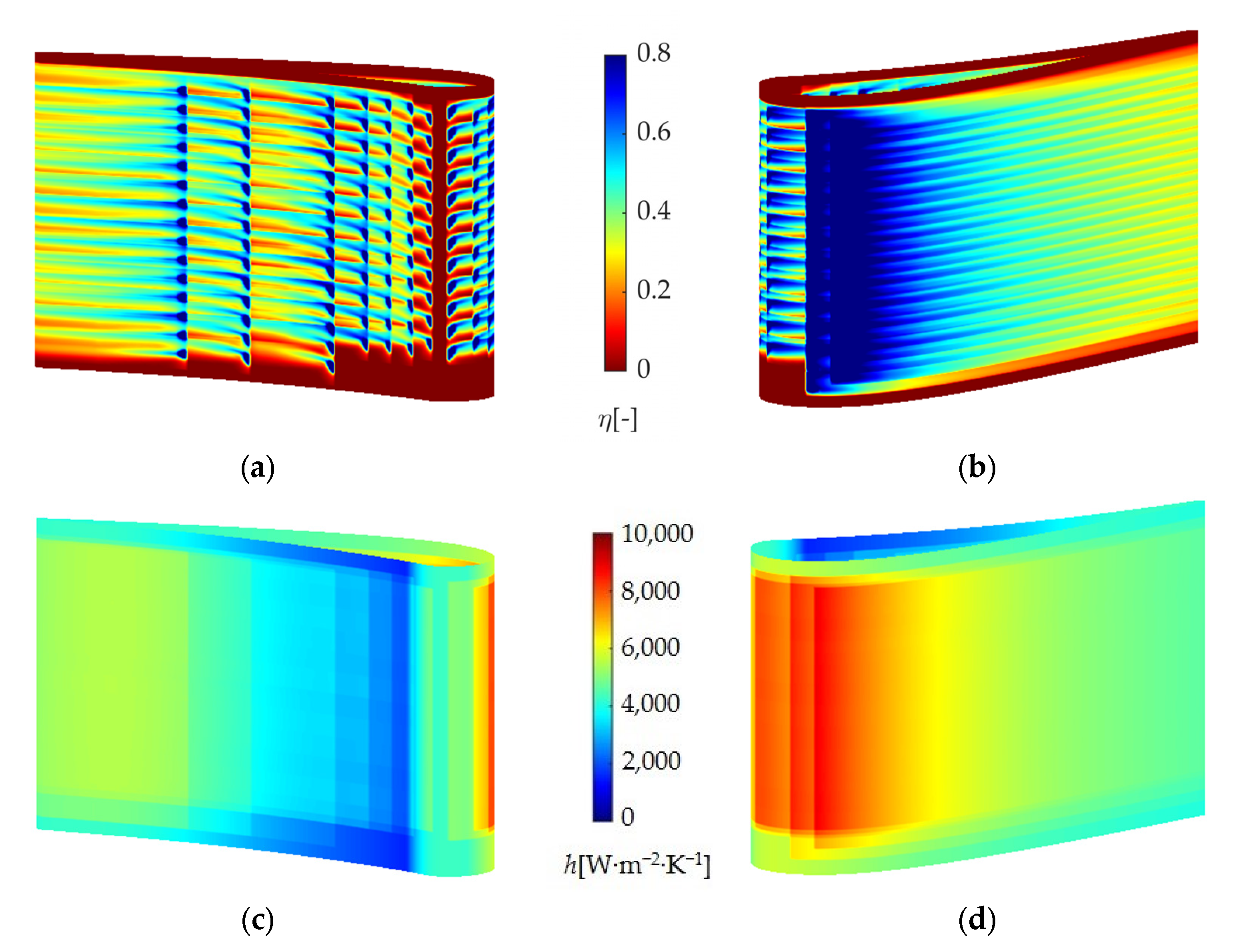
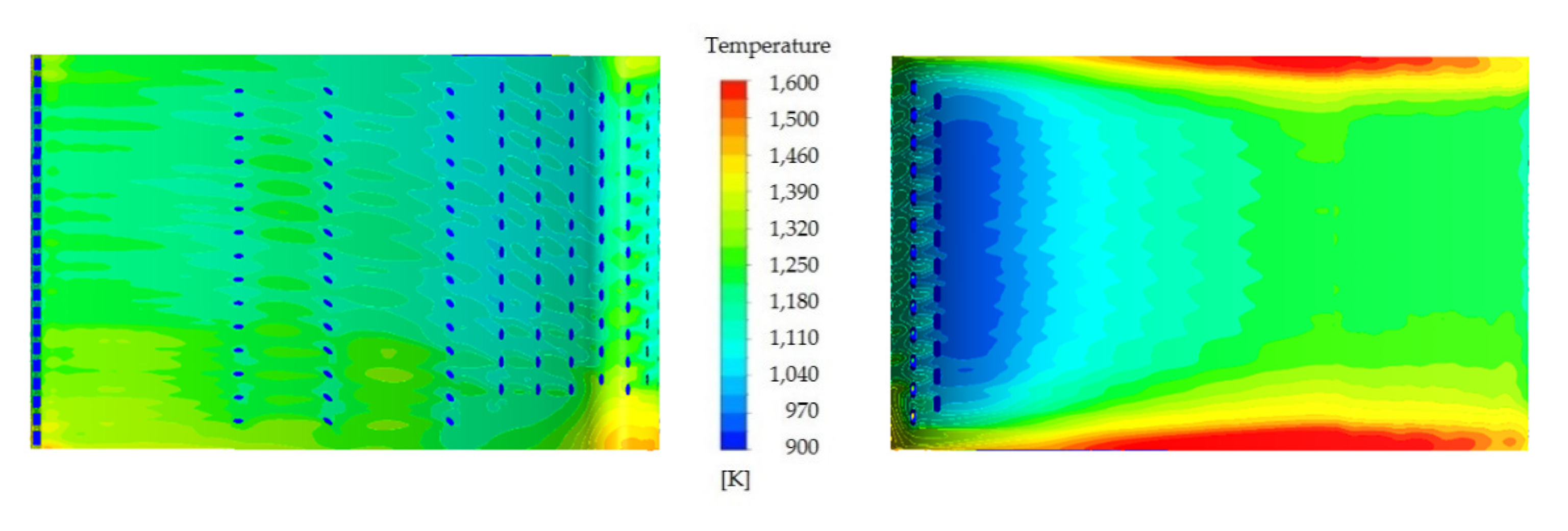
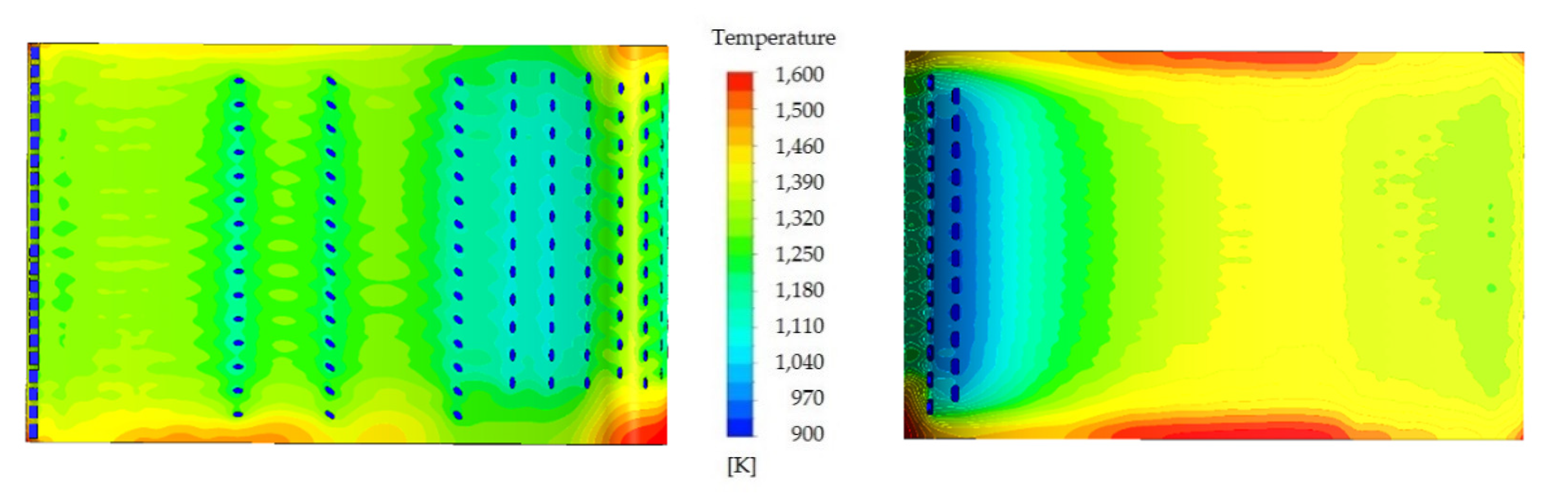
4.1. Temperature Distribution Results
4.2. Performance Evaluation of the Data-Driven Method
4.2.1. Accuracy
4.2.2. Computational Cost
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bunker, R.S. Evolution of Turbine Cooling. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Volume 1: Aircraft Engine; Fans and Blowers; Marine; Honors and Awards, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar] [CrossRef]
- Han, J. Turbine Blade Cooling Studies at Texas A&M University: 1980–2004. J. Thermophys. Heat Transf. 2006, 20, 161–187. [Google Scholar] [CrossRef]
- Heidmann, J.D.; Kassab, A.J.; Divo, E.A.; Rodriguez, F.; Steinthorsson, E. Conjugate Heat Transfer Effects on a Realistic Film-Cooled Turbine Vane. In Proceedings of the ASME Turbo Expo 2003, Collocated with the 2003 International Joint Power Generation Conference, Volume 5: Turbo Expo 2003, Parts A and B, Atlanta, GA, USA, 16–19 June 2003. [Google Scholar] [CrossRef]
- Zecchi, S.; Arcangeli, L.; Facchini, B.; Coutandin, D. Features of a Cooling System Simulation Tool Used in Industrial Preliminary Design Stage. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Volume 3: Turbo Expo 2004, Vienna, Austria, 14–17 June 2004. [Google Scholar] [CrossRef]
- Bohn, D.; Bonhoff, B.; Schrinenbom, H. Combined Aerodynamic and Thermal Analysis of a Turbine Nozzle Guide Vane. In Proceedings of the 1995 Yokohama International Gas Turbine Congress, Yokohama, Japan, 22–27 October 1995. [Google Scholar]
- Bohn, D.E.; Becker, V.J.; Kusterer, K.A. 3-D Conjugate Flow and Heat Transfer Calculations of a Film-Cooled Turbine Guide Vane at Different Operation Conditions. In Proceedings of the ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition, Volume 3: Heat Transfer; Electric Power; Industrial and Cogeneration, Orlando, FL, USA, 2–5 June 1997. [Google Scholar] [CrossRef]
- Bonini, A.; Andreini, A.; Carcasci, C.; Facchini, B.; Ciani, A.; Innocenti, L. Conjugate Heat Transfer Calculations on GT Rotor Blade for Industrial Applications: Part I—Equivalent Internal Fluid Network Setup and Procedure Description. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Volume 4: Heat Transfer, Parts A and B, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar] [CrossRef]
- Andreini, A.; Bonini, A.; Da Soghe, R.; Facchini, B.; Ciani, A.; Innocenti, L. Conjugate Heat Transfer Calculations on GT Rotor Blade for Industrial Applications: Part II—Improvement of External Flow Modeling. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Volume 4: Heat Transfer, Parts A and B, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar] [CrossRef]
- Chowdhury, N.H.K.; Zirakzadeh, H.; Han, J. A Predictive Model for Preliminary Gas Turbine Blade Cooling Analysis. J. Turbomach. 2017, 139, 091010. [Google Scholar] [CrossRef]
- Ngetich, G.C.; Murray, A.V.; Ireland, P.T.; Romero, E. A Three-Dimensional Conjugate Approach for Analyzing a Double-Walled Effusion-Cooled Turbine Blade. J. Turbomach. 2019, 141, 011002. [Google Scholar] [CrossRef]
- Amaral, S.; Verstraete, T.; Braembussche, R.V.; Arts, T. Design and Optimization of the Internal Cooling Channels of a High Pressure Turbine Blade—Part I: Methodology. J. Turbomach. 2010, 132, 021013. [Google Scholar] [CrossRef]
- Verstraete, T.; Amaral, S.; Braembussche, R.V.; Arts, T. Design and Optimization of the Internal Cooling Channels of a High Pressure Turbine Blade—Part II: Optimization. J. Turbomach. 2010, 132, 021014. [Google Scholar] [CrossRef]
- Zhang, L.J.; Jaiswal, R.S. Turbine nozzle endwall film cooling study using pressure-sensitive paint. J. Turbomach. 2001, 123, 730–738. [Google Scholar] [CrossRef]
- Gao, Z.; Wright, L.M.; Han, J. Assessment of Steady State PSP and Transient Ir Measurement Techniques for Leading Edge Film Cooling. In Proceedings of the ASME 2005 International Mechanical Engineering Congress and Exposition, Heat Transfer, Part A, Orlando, FL, USA, 5–11 November 2005; pp. 467–475. [Google Scholar] [CrossRef]
- Gao, Z.; Han, J. Influence of Film-Hole Shape and Angle on Showerhead Film Cooling Using PSP Technique. J. Heat Transf. 2009, 131, 061701. [Google Scholar] [CrossRef]
- Lowery, G.W.; Vachon, R.I. The Effect of Turbulence on Heat Transfer from Heated Cylinders. Int. J. Heat Mass Transf. 1975, 18, 1229–1242. [Google Scholar] [CrossRef]
- Kreith, F.; Manglik, R.M. Principles of Heat Transfer, 8th ed.; Cengage Learning: Boston, MA, USA, 2018; pp. 342+362. [Google Scholar]
- Baldauf, S.; Scheurlen, M.; Schulz, A.; Wittig, S. Heat flux reduction from film cooling and correlation of heat transfer coefficients from thermographic measurements at enginelike conditions. J. Turbomach. 2002, 124, 699–709. [Google Scholar] [CrossRef]
- Bogard, D.G.; Thole, K.A. Gas Turbine Film Cooling. J. Propul. Power 2006, 22, 249–270. [Google Scholar] [CrossRef]
- Qin, Y.; Ren, J.; Jiang, H. Effects of Streamwise Pressure Gradient and Convex Curvature on Film Cooling Effectiveness. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Volume 5B: Heat Transfer, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar] [CrossRef]
- Qin, Y.; Li, X.; Ren, J.; Jiang, H. Effects of compound angle on film cooling effectiveness with different streamwise pressure gradient and convex curvature. Int. J. Heat Mass Transf. 2015, 86, 482–491. [Google Scholar] [CrossRef]
- Goldstein, R.J. Film Cooling. Adv. Heat Transf. 1971, 7, 321–379. [Google Scholar] [CrossRef]
- John, P.; Sellers, J.R. Gaseous Film Cooling with Multiple Injection Stations. AIAA J. 1963, 1, 321–379. [Google Scholar] [CrossRef]
- Halila, E.E.; Lenahan, D.T.; Thomas, T.T. Energy Efficient Engine High Pressure Turbine Test Hardware Detailed Design Report; Report No.: NASA CR-167955; NASA: Washington, DC, USA, 1982; pp. 23–34.
- Stearns, E.M. Energy Efficient Engine Core Design and Performance Report; Report No.: NASA CR-168069; NASA: Washington, DC, USA, 1982; pp. 357–361.

| Experimental Conditions | Value |
|---|---|
| Hole shape (-) | Cylindrical, Fan-shaped |
| Compound angle (°) | 0, 45 |
| Blowing ratio (-) | 0.5, 0.75, 1.0, 1.2, 1.5 |
| Density ratio (-) | 1.0, 1.5 |
| Non-dimensional curvature of the external surface (-) | −1/30, 0, 1/30 |
| Non-dimensional pressure gradient along the mainstream flow direction (×10−7) | −3.0, 0, 4.8, 7.3, 10 |
| Grid Density | Cell Number | Mean Temperature of Vane’s Outer Surface |
|---|---|---|
| Low | 11,050,194 | 1208.26 K |
| Medium | 11,834,831 | 1208.68 K |
| High | 12,830,966 | 1209.52 K |
| Boundary Position | Parameter | Value |
|---|---|---|
| Mainstream inlet | Total pressure | 2.526 MPa |
| Mainstream inlet | Total temperature | 2012 K |
| Mainstream inlet | Turbulent intensity | 0.1 |
| Mainstream outlet | Static pressure | 1.51 MPa |
| Front coolant cavity’s inlet | Total pressure | 2.588 MPa |
| Front coolant cavity’s inlet | Total temperature | 883 K |
| Rear coolant cavity’s inlet | Total pressure | 2.576 MPa |
| Rear coolant cavity’s inlet | Total temperature | 883 K |
| Parameter | Data-Driven | Conventional |
|---|---|---|
| Maximum Error (K) | 53.3 | −92.7 |
| Maximum Relative Error (%) | 4.1 | −7.1 |
| Mean Error (K) | 34.5 | −75.7 |
| Mean Relative Error (%) | 2.7 | −5.9 |
| Parameter | Value |
|---|---|
| Data-driven method’s time cost (min) | 321 |
| Data-driven method’s time cost (min) | 1069 |
| Percentage decreased by simplification (-) | 69.97% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, H.; Wang, L.; Li, X.; Ren, J. Data-Driven Conjugate Heat Transfer Analysis of a Gas Turbine Vane. Processes 2022, 10, 2335. https://doi.org/10.3390/pr10112335
Cui H, Wang L, Li X, Ren J. Data-Driven Conjugate Heat Transfer Analysis of a Gas Turbine Vane. Processes. 2022; 10(11):2335. https://doi.org/10.3390/pr10112335
Chicago/Turabian StyleCui, Hao, Lang Wang, Xueying Li, and Jing Ren. 2022. "Data-Driven Conjugate Heat Transfer Analysis of a Gas Turbine Vane" Processes 10, no. 11: 2335. https://doi.org/10.3390/pr10112335
APA StyleCui, H., Wang, L., Li, X., & Ren, J. (2022). Data-Driven Conjugate Heat Transfer Analysis of a Gas Turbine Vane. Processes, 10(11), 2335. https://doi.org/10.3390/pr10112335









