Influence Mechanism of Gas–Containing Characteristics of Annulus Submerged Jets on Sealing Degree of Mixing Zone
Abstract
:1. Introduction
2. Test Device and Numerical Model
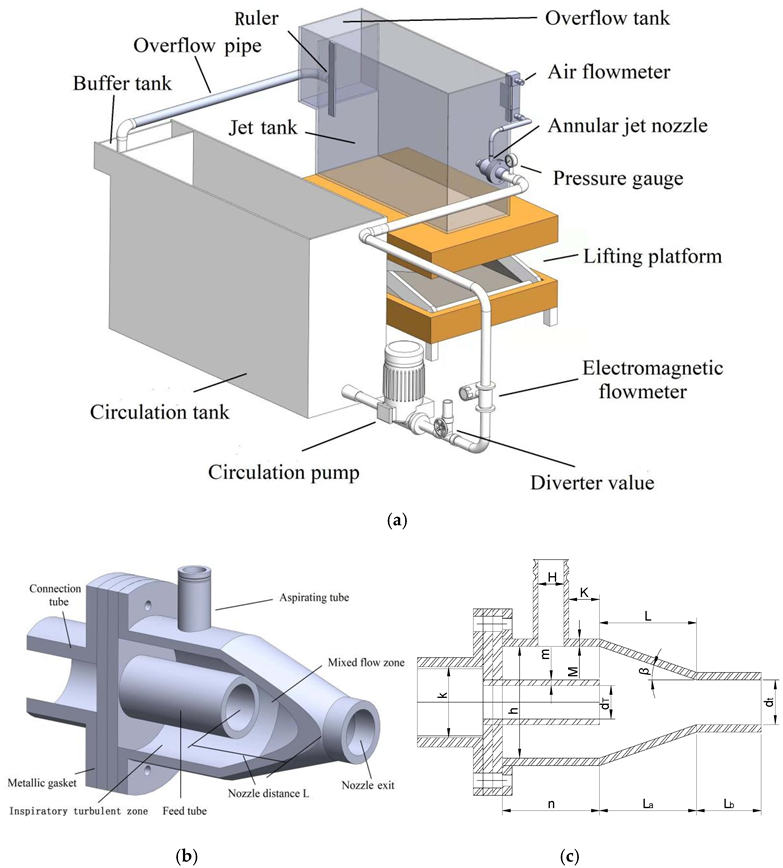
2.1. Test Device
2.2. Test Process
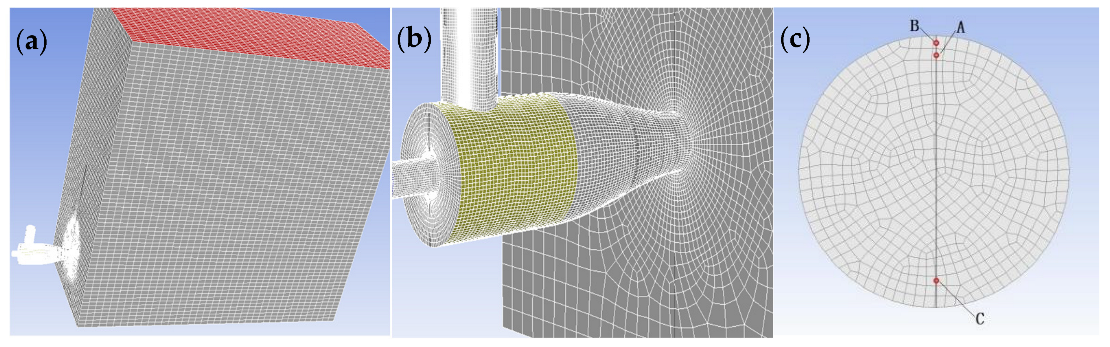
3. Numerical Model
Model Establishment
4. Analysis of Results
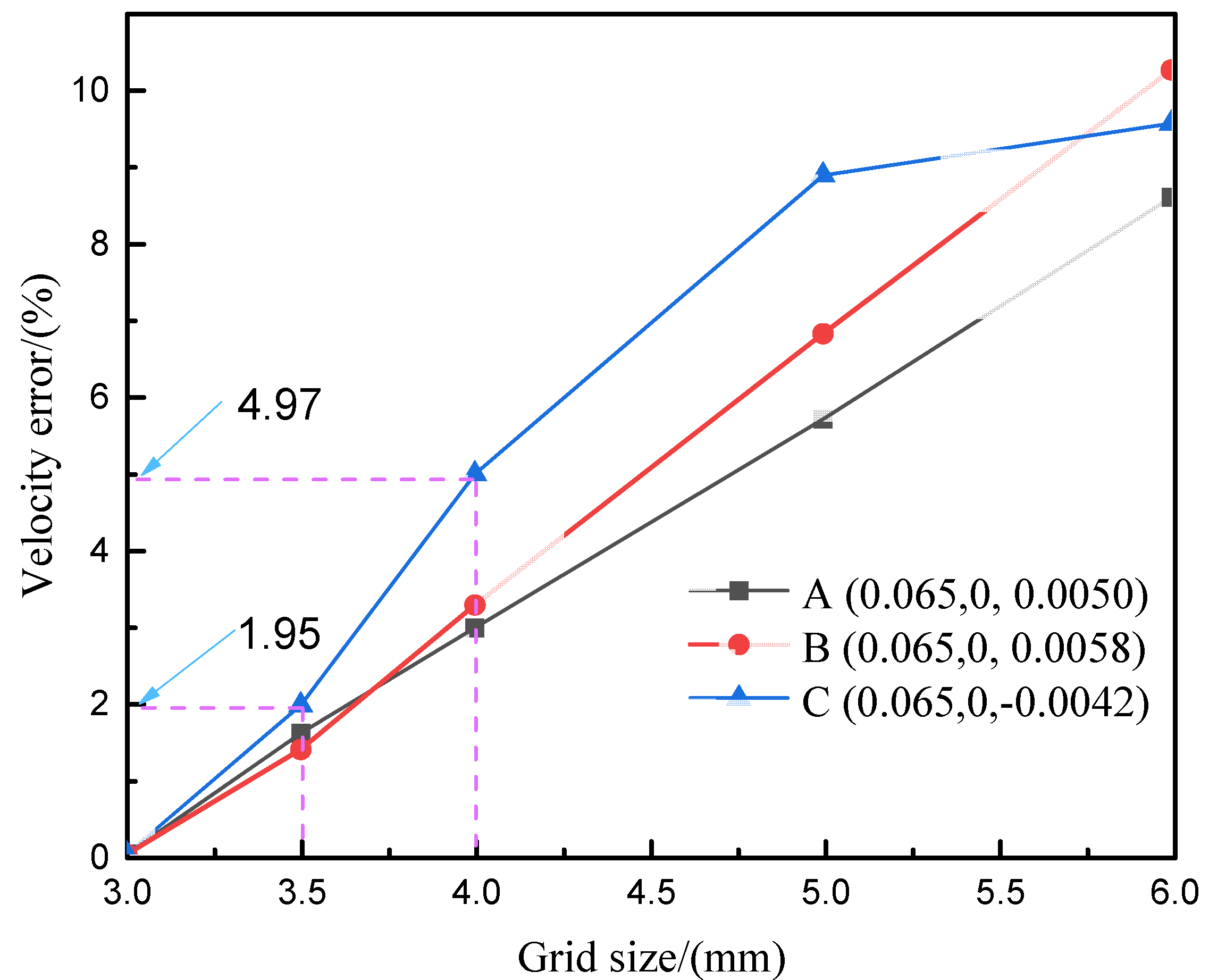
4.1. Evaluating the Reliability of Numerical Simulation
4.2. Analysis of Internal Flow Field
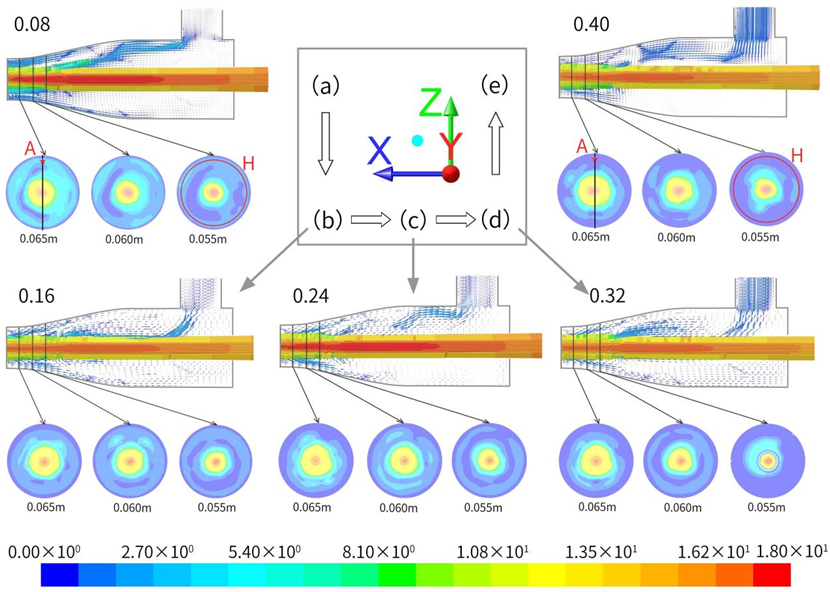
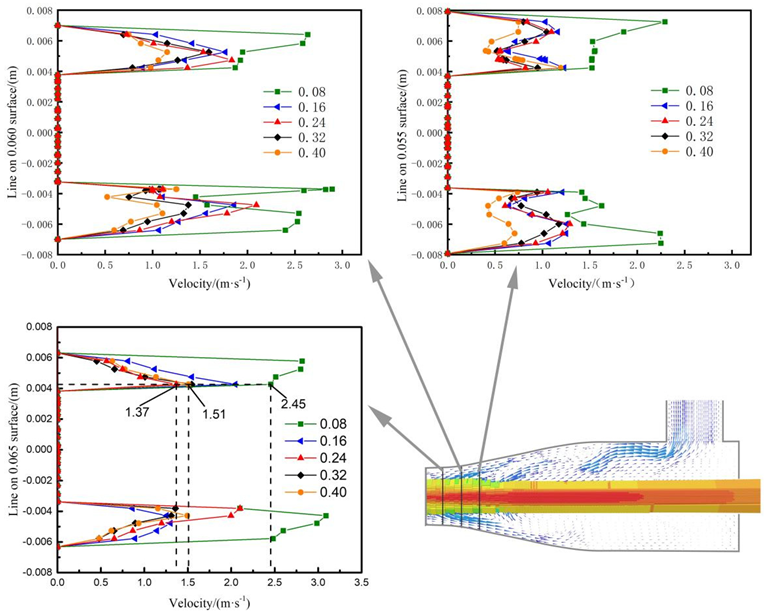
4.2.1. Variation Characteristics of Velocity Field under Different Gas–Liquid Ratios
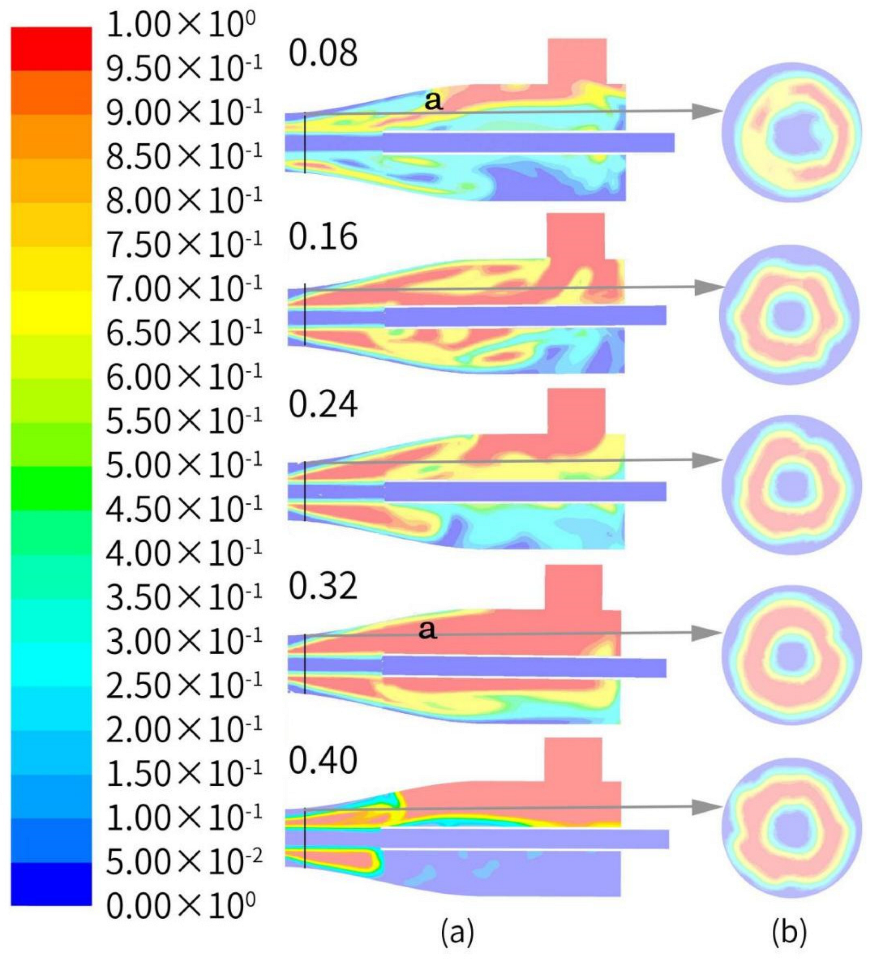
4.2.2. Distribution of Air and Liquid Volumes with Different Air–Liquid Ratios
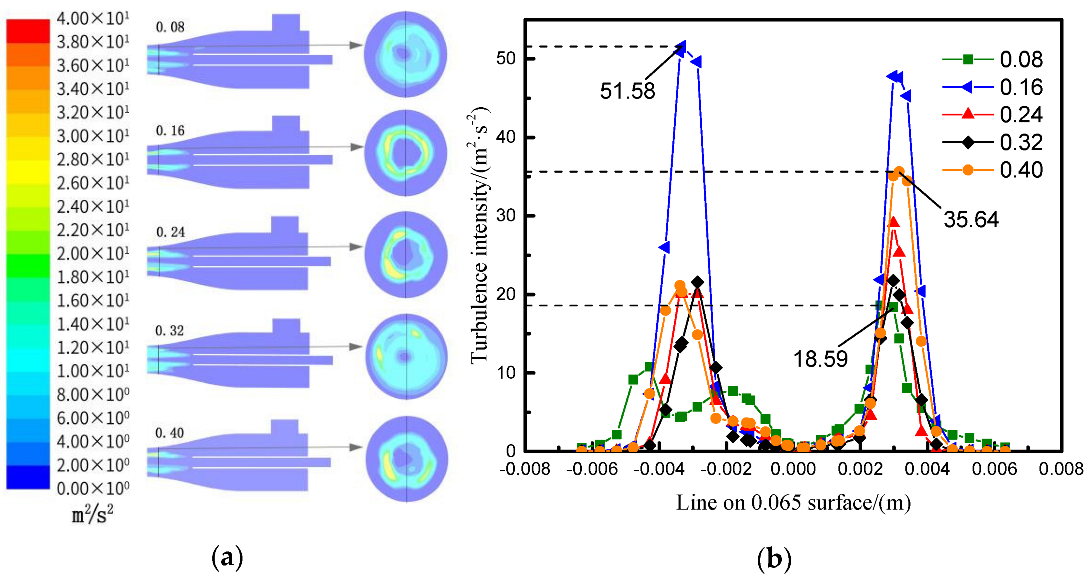
4.2.3. Distribution of Turbulence Intensity with Different Gas–Liquid Ratios
4.2.4. Distribution of Turbulence Intensity with Different Gas–Liquid Ratios
5. Conclusions
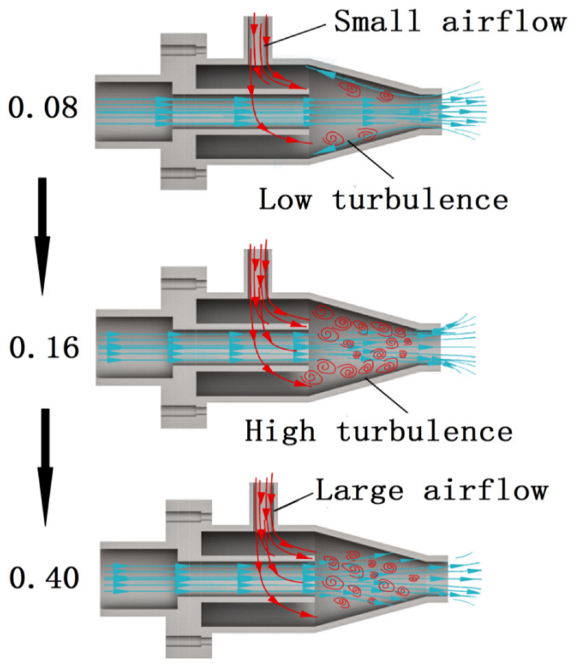
- For submerged annular jets, the degree of enclosure of the gas–water mixing zone in the annular jet nozzle increases with the increase in the air–liquid ratio. The main reason for this is that, as Gas–Containing increases, the degree of air–liquid mixing increases, and as a result, the core jet will be gradually dispersed in the radial direction to effectively enclose the gas–water mixing zone. As the air–liquid ratio further increases, the core jet will be further dispersed, causing water to bounce off the inner surface of the nozzle, and the degree of enclosure will remain unchanged. However, this phenomenon may cause energy dissipation, which is unfavorable for air suction;
- From the figure showing the distribution of gas–phase volume fraction, it can be observed that the increase in air–liquid ratio will result in a larger range of air–liquid mixture in the gas–water mixing zone. As the degree of dispersion of the water jet increases, the area of the gas–water mixing zone where water is bounced back will become larger, the energy of the water flow involved in enclosure will be attenuated, and more water in the tank will be suctioned into the nozzle. As a result, the area of the gas–water mixing zone where the gas phase is distributed will become smaller, and the range of the liquid phase will increase accordingly. This phenomenon is unfavorable for air suction and the effective utilization of jet energy;
- From the figure showing the distribution of turbulence intensity with different air–liquid ratios, it can be observed that as the air–liquid ratio increases, the water jet will be further dispersed, and the range of turbulence will gradually become larger. However, with the increase in the dispersion degree of the jet, the gas–liquid mixing becomes stronger, resulting in increases in turbulence intensity and vorticity intensity. As the degree of dispersion of the jet further increases, the area of the gas–water mixing zone with bounced−back water will become larger, resulting in lower local turbulence intensity and vorticity intensity. This effectively explains the mechanism whereby Gas–Containing affects the degree of enclosure of the gas–water mixing zone.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ji, Y.; Song, A.; Li, C.; Cao, Y. Role of Sparger Configuration in Determining Flotation Performance under Oscillatory Air Supply. Processes 2021, 9, 638. [Google Scholar] [CrossRef]
- Santander, M.; Rodrigues, R.; Rubio, J. Modified jet flotation in oil (petroleum) emulsion/water separations. Colloids Surf. A Physicochem. Eng. Asp. 2011, 375, 237–244. [Google Scholar] [CrossRef]
- Yan, X.; Yao, Y.; Meng, S.; Zhao, S.; Wang, L.; Zhang, H.; Cao, Y. Comprehensive particle image velocimetry measurement and numerical model validations on the gas–liquid flow field in a lab-scale cyclonic flotation column. Chem. Eng. Res. Des. 2021, 174, 1–10. [Google Scholar] [CrossRef]
- Wang, X.; Shuai, Y.; Zhang, H.; Sun, J.; Yang, Y.; Huang, Z.; Jiang, B.; Liao, Z.; Wang, J.; Yang, Y. Bubble breakup in a swirl-venturi microbubble generator. Chem. Eng. J. 2021, 403, 126397. [Google Scholar] [CrossRef]
- Murai, Y.; Tasaka, Y.; Oishi, Y.; Ern, P. Bubble fragmentation dynamics in a subsonic Venturi tube for the design of a compact microbubble generator. Int. J. Multiph. Flow 2021, 139, 103645. [Google Scholar] [CrossRef]
- Li, L.; Liu, J.; Wang, L.; Yu, H. Numerical simulation of a self-absorbing microbubble generator for a cyclonic-static microbubble flotation column. Min. Sci. Technol. 2010, 20, 88–92. [Google Scholar] [CrossRef]
- Wu, M.; Yuan, S.; Song, H.; Li, X. Micro-nano bubbles production using a swirling-type venturi bubble generator. Chem. Eng. Process. Process Intensif. 2021, 170, 108697. [Google Scholar] [CrossRef]
- Foronda-Trillo, F.J.; Rodríguez-Rodríguez, J.; Gutiérrez-Montes, C.; Martínez-Bazán, C. Deformation and breakup of bubbles interacting with single vortex rings. Int. J. Multiph. Flow 2021, 142, 103734. [Google Scholar] [CrossRef]
- Li, M.; Li, W.; Hu, L. Jet formation and breakup inside highly deformed bubbles. Int. J. Heat Mass Transf. 2020, 163, 120507. [Google Scholar] [CrossRef]
- Wang, S.; Tao, X. Comparison of the adhesion kinetics between air or oily bubble and long flame coal surface in flotation. Fuel 2021, 291, 120139. [Google Scholar] [CrossRef]
- Farrokhpay, S.; Filippova, I.; Filippov, L.; Picarra, A.; Rulyov, N.; Fornasiero, D. Flotation of fine particles in the presence of combined microbubbles and conventional bubbles. Miner. Eng. 2020, 155, 106439. [Google Scholar] [CrossRef]
- Islam, M.T.; Nguyen, A.V. Effect of microturbulence on bubble-particle collision during the bubble rise in a flotation cell. Miner. Eng. 2020, 155, 106418. [Google Scholar] [CrossRef]
- Ruiz-Rus, J.; Bolaños-Jiménez, R.; Sevilla, A.; Martínez-Bazán, C. Bubble formation regimes in forced co-axial air-water jets. Int. J. Multiph. Flow 2020, 128, 103296. [Google Scholar] [CrossRef] [Green Version]
- Gutiérrez-Montes, C.; Bolaños-Jiménez, R.; Sevilla, A.; Martínez-Bazán, C. Experimental and numerical study of the periodic bubbling regime in planar co-flowing air–water sheets. Int. J. Multiph. Flow 2013, 50, 106–119. [Google Scholar] [CrossRef]
- Jamali, M.; Rostamijavanani, A.; Nouri, N.M.; Navidbakhsh, M. An experimental study of cavity and Worthington jet formations caused by a falling sphere into an oil film on water. Appl. Ocean Res. 2020, 102, 102319. [Google Scholar] [CrossRef]
- Song, H.; Chang, S.; Yu, W.; Wu, K. Experimental statistics of micrometer-sized water droplet deformation and breakup behavior in continuous air jet flow. Int. J. Multiph. Flow 2021, 135, 103529. [Google Scholar] [CrossRef]
- Deng, J.; Zhang, F.X.; Tian, Z.; Xu, W.L.; Liu, B.; Wei, W.R. Laboratory model study of the effect of aeration on axial velocity attenuation of turbulent jet flows in plunge pool. J. Hydrodyn. 2015, 27, 913–918. [Google Scholar] [CrossRef]
- Park, S.K.; Yang, H.C. Experimental investigation on mixed jet and mass transfer characteristics of horizontal aeration process. Int. J. Heat Mass Transf. 2017, 113, 544–555. [Google Scholar] [CrossRef]
- Dapelo, D.; Alberini, F.; Bridgeman, J. Euler-Lagrange CFD modelling of unconfined gas mixing in anaerobic digestion. Water Res. 2015, 85, 497–511. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Ning, Z.; Lv, M.; Lü, M. Large eddy simulation of the two-phase flow pattern and bubble formation process of a flow mixing nozzle under a gas–liquid mode. Fluid Dyn. Res. 2019, 51, 055510. [Google Scholar] [CrossRef]
- Wang, C.; Wang, C.; Yu, A.; Zheng, M.; Khan, M. Effect of Closure Characteristics of Annular Jet Mixed Zone on Inspiratory Performance and Bubble System. Processes 2021, 9, 1392. [Google Scholar] [CrossRef]
- Zheng, H.; Su, Y.; Zheng, L.; Ke, H. Numerical simulation of CO2 and dye separation for supercritical fluid in separator. Sep. Purif. Technol. 2020, 236, 116246. [Google Scholar] [CrossRef]
- Zolfagharnasab, M.H.; Salimi, M.; Aghanajafi, C. Application of non-pressure-based coupled procedures for the solution of heat and mass transfer for the incompressible fluid flow phenomenon. Int. J. Heat Mass Transf. 2021, 181, 121851. [Google Scholar] [CrossRef]
- Almitani, K.H.; Alzaed, A.; Alahmadi, A.; Sharifpur, M.; Momin, M. The influence of the geometric shape of the symmetrical twisted turbulator on the performance of parabolic solar collector having hybrid nanofluid: Numerical approach using two-phase model. Sustain. Energy Technol. Assess. 2022, 51, 101882. [Google Scholar] [CrossRef]
- Garoosi, F.; Hooman, K. Numerical simulation of multiphase flows using an enhanced Volume-of-Fluid (VOF) method. Int. J. Mech. Sci. 2021, 215, 106956. [Google Scholar] [CrossRef]
- Garoosi, F.; Merabtene, T.; Mahdi, T.-F. Numerical simulation of merging of two rising bubbles with different densities and diameters using an enhanced Volume-of-Fluid (VOF) model. Ocean Eng. 2022, 247, 110711. [Google Scholar] [CrossRef]
- Cerqueira, R.F.; Paladino, E.E.; Evrard, F.; Denner, F.; van Wachem, B. Multiscale modeling and validation of the flow around Taylor bubbles surrounded with small dispersed bubbles using a coupled VOF-DBM approach. Int. J. Multiph. Flow 2021, 141, 103673. [Google Scholar] [CrossRef]
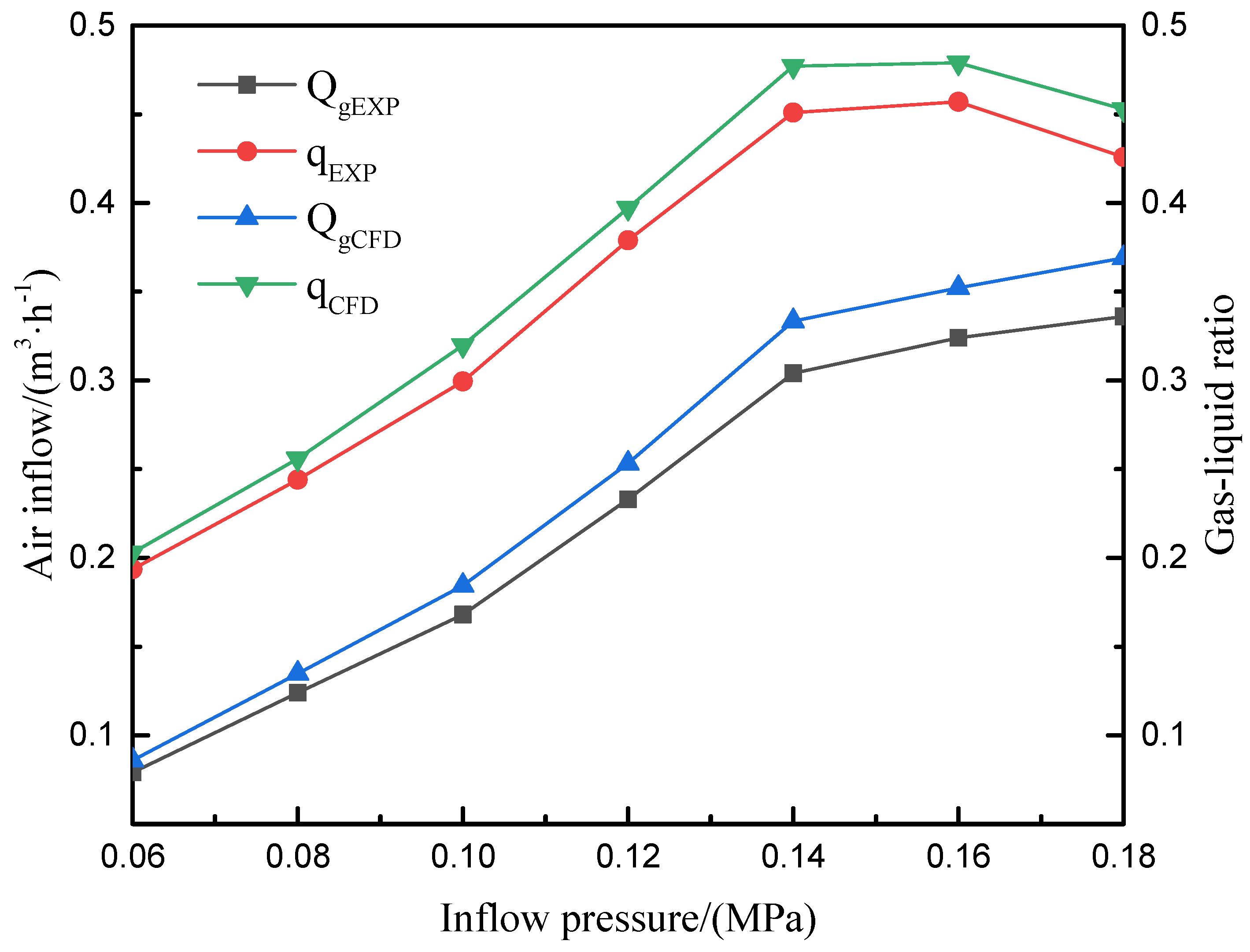

| m3/h MPa | 20 mm (EXP) | 20 mm (CFD) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.06 | 0.08 | 0.10 | 0.12 | 0.14 | 0.16 | 0.18 | 0.06 | 0.08 | 0.10 | 0.12 | 0.14 | 0.16 | 0.18 | |
| 0.079 | 0.124 | 0.168 | 0.233 | 0.304 | 0.324 | 0.336 | 0.086 | 0.135 | 0.184 | 0.253 | 0.333 | 0.352 | 0.375 | |
| 0.408 | 0.508 | 0.561 | 0.615 | 0.674 | 0.709 | 0.789 | 0.423 | 0.527 | 0.576 | 0.638 | 0.699 | 0.735 | 0.808 | |
| 0.194 | 0.244 | 0.299 | 0.379 | 0.451 | 0.457 | 0.426 | 0.203 | 0.256 | 0.320 | 0.397 | 0.477 | 0.479 | 0.464 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Wang, C.; Xie, J.; Khan, M.S. Influence Mechanism of Gas–Containing Characteristics of Annulus Submerged Jets on Sealing Degree of Mixing Zone. Processes 2022, 10, 593. https://doi.org/10.3390/pr10030593
Wang C, Wang C, Xie J, Khan MS. Influence Mechanism of Gas–Containing Characteristics of Annulus Submerged Jets on Sealing Degree of Mixing Zone. Processes. 2022; 10(3):593. https://doi.org/10.3390/pr10030593
Chicago/Turabian StyleWang, Chao, Chuanzhen Wang, Jun Xie, and Md Shakhaoath Khan. 2022. "Influence Mechanism of Gas–Containing Characteristics of Annulus Submerged Jets on Sealing Degree of Mixing Zone" Processes 10, no. 3: 593. https://doi.org/10.3390/pr10030593
APA StyleWang, C., Wang, C., Xie, J., & Khan, M. S. (2022). Influence Mechanism of Gas–Containing Characteristics of Annulus Submerged Jets on Sealing Degree of Mixing Zone. Processes, 10(3), 593. https://doi.org/10.3390/pr10030593








