Numerical Simulation and Field Test Research on Vibration Reduction of PDC Cutting of Pebbled Sandstone under Composite Impact Load
Abstract
1. Introduction
2. Simulation Method
3. Modeling of Pebbled Sandstone
3.1. Modeling Steps
- (1)
- Establish the polygon-generating area according to the size of the rock and generate points randomly in this area.
- (2)
- Take a random radius within the set granularity range to generate a circle with as the center and as the radius.
- (3)
- Judge whether intersects with the circumscribed circle of all the polygons generated, and return to Step 1 in the case of intersection.
- (4)
- Take point on the circle to generate an arbitrary regular polygon with circle as the circumscribed circle and as the vertex. The included angle between the line between point and point and the -axis square is a random angle .
- (5)
- Calculate the sum of the areas of all polygons currently generated and the volume ratio of the rock sample, , to characterize the gravel content. If , the cycle ends, where is the polygon area, is the rock model area, and is the gravel content.

3.2. Comparison and Validation
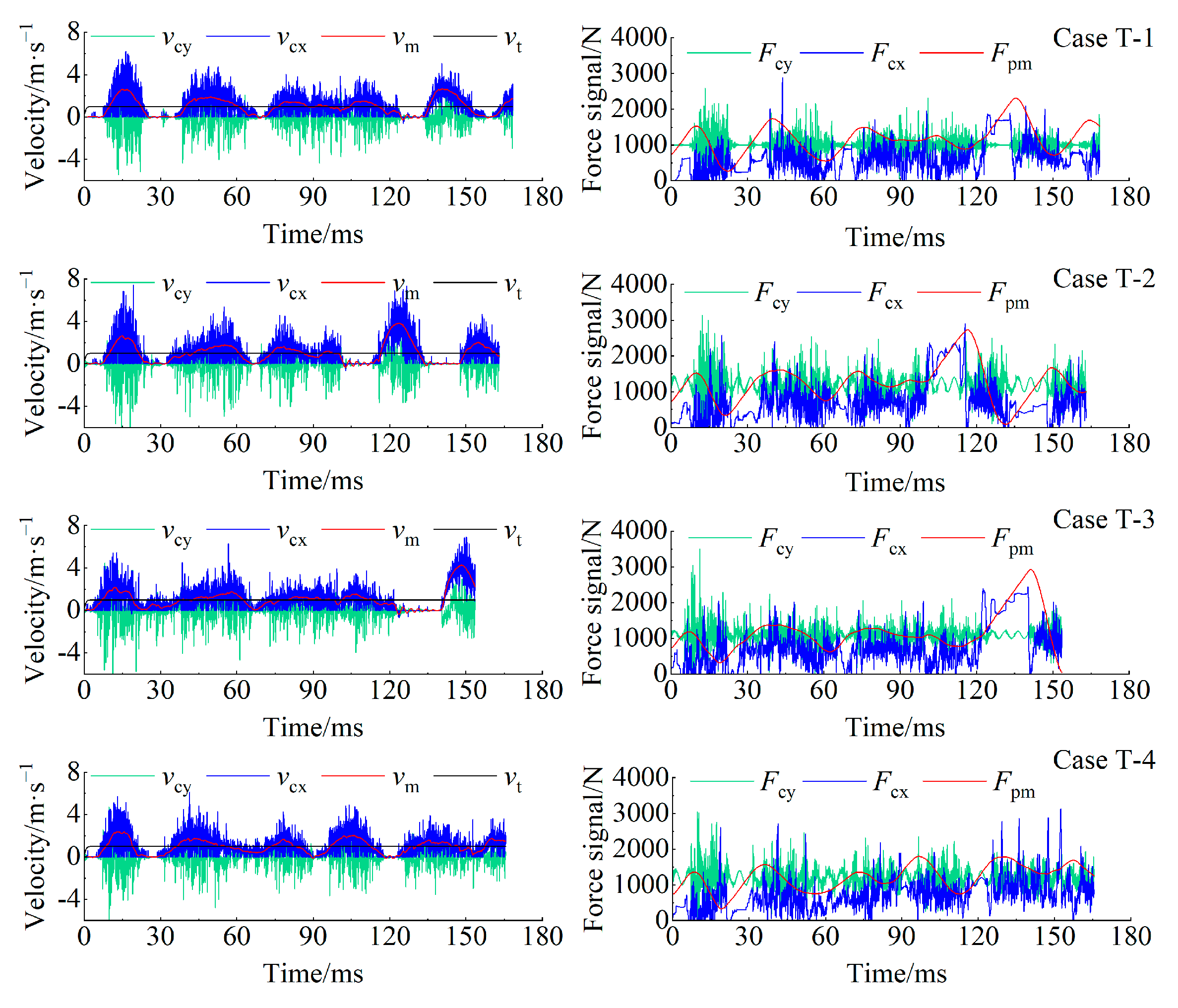
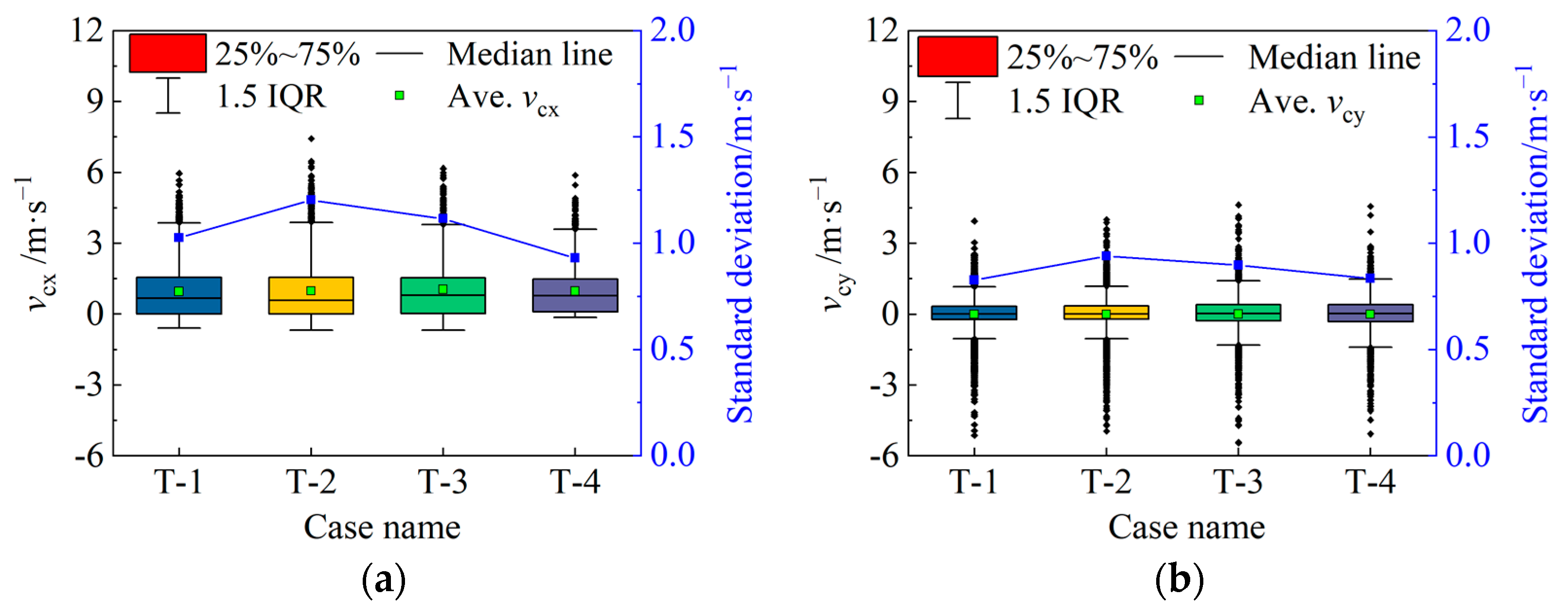
4. Simulation of PDC Cutting Pebbled Sandstone
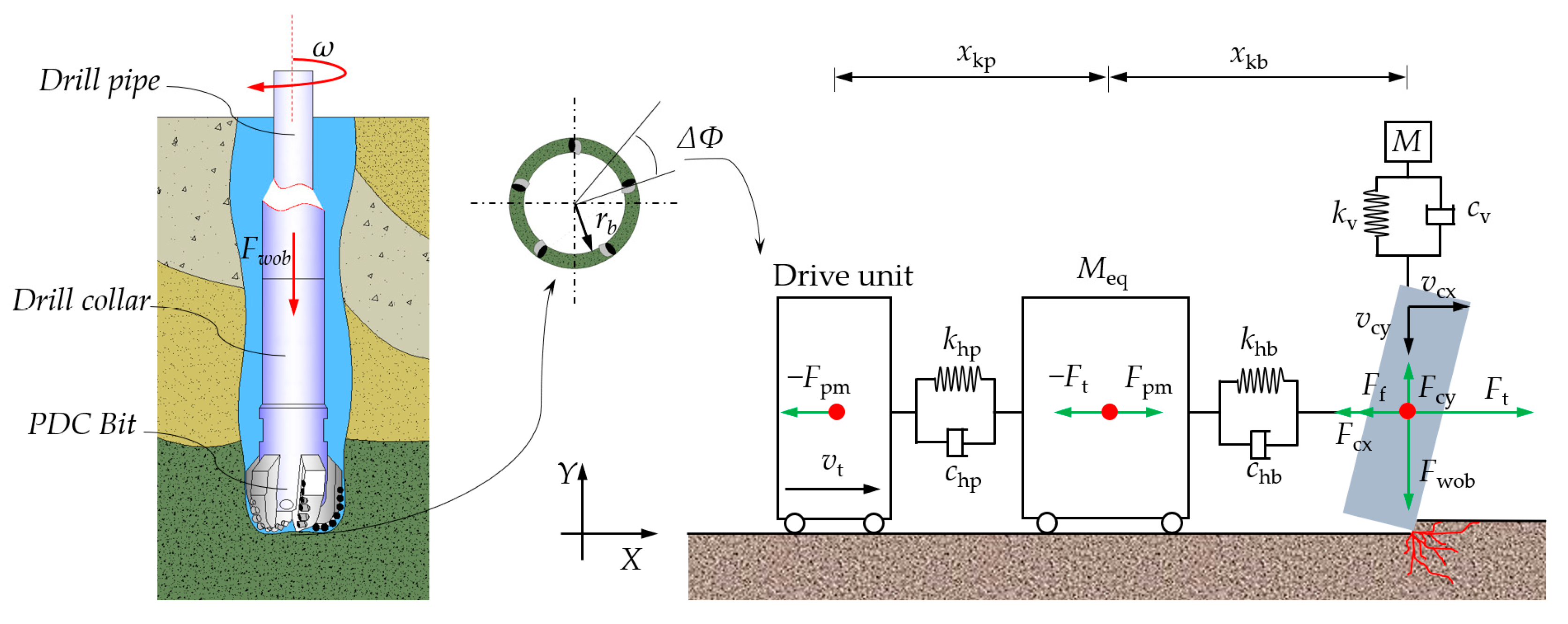
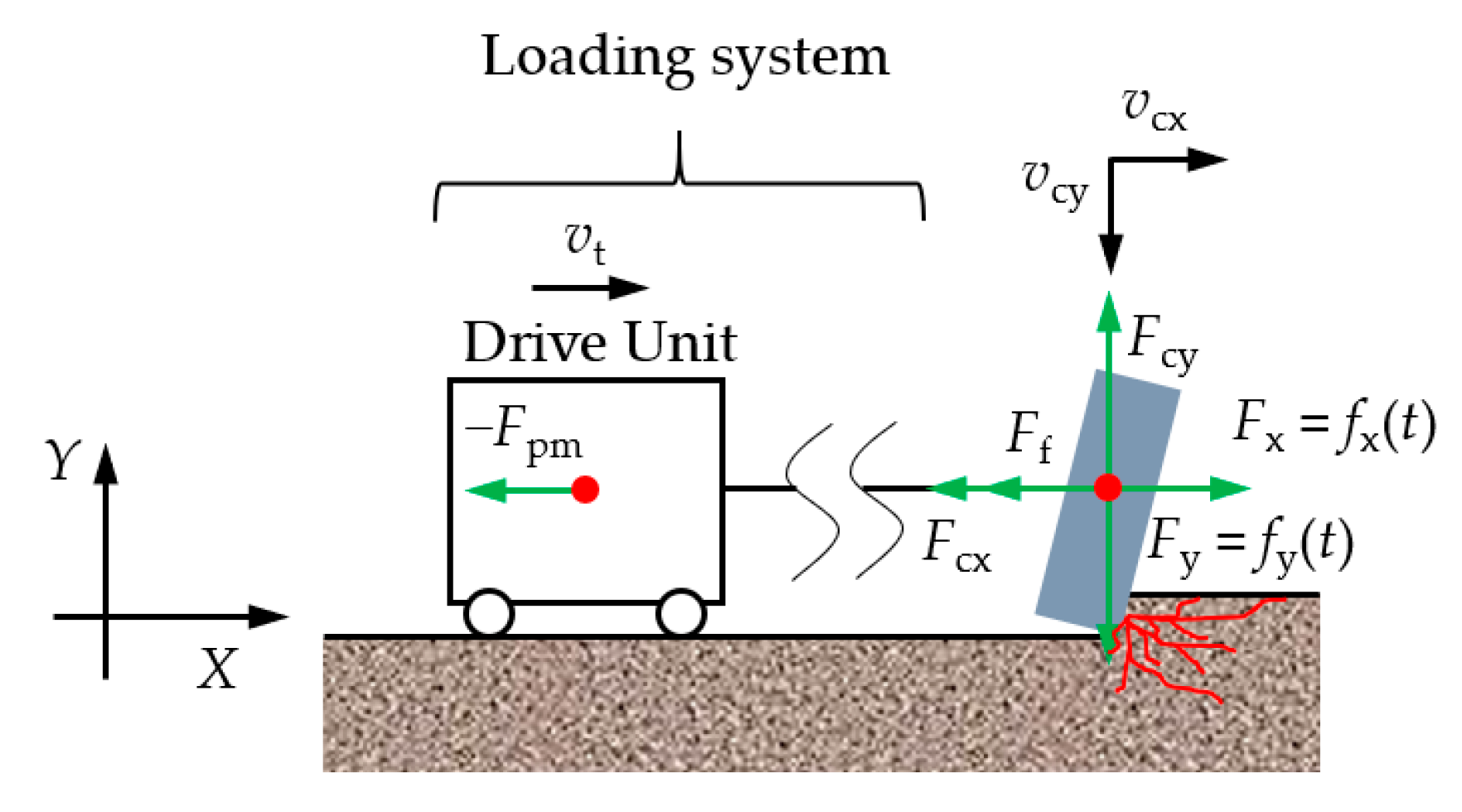
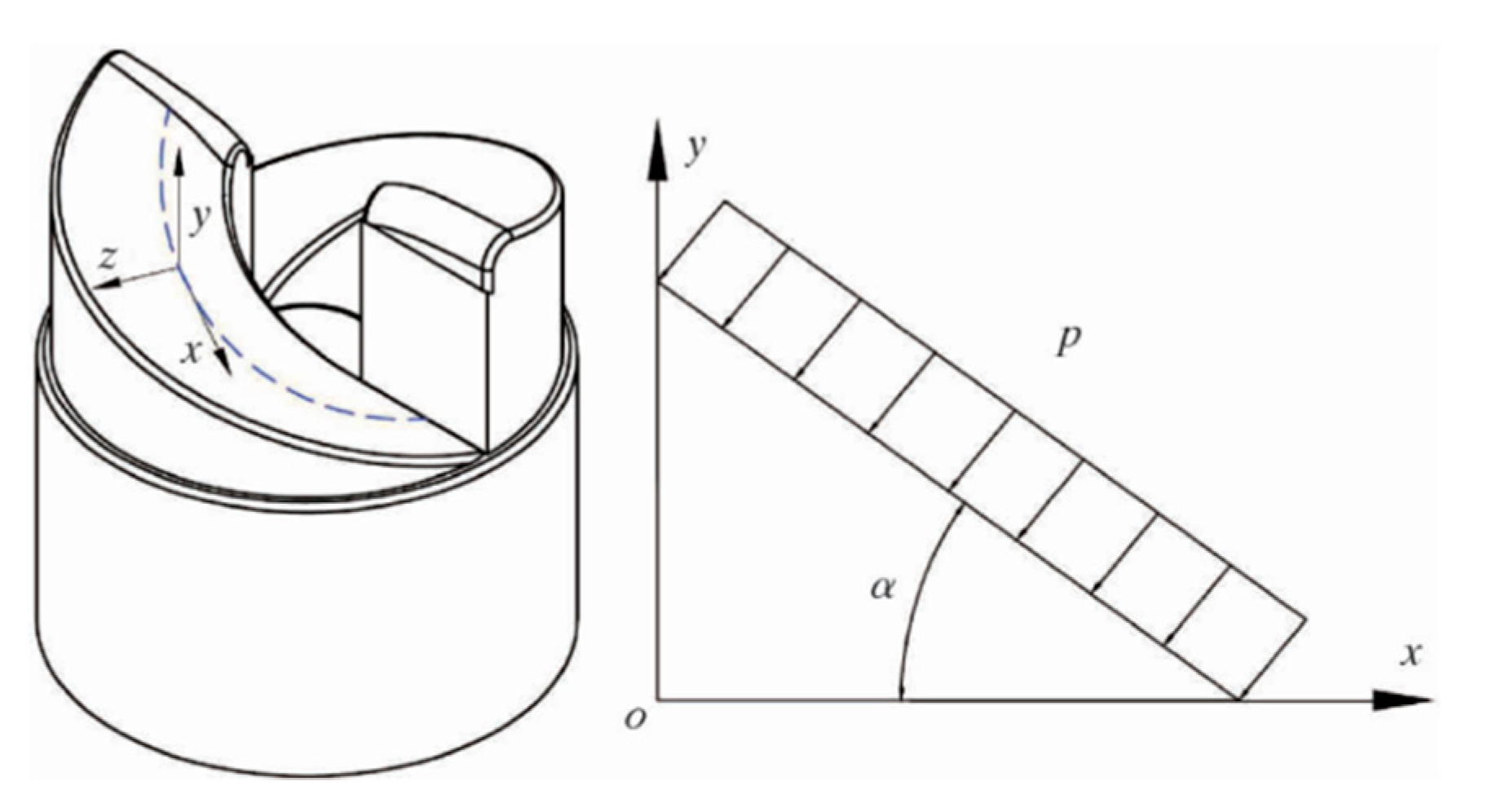
4.1. Loading Model of PDC Cutter
4.2. Physical Model
4.3. Numerical Simulation
5. Field Test of Composite Impactor
5.1. Structure Introduction
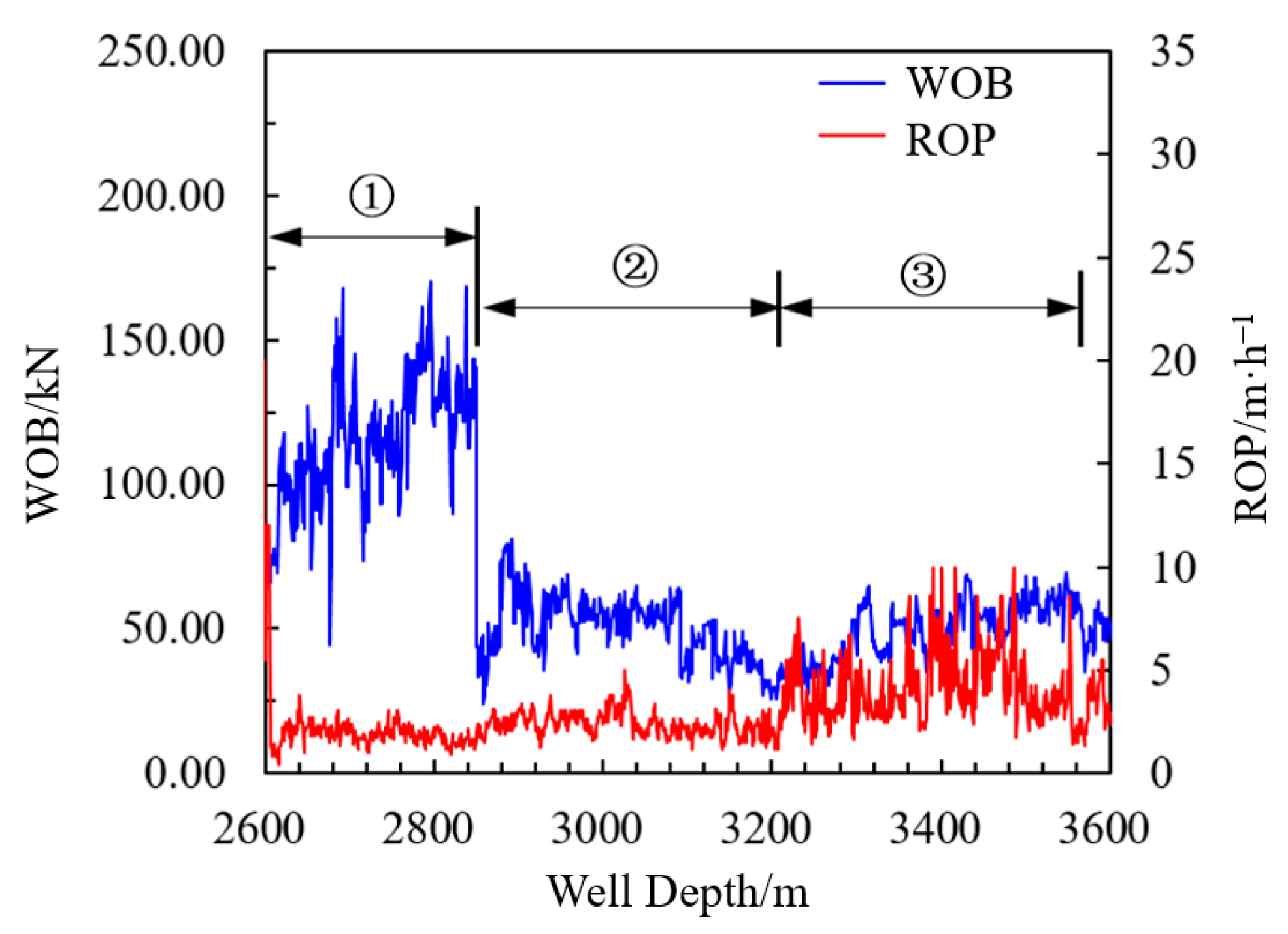
5.2. Field Drilling Test
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, P.; Ni, H.; Wang, R.; Li, Z. Modulating downhole cuttings via a pulsed jet for efficient drilling-tool development and field testing. J. Nat. Gas Sci. Eng. 2015, 27, 1287–1295. [Google Scholar] [CrossRef]
- Detournay, E.; Richard, T.; Shepherd, M. Drilling response of drag bits: Theory and experiment. Int. J. Rock Mech. Min. Sci. 2008, 45, 1347–1360. [Google Scholar] [CrossRef]
- Glowka, D.A. Use of single-cutter data in the analysis of PDC bit designs: Part 1-development of a PDC cutting force model. J. Pet. Technol. 1989, 41, 797–849. [Google Scholar] [CrossRef]
- Wojtanowicz, A.; Kuru, E. Mathematical modeling of PDC bit drilling process based on a single-cutter mechanics. J. Energy Resour. Technol. 1993, 115, 247–256. [Google Scholar] [CrossRef]
- Mishnaevsky, L.L., Jr. Physical mechanisms of hard rock fragmentation under mechanical loading: A review. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 763–766. [Google Scholar] [CrossRef]
- Black, A.D.; Walker, B.H.; Tibbitts, G.A.; Sandstrom, J.L. PDC Bit Performance for Rotary, Mud Motor, and Turbine Drilling Applications. SPE Drill. Eng. 1986, 1, 409–416. [Google Scholar] [CrossRef]
- Slnor, A.; Warren, T. SPE Annual Technical Conference and Exhibition. In Drag Bit Wear Model; Society of Petroleum Engineers: Dallas, TX, USA, 1987. [Google Scholar]
- Warren, T.; Sinor, A. Drag-bit performance modeling. SPE Drill. Eng. 1989, 4, 119–127. [Google Scholar] [CrossRef]
- Detournay, E.; Defourny, P. International journal of rock mechanics and mining sciences & geomechanics abstracts. In A Phenomenological Model for the Drilling Action of Drag Bits; Elsevier: Amsterdam, The Netherlands, 1992; pp. 13–23. [Google Scholar]
- Nandakumar, K.; Wiercigroch, M. Stability analysis of a state dependent delayed, coupled two DOF model of drill-string vibration. J. Sound Vib. 2013, 332, 2575–2592. [Google Scholar] [CrossRef]
- Chiaia, B. Fracture mechanisms induced in a brittle material by a hard cutting indenter. Int. J. Solids Struct. 2001, 38, 7747–7768. [Google Scholar] [CrossRef]
- Liu, H.Y.; Kou, S.Q.; Lindqvist, P.A.; Tang, C.A. Numerical simulation of the rock fragmentation process induced by indenters. Int. J. Rock Mech. Min. Sci. 2002, 39, 491–505. [Google Scholar] [CrossRef]
- Bilgesu, I.; Sunal, O.; Tulu, I.; Heasley, K. The 42nd US Rock Mechanics Symposium (USRMS). In Modeling Rock and Drill Cutter Behavior; American Rock Mechanics Association: San Francisco, CA, USA, 2008. [Google Scholar]
- Jalali, S.M.E.; Naghadehi, M.Z. An analytical pre-feasibility study to generate rotary-percussive concept in hard rock TBMs. J. Geol. Min. Res. 2009, 1, 140–148. [Google Scholar]
- Tulu, I.; Heasley, K. 43rd US Rock Mechanics Symposium & 4th US-Canada Rock Mechanics Symposium. In Calibration of 3D Cutter-Rock Model with Single Cutter Tests; American Rock Mechanics Association: Asheville, NC, USA, 2009. [Google Scholar]
- Mendoza, J.; Gamwo, I.; Zhang, W.; Lin, J. 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium. In Discrete Element Modeling of Rock Cutting Using Crushable Particles; American Rock Mechanics Association: Salt Lake City, UT, USA, 2010. [Google Scholar]
- Jaime, M.C. Numerical Modeling of Rock Cutting and Its Associated Fragmentation Process Using the Finite Element Method. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 2011. [Google Scholar]
- Jaime, M.C.; Zhou, Y.; Lin, J.-S.; Gamwo, I.K. Finite element modeling of rock cutting and its fragmentation process. Int. J. Rock Mech. Min. Sci. 2015, 80, 137–146. [Google Scholar] [CrossRef]
- Menezes, P.L. Influence of rock mechanical properties and rake angle on the formation of rock fragments during cutting operation. Int. J. Adv. Manuf. Technol. 2017, 90, 127–139. [Google Scholar] [CrossRef]
- Cao, L.; Sun, J.; Zhang, B.; Lu, N.; Xu, Y. Sensitivity analysis of the temperature profile changing law in the production string of a high-pressure high-temperature gas well considering the coupling relation among the gas flow friction, gas properties, temperature, and pressure. Front. Phys. 2022, 10, 1112. [Google Scholar] [CrossRef]
- Zhong, R.; Miska, S.; Yu, M.; Meng, M.; Ozbayoglu, E.; Takach, N. Experimental investigation of fracture-based wellbore strengthening using a large-scale true triaxial cell. J. Pet. Sci. Eng. 2019, 178, 691–699. [Google Scholar] [CrossRef]
- Galkin, V.I.; Martyushev, D.A.; Ponomareva, I.N.; Chernykh, I.A. Developing features of the near-bottomhole zones in productive formations at fields with high gas saturation of formation oil. J. Min. Inst. 2021, 249, 386–392. [Google Scholar] [CrossRef]
- Saksala, T. Numerical study of the influence of hydrostatic and confining pressure on percussive drilling of hard rock. Comput. Geotech. 2016, 76, 120–128. [Google Scholar] [CrossRef]
- Guarin, P.L.; Arnold, H.E.; Harpst, W.E.; Davis, E.E. Rotary Percussion Drilling. In Drilling and Production Practice; American Petroleum Institute: New York, NY, USA, 1949; p. 11. [Google Scholar]
- Melamed, Y.; Kiselev, A.; Gelfgat, M.; Dreesen, D.; Blacic, J. Hydraulic hammer drilling technology: Developments and capabilities. J. Energy Resour. Technol. 1999, 122, 1–7. [Google Scholar] [CrossRef]
- Liu, S.; Ni, H.; Zhang, H.; Wang, Y.; Xie, H. Numerical study on optimal impact angle of a single PDC cutter in impact rock cutting. Energy Rep. 2021, 7, 4172–4183. [Google Scholar] [CrossRef]
- Akbari, B.; Butt, S.; Munaswamy, K.; Arvani, F. 45th US Rock Mechanics/Geomechanics Symposium. In Dynamic Single PDC Cutter Rock Drilling Modeling and Simulations Focusing on Rate of Penetration Using Distinct Element Method; American Rock Mechanics Association: San Francisco, CA, USA, 2011. [Google Scholar]
- Xiong, C.; Huang, Z.; Shi, H.; Shi, X.; Zhang, B.; Chalaturnyk, R. Experimental Investigation into Mixed Tool Cutting of Granite with Stinger PDC Cutters and Conventional PDC Cutters. Rock Mech. Rock Eng. 2021, 55, 813–835. [Google Scholar] [CrossRef]
- Dong, G.; Chen, P. 3D Numerical Simulation and Experiment Validation of Dynamic Damage Characteristics of Anisotropic Shale for Percussive-Rotary Drilling with a Full-Scale PDC Bit. Energies 2018, 11, 1326. [Google Scholar] [CrossRef]
- Xi, Y.; Wang, W.; Fan, L.; Zha, C.; Li, J.; Liu, G. Experimental and numerical investigations on rock-breaking mechanism of rotary percussion drilling with a single PDC cutter. J. Pet. Sci. Eng. 2021, 208, 109227. [Google Scholar] [CrossRef]
- Tian, K.; Detournay, E. Influence of PDC bit cutter layout on stick–slip vibrations of deep drilling systems. J. Pet. Sci. Eng. 2021, 206, 109005. [Google Scholar] [CrossRef]
- Song, H.; Shi, H.; Ji, Z.; Wu, X.; Li, G.; Zhao, H.; Wang, G.; Liu, Y.; Hou, X. The percussive process and energy transfer efficiency of percussive drilling with consideration of rock damage. Int. J. Rock Mech. Min. Sci. 2019, 119, 1–12. [Google Scholar] [CrossRef]
- Liu, S.; Ni, H.; Jin, Y.; Zhang, H.; Wang, Y.; Huang, B.; Hou, W. Experimental study on drilling efficiency with compound axial and torsional impact load. J. Pet. Sci. Eng. 2022, 219, 111060. [Google Scholar] [CrossRef]
- Wang, W.; Liu, G.; Li, J.; Zha, C.; Lian, W. Numerical simulation study on rock-breaking process and mechanism of compound impact drilling. Energy Rep. 2021, 7, 3137–3148. [Google Scholar] [CrossRef]
- He, X.; Xu, C. Discrete element modelling of rock cutting: From ductile to brittle transition. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 1331–1351. [Google Scholar] [CrossRef]
- He, Q.; Zhu, L.; Li, Y.; Li, D.; Zhang, B. Simulating hydraulic fracture re-orientation in heterogeneous rocks with an improved discrete element method. Rock Mech. Rock Eng. 2021, 54, 2859–2879. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Potyondy, D.O. The bonded-particle model as a tool for rock mechanics research and application: Current trends and future directions. Geosyst. Eng. 2015, 18, 1–28. [Google Scholar] [CrossRef]
- Itasca Consulting Group. PFC (Particle Flowcodein 2 and 3 Dimensions), Version 5.0 [User’s Manual]; ICG. Inc.: Minneapolis, MN, USA, 2016. [Google Scholar]
- Richard, T.; Dagrain, F.; Poyol, E.; Detournay, E. Rock strength determination from scratch tests. Eng. Geol. 2012, 147–148, 91–100. [Google Scholar] [CrossRef]
- Wei, J.; Liao, H.; Wang, H.; Chen, J.; Li, N.; Liang, H.; Liu, C.; Zhang, D.; Teng, Z. Experimental investigation on the dynamic tensile characteristics of conglomerate based on 3D SHPB system. J. Pet. Sci. Eng. 2022, 213, 110350. [Google Scholar] [CrossRef]
- Saha, A.; Wiercigroch, M.; Jankowski, K.; Wahi, P.; Stefański, A. Investigation of two different friction models from the perspective of friction-induced vibrations. Tribol. Int. 2015, 90, 185–197. [Google Scholar] [CrossRef]
- Saha, A.; Wahi, P.; Wiercigroch, M.; Stefański, A. A modified LuGre friction model for an accurate prediction of friction force in the pure sliding regime. Int. J. Non-Linear Mech. 2016, 80, 122–131. [Google Scholar] [CrossRef]
- Zhang, H.; Ni, H.; Wang, Z.; Huang, B.; Liu, S.; Xu, X.; Liu, C. Discrete element modeling and simulation study on cutting rock behavior under spring-mass-damper system loading. J. Pet. Sci. Eng. 2022, 209, 109872. [Google Scholar] [CrossRef]
- He, Q.; Li, Y.; Li, D.; Zhang, C. Microcrack fracturing of coal specimens under quasi-static combined compression-shear loading. J. Rock Mech. Geotech. Eng. 2020, 12, 1014–1026. [Google Scholar] [CrossRef]
- Kyllingstad, A.; Halsey, G.W. SPE Annual Technical Conference and Exhibition, Dallas. In A Study of Slip/stick Motion of the Bit, SPE 16659; Society of Petroleum Engineers: Dallas, TX, USA, 1987. [Google Scholar]
- Richard, T.; Germay, C.; Detournay, E. A simplified model to explore the root cause of stick-slip vibrations in drilling systems with drag bits. J. Sound Vib. 2007, 305, 432–456. [Google Scholar] [CrossRef]
- Germay, C.; Denoël, V.; Detournay, E. Multiple Mode Analysis of the Self-Excited Vibrations of Rotary Drilling Systems. J. Sound Vib. 2009, 325, 362–381. [Google Scholar] [CrossRef]
- Brett, J.F. The genesis of torsional drillstring vibrations. SPE Drill. Eng. 1992, 7, 168–174. [Google Scholar] [CrossRef]
- Liu, S.; Ni, H.; Wang, X.; Wang, Y.; Wang, P. IADC/SPE Asia Pacific Drilling Technology Conference and Exhibition. In Rock-Breaking Mechanism Study of Axial and Torsional Impact Hammer and Its Application in Deep Wells; Society of Petroleum Engineers: Bangkok, Thailand, 2018. [Google Scholar]
- Zhang, H.; Ni, H.; Liu, S.; Huang, B.; Liang, H. An Axial and Torsional Percussion Hammer with Considerable Potential to Increase the Drilling Speed of High-Temperature Geothermal Wells. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Wuhan, China, 2020; p. 012131. [Google Scholar]


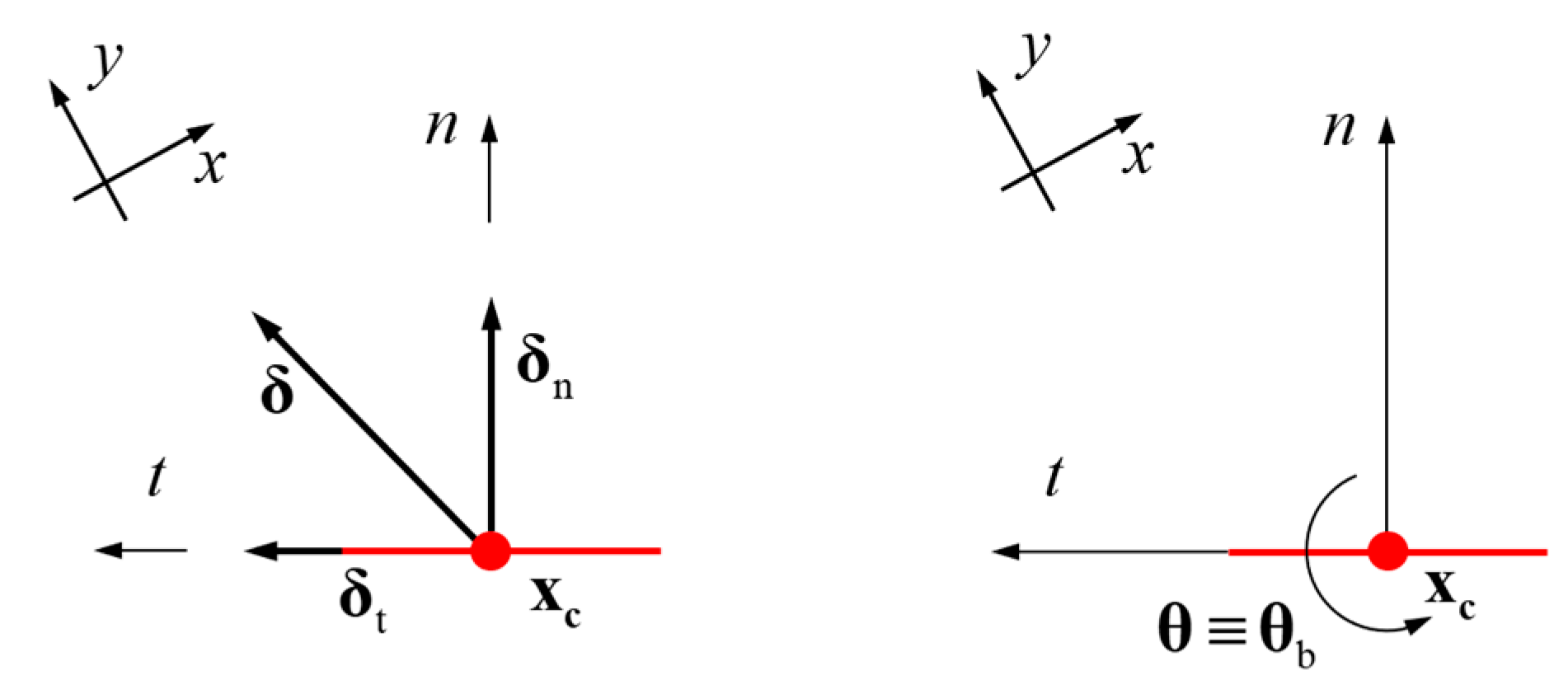
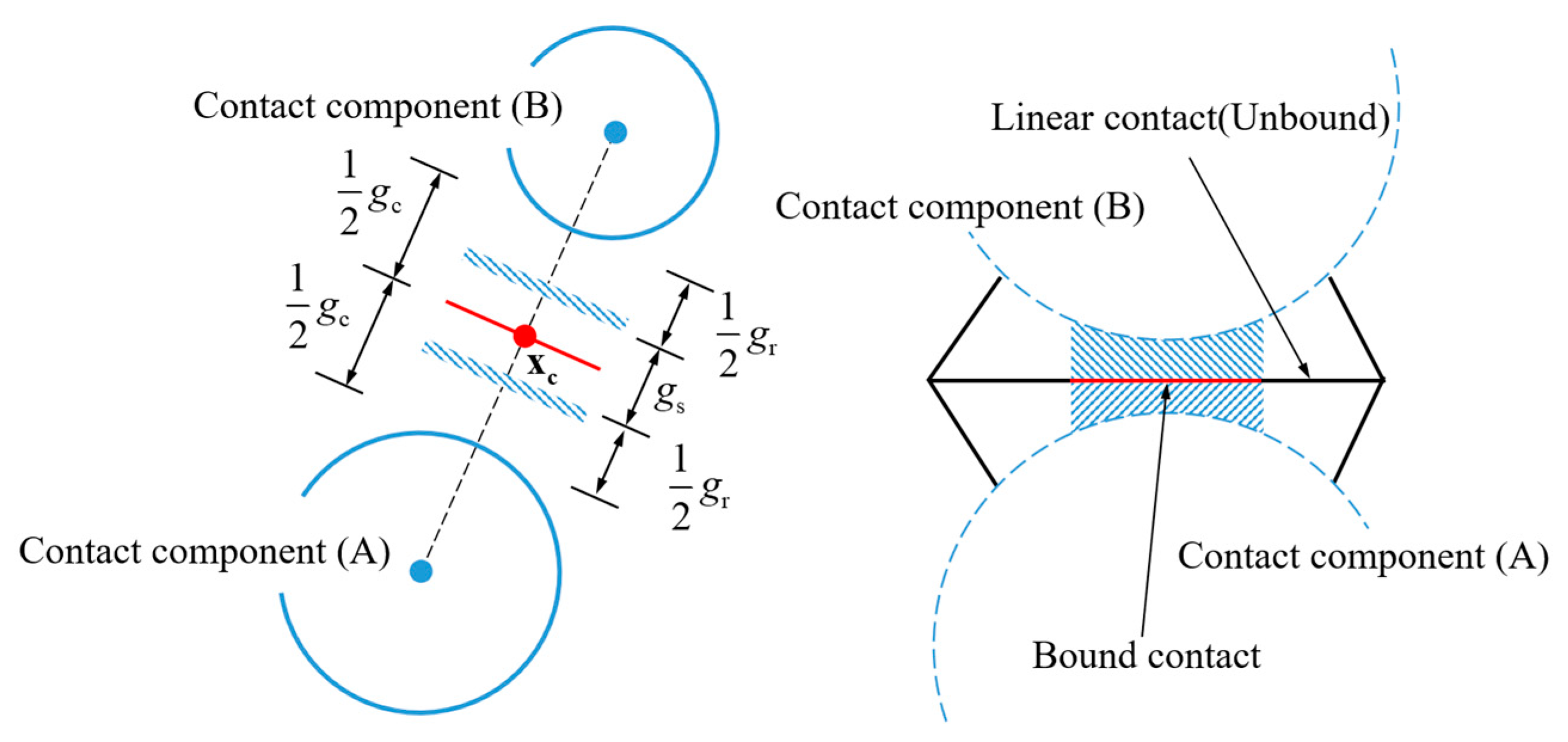
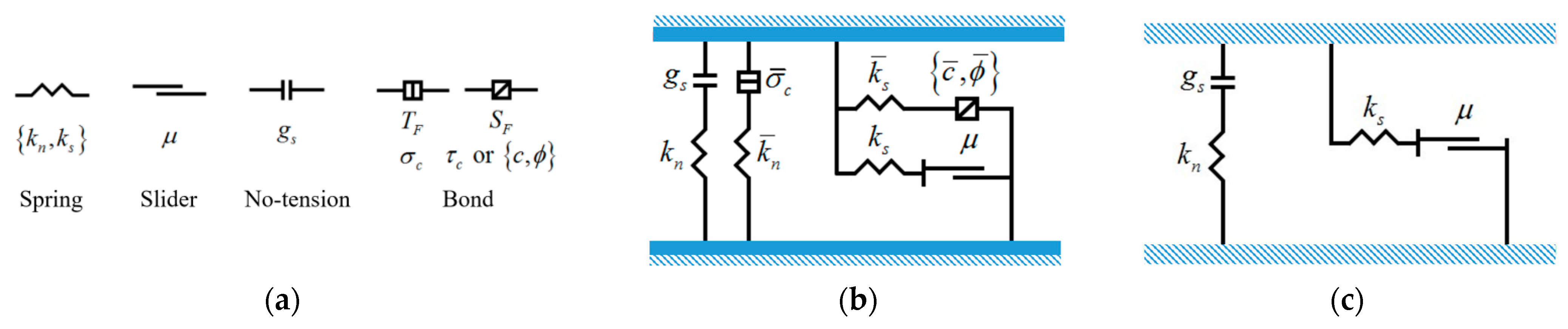

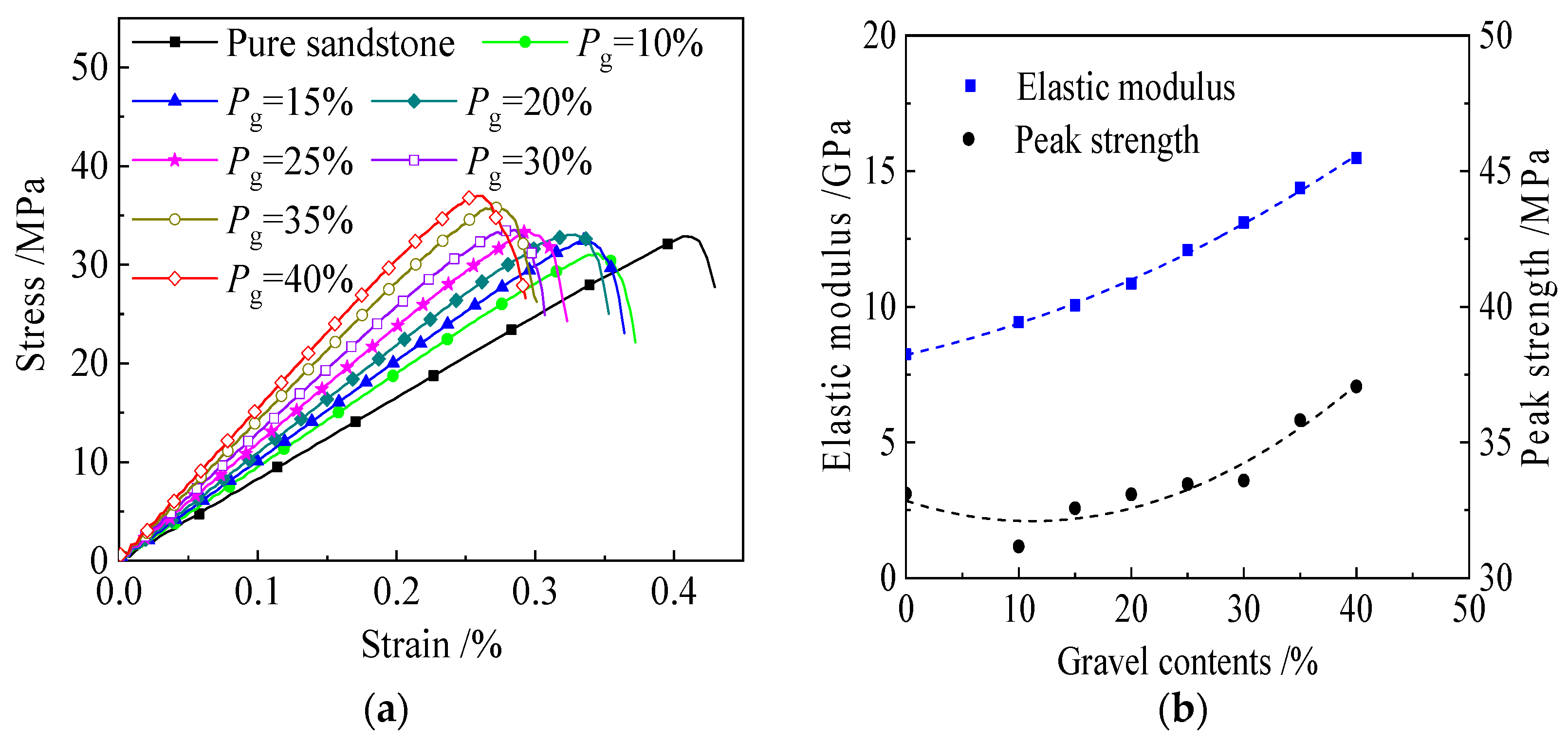



| Rock Samples | Compressive Strength/MPa | Elastic Modulus/GPa | Poisson’s Ratio |
|---|---|---|---|
| Sandstone | 33.10 | 8.25 | 0.33 |
| Sandstone model | 32.97 | 8.24 | 0.32 |
| Gravel | 203.45 | 70.47 | 0.177 |
| Gravel model | 206.95 | 70.41 | 0.177 |
| Rock Composition | Rock Matrix | Gravel |
|---|---|---|
| Particle density/(kg/cm3) | 2000 | 2650 |
| Effective modulus/GPa | 4.33 | 33.82 |
| Normal-to-shear stiffness ratio | 1.50 | 1.58 |
| Bonding effective modulus/GPa | 4.33 | 33.82 |
| Bond normal-to-shear stiffness ratio | 1.50 | 1.58 |
| Tensile strength/MPa | 9.98 | 67.20 |
| Cohesion/MPa | 11.96 | 78.33 |
| Friction angle/° | 32 | 25 |
| Friction coefficient | 0.65 | 0.65 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| vt (m·s−1) | 1 | khb (N·m−1) | 1 × 109 |
| xmax (m) | 0.16 | chp (N·m·s−1) | 5 × 104 |
| xkp (m) | 10 | α | 0.005 |
| xkb (m) | 10 | β | 0.01 |
| Fwob (N) | 200 | γ | 0.001 |
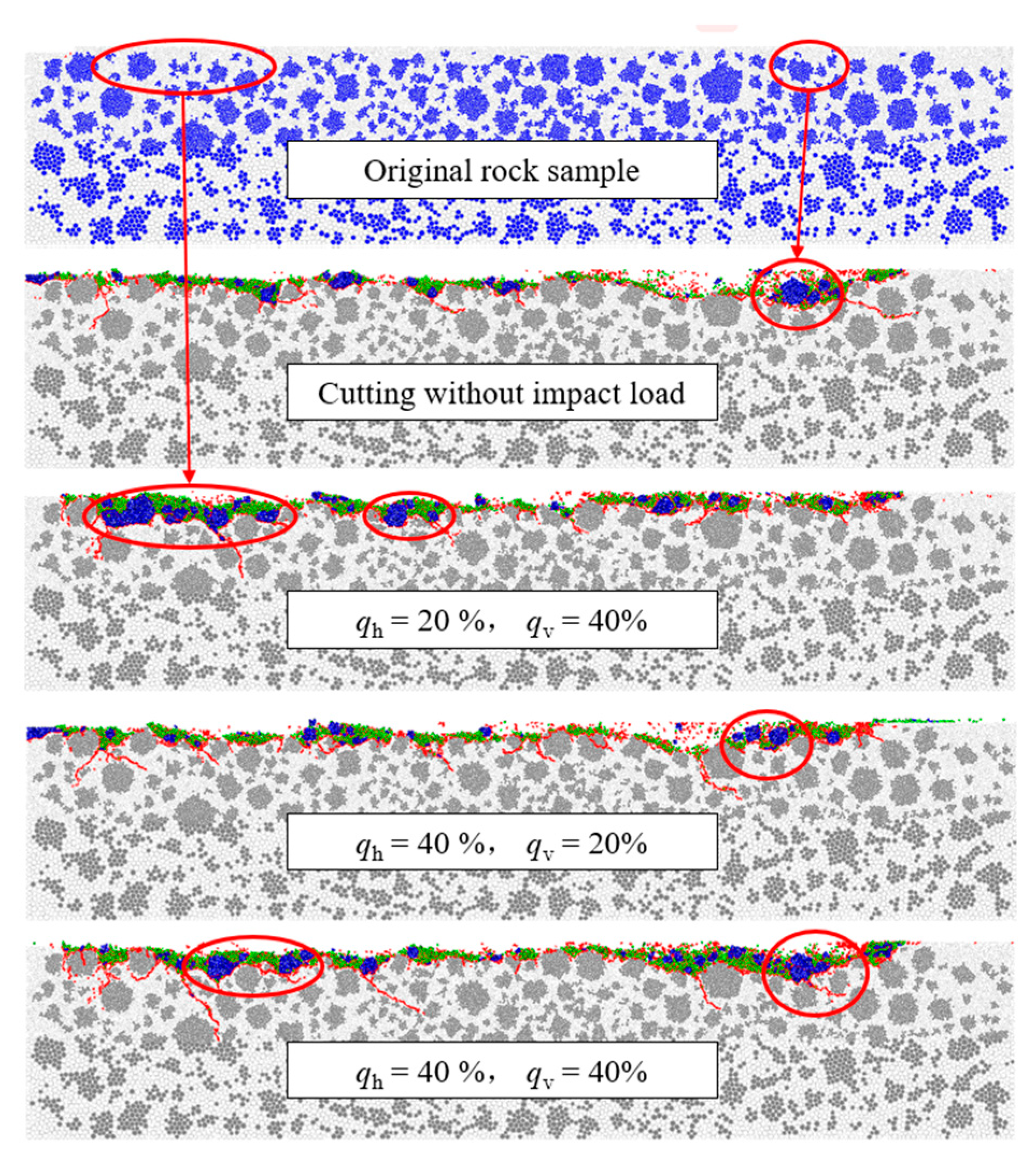
| Case | qh/% | qv/% |
|---|---|---|
| T-1 | 0 | 0 |
| T-2 | 20 | 40 |
| T-3 | 40 | 20 |
| T-4 | 40 | 40 |
| Parameters | Value |
|---|---|
| Diameter/mm | 245 |
| Spiral angle α/° | 70 |
| Number of spiral faces | 5 |
| Pressure/MPa | 2 |
| Axial load/kN | 24 |
| Torsional load/N·m | 3479 |
| Drilling Method | Conventional | Turbine Drill | Composite Impactor |
|---|---|---|---|
| Test section/m | 2612–2850 | 2850–3207 | 3207–3569 |
| WOB/kN | 115.27 | 49.95 | 49.42 |
| Standard deviation of WOB/kN | 22.97 | 11.21 | 9.81 |
| ROP/(m/h) | 1.77 | 2.25 | 3.51 |
| ROP enhancement rate/% | / | 27.12 | 98.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Ni, H.; Yang, H.; Fu, L.; Wang, Y.; Liu, S.; Huang, B.; Wang, Z.; Chen, G. Numerical Simulation and Field Test Research on Vibration Reduction of PDC Cutting of Pebbled Sandstone under Composite Impact Load. Processes 2023, 11, 671. https://doi.org/10.3390/pr11030671
Zhang H, Ni H, Yang H, Fu L, Wang Y, Liu S, Huang B, Wang Z, Chen G. Numerical Simulation and Field Test Research on Vibration Reduction of PDC Cutting of Pebbled Sandstone under Composite Impact Load. Processes. 2023; 11(3):671. https://doi.org/10.3390/pr11030671
Chicago/Turabian StyleZhang, Heng, Hongjian Ni, Henglin Yang, Li Fu, Yuan Wang, Shubin Liu, Bin Huang, Zixin Wang, and Gang Chen. 2023. "Numerical Simulation and Field Test Research on Vibration Reduction of PDC Cutting of Pebbled Sandstone under Composite Impact Load" Processes 11, no. 3: 671. https://doi.org/10.3390/pr11030671
APA StyleZhang, H., Ni, H., Yang, H., Fu, L., Wang, Y., Liu, S., Huang, B., Wang, Z., & Chen, G. (2023). Numerical Simulation and Field Test Research on Vibration Reduction of PDC Cutting of Pebbled Sandstone under Composite Impact Load. Processes, 11(3), 671. https://doi.org/10.3390/pr11030671






