Analysis of Bottomhole Rock Stress in Deep-Well Drilling Considering Thermal-Hydro-Mechanical Coupling

Abstract

Drilling is a key step in the exploitation of deep oil and gas resources. In order to clarify the stress state of the rocks and the mechanism of rock breakage in deep-well drilling, a thermal-hydro-mechanical coupling model for deep-well drilling was established, and the effects of drilling on the temperature, pressure, and stress in the formation were studied. Furthermore, the effects of the formation parameters and wellbore parameters on the bottomhole stress were analyzed. The results revealed that after the formation was drilled, the temperatures in different horizontal in situ stress directions were not significantly different, but the difference in the pore pressure between the maximum and minimum horizontal stress directions was large. The average effective stress at the bottom of the hole was the smallest, and in some areas, it was tensile stress. For deep-well drilling, as the formation pressure increased, the in situ stress increased, and the permeability decreased, leading to greater average effective stress of the bottomhole rock. As a result, it was harder to break the rock, and the drilling efficiency decreased. Reducing the wellbore pressure and wellbore temperature is conducive to forming tensile stress near the borehole axis in the bottomhole, causing tensile damage. The average effective stress of the formation near the shoulder of the drill bit was compressive stress, and it is advisable to take advantage of the rock shear failure characteristics to improve the drilling efficiency in this area. The results of this study can help us to understand the stress state of the bottomhole rocks and the mechanism of rock breakage and can provide a reference for the optimization of drilling tools and drilling parameters in deep-well drilling.

1. Introduction

With rapid economic and social development, there has been an increasing demand for energy. With the background that shallow oil and gas resources are depleted, energy resources from the deep part of the earth have become an important alternative for increasing oil and gas reserves and production [1,2]. The deep oil and gas reserves in the world are rich, and efficient development of deep oil and gas resources is of great significance to the development of the global economy [3,4]. Drilling is a key step in deep oil and gas exploitation. It not only plays a role in confirming the oil and gas reserves in deep formations but also provides oil and gas migration channels for later deep oil and gas extraction [5]. However, due to the complex lithology, high strength, strong abrasiveness, and poor drillability of deep formations [6,7,8,9], as well as the significant coupled effect of multiple physical fields during drilling [10], deep-well drilling faces the challenges of low drilling speed and efficiency, which greatly restrict the exploitation of deep oil and gas resources.

In order to increase the rock-breaking efficiency and rate of penetration (ROP) of deep-well drilling, a variety of drill bits have been developed, such as polycrystalline diamond compact (PDC) bits, composite bits, and dual-diameter PDC bits [11,12,13,14,15]. New drilling techniques have also been developed, such as high-pressure water jet drilling, electro-pulse drilling, particle jet impact drilling, and laser drilling [9,16,17,18,19]. In addition to the development of new tools and drilling techniques, analysis of the stress state of bottomhole rocks during drilling can also help clarify the mechanism of bottomhole rock breakage during drilling, which can provide references for optimizing drilling tools and drilling parameters. In this field, Peng et al. [20] used the finite element method to simulate formation stress state before drilling, during drilling, and after drilling of the formation. They found that there was stress concentration in the bottom area near the wellbore wall, which led to poor drillability of the rocks in this area. Regarding the high-pressure water jet drilling process, Li et al. [21] studied bottomhole rock stress under high-pressure water jet drilling using finite element and finite volume methods. Their results showed that the maximum principal stress of bottomhole rocks increased as the jet velocity increased. Furthermore, Wang et al. studied the stress release mechanism of deep bottomhole rock using ultra-high-pressure water jet slotting [16]. Their results suggest that the stress release was due to the combined action of three drivers, namely, horizontal stress release, stress concentration in the area away from the cutting plane, and increased pore pressure caused by rock mass expansion. Under the condition of underbalanced drilling, Li et al. [22] used the finite element method to study the stress state of bottomhole rocks, and their results indicate that the mechanical properties of the rocks near the bottomhole were affected by a number of factors, including the in situ stress, pore pressure, well diameter, and fluid column pressure. Compared to a permeable borehole wall, rocks are easier to break under impermeable borehole conditions. In view of the influence of the bit structure, Heydarshahy and Karekal [23] carried out finite element simulations to study the stress distribution characteristics under different drill bit shapes. It was found that increasing the height of the cone-shaped bit led to an increase in the high-stress area of bottomhole rocks. Shen and Peng [24] analyzed the bottomhole stress field when a dual-diameter PDC bit was used. Their results showed that there was significant equivalent stress unloading, which improved the ROP.

The above studies focused on bottomhole rock stress under different drilling techniques and different drill bit shapes but did not consider the multi-physical coupling effects of the bottomhole rocks during drilling. Actually, after the formation is drilled, because some of the rocks are replaced by the drilling fluid, the stress, temperature, and pressure of the bottomhole rock changes accordingly, and these changes impact the stress state of bottomhole rocks. This process is a complex thermal-hydro-mechanical coupling process. In order to analyze the influence of the coupling effect on bottomhole rock stress, Warren and Smith [25] established a hydro-mechanical coupling model for studying the formation stress near the bottom of a borehole and analyzed the distribution of the mean bottomhole stress under different over-balance pressures. They concluded that a high over-balance pressure was not conducive to improving the rock-breaking efficiency. Chang et al. [26] analyzed the formation stress under different bottomhole pressure differences using numerical simulation methods. Their results showed that reducing the wellbore pressure could promote bottomhole rock breakage. Chen et al. [27] used the finite difference method to analyze the formation stress near the bottom of the wellbore by considering the hydro-mechanical coupling effect during the drilling process, and they found that the rock mass expansion at the bottom of the wellbore led to a decrease in the pore pressure, thereby affecting the drilling efficiency. Hu et al. [28] carried out finite element simulations to study the dynamic variations in bottomhole rock stress and pore pressure, considering hydro-mechanical coupling. Then, Hu et al. [29] analyzed the dynamic variations in the stress field under balanced drilling conditions, and their results showed that the variations in bottomhole stress were caused by the changes in the pore pressure. In addition, Hu et al. [13,14] designed a dual-diameter PDC bit and studied the bottomhole stress release mechanism of the drill bit under the influence of coupled hydro-mechanical conditions. Their results showed that the stress concentration area at the shoulder of the reaming bit was significantly reduced, and a large stress unloading area formed at the intersection of the reaming bit and the pilot bit. Moreover, some scholars have studied the comprehensive influence of the thermal-hydro-mechanical coupling effect. For instance, Li et al. [30] studied the stress of bottomhole rock in underbalanced drilling using the finite element method. Their results suggest that both the wellbore pressure and temperature can affect bottomhole stress. Moreover, Zhang et al. [31] established an analytical model for calculating bottomhole pressure and the thermally induced near-wellbore stress. They found that when the wellbore pressure changed from overbalanced to underbalanced, the stress state of the bottomhole rocks changed from compressive stress to tensile stress. In addition, Zhang et al. [32] also analyzed bottomhole stress distribution and its influencing factors in underbalanced drilling by considering thermal-hydro-mechanical coupling.

Based on the above analysis, it can be seen that most previous studies analyzed the bottomhole rock stress while neglecting the coupling effect or only considering hydro-mechanical coupling. A few studies have considered the influence of thermal-hydro-mechanical coupling in underbalanced drilling conditions. Although underbalanced drilling is beneficial to improving the drilling efficiency, its safety is still controversial, and the related risks are high. In deep-well drilling practices, in order to ensure drilling safety, overbalanced drilling is generally used. In overbalanced drilling, the wellbore fluid under positive pressure difference will penetrate the formation. Due to the difference between the temperature and pressure of the wellbore fluid and the original formation, bottomhole rocks will be directly affected by the thermal-hydro-mechanical coupling effect. The objective of this study was to analyze the stress of bottomhole rocks during deep-well drilling by considering the thermal-hydro-mechanical coupling effect. First, a thermal-hydro-mechanical coupling model was established. Then, numerical simulations were carried out to reveal the dynamic evolution of the temperature, pressure, and stress of the bottomhole rocks. Furthermore, the mechanisms by which the formation pressure, in situ stress, formation permeability, wellbore pressure, and wellbore temperature influence bottomhole rock stress were analyzed. The results of this study can improve our understanding of bottomhole stress and the mechanism of rock breakage; moreover, the results can be used to analyze wellbore stability by combing the rock strength criterion, which is of great significance for improving the safety and efficiency of deep-well drilling.

2. Thermal-Hydro-Mechanical Coupling Model for Deep-Well Drilling

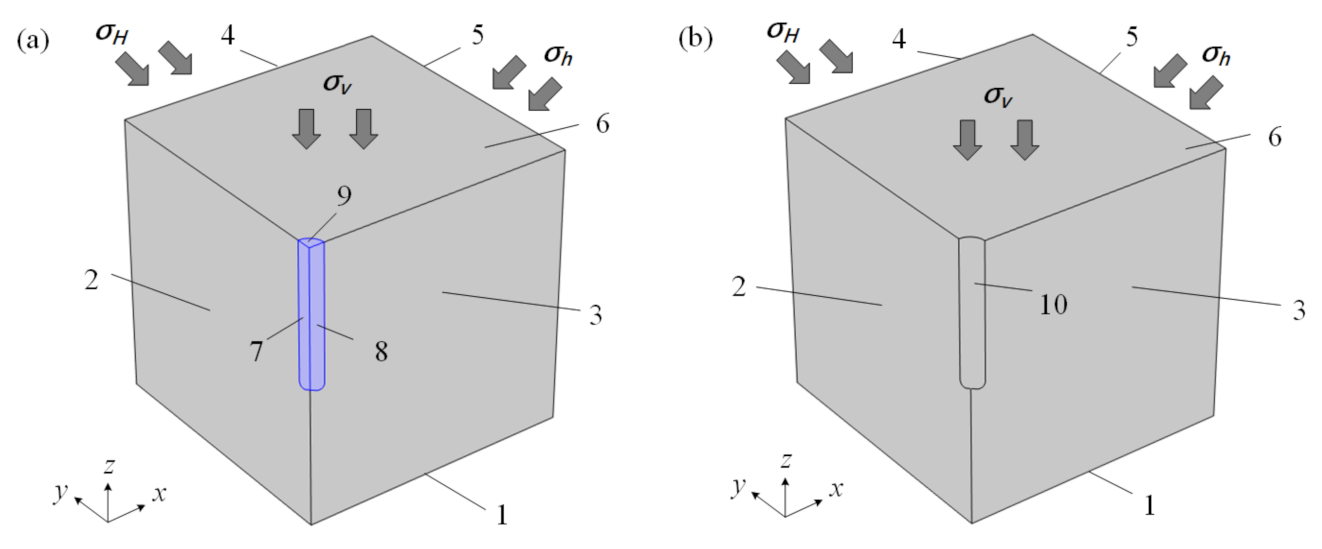
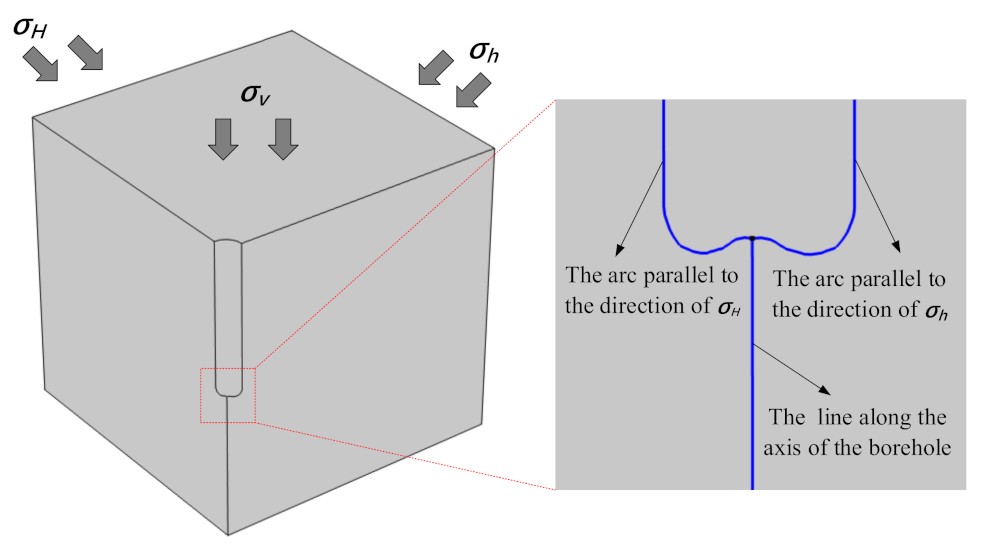
2.1. Assumptions

In order to simplify the model, the following assumptions were made.

(1)

The formation is continuous, homogeneous, isotropic, and meets the small deformation condition.

(2)

The fluid seepage in the formation is single-phase flow.

(3)

The variations in the wellbore temperature and pressure were neglected.

(4)

The effect of the water jet on bottomhole rock stress was neglected.

(5)

The influence of the thermal radiation on the wellbore temperature was neglected.

2.2. Field Equations

2.2.1. Stress Field

For porous elastic materials, when the external load, pore pressure, and temperature are considered, the constitutive equation of the porous media is [33]

$${\sigma }_{ij}=2G{\epsilon }_{ij}+\frac{2G\nu }{1-2\nu }{\epsilon }_v{\delta }_{ij}-\alpha p{\delta }_{ij}-{\beta }_{s}K\left(T-T_0\right){\delta }_{ij}$$

(1)

where

$$G=\frac{E}{2\left(1+\nu \right)},$$

(2)

$$K=\frac{2G\left(1+\nu \right)}{3\left(1-2\nu \right)},$$

(3)

and

$$\alpha =\frac{3\left({\nu }_{\mathrm{u}}-\nu \right)}{B\left(1-2\nu \right)\left(1+{\nu }_{\mathrm{u}}\right)}.$$

(4)

In Equations (1)–(4), σ_ij is the second-order stress tensor component (MPa). ε_ij is the dimensionless second-order strain tensor component. ε_v is the dimensionless volume strain; δ_ij is the Kronecker symbol, which is dimensionless. G is the shear modulus (GPa). E is the Young’s modulus (GPa). K is the bulk modulus (GPa); ν is the Poisson’s ratio. ν_u is the undrained Poisson’s ratio, which is dimensionless. B is Skempton’s coefficient, which is dimensionless. α is the dimensionless Biot coefficient. p is the pore pressure (MPa). β_s is the volumetric expansion coefficient of the rock (1/°C). T is the formation temperature (°C). T₀ is the initial formation temperature (°C).

By substituting Equation (1) into the momentum conservation equation and combining it with the deformation coordination equation, Equation (5) can be obtained.

$$G{u}_{i,jj}+\frac{G}{1-2\nu }{u}_{j,ji}-\alpha p_{,i}-{\beta }_{s}K{T}_{,i}+F_i=0,$$

(5)

where u is the displacement (m), and F_i is the body load component (MPa).

Next, Equation (5) is written in tensor notation. Without considering the body load, the governing equation of the stress field, considering thermal-hydro-mechanical coupling, is

$$G{\nabla }^2\mathit{u}+\left(\frac{G}{1-2\nu }\right)\nabla \left(\nabla \cdot \mathit{u}\right)-\alpha \nabla p-{\beta }_{s}K\nabla T=0.$$

(6)

2.2.2. Seepage Field

Considering the thermal-hydro-mechanical coupling effect, changes in the volumetric strain, pore pressure, and temperature of the formation will lead to changes in the fluid content in the pores as follows [34]

$$\zeta =\alpha \left(\nabla \cdot \mathit{u}\right)+\frac{p}{M}-{\beta }_{sf}\left(T-T_0\right),$$

(7)

where

$$M=\frac{BK}{\alpha \left(1-\alpha B\right)},$$

(8)

and

$${\beta }_{sf}=\left(\alpha -\varphi \right){\beta }_s+\varphi {\beta }_f.$$

(9)

In Equations (7)–(9), ζ is the change in the fluid content in a unit volume of rock (m³). M is the Biot’s modulus (1/MPa). ϕ is the formation porosity, which is dimensionless, and β_f is the coefficient of volumetric expansion of the fluid (1/°C).

Because the formation is considered to be a closed system, there is no external mass exchange. Therefore, the mass flux of the fluid is equal to the rate of change in the mass of the fluid. According to the law of conservation of mass, the process can be expressed as follows:

$$\frac{\partial \left({\rho }_f\zeta \right)}{\partial t}+\nabla \cdot \left({\rho }_f{v}_f\right)=0,$$

(10)

where

$$v_f=-\frac{k}{\mu }\nabla p.$$

(11)

In Equations (10) and (11), ρ_f is the fluid density (kg/m³). v_f is fluid seepage velocity (m/s). k is the formation permeability (m²). μ is the fluid viscosity (mPa·s).

When the fluid density is constant, the governing equation of the seepage field, considering thermal-hydro-mechanical coupling, is

$$\alpha \frac{\partial }{\partial t}\left(\nabla \cdot \mathit{u}\right)+\frac{1}{M}\frac{\partial p}{\partial t}-\left[\left(\alpha -\varphi \right){\beta }_s+\varphi {\beta }_f\right]\frac{\partial T}{\partial t}+\nabla \cdot \left(-\frac{k}{\mu }\nabla p\right)=0.$$

(12)

2.2.3. Temperature Field

Considering the thermal-hydro-mechanical coupling condition, according to the second law of thermodynamics, deformation of an object, changes in the pore pressure, and changes in the temperature will all lead to a change in the system’s entropy. The entropy change can be expressed as follows:

$$S=-{\beta }_{s}K\left(\nabla \cdot \mathit{u}\right)-\varphi {\beta }_{f}p+{\rho }_m{c}_m\frac{T-T_0}{T_0},$$

(13)

where

$${\rho }_m{c}_m=\left(1-\varphi \right){\rho }_s{C}_s+\varphi {\rho }_f{C}_f.$$

(14)

In Equations (13) and (14), S is the change in entropy (J/(K·m³)). C_s is the specific heat capacity of the rock (J/(kg·K)). C_f is the specific heat capacity of the fluid (J/(kg·K)). ρ_s is the density of the solid phase (kg/m³).

Based on the relationship between the change in entropy, temperature, and energy, the change in energy caused by the change in entropy can be expressed as follows:

$$Q=S\cdot T_0=-{\beta }_{s}K{T}_0\left(\nabla \cdot \mathit{u}\right)-\varphi {\beta }_f{T}_{0}p+{\rho }_m{c}_m\left(T-T_0\right),$$

(15)

where Q is the change in energy (J/m³).

The heat transfer in the formation includes thermal conduction and convection. Based on Fourier’s law of thermal conduction, the heat flux in the formation is as follows [35]:

$$\mathit{q}=-{\lambda }_m\nabla \left(T-T_0\right)+{\rho }_f{C}_f{\mathit{v}}_f\left(T-T_0\right),$$

(16)

where

$${\lambda }_m=\left(1-\varphi \right){\lambda }_s+\varphi {\lambda }_f.$$

(17)

In Equations (16) and (17), q is the heat flux (J/m). λ_s is the thermal conductivity of the rock (J/(m·K·s)). λ_f is the thermal conductivity of the fluid (J/(m·K·s)).

Since the system satisfies the law of energy conservation, the sum of the rate of change in the energy and the heat flux is zero, that is,

$$\frac{\partial Q}{\partial t}+\nabla \cdot \mathit{q}=0.$$

(18)

By substituting Equations (15) and (16) into Equation (18), the governing equation of the temperature field of the rock, considering thermal-hydro-mechanical coupling, can be obtained as follows:

$$-{\beta }_{s}K{T}_0\frac{\partial }{\partial t}\left(\nabla \cdot \mathit{u}\right)-\varphi {\beta }_f{T}_0\frac{\partial p}{\partial t}+{\rho }_m{c}_m\frac{\partial T}{\partial t}+\nabla \cdot \left[-{\lambda }_m\nabla \left(T-T_0\right)+{\rho }_f{C}_f{\mathit{v}}_f\left(T-T_0\right)\right]=0.$$

(19)

2.3. Initial and Boundary Conditions

Due to the symmetry of the formation conditions, a 1/4 formation model was established to reduce the amount of numerical computations. The side length of the formation was 2 m, and the borehole radius was 0.111 m. The geometric models before and after the drilling of the borehole in the formation are shown in Figure 1a,b. It should be noted that the numbers in the figure represent the different surface of the geometric model. Before the formation is drilled, the formation is in a state of equilibrium under in situ stress; the initial temperature of the formation is equal to the original formation temperature; and the initial formation pressure is equal to the original formation pressure. Therefore, the initial conditions of the whole system are as follows:

$$\left\{\begin{array}{c}u=0\hfill \\ p=p_i\hfill \\ T=T_i\hfill \end{array}\right. (\mathrm{when} t=0),$$

(20)

where p_i is the original formation pressure (MPa), and T_i is the original formation temperature (°C).

After the formation is drilled, some rocks are replaced by drilling fluid. At this time, the boundary conditions in the system are determined by the wellbore parameters:

$$\left\{\begin{array}{c}u=f(p_w)\hfill \\ p=p_w\hfill \\ T=T_w\hfill \end{array}\right. (\mathrm{On} {\Gamma }_{10} \mathrm{when} t>0),$$

(21)

where p_w is the wellbore pressure (MPa), and T_w is the wellbore temperature (°C).

For the outer boundary of the system, the formation displacement, temperature, and pressure remain stable. Therefore, the internal and external boundary conditions of the system are as follows:

$$\left\{\begin{array}{c}u=0\\ p=p_i\\ T=T_i\end{array}\right. (\mathrm{On} {\Gamma }_4\cup {\Gamma }_5 \mathrm{when} t>0).$$

(22)

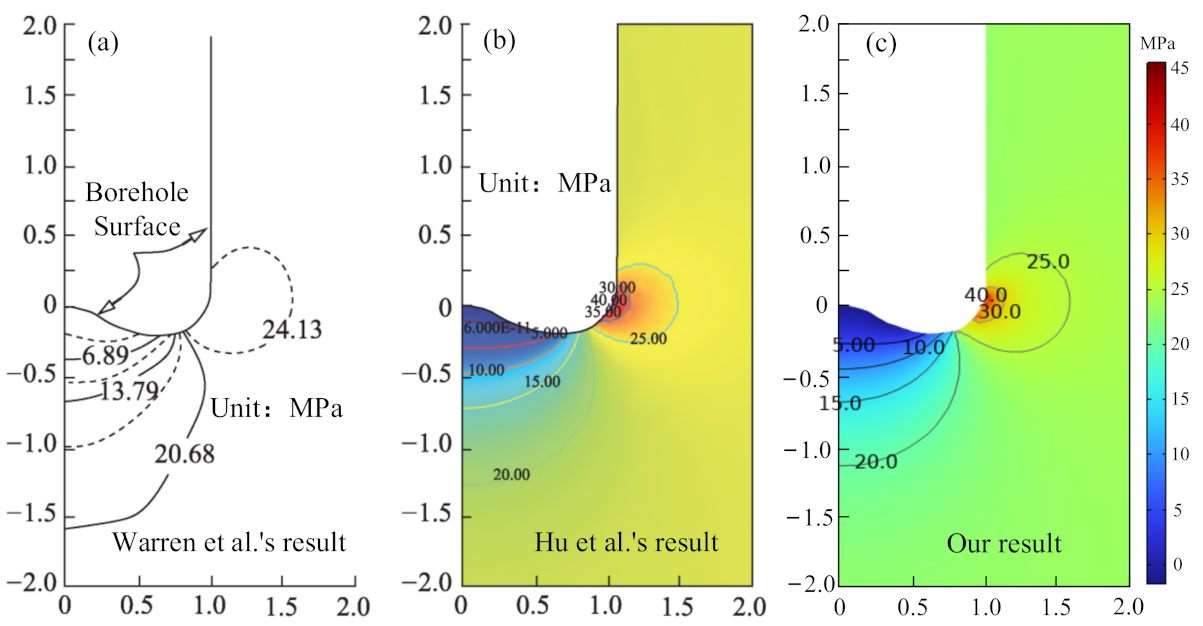
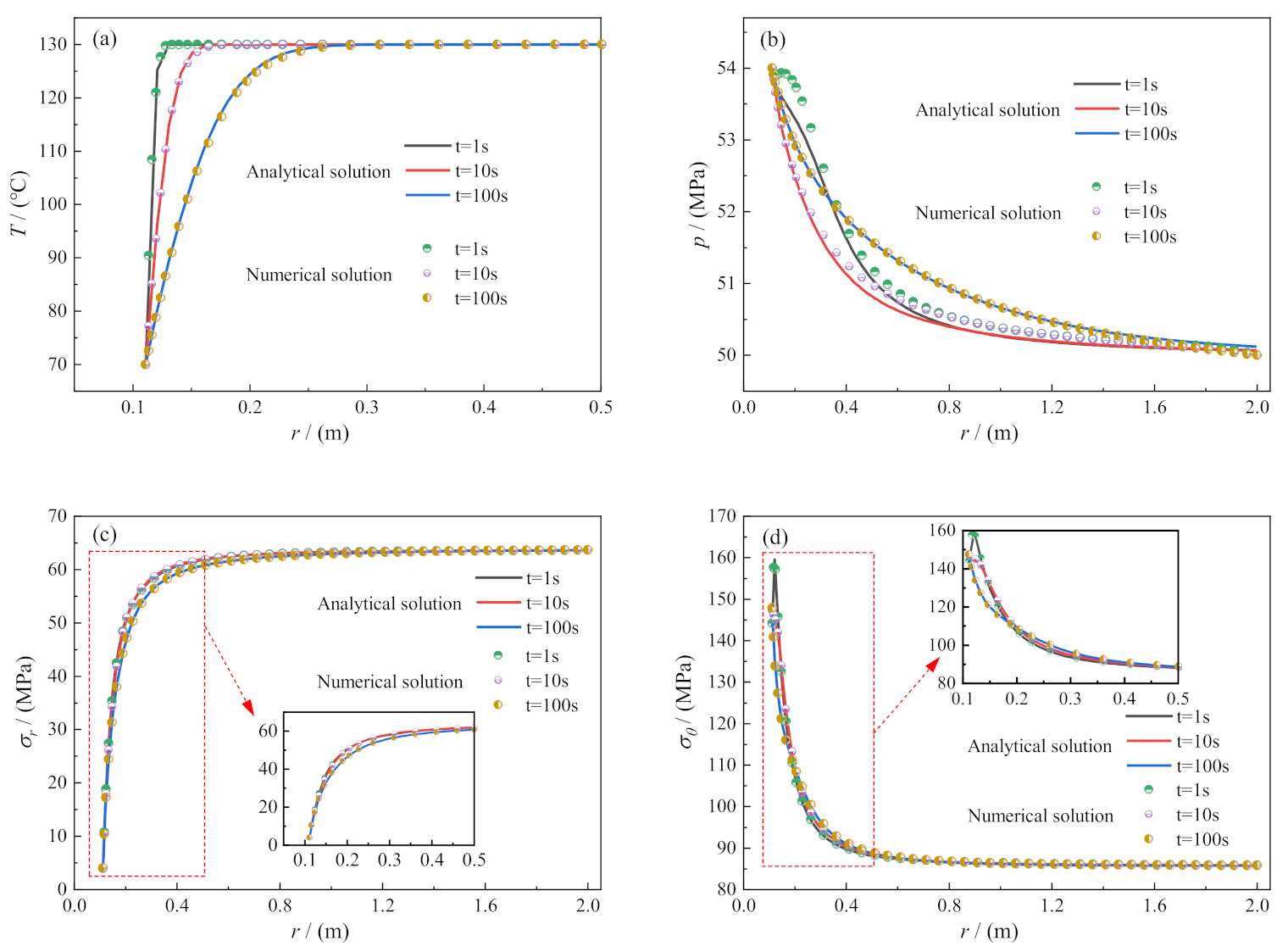
2.4. Model Solving and Validation

Since the contour of the drill bit is complex, and the model involves thermal-hydro-mechanical coupling, the finite element method was used to solve the proposed model, which was carried out in two steps. The first step was the in situ stress balance process, in which, the boundary conditions of surfaces #1, #2, #3, #7, and #8 in Figure 1a were set as the roller support. The maximum horizontal in situ stress was applied on surface #4, and the minimum horizontal in situ stress was applied on surface #5. In addition, vertical stress was applied on surfaces #6 and #9. In this way, the in situ stress distribution before drilling was simulated, which provided the prestress for subsequent drilling and eliminated the influence of the strain generated by the in situ stress on the formation deformation around the well. The second step was the simulation after the formation was drilled. In this step, the geometric elements in the blue area in Figure 1 were deleted from the model to simulate the formation after drilling. The initial conditions and internal and external boundary conditions of the model were set according to Equations (20)–(22). Next, the fully coupled solution method was used to calculate the transient changes in the formation stress, temperature, and pressure after drilling. Positive values represented compressive stress, and negative values represented tensile stress. After obtaining the stress components, the following equation was used to describe the stress components in the cylindrical coordinate system:

$$\left[\begin{array}{ccc}{\sigma }_r& {\tau }_{r\theta }& {\tau }_{rz}\\ {\tau }_{r\theta }& {\sigma }_{\theta }& {\tau }_{\theta z}\\ {\tau }_{rz}& {\tau }_{\theta z}& {\sigma }_z\end{array}\right]=\left[\begin{array}{ccc}\cos \theta & \sin \theta & 0\\ -\sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}{\sigma }_x& {\tau }_{xy}& {\tau }_{zx}\\ {\tau }_{xy}& {\sigma }_y& {\tau }_{yz}\\ {\tau }_{zx}& {\tau }_{yz}& {\sigma }_z\end{array}\right]{\left[\begin{array}{ccc}\cos \theta & \sin \theta & 0\\ -\sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]}^{\mathrm{T}},$$

(23)

where σ_r, σ_θ, σ_z, τ_rθ, τ_rz, and τ_θz are the stress components in the cylindrical coordinate system (MPa), and θ is the well circumference angle (°).

After obtaining the stress components in the cylindrical coordinate system, the three principal stresses of the bottomhole rocks were obtained:

$$\left\{\begin{array}{c}{\sigma }_i={\sigma }_r\hfill \\ {\sigma }_j=\frac{1}{2}\left({\sigma }_{\theta }+{\sigma }_z\right)+\frac{1}{2}{\left[{\left({\sigma }_{\theta }-{\sigma }_z\right)}^2+4{\tau }_{\theta z}^2\right]}^{\frac{1}{2}}\\ {\sigma }_k=\frac{1}{2}\left({\sigma }_{\theta }+{\sigma }_z\right)-\frac{1}{2}{\left[{\left({\sigma }_{\theta }-{\sigma }_z\right)}^2+4{\tau }_{\theta z}^2\right]}^{\frac{1}{2}}\end{array}\right.,$$

(24)

where σ_i, σ_j, and σ_k are the three principal stresses (MPa).

Furthermore, based on the effective stress expression, the average effective stress of the bottomhole rocks was obtained:

$$\overline{\sigma }=\frac{1}{3}\left({\sigma }_i+{\sigma }_j+{\sigma }_k\right)-\alpha p,$$

(25)

where $\overline{\sigma }$ is the average effective stress of the bottomhole rocks after drilling (MPa).

In order to verify the accuracy of the model, the bottomhole stress model proposed by Warren et al. [25] was used to calculate the bottomhole rock stress using the parameters listed in

Table 1. Basic parameters of the Warren et al. model.

No.	Parameters	Value	Units
1	Well depth, h	3048	m
2	Borehole radius, rw	0.111	m
3	Drilling fluid density, ρf	1050	kg/m3
4	Vertical in situ stress, σv	68.95	MPa
5	Wellbore pressure, pw	32.41	MPa
6	Formation pressure, p0	32.41	MPa
7	Maximum horizontal in situ stress, σH	48.26	MPa
8	Minimum horizontal in situ stress, σh	48.26	MPa
9	Young’s modulus of the rock, E	13,789.5	MPa
10	Poisson’s ratio of the rock, ν	0.25	-
11	Formation permeability, k	1	mD
12	Formation porosity, ϕ	0.15	-
13	Rock density, ρs	2262	kg/m3
14	Rock compression coefficient, cs	2.697 × 10−5	MPa−1
15	Drill bit profile code	IADC5-3-7bit	-

. The results of Warren et al.’s model are shown in Figure 2a. Hu et al. [28] also employed Warren et al.’s model to calculate the average effective stress of bottomhole rocks after drilling, using the finite element method. Their results are shown in Figure 2b. The results of the model proposed in this study using the same parameters are shown in Figure 2c. It can be seen that the results of the proposed model are consistent with those of the two previous studies. It should be noted that the influence of temperature was not considered in the above analysis. In order to further verify the thermal-hydro-mechanical coupling process, the parameters in

Table 2. Basic parameters of the thermal-fluid-solid coupling model.

No.	Parameters	Value	Units
Material parameters
1	Poisson’s ratio of the rock(drained), ν	0.291	-
2	Young’s modulus of the rock, E	26.3	GPa
3	Poisson’s ratio of the rock(undrained), νu	0.45	-
4	Skempton’s coefficient of the rock, B	0.85	-
5	Formation permeability, k	1	mD
6	Formation fluid viscosity, μ	5	mPa·s
7	Formation porosity, ϕ	0.1	-
8	Rock density, ρs	2680	kg/m3
9	Formation fluid density, ρf	1000	kg/m3
10	Specific heat capacity of the rock, Cs	890	J/(kg·K)
11	Specific heat capacity of the fluid, Cf	2510	J/(kg·K)
12	Thermal conductivity of the rock, λs	46	J/(m·K·s)
13	Thermal conductivity of the fluid, λf	26	J/(m·K·s)
14	Coefficient of volumetric expansion of the rock, βs	5 × 10−5	1/°C
15	Coefficient of volumetric expansion of the fluid, βf	2 × 10−4	1/°C
Formation parameters
16	Original formation temperature, T0	130	°C
17	Original formation pressure, p0	50	MPa
18	Maximum horizontal in situ stress, σH	132	MPa
19	Minimum horizontal in situ stress, σh	110	MPa
20	Vertical in situ stress, σv	144	MPa
Wellbore parameters
21	Borehole radius, rw	0.111	m
22	Wellbore pressure, pw	54	MPa
23	Wellbore temperature, Tw	70	°C

were used to calculate the temperature, pressure, and stress distribution along the radial direction of the borehole after the formation was drilled, using the finite element method. The numerical simulation results were compared with the analytical results [36] (Figure 3). It can be seen that the numerical simulation results obtained in this study are in good agreement with the analytical solution, which further demonstrates the accuracy of the model proposed in this study. Therefore, the proposed model can be used to study bottomhole stress in deep-well drilling, considering the thermal-hydro-mechanical coupling effect.

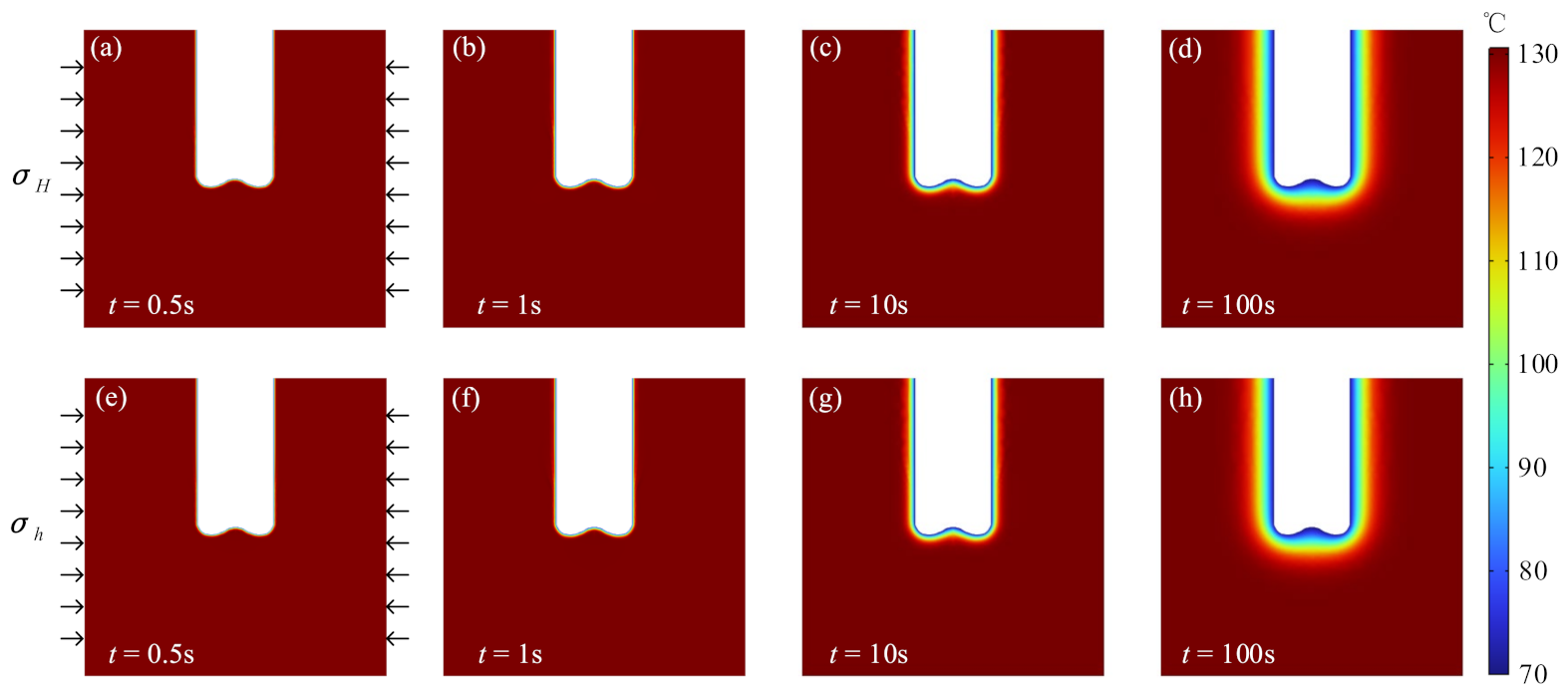
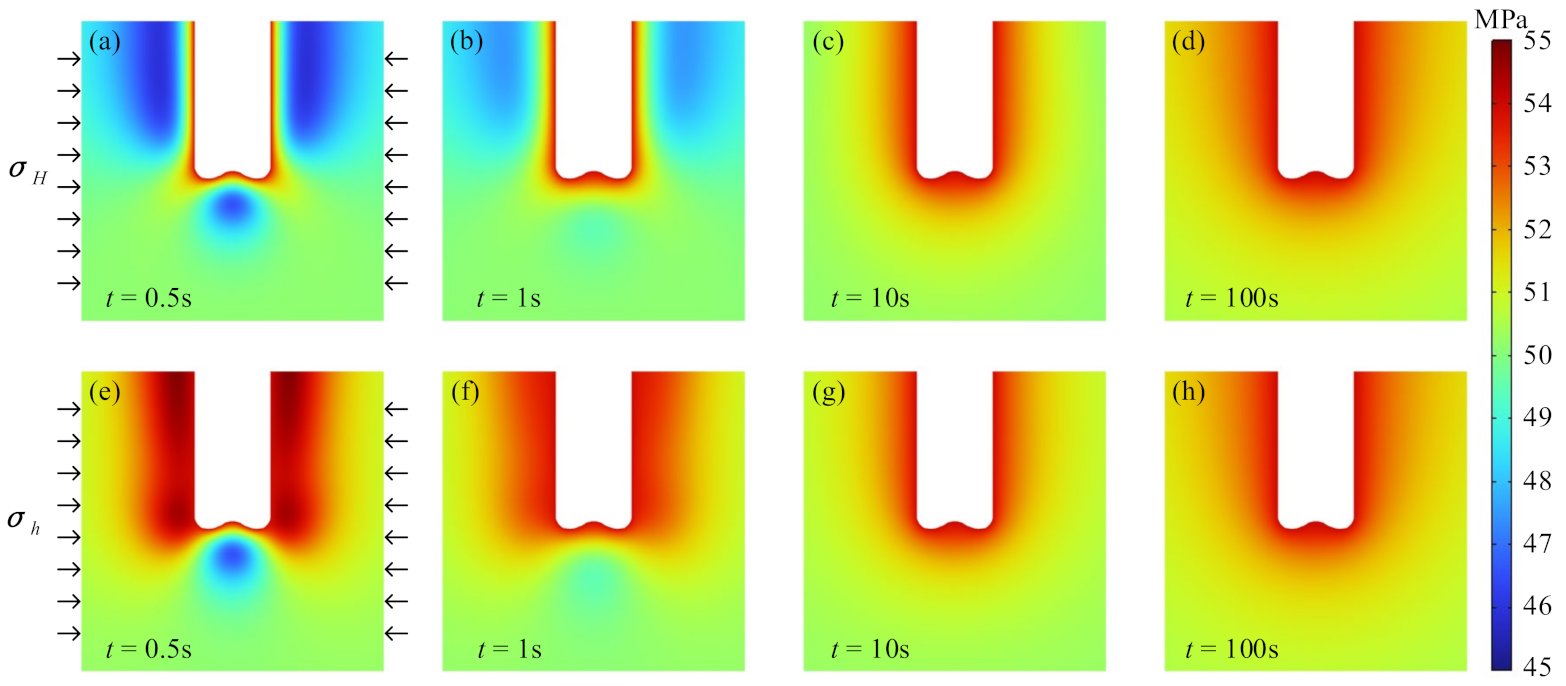
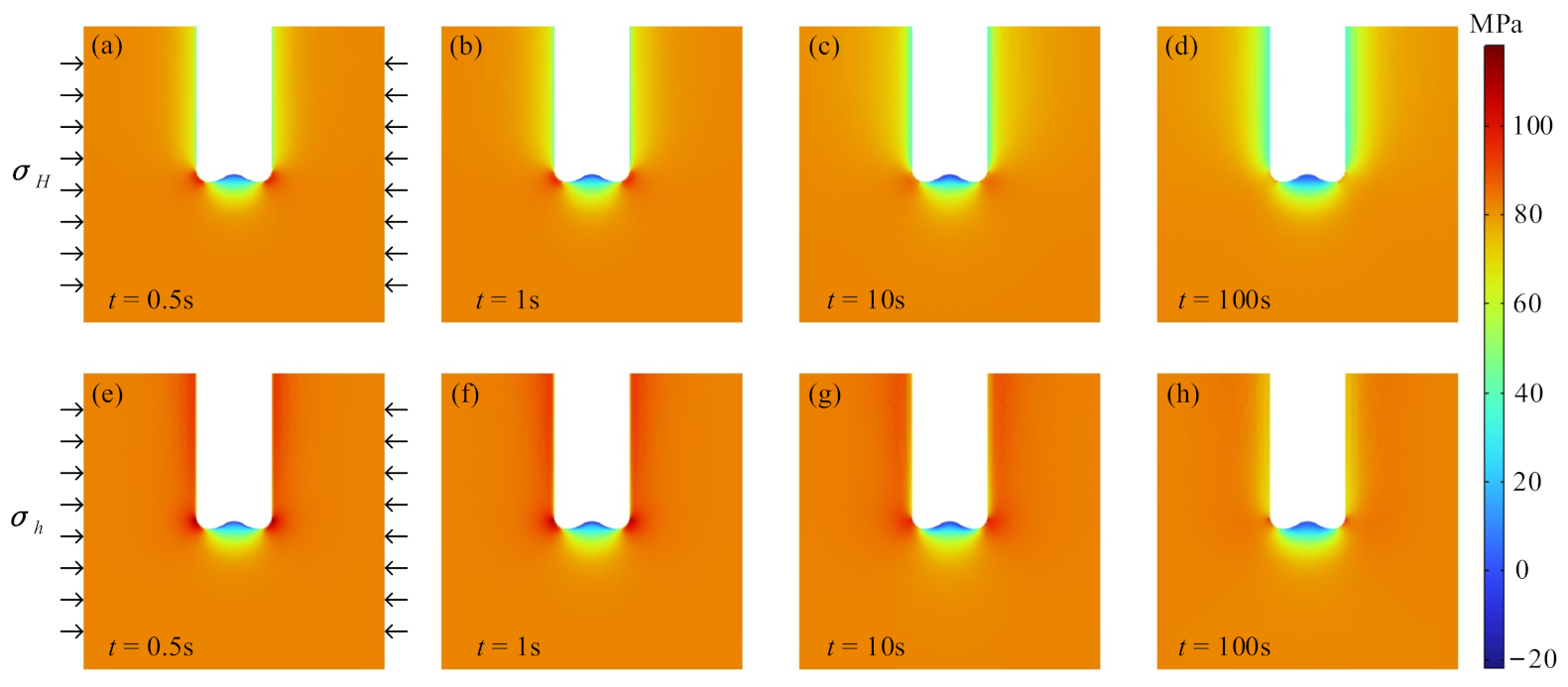
3. Distribution of Formation Temperature, Pressure, and Stress due to Drilling

Understanding the distribution and evolution of the formation temperature, pressure, and stress under the action of thermal-hydro-mechanical coupling is the basis for analyzing bottomhole rock stress and studying the mechanism of rock breakage. Therefore, based on the model proposed in this study and the parameters in Table 2, the distributions of the formation temperature, pressure, and average effective stress along the directions of the maximum and minimum horizontal in situ stresses were calculated. The results are shown in Figure 4, Figure 5 and Figure 6.

Figure 4a–d show the formation temperature in the direction of the maximum horizontal in situ stress at different drilling stages, and Figure 4e–h show the formation temperature in the direction of the minimum horizontal in situ stress at different drilling stages. It can be seen that for the homogeneous and isotropic formation modelled in this study, the temperatures around the wellbore along the directions of the maximum and minimum horizontal crustal stresses are approximately the same; that is, the change in the formation temperature caused by the deformation of the formation around the wellbore and the change in the pore pressure are small, and the formation temperature is mainly controlled by thermal conduction and thermal convection. After the formation is drilled, under the cooling effect of the drilling fluid, the temperatures of the wellbore wall and bottomhole are the same as that of the drilling fluid. Then, under the joint action of thermal conduction and convection, the low temperature zone gradually increases and expands to the deep part of the formation.

Figure 5a–d show the formation pressure in the direction of the maximum horizontal in situ stress, and Figure 5e–h show the formation pressure in the direction of the minimum horizontal in situ stress. It can be seen that shortly after the start of drilling (t = 0.5 s and t = 1 s), the formation pressures along the directions of the maximum and minimum horizontal in situ stresses are greatly different. This mainly occurs on the wellbore wall, and the difference near the bottom of the well is small. When the tangent plane of the stratum is along the direction of the maximum horizontal in situ stress, the pore pressure near the wellbore wall is the lowest. However, when the tangent plane of the stratum is along the direction of the minimum horizontal in situ stress, the pore pressure near the wellbore wall is the highest. At t = 0.5 s, the maximum difference in the pore pressure between the two directions is about 10 MPa. The main reason for this difference is that the wellbore along the direction of the maximum horizontal in situ stress is under tension, and the volume of the pores of formation rock increases under the tensile stress, which in turn leads to a decrease in the pore pressure around the wellbore. Conversely, the wellbore along the direction of the minimum horizontal in situ stress is subjected to compressive stress, and the formation is further compressed, which leads to an increase in the pore pressure around the wellbore. With the progression of drilling, the high-pressure area around the wellbore gradually spreads toward the low-pressure area; the minimum pore pressure along the direction of the maximum horizontal in situ stress gradually increases, whereas the maximum pore pressure along the direction of the minimum horizontal in situ stress gradually decreases. After a certain period of time, the pore pressures in the two directions become approximately equal.

Figure 6a–d show the average effective stress in the direction of the maximum horizontal in situ stress, and Figure 6e–h show the average effective stress in the direction of the minimum horizontal in situ stress. The results show that when the maximum horizontal in situ stress and the minimum horizontal in situ stress are not the same, the average effective stresses of the formation around the wellbore in the directions of the maximum and minimum horizontal in situ stresses after drilling are also different, and the average effective stress along the direction of the minimum horizontal in situ stress is larger than that along the direction of the maximum horizontal in situ stress. It can also be seen that the average effective stress near the shoulder of the drill bit is the largest, while the average effective stress near the centerline of the bit is the smallest. Moreover, the average effective stress is tensile stress in some areas, and the minimum average effective stress is located on the bottom of the wellbore. Starting from the centerline of the drill bit, the average effective stress at the bottomhole initially increases and then decreases along the contour of the drill bit. With the progression of drilling, the maximum average effective stress gradually decreases, and the minimum average effective stress remains stable. Moreover, the bottomhole area under tension increases slightly.

4. Factors Affecting Bottomhole Rock Stress under the Thermal-Hydro-Mechanical Coupling Effect

The influences of the formation parameters and wellbore parameters on bottomhole rock stress in deep-well drilling were investigated using the proposed model. Under each set of conditions, the parameter of interest was set to different values, while the other parameters were held constant. The average effective stress of the bottomhole rocks under different formation pressures, in situ stress, formation permeability, wellbore pressures, and wellbore temperature values were calculated. In order to facilitate the analysis, the average effective stress was calculated at three locations, namely, the drill bit contour parallel to the direction of the maximum horizontal in situ stress; the contour parallel to the direction of the minimum horizontal in situ stress; and the axis of the wellbore (Figure 7). The results are described in Section 4.1, Section 4.2, Section 4.3, Section 4.4 and Section 4.5.

4.1. Formation Pressure

The formation pressure is very important to the drilling process. The safe density window of the drilling fluid is determined based on the formation pressure. In addition, the formation pressure directly affects bottomhole rock stress during the drilling process. In order to understand the influence of the formation pressure on bottomhole rock stress, the average effective stress was calculated at the above three locations under different formation pressure values (40, 50, 60, and 70 MPa). The results are shown in Figure 8. It should be noted that the overbalance pressure was set to 4 MPa under the four formation pressure conditions, and the result was the average effective stress at 1 s after the formation had been drilled. It can be seen from Figure 8a that the average effective stress at the bottom of the wellbore was the smallest, and the average effective stress was tensile stress in some areas. The average effective stress was the largest near the shoulder of the drill bit, and there were large fluctuations in this area. In summary, the smaller the formation pressure was, the greater the average effective stress near the shoulder of the drill bit was. After the wellbore was formed, the average effective stresses of the wellbore walls parallel to the directions of the maximum and minimum horizontal in situ stresses were different. Under formation pressures of 40, 50, 60, and 70 MPa, the average effective stress of the wellbore wall parallel to the direction of the maximum horizontal in situ stress was 42.2, 33.8, 25.3, and 16.9 MPa, respectively, and the average effective stress of the wellbore wall parallel to the direction of the minimum horizontal in situ stress was 74.5, 66.0, 57.6, and 49.1 MPa, respectively. That is, the higher the formation pressure was, the lower were the average effective stresses of the wellbore wall parallel to the directions of maximum and minimum horizontal in situ stresses. It can be seen from Figure 8b that after the formation was drilled, the average effective stress at the bottomhole was the smallest. For formation pressures of 40, 50, 60, and 70 MPa, the average effective stress of the bottomhole rock near the borehole axis was −19.2, −18.3, −17.4, and −16.5 MPa, respectively, indicating that a larger formation pressure did not lead to a smaller average effective stress at the bottom of the wellbore. The increase in the average effective stress at the bottom of the hole with increasing formation pressure may have been caused by the high fluid column pressure at the bottomhole under high formation pressure conditions. With increasing depth, the average effective stress initially increased and then became stable. In the region of the formation far away from the bottom of the wellbore, due to the very limited influence of the drilling, the average effective stress was controlled by the in situ stress and the original formation pressure. Therefore, the higher the formation pressure in this region was, the smaller the average effective stress was.

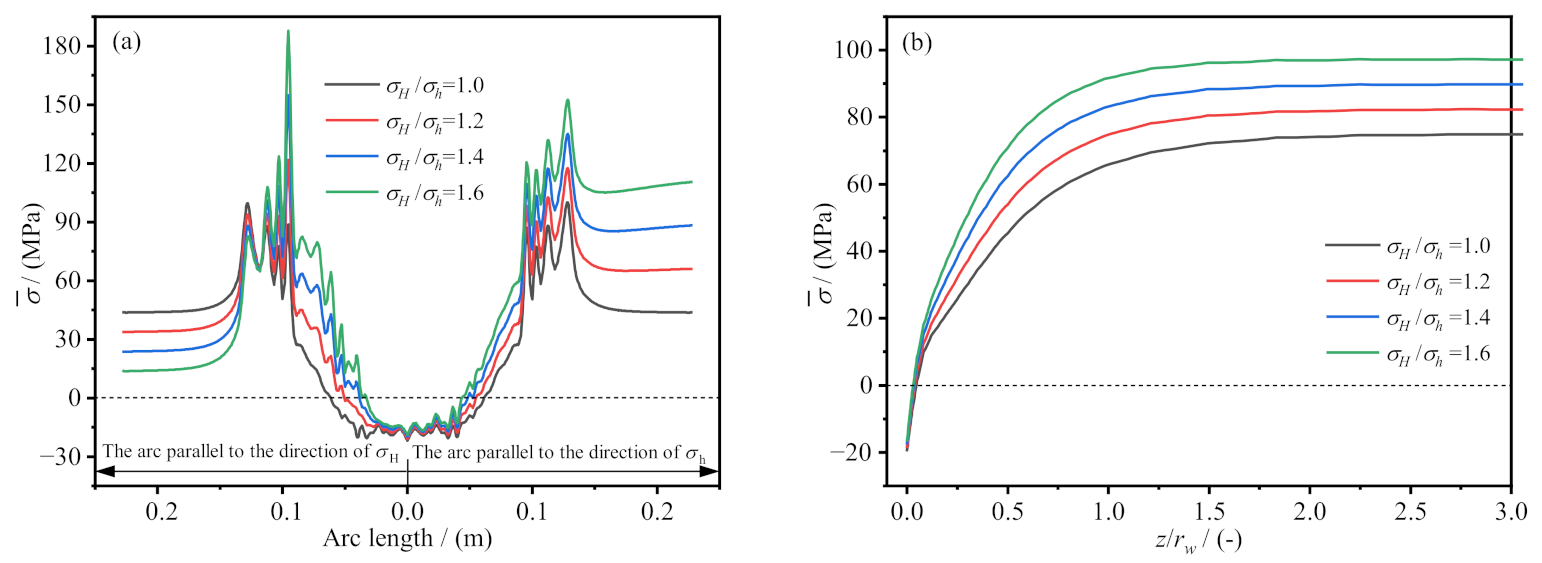
4.2. In Situ Stress

In situ stress directly affects bottomhole rock stress. In order to understand the influence of the in situ stress on the bottomhole rock stress in deep-well drilling, the maximum horizontal in situ stress was adjusted, and the average effective stress was calculated at the three locations under maximum horizontal in situ stress to minimal horizontal in situ stress ratios of 1.0, 1.2, 1.4, and 1.6, while holding the minimum horizontal in situ stress in Table 2 constant. The results are shown in Figure 9. It can be seen from Figure 9a that the in situ stress had a large influence on the bottomhole rock stress. When the maximum and minimum horizontal in situ stresses were equal, for the same arc length, the average effective stress of the wellbore parallel to the direction of the maximum horizontal in situ stress was the same as that parallel to the direction of the minimum horizontal in situ stress. When the maximum and minimum horizontal in situ stresses were not equal, the difference in the average effective stresses at the two locations was small near the center of the bottomhole. With increasing arc length, the difference in the average effective stress increased accordingly. In the bottomhole area from the center to the shoulder of the drill bit, the higher the in situ stress ratio was, the higher the average effective stress at the bottom of the hole was. However, on the wellbore wall, the average effective stresses parallel to the maximum and minimum horizontal in situ stresses exhibited different change trends. When the wellbore wall was parallel to the direction of the maximum horizontal in situ stress, the average effective stress decreased with increasing in situ stress ratio. For σ_H/σ_h ratios of 1.0, 1.2, 1.4, and 1.6, the average effective stress was 43.7, 33.8, 23.7, and 13.7 MPa, respectively. However, when the wellbore wall was parallel to the direction of the minimum horizontal in situ stress, the average effective stress increased with increasing in situ stress ratio. For σ_H/σ_h ratios of 1.0, 1.2, 1.4, and 1.6, the average effective stress was 43.7, 66.0, 88.3, and 110.5 MPa, respectively. It can be seen from Figure 9b that as the σ_H/σ_h ratio increased, the average effective stress at the bottom of the hole increased. For σ_H/σ_h ratios of 1.0, 1.2, 1.4, and 1.6, the average effective stress of the bottomhole rock near the borehole axis was −19.3, −18.3, −17.3, and −16.4 MPa, respectively. With increasing depth, the average effective stress of the formation initially increased and then became stable. In summary, the higher the in situ stress ratio was, the higher the average effective stress of the bottomhole rock was. Since the rock strength increases with increasing effective stress, the bottomhole rocks become more difficult to break under a high in situ stress, which leads to a low drilling efficiency.

4.3. Formation Permeability

After the formation is drilled, the wellbore drilling fluid filtrate penetrates the formation due to the overbalance pressure, which leads to changes in the formation pressure and temperature at the bottom of the hole. Thus, the penetration process is closely related to the formation permeability. In order to analyze the impact of permeability on bottomhole rock stress, the average effective stress of the bottomhole rocks was calculated under formation permeabilities of 10, 1, 0.1, and 0.01 mD at 1 s after the formation had been drilled. The results are shown in Figure 10. It can be seen that the formation permeability had a significant influence on the average effective stress of the bottomhole rock near the borehole axis. The lower the permeability was, the smaller the average effective stress was, and the smaller the area under tension was. At the center of the bottomhole along the borehole axis, for formation permeabilities of 10, 1, 0.1, and 0.01 mD, the average effective stress was −18.5, −18.3, −14.9, and −2.4 MPa, respectively. In the area near the shoulder of the drill bit, the difference in the average effective stress under the different permeabilities was small. As the formation depth increased, the average effective stress of the bottomhole rock initially increased and then became stable. The lower the formation permeability was, the smaller the bottomhole area disturbed by the drilling was. In the undisturbed area, the average effective stress of the rocks was the same, and it was not affected by the formation permeability. The higher the permeability was, the easier it was for the drilling fluid to penetrate the formation. Therefore, the range of the high-pressure area at the bottomhole was large when the permeability was high. Moreover, a high permeability resulted in more drilling fluid penetrating the formation; therefore, the drilling fluid had a more significant cooling effect on the bottomhole rock under the effect of thermal convection. For the above two reasons, the average effective stress of the bottomhole rocks was smaller under a low formation permeability. In terms of deep-well drilling, the greater the formation depth is, the higher the degree of formation compaction is; that is, the lower the formation permeability is, the greater the average effective stress of the formation is, and the harder it is to break the bottomhole rocks, which results in a slower ROP.

4.4. Wellbore Pressure

In order to study the influence of wellbore pressure on bottomhole rock stress, the average effective stress of the bottomhole rocks at 1 s after the formation had been drilled was calculated, under wellbore pressures of 40, 45, 50, and 55 MPa. The results are shown in Figure 11. It can be seen that in the bottomhole area near the borehole axis, the lower the wellbore pressure was, the smaller the average effective stress of the bottomhole rocks was. For wellbore pressures of 40, 45, 50, and 55 MPa, the average effective stress was −19.9, −19.3, −18.8, and −18.2 MPa, respectively. However, in the bottomhole area near the shoulder of the drill bit and the wellbore wall, the average effective stress increased with decreasing wellbore pressure. Since the maximum and minimum horizontal in situ stresses were not the same, the average effective stresses on the wellbore walls parallel to the directions of the maximum and minimum horizontal in situ stresses were also different. Specifically, the average effective stress on the wellbore wall parallel to the direction of the maximum horizontal in situ stress was significantly lower than that parallel to the direction of the minimum horizontal in situ stress. With increasing formation depth, the average effective stress of the bottomhole rocks initially increased and then became stable. In the area of the formation near the bottomhole, the average effective stress decreased with decreasing wellbore pressure. With increasing formation depth, when z/r_w was, for example, greater than 0.25, the average effective stress increased slightly with decreasing wellbore pressure. In summary, decreasing the wellbore pressure is conducive to generating tensile stress in the bottomhole formation near the borehole axis, causing tensile damage to this area. However, the average effective compressive stress of the formation near the shoulder of the drill bit is large. Therefore, the recommendation is to generate shear failure in the formation near the shoulder of the drill bit so as to improve the drilling efficiency.

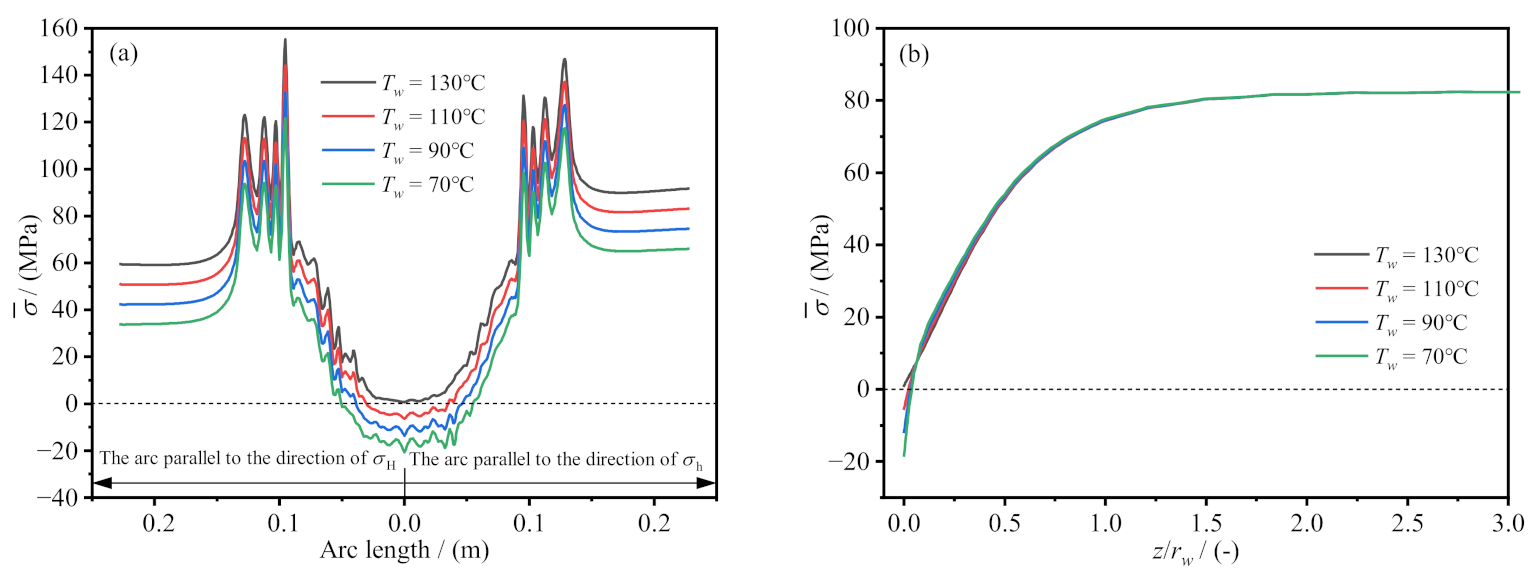
4.5. Wellbore Temperature

In deep-well drilling, due to the presence of a geothermal gradient, a deep formation generally has a high temperature. Under the cooling effect of the drilling fluid, the rock at the bottom of the wellbore will contract, thereby generating thermal stress. In order to understand the influence of wellbore temperature on bottomhole rock stress, the average effective stress was calculated at three locations in the bottomhole under wellbore temperatures of 130 °C, 110 °C, 90 °C, and 70 °C. The results are shown in Figure 12. The results show that with decreasing wellbore temperature, the average effective stress of the bottomhole rocks decreased. In the bottomhole area near the borehole axis, the average effective stress was the smallest. For wellbore temperatures of 130 °C, 110 °C, 90 °C, and 70 °C, the average effective stress at this location was 1.0, −5.4, −11.8, and −18.3 MPa, respectively. In the bottomhole area between the borehole axis and the shoulder of the drill bit, the average effective stress gradually increased and exhibited fluctuations near the shoulder. Furthermore, between the drill bit shoulder and the wellbore wall, the average effective stress initially decreased and then became stable. With increasing formation depth, the average effective stress initially increased and then became stable. The difference in the average effective stress at different wellbore temperatures gradually decreased with increasing formation depth, which was mainly due to the shorter drilling duration and the limited variation in the formation temperature at the bottomhole. In summary, a lower wellbore temperature is beneficial to reducing the average effective stress of the bottomhole formation and accelerating bottomhole rock breakage. Therefore, under the premise that the drilling fluid meets the relevant requirements, it is recommended to keep the wellbore temperature as low as possible so as to improve the drilling efficiency.

5. Conclusions

In this study, based on the laws of momentum conservation, mass conservation, and energy conservation, a thermal-hydro-mechanical coupling model for deep-well drilling was established. The finite element method was used to simulate the distribution and evolution characteristics of the formation temperature, pressure, and stress due to drilling. Finally, the thermal-hydro-mechanical coupling model was used to analyze the influences of the formation pressure, in situ stress, formation permeability, wellbore pressure, and wellbore temperature on the average effective stress of the bottomhole rock. The main conclusions of this study are as follows:

(1)

The formation temperature around the wellbore was controlled by thermal conduction and convection. The formation temperature around the wellbore wall was approximately the same in the different in situ stress directions. With the progression of drilling, the low-temperature zone gradually extended deeper within the formation. In the initial stage of drilling, the pore pressure near the wellbore wall along the direction of the maximum horizontal in situ stress was the smallest, and the pore pressure along the direction of the minimum horizontal in situ stress direction was the largest. With the progression of drilling, the difference in the pore pressure in the two directions gradually decreased.

(2)

After the wellbore was drilled, the average effective stress of the formation near the shoulder of the drill bit was the largest, and the average effective stress of the formation near the axis of the drill bit was the smallest. With the progression of drilling, the maximum average effective stress gradually decreased, while the minimum average effective stress remained stable. The bottomhole area under tension increased slightly.

(3)

In the bottomhole area near the borehole axis, the average effective stress increased with increasing formation pressure. The higher the in situ stress ratio was, the larger the average effective stress of the bottomhole rocks was. For the wellbore walls, the variation in the average effective stress was different in the different in situ stress directions. The average effective stress in the direction parallel to the maximum horizontal in situ stress decreased as the in situ stress ratio increased, whereas the average effective stress in the direction parallel to the minimum horizontal in situ stress increased as the in situ stress ratio increased.

(4)

The formation permeability had a significant effect on the average effective stress of the bottomhole rock near the borehole axis. The lower the formation permeability was, the smaller the average effective stress was, and the smaller the area under tension was. As the wellbore pressure decreased, the average effective stress of the bottomhole rocks near the borehole axis decreased. However, in the bottomhole area between the drill bit shoulder and the wellbore wall, the average effective stress increased with decreasing wellbore pressure. Reducing the wellbore temperature is beneficial to reducing the average effective stress of the bottomhole formation, thereby promoting bottomhole rock breakage.

(5)

With increasing formation depth, the average effective stress of the bottomhole rocks initially increased and then became stable. The formation permeability and wellbore temperature had greater influence on the average effective stress of the formation near the bottomhole area. However, the formation pressure and in situ stress had greater influence on the average effective stress of the formation farther away from the bottomhole area. In addition, the influence of the wellbore pressure on the average effective stress of the formation below the bottomhole area was minimal.

(6)

The present work focuses on the thermal-hydro-mechanical coupling effect on bottomhole rock stress in deep-well drilling, and the proposed model can be used to calculate the bottomhole stress, pore pressure and temperature during drilling. However, the model also exhibits some limitations. For example, the model neglected the influence of water jet, dynamic wellbore pressure, dynamic wellbore temperature, and multiphase flow in formation, and those aspects need to be improved in future work.